倒立摆的s函数建模及仿真
Matlab的一倒立摆模型的仿真

深圳大学考试答题纸(以论文、报告等形式考核专用)二○○九~二○○一零 学年度第2学期课程编号课程名称计算机控制系统主讲教师 李东 评分学 号姓名专业年级2007级光电工程学院测控技术与仪器教师评语:题目:一级倒立摆模型的仿真一、倒立摆模型的研究意义倒立摆控制系统是一个复杂的、不稳定的、非线性系统,是进行控制理论教学及开展各种控制实验的理想实验平台。
对倒立摆系统的研究能有效的反映控制中的许多典型问题:如非线性问题、鲁棒性问题、镇定问题、随动问题以及跟踪问题等。
通过对倒立摆的控制,用来检验新的控制方法是否有较强的处理非线性和不稳定性问题的能力。
同时,其控制方法在军工、航天、机器人和一般工业过程领域中都有着广泛的用途,如机器人行走过程中的平衡控制、火箭发射中的垂直度控制和卫星飞行中的姿态控制等。
故其研究意义广泛。
二、倒立摆模型的数学建模质量为m 的小球固结于长度为L 的细杆(可忽略杆的质量)上,细杆又和质量为M 的小车铰接相连。
由经验知:通过控制施加在小车上的力F (包括大小和方向)能够使细杆处于θ=0的稳定倒立状态。
在忽略其他零件的质量以及各种摩擦和阻尼的条件下,推导小车倒立摆系统的数学模型分析过程如下:如图所示,设细杆摆沿顺时针方向转动为正方向,水平向右方向为水平方向上的正方向。
当细杆摆顺时针往右运动时水平方向施加的力应该为水平向右。
现对小车和细杆摆分别进行隔离受力分析:(1)对小车有:F-F’sinθ=Mx’’(a)(2)对小球有:水平方向上运动为x+lsinθ故水平方向受力为 F’sinθ= m(x+lsinθ)’’=m(x’+lcosθθ’)’= mx’’+mlcosθθ’’-mlsinθ(θ’)^2(b)由(a)、(b)两式得F= (M+m)x’’ +mlcosθθ’’-mlsinθ(θ’)^2 <1>小球垂直方向上位移为 lcosθ故受力为F’cosθ-mg=m(lcosθ)’’=-mlθ’’sinθ-ml cosθ(θ’)^2即 F’cosθ=mg-mlθ’’sinθ-ml cosθ(θ’)^2(c)由(b)、(c)两式得cosθx’’=gsinθ- lθ’’<2>故可得以下运动方程组:F= (M+m)x ’’ +mlcos θθ’’-mlsin θ(θ’)^2cos θx ’’=gsin θ- l θ’’以上方程组为非线性方程组,故需做如下线性化处理:32sin ,cos 13!2!θθθθθ≈-≈-当θ很小时,由cos θ、sin θ的幂级数展开式可知,忽略高次项后, 可得cos θ≈1,sin θ≈θ,θ’’≈0 故线性化后运动方程组简化为 F= (M+m)x ’’ +ml θ’’ x ’’=g θ- l θ’’下面进行系统状态空间方程的求解:以摆角θ、角速度θ’、小车位移x 、加速度x ’为系统状态变量,Y 为输出,F 为输入即X=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡4321x x x x =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡x'x 'θθY=⎥⎦⎤⎢⎣⎡x θ=⎥⎦⎤⎢⎣⎡31x x由线性化后运动方程组得 x1’=θ’=x2 x2’=''θ=()Mlg m M +x1-Ml1 F X3’ =x ’=x4 x4’=x ’’=-Mm g x1+M 1 F故空间状态方程如下:X ’=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'4'3'2'1x x x x =()⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡-+0010000000010Mm gMlg m M ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡4321x x x x +⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡-M Ml 1010FY= ⎥⎦⎤⎢⎣⎡31x x =⎥⎦⎤⎢⎣⎡01000001⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡4321x x x x + 0⨯F 用MATLAB 将状态方程转化成传递函数,取M=2kg m=0.1kg l=0.5m 代入得 >>A=[0 1 0 0;20.58 0 0 0;0 0 0 1;-0.49 0 0 0] >>B=[0;-1;0;0.5] >>C=[1 0 0 0;0 0 1 0] >>D=[0;0]>> [num,den]=ss2tf(A,B,C,D,1); >> [num,den]=ss2tf(A,B,C,D,1) num =0 -0.0000 -1.0000 0 0 0 -0.0000 0.5000 -0.0000 -9.8000 den =1.0000 0 -20.5800 0 0由上可以得出角度 对力F 的传递函数:位移X 对外力F 的传递函数:三、用MATLAB 的Simulink 仿真系统进行建模58.201)()(2--=Φs s F s 24258.208.95.0)()(s s s s F s X --=1、没校正之前的θ-F 控制系统由于未加进控制环节,故系统输出发散2、加进控制环节,实现时域的稳定控制给系统加入PID 控制,设置系统稳定值为0,给系统一个初始干扰冲击信号 采用试凑法不断调整PID 参数,使系统达到所需的控制效果 当系统Kp=-100,Ti=Td=0时输出如下:Transfer Fcn-s 2s +-20.58s 42ScopePulseGeneratorConstant 1Transfer Fcn-1s +-20.582ScopePulseGeneratorIntegrator 1s Gain 3-40Gain 11Gain-K-Derivative du/dt Constant 0不断地调整参数,最后得到稳定的响应 Kp=-1000,Ti=1,Td=-40时可见调整好参数后,系统基本达到稳定,净差基本为0,超调较小,响应时间较小。
(完整word版)一级倒立摆的Simulink仿真

单级倒立摆稳定控制直线-级倒立摆系统在忽略了空'(阻力及各种摩擦Z后,町抽象成小车和匀质摆杆组成的系统,如图1所示。
图2控制系统结构假设小车质量M=0.5kg,匀质摆朴质量m=0.2kg,摆朴长度21 =0.6m, x(t)为小车的水半位移,〃为摆杆的角位移,g = 9.8m/s2o控制的目标是通过外力u⑴使得摆直立向上(即&(t) = 0) o该系统的非线性模型为:(J +inl‘)典(nilcos^)&= niglsin^ (ml cos。
)翼(M其中J二一ml+ m)&= (mlsin0)6^ + u一、非线性模型线性化及建立状态空间模型因为在工作点附近(& = 0.必0)对系统进行线竹:•化,所以可以做如下线性化处理: 03 Q1sin0« 0 --------- 、COS&Q 1-----------------3! 2!当e很小时,由COS0V sine的幕级数展开式可知,忽略高次项后, 可得cos0~l, sin0=0, 0Z 2=0:因此模型线性化后如下:(J+nil A2)0r z +mlx z z =mgl0 (a)取系统的状态变量为% = x,x2 =仪X3 = x4=灰输出y = [x OF包扌舌小车位移和摆杆的角位移.由线性化后运动方程组得故空间状态方程如下:■010 0 ■「xT■ ■x2*00-2.6727 0x21 1.8182 x3f =000 1x3+0_x4J|_x40031.1818 0-4.5455uml0f r + (M+m) x''二u (b) 其中J = -ml3■ ■ xl ■ ■Xx2x1 x30 x4&Y=xlx3X1/二x'=x2—沁—册4(M + m) 一3m44(M + m) - 3m u3(M +m)g4(M + m)l 一3ni-34(M + m)l 一311119 1 00 ''xlM00 -3mg0am xl x2‘ _4(M + m) 一3m x2 x3* ~00 01x3x4J00 3(M + m)g0[_x44(M + m)l - 3ml 044(M + m) - 3m 0一34(M + m)l - 3nil二. 通过Matlab 仿真判断系统的可控与可观性,并说明其物理意义。
matlab仿真毕设--倒立摆现代控制理论研究

内蒙古科技大学本科生毕业设计说明书(毕业论文)题目:倒立摆现代控制理论研究倒立摆现代控制理论研究摘要倒立摆系统是一个复杂的非线性、强耦合、多变量和自不稳定系统。
在控制工程中,它能有效地反映诸如可镇定性、鲁棒性、随动性以及跟踪性等许多控制中的关键问题,是检验各种控制方法的理想工具。
理论是工程的先导,它对倒立摆系统的控制研究具有重要的工程背景,单级倒立摆与火箭的飞行有关,二级倒立摆与双足机器人的行走有相似性,日常生活中的任何重心在上,支点在下的问题都与倒立摆的控制有极大的相似性,所以对倒立摆的稳定控制有重大的现实意义。
迄今,人们已经利用古典控制理论、现代控制理论及多重智能控制理论实现了多种倒立摆系统的稳定控制[5]。
倒立摆的控制方法有很多,如状态反馈控制,经典PID控制,神经网络控制,遗传算法控制,自适应控制,模糊控制等。
其控制方法已经在军工、航天、机器人和一般工业过程等领域得到了应用。
因此对倒立摆系统的控制研究具有重要的理论和现实意义,成为控制领域中经久不衰的研究课题。
本文是应用线性系统理论中的极点配置、线性二次型最优(LQR)和状态观测器等知识,设计了倒立摆系统线性化模型的控制器,通过MA TLAB仿真,研究其正确性和有效性。
通过分析仿真结果,我们知道了,状态反馈控制可以使倒立摆系统很好的控制在稳定状态,并具有良好的鲁棒性。
关键词:倒立摆;现代控制;Matlab仿真;Modern Control Theory Of Inverted PendulumAbstractInverted pendulum system is a complex nonlinear and strongly coupled,multi-variable and unstable system since.In control engineering,it can effectively reflect such stabilization,robustness,with the mobility of control and tracking,and many other key issue,It is the test ideal for a variety of control methods.Theory is the project leader,inverted pendulum control system also has important engineering research background,inverted pendulum with single-stage related torocket for the flight,Inverted pendulum and biped walking robot similar nature in any life in the center of gravity,the fulcrum in the next issue with the inverted pendulum control has a great similarity,so the stability control of inverted pendulum significant practical significance.So far,it has been the use of classical control theory,modern control theory and control theory of multiple intelligence to achieve a variety of inverted pendulum system stability control[5].Inverted pendulum control methods there are many,such as the state feedback control,the classic PID control,neural network control,genetic algorithm control,adaptive control,fuzzy control.The control method has been in military,aerospace,robotics and general industrial processes and other areas have been intended use.Therefore,the control of inverted pendulum system research has important theoretical and practical significance,of becoming enduring research topics in the field.This is the application of the theory of linear systems pole placement,linear quadratic optimal (LQR) and the state observer of such knowledge,the design of the linear inverted pendulum model of the controller,through simulation to study the correctness and effective sex.By analyzing the results of MATLAB simulation,state feedback control can make a goodcontrol of inverted pendulum system in a stable state,and has good robustness,stability control features.Key words: Inverted pendulum;Modern control;Matlab simulation;目录摘要 (I)Abstract (II)第一章绪论 (1)1.1倒立摆系统模型简介 (1)1.2倒立摆研究的背景与意义 (2)1.3国内外研究现状、水平和发展趋势 (3)1.3.1倒立摆和控制理论的发展 (3)1.3.2倒立摆的控制方法 (4)1.3.3倒立摆的发展趋势 (5)1.4本论文的主要工作介绍 (6)第二章一级倒立摆的数学模型建立及其性能分析 (7)2.1 系统的组成 (7)2.2 一级倒立摆数学模型的建立 (8)2.2.1 数学模型的建立 (8)2.2.2 系统的结构参数 (9)2.2.3 用牛顿力学方法来建立系统的数学模型 (9)2.2.4 一级倒立摆的性能分析[7] (13)2.3 本章小结 (15)第三章现代控制理论在倒立摆控制中的应用 (16)3.1 自动控制理论的发展历程 (16)3.2 经典控制理论 (18)3.2.1 PID控制现状 (18)3.2.2 PID控制的基本原理 (18)3.2.3 常用PID数字控制系统 (20)3.3 现代控制理论 (21)3.3.1 极点配置[11] (22)3.3.2 线性二次型最优的控制理论[7,8] (24)3.3.3 加权矩阵的选取 (26)3.3.4 状态观测器[7] (26)3.4 本章小结 (29)第四章MA TLAB仿真技术 (30)4.1 仿真软件——Matlab简介 (30)4.1.1 MA TLAB的优势 (30)4.2 Simulink简介 (32)4.3 S-函数简介 (33)4.3.1 用M文件创建S-函数 (34)4.4 倒立摆仿真模块的建立 (36)4.5 本章小结 (37)第五章一级倒立摆线性模型系统的仿真 (38)5.1 倒立摆控制器结构选择 (38)5.2 一级倒立摆线性模型系统仿真 (38)5.2.1 Simulink仿真 (42)5.3 本章小结 (46)结束语 (48)参考文献 (49)附录A (51)致谢 (53)第一章绪论1.1倒立摆系统模型简介倒立摆控制系统是一个复杂的、不稳定的、非线性的系统,是进行控制理论教学及开展各种控制实验的理想实验平台,但它并不是我们想象的那样抽象,其实在我们日常生活中就有很多这样的例子。
倒立摆控制器设计与仿真

摘要倒立摆系统是一个非线性自然不稳定系统, 是进行控制理论教学及开展各种控制实验的理想实验平台。
许多抽象的控制概念如控制系统的稳定性、可控性、系统收敛速度和系统抗干扰能力等,都可以通过倒立摆系统直观的表现出来。
除教学用途外,倒立摆系统的高阶次、不稳定、多变量、非线性和强耦合等特性使得许多现代控制理论的研究人员一直将它视为研究对象。
本课题以固高倒立摆系统为研究对象,通过Simulink搭建非线性模型然后将其线性化,并与数学方法近似的线性模型进行了比较。
采用根轨迹法设计出确定参数下的使系统稳定的控制器,并将其应用于倒立摆实际控制中,在摆杆角度控制器方面获得了很好的的控制效果。
最后,在MATLAB/Simulink环境下分别观察了线性模型和非线性模型的仿真情况。
本文以直线一级倒立摆系统为核心,掌握了在倒立摆系统控制方面国内外的研究情况。
通过实现对倒立摆的稳定控制,进而掌握了控制系统设计的一些基本方法。
一、绪论(一)课题研究的背景及意义倒立摆的最初研究始于上世纪50年代,由美国麻省理工学院(MIT)的控制论专家根据火箭发射助推器的原理设计而来,随着研究的深入和实际问题的推动而不断发展至今,已发展出了三级摆和四级摆。
这些研究成果具有重要的工程前景,在控制等领域中发挥了巨大的作用。
作为研究控制理论的一种非常典型的实验装置,倒立摆系统具有形象直观、结构简单、成本低廉、构件组成参数和形状易于改变的特点。
倒立摆是多种技术、多个领域的有机结合,包括机器人技术、控制理论技术、计算机控制技术等。
很多抽象的控制概念,如控制系统的稳定性、系统的可控性、系统收敛速度和抗干扰能力等,都可通过倒立摆系统直观形象的表现出来。
倒立摆控制系统本身又是一个多变量、高阶次、强耦合的非线性自然不稳定系统系统,在自动控制领域中,倒立摆仿真或者实物控制实验,已成为检验一种新的控制理论是否有效的试金石,同时也是产生一种新的控制方法所必须依据的基础实验平台。
倒立摆控制系统的Simulink仿真

倒立摆控制系统的Simulink 仿真本文针对一个倒立摆系统进行了系统的建模、求解、控制系统的设计,并且使用Simulink 对控制算法进行了仿真。
一、模型的描述倒立摆系统如图(1),设有一个倒立摆装在只能沿x 轴方向移动的小车上,图中1m 为小车的质量,2m 为摆球的质量,g 为重力加速度,l 为摆长,J 为摆的转动惯量。
当小车受到外力()f t 的作用时,小车产生位移()x t ,且摆产生角位移()t θ。
二、模型的建立下面针对该倒立摆系统进行建模求解。
当小车1m 在外力作用下产生位移()x t 时,摆球受力情况如图(2)所示。
图中2m g 为摆球2m 所受重力,222()d x t m dt 为x 方向的惯性力,2sin ()m g t θ为垂直于摆杆方向的重力分量。
在x 方向上,小车的惯性力矩为212()d x t m dt ,摆球产生的位移量为()sin ()x t l t θ+;在垂直于摆杆的方向上,摆球的转动惯性力为22()d t J dt θ;222()d x t m dt的分力为222()cos ()d x t m t dt θ。
图(1)装有倒立摆的小车 图(2)倒立摆受力图根据牛顿运动定律,按照力的平衡原理,可以分别列出该系统在x 方向上和垂直于摆杆方向上的的运动方程222122222()()[sin ()]()d x t d x t d l t m m m f t dt dt dt θ++=(1) 222222()()cos ()sin ()d t d x t J m l t m lg t dt dtθθθ+= (2) 三、模型的求解3.1微分方程组的求解联立式(1)、(2),经过方程组的恒等变形得2222222122222()()2[()cos ()]sin 2()2sin ()()2()d x t d t m m J m l t m l g t Jm l t dt dtJf t θθθθ+-=-++ (3) 2222222212221222()()[cos ()()]sin ()cos ()()()sin ()()d t d t m l t m m J m l t t dt dtm m m lg t m lf t θθθθθθ-+=-++ (4) 由式(3)、(4)令''121343()(),(),()(),()()x t t x x t x t x t x t x t θ====,可建立如下的微分方程组进行求解'12'2222221222222122'34'222422222122()()1()()(sin ()cos ()()()sin ()cos ()()())()()1()()(sin 2()2sin ()()2())2[()cos ()]x t x t d t x t x m l t t m m m lg t m l t m m J dt m lf t x t x t d t x t m l g t Jm l t Jf t m m J m l t dt θθθθθθθθθ⎧=⎪⎪=-+⎪-+⎪+⎨==-+++-⎪⎪⎪⎪⎩3.2控制系统的分析与设计在该模型中,对该倒立摆系统实施角度环、速度换的控制,并假设小车在运行过程中受到空气阻力,阻力大小与小车的速度成正比。
直线二级倒立摆建模与matlab仿真LQR
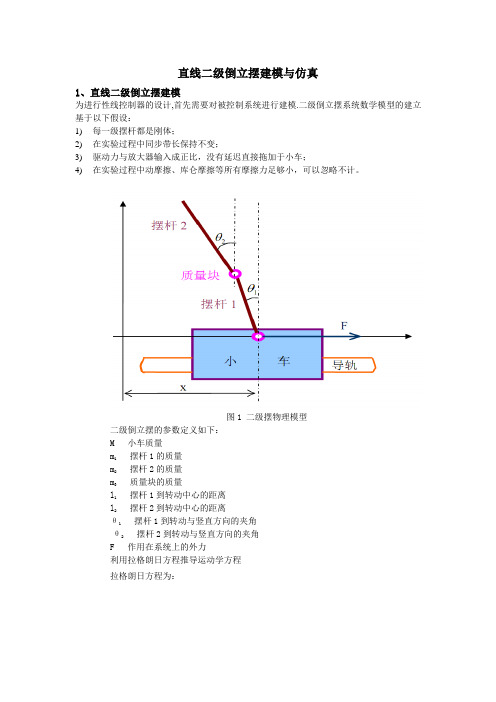
直线二级倒立摆建模与仿真1、直线二级倒立摆建模为进行性线控制器的设计,首先需要对被控制系统进行建模.二级倒立摆系统数学模型的建立基于以下假设:1)每一级摆杆都是刚体;2)在实验过程中同步带长保持不变;3)驱动力与放大器输入成正比,没有延迟直接拖加于小车;4)在实验过程中动摩擦、库仑摩擦等所有摩擦力足够小,可以忽略不计。
图1 二级摆物理模型二级倒立摆的参数定义如下:M 小车质量m1摆杆1的质量m2摆杆2的质量m3质量块的质量l1摆杆1到转动中心的距离l2摆杆2到转动中心的距离θ1摆杆1到转动与竖直方向的夹角θ2摆杆2到转动与竖直方向的夹角F 作用在系统上的外力利用拉格朗日方程推导运动学方程拉格朗日方程为:其中L 为拉格朗日算子,q 为系统的广义坐标,T 为系统的动能,V 为系统的势能其中错误!未找到引用源。
,错误!未找到引用源。
为系统在第i 个广义坐标上的外力,在二级倒立摆系统中,系统有三个广义坐标,分别为x,θ1,θ2,θ3。
首先计算系统的动能:其中错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
分别为小车的动能,摆杆1的动能,摆杆2的动能和质量块的动能。
小车的动能:错误!未找到引用源。
,其中错误!未找到引用源。
,错误!未找到引用源。
分别为摆杆1的平动动能和转动动能。
错误!未找到引用源。
,其中错误!未找到引用源。
,错误!未找到引用源。
分别为摆杆2的平动动能和转动动能。
对于系统,设以下变量: xpend1摆杆1质心横坐标 xpend2摆杆2质心横坐标 yangle1摆杆1质心纵坐标 yangle2摆杆2质心纵坐标 xmass 质量块质心横坐标 ymass 质量块质心纵坐标 又有:(,)(,)(,)L q q T q q V q q =-则有:系统总动能:系统总势能:则有:求解状态方程:可解得:使用MATLAB对得到的系统进行阶跃响应分析,执行命令:A=[0 0 0 1 0 0;0 0 0 0 1 0;0 0 0 0 1 01;0 0 0 0 0 0;0 86.69 -21.62 0 0 0;0 -40.31 39.45 0 0 0];B=[0;0;0;1;6.64;-0.808];C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];D=[0;0;0];sys=ss(A,B,C,D);t=0:0.001:5;step(sys,t)求取系统的单位阶跃响应曲线:图2 二级摆阶跃响应曲线由图示可知系统小车位置、摆杆1角度和摆杆2角度均发散,需要设计控制器以满足期望要求。
一级倒立摆的Simulink仿真

一级倒立摆的Simulink仿真第一篇:一级倒立摆的Simulink仿真单级倒立摆稳定控制直线一级倒立摆系统在忽略了空气阻力及各种摩擦之后,可抽象成小车和匀质摆杆组成的系统,如图1所示。
杆长为2λmguθ图1 直线一级倒立摆系统图2 控制系统结构假设小车质量M =0.5kg,匀质摆杆质量m=0.2kg,摆杆长度2l =0.6m,x(t)为小车的水平位移,θ为摆杆的角位移,g=9.8m/s2。
控制的目标是通过外力u(t)使得摆直立向上(即θ(t)=0)。
该系统的非线性模型为:&&+(mlcosθ)&12&=mglsinθ(J+ml2)θxJ=ml。
,其中2&&&3&=(mlsinθ)θ+u(mlcosθ)θ+(M+m)&x解:一、非线性模型线性化及建立状态空间模型&=0)对系统进行线性化,所以因为在工作点附近(θ=0,θsinθ≈θ-θ33!可以做如下线性化处理:,cosθ≈1-θ22!当θ很小时,由cosθ、sinθ的幂级数展开式可知,忽略高次项后,可得cosθ≈1,sinθ≈θ,θ’^2≈0;因此模型线性化后如下:(J+ml^2)θ’’+mlx’’=mglθ(a)mlθ’’+(M+m)x’’=u(b)其中J=ml13&,输出y=[x&,x3=θ,x4=θ取系统的状态变量为x1=x,x2=x的角位移.θ]T包括小车位移和摆杆⎡x1⎤⎡x⎤⎢x2⎥⎢x'⎥⎡x⎤⎡x1⎤即X=⎢⎥=⎢⎥ Y=⎢⎥=⎢⎥⎢x3⎥⎢θ⎥⎣θ⎦⎣x3⎦⎢⎥⎢⎥⎣x4⎦⎣θ'⎦由线性化后运动方程组得-3mg4X1’=x’=x2 x2’=x’’=x3+u4(M+m)-3m4(M+m)-3m3(M+m)g-3X3’ =θ’=x4 x4’=θ’’=x3+u4(M+m)l-3ml4(M+m)l-3ml故空间状态方程如下:⎡0⎢⎡x1'⎤⎢0⎢x2'⎥⎢X’=⎢⎥=⎢⎢x3'⎥⎢0⎢⎥⎢⎣x4'⎦⎢0⎣100⎤⎡0⎤⎥⎢⎥-3mgx14⎡⎤⎢⎥00⎥⎢⎥4(M+m)-3m⎥x2⎢4(M+m)-3m⎥⎢⎥+ ⎢⎥001⎥0⎥⎢x3⎥⎢⎥⎢⎥⎥x4⎢⎥3(M+m)g-300⎥⎣⎦⎢⎥4(M+m)l-3ml⎦⎣4(M+m)l-3ml ⎦u⎡x1'⎤⎡0⎢x2'⎥⎢0⎢⎥⎢X’=⎢x3'⎥=⎢⎥⎢0⎣x4'⎦⎢⎣0100⎤0⎡⎤x1⎡⎤⎢1.8182⎥⎢x2⎥0-2.67270⎥⎥⎢⎥ + ⎢⎥ ux3⎥001⎥⎢⎢0⎥⎢⎥⎥⎣x4⎦⎢⎥031.18180⎦⎣-4.5455⎦⎡x1⎤⎢⎥⎡x1⎤⎡1000⎤⎢x2⎥Y= ⎢⎥=⎢⎥⎢⎥⎣x3⎦⎣0010⎦x3⎢⎥⎣x4⎦二、通过Matlab仿真判断系统的可控与可观性,并说明其物理意义。
倒立摆PID控制及MATLAB仿真

摘要倒立摆系统是一个典型的快速、多变量、非线性、不稳定系统,对倒立摆的控制研究无论在理论上和方法上都有深远的意义。
本论文以实验室原有的直线一级倒立摆实验装置为平台,重点研究其PID控制方法,设计出相应的PID控制器,并将控制过程在MATLAB上加以仿真。
本文主要研究内容是:首先概述自动控制的发展和倒立摆系统研究的现状;介绍倒立摆系统硬件组成,对单级倒立摆模型进行建模,并分析其稳定性;研究倒立摆系统的几种控制策略,分别设计了相应的控制器,以MATLAB为基础,做了大量的仿真研究,比较了各种控制方法的效果;借助固高科技MATLAB实时控制软件实验平台;利用设计的控制方法对单级倒立摆系统进行实时控制,通过在线调整参数和突加干扰等,研究其实时性和抗千扰等性能;对本论文进行总结,对下一步研究作一些展望。
关键词:一级倒立摆,PID,MATLAB仿真目录第1章自动控制概述 (1)1.1 自动控制概念 (1)1.1.1 开环控制 (1)1.1.2 闭环控制 (2)1.2 自动控制系统的分类 (2)1.2.1 恒值系统、随动系统和程序控制系统 (2)1.2.2 随机系统与自动调整系统 (3)1.2.3 线性系统和非线性系统 (3)1.2.4 连续系统与离散系统 (3)1.2.5 单输入单输出系统和多输入多输出系统 (3)1.2.6 集中参数系统和分布参数系统 (4)1.3 对控制系统的性能要求 (4)1.4 典型环节 (5)1.4.1 比例环节 (5)1.4.2 积分环节 (5)1.4.3 微分环节 (6)1.4.4 惯性环节 (6)1.4.5 时滞环节 (7)第2章 MATLAB仿真软件的应用 (9)2.1 MATLAB的基本介绍 (9)2.2 MATLAB的仿真 (9)2.3 控制系统的动态仿真 (10)2.4 小结 (12)第3章直线一级倒立摆系统及其数学模型 (13)3.1 系统组成 (13)3.1.1 倒立摆的组成 (14)3.1.2 电控箱 (14)3.1.3 其它部件图 (14)3.1.4 倒立摆特性 (15)3.2 模型的建立 (15)3.2.1 微分方程的推导 (16)3.2.2 传递函数 (17)3.2.3 状态空间结构方程 (18)3.2.4 实际系统模型 (20)3.2.5 采用MATLAB语句形式进行仿真 (21)第4章 PID控制理论 (23)4.1 PID控制概述 (23)4.2 PID的控制规律 (24)4.3 数字PID控制 (25)4.3.1 位置式PID控制算法 (26)4.3.2 增量式PID控制算法 (27)4.4 常用的PID控制系统 (27)4.4.1 串级PID控制 (27)4.4.2 纯滞后系统的大林控制算法 (28)4.4.3纯滞后系统的Smith控制算法 (29)4.4.4 PID控制原理的特点 (30)4.4.5 PID参数的调整 (31)4.4.6 PID控制回路的运行 (32)第5章直线一级倒立摆的PID控制器设计与调节 (33)5.1 PID控制器的设计 (33)5.2 PID控制器设计MATLAB仿真 (35)结论 (40)致谢.......................................................................................................................错误!未定义书签。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
倒立摆的s函数建模及仿真
倒立摆是一类普遍存在于现实生活中的控制工程问题,也是机器人控制领域中的典型问题。
为了探究倒立摆的控制方法,需要进行建模和仿真研究。
本文将介绍如何对倒立摆进行s函数建模,并进行仿真研究。
一、倒立摆的建模
1. 系统假设
倒立摆系统假设为:
(1)摆杆质量可以忽略,只考虑质点的重量;
(2)摆杆的摩擦系数可以忽略;
(3)摆杆的惯性可以忽略。
2. 系统模型
假设摆杆长度为L,质点质量为m,摆杆与竖直方向成θ角度,摩擦系数为f,则可得到如下系统模型:
mx”=mgLsinθ-fx’+u
θ’=x
其中,x表示质点距离垂直方向的距离,u是外部输入信号,可用来控制系统。
3. s函数模型
根据系统模型,可以进行s函数建模。
将其转化为状态空间的形式,得到如下s函数模型:
function [sys,x0,str,ts] = pendulum(t,x,u,flag)
switch flag
% Initialization
case 0
sys = [0 0 1 2 0 1];
x0 = [0; 0];
str = [];
ts = [];
% Derivatives
case 1
sys = [x(2); (u(1)*cos(x(1))-9.8*sin(x(1)))/0.5];
% Outputs
case 3
sys = [x(1)];
% Unhandled flags
case {2, 4, 9}
sys = [];
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
二、倒立摆的仿真
倒立摆的仿真可以使用Matlab软件进行实现。
下面介绍具体的
仿真过程:
1. 创建仿真模型
打开Matlab软件,选择“Simulink”工具栏,创建一个新的模
型文件。
2. 添加控制器
在模型中添加一个控制器,用于产生外部输入信号u。
具体可选
择Proportional Integral Derivative(PI D)控制器或者其他控制器。
在控制器中输入期望值以及计算出来的偏差,根据控制器输出信号进
行控制。
3. 添加s函数模块
在模型中添加s函数模块,用于实现倒立摆的状态空间模型。
在
s函数模块中调用前面所建立的s函数模型,实现倒立摆系统的仿真。
4. 运行仿真
设置模型参数,运行仿真。
可以通过仿真结果来分析控制器的效果。
根据仿真结果,可以进一步优化控制器的设计。
三、总结
本文介绍了倒立摆的s函数建模方法以及仿真过程。
通过Matlab 软件进行仿真,可以更加直观地了解倒立摆系统的控制过程,帮助更好地掌握倒立摆系统的控制方法。
