石家庄市2011年初中毕业班知识能力测试数学试题答案
2011年河北省中考数学试题及答案

得 分
评卷人
数学试卷 第 6 页(共 12 页)
25. (本小题满分 10 分)
如图 14-1 至 14-4 中,两平行线 AB,CD 间的距离均为 6,点 M 为 AB 上一定点. 思考 如图 14-1,圆心为 O 的半圆形纸片在 AB,CD 之间 (包括 AB,CD) ,其直径 MN 在 AB 上,MN=8, .. 点 P 为半圆上一点,设∠MOP=α. 当 α=_____度时,点 P 到 CD 的距离最小,最小 值为_______ 探究一 在图 14-1 的基础上, 以点 M 为旋转中心, 在 AB, CD 之间顺时针旋转该半圆形纸片,直到不能再转动 为止,如图 14-2,得到最大旋转角∠BMO=_____度, 此时点 N 到 CD 的距离是_______. 探究二 将图 14-1 中的扇形纸片 NOP 按下面对 α 的要求 剪掉,使户型纸片 MOP 绕点 M 在 AB,CD 之间 顺时 .. 外旋转. (1)如图 14-3,当 α=60° 时,求在旋转过程中, 点 P 到 CD 的最小距离, 并请指出旋转角∠ BMO 的最大值 (2)如图 14-4,在扇形纸片 MOP 旋转过程中, 要保证点 P 能落在直线 CD 上, 请确定 α 的 取值范围. (参考数据:sin49° =4,cos41° =4,tan37° =4)
数学试卷 第 1 页(共 12 页)
游客年龄的方差分别是 S 甲 2=27,S 乙 2=19.6,S 丙 2=1.6.导游小王最喜欢带游客年龄相 近的团队,若在三个团中选择一个,则他 应选 A.甲团 B.乙团 C.丙团 D.甲团或乙团
8.一小球被抛出后,距离地面的高度 h(米)和飞行时间 t(秒)满足下面函数关系式: h=–5(t–1)2+6,则小球距离地面的最大高度是 A.1 米 B.5 米 C .6 米 D.7 米
石家庄市桥西区2011年初中毕业生升学文化课考试数学试题(含答案)
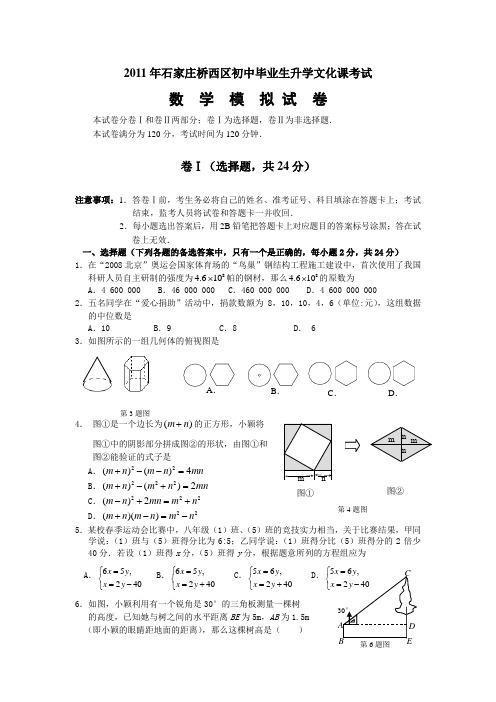
2011年石家庄桥西区初中毕业生升学文化课考试数 学 模 拟 试 卷本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题. 本试卷满分为120分,考试时间为120分钟.卷Ⅰ(选择题,共24分)注意事项:1.答卷Ⅰ前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上;考试结束,监考人员将试卷和答题卡一并收回.2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;答在试卷上无效.一、选择题(下列各题的备选答案中,只有一个是正确的,每小题2分,共24分) 1.在“2008北京”奥运会国家体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为84.610⨯帕的钢材,那么84.610⨯的原数为A .4 600 000B .46 000 000C .460 000 000D .4 600 000 000 2.五名同学在“爱心捐助”活动中,捐款数额为8,10,10,4,6(单位:元),这组数据的中位数是A .10B .9C .8D . 6 3.如图所示的一组几何体的俯视图是4. 图①是一个边长为()m n +的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是A .22()()4m n m n mn +--=B .222()()2m n m n mn +-+= C .222()2m n mn m n -+=+ D .22()()m n m n m n +-=-5.某校春季运动会比赛中,八年级(1)班、(5)班的竞技实力相当,关于比赛结果,甲同学说:(1)班与(5)班得分比为6:5;乙同学说:(1)班得分比(5)班得分的2倍少40分.若设(1)班得x 分,(5)班得y 分,根据题意所列的方程组应为A .65,240x y x y =⎧⎨=-⎩B .65,240x y x y =⎧⎨=+⎩C .56,240x y x y =⎧⎨=+⎩D .5x x ⎧⎨⎩6.如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE 为5m ,AB 为1.5m (即小颖的眼睛距地面的距离),那么这棵树高是( )第3题图图①图②第4题图第6题图A . . D . C .A .2+)m B .(32)m C .m D .4m7.如图,在平面直角坐标系中,以O (0,0),A (1,1), B (3,0)为顶点,构造平行四边形,下列各点中 不能..作为平行四边形顶点坐标的是( ) A .(-3,1) B .(4,1) C .(-2,1)D .(2,-1)8.把长为8cm 的矩形按虚线对折,按图中的虚线剪出一个直角梯形,打开得到一个等腰梯形,剪掉部分的面积为6cm 2,则打开后梯形的周长是( )A .(cmB .(cmC .22cmD .18cm 9其中<50时空气质量为优, 50≤≤100时空气质量为良,100<w ≤150时空气质量为轻度污染,若1年按365天计算,请你估计该城市在一年中空气质量达到良以上(含良)的天数为A .255B .256C .292D .29310.已知△ABC 是斜边长为1cm 的等腰直角三角形,以Rt △ABC 的斜边AC 为直角边,画第二个等腰Rt △ACD ,再以Rt △ACD 的斜边AD 为直角边,画第三个等腰Rt △ADE ,…,依此类推,第n 个等腰直角三角形的斜边长是 . A cm C .2ncm D cm 11.若n (0n ≠)是关于x 的方程220x mx n ++=的根, 则m +n 的值为( ) A .1 B .2 C .-1 D .-2 12.如图,在平面直角坐标系中有一矩形ABCD 黑色区域,其中(62)A ,, (60)B ,,C(2,1),D (2,2),有一动态扫描线为双曲线ky x=(x >0),当扫描线遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的k 的取值范围是A . 4≤k ≤6B . 2≤k ≤12C .6<k <12D . 2<k <12第8题图第7题图AB CD E FG第11题图2011年桥西区初中毕业生升学文化课考试数学模拟试卷卷Ⅱ(非选择题,共96分)注意事项:1.答卷Ⅱ前,将密封线左侧的项目填写清楚.2.答卷Ⅱ时,将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.二、填空题(本大题共6个小题,每小题3分,共18分.把答案写在题中横线上)13.函数124yx=-中,自变量x的取值范围是.14.写出含有解为x=1的一元一次不等式__ __(写出一个即可).15.如图,ABC△与A B C'''△是位似图形,且位似比是1:2,若AB=2cm,则A B''= cm,并在图中画出位似中心O.16.某商场销售额3月份为16万元,5月份为25万元,该商场这两个月销售额的平均增长率是.17.如图,整个圆表示某班参加课外活动的总人数,跳绳的人数占30%,表示踢毽的扇形圆心角是60°,踢毽和打篮球的人数比是1:2,那么表示参加“其它”活动的人数占总人数的 %.18.星期天,小明与小刚骑自行车去距家50千米的某地旅游,匀速行驶1.5小时的时候,其中一辆自行车出故障,因此二人在自行车修理点修车,用了半个小时,然后以原速继续前行,行驶1小时到达目的地.请在右面的平面直角坐标系中,画出符合他们行驶的路程S(千米)与行驶时间t(时)之间的函数图象.三、解答题(本大题共8个小题,共78分.解答应写出文字说明、证明过程或演算步骤)19.(1)(本小题满分4分)45sin60)4︒-︒+.′AB CABC′′第15题图踢毽篮球跳绳其它第17题图t(时)第18题图进入防汛期后,某地对河堤进行了加固.该地驻军在河堤加固的工程中出色完成了任务.这是记者与驻军工程指挥官的一段对话: 20.(1)(本小题满分7分)某服装厂承揽一项生产夏凉小衫1600件的任务,计划用t 天完成.(1)写出每天生产夏凉小衫w (件)与生产时间t (天)(t >4)之间的函数关系式;(2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务?通过这段对话,请你求出该地驻军原来每天加固的米数.如图,已知矩形ABCD 中,E 是AD 上的一点,F 是AB 上的一点,EF ⊥EC ,且EF =EC ,DE =4cm ,矩形ABCD 的周长为32cm ,求AE 的长.21.(本小题满分7分)为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容.为了了解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如下:请根据统计图提供的信息回答以下问题: (1)抽取的学生数为_______名;(2)该校有3000名学生,估计喜欢收听易中天《品三国》的学生有_______名; (3)估计该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的_ ___%; (4)你认为上述估计合理吗?理由是什么?《红楼梦》《品三国》《论语》博物院《庄子》内容第21(2)图第20(2)图BCA EDF四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.(1)求随机抽取一张卡片,恰好得到数字2的概率;(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树状图法说明理由,若认为不公平,请你修改规则,使游戏变得公平.23.(本小题满分8分)某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).(1)分别写出两种优惠方法购买费用y(元)与所买水性笔支数x(支)之间的函数关系式;(2)对x的取值情况进行分析,说明按哪种优惠方法购买比较便宜;(3)小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济.2362如图,已知在⊙O中,ABAC是⊙O的直径,AC⊥BD于F,∠A=30°.(1)求图中阴影部分的面积;(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.(3) 试判断⊙O中其余部分能否给(2)中的圆锥做两个底面。
河北省石家庄市2011届初中毕业班能力测试数学试题(扫描版)

2011年石家庄市初中毕业班知识能力测试数学试题参考答案一、选择题题 号 1 2 3 4 5 6 7 8 9 10 11 12 答 案 BCBADCBDCCDA二、填空题13.)5)(5(-+b b a ;14.⎩⎨⎧==2,1y x ;15.1-≠x ;16.65°;17.81;18.212+.三、解答题 19.解:1)111(2+÷-+a aa =aa a a a 1)1)(1(2+⨯-+……………………………………………………………3分 =1-a a.……………………………………………………………………………6分 当a =-2时, 原式=32. ……………………………………………………………………………8分 20. 解:(1)50t , 225t .……………………………………………………………4分(2)过点C 作CD ⊥AB 于点D ,∵在R t △ACD 中,AC =225 t ,∠DAC =45°,∴CD =25 t ,…………………………………………………………5分 又∵在R t △BCD 中,CD =25 t ,BC =50 t ,∴sin ∠B =BC CD =21,∴∠B =30°,……………………………………………………7分 ∴巡逻艇是沿北偏东30°方向追击走私快艇.…………………8分21. 解:(1) 30÷15%=200,∴同学们一共随机调查了200户.……………………2分(2) 如图2、图3所示; ………………………………………………………6分C图215%10%DB40%35%O40 户数 80 30 A C B 家长意见D 20 1050 60 70 7020AAB北 CD图1(3)A . ……………………………………………………………………………………7分 (4) 2000×(35%+40%)=1500(户).∴该社区大约有1500户家庭反对孩子上网.…………………………………………9分 22. 解:(1)∵反比例函数xky =的图象过C (2,1), ∴21k=,解得:2=k , ∴反比例函数的表达式为2y x=;……………………2分 又∵一次函数b kx y +=的图象过C (2,1),且2=k , ∴b +⨯=221,解得:3-=b ,∴一次函数的表达式为32-=x y ;…………………………………………4分 (2) 如图4,过点C 作CD ⊥y 轴于点D ,……………………………………………5分∴CD =2, 又∵一次函数表达式为32-=x y , ∴0=x 时, 3-=y ;∴OB =3,∴S △OBC =21×OB ×CD =3.………………………………………………………8分 (3)P (21,4). ………………………………………………………………………9分 23.操作探究:(1)图略; ……………………………………………………………………2分(2)①22; ② 25;③2. (5)分联想拓展:(1)340,………………………………………………………………………8分(2)13,图略. (10)分24.(1)证明:∵△ABC ∽△EDC ,∴AC BC EC CD =,∴CECDAC BC = A图4OyBC xD又∵1BCAC=,∴BC =AC , CD =CE , 又∵AC ⊥BE ,∴∠ACB =∠ECD =90︒,∴△BCD ≌△ACE ,∴ BD=AE . (3)分(2)BD=kAE ,BD ⊥AE . …………………………………………………………………4分证明:如图5,延长BD 交AE 于点F , ∵△ABC ∽△EDC ,∴AC BC EC CD =, ∴CECDAC BC = 又∵AC ⊥BE ,∴∠ACB =∠ECD =90︒,∴△BCD ∽△ACE .∴AC BCAE BD =, ∠BDC=∠AEC , ∵k AC BC =,∴k AEBD=,∴BD=kAE .……………7分 ∵∠BCD =90︒ ,∴∠CBD +∠CDB =90︒, ∴∠CBD +∠AEC =90︒, ∴BD⊥AE . …………………………………………………………………………………9分(3)BD=kAE .……………………………………………………………………………………10分 25.解:(1) 法一:设购买纪念册m 本.则18-0.2(m -6)≥13,解得:m ≤31, ∴至少买31本才能用最低价购买.…………………………………………………………3分法二:(18-13)÷0.2+6=31.法三:设购买m 本时可恰得到最低价.则18-0.2(m -6)=13,解得:m =31. ∴至少买31本才能用最低价购买.(2) ①当x ≤6时,xx W 8)1018(=-=.(x 为整数) …………………………………………………………4分②当6<x ≤31时,[]10)6(2.018---=x x W=)2.02.9(x x - =xx 2.92.02+-.( x 为整C BADE图5F新世纪教育网 精品资料 版权所有@新世纪教育网 数) ……………………………………………………………7分③当x >31时,xx W 3)1013(=-=.(x 为整数) …………………………………………………………8分 (3) 由②中x x W 2.92.02+-=,∵a =-0.2<0, 232=-ab,∴当3123≤≤x 时,W 随x 的增大而减小. ∴商店一次售出30本纪念册所获的利润,比一次售出26本纪念册所获的利润低.…………10分又∵当x =23时,纪念册的售价为18-0.2×(23-6)=14.6(元),∴商店把促销方案中:“纪念册的最低售价不低于13元”改为“纪念册的最低售价不低于14.6元”,就可以使卖的纪念册越多商店所获的利润越大. ……………………………………………12分 26.解: (1)7和4; ………………………………………………………………………………………2分 (2)当t =2.5秒时,△EBF 的面积为y =7)(21=⋅-⋅CD CF BC ,即:7)25(21=⋅-CD BC . 当t =4秒时,△EBF 的面积为y =4)(21=⋅-⋅CD CF BC ,即: ()4421=⋅-CD BC .∴4,6.CD BC =⎧⎨=⎩…………………………………………………………………………………6分(3)法一:∵BC =6,点F 的速度是每秒1个单位, ∴OP =6,∴点E 从D 运动到C 用时为6-4=2秒, 又∵CD = 4,∴点E 的运动速度为每秒2 个单位.………………………………………………………9分法二:如图6,过点A 作AG ⊥BC 于点G , ∵AB =2.5k ,AD =1.5k ,∴BG =6-1.5 k ,在Rt ABG ∆中,42+(6-1.5k )2 =(2.5k )2. ∴ k 1=2,k 2 =-6.5(不合题意舍去),即点E 的运动速度为每秒2 个单位. (4)∵k =2,∴AD =3,AB =5,∴S 梯形ABCD =18,31S 梯形ABCD =6. 由题意可知运动过程中有两个时刻△EBF 的面积等于6.①当E 在AB 上时,过点E 作EH ⊥BC 于点H , △EBH ∽△ABG ,CD A BE F H G图6图6新世纪教育网 精品资料版权所有@新世纪教育网∴BE EH AB AG=,∴EH=85t,∴18(6)625t t⨯⨯-=,解得266±=t,∵t≤2.5.∴266-= t.…………………………………………………………………………11分②当E在AD上时,14(6)62t⨯⨯-=,解得t=3.综上所述,当266-=t或3t=秒时,△EBF与梯形ABCD的面积之比为1:3.…12分。
2011河北数学中考试卷及答案

2011河北省初中毕业生升学文化课考试数 学 试 卷本试卷分卷Ⅰ和卷Ⅱ两部分:卷I 为选择题,卷Ⅱ为非选择题. 本试卷满分为120分,考试时间为120分钟.卷Ⅰ(选择题,共30分)注意事项:1.答卷Ⅰ前,考生务必将自己的姓名、准考证号、科目填涂在答题卡,考试结束,监考人员将试卷和答题卡一并收回.2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,答在试卷上无效.一、选择题(本大题共12个小题.1-6小题,每小题2分,7-12小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的 1.(11河北)计算30的结果是A .3B .30C .1D .0 2.(11河北)如图1,∠1+∠2等于A .60°B .90°C .110°D .180° 3.(11河北)下列分解因式正确的是A .-a +a 3=-a (1+a 2)B .2a -4b +2=2(a -2b )C .a 2-4=(a -2)2D .a 2-2a +1=(a -1)2 4.(11河北)下列运算中,正确的是A .2x -x =1B .x +x 4=x 5C .(-2x )3=-6x 3D .x 2y ÷y =x 25.(11河北)一次函数y =6x +1的图象不经过... A .第一象限 B .第二象限 C .第三象限 D .第四象限6.(11河北)将图2①围成图2②的正方体,则图②中的红心“”标志所在的正方形是正方体中的A .面CDHEB .面BCEFC .面ABFGD .面ADHG 7.(11河北)甲、乙、丙三个旅行团的游客人数都相等,且每团游客的平均年龄都是32岁,这三个团游客年龄的方并有分别是227S =甲,219.6S =乙,2 1.6S =丙,导游小王最喜欢带游客年龄相近的团队,若在这三个团中选择一个,则他应选 A .甲团 B .乙团 C .丙团 D .甲或乙团8.(11河北)一小球被抛出后,距离地面的高度h (米)和飞行时间t (秒)满足下面的函数关系式:h =-5(t -1)2+6,则小球距离地面的最大高度是 A .1米 B .5米 C .6米 D .7米9.(11河北)如图3,在△ABC 中,∠C =90°,BC =6,D ,E 分别在AB ,AC 上,将△ABC沿DE 折叠,使点A 落在A ′处,若A ′为CE 的中点,则折痕DE 的长为A .12B .5米C .6米D .7米图1 ① ② 图210.(11河北)已知三角形三边长分别为2,x ,13,若x 为正整数,则这样的三角形个数为A .2B .3C .5D .1311.(11河北)如图4,在长形中截取两个相同的圆作为圆柱的上、下底面,剩余的矩形作为圆住的侧面,刚好能组合成圆住.设矩形的长和宽分别为y 和x ,则y 与x 的函数图象大致是12.(11河北)根据图5中①所示的程序,得到了y 与x 的函数图象,如图5中②,若点M是y 轴正半轴上任意一点,过点M 作PQ ∥x 轴交图象于点P 、Q ,连接OP 、OQ ,则以下结论:①x <0时,y =2x②△OPQ 的面积为定值③x >0时,y 随x 的增大而增大 ④MQ =2PM⑤∠POQ 可以等于90° 其中正确结论是 A .①②④ B .②④⑤C .③④⑤D .②③⑤2011年河北省初中毕业生升学文化课考试数 学 试 卷卷Ⅱ(非选择题,共90分)注意事项:1.答卷Ⅱ前,将密封线左侧的项目填写清楚.2.答卷Ⅱ时,将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.二、填空题(本大题共6个小是,每小题3分,共18分,把答案写在题中横线上) 13.(11河北π,-4,0这四个数中,最大的数是___________.14.(11河北)如图6,已知菱形ABCD ,其顶点A 、B 在数轴上对应的数分别为-4和1,则BC =_____.图6ABCD图40 ①②ABCDO 图7C①②图815.(11河北)若︱x -3︱+︱y +2︱=0,则x +y 的值为_____________.16.(11河北)如图7,点O 为优弧ACB 所在圆的心,∠AOC =108°,点D 在AB 的延长线上,BD =BC ,则∠D =____________.17.(11河北)如图8中图①,两个等边△ABD ,△CBD 的边长均为1,将△ABD 沿AC 方向向右平移到△A ′B ′D ′的位置得到图②,则阴影部分的周长为_________18.(11河北)如图9,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”. 若小宇从编号为2的顶点开始,第10次“移位”后,则他所处顶点的编号是____________.三、解答题(本大题共8个小题,共72分,解答应写出文字说明、证明过程 或演算步骤)19.(本小题满分8分)(11河北)已知2x y =⎧⎪⎨=⎪⎩x ,yy a =+的解.求(a +1)(a -1)+7的值20.(本小题满分8分)(11河北)如图10,在6×8的网格图中,每个小正方形边长均为1,点O 和△ABC 的顶点均为小正方形的顶点.⑴以O 为位似中心,在网格图...中作△A ′B ′C ′,使△A ′B ′C ′和△ABC 位似,且位似比为1:2⑵连接⑴中的AA ′,求四边形AA ′C ′C 的周长.(结果保留根号)21.(本小题满分8分)(11河北)如图11,一转盘被等分成三个扇形,上面分别标有关-1,1,2中的一个数,指针位置固定,转动转盘后任其自由停止,这时,这个扇形恰好停在指针所指的位置,并相应得到这个扇形上的数(若指针恰好指在等分线上,当做指向右边的扇形).⑴若小静转动转盘一次,求得到负数的概率; ⑵小宇和小静分别转动一次,若两人得到的数相同,则称两人“不谋而合”,用列表法(或画树形图)求两人“不谋而合”的概率.图9图11小宇 小静(11河北)甲、乙两人准备整理一批新到的实验器材,若甲单独整理需要40分钟完工,若甲、乙共同整理20分钟后,乙需再单独整理20分钟才能完工.⑴问乙单独整理多少分钟完工?⑵若乙因工作需要,他的整理时间不超过30分钟,则甲至少整理多少分钟才能完工?23.(本小题满分9分)(11河北)如图12,四边形ABCD 是正方形,点E ,K 分别在BC ,AB 上,点G 在BA 的延长线上,且CE =BK =AG .⑴求证:①DE =DG ;②DE ⊥DG ;⑵尺规作图:以线段DE ,DG 为边作出正方形DEFG (要求:只保留作图痕迹,不写作法和证明);⑶连接⑵中的KF ,猜想并写出四边形CEFK 是怎样的特殊四边形,并证明你的猜想;⑷当1CE CB n 时,衣直接写出ABCD DEFGS S 正方形正方形的值.24.(本小题满分9分)(11河北)已知A 、B 两地的路程为240千米,某经销商每天都要用汽车或火车将x 吨保鲜品一次性由A 地运往B 地,受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.现在有货运收费项目及收费标准表,行驶路程S (千米)与行驶时间t (时)的函数图象(如图13中①),上周货运量折线统计图(如图13中②)等信息如下:货运收费项目及收费标准表⑴汽车的速度为__________千米/时, 火车的速度为_________千米/时; 设每天用汽车和火车运输的总费用分别为y 汽(元)和y 火(元),分别求y 汽、y 火与x 的函数关系式(不必写出x 的取值范围)及x 为何值时y汽>y 火; (总费用=运输费+冷藏费+固定费用) ⑶请你从平均数、折线图走势两个角度分析,建议该经销商应提前下周预定哪种运输工具,才能使每天的运输总费用较省?A BCD图11 图13①图13 ②(11河北)如图14①至图14④中,两平行线AB、CD音的距离均为6,点M为AB上一定点.思考:如图14①中,圆心为O的半圆形纸片在AB、CD之间(包括AB、CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α,当α=________度时,点P到CD的距离最小,最小值为____________.探究一在图14①的基础上,以点M为旋转中心,在AB、CD之间顺时针旋转该半圆形纸片,直到不能再转动为止.如图14②,得到最大旋转角∠BMO=_______度,此时点N到CD的距离是______________.探究二将图14①中的扇形纸片NOP按下面对α的要求剪掉,使扇形纸片MOP绕点M在AB、CD之间顺时针旋转.⑴如图14③,当α=60°时,求在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值:⑵如图14④,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请确定α的取值范围.(参考数据:sin49°=34,cos41°=34,tan37°=34)26.(本小题满分12分)(11河北)如图15,在平面直角坐标系中,点P从原点O出发,沿x轴向右以每秒1个单位长的速度运动t(t>0)秒,抛物线y=x2+bx+c经过点O和点P.已知矩形ABCD 的三个顶点为A(1,0)、B(1,-5)、D(4,0).⑴求c、b(用含t的代数式表示);⑵当4<t<5时,设抛物线分别与线段AB、CD交于点M、N.①在点P的运动过程中,你认为∠AMP的大小是否会变化?若变化,说明理由;若不变,求出∠AMP的值;②求△MPN的面积S与t的函数关系式,并求t为何值时,S=218;③在矩形ABCD的内部(不含边界),把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分,请直接..写出t的取值范围.B AD C图14①B AD C图14 ③B AD C图14 ②B AD C图14 ④M。
2011年石家庄市初中毕业生调研答案

时间/周2011年石家庄市初中毕业班调研检测数学试题参考答案一、选择题二、填空题13.<;14.4;15.1;16.54;17.16;18.S 1+ S 3= S 2. 三、解答题 19.解:11211x x x+=+--两边同乘以(x -1) , ………………………………2分1122x x +=-+-4x =.………………………………6分检验:当4x =时,x -1≠0.………………………7分所以原方程的解为4x =. ………………………8分 20. 解:(1)如图; ………………………………2分(2)∵小正方形边长为1, ∴AB 2=5,AC 2=5,BC 2=10;∴AB 2+AC 2=BC 2;∴△ABC 是直角三角形; …………………………………………6分 (3)1,5.…………………………………………………………8分 21. 解:(1)90°;……………1分(2)8;……………2分折线图如图所示;……………5分(3)甲、乙两种品牌电磁炉周销售量的中位数分别为9,10;……………7分 (4)甲的周销售折线图整体呈上升趋势,而乙的周销售折线图从第三周以后一直呈下降趋势,所以商店应经销甲品牌的电磁 炉。
…………………………………9分 22. 解:(1)(1,4);……………………1分(2)设抛物线的解析式为2()y a x h k =-+,∵抛物线顶点坐标为(1,4),∴2(1)4y a x =-+,又∵抛物线过点A (-1,0),∴044=+a ,解得 a =-1.CABED第一 第二 第三 第四 第五 第六 甲品牌销量折线统计图∴223y x x=-++(或2(1)4y x=--+为所求).…………………………4分当x=0时,y=3,∴B(0,3).………………………………………………5分(3)过点D作DH⊥x轴于点H,∵A(-1,0),B(0,3),∴OA=1,OB=3,∴S△AOB =21×OA×OB=23;又∵D (1,4),E(3,0),∴DH=4,EH=2∴S△DHE =21×DH×HE=4;又∵B(0,3),D (1,4),∴S梯形BOHD =21×(OB+DH)×OH=27;∴S四边形AEDB= S△AOB+ S梯形BOHD+ S△DHE=9 .………………………………………8分(4) m=1.……………………………………………………………………9分23.解:'A,'B.…………………………………………………………………2分探究与发现:(1)50;………………………………………………………………………3分(2)如图,在R t△AA′C中,AA′=30 ,A′C=404=10,∴AC=∴丝线至少为cm.………………7分实践与应用:18π.………………………………………10分24.(1)DM=EM;………………………………………………………………1分证明:过点E作EF∥AB交BC于点F,…………………………………………2分∵AB=AC,∴∠ABC=∠C;又∵EF∥AB,∴∠ABC=∠EFC,∴∠EFC=∠C,∴EF=EC.又∵BD=EC,∴EF=BD.又∵EF∥AB,∴∠ADM=∠MEF.′C在△DBM 和△EFM 中BD E FEM BM D FM E BD EF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DBM ≌△EFM ,∴DM=EM .…………………………………………4分 (2)成立;…………………………………………………………………………5分 证明:过点E 作EF ∥AB 交CB 的延长线于点F ,………………………………6分 ∵AB =AC ,∴∠ABC =∠C ; 又∵EF ∥AB ,∴∠ABC =∠EFC , ∴∠EFC =∠C ,∴EF =EC . 又∵BD =EC ,∴EF =BD .又∵EF ∥AB ,∴∠ADM =∠MEF .在△DBM 和△EFM 中 BD E FEM BM D FM E BD EF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DBM ≌△EFM ;∴DM=EM ; ……………………………………8分 (3)1M D M E m=.……………………………………………………………10分25.解:(1)把p =3.8代入0.0550.5p t =+,得t=60,所以五月份该公司的总销售量为60台. ……………………………………2分 (2)由题意,得0.9 1.2 1.1(60)64x y x y ++--=,∴y =2 x -20. …………………………………………5分 (3)W =(1.2-0.9)x +(1.6-1.2)y +(1.3-1.1)(60-x -y )-3.8=0.1x +0.2y +12-3.8 =0.1x +0.2(2 x -20)+8.2=0.5x +4.2. …………………………………………8分E(4)由题意得⎪⎩⎪⎨⎧≥≥≥8--6088y x y x ,即⎪⎩⎪⎨⎧≥+≥-≥8202--6082028x x x x解得:14≤x ≤24. …………………………………………10分 又∵W =0.5x +4.2中,k =0.5>0,W 随x 的增大而增大,∴当x =24时,W 的最大值为16.2.∴该公司五月份销售这三种健身器材的最大利润是16.2万.…………………12分 26.解:(1)∵∠C =90°,CD =8,CE =6,∴DE =10;……………………………………………………………1分(2)①当点P 在DA 上时,即0≤t ≤5时,∵四边形ABCD 为直角梯形,∴AD ∥BC ,∠C =90°。
2011河北中考数学试题及答案

2011河北中考数学试题及答案2011年河北中考数学试题一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 22. 已知一个直角三角形的两条直角边分别为3和4,求斜边的长度。
A. 5B. 6C. 7D. 83. 如果一个数的平方等于16,那么这个数是多少?A. ±4B. ±2C. 4D. 24. 一个圆的半径是5,求这个圆的面积。
A. 25πB. 50πC. 75πD. 100π5. 一个数列的前三项是1, 3, 6,求第四项。
A. 10B. 12C. 15D. 206. 一个长方体的长、宽、高分别是2, 3, 4,求其体积。
A. 24B. 26C. 28D. 327. 一个分数的分子是5,分母是8,这个分数化简后是多少?A. 5/8B. 1/2C. 5/4D. 1/18. 一个二次方程x^2 - 5x + 6 = 0的解是什么?A. x = 2, 3B. x = -2, -3C. x = 2, -3D. x = -2, 39. 一个函数f(x) = 2x + 3的反函数是什么?A. f^(-1)(x) = (x-3)/2B. f^(-1)(x) = (x+3)/2C. f^(-1)(x) = (x-2)/3D. f^(-1)(x) = (x+2)/310. 一个正弦函数y = sin(x)的图像,当x增加π时,图像如何变化?A. 向左平移π个单位B. 向右平移π个单位C. 向上平移π个单位D. 向下平移π个单位二、填空题(每题2分,共20分)11. 圆的周长公式是_________。
12. 一个数的绝对值是它到0的距离,例如|-5|=_______。
13. 一个多项式3x^2 - 5x + 2的首项系数是_______。
14. 一个三角形的内角和是_______度。
15. 一个数的对数函数log_a(x),当a=10时,称为_______。
2011年河北省中考数学试题及答案
2011年河北省初中毕业生升学文化课考试数学试卷卷Ⅰ(选择题,共30分)注意事项:1.答卷I前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上,考试结束,监考人员将试卷和答题卡一并收回.2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.答在试卷上无效.一、选择题(本大题共12个小题,1~6小题,每小题2分;7~12小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.计算30的结果是的算术平方根是()A.3 B.30 C.1 D.02. 如图1,∠1+∠2等于A.60°B.90°C.110°D.180°3.下列分解因式正确的是–A.–a+a3=–a(1+a2) B.2a–4b+2=2(a–2b)C.a2–4=(a–2)2D.a2–2a+1=(a–1)24.下列运算中,正确的是A.2x–x=1 B.x+x4=x5C.(–2x)3=–6x3 D.x2y÷y=x25.一次函数y=6x+1的图象不经过...A.第一象限B.第二象限C.第三象限D.第四象限6.将图2-1围成图2–2的正方体,则图2-1中的红心“”标志所在的正方形的是正方形是下文体中的A.面CDHEB.面BCEFC.面ABFG D.面ADHG7.甲、乙、丙三个旅行团的游客人数相等,且每团游客的平均年龄都是32岁,这三个团游客年龄的方差分别是S 甲2=27,S 乙2=19.6,S 丙2=1.6.导游小王最喜欢带游客年龄相近的团队,若在三个团中选择一个,则他 应选 A .甲团 B .乙团 C .丙团 D .甲团或乙团8.一小球被抛出后,距离地面的高度h (米)和飞行时间t (秒)满足下面函数关系式:h =–5(t –1)2+6,则小球距离地面的最大高度是 A .1米 B .5米 C .6米 D .7米9.如图3,在△ABC 中,∠C =90°,BC =6,D 、E 分别在AB 、AC 上将△ABC 沿DE 折叠,使点A 落在点A ´处,若A ´为CE 的中点,则折痕DE 的度A .1米B .5米C .6米D .7米10.已知三角形三边长分别为2,x ,13,若x 为正整数,则这样的三角形个数为 A .2 B .3 C .5 D .1311.如图4,在矩形中截取两个相同的圆作为圆柱的上、下底面,剩余的矩形作为圆柱的侧面,刚好能组合成圆柱.设矩形的长和宽分别为y 和x ,则y 与x 的函数图象大致是12.根据图5-1所示的程序,得到了y 与x 的函数图象,如图5-2.若点M 是y 轴正半轴上任意一点,过点M 作PQ ∥x 轴交图象于点P ,Q ,连接OP ,OQ .则以下结论: ①x <0时,y =2x②△OPQ 的面积为定值. ③x >0时,y 随x 的增大而增大 ④MQ =2PM⑤∠POQ 可以等于90°. 其中正确的是:A .①②④B .②④⑤C .③④⑤D .②③⑤2011年河北省初中毕业生升学文化课考试数 学 试 卷卷II (非选择题,共96分)注意事项:1.答卷II 前,将密封线左侧的项目填写清楚.2.答卷II 时,将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.二、填空题(本大题共6个小题,每小题3分,共18分.把答案写在题中横线上) 13.35,π,–4,0这四个数中,最大的数是_________________14.如图6,已知菱形ABCD ,其顶点A ,B 在数轴上对应的数分别为–4和1,则BC =_____________ 15.若||x –3+||y +2=0,则x +y 的值为16.如图7,点O 为优级弧ACB ⌒所在圆的圆心,∠AOC =108°,点D 在AB 延长线上,BD =BC ,则∠D = __________17. 如图8-1,两个等边△ABD ,△CBD 的边长均为1,将△ABD 沿AC 方向向右平移到△A ´B ´D ´的位置,得到图8-2,则阴影部分的周长为___________.18.如图9,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第10次“移位”后,则他所处顶点的编号是三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤) 19.(本小题满分8分)已知⎩⎨⎧x =2y =3是关于x ,y 的二元一次方程3x =y +a 的解.求(a +1)(a –1)+7的值20.(本小题满分8分)如图10,在6⨯8网格图中,每个小正方形的边长均为1,点O 和△ABC 的顶点均为小正方形的顶点.(1)以O 为位似中心,在网格图中....作△A ´B ´C ´,使△A ´B ´C ´和△ABC 位似,且位似比为1:2;(2)连接(1)中的AA ´,求四边形AA ´C ´C 的周长.(结果保留根号).如图11,一转盘被等分成三个扇形,上面分别标有–1,1,2中的一个数,指针位置固定,转动转盘后任其自由停止,这时,某个扇形会恰好停在指针所指的位置,并相应得到这个扇形上的数(若指针恰好指在等分线上,当做指向右边的扇形).(1)若小静转动转盘一次,求得到负数的概率;(2)小宇和小静分别转动转盘一次,若两人得到的数相同,则称两“不谋而合”.用列表法(或画树状图)求两人“不谋而合”的概率.22.(本小题满分8分)甲、乙两人准备整理一批新到的实验器材.若甲单独整理需要40分钟完工;若甲、乙共同事理20分钟后,乙需再单独整理20分钟才能完工.(1)问乙单独整理多少分钟完工?(2)若乙因工作需要,他整理时间不超过30分钟,则甲至少整理多少分钟才能完工?23.(本小题满分9分)如图12,四边形ABCD是正方形,点E,K分别在BC,AB上,点G在BA的延长线上,且CE=BK=A G.(1)求证:①DE=DG;②DE⊥DG(2)尺规作图:以线段DE,DG为边作出正方形DEFG(要求:只保留作图痕迹,不写作法和证明);(3)连接(2)中KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想;(4)当CECB=1n时,请直接写出S正方形ABCDS正方形DEFG的值.24.(本小题满分9分)已知A 、B 两地的路程为240千米.某经销商每天都要用汽车或火车将x 吨保鲜品一次性由A 地运往B 地.受各各因素限制,下一周只采用汽车和火车中的一种进行运输,且须提前预订.现有货运收费项目及收费标准表、行驶路程s (千米)与行驶时间t (时)的函数图象(如图13-1)、上周货运量折线统计图(如图13-2)等信息如下: 货运收费项目及收费标准表(1)汽车的速度为___________千米/时, 火车的速度为___________千米/时; (2)设每天..用汽车和火车运输的总费用分别为 y 汽 (元)和y 火 (元),分别求y汽、y 火与x的函数关系式(不必写出x 的取值范围),及x 为何值时y 汽 >y 火;(总费用=运输费+冷藏费+固定费用) (3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前为下周预定哪种运输工具,才能使每天的运输总费用较省?25.(本小题满分10分)如图14-1至14-4中,两平行线AB,CD间的距离均为6,点M为AB上一定点.思考如图14-1,圆心为O的半圆形纸片在AB,CD之间..(包括AB,CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α.当α=_____度时,点P到CD的距离最小,最小值为_______探究一在图14-1的基础上,以点M为旋转中心,在AB,CD之间顺时针旋转该半圆形纸片,直到不能再转动为止,如图14-2,得到最大旋转角∠BMO=_____度,此时点N到CD的距离是_______.探究二将图14-1中的扇形纸片NOP按下面对α的要求剪掉,使户型纸片MOP绕点M在AB,CD之间..顺时外旋转.(1)如图14-3,当α=60°时,求在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值(2)如图14-4,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请确定α的取值范围.(参考数据:sin49°=34,cos41°=34,tan37°=34)26.(本小题满分12分)如图15,在平面直角坐标系中,点P 从原点O 出发,沿x 轴向右以每秒1个单位长的速度运动t 秒(t >0),抛物线y =x 2+bx +c 经过点O 和点P .已知矩形ABCD 的三个顶点为A (1,0),B (1,–5),D (4,0).(1)求c ,b (用含t 的代数式表示);(2)当4<t <5时,设抛物线分别与线段AB ,CD 交于点M ,N .①在点P 的运动过程中,你认为∠AMP 的大小是否会变化?若变化,说明理由;若不变,求出∠AMP 的值;②求△MPN 的面积S 与t 的函数关系式,并求t 为何值时,S =218(3)在矩形ABCD 的内部(不含边界),把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分,请直接..写出t 的取值范围.。
2011河北中考数学试卷及答案解析
点评:本题考查了画位似图形.画位似图形的一般步骤为:确定位似中心,分别连接并延长位似中心和能代 表原图的关键点;根据相似比,确定能代表所作的为似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.同
《电力拖动控制线路与技能训练》试卷()
、(河北)甲、乙、丙三个旅行团的游客人数都相等,且毎团游客的平均年龄都是岁,这三个团
游客年龄的方差分别是甲,乙,丙,导游小王最喜欢带游客年龄相近的团队,若
在三个团中选择一个,则他应选( )
《电力拖动控制线路与技能训练》试卷()
、甲团 、乙团 、丙团 、甲或乙团 考点:方差。
专题:应用题。
分析:由甲,乙,丙,得到丙的方差最小,根据方差的意义得到丙旅行团的游 客年龄的波动最小.
设(,),(,), 则﹣,,
《电力拖动控制线路与技能训练》试卷()
的面积是 (﹣) ,正确; 、>时,随的增大而减小,错误; 、﹣,,正确; 、因为也行,正确; 正确的有, 故选.
点评:本题主要考查对反比例函数的性质,反比例函数图象上点的坐标特征,三角形的面积等知识点的理解和掌 握,能根据这些性质进行说理是解此题的关键. 二、填空题(共小题,每小题分,满分分)
《电力拖动控制线路与技能训练》试卷()
、第三象限 、第四象限 考点:一次函数的性质。 专题:存在型;数形结合。
分析:先判断出一次函数中的符号,再根据一次函数的性质进行解答即可. 解答:解:一次函数中>,>, 此函数经过一、二、三象限, 故选. 点评:本题考查的是一次函数的性质,即一次函数()中,当>时,函数图象经过一、 三象限,当>时,函数图象与轴正半轴相交. 、(河北)将图围成图的正方体,则图中的红心 标志所在的正方形是正方体中的( )
2011年河北中考数学试题及答案
数学试卷
第 3 页(共 14 页)
三、解答题(本大题共 8 个小题,共 72 分.解答应写出文字说明、证明过程或演算步骤) 得 分 评卷人 19. (本小题满分 8 分)
x=2 已知 是关于 x,y 的二元一次方程 3x=y+a 的解. y= 3
求(a+1) (a–1)+7 的值
得 分
评卷人 20. (本小题满分 8 分)
5.一次函数 y=6x+1 的图象不经过 ... A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.将图 2-1 围成图 2–2 的正方体,则图 2-1 中 的红心“ ”标志所在的正方形的是正方形 是下文体中的 A.面 CDHE C.面 ABFG B.面 BCEF D.面 ADHG
7.甲、乙、丙三个旅行团的游客人数相等,且每团游客的平均年龄都是 32 岁,这三个团
11.如图 4,在矩形中截取两个相同的圆作为圆柱的上、 下底面,剩余的矩形作为圆柱的侧面,刚好能组合成 圆柱.设矩形的长和宽分别为 y 和 x,则 y 与 x 的函 数图象大致是
12.根据图 5-1 所示的程序,得到了 y 与 x 的函数图象,如图 5-2.若点 M 是 y 轴正半轴上 任意一点, 过点 M 作 PQ∥x 轴交图象于点 P, Q,连接 OP,OQ.则以下结论: ①x<0 时,y=x
数学试卷
第 8 页(共 14 页)
得 分
评卷人 25. (本小题满分 10 分)
如图 14-1 至 14-4 中,两平行线 AB,CD 间的距离均为 6,点 M 为 AB 上一定点. 思考 如图 14-1,圆心为 O 的半圆形纸片在 AB,CD 之间 (包括 AB,CD) ,其直径 MN 在 AB 上,MN=8, .. 点 P 为半圆上一点,设∠MOP=α. 当 α=_____度时,点 P 到 CD 的距离最小,最小 值为_______ 探究一 在图 14-1 的基础上, 以点 M 为旋转中心, 在 AB, CD 之间顺时针旋转该半圆形纸片,直到不能再转动 为止,如图 14-2,得到最大旋转角∠BMO=_____度, 此时点 N 到 CD 的距离是_______. 探究二 将图 14-1 中的扇形纸片 NOP 按下面对 α 的要求 剪掉,使户型纸片 MOP 绕点 M 在 AB,CD 之间 顺时 .. 外旋转. (1)如图 14-3,当 α=60° 时,求在旋转过程中, 点 P 到 CD 的最小距离, 并请指出旋转角∠ BMO 的最大值 (2)如图 14-4,在扇形纸片 MOP 旋转过程中, 要保证点 P 能落在直线 CD 上, 请确定 α 的 取值范围. (参考数据:sin49° =4,cos41° =4,tan37° =4)
2011年河北省中考数学试卷及答案解析
2011年河北省中考数学试卷及答案解析一、选择题(共12小题,1-6小题每小题2分,7-12小题,每题3分,满分30分)1、(2011•河北)计算30的结果是()A、3B、30C、1D、0考点:零指数幂。
专题:计算题。
分析:根据零指数幂:a0=1(a≠0)计算即可.解答:解:30=1,故选C.点评:本题主要考查了零指数幂,任何非0数的0次幂等于1.2、(2011•河北)如图,∠1+∠2等于()A、60°B、90°C、110°D、180°考点:余角和补角。
专题:计算题。
分析:根据平角的定义得到∠1+90°+∠2=180°,即由∠1+∠2=90°.解答:解:∵∠1+90°+∠2=180°,∴∠1+∠2=90°.故选B.点评:本题考查了平角的定义:180°的角叫平角.3、(2011•河北)下列分解因式正确的是()A、﹣a+a3=﹣a(1+a2)B、2a﹣4b+2=2(a﹣2b)C、a2﹣4=(a﹣2)2D、a2﹣2a+1=(a﹣1)2考点:提公因式法与公式法的综合运用。
专题:因式分解。
分析:根据提公因式法,平方差公式,完全平方公式求解即可求得答案.解答:解:A、﹣a+a3=﹣a(1﹣a2)=﹣a(1+a)(1﹣a),故本选项错误;B、2a﹣4b+2=2(a﹣2b+1),故本选项错误;C、a2﹣4=(a﹣2)(a+2),故本选项错误;D、a2﹣2a+1=(a﹣1)2,故本选项正确.故选D.点评:本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,理解因式分解与整式的乘法是互逆运算是解题的关键.4、(2011•河北)下列运算中,正确的是()A、2x﹣x=1B、x+x4=x5C、(﹣2x)3=﹣6x3D、x2y÷y=x2考点:整式的除法;合并同类项;幂的乘方与积的乘方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年石家庄市初中毕业班知识能力测试
数学试题参考答案
一、选择题
题 号 1 2 3 4 5 6 7 8 9 10 11 12 答 案 B
C
B
A
D
C
B
D
C
C
D
A
二、填空题
13.)5)(5(-+b b a ;14.⎩⎨⎧==2
,1y x ;15.1-≠x ;16.65°;17.81;18.21
2+.
三、解答题 19.解:1
)111(2+÷-+
a a
a =a
a a a a 1)1)(1(2+⨯-+……………………………………………………………3分 =
1
-a a
.……………………………………………………………………………6分 当a =-2时, 原式=
3
2
. ……………………………………………………………………………8分 20. 解:(1)50t , 225t .……………………………………………………………4分
(2)过点C 作CD ⊥AB 于点D ,
∵在R t △ACD 中,AC =225 t ,∠DAC =45°,
∴CD =25 t ,…………………………………………………………5分 又∵在R t △BCD 中,CD =25 t ,BC =50 t ,
∴sin ∠B =
BC CD =2
1
, ∴∠B =30°,……………………………………………………7分 ∴巡逻艇是沿北偏东30°方向追击走私快艇.…………………8分
21. 解:(1) 30÷15%=200,∴同学们一共随机调查了200户.……………………2分
(2) 如图2、图3所示; ………………………………………………………6分
C
图2
15% 10%
D
B 40%
35%
O
40 户数 80 30 A
C B
家长意见
D 20 10
50 60 70 图3
70
20
A
A B
北
C
D
图1
(3)A . ……………………………………………………………………………………7分 (4) 2000×(35%+40%)=1500(户).
∴该社区大约有1500户家庭反对孩子上网.…………………………………………9分 22. 解:(1)∵反比例函数x
k
y =
的图象过C (2,1), ∴2
1k
=
,解得:2=k , ∴反比例函数的表达式为2
y x
=;……………………2分
又∵一次函数b kx y +=的图象过C (2,1),且2=k , ∴b +⨯=221,解得:3-=b ,
∴一次函数的表达式为32-=x y ;…………………………………………4分 (2) 如图4,过点C 作CD ⊥y 轴于点D ,……………………………………………5分
∴CD =2, 又∵一次函数表达式为32-=x y , ∴0=x 时, 3-=y ;∴OB =3,
∴S △OBC =
2
1
×OB ×CD =3.………………………………………………………8分 (3)P (
2
1
,4). ………………………………………………………………………9分 23.操作探究:(1)图略; ……………………………………………………………………2分
(2)①
22; ② 2
5
;③2. ……………………………………………5分
联想拓展:(1)3
40
,………………………………………………………………………8分
(2)13,图略. (10)
分
24.(1)证明:∵△ABC ∽△EDC ,∴
AC BC EC CD =,∴CE
CD
AC BC = A
图4
O
y
B
C x
D
又∵
1BC
AC
=,∴BC =AC , CD =CE , 又∵AC ⊥BE ,∴∠ACB =∠ECD =90︒,∴△BCD ≌△ACE ,
∴ BD=AE . (3)
分
(2)BD=kAE ,BD ⊥AE . …………………………………………………………………4分
证明:如图5,延长BD 交AE 于点F , ∵△ABC ∽△EDC ,∴
AC BC EC CD =, ∴CE
CD
AC BC = 又∵AC ⊥BE ,∴∠ACB =∠ECD =90︒,∴△BCD ∽△ACE .
∴
AC BC
AE BD =, ∠BDC=∠AEC , ∵k AC BC =,∴k AE
BD
=,∴BD=kAE .……………7分 ∵∠BCD =90︒ ,∴∠CBD +∠CDB =90︒, ∴∠CBD +∠AEC =90︒, ∴
BD
⊥
AE . …………………………………………………………………………………9分
(3)
BD=kAE .……………………………………………………………………………………10分 25.解:
(1) 法一:设购买纪念册m 本.
则18-0.2(m -6)≥13,解得:m ≤31, ∴至少买31本才能用最低价
购
买.…………………………………………………………3分
法二:(18-13)÷0.2+6=31.
法三:设购买m 本时可恰得到最低价.则18-0.2(m -6)=13,解得:m =31. ∴至少买31本才能用最低价购买.
(2) ①当x ≤6时,
x
x W 8)1018(=-=.(x 为整
数) …………………………………………………………4分
②当6<x ≤31时,
[]10)6(2.018---=x x W
=)2.02.9(x x - =
x
x 2.92.02+-.( x 为整
C B
A
D
E
图5
F
数) ……………………………………………………………7分
③当x >31时,
x
x W 3)1013(=-=.(x 为整
数) …………………………………………………………8分 (3) 由②中x x W 2.92.02
+-=,
∵a =-0.2<0, 232=-
a
b
,∴当3123≤≤x 时,W 随x 的增大而减小. ∴商店一次售出30本纪念册所获的利润,比一次售出26本纪念册所获的利润低.…………10分
又∵当x =23时,纪念册的售价为18-0.2×(23-6)=14.6(元), ∴商店把促销方案中:“纪念册的最低售价不低于13元”改为“纪念册的最低售价不低于14.6元”,就可以使卖的纪念册越多商店所获的利润越大. ……………………………………………12分 26.解: (1)7和4; ………………………………………………………………………………………2分 (2)当t =2.5秒时,△EBF 的面积为y =
7)(2
1
=⋅-⋅CD CF BC ,
即:7)25(21=⋅-CD BC . 当t =4秒时,△EBF 的面积为y =4)(2
1
=⋅-⋅CD CF BC ,即: ()4421=⋅-CD BC .
∴4,
6.
CD BC =⎧⎨
=⎩…………………………………………………………………………………
6分
(3)法一:
∵BC =6,点F 的速度是每秒1个单位, ∴OP =6,
∴点E 从D 运动到C 用时为6-4=2秒, 又∵CD = 4,
∴点E 的运动速度为每秒2 个单位.………………………………………………………9分
法二:如图6,过点A 作AG ⊥BC 于点G , ∵AB =2.5k ,AD =1.5k ,∴BG =6-1.5 k ,
在Rt ABG ∆中,42+(6-1.5k )
2 =(2.5k )2. ∴ k 1=2,k 2 =-6.5(不合题意舍去),
即点E 的运动速度为每秒2 个单位. (4)∵k =2,∴AD =3,AB =5,∴S 梯形ABCD =18,
31
S 梯形ABCD =6. 由题意可知运动过程中有两个时刻△EBF 的面积等于6.
①当E 在AB 上时,过点E 作EH ⊥BC 于点H , △EBH ∽△ABG ,
C
D A B
E
F H G
图6
图6
∴BE EH AB AG
=,
∴EH=8
5
t,
∴18
(6)6
25
t t
⨯⨯-=,解得
2
6
6±
=
t,∵t≤2.5.
∴
26
6-
= t.…………………………………………………………………………11分
②当E在AD上时,1
4(6)6
2
t
⨯⨯-=,解得t=3.
综上所述,当
26
6-
=
t或3
t=秒时,△EBF与梯形ABCD的面积之比为1:3.…12分。
