2017-2018学年 押高考数学第18题-试题君之每日一题君2018年高考数学(理)四轮复习 Word版含解析
答案与解析:2018高考数学押题原创卷03(理)
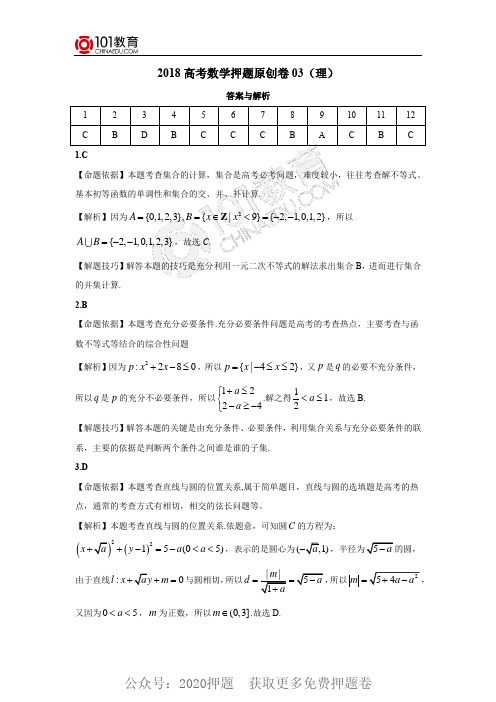
高为 2,所以该几何体的表面积为 1 1 2 21 2 1 1 2 1 2 2 6 3 .
22
2
2
2
故选 C.
【解题技巧】解答本题的技巧是根据三视图确定几何体的面以及各个面的形状,再求表面积.
8.B 【命题依据】本题考查基本不等式,基本不等式是高考热频考点,尤其是基本不等式的变形
5.C 【命题依据】本题考查简单的线性规划,简单的线性规划是高考必考问题,难度中等,理科 往往考查的是线性目标函数含参数,或者约束条件含参数的求最值问题.
【解析】如图所示,可行域大致入下图,可知 z 2x y+1在 (2 a, a) 取得最大值,所以 4 3a 1 2,所以 a 1.故选 C.
x1
x2
=
1
5 k
2
0 ,所以只需要1 k 2
0 ,即
k (1,1) .
x1
x2
4k 1 k2
,
x1x2
又因为 g(x) x3 3x 2 e ,g(x) 3x2 3 ,所以 g(x) x3 3x 2 e e 在 x [1,1]
公众号:2020押题 获取更多免费押题卷
单调递减, x [1, 2]上单调递增,所以 g(x)min g(1) e , 所以 0 1 1 1 ,解之得 a 1 .故选 C.
向前推导,找到输出值的可能取值.
10.C
【命题依据】本题考查几何体的外接球问题,几何体的外接球,或内切球问题是全国卷的一
大特色,本题主要围绕外接球或内切球的多种可能性,求表面积与体积.
【解析】设外接球的半径为 r ,当球心在四棱锥内部时,可得四棱锥的高为 3r ,四棱锥的 2
底面边长 a 满足 ( 2a )2 r2 ( r )2 3r2 ,所以 a 6r ,所以斜高为 42r ,所以四棱
2018年6月1日 押高考数学第21题-试题君之每日一题君20

6月1日 押高考数学第21题1.已知函数2()e x f x ax x =+-. (1)当0≥a 时,求函数)(x f 的极小值;(2)当0<a 时,若函数)(x f 在区间[1,)+∞上是增函数,求a 的取值范围.2.设函数2()(()e )x f x x ax a a -=+-⋅∈R .(1)当0a =时,求曲线()y f x =在点(1,(1))f --处的切线方程;(2)设2()1g x x x =--,若对任意的[0,2]t ∈,存在[0,2]s ∈使得()()f s g t ≥成立,求a 的取值范围.(2) 函数)(x f 在区间[1,)+∞上是增函数,∴()e 210x f x ax '=+-≥在[1,)+∞上恒成立,1e 2x a x-∴≥在[1,)+∞上恒成立,设1e ()(1)x g x x x -=≥,则2e e 1()(1)x x x g x x x-+-'=≥, 设()e e 1(1)x x h x x x =-+-≥,则()e e e e 0x x x x h x x x '=--+=-<,)(x h ∴在区间[1,)+∞上是减函数,()(1)e e 110h x h ∴≤=-+-=-<,0)(<'∴x g ,∴)(x g 在区间[1,)+∞上是减函数,()1e g x ∴≤-,21e a ∴≥-,又0<a ,1e 02a -∴≤<, 所以a 的取值范围是1e [,0)2-. 2.【解析】(1)当a =0时,因为,所以,, 又因为, 所以曲线在点(1,)处的切线方程为.①当0a -≤,即0a ≥时,在上恒成立,在上为单调递增函数, 则的最大值为, 由,得a .②当02a <-<,即20a -<<时, 当时,,为单调递减函数,当时,,为单调递增函数. 所以的最大值为或,由1a -≥,得1a ≤-;由,得a .又因为20a -<<,所以21a -<≤-.今日收获如何?总结一下吧!。
2018年全国高考数学试题18大专题汇总考前复习资料

2018年全国高考数学试题18大专题汇总考前复习资料(01集合)一、选择题:1.(2018年北京文)已知集合{}2A x x =<,{}–2,0,1,2B =,则A B =I( )A.{}0,1B.{}–1,0,1C.{}–2,0,1,2D.{}–1,0,1,21.【参考答案】A 【试题解析】2x <Q ,22x ∴-<<,因此{}(){}2,0,1,22,20,1A B =--=I I ,故选A.2.(2018年北京理)已知集合A ={x ||x |<2},B ={–2,0,1,2},则A I B =( ) (A){0,1} (B){–1,0,1} (C){–2,0,1,2} (D){–1,0,1,2} 2.【参考答案】A 【试题解析】2x <Q ,22x ∴-<<,因此{}(){}2,0,1,22,20,1A B =--=I I ,故选A.3.(2018浙江)已知全集U ={1,2,3,4,5},A ={1,3},则=U A ð( ) A.∅ B.{1,3} C.{2,4,5} D.{1,2,3,4,5} 3.答案:C【试题解答】:由题意知U C A ={2,4,5}.4.(2018天津文)设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-≤<R ,则()A B C =U I ( )(A){1,1}- (B){0,1} (C){1,0,1}- (D){2,3,4}4.【参考答案】C【试题解析】由并集的定义可得{}1,0,1,2,3,4A B =-U , 结合交集的定义可知:(){}1,0,1A B C =-U I .故选C. 5 (2018天津理)设全集为R ,集合{02}A x x =<<,{1}B x x =≥,则()=R I A B ð ( ) (A){01}x x <≤ (B){01}x x << (C){12}x x ≤< (D){02}x x <<5.【参考答案】B 【试题解析】由题意可得{}1B x x =<R ð,结合交集的定义可得(){}01A B x =<<R I ð,故选B.6.(2018全国新课标Ⅰ文)已知集合{}02A =,,{}21012B =--,,,,,则A B =I ( )A.{}02,B.{}12, C.{}0D.{}21012--,,,,6.答案:A【试题解答】:{0,2}A B ⋂=,故选A.7.(2018全国新课标Ⅰ理)已知集合{}220A x x x =-->,则A =Rð( )A.{}12x x -<<B.{}12x x -≤≤C.}{}{|1|2x x x x <->UD.}{}{|1|2x x x x ≤-≥U7. 答案:B【试题解答】:{|2A x x =>或1}x <-,则{|12}R C A x x =-≤≤.8.(2018全国新课标Ⅱ文)已知集合{}1,3,5,7A =,{}2,3,4,5B =,则A B =I ( ) A.{}3 B.{}5 C.{}3,5 D.{}1,2,3,4,5,78.【参考答案】C 【试题解析】{}1,3,5,7A =Q ,{}2,3,4,5B =,{}3,5A B ∴=I ,故选C.9.(2018全国新课标Ⅱ理)已知集合(){}223A x y xy x y =+∈∈Z Z,≤,,,则A 中元素的个数为( ) A.9 B.8 C.5 D.4 9.【参考答案】A【试题解析】223x y +≤Q ,23x ∴≤,x ∈Z Q ,1x ∴=-,0,1,当1x =-时,1y =-,0,1;当0x =时,1y =-,0,1; 当1x =-时,1y =-,0,1;所以共有9个,故选A. 10.(2018全国新课标Ⅲ文、理)已知集合{}|10A x x =-≥,{}012B =,,,则A B =I ( )A.{}0B.{}1C.{}12,D.{}012,,10.答案:C【试题解答】:∵{|10}{|1}A x x x x =-≥=≥,{0,1,2}B =,∴{1,2}A B =I .故选C. 二、填空题:1.(2018江苏)已知集合{0,1,2,8}A =,{1,1,6,8}B =-,那么A B =I ▲ .1.【参考答案】{}1,8【试题解析】由题设和交集的定义可知,{}1,8A B =I .(02常用逻辑用语) 一.选择题:1.(2018年北京文)设a ,b ,c ,d 是非零实数,则“ad bc =”是“a ,b ,c ,d 成等比数列”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件 1.【参考答案】B【试题解析】当4a =,1b =,1c =,14d =时,a ,b ,c ,d 不成等比数列,所以不是充分条件;当a ,b ,c ,d 成等比数列时,则ad bc =,所以是必要条件.综上所述,“ad bc =”是“a ,b ,c ,d 成等比数列”的必要不充分条件.故选B.2.(2018年北京理)设a ,b 均为单位向量,则“33-=+a b a b”是“a ⊥b ”的( )(A)充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件 (D)既不充分也不必要条件 2.【参考答案】C 【试题解析】2222223333699+6a b a b a b a b a a b b a a b b -=+⇔-=+⇔-⋅+=⋅+,因为a ,b 均为单位向量,所以2222699+6=0a a b b a a b b a b a b -⋅+=⋅+⇔⋅⇔⊥,即“33a b a b-=+”是“a b ⊥”的充分必要条件.故选C.3.(2018浙江)已知平面α,直线m ,n 满足m ⊄α,n ⊂α,则“m ∥n ”是“m ∥α”的( ) A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件 3..答案:A【试题解答】:若“//m n ”,平面外一条直线与平面内一条直线平行,可得线面平行,所以“//m α”;当“//m α”时,m 不一定与n 平行,所以“//m n ”是“//m α”的充分不必要条件.4. (2018上海)已知a R ∈,则“1a﹥”是“1a 1﹤”的( )(A)充分非必要条件 (B)必要非充分条件 (C)充要条件 (D)既非充分又非必要条件5.(2018天津文)设x ∈R ,则“38x >”是“||2x >” 的( )(A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件 (D)既不充分也不必要条件 5.【参考答案】A【试题解析】求解不等式38x >可得2x >,求解绝对值不等式2x >可得2x >或2x <-, 据此可知:“38x >”是“2x >” 的充分而不必要条件.故选A.6.(2018天津理)设x ∈R ,则“11||22x -<”是“31x <”的 ( ) (A)充分而不必要条件 (B)必要而不充分条件(C)充要条件 (D)既不充分也不必要条件6.【参考答案】A【试题解析】绝对值不等式111110122222x x x -<⇔-<-<⇔<<,由311x x <⇔<,据此可知1122x -<是31x <的充分而不必要条件.故选A.二.填空题:(03函数的性质及其应用) 一、选择题1. (2018上海)设D 是含数1的有限实数集,f x ()是定义在D 上的函数,若f x ()的图像绕原点逆时针旋转π6后与原图像重合,则在以下各项中,1f()的可能取值只能是( )(A)3 (B)3(C)3(D)02.(2018浙江)函数y=||2x sin2x的图象可能是( )A. B. C. D.2.答案:D【试题解答】:令||()2sin2xy f x x==,||||()2sin(2)2sin2()x xf x x x f x--=-=-=-,所以()f x 为奇函数①;当(0,)x pÎ时,||20x>,sin2x可正可负,所以()f x可正可负②.由①②可知,选D.3.(2018天津文)已知13313711log,(),log245a b c===,则,,a b c的大小关系为( )(A)a b c>> (B)b a c>> (C)c b a>> (D)c a b>>3.【参考答案】D【试题解析】由题意可知:3337log3log log92<<,即12a<<,1103111444⎛⎫⎛⎫⎛⎫<<<⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,即01b<<,133317log log5log52=>,即c a>,综上可得:c a b>>.故选D.4.(2018天津理)已知2log e =a ,ln 2b =,121log 3c =,则a ,b ,c 的大小关系为 ( )(A) a b c >> (B) b a c >> (C) c b a >> (D) c a b >>4.【参考答案】D【试题解析】由题意结合对数函数的性质可知:2log e 1a =>,()21ln 20,1log e b ==∈,12221log log 3o 3e l g c ==>,据此可得c a b >>,故选D.5.(2018全国新课标Ⅰ文)设函数()201 0x x f x x -⎧=⎨>⎩,≤,,则满足()()12f x f x +<的x 的取值范围是( ) A.(]1-∞-, B.()0+∞, C.()10-, D.()0-∞,5.答案:D 【试题解答】:取12x =-,则化为1()(1)2f f <-,满足,排除,A B ;取1x =-,则化为(0)(2)f f <-,满足,排除C ,故选D .6.(2018全国新课标Ⅰ理)已知函数e 0()ln 0x xf x x x ⎧≤=⎨>⎩,,,,()()g x f x x a =++.若g (x )存在2个零点,则a 的取值范围是( )A.[–1,0)B.[0,+∞)C.[–1,+∞)D.[1,+∞) 6. 答案:C【试题解答】:∵()()g x f x x a =++存在2个零点,即()y f x =与y x a =--有两个交点,)(x f 的图象如下:要使得y x a =--与)(x f 有两个交点,则有1a -≤即1a ≥-,∴选C.7.(2018全国新课标Ⅱ文、理)函数()2e e x xf x x --=的图像大致为( )7.【参考答案】B【试题解析】0x ≠Q ,()()2e e x xf x f x x ---==-,()f x ∴为奇函数,舍去A,()11e e 0f -=->Q ,∴舍去D ;()()()()()243e e e e 22e 2e xx x x x xx xx x f x x x ---+---++='=Q ,2x ∴>,()0f x '>,所以舍去C ;因此选B.8.(2018全国新课标Ⅲ文)下列函数中,其图像与函数ln y x =的图像关于直线1x =对称的是( )A.ln(1)y x =-B.ln(2)y x =-C.ln(1)y x =+D.ln(2)y x =+8.答案:B【试题解答】:()f x 关于1x =对称,则()(2)ln(2)f x f x x =-=-.故选B.9.(2018全国新课标Ⅲ文、理)函数422y x x =-++的图像大致为( )9.答案:D【试题解答】:当0x =时,2y =,可以排除A 、B 选项;又因为322424(22y x x x x x '=-+=-+-,则()0f x '>的解集为22(,(0,22-∞-U ,()f x 单调递增区间为2(,)2-∞-,2(0,2;()0f x '<的解集为22(,)22-+∞U ,()f x 单调递减区间为2(,0)2-,2,)2+∞.结合图象,可知D 选项正确.10.(2018全国新课标Ⅱ文、理)已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)f f f ++(50)f ++=L ( ) A.50- B.0 C.2 D.5010.【参考答案】C【试题解析】因为()f x 是定义域为(),-∞+∞的奇函数,且()()11f x f x -=+,所以()()11f x f x +=--,()()()311f x f x f x ∴+=-+=-,4T ∴=,因此()()()()()()()()()()1235012123412f f f f f f f f f f ++++=+++++⎡⎤⎣⎦L ,因为()()31f f =-,()()42f f =-,所以()()()()12340f f f f +++=, ()()()222f f f =-=-Q ,()20f ∴=,从而()()()()()1235012f f f f f ++++==L ,选C.11.(2018全国新课标Ⅲ理)设0.2log 0.3a =,2log 0.3b =,则( )A.0a b ab +<<B.0ab a b <+<C.0a b ab +<<D.0ab a b <<+11.答案:B 【试题解答】:∵0.2log 0.3a =,2log 0.3b =,∴0.31log 0.2a =,0.31log 2b =,∴0.311log 0.4a b +=,∴1101a b <+<即01a bab +<<,又∵0a >,0b <,∴0ab a b <+<,故选B.二、填空:1.(2018年北京理)能说明“若f (x )>f (0)对任意的x ∈(0,2]都成立,则f (x )在[0,2]上是增函数”为假命题的一个函数是__________. 1.【参考答案】sin y x =(答案不唯一)【试题解析】令()(]00402x f x x x =⎧⎪=⎨-∈⎪⎩,,,,则()()0f x f >对任意的(]0,2x ∈都成立, 但()f x 在[]0,2上不是增函数.又如,令()sin f x x =,则()00f =,()()0f x f >对任意的(]0,2x ∈都成立,但()f x 在[]0,2上不是增函数.2. (2018上海)设常数a R ∈,函数f x x a =+()㏒₂(),若f x ()的反函数的图像经过点31(,),则a= 。
2018年5月20日 押高考数学第11题-试题君之每日一题君2

5月20日 押高考数学第11题
1.过抛物线2:4C y x =的焦点F ,C 于点M (M 在x 轴上方),l 为C 的准线,点N 在
l 上且MN l ⊥,则M 到直线NF 的距离为
A B .
C .
D .
2.已知双曲线的右焦点为,其中一条渐近线与圆交于两点,
为锐角三角形,则双曲线的离心率的取值范围是 A . B .
C .
D .
3.已知椭圆:的右焦点为,为坐标原点,为轴上一点,点是直线与椭圆的一
个交点,且
,则椭圆的离心率为
A .
B .
C .
D .
2.【答案】D
【解析】双曲线
的右焦点为,一条渐近线方程为,
圆的圆心坐标为,半径为,
由渐近线与圆交于两点,为锐角三角形,可得:可得
又可得可得:,由可得
所以双曲线的离心率的取值范围是.
故选D . 3.【答案】A
【解析】设左焦点为因为
,所以, 设
,如图所示,由题意可得
,所以
122|||1
|||3
||AF OM AF OF ==, 则,解得,
所以,解得,故选A .
今日收获如何?
总结一下吧!。
2018年5月31日 押高考数学第20题-每日一题2018年高考数学(理)四轮复习

押高考数学第20题1.在直角坐标系xOy 中,已知一动圆经过点(2,0)且在y 轴上截得的弦长为4,设动圆圆心的轨迹为曲线C .(1)求曲线C 的方程;(2)过点(1,0)作互相垂直的两条直线1l ,2l ,1l 与曲线C 交于A ,B 两点,2l 与曲线C 交于E ,F 两点,线段AB ,EF 的中点分别为M ,N ,求证:直线MN 过定点P ,并求出定点P 的坐标.2.已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ,B A ,是椭圆C 上两点,O 是坐标原点,且2AB OB =,4||||11=+BF AF ,离心率为21. (1)求椭圆C 的方程;学-(2)过1F 作两条相互垂直的直线21,l l 分别交椭圆于P Q 、和M N 、,求PQ MN +的取值范围.1.【解析】(1)设圆心(,)C x y ,依题意有2224(2)x x y +=-+,即得24y x =,∴曲线C 的方程为24y x =.(2)易知直线1l ,2l 的斜率存在且不为0,设直线1l 的斜率为k ,11(,)A x y ,22(,)B x y ,则直线1l :(1)y k x =-,1212(,)22x x y y M ++, 由24(1)y x y k x ⎧=⎨=-⎩得2222(24)0k x k x k -++=,2242(24)416160k k k ∆=+-=+>,12242x x k +=+,12124(2)y y k x x k +=+-=,∴222(1,)M k k+. 同理得2(12,2)N k k +-.当1k =或1k =-时,直线MN 的方程为3x =;当1k ≠且1k ≠-时,直线MN 的斜率为21k k -, ∴直线MN 的方程为222(12)1k y k x k k+=---,即2(1)(3)0k y x k -+-=, ∴直线MN 过定点P ,其坐标为(3,0).学-综上所述,直线MN 过定点P ,其坐标为(3,0).(2)①当直线MN PQ ,有一条斜率不存在时,437PQ MN +=+=.②当PQ 斜率存在且不为0时,设方程为(1)y k x =+,1122(,),(,)P x y Q x y . 联立方程,得⎪⎩⎪⎨⎧=++=134)1(22y x x k y ,消去y 整理得01248)43(2222=-+++k x k x k . 2221222143124,438k k x x k k x x +-=+-=+∴. 221212(1)[()4]PQ k x x x x ∴=++-2(1)k +22222431244)438(k k k k +-⨯-+-=2243)1(12k k ++. 把1k-代入上式,得2234)1(12k k MN ++=, 222284(1)(43)(34)k PQ MN k k +∴+=++, 设1),0(12>≠+=t k k t ,28411+12PQ MN t t∴+=-+,1t >, 设211()12g t t t =-++=449)211(2+--t ,1t >, 令t m 1=,则)1,0(1∈=t m ,)(m g =449)21(2+--m (10<<m ), ∴449)()(12≤=<t g m g ,∴7)(84748<≤t g , 48[7)7PQ MN ∴+∈,.综上,PQ MN 的取值范围是[7,748]. 今日收获如何?总结一下吧!。
2018年5月4日 选修部分-试题君之每日一题君2018年高考

课时达标第2讲[解密考纲]考查命题及其相互关系、充分条件及必要条件的定义,与高中所学知识交汇考查,常以选择题、填空题的形式呈现,考卷中常排在靠前的位置.一、选择题1.(2016·上海卷)设a∈R,则“a>1”是“a2>1”的(A)A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件解析当a>1时,a2>1;当a2>1时,a>1或a<-1.故选A.2.原命题为“△ABC中,若cos A<0,则△ABC为钝角三角形”,关于其逆命题、否命题、逆否命题真假性的判断依次如下,正确的是(B)A.真、真、真B.假、假、真C.真、真、假D.真、假、假解析因为cos A<0,0<A<π,则A必为钝角,△ABC为钝角三角形,所以原命题为真,从而逆否命题也为真;△ABC为钝角三角形,可能是B或C为钝角,A为锐角,则cos A>0,所以逆命题为假,从而否命题也为假.故选B.3.l1,l2表示空间中的两条直线,若p:l1,l2是异面直线,q:l1,l2不相交,则(A) A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充要条件D.p既不是q的充分条件,也不是q的必要条件解析两直线异面,则两直线一定无交点,即两直线一定不相交;而两直线不相交,有可能是平行,不一定异面,故两直线异面是两直线不相交的充分不必要条件.故选A.4.(2018·河北邯郸二中期中)已知命题p:(x-3)(x+1)>0,命题q:x2-2x+1>0,则命题p是命题q的(A)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析由p:(x-3)(x+1)>0,得x<-1或x>3,由命题q:x2-2x+1>0,解得x≠1,由于p⇒q成立,q⇒p不成立,即命题p是命题q的充分不必要条件.故选A.5.A={x||x-1|≥1,x∈R},B={x|log2x>1,x∈R},则“x∈A”是“x∈B”的(B) A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析由已知得A=(-∞,0]∪[2,+∞),B=(2,+∞),若“x∈B”,则必有“x∈A”,反之不成立,即得“x∈A”是“x∈B”的必要不充分条件.故选B.6.下列四个选项中错误的是( B )A .命题“若x ≠1,则x 2-3x +2≠0”的逆否命题是“若x 2-3x +2=0,则x =1”B .若p ∨q 为真命题,则p ,q 均为真命题C .若命题p :∀x ∈R ,x 2+x +1≠0,则¬p :∃x 0∈R ,x 20+x 0+1=0D .“x >2”是“x 2-3x +2>0”的充分不必要条件解析 对于A 项,显然是正确的;对于B 项,根据复合命题的真值表知,有p 真q 假、p 假q 真、p 真q 真三种情况,故B 项是错误的;对于C 项,由全称命题的否定形式知C 项是正确的;对于D 项,x 2-3x +2>0的解是x >2或x <1,故D 项是正确的.二、填空题7.已知命题p :若a >b >0,则log 12a <log 12b +1,命题p 的原命题、逆命题、否命题、逆否命题中真命题的个数为__2__.解析 ∵a >b >0,∴log 12a <log 12b , ∴命题p 为真命题,其逆命题为:若log 12a <log 12b +1,则a >b >0, ∵a =2,b =2时,log 12a <log 12b +1,而a =b . ∴逆命题为假命题.根据命题与其逆否命题的真假相同,逆命题与否命题互为逆否命题,知命题p 的原命题、逆命题、否命题、逆否命题中只有原命题及其逆否命题是真命题.8.记不等式x 2+x -6<0的解集为集合A ,函数y =lg(x -a )的定义域为集合B .若“x ∈A ”是“x ∈B ”的充分条件,则实数a 的取值范围为__(-∞,-3]__.解析 由x 2+x -6<0,得-3<x <2,即A =(-3,2),由x -a >0,得x >a ,即B =(a ,+∞),若“x ∈A ”是“x ∈B ”的充分条件,则A ⊆B ,则a ≤-3.9.能够说明“设a ,b ,c 是任意实数,若a >b >c ,则a +b >c ”是假命题的一组整数a ,b ,c 的值依次为__-1,-2,-3(答案不唯一)__.解析 取a =-1,b =-2,c =-3,满足a >b >c ,但a +b =-3=c ,不满足a +b >c ,故“设a ,b ,c 是任意实数,若a >b >c ,则a +b >c ”是假命题的一组整数a ,b ,c 的值依次为-1,-2,-3.三、解答题10.(2018·山东邹平月考)写出“若x =2,则x 2-5x +6=0”的逆命题、否命题、逆否命题,并判断其真假.解析 逆命题:若x 2-5x +6=0,则x =2,是假命题;否命题:若x ≠2,则x 2-5x +6≠0,是假命题;逆否命题:若x 2-5x +6≠0,则x ≠2,是真命题.11.已知函数f (x )=lg(x 2-2x -3)的定义域为集合A ,函数g (x )=2x -a (x ≤2)的值域为集合B .(1)求集合A ,B ;(2)已知命题p :m ∈A ,命题q :m ∈B ,若綈p 是綈q 的充分不必要条件,求实数a 的取值范围.解析 (1)A ={x |x 2-2x -3>0}={x |(x -3)(x +1)>0}={x |x <-1或x >3},B ={y |y =2x -a ,x ≤2}={y |-a <y ≤4-a }.(2)∵¬p 是¬q 的充分不必要条件,∴q 是p 的充分不必要条件,∴B A ,∴4-a <-1或-a ≥3,∴a ≤-3或a >5,即实数a 的取值范围是(-∞,-3]∪(5,+∞).12.已知p :x 2-8x -20≤0,q :x 2-2x +1-m 4≤0.(1)若p 是q 的必要条件,求m 的取值范围;(2)若¬p 是¬q 的必要不充分条件,求m 的取值范围.解析 由x 2-8x -20≤0,得-2≤x ≤10,即p :-2≤x ≤10,q :1-m 2≤x ≤1+m 2.(1)若p 是q 的必要条件,则⎩⎪⎨⎪⎧1-m 2≥-2,1+m 2≤10,即⎩⎪⎨⎪⎧ m 2≤3,m 2≤9,即m 2≤3,解得-3≤m ≤ 3. 故m 的取值范围是[-3,3]. (2)∵¬p 是¬q 的必要不充分条件, ∴q 是p 的必要不充分条件,即⎩⎪⎨⎪⎧ 1-m 2≤-2,1+m 2≥10,即m 2≥9,解得m ≥3或m ≤-3. 故m 的取值范围是(-∞,-3]∪[3,+∞).。
2017年7月5日 郡县制度-试题君之每日一题君2018年高考
2017年7月5日郡县制度高考频度:★★★★☆ 难易程度:★★★★☆(2017年江苏高三检测)据江苏尹湾汉墓出土的东海郡《集簿》记载,当时东海郡有“县、邑、侯国卅八:县十八,侯国十八,邑二。
乡百七十,□百六,里二千五百卅四,正二千五百卅二人。
亭六百八十八,卒二千九百七十二人”。
此记载A.说明封国仍是朝廷的严重威胁B.佐证了西汉时期曾在地方分封诸侯C.表明西汉尚未推行郡县制D.填补了县以下基层机构的史籍空白【参考答案】B【解题必备】秦朝郡县制度的概况及与分封制的比较1.郡县制度(1)推行:秦统一之初,在全国范围内实行郡县制。
(2)内容①郡设郡守、郡丞和郡尉。
②郡下设若干县,县置县令(长)、县丞和县尉。
③县以下有乡、里等基层机构。
(3)作用:加强了皇帝对全国的统治。
郡县制是古代中国继宗法制和分封制之后出现的以郡统县的两级地方行政制度,是古代中国中央集权制在地方政权上的体现,形成于春秋战国时期,盛行于秦汉时期。
春秋战国时期,一些诸侯国已经在一些新兼并的地区设置了郡县,产生了郡统辖县的两级地方行政组织。
它彻底打破了传统的贵族分封制,奠定了古代中国大一统的基础,提高了行政效率,强化了中央对地方的统治。
④官吏权利:诸侯拥有封地和爵位;官吏只有俸禄,没有封地。
⑤历史作用:诸侯国拥有很强的地方独立性,容易发展为割据势力;郡县则是地方行政机构,有利于中央集权的加强和国家的统一。
2002年在湖南省湘西里耶古城发现大量的秦简,其中Jl(12)10简内容是(正面):廿六年(即公元前221年)六月癸酰(丑),遥(迁)陵拔(应为“掾”,吏)訓(刑讯)蛮、衿(蛮荆)。
(背面):鞫(ju,审讯犯人)之,越人以城邑反。
下列选项中对上述材料理解最准确的是A.秦朝统治范围最远已达湖南B.秦朝郡县制度得到全面推广C.楚国遗民流窜到湘江流域D.秦朝制度推广激化了社会矛盾阅读下列材料,回答问题。
材料一自殷以前,天子诸侯君臣之分未定也……盖诸侯之于天子,犹后世诸侯之于盟主,未有君臣之分也……逮克殷践奄,灭国数十,而新建之国皆其功臣、昆弟、甥舅,本周之臣子;而鲁、卫、晋、齐四国,又以王室至亲为东方大藩……由是天子之尊,非复诸侯之长而为诸侯之君……盖天子诸侯君臣之分始定于此。
答案与解析:2018高考数学押题原创卷04(理)
双曲线上一点与两顶点所在直线斜率的乘积,该乘积为定值
b2 a2
,然后可求离心率.
11.B 【命题依据】开放型题目是最近今年全国卷的热点题目. 【解析】由题,
a1 3 20 21, a2 5 20 22, a3 6=21+22, a4 9=20 +23, a5 10=21+23, a6 12=22 +23,...
直接通分,再转化,也能转化为均值不等式或双勾函数求最值.也可以通分后求导,找单调
区间,进而求最值.
10.B
【命题依据】以双曲线为背景,求离心率问题已经成为高考题中常见题.本题充分将圆与双
曲线融合,既考查圆的基本性质,又考查双曲线的基本知识,属于难题.
【解析】由题, NB NA ,所以 KNB KNA 1,
2)2 1 21 1 .
2
2
【解题技巧】解答本题的关键是正确的分割图形,找出图形的对称性. 17.【命题依据】2017 年全国卷考察三角函数,今年考察数列的可能性相当大.
【解析】(1)当 n 1时, a1 1.
因为 Sn 2an 1(n N*) ①,所以 Sn1 2an1 1②,②-①式可得 an1 2an1 2an ,即
0,
1 3
,
2 3
1-
1 n 1
1 , 2(1
1) n 1
2
11
1
... 2
T2 T3
Tn1
【解题技巧】等比数列求通项,等差数列求和,以及裂项求和.
18.【命题依据】正态分布
公众号:2020押题 获取更多免费押题卷
【解析】(1) x 79+80+85+85+90+93+95+96+97+100 90 , 10
2018年4月7日 周末培优-试题君之每日一题君2018年高考
4月7日 周末培优高考频度:★★★★★ 难易程度:★★★★☆典例在线已知函数()()23,33,3x x f x x x ⎧-≤⎪=⎨-->⎪⎩,函数()()3g x b f x =--,其中b ∈R ,若函数()()y f x g x =-恰有4个零点,则实数b 的取值范围是 A .11,4⎛⎫-+∞ ⎪⎝⎭B .113,4⎛⎫--⎪⎝⎭C .11,4⎛⎫-∞-⎪⎝⎭D .()3,0-【参考答案】B【名师点睛】本小题主要考查分段函数的图象与性质,考查零点问题的求解方法.题目所给函数()f x 是一个分段函数,那么函数()3f x -也是一个分段函数,所以两个结合起来,将函数分成三个部分,将三段函数解析式求解出来后画出图象,即可得到b 的范围.学霸推荐1.已知函数()exf x y =在其定义域上单调递减,则函数()f x 的图象可能是A .B .C .D .2.已知函数()()()2ln 2,2ex xf x x ax a xg x =-+-=-. (1)求函数()f x 的极值;(2)若对任意给定的(]00,e x ∈,方程()()0f x g x =在(]0,e 上总有两个不相等的实数根,求实数a 的取值范围.1.【答案】A 【解析】∵函数()e xf x y =在其定义域上单调递减,∴()()()[]0e e xxf x f x f x -''=≤在定义域上恒成立,且不可恒为0,即()()f x f x ≥'恒成立.结合函数()f x 的图象及导数的几何意义可得选项A 满足条件.故选A . 2.【答案】(1)0a ≤时,()f x 无极值;0a >时,极大值为11ln1a a +-;(2)232ee e ea +≤<+.(2)由题意知()()12,e e x xx xg x g x '-=-=, 令()0,g x '>得()(),1,x g x ∈-∞单调递增;令()0,g x '<得()()1,x g x ∈+∞,递调递减.所以(]0,e x ∈时,()12,2e g x ⎛⎤∈-- ⎥⎝⎦.依题意,()()max 10e 1e 2a f g x a f ⎧<<⎪⎪⎪⎛⎫>⎨ ⎪⎝⎭⎪⎪≤-⎪⎩,由()2e 1e 2e e 2f a a =-+-≤-,得232ee ea +≥+, 由1111ln 12e f a a a ⎛⎫=+->-⎪⎝⎭,得11ln 1e a a -+<, 令()11ln eh a a a =-+,易知()h a 单调递增,且()e 1h =, ∴11ln 1e a a -+<,即()0,e a ∈, 综上所述,232ee e ea +≤<+. 【思路点拨】(1)对函数()f x 中的x 求导,对a 进行分类讨论,结合单调性即可得函数()f x 的极值;(2)对函数()g x 中的x 求导,得()g x 的单调性,从而得()g x 的值域,根据方程()()0f x g x =在(]0,e 上总有两个不相等的实数根,只需满足()()max 10e 1e 2a f g x a f ⎧<<⎪⎪⎪⎛⎫>⎨ ⎪⎝⎭⎪⎪≤-⎪⎩,即可求得实数a 的取值范围.【名师点睛】涉及函数的零点问题、方程解的个数问题、函数图象交点个数问题,一般先通过导数研究函数的单调性、最大值、最小值、变化趋势等,再借助函数的大致图象判断零点、方程根、交点的情况,归根到底还是研究函数的性质,如单调性、极值,然后通过数形结合的思想找到解题的思路.。
押高考数学第8题-学易试题君之每日一题君2018年高考数学(理)四轮复习
【解析】模拟程序的运行,可得S=0,i=1,
执行循环体,S=290,i=2;
不满足判断框内的条件,执行循环体, ;
不满足判断框内的条件,执行循环体, ;
不满足判断框内的条件,执行循环体, ;
不满足判断框内的条件,执行循环体, ;
不满足判断框内的条件,执行循环体, ;
不满足判断框内的条件,执行循环体, ;
1、按住ctrl键单击链接即可打开专题链接
2、复制链接到网页
5月17日押高考数学第8题
1.执行如下图所示的程序框图,则输出的
A. B.
C. D.
2.执行如图所示的程序框图,令 ,若 ,则实数a的取值范围是
A. B.
C. D.
3.《九章算术》中有这样一则故事:“今有良马与驽马发长安,至齐.齐去长安三千里.良马初日行一百九十三里,日增一十二里;驽马初日行九十七里,日减二里.”为了计算每天良马和驽马所走的路程之和,设计框图如下图.若输出的 的值为360,则判断框中可以填
A.23B.47
C.24D.48此时结束循环.
故选B.
【名师点睛】像这种程序框图的问题,一般直接按照程序框图运行该程序即可找到输出值S.本题考查到了数列里的裂项相消法求和.即 ,裂项时,不要漏掉了后面的 .裂项相消是数列的一种重要的求和方法,是高考考查的重点,所以大家要理解掌握并灵活运用.
不满足判断框内的条件,执行循环体, .
由题意,此时,应该满足判断框内的条件,退出循环,输出 的值为360.
可得判断框中的条件为 .
故选C.
今日收获如何?
总结一下吧!
学易试题君之每日一题君2018年高考数学(理)四轮复习
专题下载链接:/a763267.html
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年 押高考数学第18题
1.如图,四棱锥P ABCD -中,PD ABCD ⊥平面,底面ABCD 是梯形,AB ∥CD ,BC CD ⊥,AB=PD=4,
CD=2,22AD =,M 为CD 的中点,N 为PB 上一点,且(01)PN PB λλ=<<.
(1)若1
4
λ=
时,求证:MN ∥平面PAD ; (2)若直线AN 与平面PBC 所成角的正弦值为
25
5
,求异面直线AD 与直线CN 所成角的余弦值. 2.如图,AB 为圆O 的直径,点C 为圆O 上的一点,且AC BC 3=,点D 为线段AB 上一点,且
DB AD 3
1
=
,PD 垂直于圆O 所在的平面.
(1)求证:⊥CD 平面PAB ;
(2)若BD PD =,求二面角A PB C --的余弦值.
3.如图,在等腰三角形ABC 中,BA =BC =2,30ACB ∠=︒,在菱形BCDE 中,1
cos 4
CBE ∠=
,AE =3. (1)求证:平面ABC ⊥平面AEC ;
(2)设直线CE 与平面ABE 所成的角为θ,求sin θ.
∴四边形DMNE 是平行四边形, ∴MN ∥DE ,
又DE ⊂平面PAD ,MN ⊄平面PAD ,
∴MN ∥平面PAD .
(2)如图所示,过点D 作DH ⊥AB 于H ,则DH ⊥CD .以D 为坐标原点建立空间直角坐标系D −xyz . 则D (0,0,0),M (0,1,0),C (0,2,0),B (2,2,0),A (2,−2,0),P (0,0,4), ∴()()2,0,0,0,2,4CB CP ==-,()()
2,2,42,2,4AN AP PN AP PB λλ=+=+=-+-
()22,22,44λλλ=-+-.
该平面PBC 的法向量为(),,x y z =n ,则由20
240
CB x CP y z ⎧⋅==⎪⎨⋅=-+=⎪⎩n n ,得02x y z =⎧⎨=⎩,令z =1,得()0,2,1=n .
该直线AN 与平面PBC 所成的角为θ,则
()()()
222
8
25sin cos 55222244AN AN AN θλλλ⋅=⋅=
=
=
⋅
-+++-n n n
,解得1
,3
λ= ∴()228248,,,,2,2,0333333N CN AD ⎛⎫⎛⎫
=-=-
⎪ ⎪⎝⎭⎝⎭
,,, 设直线AD 与直线CN 所成的角为α, 则442
cos cos ,14221
223
AD CN α==
=⨯
. 所以直线AD 与直线CN 所成角的余弦值为
4214
.
【名师点睛】(1)利用向量法求线面角的方法:
①分别求出斜线和它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(锐角或直角时)或其补角(钝角时);
②通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角或钝角的补角,取其余角就是斜线与平面所成的角.
(2)利用直线的方向向量求异面直线所成的角时,要注意直线方向向量的夹角和异面直线所成角的区别,不要得到错误的结论.
(2)解:由(1)可建立如图所示的空间直角坐标系xyz D -. 设2=AC ,则)3,0,0(),0,3,0(),0,0,3(),0,0,0(P B C D .
(3,0,3),(0,3,3)PC PB ∴=-=-.
设向量(,,)x y z =n 为平面PBC 的一个法向量,则0
PC PB ⎧⋅=⎪⎨⋅=⎪⎩n n ,即⎩⎨⎧=-=-033033z y z x ,
z y z x ==∴,3,取1=z ,则(3,1,1)=n 为平面PBC 的一个法向量.
又(3,0,0)DC =为平面PAB 的一个法向量,
315
cos ,553
DC =
=⨯∴n , ∴二面角A PB C
--
的余弦值为
5
15
.
∴222cos CE BC BE BC BE CBE =
+-⨯⨯∠=1
222224
+-⨯⨯⨯=3,
∵O 为AC 中点,∴OE AC ⊥,且2236
322
OE CE OC =-=-
=
,
∴22
213
222
OB OE BE +=+==,∴OE OB ⊥, ∵AC
OB O =,∴OE ⊥平面ABC ,
∵OE ⊂平面ACE ,∴平面ABC ⊥平面AEC .
设平面ABE 的法向量为m =(,,)x y z ,则00
AB BE ⎧⋅=⎪⎨⋅=⎪⎩m m ,即62
022
26022
x y y z ⎧+=⎪⎪⎨⎪-+=⎪⎩,
取1x =,则3,1y z =-=-,所以平面ABE 的一个法向量为m =(1,3,1)--,
则sin |cos ,|CE θ=m =22222
66
|10(3)(1)|2266()()1(3)(1)22
-
⨯+⨯-+⨯--+⨯+-+-=10
5.
今日收获如何?
总结一下吧!。
