第三章 力偶系
工程力学(静力学与材料力学)第三章力偶系详解

FB
r M2 0 ∑ M = 0 , FA sin
M 2 2r FA
M2 = 4M1 = 8kNm
2M 1 FO FB FA 8kN r
• 作业3-1,3-4,3-8
考虑CB部分为二力构件,得:
FC FA FB FC
例3-4
图示机构自重不记。圆轮上的销子 A 放在 摇杆 BC上的光滑导槽内。M 1 = 2kNm,OA = r = 0.5m 。图示位置OA⊥OB,α = 30°,且系统平衡。 求作用于摇杆 BC 上力偶的矩 M 2 及 O、B 支座的反 力。 解:受力分析
M1
R
F1
M
F2
2
M1 + M2 = rBA×F1 + rBA×F2 = rBA×( F1 + F2 ) = rBA×R = M
如有n个力偶,按上法依次合成, 最后得一力偶,合力偶矩矢为 M = M1 +M2 + … +Mn = ∑M I
B
rBA
A
F2
F1
任意个力偶可以合成为一个 合力偶,这个合力偶矩矢等于各 分力偶矩矢的矢量和。 M = M 1+ M 2+ … + M n = ∑M i
性质三
证:
力偶没有合力
仍用反证法,即假定力偶有合力,那么总可 找到一个与此力大小相等,方向相反而作用线 共线的力与此力平衡,即力与力偶相平衡。与 性质二矛盾。
性质一、二和三告诉我们力偶只能与力偶等 效而不能与单个力等效。
•力偶只能与力偶相平衡 力偶只能与力偶相平衡
§3-4 力偶系的合成
设有两个力偶,由性质一,将 力偶中两力分别移到两力偶作用面 交线上的两点 A 和 B,可得到两个 汇交力系,其合力分别为R 、 R ’ 。
工程力学 第3章 力偶系
M 2 F2 , F2'
M F1'
r1
F F1 F2 F ' F1' F2'
F2' MR F, F '
F2
F1 F
M2
MR r F ' r (F1'F2 ') r F1'r F2 '
M1 M2
结论:两个力偶的合成仍然为力偶,且
第三章 力偶系
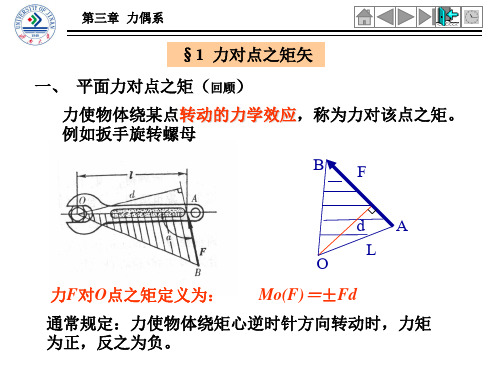
§1 力对点之矩矢 一、 平面力对点之矩(回顾)
力使物体绕某点转动的力学效应,称为力对该点之矩。 例如扳手旋转螺母。
BF
dA L
O
力F对O点之矩定义为: Mo(F)=±Fd
通常规定:力使物体绕矩心逆时针方向转动时,力矩 为正,反之为负。
第三章 力偶系
二、力对点之矩矢量 1、空间力矩三个要素:
一、力偶 在日常生活和工程实际中经常见到物体受动两个大小相等、 方向相反,但不在同一直线上的两个平行力作用的情况。例如
第三章 力偶系
B d
F’
F A
M
B
F
rBA
F’ d A
1. 定义:在力学中把这样一对等值、反向而不共线的平行力 称为力偶,用符号 ( F , F′)表示。
两个力作用线之间的垂直距离 d 称为力偶臂, 两个力作用线所决定的平面称为力偶的作用面。
x (F ) y (F )
yFz zFx
zFy xFz
M
z
(F
)
xFy
yFx
力对点之矩在各坐标轴上的投影
MO z
O xr
工程力学(第三章)

MR
y
MR Mz cos MR
§3-6
力偶系的平衡条件
M 0
平衡: 力偶系平衡的充要条件是 其合力偶矩矢为零。
即:力偶系平衡
一、平面力偶系的平衡条件
M R M(代数和) i
M 0
平面力偶系的平衡方程
§3-6
力偶系的平衡条件
M 0
平衡: 力偶系平衡的充要条件是 其合力偶矩矢为零。
力对点之矩矢
作用: 用来度量力使物体绕某点转动效应的量。
(代数量) 一、平面中力对点之矩(力矩)
F
O
h
定义:M O
F Fh
正负号规定: 力使物体绕矩心逆转为正,顺转为负。
作用: 用来度量力使物体绕某点转动效应的量。 1、平面问题
(代数量) 力矩作用面
矩心 O h
力臂
定义: M O F Fh
A
O x
y
Fx
z
y
Fy
x
A x, y, z ,
F Fx , Fy , Fz
(一)、力对点的矩
1、平面问题
MO
F Fh
MO F
O
h
z
F
F
2、空间问题
MO F r F
x
(二)、力对轴的矩
空间: 力偶对空间任一点的矩矢恒等于力偶矩矢, 而与矩心位置无关。
性质二 力偶可在其作用面内任意移转,或移到另
一平行平面,而不改变对刚体的作用效应。
= =
F
F
F
F
工程力学 04力偶系.ppt

§3-1、力对点之矩矢
(3)力对点之矩矢的基本性质 作用于刚体上的二力对刚体产生的绕一点的转动效应, 可以用该点的一个矩矢来度量,这个矩矢等于二力分别 对该点之矩矢的矢量和。
即 MO =MO (F1 )+MO (F2 )
推广:力系(F1,F2,- - -,Fn)对刚体产生的绕一点的
(2)力F与z轴相交
2019年11月10日星期日
理论力学
Theoretical Mechanics
§3-2、力对轴之矩
5.力对任意l 轴(方向l°)之矩
Ml (F) MA(F)l
A为l 轴上任意一点
z
F
M A(F)
r l轴
y
对任意l 轴之矩的几何意义
A
l x
定理:力对点的矩矢在通过该点的任意轴上的投影等于这力
§3-1、力对点之矩矢
力对物体可以产生 移动效应--取决于力的大小、方向 转动效应--取决于力矩的大小、方向
一.平面力系中力对点之矩(代数量)
简称力矩
1.现象
2.定义 M0 F F d
F
o 力矩中心
d 力臂
力矩作用面
两个要素:
大小:力F与力臂的乘积 方向:转动方向
2019年11月10日星期日
同理:
Mx(F)= Fz y Fy z
My(F ) = Fx z Fz x
2019年11月10日星期日
理论力学
Theoretical Mechanics
§3-2、力对轴之矩 空间力对点的矩与空间力对轴的矩的关系(力矩关系定理):
Mo (F )x yFz zFy M x (F )
理论力学第3章-力偶系

例 3-1 图示机构,各杆自重不计,在两力偶作用下处于平 衡。已知:M1 = 100 N · m,O1A = 40 cm,O2B = 60 cm。 试求力偶矩M2的大小。 B A FB F B FA
30 o
B
O1
B
A FA M2
M1 FO1 O1 A M1
M
2
O2
O2
FO2
解:取O1A杆为研究对象,受力如图所示,
若两个力偶对刚体的作用效应相同,则称这二力 偶等效。
两力偶的等效条件 :力偶矩矢相等,即
M1 M2
(3-2) FR'
B'
证明:
A'
FR F1 FR F'
A B
FR' F1'
F
力偶(FR,FR' ) 代了原力偶(F,F' ) 并与原力偶等效。
A'
FR
FR'
B'
D F' C
比较(F,F')和(FR,FR')可得 M(F,F')=2△ABD=M(FR,FR') =2 △ABC
合力偶矩矢的大小和方向余弦为
M ( M x )2 ( M y )2 ( M z )2 (280)2 1602 (800)2 862.55 kN m
M cos( M , i )
280 0.3246 M 862.55 My 160 cos( M , j ) 0.1855 M 862.55
1 3 200 280kN m 5 5 4 M y M y M 1 y M 2 y 0 200 160kN m 5 2 M z M z M1z M 2 z 400 5 0 800kN m 5 M x M x M1x M 2 x 400 5
第三章 力偶系

QA RF
F' R'
B Q'
(3)将R, R'分别移到A', B'点,则(R, R')与原力偶等效
(4)最后将力偶(R, R')的力臂调整到与原力偶相等
19
§3-5、力偶系的合成
设作用于刚体上的任意两个力偶M1,M2, 总能将其等效为两个共力臂的力偶:
z
Fz
力 F 对 z 轴之矩:
M z (F ) xFy yFx
F
Fy
k Fx z
ij
x
y
x
y
Fx
Fxy
力 F 对 x 轴与 y 轴之矩: M x (F ) yFz zFy
M y (F ) zFx xFz
10
问题:力对轴之矩与力对轴上一点之矩有什么关系?
z
力对轴之矩 M x (F ) yFz zFy M O M Oz
力偶(F, F’ )是特殊的力系,对O点 的合力矩为:
F ' F
F
B rBA
A d
F’
rB
rA
O
MO MO(F) MO(F')
rA F rB F '
rA F rB (F )
(rA rB ) F rBA F
M
M = Fd
B rBA
F’
力偶矩矢
F A
注:力偶矩矢垂直于力偶所在的平面,其大小和方向与取矩点 无关。
合力偶的方向:
cos(MR, i)
Mx MR
cos(MR, j)
My MR
工程力学第三章 力 偶 系
§3-5 力偶系的合成 对于任意一个力偶系,可以将力偶矩矢移到一个汇交点, 再按照矢量合成的方法将矢量合成为一个合矢量,这个合矢 量就是力偶系的合力偶。而且有:
MR = M1+ M2+ + Mn = ∑M
对于平面力偶系,力偶只有顺时针和逆时针两种转向,所 以力偶可以看成代数量规定:逆时针为正、顺时会为负。 所以平面力偶系的合力偶
MR = M1+ M2+ …+ Mn = ∑M
§3-6 力偶系的平衡条件 对于任意一个力偶系,它的平衡条件是合力偶矩矢为零。
即:MR = ∑M = 0
M1x+ M2x+ + Mnx = ∑Mx = 0 M1y+ M2y+ + Mny = ∑My = 0 M1z+ M2z+ + MnZ = ∑Mz = 0
二、空间中力对点之矩 M0(F)= r × F
§3-2力对轴之矩 一、力对轴之矩的概念
1、定义:对力使它所作用的物体绕轴转动效果的度量。 它是一个代数量。
2、特例:力与轴平行: MZ(F)=0 力与轴相交: MZ(F)=0
力与轴在同一平面内时力对轴之矩为零。 3、合力矩定理:合力对任一轴之矩等于各分力对同一 轴之矩的代数和。
§3-4 力偶的等效条件和性质 一、力偶的等效条件(41页) 两个力偶的等效条件是它们的力偶矩矢相等。 二、力偶的性质 1、力偶不能与一个力等效,也不能与一个力平衡。 2、力偶可在其作用面内任意转移,或移到另一平行平 面,而不改变对刚体的作用效果。
=
=
=
3、在保持力偶的转向和力偶矩的大小不变的条件下, 可以同时改变力偶中力和力偶臂的大小,而不改变 力偶对刚体的作用。
力偶

力偶矩的符号
M
3.只要保持力偶矩不变,力偶可在其作用面 内任意移转,且可以同时改变力偶中力的大小与 力臂的长短,对刚体的作用效果不变.
=
=
=
ABC?ABD ABC ABD
例2-8 已知:q,l; 求: 合力及合力作用线位置. 解:取微元如图
x q q l l x 1 P q dx ql 0 l 2
由合力矩定理
得
x2 P h q dx x q dx 0 0 l
l l
2 h l 3
例2-9
M 已知: 1 M 2 10N m, M 3 20N m, l 200mm ;
F cos θ r 78.93N m
例2-7
F 已知: , , xB , yB , l;
求:平衡时,CD杆的拉力.
解: CD为二力杆,取踏板 由杠杆平衡条件
F cos yB F sin xB FCD l 0
解得 FCD
F cos y B F sin xB l
解得 FCy 1.5kN
例2-6
已知: F=1400N, θ 20 , r 60mm
求: M O F .
解:直接按定义
MO
F F h F r cos θ
78.93N m
按合力矩定理 M O F M O Ft M O Fr
M O FR M O Fi M O FR xi Fiy yi Fix
§3-2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章力偶系
习题
3.1 如图3.1A、B、C、D均为滑轮,绕过B、D两轮的绳子两端的拉力为400N,绕过A、C两轮的绳子两端的拉力F为300N,α=30°。
求这两力偶的合力偶的大小和转向。
滑轮大小忽略不计。
题3.1图
解:两力偶的矩分别为
1400sin60240400cos60200123138
M N mm =∙+∙=∙
2300sin30480300cos30200123962
M N mm =∙+∙=∙
合力偶矩为
12247.1
M M M N m
=+=∙(逆时针转向)
3.2 已知粱AB上作用一力偶,力偶矩为M,粱长为L,粱重不计。
求在图3.2中a,b,c三种情况下,支座A和B的约束力。
18
题3.2图
解:AB 梁受力如个图所示, 由
0i M =∑,对图(a )(b)有
0RA F l M -=
得
RA NB
M F F l
== 对图(c )有
cos 0RA F l M θ-=
得
cos RA NB M
F F l θ
==
3.3 齿轮箱的两个轴上作用的力偶如图所示,它们的力偶矩的大小分别为M 1=500 N ·m ,M 2=125N ·m 。
求两螺栓处的铅垂约束力。
图中长度单位为cm 。
NB
F RA
F RA
F F 3
l NB
F RA
F
19
题3.3图
F
F '
解:
1200M Fd M M =+-=合,
750F N =-
力的方向与假设方向相反
3.4 汽锤在锻打工件时,由于工件偏置使锤头受力偏心而发生偏斜,它将在导轨DA 和BE 上产生很大的压力,从而加速导轨的磨损并影响锻件的精度。
已知锻打力F=1000kN ,偏心距e =20mm ,试求锻锤给两侧导轨的压力。
题3.4图
N1
F N2
F
解:锤头受力如图,这是个力偶系的平衡问题, 由
10,0i
N M
F e F h =-=∑
解得
1220N N F F h
==
KN
20
3.5四连杆机构在图示位置平衡,已知OA =60 m ,BC =40 cm , 作用在BC 上力偶的力偶矩大小M 1=1 N ·m ,试求作用在OA 上力偶的力偶矩大小M 1和AB 所受的力F AB 。
各杆重量不计。
题3.5
图
解:CA 和OB 分别受力如图 由
0i
M
=∑
2sin300BA F CB M *-= 10AB M F OA -*=
解得
5AB F N = (拉) 13M N m =⋅
3.6 齿轮箱三根轴上分别作用有力偶,它们的转向如图所示,各力偶矩的大小为1M =36kN ·m ,2M =6 kN ·m ,3M =6kN ·m ,试求合力偶矩。
题3.6
图
解: 23sin 40cos400.74x M M M N m =-=-⋅
13sin 4032.14y M M M N m =-=⋅ 2cos40 4.6z M M N m ==⋅
21
32.48M N m ==⋅
3.7 1O 和2O 圆盘与水平轴AB 固连,1O 盘垂直z 轴,2O 盘垂直x 轴,盘面上分别作用力偶
),(11F F
' ,),(2
2F F '如图所示。
如两盘半径为r =20 cm ,31=F N ,52=F N ,AB =80 cm ,不计构件自重,试计算轴承A 和B 处的约束力。
题3.7图
Bz
Az
F Ax
F Bx
解:取整体为研究对象,由于构件自重不计,主动力为两力偶,由力偶只能由力偶来平衡的性质,轴承A ,B 处的约束力也应该形成力偶。
设A ,B 处的约束力为,,,Ax Az Bx Bz F F F F ,方向如图,由力偶系的平衡方程,
有
20,4008000x
Az M mmF mmF =-=∑ 10,4008000y
Ax M
mmF mmF =+=∑
解得
1.5,
2.5
A x
B x B z A z F F N F F N ==-==。
