2018届全国高三考前密卷(三)数学文试题
2018届全国高三考前密卷(一)数学(文科)试卷

2018届全国高三考前密卷(一)数学(文科)试卷本试题卷共10页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知i 为虚数单位,则2(34)2i i i+--()=( )A .5B .5iC .712--55iD .712-+55i2.已知M 是函数y =的定义域,N 是函数24y x =-的值域,则MIN =( ) A .1,2⎛⎤-∞ ⎥⎝⎦ B .14,2⎡⎫-⎪⎢⎣⎭C .RD .∅3.执行下面的程序框图,若10P =,则输出的S 等于( )A .10231024 B .10251024 C .10471048 D .104910484.已知O 是平面内一点,,A B C ,是平面内不共线的三点,若OA OB OB OC OC OA ∙=∙=∙,O 一定是ABC ∆的( )A .外心B .重心 C.垂心 D .内心5.有一几何体,其三视图如图所示: 网格纸上小正方形的边长为1,则该几何体的体积为( )A .5B .10 C.203 D .2536.已知数列{}n a 的前n 项和为n S ,若323n n n S a =-,则2018a =( ) A .20181A- B .201836- C.201817()22- D .2018110()33-7.已知sin()sin 3παα++=,则7sin()6πα+=( )A . C.45 D .4-58.函数()f x 在定义域R 内可导,若()(2)f x f x =-,且1'()0x f x -<(),若1(0),(),(3)2a fb fc f ===,则,,a b c 的大小关系是( )A .c a b >>B .a c b >> C.a b c >> D .b a c >> 9.若A B 、为对立事件,其概率分别为41()=,()P A p B x y=,则x y +的最小值为( ) A .10 B .9 C.8 D .6 10.若()2cos()f x x k ωϕ=++,对任意实数t 都有()()33f t f t ππ+=-成立,且()13f π=-,则实数k 的值等于( )A .-3或1B .1 C.-1或3 D .-311.双曲线2222:1(0,0)x y C a b a b-=>>,过虚轴端点且平行于x 轴的直线交于,A B 两点,F为双曲线的一个焦点,且有AF BF ⊥,则双曲线的离心率为( ) A.2D12.曲线3y x =上一点B 处的切线l 交x 轴于点A ,OAB ∆(O 为原点)是以A 为顶点的等腰三角形,则切线l 的倾斜角为( )A .30B .45 C.60 D .120第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知实数,x y 满足2022020x y x y x y --≤⎧⎪-+≥⎨⎪++≥⎩,则32z x y =-+的最小值为 .14.设抛物线24E y x =:,其焦点为F ,准线l 与x 轴的交点为A ,过抛物线E 上一点p (第一象限内) 做l 的垂线PQ ,垂足为Q ,若四边形AFPQ 的周长为16,则点P 的坐标为 .15.在平行四边形ABCD 中,0AB BD ∙=且1AB =,2BD =BD 折起使平面ABD ⊥平面BCD ,则三棱锥A BDC -的外接球的表面积为 .16.数列{}n a 中,n S 为数列{}n a 的前n 项和,且11a =,22(2)21n n Sna n S =≥-,则这个数列前{}n a 项和公式n S = .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在ABC ∆中,点,,A B C 的对边长分别为,,a b c ,(()3a b c a b c ac ++-+=)(1)求B 的大小. (2)设(sin ,2),(cos ,sin )u r A xos C A B m n ==,且a c<,求u rp m n=∙的取值范围. 18.在四棱锥P ABCD -中,PA ⊥平面ABCD ,ABC ∆是正三角形,AC 与BD 的交点为M ,又4PA AB ==,AD CD =,120CDA ∠=,点N 是CD 的中点.(1) 求证: 平面PMN ⊥平面PAB ; (2) 求点M 到平面PBC 的距离.19.为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30 天) 的快递件数记录结果中随机抽取10 天的数据,制表如下每名快递员完成一件货物投递可获得的劳务费情况如下:甲公司规定每件4.5元; 乙公司规定每天35件以内(含35件) 的部分每件4元,超出35件的部分每件7元.(1) 根据表中数据写出甲公司员工A 在这10天投递的快递件数的平均数和众数;(2) 为了解乙公司员工B 的每天所得劳务费的情况,从这10天中随机抽取1天他所得的劳务费记为X (单位: 元),求>182X 的概率;(3) 根据表中数据估算两公司的每位员工在该月所得的劳务费.20.已知椭圆2222:(0)x y E a b a b+=>>的离心率为12,右焦点F 是抛物线2:2(0)C y px p =>的焦点,抛物线过点2(,过点F 的直线l 交椭圆于,A B 两点。
2018届全国高三考前密卷(三)数学理科试题

2018届全国高三考前密卷(三)数学理科试卷本试题卷共10页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知i 虚数单位,复数533i i ++对应的点在复平面的( )A .第一象限B .第二象限C .第三象限D .第四象限 2.已知集合{|}A x x a =≤,21221{|lo g (4)lo g }5B x x x =-≥,若AB =∅,则实数a 的取值范围为( )A .(1,5)-B .[0,4]C .(,1]-∞-D .(,1)-∞-3.设a ,b ,c ,d ,x 为实数,且0b a >>,c d >,下列不等式正确的是( ) A .d a c d -<- B .b b x a a x+≥+ C .c db a > D .||||a a x bb x +≤+4.设随机变量2(,)N ξμσ,则使得(3)(3)1P m P ξξ≤+>=成立的一个必要不充分条件为( )A .1m =或2m =B .1m = C.1m =- D .23m =-或2m =5.执行如图所示的程序框图,若输出的结果3S =,则判断框内实数M 应填入的整数值为( )A .998B .999 C.1000 D .10016.已知公差不为0的等差数列{}n a 的前n 项和为n S ,若2297a a =,则下列选项中结果为0的是( )A .9aB .7a C.15S D .16S7.设1A ,2A 分别为双曲线2222:1x y C ab-=(0a >,0b >)的左、右顶点,过左顶点1A 的直线l 交双曲线右支于点P ,连接2A P ,设直线l 与直线2A P 的斜率分别为1k ,2k ,若1k ,2k 互为倒数,则双曲线C 的离心率为( )A .12B D .8.如图所示,网格纸上小正方形的边长为1,粗实线画出的是几何体的三视图,则该几何体的体积为( )A .816π-B .8π C.16 D .81π+9.已知曲线33y x x =-和直线y x =所围成图形的面积是m ,则5()y x m ++的展开式中3x项的系数为( )A .480B .160 C.1280 D .64010.在平面直角坐标系中,O 为坐标原点,(0,4)A ,(2,0)A B =,(2,0)A B =,(1,1)B C B A -=-,设(,)P x y ,A P m A B n A C =+,若0m ≥,0n ≥,且1m n +≤,则2x y +的最大值为( )A .7B .10 C.8 D .1211.如图所示,椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.根据椭圆的光学性质解决下题:已知曲线C 的方程为2244x y+=,其左、右焦点分别是1F ,2F ,直线l 与椭圆C 切于点P ,且1||1P F =,过点P 且与直线l 垂直的直线'l 与椭圆长轴交于点M ,则12||:||F M F M =( )A B .1:1:3 D .1:12.将给定的一个数列{}n a :1a ,2a ,3a ,…按照一定的规则依顺序用括号将它分组,则可以得到以组为单位的序列.如在上述数列中,我们将1a 作为第一组,将2a ,3a 作为第二组,将4a ,5a ,6a 作为第三组,…,依次类推,第n 组有n 个元素(*n N ∈),即可得到以组为单位的序列:1()a ,23(,)a a ,456(,,)a a a ,…,我们通常称此数列为分群数列.其中第1个括号称为第1群,第2个括号称为第2群,第3个数列称为第3群,…,第n 个括号称为第n 群,从而数列{}n a 称为这个分群数列的原数列.如果某一个元素在分群数列的第m 个群众,且从第m 个括号的左端起是第k 个,则称这个元素为第m 群众的第k 个元素.已知数列1,1,3,1,3,9,1,3,9,27,…,将数列分群,其中,第1群为(1),第2群为(1,3),第3群为(1,3,23),…,以此类推.设该数列前n 项和12n N a a a =+++,若使得14900N >成立的最小n a 位于第m 个群,则m =( ) A .11 B .10 C.9 D .8第Ⅱ卷二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若函数3()lo g (19)xf x k x =++为偶函数,则k = .14.已知993sin ()co sco s()sin1471475x x ππππ-+-=,3(,)2x ππ∈,则tan 2x = .15.中华民族具有五千多年连绵不断的文明历史,创造了博大精深的中华文化,为人类文明进步作出了不可磨灭的贡献.为弘扬传统文化,某校组织了国学知识大赛,该校最终有四名选手A 、B 、C 、D 参加了总决赛,总决赛设置了一、二、三等奖各一个,无并列.比赛结束后,C 对B 说:“你没有获得一等奖”,B 对C 说:“你获得了二等奖”;A 对大家说:“我未获得三等奖”,D 对A 、B 、C 说:“你妈三人中有一人未获奖”,四位选手中仅有一人撒谎,则选手获奖情形共计 种.(用数字作答)16.已知G 为A B C ∆的重心,点P 、Q 分别在边A B ,A C 上,且存在实数t ,使得P G t P Q =.若A P A B λ=A Q A C μ=,则11λμ+= .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 在A B C ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知2co s 2a B c b =-. (1)求角A 的大小;(2)若A B C ∆的面积2S =,D 为B C 边的中点,2A D =,求b c +.18. 市场份额又称市场占有率,它在很大程度上反映了企业的竞争地位和盈利能力,是企业非常重视的一个指标.近年来,服务机器人与工业机器人以迅猛的增速占据了中国机器人领域庞大的市场份额,随着“一带一路”的积极推动,包括机器人产业在内的众多行业得到了更广阔的的发展空间,某市场研究人员为了了解某机器人制造企业的经营状况,对该机器人制造企业2017年1月至6月的市场份额进行了调查,得到如下资料:(1)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程,并预测该企业2017年7月份的市场份额;(2)如图是该机器人制造企业记录的2017年6月1日至6月30日之间的产品销售频数(单位:天)统计图.设销售产品数量为s ,经统计,当0200s ≤≤时,企业每天亏损约为200万元,当200400s <≤时,企业平均每天收人约为400万元;当400s >时,企业平均每天收人约为700万元。
2018届全国高三考前密卷(三)数学(理)试题

2018届全国高三考前密卷(三)数学(理科)试卷本试题卷共10页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合12|A x y x ⎧⎫==⎨⎬⎩⎭,{}|ln(1)B x y x ==+,则A B =( )A .[0,)+∞B .(0,1)C .(1,)-+∞D .(,1)-∞-2.下面是关于复数2z i =-的四个命题:1p :||5z =;2p :234z i =-;3p :z 的共轭复数为2i -+;4p :z 的虚部为1-,其中真命题为( ) A .2p ,3pB .1p ,2pC .2p ,4pD .3p ,4p3.我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金箠,长五尺,一头粗,一头细,在粗的一端截下1尺,重四斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”设该金箠由粗到细是均匀变化的,则金箠的重量为( ) A .15斤B .14斤C .13斤D .12斤4.若某多面体的三视图(单位:cm )如图所示,则此多面体的体积是( )A .378cm B .323cm C .356cmD .312cm5.已知函数())cos 22f x x x π=--,若要得到一个奇函数的图象,则可以将函数()f x 的图象( )A .向左平移6π个单位长度 B .向右平移6π个单位长度 C .向左平移12π个单位长度D .向右平移12π个单位长度6.已知函数(12)3,1,()ln ,1a x a x f x x x -+<⎧=⎨≥⎩的值域为R ,那么实数a 的取值范围是( )A .(,1]-∞-B .1(1,)2-C .1[1,)2-D .1(0,)27.《红海行动》是一部现代海军题材影片,该片讲述了中国海军“蛟龙突击队”奉命执行撤侨任务的故事.撤侨过程中,海军舰长要求队员们依次完成六项任务,并对任务的顺序提出了如下要求:重点任务A 必须排在前三位,且任务E 、F 必须排在一起,则这六项任务的不同安排方案共有( ) A .240种B .188种C .156种D .120种8.运行如图所示的程序框图,则输出的结果S =( )A .14B .30C .62D .1269.ABC ∆的三个内角A ,B ,C 的对边分别为a ,b ,c ,若2B A =,cos cos cos 0A B C >,则sin a Ab的取值范围是( )A .B .C .1(2D .1)210.已知如图所示的三棱锥D ABC -的四个顶点均在球O 的球面上,ABC ∆和DBC ∆所在的平面互相垂直,3AB =,AC =BC CD BD ===O 的表面积为( )A .4πB .12πC .16πD .36π11.已知S 为双曲线22221x y a b-=(0a >,0b >)上的任意一点,过S 分别引其渐近线的平行线,分别交x 轴于点M ,N ,交y 轴于点P ,Q ,若11()(||||)4||||OP OQ OM ON +⋅+≥恒成立,则双曲线离心率e 的取值范围为( ) A .(1,2]B .[2,)+∞ C. D.)+∞12.已知函数()||xx af x e e=+(a R ∈)在区间[]0,1上单调递增,则实数a 的取值范围是( ) A .(1,1)-B .(1,)-+∞C .[]1,1-D .(0,]+∞第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.已知1sin cos 5θθ+=,(,)2πθπ∈,则tan θ= . 14.已知实数x ,y 满足条件2,22,1,y x x y x ≤⎧⎪+≥⎨⎪≤⎩则3y x +的最大值为 .15.在矩形ABCD 中,2AB =,1BC =,E 为BC 的中点,若F 为该矩形内(含边界)任意一点,则AE AF ⋅的最大值为 .16.下列命题正确的是 .(写出所有正确的命题的序号) ①若奇函数()f x 的周期为4,则函数()f x 的图象关于(2,0)对称; ②如(0,1)a ∈,则111aaa a++<;③函数1()ln1xf x x+=-是奇函数; ④存在唯一的实数a使()lg(f x ax =为奇函数.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.若正项数列{}n a 的前n 项和为n S ,首项11a =,1)n P S +点在曲线2(1)y x =+上.(1)求数列{}n a 的通项公式n a ; (2)设11n n n b a a +=⋅,n T 表示数列{}n b 的前n 项和,若n T a ≥恒成立,求n T 及实数a 的取值范围.18.2016年1月1日,我国实行全面二孩政策,同时也对妇幼保健工作提出了更高的要求.某城市实行网格化管理,该市妇联在网格1与网格2两个区域内随机抽取12个刚满8个月的婴儿的体重信息,体重分布数据的茎叶图如图所示(单位:斤,2斤=1千克),体重不超过9.8千克的为合格.(1)从网格1与网格2分别随机抽取2个婴儿,求网格1至少有一个婴儿体重合格且网格2至少有一个婴儿体重合格的概率;(2)妇联从网格1内8个婴儿中随机抽取4个进行抽检,若至少2个婴儿合格,则抽检通过,若至少3个合格,则抽检为良好,求网格1在抽检通过的条件下,获得抽检为良好的概率; (3)若从网格1与网格2内12个婴儿中随机抽取2个,用X 表示网格2内婴儿的个数,求X 的分布列与数学期望.19.如图,在四棱锥P ABCD -中,底面ABCD 是平行四边形,135BCD ∠=︒,侧面PAB ⊥底面ABCD ,90BAP ∠=︒,2AB AC PA ===,E ,F 分别为BC ,AD 的中点,点M 在线段PD 上.(1)求证:EF ⊥平面PAC ;(2)若直线ME 与平面PBC 所成的角和直线ME 与平面ABCD 所成的角相等,求PMPD 的值.20.已知椭圆C 的中心在原点,对称轴为坐标轴,椭圆C 与直线24x y +=相切于点3(,1)2P . (1)求椭圆C 的标准方程;(2)若直线l :y kx t =+与椭圆相交于A 、B 两点(A ,B 不是长轴端点),且以AB 为直径的圆过椭圆C 在y 轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标. 21.已知函数2()2ln f x x x a x =--,()g x ax =. (1)求函数()()()F x f x g x =+的极值;(2)若不等式sin ()2cos xg x x≤+对0x ≥恒成立,求a 的取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线1C的参数方程为2cos ,x y αα=⎧⎪⎨=⎪⎩(α为参数),将曲线1C 上各点的横坐标都缩短为原来的122C ,在极坐标系(与直角坐标系xOy 取相同的单位长度,且以原点O 为极点,以x 轴非负半轴为极轴)中,直线l的极坐标方程为cos()4πρθ+=-(1)求直线l 和曲线2C 的直角坐标方程;(2)设点Q 是曲线2C 上的一个动点,求它到直线l 的距离的最大值. 23.选修4-5:不等式选讲已知0a >,0b >,且222a b +=.(1)若2214|21||1|x x a b+≥---恒成立,求x 的取值范围; (2)证明:5511()()4a b a b++≥.数学(理)试卷答案一、选择题1-5:ACAAC 6-10:CDCDC 11、12:DC 二、填空题 13.43-14.12 15.9216.①③ 三、解答题17.解:(1)由211)n S +=1=,所以数列1为公差的等差数列,(1)1n =-⨯,即2n S n =,由公式11,1,,2n n n S n a S S n -=⎧=⎨-≥⎩,得1,1,21,2,n n a n n =⎧=⎨-≥⎩所以21n a n =-. (2)因为111111()(21)(21)22121n n n b a a n n n n +===--+-+, 所以11(1)221n T n =-+, 显然n T 是关于n 的增函数,所以n T 有最小值. 由于n T a ≥恒成立,所以13a ≤, 于是a 的取值范围是1[,)3+∞.18.解:(1)由茎叶图知,网格1内体重合格的婴儿数为4,网格2内体重合格的婴儿数为2,则所求概率2242228455(1)(1)84C C P C C =--=.(2)设事件A 表示“2个合格,2个不合格”;事件B 表示“3个合格,1个不合格”;事件C 表示“4个全合格”;事件D 表示“抽检通过”;事件E 表示“抽检良好”.∴223144444444488853()()()()70C C C C C P D P A P B P C C C C =++=++=,314444448817()()()70C C C P E P B P C C C =+=+=,则所求概率()17()53P D P P E ==. (3)由题意知,X 的所有可能取值为0,1,2,∴2821214(0)33C P X C ===,114821216(1)33C C P X C ===,242121(2)11C P X C ===, ∴X 的分布列为∴()0123333113E X =⨯+⨯+⨯=. 19.(1)证明:在平行四边形ABCD 中,因为AB AC =,135BCD ∠=︒,所以AB AC ⊥,由E ,F 分别为BC ,AD 的中点,得//EF AB ,所以EF AC ⊥. 因为侧面PAB ⊥底面ABCD ,且90BAP ∠=︒,所以PA ⊥底面ABCD . 又因为EF ⊂底面ABCD ,所以PA EF ⊥, 又因为PAAC A =,PA ⊂平面PAC ,AC ⊂平面PAC ,所以EF ⊥平面PAC .(2)解:因为PA ⊥底面ABCD ,AB AC ⊥,所以AP ,AB ,AC 两两垂直, 以AB ,AC ,AP 分别为x ,y ,z ,建立空间直角坐标系,则(0,0,0)A ,(2,0,0)B ,(0,2,0)C ,(0,0,2)P ,(2,2,0)D -,(1,1,0)E , 所以(2,0,2)PB =-,(2,2,2)PD =--,(2,2,0)BC =-, 设PMPDλ=([]0,1λ∈),则(2,2,2)PM λλλ=--, 所以(2,2,22)M λλλ--,(12,12,22)ME λλλ=+--,易得平面ABCD 的法向量(0,0,1)m =.设平面PBC 的法向量为(,,)n x y z =,由0n BC ⋅=,0n PB ⋅=,得220,220,x y x z -+=⎧⎨-=⎩令1x =,得(1,1,1)n =,因为直线ME 与平面PBC 所成的角和此直线与平面ABCD 所成的角相等,所以|cos ,||cos ,|ME m ME n <>=<>,即||||||||||||ME m ME n ME m ME n ⋅⋅=⋅⋅,所以|22|||λ-=, 解得32λ=32λ=. 综上可得:PM PD =. 20.解:(1)设椭圆为22221x y m n+=(0m >,0n >且m n ≠),则它在点3(,1)2P 处的切线为22321xy m n +=,它与24x y +=表示同一直线, ∴23224m =,2114n=,∴23m =,24n =,故所求椭圆的方程为22143y x +=. (2)设11(,)A x y ,22(,)B x y ,联立22,1,43y kx t y x =+⎧⎪⎨+=⎪⎩得222(34)63(4)0k x ktx t +++-=,22223612(34)(4)0k t k t ∆=-+->,得22430k t +->,122634kt x x k +=-+,21223(4)34t x x k -=+,22221212121224(3)()()()34t k y y kx t kx t k x x kt x x t k -=++=+++=+, ∵以AB 为直径的圆过椭圆的上顶点(0,2)D , ∴1AD BD k k =-,即1212221y y x x --⋅=-, ∴1212122()40y y x x k x x ⋅+⋅-++=,即1212122()440y y x x k x x t +-++-=,即2222224(3)3(4)62440343434t k t ktk t k k k ---+-⋅+-=+++,即271640t t -+=,∴27t =或2t =, 当2t =时,直线2y kx =+过定点(0,2)与已知矛盾;当27t =时,直线27y kx =+过定点2(0,)7满足22430k t +->, 所以,直线l 过定点,定点坐标为2(0,)7.21.解:(1)2()2ln F x x x a x ax =--+,22(2)(2)(1)'()x a x a x a x F x x x+--+-==,∵()F x 的定义域为(0,)+∞, ①02a-≤,即0a ≥时,()F x 在(0,1)上递减,()F x 在(1,)+∞上递增,()1F x a =-极小,()F x 无极大值;②012a <-<,即20a -<<时,()F x 在(0,)2a -和(1,)+∞上递增,在(,1)2a-上递减, 2()()ln()242a a aF x F a a =-=---极大,()(1)1F x F a ==-极小;③12a-=,即2a =-时,()F x 在(0,)+∞上递增,()F x 没有极值; ④12a ->,即2a <-时,()F x 在(0,1)和(,)2a -+∞上递增,()F x 在(1,)2a-上递减,∴()(1)1F x F a ==-极大,2()()ln()242a a aF x F a a =-=---极小.综上可知:0a ≥时,()1F x a =-极小,()F x 无极大值;20a -<<时,2()()ln()242a a aF x F a a =-=---极大,()(1)1F x F a ==-极小;2a =-时,()F x 没有极值;2a <-时,()(1)1F x F a ==-极大,2()()ln()242a a aF x F a a =-=---极小.(2)设sin ()2cos x h x ax x =-+(0x ≥),212c o s'()(2c o s )xhx a x+=-+,设cos t x =,则[]1,1t ∈-,212()(2)t t t ϕ+=+,432(2)(1)2(1)'()0(2)(2)t t t t t t ϕ-+---==≥++, ∴()t ϕ在[]1,1-上递增,∴()t ϕ的值域为11,3⎡⎤-⎢⎥⎣⎦, ①当13a ≥时,'()0h x ≥,()h x 为[0,)+∞上的增函数, ∴()(0)0h x h ≥=,适合条件;②当0a ≤时,∵1()0222h a ππ=⋅-<,∴不适合条件; ③当103a <<时,对于02x π<<,sin ()3x h x ax <-, 令sin ()3x T x ax =-,cos '()3x T x a =-, 存在(0,)2x π∈,使得0(0,)x x ∈时,'()0T x <,∴()T x 在0(0,)x 上单调递减,∴0()(0)0T x T <=,即在0(0,)x x ∈时,()0h x <,∴不适合条件.综上,a 的取值范围为1[,)3+∞.22.解:(1)因为直线l的极坐标方程cos()4πρθ+=-所以有cos sin 40ρθρθ-+=,即直线l 的直角坐标方程为:40x y -+=,因为曲线1C的参数方程为2cos ,x y αα=⎧⎪⎨=⎪⎩(α为参数),经过变换后cos ,sin x y αα=⎧⎨=⎩(α为参数), 所以化为直角坐标方程为:221x y +=.(2)因为点Q 在曲线2C 上,故可设点Q 的坐标为(cos ,sin )αα, 从而点Q 到直线l的距离|)4|d πα++==, 由此得,当cos()14πα+=时,d取得最大值,且最大值为1.23.解:(1)设,1,1|21||1|32,1,21,.2x x y x x x x x x ⎧⎪≥⎪⎪=---=-≤<⎨⎪⎪-<⎪⎩ 由222a b +=,得221()12a b +=, 故22222222221411414()()(14)22b a a b a b a b a b +=++=+++19(1422≥++=, 所以9|21||1|2x x ≥---. 当1x ≤时,92x ≤,得912x ≤≤; 当112x ≤<时,9322x -≤,解得136x ≤,故112x ≤<; 当12x <时,92x -≤,解得92x ≥-,故9122x -≤<. 综上,9922x -≤≤. (2)55554411()()b a a b a b a b a b ++=+++5522222()2b a a b a b a b=+++-22222222()2()4a b a b a b ≥++=+=.。
2018届全国高三考前密卷数学(理科)卷

2018届全国高三考前密卷数学(理科)试卷本试题卷共10页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{1,}M x =,{0,2}N =,若{2}MN =,则A B 为( )A .{0,1}B .{0,2}C .{1,2}D .{0,1,2}2.复数1ii -的共轭复数为( ) A .1122i -+ B .1122i + C .1122i -- D .1122i -3.执行如图所示的程序框图,输出的S 值为( )A .-10B .-3C .4D .5 4.函数212()log ()f x x x =-的单调增区间为( )A .1(,)2-∞ B .1(0,)2 C. 1(,)2+∞ D .1(,1)25.某学校计划在周一至周四的艺术节上展演《雷雨》《茶馆》《天籁》《马蹄声碎》四部话剧,每天一部,受多种因素影响,话剧《雷雨》不能在周一和周四上演,《茶馆》不能在周一和周三上演,《天籁》不能在周三和周四上演,《马蹄声碎》不能在周一和周四上演,那么下列说法正确的是( )A .《雷雨》只能在周二上演B .《茶馆》可能在周二或周四上演 C. 周三可能上演《雷雨》或《马蹄声碎》 D .四部话剧都有可能在周二上演 6.我国古代数学名著《九章算术·均输》中记载了这样一个问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何?”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”(“钱”是古代一种重量单位).这个问题中,等差数列的通项公式为( )A .1766n -+(*,5n N n ∈≤) B .1362n +(*,5n N n ∈≤) C. 1766n + (*,5n N n ∈≤) D .1362n -+,(*,5n N n ∈≤)7.我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高,意思是两等高立方体,若在每一等高处的截面积都相等,则两立方体的体积相等,已知某不规则几何体与如图所示的几何体满足“幂势同”,则该不规则几何体的体积为( )A .42π-B .8π- C. 483π-D .82π- 8.如图在边长为1的正方形组成的网格中,平行四边形ABCD 的顶点D 被阴影遮住,请设法计算AB AD ∙=( )A .10B .11 C.12 D .139.先后掷一枚质地均匀骰子(骰子的六个面上分别标有1,2,3,4,5,6个点)两次,落在水平桌面后,记正面朝上的点数分别为,x y ,设事件A 为“x y +为偶数”,事件B 为“,x y 中有偶数,且x y ≠”,则概率(|)P B A =( ) A .13 B .14 C. 15 D .1610.点,,,A B C D 在同一个球面上,AB BC ==2AC =,若球的表面积为254π,则四面体ABCD 体积最大值为( ) A .14 B .12 C. 23D .2 11.设双曲线2222:1x y C a b-=(0,0a b >>)的左右焦点分别为12,F F ,以12F F 为直径的圆与双曲线左支的一个交点为P ,若以1OF (O 为坐标原点)为直径的圆与2PF 相切,则双曲线C 的离心率为( )A.34-+C..37+ 12.已知函数()f x 是定义在R 上的偶函数,且(1)(1)f x f x --=-,当[1,0]x ∈-时,3()f x x =-,则关于x 的方程()cos f x x π=在51[,]22-上的所有实数解之和为( )A .-7B .-6 C. -3 D .-1二、填空题(每题5分,满分20分,将答案填在答题纸上)13.设实数,x y 满足202600x y x y x -+≤⎧⎪-+≥⎨⎪≥⎩,则目标函数y z x =的最小值为 .14.已知(13)n x +的展开式中,含有2x 项的系数是54,则n = .15.如图,在平面直角坐标系中,分别在x轴与直线1)y x =+上从左向右依次取点,k k A B ,1,2,k =,其中1A 是坐标原点,使1k k k A B A +∆都是等边三角形,则101011AB A ∆的边长是 .16.已知点A 在椭圆221259x y +=上,点P 满足(1)AP OA λ=-(R λ∈)(O 是坐标原点),且72OA OP ∙=,则线段OP 在x 轴上的设影长度的最大值为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.已知函数231())sin()cos ()2222f x x x x πππ=--++-. (1)求函数()f x 的单调递增区间;(2)已知在ABC ∆中,,,A B C 的对边分别为,,a b c ,若()1f A =,2a =,求ABC ∆面积的最大值.18. 2017年5月27日当今世界围棋排名第一的柯洁在与AlphaGo 的人机大战中中盘弃子认输,至此柯洁与AlphaGo 的三场比赛全部结束,柯洁三战全负,这次人机大战再次引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查,根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.(1)请根据已知条件完成下面22⨯列联表,并据此资料你是否有95%的把握认为“围棋迷”与性别有关?(2)将上述调查所得到的频率视为概率,现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名学生中的“围棋迷”人数为X ,若每次抽取的结果是相互独立的,求X 的分布列,数学期望和方差. 独立性检查临界值表:(参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++)19. 底面为菱形的直棱柱1111ABCD A BC D -中,,E F 分别为棱11A B ,11A D 的中点.(1)在图中作出一个平面α,使得BD α⊂,且平面//AEF α.(不必给出证明过程,只要求作出α与直棱柱1111ABCD A BC D -的截面.)(2)若12AB AA ==,060BAD ∠=求平面AEF 与平面α的距离d . 20. 在平面直角坐标系xOy 中,点1(1,0)F -,2(1,0)F ,动点M 满足124OF OM OF OM -+-=.(1)求动点M 的轨迹E 的方程;(2)若直线y kx m =+与轨迹E 有且仅有一个公共点Q ,且与直线4x =-相交于点R ,求证:以QR 为直径的圆过定点1F . 21. 已知函数1()xf x e ax=+(0,0a x ≠≠)在1x =处的切线与直线(1)20180e x y --+=平行.(1)求a 的值并讨论函数()y f x =在(,0)x ∈-∞上的单调性; (2)若函数1()()1g x f x x m x=--++(m 为常数)有两个零点12,x x (12x x <) ①求实数m 的取值范围; ②求证:120x x +<请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线C 的参数方程为cos 2sin x a ty t =⎧⎨=⎩,(t 为参数,0a >)以坐标原点O为极点,以x 轴的正半轴为极轴建立极坐标系,已知直线l 的极坐标方程为cos()4πρθ+=-(1)设P 是曲线C 上的一个动点,当2a =时,求点P 到直线l 的距离的最小值; (2)若曲线C 上的所有点均在直线l 的右下方,求实数a 的取值范围. 23.选修4-5:不等式选讲已知函数()121f x x x =--+的最大值为m . (1)作出函数()f x 的图象;(2)若22223a c b m ++=,求2ab bc +的最大值.试卷答案一、选择题1-5:DCADC 6-10:DBBAC 11、12:DA 二、填空题13. 2 14. 4 15. 512 16. 15 三、解答题 17. 解:(1)231()cos()sin()cos ()2222f x x x x πππ=--++-21cos sin 2x x x =+-12cos 22x x =- sin(2)6x π=-令222262k x k πππππ-≤-≤+(k Z ∈),解得63k x k ππππ-≤≤+(k Z ∈),所以()f x 的单调递增区间为[,]63k k ππππ-+(k Z ∈). (2)由(1)知()sin(2)16f A A π=-=因为(0,)A π∈,所以3A π=.在ABC ∆中,由余弦定理得2222cos a b c bc A =+- 又2a =,则2242b c bc bc bc bc =+-≥-=,当且仅当2b c ==时,等号成立. 所以bc 取最大值,最大值为4,所以ABC ∆面积的最大值为11sin 4222ABC S bc A ∆==⨯⨯=18.由频率分布直方图可知,(0.0200.005)1010025+⨯⨯=所以在抽取的100人中,“围棋迷”有25人,从而22⨯列联表如下22()()()()()n ad bc K a b c d a c b d -=++++2100(30101545)100 3.0304555752533⨯-⨯==≈⨯⨯⨯ 因为3.030 3.841<,所以没有95%的把握认为“围棋迷”与性别有关.(2)由频率分布直方图知抽到“围棋迷”的频率为0.25,将频率视为概率,即从该地区抽取1名“围棋迷”的概率为14. 由题意知,1~(3,)X B ,从而X 的分布列为故()344E X =⨯=,()34416D X =⨯⨯=. 19. (1)如图,取11B C 的中点M ,11D C 的中点N ,连结BM ,MN ,ND ,则平面BMND 即为所求平面α.(2)如图,连接AC ,AC 交BD 于点O , ∵在直棱柱1111ABCD A BC D -中,底面为菱形, ∴AC BD ⊥,∴分别以,DB AC 所在直线为,x y 轴,O 为原点建立如图所示空间直角坐标系, 又∵所有棱长为2,060BAD ∠=,∴(0,A ,(1,0,0)B ,C ,(1,0,0)D -,1(0,A ,1(1,0,2)B ,1(1,0,2)D -∴1(,2)2E ,1(,2)2F -∴1(2AE =,1(2AF =-,(1AB =,设平面AEF 的法向量(,,)n x y z =,则00n AE n AF ⎧∙=⎪⎨∙=⎪⎩,即12021202x y z x y z ⎧+=⎪⎪⎨⎪-++=⎪⎩令y =(0,43,3)n =-,57n =,∴点B 到平面AEF的距离19AB n h n ∙===, ∴平面AEF 与平面α的距离d =20. (1)解:因为12124OF OM OF OM MF MF -+-=+= 即124MF MF +=由椭圆定义可知动点M 的轨迹是以12,F F 为焦点的椭圆 所以2,1a c ==,2223b a c =-=所以椭圆C 的方程为22143x y +=. (2)证明:由22143x y y kx m ⎧+=⎪⎨⎪=+⎩, 消去y 得222(43)84120k x kmx m +++-= 如图,设点00(,)Q x y ,依题意0m ≠, ∵直线y kx m =+与轨迹E 有且仅有一个公共点 ∴由222(8)4(43)(412)0km k m ∆=-+-=, 可得2243m k =+.此时02443km x k =-+,02343m y k =+,即04k x m =-,03y m=, ∴43(,)k Q m m -, 由4y kx m x =+⎧⎨=-⎩,解得4y k m =-+ ∴(4,4)R k m --+由1(1,0)F - 可得143(1,)k QF m m=--,1(3,4)RF k m =- ∴11433(1)(4)0k QF RF k m m m ∙=---= ∴11QF RF ⊥∴以QR 为直径的圆过定点1F .21.解:(1)'21()x f x e ax=-, '1(1)1f e e a =-=-,∴1a =. ∴2'2211()x x x e f x e x x-=-= 令2()1xh x x e =-,则'2()(2)x h x x x e =+∴(,2)x ∈-∞-时,'()0h x >;(2,0)x ∈-时,'()0h x <.则()h x 在(,2)-∞-上单调递增,在(2,0)-上单调递减.∴在(,0)x ∈-∞时,24()(2)10h x h e ≤-=-<, 即(,0)x ∈-∞时,'()0f x <, ∴函数()f x 在(,0)x ∈-∞上单调递减.(2)①由条件可知,()1x g x e x m =-++,则'()1x g x e =-∴()g x 在(,0)-∞上单调递减,在(0,)+∞上单调递增;要使函数有两个零点,则min ()(0)20g x g m ==+<∴2m <-.②证明:由①可知120x x <<,∴20x -<,又12,x x 是两个零点∴2212222()()()()2x x g x g x g x g x e ex ---=--=-- 令()2x x m x e e x -=--(0x >)则'()20x x m x e e -=+->,∴()(0)0m x m >=即12()()g x g x >-又()g x 在(,0)-∞上单调递减,∴12x x <-,即120x x +<22.解:(1)由cos()4πρθ+=-)x y -=- 即直线l 的方程为40x y -+=,依题意,设(2cos ,2sin )P t t ,则点P 到直线l的距离d==2sin()4t π=-- ∴当242t k πππ-=+,k Z ∈时,min 2d =.(2)∵曲线C 上的所有点均在直线l 的右下方,∴对任意t R ∈,有cos 2sin 40a t t -+>恒成立,)4t ϕ-<(其中tan 2a ϕ=)恒成立,4,又0a >,解得0a <<故实数a的取值范围为.23.解:(1)12,21()1213,122,1x x f x x x x x x x ⎧+≤-⎪⎪⎪=--+=--<<⎨⎪--≥⎪⎪⎩(2)由(1)可知32m =∵2222222323()2()242m a c b a b c b ab bc ==++=+++≥+, ∴324ab bc +≤ ∴2ab bc +的最大值为34, 当且仅当12a b c ===时,等号成立.。
2018届全国高三考前密卷(一)数学文科试题

2018届全国高三考前密卷(一)数学试题(文科)本试题卷共10页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}2,1,0,1,2A =--,{}=0B x x ≥则=A R (C B )( ) A .{}12, B .{}-2-1, C .{}012,, D .{}-2-10,, 2.已知,a R i ∈为虚数单位。
若复数1a iz i-=+是纯虚数.则a 的值为( ) A .-1 B .0 C .1 D .23.中国人民银行发行了2018中国戊戌(狗)年金银纪念币一套,如下图所示是一枚3克圆形金质纪念币,直径18mm ,某同学为了算图中装饰狗的面积.他用1枚针向纪念币上投掷500次,其中针尖恰有150次落在装饰狗的身体上,据此可估计装饰狗的面积大约是( )A .24865mm π B .22435mm π C .224310mm π D .224320mm π4.若31cos()23πα-=,且-22ππα≤≤,则sin 2a 的值为( )A .-9 B .-9 C.9 D .95.下列说法中正确是( )A.若命題0p x R ∃∈:,使得20010x x ++<,则P x R ⌝∀∈:,均有210x x ++> B.若“P q ∨”是真命题,则p 一定是真命题C.已知x R ∈则“1x >”是“112x<()”的必要不充分条件 D.命题“若x y ≠”,则sin sin x y ≠的逆命题是真命题 6.执行如下图所示的程序框图,则输出的=S ( )A .32 B .85 C.53D .2 7.一个几何体的视图如下图所示,则该几何体的外接球的表面积为( )A .9πB .8π C.5π D .4π 8.函数1()11xf x nx+=-的大致图象为( )9.已知αβγ、、表示不同的平面,a b 、表示不同的直线,下列命题中正确的是( ) A .如果//a α,αβ⊥,那么a β⊥ B .如果αβ⊥,βγ⊥,那么//αγ C. 如果//a b ,/b α,那么//a α D .如果//a α,a β⊥,那么αβ⊥ 10.已知函数2()4sin (+2sin()2(0)284x f x x ωππωω=--->)的图象关于点304π(,)对称.且()f x 在区间203π(,)上单调,则ω的值为( )A .2B .103 C.23 D .3811.已知双曲线2222:10,0)x y C a b a b-=>>(的左、右顶点分别为A B 、.点F 为双曲线的左焦点,过点F 作垂直于x 轴的直线分别在第二、第三象限交双曲线C 于P 、Q 两点,连接PB 交y 轴于点E ,连接AE 交QF 于点M ,且2QM MF =,则双曲线C 的离心率为( )A.2 C.3 D .5 12.已知函数222()25,()xx f x x ax g x e +=++=若对[][]122,1,1,1x x ∀∈--∃∈-,使得12()()f x g x ≤成立,则实数a 的最小值是( ) A.74C.2 D .3 第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量(1,0)(,2),2a b a b a b λ==-=+,则λ= .14.设变量,x y 满足约束条件0034x y x y x y +≥⎧⎪-≥⎨⎪+≤⎩,则32x y +的最大值为 .15.已知锐角ABC ∆的内角A B C 、、的对边分别为a b c 、、,且2cos 2,2a C c b a +==,则ABC ∆的最大值为 .16.已知F 为抛物线24E y x =:的焦点,过F 作倾斜角为α的直线l 与抛物线E 交于A B、两点,过A B 、向E 的准线作垂线,垂足分别为C D 、,设CD 的中点为M 若(0,)6πα∈,则MF 的取值范是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 已知{}n a 是公差为2的等差数列.数列{}n b 满足112b =,214b =,且11()n n n n a b nb b n N *++=+∈(I)求数列{}n a 和{}n b 的通项公式; (Ⅱ)设2221log log n n n c b b +=∙,数列{}n c 的前n 项和为n S ,证明:34n S <18. 党的十九大报告指出,要推进绿色发展,倡导“简约知适度、绿色低碳”的生活方式,开展创建“低碳生活,绿色出行”等行动.在这一号召下,越来越多的人秉承“能走不骑,能骑不坐,能坐不开”的出行理念,尽可能采取乘坐公交车骑自行车或步行等方式出行,减少交通拥堵,共建清洁、畅通高效的城市生活环境.某市环保机构随机抽查统计了该市部分成年市民某月骑车次数,统计如下:联合国世界卫生组织于2013年确定新的年龄分段:44岁及以下为青年人,45岁至59岁为中年人,60岁及以上为老年人.(I)若从被抽查的该月骑车次数在[]4060,的老年人中随机选出两名幸运者给予奖励,求其中一名幸运者该月骑车次数在[)4050,之间,另一名幸运者该月骑车次数在[)5060,之间的概率; (Ⅱ)用样本估计总体的思想,解决如下问题:(i )估计该市在32岁至44岁年龄段的一个青年人每月骑车的平均次数;(ii ) 若月骑车次数不少于30次者称为“骑行爱好者”,根据这些数据,能否在犯错误的概率不超过0.001的前提下认为“骑行爱好者”与“青年人”有关? 参考数据:22()=()()()()n ad bc K a b c d a c b d -++++ 19. 如下图,四梭锥-P ABCD 中,PA ⊥底面ABCD ,//,3,4AD BC PA AB AC AD BC =====,M 为线段AD 上一点,2AM MD =,N 为PB 的中点.(I)证明://MN 平面PCD ; (Ⅱ)求四面体M BCN -的体积.20.已知椭圆2215x y +=的右焦点为F ,坐标原点为O .椭圆C 的动弦AB 过右焦点F 且不垂直于坐标轴,AB 的中点为N ,过F 且垂直于线段AB 的直线交射线ON 于点M (I)证明:点M 在直线52x =上; (Ⅱ)当四边形OAMB 是平行四边形时,求MAB ∆的面积. 21. 已知函数2(1)()11x f x nx x -=-+,2()1(1)(,)g x x nx n x m n R =--∈. (I)若函数(),()f x g x 在区间01(,)上均单调且单调性相反,求实数n 的取值范围;(Ⅱ)若0a b <<,证明112a b a bna nb -+<-请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程已知直线l的参数方程为1212x y t ⎧=--⎪⎪⎨⎪=⎪⎩ (t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,圆C 的极坐标方程为22cos()3πρθ=-. (I)求圆C 的直角坐标方程;(II)若(,)p x y 是直线l 与圆面22cos()3πρθ≤-的公共点,y +的取值范围. 23.选修4-5:不等式选讲 已知函数()1f x x =+.(I)求不等式()63f x x ≤--的解集;(Ⅱ)若正数,m n 满 足2m n mn +=求证:()(2)8f m f n +-≥.数学试题(文科)参考答案一、选择题:(每小题5分,共60分)(1~5)BCCAD (6~10)BADDC (11~12)BC 二、填空题:(每小题5分,共20分) 13、1214、5 15、 16、(4,)+∞三、解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.) 17、解:(Ⅰ)由题意可知,1n =时121213a b b b a =+⇒=,又公差为2,故21n a n =+. 从而有111(21)2n n n n n n b nb b b b ++++=+⇒=,故数列{}n b 是公比为12的等比数列 又112b =,所以1()2nn b =; (Ⅱ)由(Ⅰ)知22211111()log log (2)22n n n c b b n n n n +===-⋅++.故1111111111(1)232435112n S n n n n =-+-+-++-+--++ 13113233()221242(1)(2)4n n n n n +=--=-<++++. 18、解:(Ⅰ)问题即从该月骑车次数在 [40,50)的4位老年人和[50,60]的2位老年人中随机抽取两人,每一段各抽取一人的概率.将6位老人分别记为,,,a b c d 和,A B ,则所有的抽法有(,)a b ,(,)a c ,(,)a d ,(,)a A ,(,)a B ,(,)b c ,(,)b d , (,)b A ,(,)b B ,(,)c d ,(,)c A ,(,)c B ,(,)d A ,(,)d B ,(,)A B 共15种,其中满足条件的抽法有(,)a A ,(,)a B , (,)b A ,(,)b B , (,)c A ,(,)c B ,(,)d A ,(,)d B 共8种, 故所求概率为815P =. (Ⅱ)(i )1252815202514035604515055168304112282014060150410⨯+⨯+⨯+⨯+⨯+⨯=≈+++++(次)(ii )根据题意,得出如下22⨯列联表221800(100800700200)1810.82830015008001000K ⨯⨯-⨯==>⨯⨯⨯根据这些数据,能在犯错误的概率不超过0.001的前提下认为“骑行爱好者”与“青年人”有关.19、解:(Ⅰ)由已知得113AM AD ==,2,DM ∴= 取CP 的中点T ,连接,DT TN ,由N 为PB 中点知//TN BC ,221==BC TN . 又//AD BC ,故TN //DM ,四边形DMNT 为平行四边形,于是//MN DT . 因为DT ⊂平面PCD ,⊄MN 平面PCD ,所以//MN 平面PCD (Ⅱ)因为⊥PA 平面ABCD ,N 为PB 的中点, 所以N 到平面ABCD 的距离为1322PA =. 取BC 的中点E ,连结AE .由3==AC AB 得BC AE⊥,522=-=BE AB AE .由//CAM B 得M 到BC 的距离为5,故525421=⨯⨯=∆BCM S . 所以四面体M BCN -的体积132M BCN N BCMBCM PA V V S --∆==⨯⨯=20.解:(Ⅰ)易知(2,0)F ,设AB 所在直线为:(2)y k x =-(0)k ≠,11(,)A x y ,22(,)B x y联立方程组2215(2)x y y k x ⎧+=⎪⎨⎪=-⎩,化简得2222(51)20(205)0k x k x k +-+-=由韦达定理得21222051k x x k +=+,212220551k x x k -=+,则222102(,)5151k kN k k -++,从而ON 所在直线方程为15y x k =- 又FM 所在直线方程为1(2)y x k =--,联立两直线方程解得52M x =. 所以点M 在直线52x =上.(Ⅱ)∵点N 是AB 的中点,且四边形OAMB 是平行四边形 ∴点N 是OM 的中点由(Ⅰ)知222102(,)5151k k N k k -++,51(,)22M k -,则22210515143k k k =⇒=+ 此时121255,28x x x x +==12|||AB x x =-==||1FM ==.从而1||||2MAB S AB FM ∆=⋅=21、 解:(Ⅰ)()()0)1(1141)(22'>+-=+-=x x x x x x f ,所以()x f 在()1,0上单调递增. 由已知)(x g 在()1,0上均单调且单调性相反得)(x g 在()1,0上均单调递减. 所以021ln )('≤-+=nx x x g 在()1,0上恒成立,即x x n 1ln 2+≥,令()()()1,01ln ∈+=x x x x ϕ,0ln )(2'>-=xxx ϕ 所以()x ϕ在()1,0上单调递增,()()11=<ϕϕx ,所以12≥n 即21≥n .(Ⅱ)由(Ⅰ)()1)1(2ln +--=x x x x f 在()1,0上单调递增,()()011)1(2ln =<+--=f x x x x f 即1)1(2ln +-<x x x ,令()1,0∈=b a x 得()b a b a ba b a b a +-=+⎪⎭⎫ ⎝⎛-<2112ln ,0ln <b a ∴.2ln ln b a b a b a +<-- 在(Ⅰ)中,令,21=n 由)(x g 在()1,0上均单调递减得:0)1()(=>g x g 所以()0121ln 2>--x x x ,即⎪⎭⎫⎝⎛->x x x 121ln ,取()1,0∈=ba x 得 ⎪⎪⎭⎫⎝⎛->a b b a b a 21ln ,即ab b a b a ->-ln ln ,由0ln ln <-b a 得:.ln ln b a b a ab --< 综上:.2ln ln ba b a b a ab +<--<请考生在22~23两题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B 铅笔在答题卡上把所选题目对应题号右侧的方框涂黑. 22. 解(Ⅰ)∵圆C 的极坐标方程为22cos()3πρθ=-⇒22212cos()2(cos )322πρρθρρθθ=-⇒=- 又222,cos ,sin x y x y ρρθρθ=+==,22,x y x ∴+-∴圆C的普通方程为220,x y x ++=(Ⅱ)解法一:设z y =+,圆C 的方程220,x y x ++=即221()(12x y ++=,∴圆C的圆心是1(2C -,半径1r = 将直线l的参数方程1212x y t ⎧=-⎪⎪⎨⎪⎪⎩(t为参数)代入z y =+,得z t =- 又∵直线l过1(2C -,圆C 的半径是1, 11,11t t ∴-≤≤∴-≤-≤,y +的取值范围是[]1,1-.解法二:圆C的方程220,x y x ++=即221()(12x y ++=,- 11 - 将直线l的参数方程1212x y t ⎧=-⎪⎪⎨⎪⎪⎩(t为参数)化为普通方程:1()232y x -=-+ ∴直线l 与圆C的交点为A和(B ,故点P 在线段AB 上 从而当(,)P x y与点A重合时,max )1y +=; 当(,)P x y与点(B重合时,min )1y +=-. 23. 解:(Ⅰ)此不等式等价于()|3|6|1||3|6f x x x x +-≤⇒++-≤.法一:由绝对值不等式的几何意义得不等式的解集为[]2,4x ∈-.法二:由|1||3|6x x ++-≤⇒1136x x x <-⎧⎨--+-≤⎩或13136x x x -≤≤⎧⎨++-≤⎩或3136x x x >⎧⎨++-≤⎩21x ∴-≤<-或3x -≤≤1或34x <≤不等式的解集为[]2,4x ∈-. (Ⅱ)证明:21120,0,2,22(),28222m n m n m n mn m n m n m n +>>+=+=⋅≤∴+≥ 当且仅当2422m n m m n mn n ==⎧⎧⇒⎨⎨+==⎩⎩时取等号.()(2)|1||12||(1)(12)|28f m f n m n m n m n ∴+-=++-≥+--=+≥ 当且仅当11202n n -≤⇒≥时取等号.∴()(2)8f m f n +-≥.。
2018年高考理科数学全国卷3(含答案与解析)
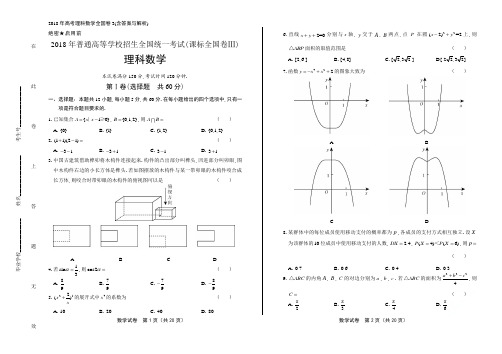
2018年高考理科数学全国卷3(含答案与解析) 数学试卷 第1页(共20页) 数学试卷 第2页(共20页) 绝密★启用前 2018年普通高等学校招生全国统一考试(课标全国卷Ⅲ)
理科数学
本试卷满分150分,考试时间120分钟. 第Ⅰ卷(选择题 共60分)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合{10}Axx∣≥,{0,1,2}B,则AB ( ) A.{0} B.{1} C.{1,2} D.{0,1,2} 2.()(1i2i) ( ) A.3i B.3i C.3i D.3i 3.中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是 ( )
A B C D 4.若1sin3,则cos2 ( )
A.89 B.79 C.79 D.89 5.252()xx的展开式中4x的系数为 ( ) A.10 B.20 C.40 D.80
6.直线2=0xy分别与x轴,y交于A,B两点,点P在圆22(2)=2xy上,则ABP△面积的取值范围是 ( )
A.[2,6 ] B.[4,8] C.[2,32 ] D[ 22,32] 7.函数422yxx的图象大致为 ( )
A B C D 8.某群体中的每位成员使用移动支付的概率都为p,各成员的支付方式相互独立.设X为该群体的10位成员中使用移动支付的人数,2.4DX,()6(4)PXPX<,则p ( ) A.0.7 B.0.6 C.0.4 D.0.3 9.ABC△的内角A,B,C的对边分别为a,b,c.若ABC△的面积为2224abc,则
C ( )
A.π2 B.π3 C.π4 D.π6
2018年新课标I、II、III数学(文)(理)高考真题试卷(Word版含答案)
2018 年一般高等学校招生全国一致考试( Ⅰ卷 )文科数学注意事项:1.答卷前,考生务势必自己的九名、考生号等填写在答题卡和试卷指定地点上.2.回答选择题时,选出每题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需变动,用橡皮擦洁净后,再选涂其余答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题(此题共 12 小题,每题 5 分,共60 分.在每题给出的四个选项中,只有一项是切合题目要求的.)1.已知会合 A 0,2 ,B 2 , 1,0 ,1,2 ,则AIB ()A. 0,2 B. 1,2 C. 0 D. 2, 1,0 ,1,21 i,则 z ()2.设z 2i1 iA.0 B.1C. 1 D. 2 23.某地域经过一年的新乡村建设,乡村的经济收入增添了一倍.实现翻番.为更好地认识该地域乡村的经济收入变化状况,统计了该地域新乡村建设前后乡村的经济收入组成比率.获得以下饼图:则下边结论中不正确的选项是()A.新乡村建设后,栽种收入减少B.新乡村建设后,其余收入增添了一倍以上C.新乡村建设后,养殖收入增添了一倍D.新乡村建设后,养殖收入与第三家产收入的总和超出了经济收入的一半4.记 S n为等差数列a n的前n项和.若 3S3 S2 S4, a1 2 ,则 a3 ()A.12 B.10 C.10 D. 125.设函数 f x x 3a 1 x 2ax .若 f x 为奇函数, 则曲线 yf x 在点 0 ,0 处的切线方程为()A . y2xB . y xC . y 2xD . y x6.在 △ ABC 中, AD 为 BC 边上的中线,uuurE 为 AD 的中点,则 EB ()A . 3 uuur1 uuurB . 1 uuur 3 uuur4 AB4 AC 4 AB AC4 C . 3 uuur 1 uuur D . 1 uuur 3 uuur 4 AB4 AC4 AB AC47.某圆柱的高为 2,底面周长为 16,其三视图以下图,圆柱表面上的点 M 在正视图上的对应点为 A ,圆柱表面上的点 N 在左视图上的对应点为 B ,则在此圆柱 侧面上,从 M 到 N的路径中,最短路径的长度为( )A .2 17B .2 5C .3D .28.设抛物线 C :y24 x 的焦点为 F ,过点2 ,0 且斜率为2的直线与 C 交于 M , N 两点,3uuuur uuur ()则FM FNA .5B . 6C .7D . 89.已知函数 f xx, ≤0 , f xf x x a (),若 g x 存在 2 个零点, 则 a 的exln x ,x 0取值范围是A . 1,0B . ,C . 1,D . 1,10.下列图来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆组成,三个半圆的直径分别为直角三角形ABC 的斜边 BC ,直角边 AB , AC , △ ABC 的三边所围成的地区记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ,在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p 1 , p 2 , p 3 ,则( )A . p 1 p 2B . p 1 p 3C . p 2 p 3D . p 1 p 2p 3211.已知双曲线 C :xy 2 1 , O 为坐标原点, F 为 C 的右焦点,过 F 的直线与 C 的两条渐 3近线的交点分别为 M , N .若 △ OMN 为直角三角形,则 MN () A .3B . 3C .2 3D . 4212.设函数 f x2 x, ≤ 0,则知足 f x 1f 2x 的 x 的取值范围是()x 01,yA .,1B . 0,C . 1,0D . ,0二、填空题(此题共 4 小题,每题 5 分,共 20 分)13.已知函数 f xlog 2 x 2 a ,若 f 31 ,则 a________.x 2 y 2 ≤ 014.若 x ,y 知足拘束条件x ≥ 0 ,则 z3x 2 y 的最大值为 ________.y 1y ≤ 015.直线 y x 1 与圆 x 2y 2 2 y 3 0 交于 A ,B 两点,则 AB________ .16. △ ABC 的内角 A ,B ,C 的对边分别为 a ,b ,c ,已知 b sinC csin B4asin Bsin C ,b 2c 2 a 2 8 ,则 △ ABC 的面积为 ________.三、解答题(共70 分。
全国三卷高考理科试卷全套(2018年精校Word版含答案)语文理科数学英语理综试卷
全国三卷理科全套试题及答案汇总2018年普通高等学校招生全国统一考试目录2018年普通高等学校招生全国统一考试全国三卷语文试题................ 2018年普通高等学校招生全国统一考试全国三卷语文试题答案............ 2018年普通高等学校招生全国统一考试全国三卷理科数学................ 2018年普通高等学校招生全国统一考试全国三卷理科数学答案............ 2018年普通高等学校招生全国统一考试全国三卷英语试题................ 2018年普通高等学校招生全国统一考试全国三卷英语试题答案............ 2018年普通高等学校招生全国统一考试全国三卷理科综合试题............ 2018年普通高等学校招生全国统一考试全国三卷理科综合试题答案........绝密★启用前2018年普通高等学校招生全国统一考试语文试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
对城市而言,文明弹性是一个城市体在生存、创新、适应、应变等方面的综合状态、综合能力,是公共性与私人性之间、多样性与共同性之间、稳定性与变迁性之间、柔性与刚性之间的动态和谐,过于绵柔、松散,或者过于刚硬、密集,都是弹性不足或丧失的表现,是城市体出现危机的表征。
当代城市社会,尤其需要关注以下文明弹性问题。
其一,空间弹性。
城市具有良好空间弹性的一个重要表现,是空间的私人性与公共性关系能够得到较为合理的处理。
任何城市空间都是私人性与公共性的统一,空间弹性的核心问题,就是如何实现空间的公共性与私人性的有机统一、具体转换。
2018全国卷3高考试题及答案理科数学.doc
绝密★启封并使用完毕前试题类型:2018年普通高等学校招生全国统一考试理科数学注意事项: 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷3至5页. 2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3.全部答案在答题卡上完成,答在本试题上无效. 4. 考试结束后,将本试题和答题卡一并交回.第Ⅰ卷一. 选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合S ={}{}(x 2)(x 3)0,T 0S x x x =--≥=I > ,则ST =(A) [2,3] (B)(-∞ ,2] [3,+∞) (C) [3,+∞) (D)(0,2] [3,+∞) (2)若z=1+2i ,则41izz =- (A)1 (B) -1 (C) i (D)-i(3)已知向量1(,22BA = ,31(),2BC = 则∠ABC= (A)300 (B) 450 (C) 600 (D)1200(4)某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图。
图中A 点表示十月的平均最高气温约为150C ,B 点表示四月的平均最低气温约为50C 。
下面叙述不正确的是(A) 各月的平均最低气温都在00C以上(B) 七月的平均温差比一月的平均温差大(C) 三月和十一月的平均最高气温基本相同 (D) 平均气温高于200C 的月份有5个 (5)若3tan 4α=,则2cos 2sin 2αα+= (A)6425 (B) 4825 (C) 1 (D)1625(6)已知432a =,344b =,1325c =,则(A )b a c << (B )a b c <<(C )b c a <<(D )c a b << (7)执行下图的程序框图,如果输入的a =4,b =6,那么输出的n =(A )3 (B )4 (C )5 (D )6(8)在ABC △中,π4B,BC 边上的高等于13BC ,则cos A(A (B (C )10(D )310(9)如图,格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为(A )18+(B )54+ (C )90 (D )81(10) 在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球,若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是 (A )4π (B )92π(C )6π (D )323π(11)已知O 为坐标原点,F 是椭圆C :22221(0)x y a b a b+=>>的左焦点,A ,B 分别为C的左,右顶点.P 为C 上一点,且PF ⊥x 轴.过点A 的直线l 与线段PF 交于点M ,与y 轴交于点E .若直线BM 经过OE 的中点,则C 的离心率为 (A )13(B )12(C )23(D )34(12)定义“规范01数列”{a n }如下:{a n }共有2m 项,其中m 项为0,m 项为1,且对任意2k m ≤,12,,,k a a a 中0的个数不少于1的个数.若m =4,则不同的“规范01数列”共有(A )18个(B )16个(C )14个(D )12个第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22)题~第(24)题为选考题,考生根据要求作答.二、填空题:本大题共3小题,每小题5分(13)若x,y满足约束条件{x−y+1≥0 x−2y≪0x+2y−2≪0则z=x+y的最大值为_____________.(14)函数y=sin x−√3cos x的图像可由函数 y=sin x+√3cos x的图像至少向右平移_____________个单位长度得到。
2018高考真题全国1卷-3卷数学理正文
2018年普通高等学校招生全国统一考试理科数学 (全国 Ⅰ 卷)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2018·高考全国卷Ⅰ)设z =1-i1+i +2i ,则|z |=( )A .0 B.12 C .1D. 22.(2018·高考全国卷Ⅰ)已知集合A ={x |x 2-x -2>0},则∁R A =( ) A .{x |-1<x <2} B.{x |-1≤x ≤2} C .{x |x <-1}∪{x |x >2}D.{x |x ≤-1}∪{x |x ≥2}3.(2018·高考全国卷Ⅰ)某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是( ) A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4.(2018·高考全国卷Ⅰ)记S n 为等差数列{a n }的前n 项和.若3S 3=S 2+S 4,a 1=2,则a 5=( )A .-12 B.-10 C .10D.125.(2018·高考全国卷Ⅰ)设函数f (x )=x 3+(a -1)x 2+ax .若f (x )为奇函数,则曲线y =f (x )在点(0,0)处的切线方程为( )A .y =-2x B.y =-x C .y =2xD.y =x6.(2018·高考全国卷Ⅰ)在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB →=( )A.34AB →-14AC →B.14AB →-34AC →C.34AB →+14AC → D.14AB →+34AC → 7.(2018·高考全国卷Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为( )A .217 B.2 5 C .3D.28.(2018·高考全国卷Ⅰ)设抛物线C :y 2=4x 的焦点为F ,过点(-2,0)且斜率为23的直线与C 交于M ,N 两点,则FM →·FN →=( )A .5 B.6 C .7D.89.(2018·高考全国卷Ⅰ)已知函数f (x )=⎩⎪⎨⎪⎧e x , x ≤0ln x , x >0,g (x )=f (x )+x +a .若g (x )存在2个零点,则a 的取值范围是( )A .[-1,0) B.[0,+∞) C .[-1,+∞)D.[1,+∞)10.(2018·高考全国卷Ⅰ)下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC 的斜边BC ,直角边AB ,AC .△ABC 的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p 1,p 2,p 3,则( )A .p 1=p 2 B.p 1=p 3 C .p 2=p 3D.p 1=p 2+p 311.(2018·高考全国卷Ⅰ)已知双曲线C :x 23-y 2=1,O 为坐标原点,F 为C 的右焦点,过F 的直线与C 的两条渐近线的交点分别为M ,N .若△OMN 为直角三角形,则|MN |=( )A.32B.3 C .2 3D.412.(2018·高考全国卷Ⅰ)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )A.334B.233C.324D.32二、填空题:本题共4小题,每小题5分,共20分.13.(2018·高考全国卷Ⅰ)若x ,y 满足约束条件⎩⎪⎨⎪⎧x -2y -2≤0x -y +1≥0y ≤0,则z =3x +2y 的最大值为________.14.(2018·高考全国卷Ⅰ)记S n 为数列{a n }的前n 项和.若S n =2a n +1,则S 6=________.15.(2018·高考全国卷Ⅰ)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有________种.(用数字填写答案)16.(2018·高考全国卷Ⅰ)已知函数f (x )=2sin x +sin 2x ,则f (x )的最小值是________. 三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17.(2018·高考全国卷Ⅰ)在平面四边形ABCD 中,∠ADC =90°,∠A =45°,AB =2,BD =5.(1)求cos ∠ADB ; (2)若DC =22,求BC .18.(2018·高考全国卷Ⅰ)如图,四边形ABCD 为正方形,E ,F 分别为AD ,BC 的中点,以DF 为折痕把△DFC 折起,使点C 到达点P 的位置,且PF ⊥BF .(1)证明:平面PEF ⊥平面ABFD ; (2)求DP 与平面ABFD 所成角的正弦值.19.(2018·高考全国卷Ⅰ)设椭圆C :x 22+y 2=1的右焦点为F ,过F 的直线l 与C 交于A ,B 两点,点M 的坐标为(2,0).(1)当l 与x 轴垂直时,求直线AM 的方程; (2)设O 为坐标原点,证明:∠OMA =∠OMB .20.(2018·高考全国卷Ⅰ)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验.设每件产品为不合格品的概率都为p (0<p <1),且各件产品是否为不合格品相互独立.(1)记20件产品中恰有2件不合格品的概率为f (p ),求f (p )的最大值点p 0.(2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的p 0作为p 的值,已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.(ⅰ)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X ,求EX ;(ⅱ)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?21.(2018·高考全国卷Ⅰ)已知函数f (x )=1x -x +a ln x .(1)讨论f (x )的单调性;(2)若f (x )存在两个极值点x 1,x 2,证明:f (x 1)-f (x 2)x 1-x 2<a -2.22.(2018·高考全国卷Ⅰ)在直角坐标系xOy 中,曲线C 1的方程为y =k |x |+2.以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ2+2ρcos θ-3=0.(1)求C 2的直角坐标方程;(2)若C 1与C 2有且仅有三个公共点,求C 1的方程. 23.(2018·高考全国卷Ⅰ)已知f (x )=|x +1|-|ax -1|. (1)当a =1时,求不等式f (x )>1的解集;(2)若x ∈(0,1)时不等式f (x )>x 成立,求a 的取值范围.22018年普通高等学校招生全国统一考试理科数学 (全国 Ⅱ 卷)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2018·高考全国卷Ⅱ)1+2i 1-2i=( )A .-45-35iB .-45+35iC .-35-45iD .-35+45i2.(2018·高考全国卷Ⅱ)已知集合A ={(x ,y )|x 2+y 2≤3,x ∈Z ,y ∈Z },则A 中元素的个数为( )A .9B.8C .5D.43.(2018·高考全国卷Ⅱ)函数f (x )=e x -e -xx 2的图象大致为( )4.(2018·高考全国卷Ⅱ)已知向量a ,b 满足|a|=1,a·b =-1,则a·(2a -b )=( ) A .4 B.3 C .2D.05.(2018·高考全国卷Ⅱ)双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为3,则其渐近线方程为( )A .y =±2x B.y =±3x C .y =±22xD.y =±32x6.(2018·高考全国卷Ⅱ)在△ABC 中,cos C 2=55,BC =1,AC =5,则AB =( )A .4 2 B.30 C.29D.2 57.(2018·高考全国卷Ⅱ)为计算S =1-12+13-14+…+199-1100,设计了右侧的程序框图,则在空白框中应填入( )A .i =i +1B .i =i +2C .i =i +3D .i =i +48.(2018·高考全国卷Ⅱ)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( )A.112B.114C.115D.1189.(2018·高考全国卷Ⅱ)在长方体ABCD -A 1B 1C 1D 1中,AB =BC =1,AA 1=3,则异面直线AD 1与DB 1所成角的余弦值为( )A.15B.56C.55D.2210.(2018·高考全国卷Ⅱ)若f (x )=cos x -sin x 在[-a ,a ]是减函数,则a 的最大值是( )A.π4B.π2C.3π4D.π11.(2018·高考全国卷Ⅱ)已知f (x )是定义域为(-∞,+∞)的奇函数,满足f (1-x )=f (1+x ),若f (1)=2,则f (1)+f (2)+f (3)+…+f (50)=( )A .-50 B.0 C .2D.5012.(2018·高考全国卷Ⅱ)已知F 1,F 2是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,A 是C 的左顶点,点P 在过A 且斜率为36的直线上,△PF 1F 2为等腰三角形,∠F 1F 2P =120°,则C 的离心率为( )A.23B.12C.13D.14二、填空题:本题共4小题,每小题5分,共20分.13.(2018·高考全国卷Ⅱ)曲线y =2ln(x +1)在点(0,0)处的切线方程为________. 14.(2018·高考全国卷Ⅱ)若x ,y 满足约束条件⎩⎪⎨⎪⎧x +2y -5≥0x -2y +3≥0x -5≤0,则z =x +y 的最大值为________.15.(2018·高考全国卷Ⅱ)已知sin α+cos β=1,cos α+sin β=0,则sin(α+β)=________.16.(2018·高考全国卷Ⅱ)已知圆锥的顶点为S,母线SA,SB所成角的余弦值为78,SA与圆锥底面所成角为45°.若△SAB的面积为515,则该圆锥的侧面积为________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17.(2018·高考全国卷Ⅱ)记S n为等差数列{a n}的前n项和,已知a1=-7,S3=-15.(1)求{a n}的通项公式;(2)求S n,并求S n的最小值.18.(2018·高考全国卷Ⅱ)下图是某地区2000年至2016年环境基础设施投资额y(单位:亿元)的折线图.为了预测该地区2018年的环境基础设施投资额,建立了y与时间变量t的两个线性回归模型.根据2000年至2016年的数据(时间变量t的值依次为1,2,…,17)建立模型①:y^=-30.4+13.5 t;根据2010年至2016年的数据(时间变量t的值依次为1,2,…,7)建立模型②:y^=99+17.5t.(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;(2)你认为用哪个模型得到的预测值更可靠?并说明理由.19.(2018·高考全国卷Ⅱ)设抛物线C:y2=4x的焦点为F,过F且斜率为k(k>0)的直线l与C交于A,B两点,|AB|=8.(1)求l的方程;(2)求过点A,B且与C的准线相切的圆的方程.20.(2018·高考全国卷Ⅱ)如图,在三棱锥P-ABC中,AB=BC=22,P A=PB=PC=AC=4,O为AC的中点.(1)证明:PO⊥平面ABC;(2)若点M在棱BC上,且二面角M-P A-C为30°,求PC与平面P AM所成角的正弦值.21.(2018·高考全国卷Ⅱ)已知函数f (x )=e x -ax 2. (1)若a =1,证明:当x ≥0时,f (x )≥1; (2)若f (x )在(0,+∞)只有一个零点,求a .22.(2018·高考全国卷Ⅱ)在直角坐标系xOy 中,曲线C 的参数方程为⎩⎪⎨⎪⎧x =2cos θy =4sin θ(θ为参数),直线l 的参数方程为⎩⎪⎨⎪⎧x =1+t cos αy =2+t sin α(t 为参数).(1)求C 和l 的直角坐标方程;(2)若曲线C 截直线l 所得线段的中点坐标为(1,2),求l 的斜率. 23.(2018·高考全国卷Ⅱ)设函数f (x )=5-|x +a |-|x -2|. (1)当a =1时,求不等式f (x )≥0的解集; (2)若f (x )≤1,求a 的取值范围.2018年普通高等学校招生全国统一考试理科数学 (全国 Ⅲ 卷)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2018·高考全国卷Ⅲ)已知集合A ={x |x -1≥0},B ={0,1,2},则A ∩B =( ) A .{0} B .{1} C .{1,2} D .{0,1,2} 2.(2018·高考全国卷Ⅲ)(1+i)(2-i)=( ) A .-3-i B.-3+i C .3-iD.3+i3.(2018·高考全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )4.(2018·高考全国卷Ⅲ)若sin α=13,则cos 2α=( )A.89B.79 C .-79D.-895.(2018·高考全国卷Ⅲ)(x 2+2x)5的展开式中x 4的系数为( )A.10 B.20C.40 D.806.(2018·高考全国卷Ⅲ)直线x+y+2=0分别与x轴,y轴交于A,B两点,点P在圆(x -2)2+y2=2上,则△ABP面积的取值范围是()A.[2,6] B.[4,8]C.[2,32] D.[22,32]7.(2018·高考全国卷Ⅲ)函数y=-x4+x2+2的图象大致为()8.(2018·高考全国卷Ⅲ)某群体中的每位成员使用移动支付的概率都为p, 各成员的支付方式相互独立.设X为该群体的10位成员中使用移动支付的人数,DX=2.4,P(X=4)<P(X=6),则p=()A.0.7 B.0.6 C.0.4 D.0.39.(2018·高考全国卷Ⅲ)△ABC的内角A,B,C的对边分别为a,b,c.若△ABC的面积为a2+b2-c24,则C=()A.π2 B.π3C.π4 D.π610.(2018·高考全国卷Ⅲ)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为93,则三棱锥D-ABC体积的最大值为() A.12 3 B.18 3C.24 3 D.54 311.(2018·高考全国卷Ⅲ)设F1,F2是双曲线C:x2a2-y2b2=1(a>0,b>0)的左,右焦点,O是坐标原点.过F2作C的一条渐近线的垂线,垂足为P.若|PF1|=6|OP|,则C的离心率为()A. 5B.2C. 3D. 212.(2018·高考全国卷Ⅲ)设a =log 0.20.3,b =log 20.3,则( ) A .a +b <ab <0 B.ab <a +b <0 C .a +b <0<abD.ab <0<a +b二、填空题:本题共4小题,每小题5分,共20分.13.(2018·高考全国卷Ⅲ)已知向量a =(1,2),b =(2,-2),c =(1,λ).若c ∥(2a +b ),则λ=________.14.(2018·高考全国卷Ⅲ)曲线y =(ax +1)e x 在点(0,1)处的切线的斜率为-2,则a =________.15.(2018·高考全国卷Ⅲ)函数f (x )=cos(3x +π6)在[0,π]的零点个数为________.16.(2018·高考全国卷Ⅲ)已知点M (-1,1)和抛物线C :y 2=4x ,过C 的焦点且斜率为k 的直线与C 交于A ,B 两点.若∠AMB =90°,则k =________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤. 17.(2018·高考全国卷Ⅲ)等比数列{a n }中,a 1=1,a 5=4a 3. (1)求{a n }的通项公式;(2)记S n 为{a n }的前n 项和.若S m =63,求m .18.(2018·高考全国卷Ⅲ)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;(2)求40名工人完成生产任务所需时间的中位数m ,并将完成生产任务所需时间超过m 和不超过m 的工人数填入下面的列联表:超过m不超过m第一种生产方式第二种生产方式(3)根据(2)附:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),P (K 2≥k )0.050 0.010 0.001 k3.8416.63510.82819.(2018·高考全国卷Ⅲ)如图,边长为2的正方形ABCD 所在的平面与半圆弧CD ︵所在平面垂直,M 是CD ︵上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC;(2)当三棱锥M -ABC 体积最大时,求平面MAB 与平面MCD 所成二面角的正弦值. 20.(2018·高考全国卷Ⅲ)已知斜率为k 的直线l 与椭圆C :x 24+y 23=1交于A ,B 两点,线段AB 的中点为M (1,m )(m >0).(1)证明:k <-12;(2)设F 为C 的右焦点,P 为C 上一点,且FP →+F A →+FB →=0.证明:|FA →|,|FP →|,|FB →|成等差数列,并求该数列的公差.21.(2018·高考全国卷Ⅲ)已知函数f(x)=(2+x +ax 2)ln (1+x)-2x. (1)若a =0,证明:当-1<x<0时,f(x)<0;当x>0时,f(x)>0; (2)若x =0是f(x)的极大值点,求a.22.(2018·高考全国卷Ⅲ)在平面直角坐标系xOy 中,⊙O 的参数方程为⎩⎪⎨⎪⎧x =cos θy =sin θ(θ为参数),过点(0,-2)且倾斜角为α的直线l 与⊙O 交于A ,B 两点.(1)求α的取值范围;(2)求AB 中点P 的轨迹的参数方程.23.(2018·高考全国卷Ⅲ)设函数f(x)=|2x +1|+|x -1|. (1)画出y =f(x)的图象;(2)当x ∈[0,+∞)时,f(x)≤ax +b ,求a +b 的最小值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018届全国高三考前密卷(三)文科数学本试题卷共10页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{|(3)0}A x N x x =∈-≥,{|22}B x x =-≤≤,则AB =( )A .{|02}x x ≤≤B .{0,1,2}C .{|02}x x <<D .{0,1}2.已知复数13ai z i+=-(a R ∈,i 为虚数单位)是纯虚数,则a 的值为( ) A .3 B .13 C .3- D .13-3.已知()cos 3cos 22sin cos παααπα⎛⎫-- ⎪⎝⎭=-+,则tan α=( ) A .15 B .23- C .12D .5- 4.甲,乙,丙三位同学被选中参加校运会的仪仗队,现编排这三位同学分别站在队伍的前三排(每两人均不在同一排),则甲或乙站第一排的概率为( ) A .23 B .35 C .16 D .135.已知某几何体的三视图如图所示,则该几何体的体积为( )A .28B .3C .283D .22+6.已知函数2()2f x x x =+,执行如图所示的程序框图,则输出的k 值是( )A .4B .5C .6D .8 7.已知圆的方程为,直线恒过点,则“直线的斜率为”是“与圆相切”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件8.某月在旅游旺季的一景区有一织女织土布卖,随着游客增多,从本月1号至30号共织了390尺布,且从2号开始,每天比前一天多织相同量的布,第1天织了5尺布,求她在该月中的14号15号16号17号这4天共织了多少尺布?( )A .55B .52C .39D .26 9.将函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭的图象上所有点的横坐标缩短到原来的12倍,纵坐标不变,再向左平移24π个单位长度,得到函数()y g x =的图象,则下列对函数()y g x =的叙述正确的是( )A .函数()2sin 3g x x π⎛⎫=+⎪⎝⎭B .函数()g x 的周期为πC .函数()g x 的一个对称中心点为,012π⎛⎫-⎪⎝⎭ D .函数()g x 在区间,63ππ⎡⎤⎢⎥⎣⎦上单调递增 10.椭圆C :22221(0)x y a b a b+=>>的两焦点为1F 、2F ,P 为椭圆C 上一点,且2PF x ⊥轴,点,22c c G ⎛⎫⎪⎝⎭到1F P 的距离为2c,则椭圆C 的离心率为( ) A .14 B .12 CD11.若方程26x y +=,在x ,y 满足的不等式组23262x y x y x y a +≥⎧⎪-≤⎨⎪-≥⎩,所表示的平面区域内有解,则实数a 的取值范围是( )A .(,0]-∞B .[1,)+∞C .(,1]-∞D .以上都不正确12.已知函数231(0)()3log (0)x x f x x x ⎧≤⎪=⎨⎪>⎩,函数()g x 是周期为2的奇函数,且当[0,1]x ∈时,234()log (1)g x x x =-+,则函数()()()F x f x g x =-的零点个数是( )A .8B .7C .6D .5二、填空题(本大题共4小题,每小题5分,共20分)13.命题“00x ∃>,20020x mx +->”的否定是 .14.已知向量(,1)a s t =-,(1,1)b =,且a b a b -=+,则st 的最大值为 . 15.抛物线24y x =的焦点为F ,过F 的直线与抛物线交于A ,B 两点,且满足4AFBF=,点O 为原点,则AOF ∆的面积为 .16.数列{}n a 的前n 项和2(1)2n n n S +⎡⎤=⎢⎥⎣⎦,数列{}n b 满足2n n a b n =,则对于任意的正整数n ,下列结论正确的是 .①112231n n n nb b b b b b b b ++++⋅⋅⋅+=; ②12112n b b b n++⋅⋅⋅+<; ③122225124n b b b n ++⋅⋅⋅+<; ④12111112n n n b b b b b +++⋅⋅⋅+=. 三、解答题(共70分.解答应写出文字说明、证明过程或演算步骤)17.在三角形ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且sin sin B C =,1)(sin sin )2sin A B C -=.(1)求角B 的大小;(2)若ABC ∆的面积为a ,b ,c 的值.18.某校想了解高二数学成绩在学业水平考试中的情况,从中随机抽出50人的数学成绩作为样本并进行统计,频率分布表如下表所示.(1)据此估计这次参加数学考试的高二学生的数学平均成绩;(2)从这五组中抽取14人进行座谈,若抽取的这14人中,恰好有2人成绩为50分,7人成绩为70分,2人成绩为75分,3人成绩为80分,求这14人数学成绩的方差; (3)从50人的样本中,随机抽取测试成绩在[50,60](90,100]内的两名学生,设其测试成绩分别为M ,N .(i )求事件“30M N ->”的概率;(ii )求事件“3600MN ≤”的概率.19.如图,在等腰梯形ADEB 中,//BE AD ,且2224AD BE AB BC ====,沿BC 翻折使得平面ABC ⊥平面BCDE ,得到四棱锥A BCDE -,若点F 为AE 的中点.(1)求证://AC 平面BDF ; (2)求点C 到平面ABE 的距离.20.已知圆心为(0,)(0)C s s >C 被直线3410x y ++=截得的弦长为4,等轴双曲线M 的上焦点是圆C 的圆心. (1)求双曲线M 的标准方程;(2)(2,0)D -,(2,0)E 为x 轴上的两点,若圆C 内的动点P 使得PD ,PO ,PE 成等比数列(O 为原点),求PD PE ⋅的取值范围. 21.已知函数()ln (0)kf x x k x=+>. (1)曲线()y f x =在点(1,(1))f 处的切线斜率为1-,求该切线方程;(2)若函数()2f x ≥在区间[1,]e 上恒成立,且存在0[1,]x e ∈使得0()2f x =,求k 的值.请考生在22、23两题中任选一题作答,并用2B 铅笔在答题卡上把所选题目的题号涂黑.注意所做题目的题号必须与所涂题目的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线C 的参数方程为cos 2sin x a ty t =⎧⎨=⎩(t 为参数,0a >),已知直线l 的方程为40x y -+=.(1)设P 是曲线C 上的一个动点,当2a =时,求点P 到直线l 的距离的最小值; (2)若曲线C 上的所有点均在直线l 的右下方,求a 的取值范围.23.选修4-5:不等式选讲已知函数2()2f x x =+,()1g x x a x =---,a R ∈. (1)若4a =,求不等式()()f x g x >的解集;(2)若对任意的12,x x R ∈,不等式12()()f x g x ≥恒成立,求实数a 的取值范围.文科数学参考答案一、选择题1-5: BADAC 6-10: CABCB 11、12:AC二、填空题13. 202x x mx ∀>+-,≤0 14.1415. 2 16. ①③④ 三、解答题17.解:(Ⅰ)∵sin sin B C =,1)(sin sin )2sin A B C -=,∴sin sin 1)sin A B C -=,∴由正弦定理可得:b c =,1)a b c -=,得a =,∴222222cos 2a c b B ac +-===又∵(0)B ∈π,, ∴6B π=.(Ⅱ)∵ABC △的面积为,∴2111sin 222ac B =⨯=4c =,∴由(Ⅰ)可得4b a ==,. 18.解:(Ⅰ)先求得a 为9,b 为0.40. 估计高二学生的数学平均成绩为:550.04650.18750.4850.32950.0676.8⨯+⨯+⨯+⨯+⨯=.(Ⅱ)这14人数学成绩的平均分为:5027077528037014x ⨯+⨯+⨯+⨯==,∴这14人数学成绩的方差为:222221575[2(5070)7(7070)2(7570)3(8070)]147s =-+-+-+-=. (Ⅲ)(i )由频数分布表知,成绩在[5060],内的人数有2人,设其成绩分别为x ,y ; 在(90100],内的人数有3人,设其成绩分别为a ,b ,c ,若[5060]M N ∈,,时,只有()x y ,一种情况;若(90100]M N ∈,,时,有()a b ,,()b c ,,()a c ,三种情况; 若M N ,分别在[5060],和(90100],内时,有:共6种情况,∴基本事件总数为10种,事件“||30M N ->”所包含的基本事件有6种, ∴63(||30)105P M N ->==. (ii )事件3600MN ≤的基本事件只有()x y ,这一种, ∴1(3600)10P MN =≤. 19.(Ⅰ)证明:如图,连接CE 交BD 于点H ,连接HF , 因为四边形BCDE 是菱形, 所以点H 为CE 的中点, 又点F 是AE 的中点, 所以//AC HF ,又因为AC ⊄平面BDF ,且HF ⊂平面BDF , 所以//AC 平面BDF .(Ⅱ)解:如图4,取BC 的中点O ,连接OA ,OE ,CE , 因为等边ABC △的边长为2,则在BOE △中,1260OB BE CBE ==∠=︒,,, ∴90BOE ∠=︒, 即OE BC ⊥,因为ABC △是等边三角形,所以OA BC ⊥, 因为平面ABC ⊥平面BCDE , 又因为平面ABC平面BCDE BC =,且OA ⊂平面ABC ,所以OA ⊥平面BCDE ,在BCE △中,2BC BE ==,60CBE ∠=︒,所以BCE S =△在ABE △中,因为2AB BE AE ===,ABE S =△ 设点C 到平面ABE 的距离为d ,则由A BCE C ABE V V --=,得1133BCE ABE S AO S d ⨯⨯=⨯⨯△△,解得d =, 所以点C 到平面ABE20.解:(Ⅰ)双曲线的焦点(0)C s ,, 圆心C 到直线3410x y ++=的距离|41|15s d +=,得1s =, 故圆C 的标准方程为22(1)5(01)x y C +-=,,, 双曲线M 的上焦点为(01),, ∴2221122a b c ===,双曲线M 的标准方程为221122y x -=1. (Ⅱ)设()P x y ,,∵||||||PD PO PE ,,成等比数列,222(2)x x y -=+,整理得222x y -=,故222(2)(2)42(1)PD PE x y x y x y y =-----=-+=-,,,由于P 在圆C 内,则2222(1)52x y x y ⎧+-<⎪⎨-=⎪⎩,, 得210y y --<y <<,则220y <=⎝⎭≤∴22(1)[21y -∈-,,则PD PE的取值范围是[21-,.21.解:(Ⅰ)由()ln (0)k f x x k x =+>,2()x kf x x -'=,(1)1f k '=-,由切线斜率为1-,得11k -=-,解得2k =,则(1)2f =,∴函数()f x 在1x =处的切线方程是2(1)y x -=--,即30x y +-=. (Ⅱ)即函数()f x 在区间[1e],上有最小值2. 由(Ⅰ)知,2()[1e]x kf x x x -'=∈,,, ①当1e k <<时,在区间[1]k ,上有()0f x '≤,函数()f x 在区间[1]k ,上单调递减; 在区间(e]k ,上有()0f x '>,函数()f x 在区间(e]k ,上单调递增, ∴()f x 的最小值是()ln 1f k k =+, 由ln 12k +=,得e k =,与1e k <<矛盾; ②当e k =时,()0f x '≤,()f x 在[1e],上递减, ∴()f x 的最小值是(e)2f =,符合题意; ③当e k >时,显然()f x 在区间[1e],上递减, 最小值是(e)12ekf =+>,与最小值是2矛盾; 综上,e k =.22.【选修4−4:坐标系与参数方程】解:(Ⅰ)依题意,设(2cos 2sin )P t t ,,则点P 到直线l 的距离2cos d t π⎛⎫===+ ⎪4⎝⎭,当2t k π+=π+π4,即2t k 3π=π+4,k ∈Z时,min 2d =,故点P 到直线l的距离的最小值为2.(Ⅱ)因为曲线C 上的所有点均在直线l 的右下方,所以对t ∀∈R ,有cos 2sin 40a t t -+>恒成立,)4t ϕ+>-2tan a ϕ⎛⎫= ⎪⎝⎭其中恒成立,4<,又0a >,所以0a <<故a的取值范围为(0,.23.【选修4−5:不等式选讲】解:(Ⅰ)当4a =时,22|4||1|x x x +>---.34()|4||1|251431x g x x x x x x -⎧⎪=---=-+<<⎨⎪⎩,≥,,,,≤,①当4x ≥时,223x +>-恒成立,∴4x ≥;②当14x <<时,2225x x +>-+,即2230x x +->,即1x >或3x <-. 综合可知:14x <<;③当1x ≤时,223x +>,则1x >或1x <-,综合可知:1x <-. 由①②③可知:{|1x x <-或1}x >.(Ⅱ)当1a >时,1()12111a x a g x a x x a a x -⎧⎪=+-<<⎨⎪-⎩,≥,,,,≤,()g x 的最大值为1a -,要使12()()f x g x ≥,故只需21a -≥,则3a ≤,∴13a <≤;当1a ≤时,11()2111a x g x x a a x a x a -+⎧⎪=--<<⎨⎪-⎩,≥,,,,≤,()g x 的最大值为1a -,要使12()()f x g x ≥,故只需21a -≥,∴1-≤≤.aa-≥,从而11综上讨论可知:13-≤≤.a。
