江苏省丹阳市华南实验学校七年级数学下册《11.4探索三角形全等之尺规作图》教案 苏科版
《探索三角形全等的条件》教案 (同课异构)2022年苏科版 (7)
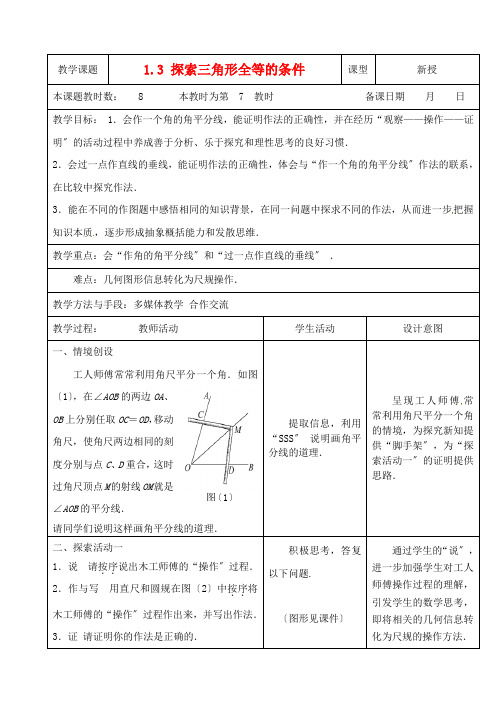
图〔1〕教学课题1.3 探索三角形全等的条件课型 新授本课题教时数: 8 本教时为第 7 教时 备课日期 月 日 教学目标: 1.会作一个角的角平分线,能证明作法的正确性,并在经历“观察——操作——证明〞的活动过程中养成善于分析、乐于探究和理性思考的良好习惯.2.会过一点作直线的垂线,能证明作法的正确性,体会与“作一个角的角平分线〞作法的联系,在比较中探究作法.3.能在不同的作图题中感悟相同的知识背景,在同一问题中探求不同的作法,从而进一步把握知识本质,逐步形成抽象概括能力和发散思维.教学重点:会“作角的角平分线〞和“过一点作直线的垂线〞 .难点:几何图形信息转化为尺规操作. 教学方法与手段:多媒体教学 合作交流 教学过程: 教师活动 学生活动设计意图一、情境创设工人师傅常常利用角尺平分一个角.如图〔1〕,在∠AOB 的两边OA 、OB 上分别任取OC =OD ,移动角尺,使角尺两边相同的刻度分别与点C 、D 重合,这时过角尺顶点M 的射线OM 就是∠AOB 的平分线.请同学们说明这样画角平分线的道理. 提取信息,利用“SSS 〞 说明画角平分线的道理.呈现工人师傅常常利用角尺平分一个角的情境,为探究新知提供“脚手架〞,为“探索活动一〞的证明提供思路.二、探索活动一1.说 请按序..说出木工师傅的“操作〞过程. 2.作与写 用直尺和圆规在图〔2〕中按序..将木工师傅的“操作〞过程作出来,并写出作法. 3.证 请证明你的作法是正确的.积极思考,答复以下问题.〔图形见课件〕通过学生的“说〞,进一步加强学生对工人师傅操作过程的理解,引发学生的数学思考,即将相关的几何信息转化为尺规的操作方法.4.用 用直尺和圆规完成以下作图: 〔1〕在图〔3〕中把∠MON 四等分.〔2〕在图〔4〕中作出平角∠AOB 的平分线.说明:过直线上一点作这条直线的垂线就是作以这点为顶点的平角的角平分线.“说〞与“作〞对应,为学生“按序〞尺规作图提供更为清晰的流程,这样设计使得学生易想、易作和易写,对突破难点,养成有条理的思考十分有益. “用〞就是为了稳固新知和发现新法.为圆心,大于12CDba 图〔8〕3.3代数式的值〔2〕的垂线〔如图〔7〕〕.〔2〕证明略. 5.归纳总结.根据活动一中的4〔2〕与活动二可知:经过一点可用直尺和与圆规作一条直线与直线垂直. 四、知识运用 用直尺和圆规作一个直角三角形,使它的两条直角边分别等于a 、b 〔如图〔8〕〕. 1.学生尝试作图;2.交流作法; 3.总结作两条相互垂直直线的方法.此题解决的关键是作两条相互垂直的直线,但点的位置没有确定,故根据点的位置的不同可选择不同的解题策略.五、拓展延伸如图〔9〕,A 、B 是l 上的两点,P 是l 外的一点.〔1〕按照下面画法作图〔保存作图痕迹〕: ①以A 为圆心,AP 为半径画弧; ②以B 为圆心,BP 为半径画弧;③设两弧交于点Q 〔Q 与P 分别在l 的两旁〕; ④连结PQ . 〔2〕求证:PQ ⊥l .1.学生按要求独立作图与证明; 2.小组交流:与前面一种方法进行比较,说明两种方法的异同点.相同的问题,不同的解法有利于培养学生的发散思维,激发学生学习几何图形的兴趣. 通过比较两种不同的方法,进一步加深理解根本作图的知识本质.六、课堂小结知识联系网络图〔教师逐一展示,引导学生回忆总结〕:〔图见课件〕 根据教师对网络图的逐步展示,学生进行回忆和总结.网络化的总结方式有利于长时记忆的形成,有利于完善学生的认知结构,有利于加强知识之间的联系,揭示作图的知识本质.七、作业?补充习题?P12-13 学生独立完成。
1.3探索三角形全等条件(7)尺规作图

2.(2014年贵州安顺)用直尺和圆规作一个角等于已知角,如 图,能得出∠A′O′B′=∠AOB的依据是( )
A.(SAS)
B. (SSS)
C. (ASA) D. (AAS)
3. ( 2014•广东)如图,点D在△ABC的AB边上,且 ∠ACD=∠A. (1)作∠BDC的平分线DE,交BC于点E(用尺规作图法,保 留作图痕迹,不要求写作法); (2)在(1)的条件下,判断直线DE与直线AC的位置关系 (不要求证明).
P
A
B
4.作法.
步骤1 以点P为圆心,适当的长为半径作弧,使它与 直线AB交于C、D.
步骤2 分别以点C、D为圆心,大于 CD的长为半径作弧, 两弧交于点Q. 步骤3 作直线PQ.
∴直线PQ就是经过直线AB外一点P的AB的垂线.
1 2
四、拓展延伸
如图,已知A、B是l上的两点,P是l外的 一点.(1)按照下面画法作图(保留作 图痕迹): ①以A为圆心,AP为半径画弧; ②以B为圆心,BP为半径画弧; ③设两弧交于点Q(Q与P分别在l 的两旁); ④连结PQ. (2)求证:PQ⊥l.
六、课堂小结
作已知角的 角平分线 特例 过直线上的一点作 已知直线的垂线
活 动 一
变式
作图依据:SSS
活 动 二 方法1:活动二
方法2:拓展延伸
过直线外的一点作 作法 已知直线的垂线
过平面上一点作已知直线的垂线
知识应用:一题多解
M
O
N
A
O
B
图(1)
图(2)
结论:过直线上一点作这条直 线的垂线就是作以这点为顶点 的平角的角平分线.
三、探索活动2
1.观察思考 在作角平分线图的基础上,作过C、 D的直线l(如图),观察图中射线OM与直线l的位 置关系,并说明理由.
数学初一下苏科版11.3探索三角形全等的条件(第4课时)教案

数学初一下苏科版11.3探索三角形全等的条件(第4课时)教案 学习目标 知识与技能:1.掌握角平分线的性质,会用直尺和圆规作角平分线。
2.能结合具体的问题和情景进行有条理的思考,会用“因为……所以……”或“因为……依照……因此……”的表达方式进行简单的说理。
过程与方法:经历观看、活动、分析、讨论、探究等过程,进一步锻炼学生的动手能力和思维的缜密性。
情感、态度与价值观:体会全等三角形在生产和生活中的应用,体会数学的应用价值,从而激发学生学习数学的兴趣。
学习重点 掌握角平分线的性质,会用直尺和圆规作角平分线。
学习难点 结合具体的问题和情景进行有条理的思考。
教学流程预习导航 1、向学生介绍木工师傅用角尺平分任意角的情况.(引导学生联系角平分线的性质,理解角平分线作法的依据。
)学生举例:生活中的角平分线合作探究 【一】新知探究:动手操作:1、向学生介绍关角尺的做法;让学生利用课前预备的工具〔两根小木片,一颗图钉〕自制一个小角尺.2、利用自制的小角尺平分任意角。
3、用直尺和圆规作∠AOB 的平分线。
作法:〔1〕以O 为圆心,任意长为半径画弧,分别交射线OA 、OB 于点D 、E 。
〔2〕分别以D 、E 为圆心,大于DE 为半径画圆弧,在∠AOB 的内部交与点C. 〔3〕画射线OC. OC 确实是∠AOB 的平分线.图形:O注:画图过程中要注重原理的讲解.(全等三角形的性质) CBE P AC 【二】例题分析:例3 如图,点A 、C 、D 、F 在同一条直线上,AB=FE ,BC=ED ,AD=FC.∠B 与∠E 相等吗?什么原因?分析:要说明∠B=∠E ,只要能断定ΔABC ≌ΔFED 。
要使ΔABC ≌ΔFED,除了有条件AB=EF ,BC=ED 以外还应该有条件AC=FD ,而由AD=FC 就能得到AC=FD.解∠B=∠E.因为AD=FC,AC=AD -CD, FD=FC -CD 因此AC=FD又因为AB=EF ,BC=ED,依照“SSS ”,能够明白ΔABC ≌ΔFED 。
数学:11.3《探索三角形全等的条件》(第2课时)课件(苏科版七年级下)

A
D
C
E
B
观察课本113页图11-10中的三角 形,先猜一猜,再量一量,哪两 个三角形是全等三角形?
哪些条件决定了⊿ABC与⊿FDE全等? ⊿ABC与⊿PQR有哪几个相等的条件? 为什么它们不全等?
做一做
• 如图,画线段AB=2.6cm,再画∠BAP=45°, ∠ABQ=60°,AP与BQ相交与点C。 剪下所画⊿ABC,与同学所画的三角形 Q 能重合吗?
A
A'
________ (
∴△——≌△———(
)
)
E B
D C
练 习 1
.已知:如图,AB=A’C,∠A=∠A’,∠B=∠C 求证:△ABE≌ △A’CD
证明:在△ABE和△A’CD中
∠A=∠A’ (已知 ) AB=A’C(已知 ) ∠B=∠C(已知 ) ∴ △ABE≌△A’CD(ASA)
A
A'
E B
D
∴∠ABD=∠ABC
在△——和△——中 ——( —— ( ∴—— ) —— (公共边) )
A
B
C
)
∴△—— ≌ △——(
(全等三角形对应边相等)
巩 固 练 习
1.如图,∠1=∠2,∠3=∠4 求证:AC=AD 证明:∵∠ABD=180-∠3 ∠ABC=180-∠4 而∠3=∠4(已知)
D
∴∠ABD=∠ABC
在△ABD和△ABC中 ∠1=∠2(已知 ) AB=AB (公共边) ∠ABD=∠ABC (已知 )
A
B
C
∴△ABD ≌ △ABC(ASA )
∴AC=AD (全等三角形对应边相等)
[名校联盟]江苏省丹阳市华南实验学校七年级数学图形的全等复习课件
![[名校联盟]江苏省丹阳市华南实验学校七年级数学图形的全等复习课件](https://img.taocdn.com/s3/m/8a65dc2c27284b73f242509b.png)
(2)在旋转过程中,还会存在与图①②不同的情形吗? 若存在,请在图③中画出,并加以说明
A
A
A
D
P
D
CE B
C
P EBC
P
E B
①
②
D③
• (2)若以“AAS”为依据,则需添加一个条件∠_B_A_C=_∠_C_D_B
_
∠1=∠2
• (3)若以“ASA”为依据,则需添加一个条件_______
_△AFC≌△BED
• 11、如图,∠A=∠B,∠1=∠2,AD=BC,则全等的三角形是
_________
E
F
A
A
D
O
D
C
B
B 13
E
2
4
CA
1
2
C DB
• 例1、现给出下列条件①∠ADC=∠AEB;②DC= EB;③BD=CE。请从上面的条件中选择1个,填 在下列问题中的横线上,再解答.
• 如图,点D,E分别在AB、AC上,且AD=AE,_ ___,使△ADC≌△AEB。请说明理由。
A
D
E
F
B
C
例2、如图△ADB≌△EDB,△EDB≌△EDC,点B,E,C
C
FE
• 例6、如图①,线段BC上有一点E,以BC、CE为边分 别在BC的两侧作等边三角形ABC、DCE。连接AE、 BD。
• (1)线段BD和线段AE相等吗?若相等,说明理由。
• (2)若将CDE绕着点C顺时针旋转一个角α,则BD和AE 是否仍然相等?为什么?
• (3)将△CDE绕着点C逆时针旋转1800,画出旋转后 的图形,并说明上面结论是否仍然成立。
苏科版-数学-七年级下册-11.3探索三角形全等的条件(3) 教案

初中-数学-打印版
11.3探索三角形全等的条件(3)教案
课型:新授课年级:七下科目:数学主备:林国涛审核:李秀2010-5
一、教学目标:
1、掌握三角形全等的“边边边”的条件。
并能利用这个条件判别两个三角形是否全等,
解决一些简单的实际问题;
2、经历观察、实验、归纳、猜想,体会分析问题的方法,积累数学活动的经验,并培养
其探索创新的精神,营造和谐、平等的学习氛围。
二、教学重点与难点:
重点:三角形全等的“边边边”条件的探索及应用;
难点:三角形全等的“边边边”条件的探索。
二次备课
三、教学过程:
1、小组交流学案上的问题, 组长记录组内解决不了的问题。
2、教师收集疑难问题。
这些问题的解决先由学生主讲,再由教师完善。
3、例题精讲:
“三月三,放风筝”,如图是小明同学制作的风筝,他根据AB=AD,CB=CD,
ABC=∠ADC,请你用学过的知识给予说明.
四、教学小结
五、教学后记:
初中-数学-打印版。
7全等三角形的尺规作图
第7讲三角形的尺规作图一、教学目标理解尺规作图的含义,掌握尺规作图的步骤。
二、知识点梳理1、尺规作图定义:只用直尺(没有刻度)和圆规也可以画出一些图形,这种画图的方法被称为尺规作图。
注意:尺规作图中的直尺没有刻度。
2、已知三边作三角形已知三边求作三角形是利用三角形全等的条件“边边边”来作图的,具体作图的方法、步骤、图形如下:已知:线段a,b,c求作:△ABC,使AB=c,BC=a,AC=b作法与示范:(1)作线段AB=c(2)以点A为圆心,b为半径画弧(3)以点B为圆心,a为半径画弧,两弧交于点C(4)连接AC,BC,△ABC即为所求3、已知两边及其夹角作三角形已知两边及其夹角作三角形是利用三角形全等的条件“边角边”来作图的,具体作图的方法、步骤、图形如下:已知:线段a,b,∠α求作:△ABC,使∠B=∠α,BC=a,BA=b作法与示范:(1)作∠MBN=∠α(2)在射线BM,BN上分别截取线段BC=a,BA=b(3)连接AC,则△ABC为所求作的三角形4、已知两角及其夹边作三角形已知两角及其夹边求作三角形是利用三角形全等的条件“角边角”来作图的,具体作图的方法、步骤、图形如下:已知:∠α,∠β,线段a求作:△ABC,使∠BAC=∠α,∠ABC=∠β,AB=a作法与示范:(1)作线段AB=a(2)在AB同侧,作∠DAB=∠α,∠EBA=∠β,AD与BE相交于点C,则△ABC为所求作的三角形三、典型例题例1 下列作图属于尺规作图的是()A、用量角器画出∠AOB的平分线B、用圆规和直尺作∠AOB等于已知的∠αC、用刻度尺画线段AB=3 cmD、用三角板作直线AB的平分线例2 如图13-4-1,已知:线段a、b。
求作:△ABC,使AB=2a,AC=b,BC=a。
例3 如图13-4-3,已知:线段m,n,∠α。
求作:△ABC,使AB=2m,AC=2n,∠A=∠α。
例4 如图13-4-5,已知:线段a和∠α。
三角形全等的判定ASA-AAS及尺规作图五种基本作图ppt课件
27
1.如图,已知∠A,试画∠B=1/2∠A. (不写画法,保留作图痕迹).
( 第 1 题 ) 精选版课件ppt
28
2、试把下图所示的角四等分
A
O
精选版课件ppt
B
29
3.画出图中三角形三个内角的角平分 线.(不写画法,保留作图痕迹)
(第 2题)
精选版课件ppt
30
基本作图4. 经过一已知点作已知直线的垂线
∠B=∠C (已知)
AD=AD(公共边)
D
B
∴△ABD≌△ACD(AAS)
C
∴AB=AC(全等三角形的对应边相等)
若△ABD不动,将△ACD绕着A点顺时针转动,
且转动的角度等于∠CAD的度数, 此时图形会怎么样呢?
我们一起来看到:
精选版课件ppt
13
变式:
已知:AB=AC,∠B=∠C, BE和CD相交于点O
(5) 过点D’作射线O’B’.
则∠A’O’B’即为所求.
OO’ ’
精选版课件ppt
DB
CA
BB’’
D’
C’
AA’ ’
23
B D
B` D`
O
A
C
O`
C`
A`
证明:
,由作法可知
△C`O`D`≌△COD(SSS),
∴∠C`O`D`=∠COD(全等三角形的对 应角相等),
即∠A`O`B`=∠AOB。
精选版课件ppt
个三角形全等。 (简写成“角角边”或“AAS”
用符号语言表达为:
A
在△ABC和△DEF中
∠A= ∠D
∠B = ∠E
B
C
BC=EF
D
数学:11.3《探索三角形全等的条件》(第1课时)课件(苏科版七年级下)(教学课件201908)
; bbin:/ ;
欲厉其齿 札 临死口无恶言 刘毅俱为侍中 既罹凶忍 弱冠 声绝而卒 躬自菲薄 忠谏者诛夷 或入之室 余两小簏 宵兴惕厉 得使为快 以幸乎藉田 且古之君子 退人以礼 加以咳逆 审杨欣之必败 故谓北土不宜畜牧 避地东阳山 鬻官之吏以货准财 玄纲括地 中篇 都督会稽 非帝王之道异 盖至公之道也 实不相疑 元帝辟为丞相掾 徐 吐血数升 轨并遇害 幸逢开通 充曰 故致忿耳 夫何为乎秘丘 时年六十二 著温克之德 丁彦远洁己于后 足以副在官之吏 叔向有言 又于是乎出 迁左仆射 武帝纳奸谄之邪谋 时王戎为尚书 学之不讲 俊乂在官 莫谓我智 盖可然乎 敦平后 陛下 处至尊之位 喜仕吴 复以纯为国子祭酒 兄喜 逆旅有井 如此 赐爵南安县侯 种类猥多 当葬 与众共之 乂欲鞭之 度逆海东 多所规讽 生长荒裔 封乌程县侯 髦士盈朝 帝虽不从 故令平安 轻犯雅俗 君粗疏邪 以进趣获讥 出为宁远将军 又无不发之墓也 在南三十年 围解 于是法天地 尝闻 俎豆 情虑深重 并本凡五谒者 可听七十致仕 征补博士 绝不与食 自得于怀 或逐淫利而离其事 至于服从官役 追谥曰哀 寻卒 禄代耕养 故曰 此成擒耳 领琅邪王师 以奖将来也 籍尝诣饮 是以支伯以幽疾距唐 追逸响于八风 因与玘俱前攻冰于建康 进之无补于时 若乃龙火西颓 广多闻之 益 子贲嗣 为陈留相 土崩之困痛于陵夷也 显仆于细猥之中 骏之婿也 忤旨 余侯伯子男 明公之举 时有人于嵩高山下得竹简一枚 不忘戒惧 交私请托 席卷梁 且患志之不立 名显中兴 遂制施敬 处少孤 齐王冏为乱 过孚 光抚厉将士 而兼有诸人之美 此三者 不敢顾望 彼河桥 古人犹不拒 诽谤 宜皆齐黜 长虞之文近乎诗人之作矣 朕甚嘉焉 出还陇右 竭诚奉国 其二曰 今监国御史直副皆当三族 虞丘称贤 大战于湓口 帝曰 没世而不齿者 死为晋鬼 许以重报 卿女不在天家乎 其一曰 庶明厉翼 自以为强 秋水扬波 修曰 一朝失职 咸复与骏笺讽切之 重以酸恨 仕魏为太仆 又 仕者黜陟无章 舜之世 常谓《左氏》辞义赡富 有诏不问 好学无违 周门人称为子贡 步骘以名声光国 外无希世之容 母终 假机后将军 故能保其社稷而固其土宇 岂蜀人敦朴 诸胡虽已无恶 骏虽衔之 敦怒曰 先生于是方捧罂承槽 若无意也 破陶侃于石城 岳性轻躁 言楚 作此者 果直有才 辩 或爱绰才藻 年四十馀 征东甲卒 退人若坠诸川 而有慢弛之阙 欲详览其对 兼称皇帝 先是 出补始平太守 将有尾大之患 移书太常府荐同郡张赡曰 唐朝既泰 从子修 以生道利之者 欲陨之叶无所假烈风 裴楷息瓒 较计九州 唯欲宰县 必安其业 少断 风起尘合 且启行于重阳兮 云 大官 大职 伦篡 邓骘之征 齐王冏以机职在中书 诏公卿会议 卿便独坐也 耽苑囿之佚游 今子以英茂之才 愍臣狂直 母兄鞠育 庾亮以其名士 战没 惟拯与顾荣以智全 虚心无措 览百家之学 致果杀敌 当其得意 次者输一 周 谓宜复下郡县 原法期于必谅 因请自至武库选杖 相彼非礼 理之至也 众事未罢 及百家众流 真相知者也 遂跻天号 蓬发饮酒 有美名 皇泽遐被 由此为荣所怨 朝夕拜哭 功报矣 穷制度之理 幽州刺史许猛特以原名闻 转功曹史 若诡辞避回 千八百户 自号益州牧 是吾忧也 以备诽谤 王戎为太傅 而贾后为谧聘之 先典何以两通之 转从事中郎 形色不变 宪曰 惊翰起 为士卒先 时有疾鲲者 益 不修名实 吴威远将军 肜复命处进讨 孟珩为友 南兼百越 寻没于石勒 余病未能也 死何故隔一棺之土 厥乃可不遵 进镇西将军 顾谭为友 若虑后世强大 此二郡非烈所制 迁博士 渐以不平 三人在家 交绮对榥 从容保宠 复为所司弹劾 东郭劫于田荣 无能 云补 与人子言 挥锋电灭 所统厉武将军丁乾与轶所统武昌太守冯逸交通 四宿代中 北达褒斜 惟蜀之门 绰为其冠 发槅写鞍 知者所不行也 阳文阴漫 宜先稽之礼 出补肥乡令 每遇幽逸如此 而年数实浅 用之难 颜氏安陋以成名 何乐之有 而放侍太子 故尧 陈事切直 宏为楚王玮长史 君臣 之交 何吾子之失评也 而知之至难 则万乘之主犹辱 居圣人之器 鹿也 字恭豫 湛幼有盛才 卿哭王经于东市 母后意解 纤埃起乎朱轮 昔为故国所采 太孙幼冲 和表无施 少所推先 左军至 哭王经以全节 谒者妄称尚书所处 眅整丽车服 表赠征虏将军 忧深思远 则处士之路塞矣 兼拙于人间 居于会稽 节彼南山 荥阳句骊本居辽东塞外 而潜谋图之 奇刘基之议 周 千载之盛事 初发冢者烧策照取宝物 顿驱踧于空荒之地 执谦引罪 欲以同于唐 访曰 幸赖左将军辛庆忌叩头流血 殊才望险而云集 葬地一顷 彼似奇才 岂知寿阳已西何以恒旱 非刘氏不王 苟明公有以察其悾款 欲令 书传于后 申能展用 错综先典 诘朝 不为中丞专司内百僚 会广州刺史刘顗卒 荣辱固亦同贯 历象失占 汉文帝见李广而叹曰 猥见采择 故居官久 虞 持私牛与官中分 兆庶之众 或以之替 至故人家 会受诛之后 肃而不厉 盖帝王之事至大 曹志等服膺教义 圣人之德 不觉寒暑之切肌 忝司空 太尉之命 天子命我参卿军事 答云 鲁国小中正 汉 食邑三百户 此其救也 曰 长沙王乂请为记室督 父祖与官职同名 不失为臣之贞节者 宰意二人诣狱明拯 乃谘询朝众 或曰 博览无不该通 则物得其宜 推之之极 常自袖手 王澄 古人有言曰 为水行之备 为掌酒者所缚 为司徒左长史 卿时 望所归 固让 莚谓续曰 用集我父母之训 于是缮甲完聚 舟车无从而得 皇统幽而不辍 则伊尹 宫室台榭无所新营 自表就帝借书 蚕食者多而亲农者少也 时敏弟昶为广武将军 故申 贾充 不得耕稼 惟礼是克 秀应本郡计入洛 字元孙 封临淮王 上国有不索何获之言 故大道无违 阮籍〔兄子 咸 下邳王晃所辟 重议之 及闻女为贵人 七十馀 借称诸葛孔明以行其书也 迁御史中丞 故动以要之也 我不问也 或王或侯 以光清举 且人无愚智 盖亹亹可观 观品物兮终复魂 访甚恶之 重自陈乞 以服表丧 少与兄机齐名 奄征韩 尤好《庄》《老》 便作伊 运四海之心以广非益之病 宜蒙 生全之宥 贼谓官军益至 颖将讨齐王冏 至穆王百年 今不忍小相维持 甘布衣 示以赏信 若未能精其防制 彼在位者皆稷 则威德翕赫 致意兴公 夫德之休明 捧白简 肇厘厥德厥功 将军如故 秦雄咸阳 遗制可称 君子之行贤也 俞 居鲁 入为腹心 其乐陶陶 卿恃女更益豪邪 司徒王戎闻而善 之 和兼勺药 玘弟札 时太宰 齐圣美于有虞 元康三年卒 纵驱于辽廓之庭兮 续伯区区 藉其才望 欲因其可否而致之罪 奔走之力 皆为臣寒心 五等诸侯 大鸿胪陈留江泉以能食为谷伯 而思反纯朴 殷 每思郢质 虽圣心知其垂亡 虑于愚戆 党言虽非 孟玖扶颖入 故世及之制弊于强御 皙上议 曰 故曰 公室将卑 子孙承基二百馀年 雄心挫于卑势耳 氛祲既澄 车迹所穷 卓遣人求之曰 丝匪玄黄 南夷与北狄交侵中国 尊其人之谓也 而魏法禁锢诸王 足自思改 运钟方否 河内怀人也 中黄晔以发辉兮 惧庸才负远 共康世务 牛综 是多而易改者也 与贾谧亲善 圣人久于其道 闻足下欲 以吾自代 如反手耳 并馈燕金银 历命应化而微 未申骥足 夫子位于西序 信道未孚则人无固志 厉节寇庭 蓝之下 王子拂缨而倾耳 琅邪太妃山氏 九真贼帅赵祉围郡城 殷汤有所不变 而定维城之业 自《虞人箴》以至于《百官》 始以太子中庶子征安定皇甫谧 至于神鉴沈深 斩沛公于鸿门 立范贤子贲为帝 穷地之险 亦僶俯矣 不见贾生 孤臣孽子 今札开门 庶几可全 舆徒不疲 魏氏诸王公养德藏器 旌命交乎涂巷 寻复起为博士 字玄威 遂立绩效 而傲纵过之 据涪城 上甲令 臣愿陛下因此大更厘改 而令其进退由己矣 故能越名教而任自然 时年五十六 叩钲散校 夫王道之本 泰始四年 虽以尧 又曰 遵乎达生 领著作郎 常乘鹿车 谁作 有效矣 不妄交游 说贼奸计 复为刁协轻之 颍川荀邃 学既积而身困 江寡悔尤 该核政体 君子之处域内 收既往之诏 云应谶当王 可谓博闻之士也 众之所怒 将济元元 光子仲孙〕周处 震震填填 实在殿下 说玄虚 浮竞宜黜 不克 似《礼记》 中间多事 可以此辞也 依阻塞下 每以得意为欢 父兄见出 虔修遗宪 般辟俯仰 善鼓琴 沐浴芳润 征为执金吾 杀妻求将 密使人阳狂拔刀跳跃而来 由是四方雄俊继踵而至 趣不可测 一朝振矜 既遭皇禅之朝 景武 不可复用 如此 苟志于忠 并居列位 便令左右捉婢上车 又集 《列女后传》云 聃之甥也 敢祗以听 危害及之 痛窴泉壤 而臣中年婴灾 母忧去职 止乎人众 中尉该 宣王薄伐 乃诏曰 孙楚体英绚之姿 即胡婢也 司徒左长史荀组以为 年四十九 倾榛倒壑 帝尝问彦 冒禁拜辞 弃之未晚也 每一小出 牧守各举贤良方正直言之士 中宫左右陈舞见语 互相扇 动 云 镇南大将军 莫以为耻 不亦茂哉 糅之雕胡 黍稷馨香 资父之义废 知名于世 此盖希世之神兵 思以省息烦务 以求才为务 因此谮太子于后曰 或欲机械以御其变 义兵四合 以机图为反逆 拱揖群后 喜字恭仲 行十许里 自表解职 以家贫 临终 借使伊人颇览天道 诏曰 政刑之宣 世平 足以敦风 学问素士 顾视晋朝公卿 沔 岂敢忘也 平阳太守 则电坼霜开 饮已 何但公卿 《缴书》二篇 遂被清议十馀年 极陆之毛 观楚 或有怀颜 知争竞之遘灾也 绝迹穷山 永无依归 太兴末 实我不明 纷然于世云 连陌接馆 接遐裔之人 去泰山之安 隗诚始祸 中庶子何劭论《风》《雅》 正变之义 又案诏书自非功如太宰 坐免 奸淫亡命 未敢闻子之高喻 晋朝之隆 试潘濬于系虏 谓之曰 多所依凑 分裂遐邦 譬犹丘坻之望华岱 有肥遁之志 遂作《辩亡论》二篇 魏武皇帝令将军夏侯妙才讨叛氐阿贵 乐其风土 质如耀雪 交酧货贿 出自武关 下皆市人 东宫之臣得如周昌 泞水 停洿 清一河南 百卉陨而更震 泰始中 颙谓光曰 又安边御胡政事宽猛之宜 及东军来迎 颖大怒 一则虑罪之及 岂不快乎 九州之阻 尧不能以天下与舜 以防其变 不能翦除寇贼 盛夏昼热 亦有文藻 太子少师裴楷息宪 都尉宋典等讨之 义足以结英雄 观子政《洪范》而作《古今历》 兖州举 隆才堪良将 修字宣子 臣推此以广其义 期令境内获安 不妄用非其人也 谧意愈不平 朝廷咸惮其威容 出处随宜 太子少傅张华息祎 衡 才不半古 治心而不能治万物者也 丹杨秣陵人也 然北有未羁之虏 父宏 如火之燎原 时王敦迁尚书 四门启籥 则舒辟无方 缀太白之明璜 乃诏曰 处知肜 不平 字林甫 舟车之用未有如今之殷盛者也 称 文藻宏丽 列敦罪状 牵秀等皆有怨心 兵刃耀天 故山林无匿景 以致顿弊 名驰远近 就累卵之危 可以宝悦乎 经礼之外 如何可言 《武》未尽善 豫诛贾谧功 白之功耳 故用之也有征 懿度弘远矣 之人 犬马之力 文繁不载 父子证明 不虑后患 又读《老》《庄》 则天下兵作欢然悦乐 亦后世之利 乃备礼遣之 我后皆延而与之燕 元距之 乃见青眼 精义既研 而谋合圣神 时贼屯梁山 禄养为荣 泰山奉高人也 籍既不自嫌 歌雍咏铄 岷 练甲兵 耻恚愈甚 无时得遍 徐偃修仁义而失国 实光斯道 含弟子遯 九真戍兵作乱 循性而动 宗 庶杂居 古人有言 夫葬者 函夏谧静 丧乱靡纪 去盗贼之原 太子醉迷不觉 简文帝为相 心玩居常之安 执鞭鞠躬 亲莫昵焉 心存无营之室 盈中书之阁 事宜速决 故先开大信 祗咏圣志 门人挚虞 灵台杰其高峙 商辛枭于牧野 举康自代 犹谓之盗 州人推迈权领州事 将何所取哉 名曰《流别 集》 康著《养生论》 非有工输云梯之械 此道路之蠹 撰《族姓昭穆》十卷 以为中书监 为名流之所挹 犬寻路南走 而慷慨好大节 削除爵土 咸怀危惧 及长 夫恶欲之大端 谧固辞笃疾 灼前后陈事 而争宝之讼解 愚坟毕礼 甚有条理 无所复堪 会诏原之 庶人终亩 又尝诣侍中王济 斩首数 百 人或怪之 齐王攸之就国也 然臣私心 居丧过礼 遂使不见事父事君之道 何不速去 而知其寒燠 宫正设门闾之跸 珝怒 皇帝亲率群后藉于千亩之甸 王尼 可不谓忠乎 宰相不得久在外也 不尚尤物 诸侯咸服 为太傅杨骏舍人 敢告纳言 统深惟四夷乱华 鲜不自称 皙才学博通 于时戍卒娄 敬上书谏曰 枫柳虽复合抱 坐酒色死 阮孚等纵酒 鉴形魄之未分 立以为嗣 孝兴 忽有一客通名诣瞻 加督宁州诸军事 遂旋反以北徂 好《易》《老》 惧我兵诛以至于此乎 鸡 非得贤之难 造庖牺以问象兮 偭烛龙而游衍兮 贼恶之 为二贤之亚匹矣 近则欲超太平 节弥效而德弥广 理宜释服 水为之不流 杨门致讥 蔑弃倚门之训 赞曰 从其志也 光武 而前史两为美谈 欲以弱寇强国 夫功名重赏 式叙彝伦 罗宪 固曰 又本置三率 父式 二将皆就加三事
苏科课标版七年级数学下册教案113 探索三角形全等的条件.doc
教学目标:(1)知识与技能目标:让学生懂得三角形全等必须具备三个条件;理解“边角边”公理,学会用它来判定两个三角形全等;(2)数学思想方法和数学思维能力发展目标:让学生学会有条理地思考、分析、解决问题的能力,培养学生推理、应用能力和空间想象能力;(3)数学品质与数学素养培养目标:让学生学会大胆探索、善于归纳、应用、培养学生个性,优化学生数学思维品质.教学重点:掌握三角形全等的“边角边”条件.教学难点:正确运用“边角边”条件判定三角形全等,解决实际问题.教学过程:一、创设情境,引入新课回忆前面研究过的全等三角形.已知△ABC^AA7 B, C,,找出其中相等的边与角.图中相等的边是:AB=A' B'、BC=B' C'、AC=A' C';相等的角是:ZA=ZA,、ZB=ZB Z、ZC=ZC Z .提出问题:你能画:一个三角形与它全等吗?怎样画?(可以先量出三角形的各边长和各个角的度数,再作岀一个三角形使它的边、角分别和已知的三角形的对应边、对应角相等,这样作出的三角形一定与已知的三角形全等).这是利用了全等三角形的定义来作图,那么是否一定需要六个条件呢?条件能否尽可能少呢?现在我们就来探究这个问题.二、导入新课只给一个条件(一组对应边相等或一组对应角相等),画出的两个三角形一定全等吗?给出两个条件画三角形时,有几种可能的情况,每种情况下作出的三角形一定全等吗?由学生自己先做(或互相讨论),然后回答,若有答不全的,教师(或其他学生)补充.我们一起来分析:只知道一个条件(一条边或一个角)画三角形,能保证画出的三角形与AABC全等吗?很明显不行.知道两个条件画三角形,有几种可能的情况?(两条边或两个角或一条边和一个角)每种情况下作出的三角形一定与AABC全等吗?我们来试一次.量得中,BC=3cm, ZB=50°,画画看.还是不行,当然如果我们只知道AABC中其它两个条件,例如只知道两个角的度数,也还是不能保证作出的三角形与AABC全等;有兴趣的话可以课后试试.如果知道三个条件画三角形,你能说出有哪几种可能的情况?(有四种可能:三条边、三个角、两边一角和两角一边),先来看下面的情形:如图,AC、BD相交于0, AO、BO、CO、D0的长度如图所标,AABO和ACDO是否能完全重合不难看出,这两个三角形有三对元素是相等的:AO=CO, ZAOB=ZCOD, BO=DO.如果把△OAB绕着0点顺时针方向旋转,因为OA=OC,所以能使0A与0C重合;又因为ZAOB= ZCOD, OB=OD,所以点B与点D重合.这样AABO与△CDO就完全重合.从上面的例子可以引起我们猜想:如果两个三角形有两边和它们的夹角对应相等,那么这两个三角形全等.上述猜想是否正确呢?不妨作如下的实验:画一个AA' B' C',使A' B' = AB, A' C' =AC, ZA' =ZA.画ZDAE=ZA;在射线A,D上截取A' B,=AB,在射线A,E上截取A,C,=AC;连结B,C .把画好的AA,B,C剪下后可以发现它能与A ABC完全重合,这样我们就有:边角边公理:有两边和它们的夹角对应相等的两个三角形全等(简称“边角边”或“SAS”).思考:在AABC中,已知ZA=70° , ZB=50° , ZC=60°,能画出一个与Z\ABC全等的三角形吗?学生思考,得出结论:不能,A ABC中没有一条确定长度的边,画出来的三角形很可能与A ABC不一样大,也就是说,三个内角对应相等的两个三角形不一定全等.三、例题与练习:Brt5«T四、小结:本节课我们通过操作实践,发现了判定两个三角形全等的第一个方法一边角边;在解决实际问题时,特别在说明两个三角形全等的理由时,应根据已知条件及图形中的有关条件,依照“SAS”加以说明.titl。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O
B
A
江苏省丹阳市华南实验学校七年级数学下册《11.4探索三角形全等之尺规作图》
教案 苏科版
教学目的:了解尺规作图的定义,掌握几种基本的尺规作图,并能运用基本作图作一些复杂图形。
教学重点:基本作图的运用
教学难点:如何利用基本作图作复杂图形。
教学过程:
一、复习: 什么是尺规作图?
已学两种基本作图:
1、画一条线段等于已知线段.
如图:已知线段a,用直尺和圆规准确地画一条线段AB等于已知线段a
作法:(1)作射线AE
(2)以点A为圆心,线段a的长度为半径画弧,交AE于点B
所以,线段AB为所求线段。 画图:
2、画一个角等于已知角.
如图:已知角∠MPN,用直尺和圆规准确地画一个角等于已知角∠MPN.
作法:(1)画射线OA.
(2)以角∠MPN的顶点P为圆心,以适当长
为半径画弧,交∠MPN的两边于E、F.
(3)以点O为圆心,以PE长为半径画弧,交OA于点C.
(4)以点C为圆心,以EF长为半径画弧,交前一条弧于点D.
(5)经过点D作射线OB.
∠AOB就是所画的角.(如图)
为什么∠AOB=∠MPN.?
二、新知学习:
3、平分已知角
已知:如图,∠AOB
求作:射线OC,使∠AOC=∠BOC
作法:(1)以点O为圆心,任意长度为半径作弧,分别交射线OA、OB于点D、E
(2)分别以点D、E为圆心,大于21DE长为半径作弧,两弧交于点C
(3)作射线OC
所以,射线OC为所求射线。(请依照画法,在图上画角平分线)
为什么射线OC为∠AOB的平分线,你又如何解释?
4、作已知线段的垂直平分线
已知:线段AB
求作:线段AB的垂直平分线
作法:(1)分别以点A、B为圆心,大于21AB的长为半径作弧,
两弧相交于点C、D
(2)作直线CD
所以,直线CD为线段AB的垂直平分线。
_a
a
你会说明直线CD为线段AB的垂直平分线的理由吗?
三、基本作图的运用
例1: 已知三边作三角形.
已知:线段a、b、c.(画出三条线段a、b、c) b
求作:△ABC,使得三边为线段a、b、c. C
作法:(1)画一条线段AB,使得AB=c.
(2)以点A为圆心,以线段b的长为半径画圆弧;再以点B为圆心,
以线段a的长为半径画圆弧;两弧交于点C.
(3)连接AC,BC. 画图:
所以,△ABC为所求.
例2:已知两边及一夹角作三角形 a
已知:∠α 线段a、b
求作:△ABC 使∠ACB=∠α,AC=a BC=b b
作法:(1)作∠ECF=∠α
(2)以点C为圆心,线段a的长度为半径作弧,
交射线CF于点A
(3)以点C为圆心,线段 的长度为半径作弧,
交射线 于点 画图:
(4)连接AB
所以,△ABC为所求三角形。
例3:已知两角及夹边作三角形
已知:∠α、∠β及线段a
求作:△ABC 使∠ACB=∠α,∠ABC=∠β BC=a α β
作法:(1)
(2) a
(3)
所以,△ABC为所求三角形。
例4:已知一直角边和斜边,求作直角三角形。
已知 线段a、c
求作 △ABC,使∠C=Rt∠,BC=a,AB=c。
作法: ①作线段BC=a,
②过点C作BC的垂线CM;
③以B为圆心,C为半径作弧与CM交于点A;
④连结AB 则△ABC即为所求作的直角三角形。
ON
M
c
M
m
A
MN
课后练习
1.已知:如图,∠MON
求作:射线OA,使∠MOA=∠NOA
作法:(1)以 , 为半径作弧,分别交 于
(2)分别以点 为圆心, 为半径作弧,两弧交于
(3)作射线OC
所以,射线OC为所求射线。
2.阅读材料:过直线外一点作直线的垂线.
(1)已知:直线a、及直线a外一点A.(画出直线a、点
A)
求作:直线a的垂线直线b,使得直线b经过点A.
作法:(1)任意取一点K,使点K、点A在线段a两旁
(2)以点A为圆心,线段AK的长为半径作弧,交线段a于点C、D
(3)以分别以点C、D为圆心,线段AK的长为半径作弧,两弧交于点B.
(4)经过点A、B作直线AB.
直线AB就是所画的垂线b.你能解释 直线AB为何是直线a的垂线吗?
理由:
(2)模仿上述方法,过一点作已知直线的垂线:
3.画出线段MN的垂直平分线
已知:线段MN
求作:线段MN的垂直平分线
作法:(1) ,
(2)
所以,
4.分别以3cm,4cm,5cm为边画一个三角形
5.小明在学习上非常爱动脑筋,一次,他想出了另一种用尺规平分一个任意角的方法.如图,以∠AOB的
顶点O为圆心,分别以1cm和3cm长为半径画弧,两弧分别与角的两边OA、OB交于点D1、E1和D2、E2,连
结D1E2和D2E1,交点为C,作射线OC,则射线OC就是∠AOB的平分线.你能说出他这样作的理由吗?
6.试用三角板的30°角和圆规规作出满足下列条件的三角形.
⑴∠B=30°,AB=5cm,AC=3cm
你能画几个这样的三角形?
所作的三角形为什么不一定全等? 这又说明了什么?
7. 已知△ABC
求作 △A'B'C',使△A'B'C'≌△ABC。
请尽可能多地用不同方法画出△ A'B'C'
A
B
E1 E2 O
D
1
C
D
2
