静电场之均匀带电圆环-圆盘和圆圈在轴线上的电场共15页
静电场之均匀带电圆环-圆盘和圆圈在轴线上的电场共17页文档

31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确
静电场习题课讲稿PPT课件

L
第10页/共114页
例 求一均匀带电圆环轴线上任一点 x处的电场。
已知: q 、R 、 x。
dq
y
R
d Ey p
d Ex
x
d Ey
x
dE
第11页/共114页
课堂练习:
1.求均匀带电半圆环圆心处的 E,已知 R、
电荷元dq产生的场
dE
dq
4 0 R2
Y
根据对称性 dEy 0
dq
dEx
r dS E
第41页/共114页
dS
E
r
第42页/共114页
r>R
电通量
e E dS E4r 2
电量
qi q
r
高斯定理
E4r 2 q 0
场强
q
E 4 0r 2
第43页/共114页
E
R
高斯面
均匀带电球体电场强度分布曲线
E
E
R
qr E 40R3
q
ε 40r 2
O
r
O
R
第44页/共114页
E
E
均匀带电球面
E
E
E
dS
R
r
E
第36页/共114页
E
高斯面
E
E
E
E
E
dS
rE
E
高斯面
E
R
E
E
第37页/共114页
rR
e
qi
E2 q
dS E2 dS E2 4r 2
s2
E2 4r 2 q 0
+
+ +
+ R
第五章 电场强度
第五章 静电场
例3 正电荷 q 均匀分布在半径为 R 的圆环上. 的圆环上. 的电场强度. 计算在环的轴线上任一点 P 的电场强度.
y dq = λdl
q R
o
r
q (λ = ) 2π R
x
P
v dE =
x
1 λdl v er 2 4π ε0 r
clc2000@
z
桂林电子科技大学十院
第五章 静电场
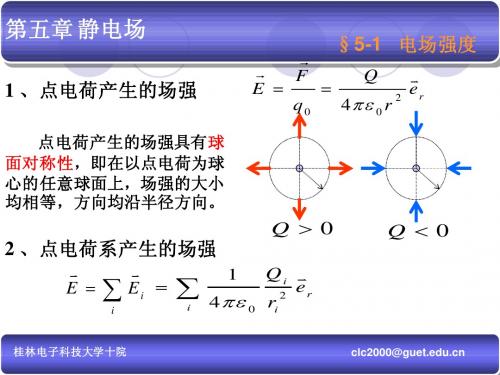
1 、点电荷产生的场强
点电荷产生的场强具有球 点电荷产生的场强具有球 面对称性, 面对称性,即在以点电荷为球 心的任意球面上, 心的任意球面上,场强的大小 均相等,方向均沿半径方向。 均相等,方向均沿半径方向。
r r F Q v ∴E = = e 2 r q 0 4πε 0 r
§5-1 电场强度
2 2 32
E=
由例3 由例 q x
y
r
dq = σ 2π rdr
(x + r )
2 2 1/2
o
R
v x P dE x
dr
q = σ πR
2
clc2000@
z
桂林电子科技大学十院
第五章 静电场
σx 1 1 E = ( − ) 2ε 0 x2 x2 + R2 σ x << R 无限大均匀带电平面 讨 论 (1) R → ∞ , E ≈ 2ε 0 σ <0 σ >0
几个常用的电场公式 (1)无限长均匀带电 无限长均匀带电 细棒的场强 (2)圆环在其中轴线上 圆环在其中轴线上 任意点产生的场强 (3)无限大均匀带电 无限大均匀带电 平面产生的场强
桂林电子科技大学十院
λ E = 2 πε 0 a
静电场之均匀带电圆环-圆盘和圆圈在轴线上的电场共17页文档

谢谢!
36、自己的鞋子,自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔,思而不学则殆。——孔子
静电场之均匀带电圆环-圆盘和圆圈在 轴线上的电场
•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
7、心急吃不了热汤圆。
•
Hale Waihona Puke 8、你可以很有个性,但某些时候请收 敛。
•
9、只为成功找方法,不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
叠加法求均匀带电球体电场问题

叠加法求均匀带电球体电场问题郭泓昊;张雅男;李庆芳【摘要】In the existing textbooks,the formula for calculating the electric field intensity on the axis of a uniform charged disk is introduced without the relationship between the relative position of field point to disk and the direction of electric field intensity.If the formula is used to calculate the field intensity distribution of a uniform charged sphere,it will get erroneous results.By introducing symbolic function into the formula of electric field intensity on the axis of the uniform charged disk,the field strength and the direction can be obtained together.Applying the new method to the calculation of electric field of the uniform charged sphere,results are exactly same as the results obtained by Gauss theorem.It is suggested that the formula of electric field intensity on the axis of charged discs should be improved in current textbooks.%现有教材中计算均匀带电圆盘轴线电场强度公式,只得到场强大小,没有明确给出场点和圆盘的相对位置与场强方向之间的关系.若根据场强叠加的方法利用此公式计算均匀带电球体的场强分布,容易得到错误的结果.将符号函数引入均匀带电圆盘轴线上电场强度计算式,可以得到场强大小及相对于圆盘的方向,清楚而准确地给出均匀带电圆盘轴线电场强度.利用该公式再次求解均匀带电球体电场,结果与利用高斯定理得到的结果完全相符.【期刊名称】《物理与工程》【年(卷),期】2018(028)001【总页数】4页(P119-122)【关键词】带电圆盘;叠加法;带电球体;静电场【作者】郭泓昊;张雅男;李庆芳【作者单位】南京信息工程大学,江苏南京 210044;南京信息工程大学,江苏南京210044;南京信息工程大学,江苏南京 210044【正文语种】中文大学物理在静电场章节中,先是讲解了点电荷的电场强度计算方法,然后利用场强叠加原理先后求出均匀带电圆环、均匀带电圆盘等电荷均匀分布的带电体轴线上的电场分布。
9.0静电场之基本内容

空间某点的所产生的场强等于各个 ri是电荷Qi到场点P的矢径。 点电荷在该点产生场强的矢量和 当电荷连续分布时,可将带电体分成许 dE = dq 3 r 4πε 0 r 多点电荷,每个点电荷产生的场强为 全部电荷产生 E = 1 dq r 4πε 0 ∫ r 3 的合场强为 点电荷dq可根据线密度λ, 面密度σ或体密度ρ决定 dq = λdl,dq = σdS和dq = ρdV。
4.典型源电荷的电场 (1)点电荷 E = 1 Q r 4πε 0 r 3 的电场为 其中r是点电荷 Q到场点的矢径。 Q>0 Q<0 r r P E EP
点电荷产生的场强与其电量Q成正比, 与场点到点电荷的距离的平方成反比, 方向在场点到点电荷的连线上。 正点电荷产生场强的方向沿径向向外, 负点电荷产生场强的方向沿径向向内。 (2)无限长均匀带 E = λ r 2 ε 2 π r 电直线的场强为 0
n
θ
E
∫
S
E ⋅ dS 对于封闭的曲面,通常取外
法线方向为曲面的正方向。
7.高斯定理:在静电场中,通过任一闭合曲面(称为高 斯面)的电通量等于该曲面包围的电量的代数和除以ε0
ΦE =
∫
S
E ⋅ dS =
1
ε0
高斯定理说明电场是有源场,正电荷 q ∑ i
i
是电场的源头,负电荷是电场的汇尾。
注意:任何一点的场强E是所有电荷在 该处产生的,而 ∑ qi 是高斯面内的电 i 荷,不包括高斯面外的电荷,因为高 斯面外的电荷产生的电通量为零。
湖南大学物电院周群益第九章第九章静电场静电场基本内容基本内容范例范例92电偶极子的电场电偶极子的电场范例范例93均匀带电线段的电场均匀带电线段的电场范例范例91点电荷的电场点电荷的电场范例范例94平行直线电荷的电场平行直线电荷的电场范例范例95均匀带电圆环圆盘和圆圈在轴线上的电场均匀带电圆环圆盘和圆圈在轴线上的电场范例范例98直线电荷与共面带电线段之间的作用力直线电荷与共面带电线段之间的作用力范例范例97均匀带电圆柱面圆柱体和圆柱壳的电场均匀带电圆柱面圆柱体和圆柱壳的电场范例范例99直线电荷与共面圆弧电荷之间的作用力直线电荷与共面圆弧电荷之间的作用力范例范例910点电荷在有孔带电平面轴线上的运动规律点电荷在有孔带电平面轴线上的运动规律范例范例96均匀带电球面球体以及球壳的电场均匀带电球面球体以及球壳的电场基本内容基本内容1
圆环圆点处电场公式
圆环圆点处电场公式圆环圆点处的电场公式可以通过叠加原理来推导。
假设我们有一个半径为R的均匀带电圆环,其上电荷密度为λ(单位长度的电荷量)。
我们想要找出圆环中心(即圆点)处的电场强度。
由于圆环是均匀的,我们可以将圆环分割成许多小段,每段都可以看作是一个点电荷。
然后,我们可以计算每段在圆点处产生的电场,并将它们叠加起来以得到总电场。
对于圆环上的任意一点,其到圆点的距离是R(因为是从圆点到圆环上的点的距离)。
假设我们考虑一小段圆环,其弧长为Δl,那么这段圆环上的电荷量就是λΔl。
点电荷在距离r处产生的电场强度E可以用以下公式表示:E = (k * q) / r^2其中,k是库仑常数,q是点电荷的电荷量,r是点到电荷的距离。
因此,对于圆环上的这一小段Δl,它在圆点处产生的电场强度是:E_Δl = (k * λΔl) / R^2由于电场是矢量,我们需要考虑方向。
对于圆环上的每一点,其在圆点处产生的电场方向都是沿着从圆点到该点的连线,并且方向是向外的(如果电荷是正的话)。
由于圆环是对称的,这些电场分量在水平方向上会相互抵消,只剩下垂直方向上的分量。
因此,我们只需要考虑垂直方向上的电场分量。
为了得到总电场,我们需要将圆环上所有小段产生的电场叠加起来。
由于圆环是对称的,我们可以只考虑四分之一圆环(例如上半部分的右半边),然后将其结果乘以4。
这样,总电场强度就是:E_total = 4 * ∫(k * λ* sin(θ) / R^2) dθ其中,θ是从正x轴到考虑的点与圆心的连线的角度,积分范围是从0到π/2。
进行积分后,我们得到:E_total = (2 * k * λ) / R这就是圆环中心处的电场强度的公式。
注意,这个公式假设了圆环是均匀的,并且只考虑了电场在垂直方向上的分量。
如果圆环不是均匀的,或者我们想要考虑其他位置的电场,那么计算会变得更加复杂。
09-4静电场的环路定理和电势
19
19
J
一个电子伏特的能量
9.4 静电场的环路定理和电势
9.4.3 电势的计算
一、点电荷q的电场中任一场点的电势
无穷远处为电势零点
V ( P)
P
E dl E dr P Edr P
q q dr 2 r 4 πε r 4πε 0 r 0
电场指向电势降落方向
沿电场线方向移动正电荷,电场力做正功, 正电荷的电势能减少,故电势减小。
9.4 静电场的环路定理和电势
我们的心脏附近 的等电势线(类似于 电偶极子)
9.4 静电场的环路定理和电势
电势差
9.5.2 电场强度与电势梯度 E
U AB VA VB V
U AB E l El cos
9.4 静电场的环路定理和电势
电势是相对的,电势差是绝对的
电势差 U V V PQ P Q
单位:1V=1J/C
P
Q
E dl
二、电势零点 1、电荷只分布在有限区域时,电势零点通常选在无 穷远处。 VP E dl 设Q点在无限远,VQ=0
P
2、 电荷分布延伸到无限远;可选取场中任一点, 合理选择电势零点可使问题简化。
y
P( x, y)
p cos V 4 π 0 r 2
在图示的Oxy坐标系中
q
r
O
r
r
q
r x y
2 2
2
l
x
cos
x x2 y 2
px V 2 2 3/ 2 4 π 0 ( x y )
9.4 静电场的环路定理和电势
电磁场试卷
PART1一、选择题1。
若一个矢量函数的旋度恒为零,则此矢量可以表示为某一个(C )函数。
A.矢量的散度 B.矢量的旋度C.标量的梯度2. 自由空间的电位函数,则点处的电场强度( A ).A. v/m B. v/m C. v/m3. 损耗媒质中的平面电磁波,其波长随着媒质电导率σ的增大,将( B )。
A。
变长B. 变短C. 不变4。
平行极化波在不同媒质分界面上无反射的条件是( A )。
A。
B。
C. (为入射角,为布儒斯特角)5. 频率f=1MH Z的均匀平面波在电导率,磁导率H/m的良导体中传播时,趋肤深度(或穿透深度)( A )。
A. B。
C.6.在导波系统中,存在TEM 波的条件是( C ).A.B.C。
7. 点电荷产生的电场强度随距离变化的规律为( B )。
A. B. C。
8。
导电媒质中,已知电场强度,则媒质中位移电流密度的相位与传导电流密度的相位( A )A。
相差 B. 相差 C。
相同9. 恒定电场中,当( A )时,两种媒质的分界面上的自由面电荷为零.A. B.C.10。
设矩形波导的截止频率为,工作频率为的电磁波在该波导中传播的条件是( B )。
A. =B。
>C。
<二、简答题(每小题10分,共20分)1.麦克斯韦方程组的微分形式是什么?对于静态场,其形式又如何?2. 简要说明均匀平面波在导电媒质中的传播特点。
①是一个横电磁波(TEM波),电场和磁场都在垂直于传播方向的横向平面内②在传播过程中有损耗,电场和磁场的振幅有衰减,波形要发生变化③是复数,和不同相位④波的相速不仅与媒质参数有关,还与频率有关,是色散波⑤电场能量密度小于磁场能量密度。
三、计算题1.通过解电位的泊松方程和拉普拉斯方程,确定球形电子云内部和外部的电位和电场.已知电子云内部区域,有均匀的体电荷密度;在电子云外部区域中,。
(由于电荷分布的球对称性,在球坐标中,电位仅是的函数)解:由于电荷分布的球对称性,在球坐标中,电位仅是的函数,其满足的微分方程为由此解出和满足的边界条件为时,为有限值;时,;于是有,由此得到 ,所以2. 一右旋圆极化波从空气中垂直入射到位于z=0处的理想导体平面上,已知电磁波的工作频率为100MHz,入射波电场强度的复数形式为试求:①平面波的传播常数和波阻抗;②空气中反射波的电场强度的复数表示式,并说明反射波的极化状态;③反射波的磁场强度的复数表示式;④空气中总电场强度的瞬时表达式.解:①沿+z方向传播的右旋圆极化波②设反射波电场的复数形式为=由理想导体表面电场所满足的边界条件,在z=0时有得这是一个沿-方向传播的左旋圆极化波。
均匀带电圆盘轴线上一点的场强PPT教案
设圆环带电量为 q ,半径为R
解:由对称性可知,p点场强只有X分量
E qdEx
dE cos
L
dq
4 0r 2
cos
cos 4 0r 2
dq
L
E
cos q 4 0r 2
4
qx 0(R2
x
2
)
3 2
dE
X
讨论:当求场点远大于环的半径时,
E
q
4 0 x2
q 方说向明在远X离轴环上心,的正场负强由相当于的点正电负荷决的定场。。L
静电力的叠加原理:
F0
n i 1
F0i
n i 1
1
4 0
q0qi r02i
rˆ0i
第4页/共20页
q1
rO1
rO 3
q3 rO 4
q4
qo
rO 2 q2
1.2电场和电场强度
一、电场(electric field)的物质性:
1. 电 荷 之 间 的 相互 作用是 通过电 场传递 的,或 者说电 荷周围 存 在 有 电 场 ,引入 该电场 的任何 带电体 ,都受 到电场 的作用 力 , 这 就 是 所渭的 近距作 用。
rˆ
E
n Ei
i 1
1
4 0
n i 1
qi ri2
rˆi
q2
第8页/共20页
三、任意带电体(连续带电体)电场中的场强:
将带电体分成很多元电荷 dq
p 的场强
dE
1
4
0
dq r2
rˆ
,先求出它在任意场点
dE
对场源求积分,可得总场强: dq
E
dE
1
