湖南省茶陵县世纪星实验学校七年级数学上册 第二章 一次式的加法和减法学案2(无答案) 湘教版
七年级数学上册《第二章 整式的加法和减法》练习题-带答案(湘教版)

七年级数学上册《第二章整式的加法和减法》练习题-带答案(湘教版)一、选择题1.计算3a-2a的结果正确的是( )A.1B.aC.-aD.-5a2.已知-4x a y+x2y b=-3x2y,则a+b的值为( )A.1B.2C.3D.43.下列变形中,不正确的是( )A.a+(b+c﹣d)=a+b+c﹣dB.a﹣(b﹣c+d)=a﹣b+c﹣dC.a﹣b﹣(c﹣d)=a﹣b﹣c﹣dD.a+b﹣(﹣c﹣d)=a+b+c+d4.下面计算正确的是( )A.6a-5a=1B.a+2a2=3a2C.-(a-b)=-a+bD.2(a+b)=2a+b5.已知a﹣b=5,c+d=﹣3,则(b+c)﹣(a﹣d)的值为( )A.2B.﹣2C.8D.﹣86.一个多项式加上3y2﹣2y﹣5得到多项式5y3﹣4y﹣6,则原来的多项式为( )A.5y3+3y2+2y﹣1B.5y3﹣3y2﹣2y﹣6C.5y3+3y2﹣2y﹣1D.5y3﹣3y2﹣2y﹣17.一个多项式A与多项式B=2x2-3xy-y2的和是多项式C=x2+xy+y2,则A等于( )A.x2-4xy-2y2B.-x2+4xy+2y2C.3x2-2xy-2y2D.3x2-2xy8.关于x、y的代数式(﹣3kxy+3y)+(9xy﹣8x+1)中不含有二次项,则k=( )A.3B.13 C.4 D.14二、填空题9.化简:2a﹣(2a﹣1)=___________.10.如果3x2y3与x m+1y n-1的和仍是单项式,则(n-3m)2026的值为.11.不改变2-xy+3x2y-4xy2的值,把前面两项放在前面带有“+”号的括号里, 后面两项放在前面带有“-”号的括号里,得_______.12.已知a2﹣ab=10,ab﹣b2=﹣6,则a2﹣2ab+b2=.13.若三个连续奇数中间一个是2n+1(n≠0的整数),则这三个连续奇数的和为.14.设A,B,C均为多项式,小方同学在计算“A﹣B”时,误将符号抄错而计算成了“A+B”,得到结果是C,其中A=12x2+x﹣1,C=x2+2x,那么A﹣B=________.三、解答题15.化简:2a+2(a+1)﹣3(a﹣1);16.化简:﹣3(2x2﹣xy)+4(x2+xy﹣6).17.化简:(8xy﹣x2+y2)﹣3(﹣x2+y2+5xy)18.化简:3a2b+{ab﹣[3a2b﹣2(4ab2+12ab)]}﹣(4a2b+ab).19.先化简再求值:5x2y﹣4xy2+[3xy2﹣(4x2y﹣xy2)],其中x=﹣2,y=﹣3.20.证明:多项式16+a﹣{8a﹣[a﹣9﹣3(1﹣2a)]}的值与字母a的取值无关.21.若|3x+6|+(3﹣y)2=0,求多项式3y2﹣x2+(2x﹣y)﹣(x2+3y2)的值.22.某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元,在促销活动期间,该厂向客户提供了两种优惠方案(客户只能选择其中一种优惠方案):①买一套西装送一条领带;②西装按原价的9折收费,领带按原价的8折收费.在促销活动期间,某客户要到该服装厂购买x套西装,y条领带(y>x).(1)该客户选择两种不同的方案所需总费用分别是多少元?(用含x、y的式子表示并化简)(2)若该客户需要购买10套西装,22条领带,则他选择哪种方案更划算?(3)若该客户需要购买15套西装,40条领带,则他选择哪种方案更划算?参考答案1.B2.C3.C.4.C5.D.6.D7.B8.A.9.答案为:110.答案为:111.答案为:(2-xy)-(-3x2y+4xy2)12.答案为:16.13.答案为:6n+3.14.答案为:﹣2.15.解:2a+2(a+1)﹣3(a﹣1)=2a+2a+2﹣3a+3=a+5.16.解:﹣3(2x2﹣xy)+4(x2+xy﹣6)=﹣6x2+3xy+4x2+4xy﹣24=﹣2x2+7xy﹣24.17.解:原式=8xy﹣x2+y2+3x2﹣3y2﹣15xy=2x2﹣2y2﹣7xy.18.解:原式=3a2b+ab﹣3a2b+8ab2+ab﹣4a2b﹣ab=﹣4a2b+8ab2+ab.19.解:原式=5x2y﹣4xy2+3xy2﹣4x2y+xy2=x2y当x=﹣2,y=3时,原式=12.20.证明:16+a﹣{8a﹣[a﹣9﹣3(1﹣2a)]}=16+a﹣{8a﹣[a﹣9﹣3+6a]}=16+a﹣{8a﹣a+9+3+6a}=16+a﹣8a+a﹣9﹣3+6a=4.故多项式的值与a的值无关.21.解:∵|3x+6|+(3﹣y)2=0∴3x+6=0,3﹣y=0解得:x=﹣2,y=3则原式=3y2﹣x2+2x﹣y﹣x2﹣3y2=﹣2x2+2x﹣y=﹣8﹣4﹣3=﹣15.22.解:(1)按方案①购买,需付款:200x+(y﹣x)×40=(40y+160x)元;该客户按方案②购买,需付款:200x•90%+40y•80%=(180x+32y)(元);(2)当x=10,y=22时,按方案①购买,需付款:40×22+160×10=2480(元);该客户按方案②购买,需付款:180×10+32×22=2504(元);∵2480<2504∴按方案①更划算;(3)当x=15,y=40时,按方案①购买,需付款:40×40+160×15=4000(元);该客户按方案②购买,需付款:180×15+32×40=3980(元);∵4000>3980∴按方案②更划算.。
七年级数学上册第二章整式的加减整式的加减《整式的加减运算》

教学设计:2024秋季七年级数学上册第二章整式的加减整式的加减《整式的加减运算》教学目标(核心素养)1.知识与技能:学生能够理解整式加减运算的意义,掌握整式加减的基本法则,能够准确进行整式的加减运算。
2.数学思维:培养学生的代数运算能力,通过整式加减运算的练习,提高学生的逻辑思维和抽象思维能力。
3.情感态度:激发学生对数学学习的兴趣,体验代数运算的简洁性和美感,培养耐心和细致的学习态度。
教学重点•整式加减的基本法则及其应用。
•准确进行整式加减运算,特别是含有同类项的整式运算。
教学难点•理解整式加减运算中同类项合并的必要性。
•在复杂整式中准确应用加减法则进行运算,避免符号错误和运算顺序错误。
教学资源•多媒体课件(包含整式加减运算示例、练习题)•黑板及粉笔(用于板书关键概念和例题)•学生笔记本(用于记录课堂笔记和练习)•实物教具(如可拆卸的代数式卡片,用于直观展示整式加减过程)教学方法•直观演示法:利用多媒体课件和实物教具,直观展示整式加减的过程和结果。
•讲授法:结合具体例子,详细讲解整式加减的基本法则和运算步骤。
•练习巩固法:通过分层练习,巩固学生对整式加减运算的掌握。
•合作学习法:组织小组合作,让学生共同解决整式加减运算中的问题,促进相互学习和交流。
教学过程要点导入新课•复习引入:回顾整式的概念、同类项以及去括号法则,为整式加减运算做铺垫。
•情境导入:通过一个实际问题(如计算两个多边形面积的差或和),引导学生思考如何用整式表示并求解,引出整式加减运算的必要性。
新课教学•整式加减法则:明确整式加减的基本法则(即同类项相加减,非同类项不能合并)。
•示例演示:选取几个典型例题,逐步演示整式加减的过程,强调同类项合并和符号处理。
•注意事项:提醒学生在运算过程中注意符号的正确性、同类项的准确识别以及运算顺序的遵循。
课堂小结•知识回顾:总结整式加减的基本法则和运算步骤,强调其在代数运算中的重要性。
•方法提炼:引导学生提炼整式加减运算的技巧,如先识别同类项再合并、注意符号变化等。
湖南省茶陵县世纪星实验学校七年级数学《一元一次方程的应用(行舟问题)》教案
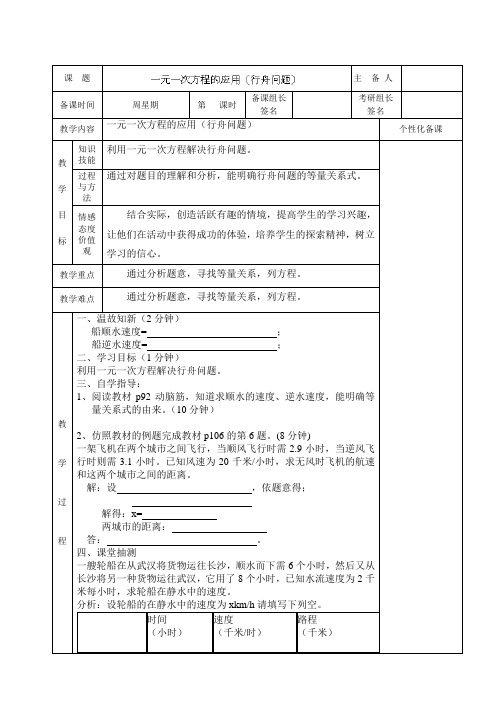
时间
(小时)
速度
(千米/时)
路程
(千米)
顺水航行
逆水航行
等量关系为:
解:
五、课堂小结
学会的知识
存在的问题
六、当堂达标
一只小船在静水中的速度为10千米/时,今往返于某河段上,逆流时用9小时,顺流时用6小时
1)、求该河的水流速度。
2)、求该船的顺水速度。
3)、求小船往返一次航行的路程。
【为了同学们将来的学习,在此补助了一道浓度问题,相信同学们能战胜它】
(选做题)要配制含糖6%的糖水700克,已有含糖5%的糖水200克,还需加入含糖8%的糖水及水各多少克?
教
学
反
思
教学重点
通过分析题意,寻找等量关系,列方程。
教学难点
通过分析题意,寻找等量关系,列方(2分钟)
船顺水速度=;
船逆水速度=;
二、学习目标(1分钟)
利用一元一次方程解决行舟问题。
三、自学指导:
1、阅读教材p92动脑筋,知道求顺水的速度、逆水速度,能明确等量关系式的由来。(10分钟)
2、仿照教材的例题完成教材p106的第6题。(8分钟)
一架飞机在两个城市之间飞行,当顺风飞行时需2.9小时,当逆风飞行时则需3.1小时。已知风速为20千米/小时,求无风时飞机的航速和这两个城市之间的距离。
解:设,依题意得;
解得:x=
两城市的距离:
答:。
四、课堂抽测
一艘轮船在从武汉将货物运往长沙,顺水而下需6个小时,然后又从长沙将另一种货物运往武汉,它用了8个小时,已知水流速度为2千米每小时,求轮船在静水中的速度。
课题
主备人
湖南省茶陵县世纪星实验学校七年级数学上册 第二章 4 单项式教案 湘教版
单项式
课时 备课组长 签名
主
备 人
考研组长 签名 个性化备课
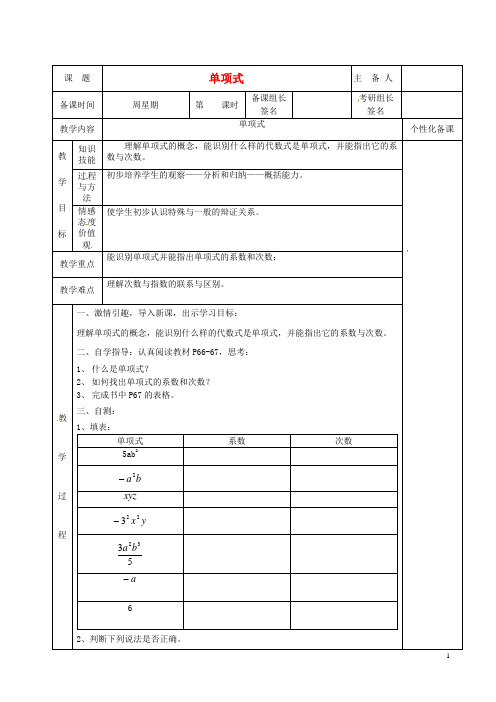
单项式 理解单项式的概念,能识别什么样的代数式是单项式,并能指出它的系 数与次数。 初步培养学生的观察——分析和归纳——概系。
教 学 反 思
2
2
系数
次数
a 2b
过
xyz
32 x 2 y
程
3a 2 b 3 5
a
6
2、判断下列说法是否正确。
1
(1) 单项式 k 没有系数也没有次数; ) ( (2) 单项式 2 10 a 系数是 2,次数是 5; ) (
3 2
(3) -2008 也是一个单项式; ( (4) 单项式
) )
8 5 8 ab 系数是 ,次数是 6;( 9 9
四、讨论答疑: 写出一个系数为正整数,次数为 8,只含有字 母 x、y 的单项式,你能写出多 少个? 五、小结:这节课你有什么收获? 六、当堂达标: 1、 单项式 系数 次数
6 2 x yz 7
x y3
x 2 yz 3 4
-s
0.1
2、写出系数是-46,且含有 a、 b、c 三个字母的 10 次单项式. 。 3、 写出一个系数为负分数只含有x、y两个字母的 6 次单项式。 。
教学重点 教学难点
能识别单项式并能指出单项式的系数和次数; 理解次数与指数的联系与区别。
一、激情引趣,导入新课,出示学习目标: 理解单项式的概念,能识别什么样的代数式是单项式,并能指出它的系数与次数。 二、自学指导:认真阅读教材 P66-67,思考: 1、 什么是单项式? 2、 如何找出单项式的系数和次数? 3、 完成书中 P67 的表格。 教 三、自测: 1、填表: 单项式 学 5ab
2024年新湘教版7年级上册数学 2.4 第2课时 整式的加减

= -6xy.
(2) (4y - 5) - 3(1 - 2y).
(2) 原式 = 4y - 5 - 3 + (-3)×(-2y)
= 4y - 5 - 3 + (-3)×(-2)×y
= 4y - 8 + 6y
= 10y - 8.
由于结中不含 x,所以不论 x 取何值,原式的值都是 1.
2. 计算:
(1) - ab3 + 2a3b- a2b-ab3- a2b-a3b; (2) (7m2-4mn-n2)-(2m2-mn + 2n2); (3) -3(3x + 2y)-0.3(6y-5x);(4) ( a3-2a-6)- ( a3-4a-7).
例2 计算:
解 (1) (4x2-5xy+3y2)-(3x2+2y2)
=4x2-5xy+3y2-3x2-2y2
=x2-5xy+y2.
提问:将 (2)、(3) 与 (1) 进行比较,它们有什么区别吗?
(1) (4x2-5xy+3y2)-(3x2+2y2);
(2) [4×(-2)2-5×(-2)×3+3×32)]-[(3×(-2)2+2×32)];
(2) [4×(-2)2-5×(-2)×3+3×32)]-[(3×(-2)2+2×32)];
例2 计算:
验算一下吧!
(1) (4x2-5xy+3y2)-(3x2+2y2);
(3) [4×(-b)2-5×(-b)×c+3×c2)]-[(3×(-b)2+2×c2)].
解:(3) 将等式 ① 中的 x 用-b 代入,y 用 c 代入,则
-72b
+
湘教版七年级数学上册《2章 代数式 2.5 整式的加法和减法 2.5整式的加法和减法(2)》优课教学设计_6

第2课时 去括号
探究:
ab c 5 2 -1 -6 -4 3
a+(-b+c)
2
1
你发现了什么?
a+(-b+c)=a-b+c
a-b+c
2 1
动脑筋
根据加法结合律,去掉下面式子中的括号, 填空:
a + ( b + c ) = ___a__+__b_+__c__; a + ( b - c ) = ___a_+__b_-__c___.
(4)-2(6-x)=-12+2x 对
练练:
一、去括号:
(1).a+(-3b-2a) = a-3b-2a; (2).(x+2y)-(-2m-n) = x+2y+2m+n; (3).6m-3(-x+2y) = 6m+3x-6y; (4).(a-b)-(-c+d) = a-b+c-d; (5).2(m+n)-5(3a-d)= 2m+2n-15a+5d; (6).-(-a+2b)-(3c-d-2e)= a-2b-3c+d+2e.
动脑筋
a–(b-c)= a+(-b+c)= a - b + c ;
a–(-b-c)=a+(b+c)= a + b + c .
由上面的式子有什么变化规律?
结论
一般地,有下列去括号法则:
括号前是“-”号,把括号和它前面的
“-”号去掉,原括号里各项的符号都要改变
.
我要去 掉括号
我的符号 全变了!
湘教版七年级数学上册《2章 代数式 2.5 整式的加法和减法 2.5整式的加法和减法(2)》优课教学设计_13
同的表达方式列出代数式吗? (2)这两个代数式的值相等吗?为什么?
问题二:若阅览室内原有a位同学.后来有些同学因上课要
离开,第一批走了b位同学,第二批又走了c位同学.
思考:(1)试用两种方式写出阅览室内还剩下的同学人数. (2)你能从中发现什么关系?
探究一:括号前是“+”号
a+(b+c)=a+b+c ① 观察等式①,发现括号前是“+”号时的变化规律: (1)根据字母表示数,从运算顺序来看,等式左边与右边有什 么不同,为什么值不变? (2)去括号后,括号内各项的符号(正负号)有什么变化?
这也符合以上发现的去括号规律。 通过上述过程,我们可以发现:
(1)填空:a+(b-c)=a+ ×(b-c)=
=
;
a-(b-c)=a+ ×(b-c)=
=
.
(2)请仿照上述过程完成去括号:a-3(b-c).
(3)想一想,上面两题的去括号,实际上我们是用什么方法做的?
理解应用,巩固提升
3.先去括号,再合并同类项: (1)-(x-y)+(-x-y);
()
(2)-4(x-y)+(y-1)=-4x-y+y-1=-4x-1 . ( )
2.去括号:
(1)+(3 x-2)=
; (2)-(x-3y)=
;
(3)-(-2x+7)=
; (4)-2(-a-b)= .
3.计算:
(1)x y-(3 x-2 x y)+(3 x y-2 x).
(2)2(a-3)-3(a+1)
(2)(a²+2ab+b²)-(a²-2ab+b²); (3)3(2x²-y²)-2(3y²-2x²).
小结反思,回味新知
1.畅谈收获:本节课你收获了什么?(知识、能力、方法等方面) 2. 在去括号时,我们应注意什么?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
湖南省茶陵县世纪星实验学校七年级数学上册 第二章 一次式的加
法和减法学案2 湘教版
三.学生自测
自测:
一、判断题
1、cabcba ( )
2、dcbadcba ( )
3、bambam22 ( )
4、1313ayxayx ( )
二、计算
①2332mmm ②2534xx
三、先化简,再求值。
3235143127xxxx,其中
2
四.当堂达标
一、填空题:
1、2(3x-2y)= ;-2(a+b-c)= .
2、-2a+1的相反数是 .
3、3x与-5x的和是 ,3x与-5x的差是 .
二、计算:
⑴ -2(3a-5)+5 ⑵ 1332xx
124353mmm (4)
babaa23352
三、先化简,再求值。
求代数式512216aaaa的值,其中
