数学学习指南16.2.3整数指数幂导学案1
八年级数学下册《16.2整数指数幂》学案(1) 新人教版

八年级数学下册《16.2整数指数幂》学案(1)新人教版【温故知新】1、正整数指数幂的性质:(1)= (m、n是正整数)(2)= ( m、n是正整数),(3)(ab)n= (n是正整数),(4)= (a≠0,m、n是正整数,m>n),(5)= (n是正整数),(6)a 0 = (a≠0)2、计算:=;=。
一方面:==另一方面:==则归纳:一般的,规定:n 是整数,即任何不等于零的数的-n(n为正整数)次幂,等于_____________________、3、试一试:4、思考:当指数引入负指数后,对于1中幂的这些运算法则是否仍然适用?= = == ,即=== =,即==1 = ,即=归纳:当m、n 是任意整数时,都有=【精讲点拨】例题、计算(1)(2)【巩固训练】1、(x-1)0=1成立的条件是、2、 (x-1)-2= ;(-)-2= ;0、1-3= ;a-3= ;a-2bc-2= ;3、= ,= ,= , =4、计算(1)(2) (3)(4)【温故知新】1、(1)用科学记数法表示 =__________,=_______, -=_______,2、93=_________ (2)用科学记数法(a10n)表示绝对值大于10的数时,1 ≤│a│<10 ,n为 ____________ 、2、填空:___________ __________ ___________________ _________=___________你发现用10的负整数指数幂表示0、0000┉┉001这样较小的数有什么规律吗?指数与运算结果的0的个数有什么关系?一般地,10的-n 次幂,在1前面有________个0。
【学以致用】1 用科学记数法表示下列各数(1)0、000 000001=____________, (2)0、0012=_____________,(3)0、000 000345=____________, (4)-0、000 03=____________,(5)0、000 000 0108=___________, (5)3780 000=____________小结:一个数M的绝对值大于1, a中n为正整数;绝对值小于1, a 中n为负整数;2 用小数表示下列各数(1)7、2=____________ (2)1、5=____________ 练习:下列是用科学记数法表示的数,写出原来的数。
《整数指数幂(第1课时)》导学案

第2课时1.知道分式混合运算的顺序,能熟练进行分式的混合运算.2.通过对分式的混合运算,提高思维的整体性和灵活性.3.重点:能熟练进行分式的混合运算.问题探究一分式的混合运算阅读教材“例7”至“例8”的内容,请你完善下列解题过程:1.计算:(错误!未找到引用源。
)2÷错误!未找到引用源。
-错误!未找到引用源。
.2.化简:(错误!未找到引用源。
-错误!未找到引用源。
)÷错误!未找到引用源。
.【归纳总结】分式的混合运算顺序与分数一样:先算,再算,最后算,有括号先算的,同级运算按的顺序进行.【预习自测】(1)化简:错误!未找到引用源。
÷(1-错误!未找到引用源。
)=.(2)1+x÷(y·错误!未找到引用源。
)=.互动探究1:见教材“习题15.2”第6题第(4)小题.互动探究2:化简:(错误!未找到引用源。
-错误!未找到引用源。
)·错误!未找到引用源。
.(尝试用多种方法计算)【方法归纳交流】计算时既可按运算顺序进行,也可以根据式子的特点,先去括号运算.互动探究3:化简(x-错误!未找到引用源。
)÷(1-错误!未找到引用源。
)的结果是( )A.错误!未找到引用源。
B.x-1C.错误!未找到引用源。
D.错误!未找到引用源。
互动探究4:已知y=错误!未找到引用源。
÷错误!未找到引用源。
-错误!未找到引用源。
,试说明在等式右边式子有意义的条件下,不论x为何值,y的值总是不变.【方法归纳交流】在解决此类问题时,一般是,化简后的式子一般是一个.互动探究5:先将代数式(x-错误!未找到引用源。
)÷(1+错误!未找到引用源。
)化简,再从-3<x<3的范围内,选取一个合适的整数x代入求值.。
16.2.3整数指数幂
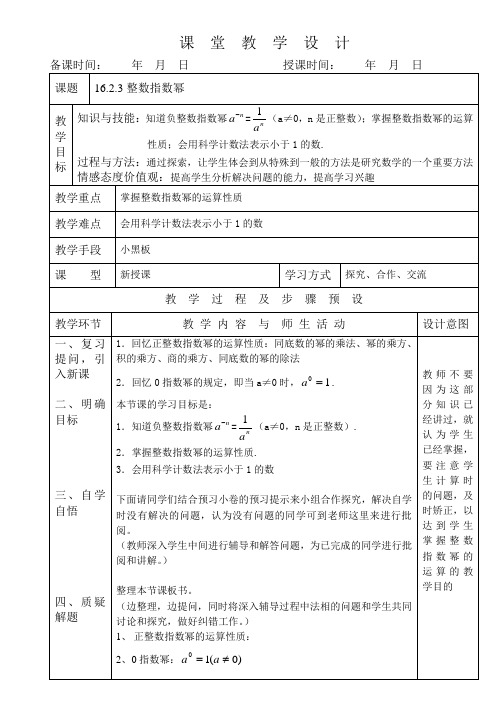
米,把 1 纳米的物
体放到乒乓球上,就如同把乒乓球放到地球上,1 立方毫米的空间 可以放多少个 1 立方纳米的物体? 完成教材中第 25 页、第 26 页练习题。 (优生做完找老师批改;中、下等生到黑板上做,如果有问题可以 问优生或者老师,使中、下等生能有所提高,优生能有精力做课外 辅导题。 ) 本节课你都学会了哪些知识?(结合学习目标进行总结)
板 书 设 计 16.2.3 整数指数幂
1、正整数指数幂的运算性质:同底数的幂的乘法、 幂的乘方、积的乘方、商的乘方、同底数的幂的除法 2、0 指数幂: a 1(a 0)
0
4、用科学计数法表示小于 1 的数 例 11(见上)
3、整数指数幂:
教 学 反 思 与 评 析
学情分析: 成功之处: 教学效果反思 不足之处: 改进措施:
因为这部 分知识已 经讲过,就 认为学生 已经掌握, 要注意学 生计算时 的问题,及 时矫正,以 达到学生 掌握整数 指数幂的 运算的教 学目的
四 、 质 疑 (边整理,边提问,同时将深入辅导过程中法相的问题和学生共同 解题 讨论和探究,做好纠错工作。 )
1、 正整数指数幂的运算性质: 2、0 指数幂: a 1(a 0)
教学重点 教学难点 教学手段 课 型
掌握整数指数幂的运算性质 会用科学计数法表示小于 1 的数 小黑板 新授课
学习方式 教 学 过 程 及 步 骤 预
探究、合作、交流
设 设计意图
教学环节
教 学 内 容 与
师 生 活 动
一 、 复 习 1.回忆正整数指数幂的运算性质:同底数的幂的乘法、幂的乘方、 提 问 , 引 积的乘方、商的乘方、同底数的幂的除法 教师不要 入新课 0 2.回忆 0 指数幂的规定,即当 a≠0 时, a 1 . 二 、 明 确 本节课的学习目标是: 1 目标 n 1.知道负整数指数幂 a = n (a≠0,n 是正整数). a
《整数指数幂》第1课时导学案

整数指数幂 导学案学习目标:1、掌握整数指数幂的运算性质,并能运用它进行整数指数幂的运算。
2、通过分式的约分与整数指数幂的运算方法对比经历探索整数指数幂的运算性质的过程,理解性质的合理性。
学习过程【温故知新】正整数指数幂的性质:(1)m a ·n a = (m 、n 是正整数) (2)()m n a = (m 、n 是正整数),(3)(ab )n = (n 是正整数),(4)m a ÷n a = (a≠0,m 、n 是正整数,m>n ),(5)()n a b= (n 是正整数) , (6)a 0 = (a≠0)【预习导学】预习P18-201、计算:5255÷= ;731010÷= 。
一方面:5255÷=35255--= 731010÷=()()1010=另一方面:5255÷=3525155= 731010÷=()()()=1010 则()()==--4310,5归纳:一般的,规定:())0(≠=-a a n n 是整数,即任何不等于零的数的-n (n 为正整数)次幂,等于_____________________.2、试一试:=-35 =-22 =-2)2(x3、思考:当指数引入负指数后,对于1中幂的这些运算法则是否仍然适用?2a ·5a -= 251a a =25a a =)(1=3-a )5(2-+=a ,即2a ·5a -=)(2+a 2a -·5a -=2511a a = 71a =)(a )5(2-+-=a ,即2a -·5a -=)(2+-a 0a ·5a -=1×51a =5-a )5(0-+=a ,即0a ·5a -=)()(+a 归纳:当m 、n 是任意整数时,都有m a ·n a = 【精讲点拨】例题、计算(1)233(2)x y -- (2)231()3ab --·3256a b -【基础训练】1. (x-1)0=1成立的条件是 .2. (x-1)-2= ;(-13)-2= ;0.1-3= ;a -3= ;a -2bc -2= ;3.(a-1)-2bc -2=4.2a ·2()a --3()a -= ,21()a --= ,1a --= , 21()a -⎡⎤-⎣⎦=5.计算(1)2313()x y x y -- (2)23223(2)()ab c a b ---÷ (3)033212009(2)()(3)2--+-+-+-(4) 2101(1)()5(2010)2π--+-÷- (5)31220128(1)()72---⎡⎤--⨯-⨯-⨯⎣⎦6.利用负指数幂将下列分式化为幂的乘法。
八年级数学上册《1623整数指数幂》学案1

八年级数学上册《1623整数指数幂》学案116、2、3 整数指数幂[学习目标]1、理解负整数指数幂的性质,正确熟练地运用整数指数幂公式进行计算。
2、通过幂指数扩展到全体实数,培养学生抽象的数学思维能力,运用公式进行计算,培养学生综合解题的能力和计算能力3、在数学公式中渗透公式的简洁美、和谐美,随着学习知识范围的扩展,产生对新知识的渴望与追求的积极情感,让学生形成辩证统一的哲学观和世界观。
[重点、难点]重点:理解负整数指数幂的性质,会运用性质进行计算。
难点:理解负整数指数幂公式中字母的取值范围。
[学习过程]课前自主练1、若(x-3)0有意义,则x=_______;若(2x-1)0无意义,则x______、2、还记得幂的性质吗?请填一填、(1)aman=______(m、n是正整数)、(2)(am)n=______(m、n 是正整数)、(3)(ab)n=______(n为正整数)、(4)aman=______(a≠0,m、n是正整数,m>n)、(5)()n=_______(n是正整数)、(6)(a)0=______(a_______)、一、创设情境,导入新课:1、同底数幂除法公式中,m、n有什么限制吗?2、若,则a。
3、计算:=;=。
二、合作交流,解读探究:一方面:==另一方面:==则归纳:一般的,规定:n是整数,即任何不等于零的数的-n (n为正整数)次幂,等于这个数的n次幂的倒数。
试一试:。
三、应用迁移,巩固提高:例1、计算:1、2、3、4、5、6、(脑力风暴)想一想:从上题的解题过程中你发现了什么?我们引进了零指数和负整数指数幂,指数的范围已经扩大到了全体整数,那么以前所学的幂的性质是否依然成立呢?例2:判断下列式子是否成立:(1)(2);(3)例3:典型例题计算:(1)(2)小组合作思考完成小组活动探究:正确把负指数幂转化为正指数幂(基本技能题)若(x-3)-2有意义,则x_______;若(x-3)-2无意义,则x_______、(基本技能题)5-2的正确结果是()A、-B、C、D、-(基本技能题)化简(-2m2n-3)(3m-3n-1),使结果只含有正整数指数幂。
16.2.3整数指数幂1

16.2.3整数指数幂1备课人 :杨玉英一、学习目标 :1.知道负整数指数幂n a -=na 1(a ≠0,n 是正整数 2.掌握整数指数幂的运算性质.重点:掌握整数指数幂的运算性质.难点:认识负整数指数幂的产生过程及幂运算法则的扩展过程.二、预习提纲:1.回顾已学过的正整数指数幂的运算性质:(1)同底数的幂的乘法:_______________________ .(2)幂的乘方:_______________________________ .(3)积的乘方:________________________ .(4)同底数的幂的除法:________________________.(5)商的乘方:________________________________.(6)0指数幂,即当a ≠0时,___________2.计算 (两种方法)53a a ÷=________________________; .3.反思归纳: .4.思考:引入负整数指数和0指数后,正整数幂的公式还能用吗?反思归纳:5.例题分析:例1 (1)321)(b a - (2) 32222)(---∙b a b a例2 下列等式时否正确,为什么?(1)n m n m aa a a -∙=÷ (2)n n nb a b a -=)(三、讨论与交流要求:以小组为单位对预习提纲的内容展开交流,并准备展示内容.四、展示与点评要求:以小组为单位对预习提纲的内容进行展示,其他小组进行质疑、点评,教师做适当补充.五、当堂检测:A 组:1.填空:(1)03=_______. 23-=_______; (2)0(3)-=_______.2(3)--=_______; (3)0b =_______.2b -=______(b ≠0)B 组:2.计算:(1)2313()x y x y --(2)2323(2)()ab c a b --÷C 组: ⎪⎭⎫ ⎝⎛-÷⎪⎭⎫⎝⎛----42318521q p q p作业1. 若(x -3)-2有意义,则x _______;若(x-3)-2无意义,则x _______.2 . 5-2的正确结果是( ) A .-125 B .125C .110D .-110 3. 化简(-2m 2n -3)·(3m -3n -1),使结果只含有正整数指数幂。
16.2.3整数指数幂
1.(1)-4(2)4(3)1(4)1(5) (6)
2.(1) (2) (3)
第四步:课后练习
1.用科学计数法表示下列各数:
0.000 04,-0. 034, 0.000 000 45, 0. 003 009
2.计算
(1
) (3×10-8)×(4×103)(2) (2×10-3)2÷(10-3)3
(P26)例11.
[分析]是一个介绍纳米的应用题,是应用科学计数法表示小于1的数.
第三步:随堂练习
1.填空
(1)-22=(2)(-2)2=(3)(-2)0=
(4)20=(5)2-3=(6)(-2)-3=
2.计算
(1) (x3y-2)2(2)x2y-2·(x-2y)3(3)(3x2y-2)2÷(x-2y)3
16.2.3整数指数幂
教学目标
1.知道负整数指数幂 = (a≠0,n是正整数).
2.掌握整数指数幂的运算性质.
3.会用科学计数法表示小于1的数.
重点、难点
重点:掌握整数指数幂的运算性质.
难点:会用科学计数法表示堂知识使学生懂得任何事物之间是相互联系的,理论来源于实践,服务于实践。能利用事物之间的类比性解决问题。
教学过程
教学设计与师生互动
备注
第一步:课堂引入
1.回忆正整数指数幂的运算性质:
(1)同底数的幂的乘法: (m,n是正整数);
(2)幂的乘方: (m,n是正整数);
(3)积的乘方: (n是正整数);
(4)同底数的幂的除法: ( a≠0,m,n是正整数,m>n);
(5)商的乘方: (n是正整数);
2.回忆0指数幂的规定,即当a≠0时, .
答案:1.(1)4×10-5(2) 3.4×10-2(3)4.5×10-7(4)3.009×10-3
16.2.3整数指数幂(1)
新世纪教育网 www.xsjjyw.com 精品资料 版权所有@新世纪教育网 新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@新世纪教育网 1 16.2.3整数指数幂(1) 一、教学目标 1、经历探索负整数指数幂和零指数幂的运算性质的过程,进一步体会幂的意义,发展代数推理能力和有条理的表达能力。 2、了解负整数指数的概念,了解幂运算的法则可以推广到整指数幂。 3、会进行简单的整数范围内的幂运算。 二、教学重点 负整数指数幂的概念 三、教学难点 认识负整数指数幂的产生过程及幂运算法则的扩展过程。 四、教学设计 教学过程 温故知新 1、 你还记得下面这些算式的算式的算法吗?比一比,看一看谁做得又快又好: (1)3533 (2)40aa(3)33()x(4)4()mn(5)53aa(6)77xx(7)7833 2、你还记得01(0)aa是怎么得到的吗? 探究新知 根据除法的意义填空,看看计算结果有什么规律?
(1)781333 (2)571101010(3)351aaa 如果我们要使运算性质mnmnaaa在这里(mn即时)也可以适用,你认为该作怎样的规定呢? 教师可以鼓励学生先运用自己的语言进行描述,然后自学课本第P23页。要指出有了这一
新规定后,mnmnaaa的适用范围就扩大到所有整数指数。 应用新知 课本第25页练习第1题。 新世纪教育网 www.xsjjyw.com 精品资料 版权所有@新世纪教育网 新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@新世纪教育网 2 对第(2)小题的计算要求学生看明底数,并写出中间的转化过程,教师可示范。 再探新知
1、 现在我们考虑:在引入负整数指数和零指数后,mnmnaaa(m、n是正整数)这条性质能否扩大到m、n是整数的情形?请完成下列填空:
(人教版初中数学)16.2.3 整数指数幂(1)
16.2.3 整数指数幂(1)知识领航:任何一个不等于零的数的零次幂等于1, 即)0(10≠=a a当n 为正整数时,nn a a 1=- ()0≠a 正整数指数幂运算性质也可以推广到整数指数幂.e 线聚焦【例】 计算:(1)()3223--y x , (2)()3322232n m n m --⋅.分析:可先运用幂的运算性质进行计算,再化成正整数指数的形式.解:(1)()3223--y x =()()323233----y x =66271y x -=6627x y . (2)()3322232n m n m --⋅=334434n m n m --⋅=112-mn =nm 12. 双基淘宝 ◆仔细读题,一定要选择最佳答案哟!1.若m,n 为正整数,则下列各式错误的是( )A .n m n m a a a a -⋅=÷ B.n n n b a b a -=⎪⎭⎫ ⎝⎛ C.()mn n ma a =-- D. n n am am 1=- 2.下列计算正确的是( )A.()110-=- B.15.0210=⎪⎭⎫ ⎝⎛- C. ()111-=-- D.()()235x x x -=-÷- 3.若25102=x ,则x -10等于( ) A.51- B.51 C.501 D.6251 4.若31=+-a a ,则22-+a a 等于( )A. 9B. 1C. 7D. 115已知p x 21+= ,p y -+=21,则用x 表示y 的结果是( ) A. 11-+x x B.12++x x C.1-x x D.x -2 6.计算:()()12211--+-n n =______________(n 为整数) 7.计算:()____________221=---8.化简:()))((2211---+-+y x y x yx =______________ 9.已知:57,37==n m ,则=-n m 27________________. 10.已知:9432827321=⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛--x x , 则x=_____________ 综合运用 ◆认真解答,一定要细心哟!11.计算:(1)10123)326(34--⎪⎭⎫ ⎝⎛⋅-⋅- (2)()32132----xy b a(3)()111)(2----⋅+-b a b a ab(4)⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛----42318521q p q p(5)321232223⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛----y x c b a (6)23323322⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛+--ππππ 12.已知:a xx =+-1,求22-+x x 和44-+x x 的值拓广创新◆试一试,你一定能成功哟! 13.求满足2151691089=⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛c b a 的一切整数a,b,c 的值.。
《整数指数幂》第1课时导学案
教师寄语春来春去,燕离燕归,枝条吐出点点新绿,红花朵朵含苞欲放,杨柳依依书写无悔年华,白云点点唱响人生奋斗的凯歌,微冷的春风淡去了烟尘与伤痛,沉淀在内心的却是缤纷的梦想以及那收获前的耕耘与奋斗。
整数指数幂 导学案学习目标:1、掌握整数指数幂的运算性质,并能运用它进行整数指数幂的运算。
2、通过分式的约分与整数指数幂的运算方法对比经历探索整数指数幂的运算性质的过程,理解性质的合理性。
学习过程【温故知新】正整数指数幂的性质:(1)m a ·n a = (m 、n 是正整数) (2)()m n a = (m 、n 是正整数),(3)(ab )n = (n 是正整数),(4)m a ÷n a = (a≠0,m 、n 是正整数,m>n ),(5)()n a b= (n 是正整数) , (6)a 0 = (a≠0)【预习导学】预习P18-201、计算:5255÷= ;731010÷= 。
一方面:5255÷=35255--= 731010÷=()()1010=另一方面:5255÷=3525155= 731010÷=()()()=1010 则()()==--4310,5归纳:一般的,规定:())0(≠=-a a n n 是整数,即任何不等于零的数的-n (n 为正整数)次幂,等于_____________________.2、试一试:=-35 =-22 =-2)2(x3、思考:当指数引入负指数后,对于1中幂的这些运算法则是否仍然适用?2a ·5a -= 251a a =25a a =)(1=3-a )5(2-+=a ,即2a ·5a -=)(2+a2a -·5a -=2511a a = 71a=)(a )5(2-+-=a ,即2a -·5a -=)(2+-a 0a ·5a -=1×51a =5-a )5(0-+=a ,即0a ·5a -=)()(+a 归纳:当m 、n 是任意整数时,都有m a ·n a = 【精讲点拨】例题、计算(1)233(2)x y -- (2)231()3ab --·3256a b -【基础训练】1. (x-1)0=1成立的条件是 .2. (x-1)-2= ;(-13)-2= ;0.1-3= ;a -3= ;a -2bc -2= ;3.(a-1)-2bc -2=4.2a ·2()a --3()a -= ,21()a --= ,1a --= , 21()a -⎡⎤-⎣⎦=5.计算(1)2313()x y x y -- (2)23223(2)()ab c a b ---÷ (3)033212009(2)()(3)2--+-+-+-(4) 2101(1)()5(2010)2π--+-÷- (5)31220128(1)()72---⎡⎤--⨯-⨯-⨯⎣⎦6.利用负指数幂将下列分式化为幂的乘法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
数学学习指南
课题:
16.2.3整数指数幂1 备:3.11 授:3. 课时数:
学习目标:
1、掌握整数指数幂的运算性质,并能运用它进行整数指数幂的运算。
2、通过分式的约分与整数指数幂的运算方法对比经历探索整数指数幂的运算性质的过程。
(一)独立自主学习
1.正整数指数幂的性质:(1)ma·na= (m、n是正整数)
(2)()mna= ( m、n是正整数), (3)(ab)n= (n是正整数),
(4)ma÷na= (a≠0,m、n是正整数,m>n),
(5)()nab= (n是正整数) , (6)a 0 = (a≠0)
2.预习P18-20完成下列习题
(1)、计算:5255= ;731010= 。
一方面:5255=35255 731010=1010
另一方面:5255=3525155 731010 =1010
则4310,5
归纳:一般的,规定:)0(aann是整数,即任何不等于零的数的-n(n为正整
数)次幂,等于_____________________.
(2)、试一试:35 22 2)2(x
(3)、思考:当指数引入负指数后,对于1中幂的这些运算法则是否仍然适用?
2a·5a=251aa=25aa =)(1=3a)5(2a ,即2
a
·5a=)(2a
2a·5a=2511aa= 71a=)(a)5(2a,即2a·5a
=)(2a
0a·5a=1×51a =5a)5(0a ,即0
a
·5a=)()(a
归纳:当m、n是任意整数时,都有ma·na=
(二)小组合作学习
2
(1)233(2)xy (2)231()3ab·3256ab
(三)知识达标检验
1. (x-1)0=1成立的条件是 .
2. (x-1)-2= ;(-13)-2= ;0.1-3= ;a-3= ;a-2bc-2= ;
3.(a-1)-2bc-2=
4.2a·2()a3()a= ,21()a= ,1a= , 21()a=
5、计算
(1)033212009(2)()(3)2 (2)2101(1)()5(2010)2
(3)31220128(1)()72 (4)32122)2(2baba
6. 把下列各式写成分式。
(1)、232nm (2)、21)()(yxyx (3)、2)2(2ba
7. 求下列各式中x的值:(1)82x (2)22738x (3)163x (4)1001020.52x
(5)0.0003=310x
8.化简:(x-1+y-1)(x+y)-1.
课后作业:教材P23——7
课后思考:计算:
(1)2023)1.0(14.3)301()101( (2)232221)()3(nmnm
