中心对称图形阶段复习一(至平行四边形)
中心对称复习

第九章 中心对称图形复习(1)复习目标:1、认识图形的旋转及性质,会根据要求画旋转图形。
2、认识中心对称图形及其性质,会设计一些中心对称图案。
3、理解并掌握平行四边形及特殊的平行四边形的性质、判定及其应用。
【学习重难点】理解并掌握平行四边形及特殊的平行四边形的性质、判定及其应用。
学习过程:【课前准备】知识点回顾:【知识点 1】旋转的概念: 这个定点称为 ,旋转的角度称为 。
图形的旋转不改变图形的 。
旋转的性质:(1)旋转前后的图形 (2) 的距离相等, (3)每一对对应点与 的连线所成的角彼此相等。
〖基础回顾〗1、下列现象属于旋转的是 ( )A.摩托车在急刹车时向前滑动B.飞机起飞后冲向空中的过程C.幸运大转盘转动的过程D.笔直的铁轨上飞驰而过的火车2、在图形旋转中,下列说法错误的是 ( )A.图形上各点的旋转角度相同B. 旋转不改变图形的大小、形状;C.由旋转得到的图形也一定可以由平移得到D. 对应点到旋转中心距离相等【知识点 2】中心对称:中心对称的性质:成中心对称的两个图形对称点连线都过 ,并且被对称中心 。
中心对称图形:中心对称图形的作图方法: 中心对称与中心对称图形之间的关系:轴对称图形与中心对称图形区别与联系: 〖基础回顾〗1、下面扑克中是中心对称的是( )A B C D2、在线段、角、平行四边形、长方形、等腰梯形、圆、等边三角形中,是中心对称图形的是_____,是轴对称图形的有_____,既是中心对称图形又是轴对称图形的是______。
3、作出ABC △关于点o 的对称图形A B C '''△.【知识点 3】利用中心对称的特点、性质设计中心对称图案〖基础回顾〗图①、图②均为76⨯的正方形网格,点A B C 、、在格点上.(画一个即可)在图①,②中分别确定格点D ,E 并画出以A B C D 、、、和A B C E 、、、为顶点的四边形,使其为轴对称和中心对称图形。
中心对称图形--平行四边形全章复习与巩固(提高)知识讲解
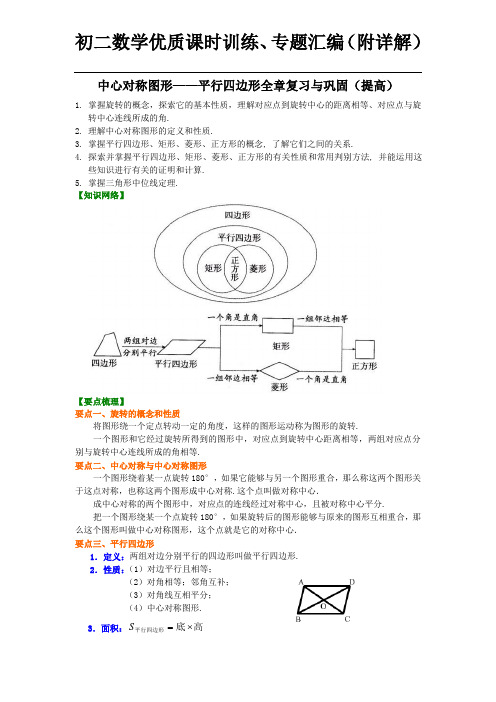
中心对称图形——平行四边形全章复习与巩固(提高) 1. 掌握旋转的概念,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角.2. 理解中心对称图形的定义和性质.3. 掌握平行四边形、矩形、菱形、正方形的概念, 了解它们之间的关系.4. 探索并掌握平行四边形、矩形、菱形、正方形的有关性质和常用判别方法, 并能运用这些知识进行有关的证明和计算.5. 掌握三角形中位线定理. 【知识网络】【要点梳理】要点一、旋转的概念和性质 将图形绕一个定点转动一定的角度,这样的图形运动称为图形的旋转.一个图形和它经过旋转所得到的图形中,对应点到旋转中心距离相等,两组对应点分别与旋转中心连线所成的角相等.要点二、中心对称与中心对称图形一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称.这个点叫做对称中心.成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分. 把一个图形绕某一个点旋转180°,如果旋转后的图形能够与原来的图形互相重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.要点三、平行四边形1.定义:两组对边分别平行的四边形叫做平行四边形.2.性质:(1)对边平行且相等;(2)对角相等;邻角互补;(3)对角线互相平分;(4)中心对称图形.3.面积:高底平行四边形⨯=S4.判定:边:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形.角:(4)两组对角分别相等的四边形是平行四边形;(5)两组邻角分别互补的四边形是平行四边形.边与角:(6)一组对边平行,一组对角相等的四边形是平行四边形; 对角线:(7)对角线互相平分的四边形是平行四边形.要点诠释:平行线的性质:(1)平行线间的距离都相等;(2)等底等高的平行四边形面积相等.要点四、矩形1.定义:有一个角是直角的平行四边形叫做矩形.2.性质:(1)具有平行四边形的所有性质;(2)四个角都是直角;(3)对角线互相平分且相等;(4)中心对称图形,轴对称图形.3.面积:宽=长矩形⨯S4.判定:(1) 有一个角是直角的平行四边形是矩形.(2)对角线相等的平行四边形是矩形.(3)有三个角是直角的四边形是矩形.要点诠释:由矩形得直角三角形的性质:(1)直角三角形斜边上的中线等于斜边的一半;(2)直角三角形中,30度角所对应的直角边等于斜边的一半.要点五、菱形1. 定义:有一组邻边相等的平行四边形叫做菱形.2.性质:(1)具有平行四边形的一切性质;(2)四条边相等;(3)两条对角线互相平分且垂直,并且每一条对角线平分一组对角;(4)中心对称图形,轴对称图形.3.面积:2对角线对角线高==底菱形⨯⨯S 4.判定:(1)一组邻边相等的平行四边形是菱形;(2)对角线互相垂直的平行四边形是菱形;(3)四边相等的四边形是菱形.要点六、正方形1. 定义:四条边都相等,四个角都是直角的四边形叫做正方形.2.性质:(1)对边平行;(2)四个角都是直角;(3)四条边都相等;(4)对角线互相垂直平分且相等,对角线平分对角;(5) 两条对角线把正方形分成四个全等的等腰直角三角形;(6)中心对称图形,轴对称图形.3.面积:=S 正方形边长×边长=12×对角线×对角线 4.判定:(1)有一个角是直角的菱形是正方形;(2)一组邻边相等的矩形是正方形;(3)对角线相等的菱形是正方形;(4)对角线互相垂直的矩形是正方形;(5)对角线互相垂直平分且相等的四边形是正方形;(6)四条边都相等,四个角都是直角的四边形是正方形.【典型例题】类型一、旋转与中心对称图形1、如图,在△ABC 中,∠CAB=75°,在同一平面内,将△ABC 绕点A 旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )A .30°B .35°C .40°D .50°【思路点拨】根据旋转的性质可得AC=AC′,∠BAC=∠B′AC′,再根据两直线平行,内错角相等求出∠ACC′=∠CAB ,然后利用等腰三角形两底角相等求出∠CAC′,再求出∠BAB′=∠CAC′,从而得解.【答案】A ;【解析】解:∵△ABC 绕点A 旋转到△AB′C′的位置,∴AC=AC′,∠BAC=∠B′AC′,∵CC′∥AB,∠CAB=75°,∴∠ACC′=∠CAB=75°,∴∠CAC′=180°-2∠ACC′=180°-2×75°=30°,∵∠BAB′=∠BAC -∠B′AC,∠CAC′=∠B′AC′-∠B′AC,∴∠BAB′=∠CAC′=30°.故选A .【总结升华】本题考查了旋转的性质,主要利用了旋转变换只改变图形的位置不改变图形的形状与大小的性质,等腰三角形两底角相等的性质,平行线的性质. 类型二、平行四边形2、(优质试题•菏泽)如图,点O 是△ABC 内一点,连结OB 、OC ,并将AB 、OB 、OC 、AC 的中点D 、E 、F 、G 依次连结,得到四边形DEFG .(1)求证:四边形DEFG是平行四边形;(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.【思路点拨】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC,DG∥BC且DG=BC,从而得到DE=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;(2)先判断出∠BOC=90°,再利用直角三角形斜边的中线等于斜边的一半,求出EF即可.【答案与解析】解:(1)∵D、G分别是AB、AC的中点,∴DG∥BC,DG=BC,∵E、F分别是OB、OC的中点,∴EF∥BC,EF=BC,∴DG=EF,DG∥EF,∴四边形DEFG是平行四边形;(2)∵∠OBC和∠OCB互余,∴∠OBC+∠OCB=90°,∴∠BOC=90°,∵M为EF的中点,OM=3,∴EF=2OM=6.由(1)有四边形DEFG是平行四边形,∴DG=EF=6.【总结升华】此题主要考查了平行四边形的判定和性质,三角形的中位线,直角三角形的性质,解本题的关键是判定四边形DEFG是平行四边形.举一反三:【变式】已知△ABC中,AB=3,AC=4,BC=5,分别以AB、AC、BC为一边在BC边同侧作正△ABD、正△ACE和正△BCF,求以A、E、F、D四点为顶点围成的四边形的面积.【答案】证明:∵ AB=3,AC=4,BC=5,∴∠BAC=90°∵△ABD、△ACE和△BCF为正三角形,∴AB=BD=AD,AC=AE=CE,BC=BF=FC ,∠1+∠FBA=∠2+∠FBA=60°∴∠1=∠2易证△BAC≌△BDF(SAS),∴DF=AC=AE=4,∠BDF=90°同理可证△BAC≌△FEC∴AB=AD=EF=3∴四边形AEFD是平行四边形(两组对边分别相等的四边形是平行四边形)∵DF∥AE,DF⊥BD延长EA交BD于H点,AH⊥BD,则H为BD中点∴平行四边形AEFD的面积=DF×DH=4×32=6.类型三、矩形3、如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.(1)求证:四边形EFGH是矩形;(2)若E、F、G、H分别是OA、OB、OC、OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.【答案与解析】(1)证明:∵四边形ABCD是矩形,∴OA=0B=OC=OD,∵AE=BF=CG=DH,∴AO-AE=OB-BF=CO-CG=DO-DH,即:OE=OF=OG=OH,∴四边形EFGH是矩形;(2)解:∵G是OC的中点,∴GO=GC,∵DG⊥AC,∴∠DGO=∠DGC=90°,又∵DG=DG,∴△DGC≌△DGO,∴CD=OD,∵F是BO中点,OF=2cm,∴BO=4cm,∵四边形ABCD是矩形,∴DO=BO=4cm,∴DC=4cm,DB=8cm,==.∴矩形ABCD的面积=4×2【总结升华】本题主要考查矩形的判定,首先要判定四边形是平行四边形,然后证明对角线相等.举一反三:(优质试题秋•太康县期中)如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,【变式】垂足为N,且AB=6,BC=10,MN=1.5,求△ABC的周长.【答案】解:延长线段BN交AC于E.∵AN平分∠BAC,在△ABN和△AEN中,∴△ABN≌△AEN(SAS),∴AE=AB=6,BN=NE,又∵M是△ABC的边BC的中点,∴CE=2MN=2×1.5=3,∴△ABC的周长是AB+BC+AC=6+10+6+3=25.4、在Rt△ABC中,∠ACB=90°,BC=4.过点A作AE⊥AB且AB=AE,过点E分别作EF⊥AC,ED⊥BC,分别交AC和BC的延长线与点F,D.若FC=5,求四边形ABDE的周长.【思路点拨】首先证明△ABC≌△EAF,即可得出BC=AF,AC=EF,再利用勾股定理得出AB的长,进而得出四边形EFCD是矩形,求出四边形ABDE的周长即可.【答案与解析】解:∵∠ACB=90°,AE⊥AB,∴∠1+∠B=∠1+∠2=90°.∴∠B=∠2.∵EF⊥AC,∴∠4=∠5=90°.∴∠3=∠4.在△ABC和△EAF中,∵342BAB AE∠=∠⎧⎪∠=∠⎨⎪=⎩,,∴△ABC≌△EAF(AAS).∴BC=AF,AC=EF.∵BC=4,∴AF=4.∵FC=5,∴AC=EF=9.在Rt△ABC中,=..∵ED⊥BC,∴∠7=∠6=∠5=90°.∴四边形EFCD是矩形.∴CD=EF=9,ED=FC=5.∴四边形ABDE的周长.【总结升华】此题主要考查了全等三角形的判定以及矩形的判定与性质和勾股定理等知识,根据已知得出AC=EF=9是解题关键.类型四、菱形5、如图,平行四边形ABCD中,AB⊥AC,AB=1,BC AC,BD 相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;(2)试说明在旋转过程中,线段AF与EC总保持相等;(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.【思路点拨】(1)当旋转角为90°时,∠AOF=90°,由AB⊥AC,可得AB∥EF,即可证明四边形ABEF为平行四边形;(2)证明△AOF≌△COE即可;(3)当EF⊥BD时,四边形BEDF为菱形,又由AB⊥AC,AB=1,易求得OA=AB,即可得∠AOB=45°,求得∠AOF=45°,则可得此时AC绕点O顺时针旋转的最小度数为45°.【答案与解析】(1)证明:当∠AOF=90°时,AB∥EF,又AF∥BE,∴四边形ABEF为平行四边形.(2)证明:四边形ABCD为平行四边形,∴AO=CO,∠FAO=∠ECO,∠AOF=∠COE.∴△AOF≌△COE∴AF=CE(3)四边形BEDF可以是菱形.理由:如图,连接BF,DE,由(2)知△AOF≌△COE,得OE=OF,∴EF与BD互相平分.∴当EF⊥BD时,四边形BEDF为菱形.AC==,在Rt△ABC中,2。
中心对称图形-平行四边形全章复习与巩固.docx

中心对称图形 -- 平行四边形全章复习与巩固一、目标与策略明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!学习目标:掌握旋转的概念,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角..理解中心对称图形的定义和性质掌握平行四边形、矩形、菱形、正方形的概念, 了解它们之间的关系.探索并掌握平行四边形、矩形、菱形、正方形的有关性质和常用判别方法, 并能运用这些知识进行有关的证明和计算.掌握三角形中位线定理.学习策略:旋转这一图形的变换在中考中应用很广泛的,在解决这类问题的时候,一定要抓住旋转中心和旋转角度,旋转前后图形是全等的。
;对三种特殊平行四边形之间的联系和区别有了更进一步的认识,达到体会探索过程,疏理探索思路的目的,学生整理本堂课复习的知识,构建完整的知识体系;比较三种特殊平行四边形的性质和判定的异同及联系,梳理知识点,对比特点,加深理解,达到梳理知识的目的.能够熟练掌握平行四边形和特殊四边形的性质和判定,并运用其性质与判定解决有关问题.二、学习与应用“凡事预则立,不预则废”.科学地预习才能使我们上课听讲更有目的性和针对知识回顾——复习学习新知识之前,看看你的知识贮备过关了吗1.在四边形ABCD中,对角线AC= BD,那么顺次连结四边形ABCD 各边的中点所得的四边形一定是.2. M 、N、P、 Q 顺次为四边形ABCD各边的中点,下面条件使四边形MNPQ 为正方形的条件是.3.已知三角形三边长分别为a、b、c,它的三条中位线组成一个新的三角形,这个新三角形的三条中位线又组成一个小三角形,这个小三角形的三条中位线又组成一个新小三角形,则最小的三角形的周长是.4.如果梯形的一底为6,中位线为8,则另一底为.5.梯形的上底长4cm,下底长 6cm ,则梯形的中位线长为.要点梳理——预习和课堂学习认真阅读、理解教材,尝试把下列知识要点内容补充完整,带着自己预习的疑惑认真听要点一、旋转的概念和性质一个图形和它经过旋转所得到的图形中,对应点到旋转中心距离与旋转中心连线所成的角.,两组对应点分别要点二、中心对称与中心对称图形成中心对称的两个图形中,对应点的连线经过,且被对称中心把一个图形绕某一个点旋转180°,如果旋转后的图形能够与原来的图形互相这个图形叫做中心对称图形,这个点就是它的对称中心.要点三、平行四边形1.定义:两组对边分别平行的四边形叫做平行四边形.2.性质:(1)对边且;(2)对相等;( 3)对角线互相;(4)对称图形..角互补;,那么3.面积:S平行四边形底高4.判定:边:( 1)两组对( 2)两组对边分别( 3)一组对边角:(4)两组对角分别( 5)两组邻角分别边与角:(6)一组对边对角线:(7)对角线互相分别平行的四边形是平行四边形;的四边形是平行四边形;的四边形是平行四边形.的四边形是平行四边形;的四边形是平行四边形.,一组相等的四边形是平行四边形;的四边形是平行四边形.要点四、矩形1.定义:有一个角是的平行四边形叫做矩形2.性质:(1)具有平行四边形的所有性质;( 2)四个角都是;.( 3)对角线互相平分且( 4)中心对称图形,3.判定:(1) 有一个( 2)对角线(3)有三个角是;对称图形 .是直角的平行四边形是矩形的平行四边形是矩形.的四边形是矩形..要点五、菱形1. 定义:有一组相等的平行四边形叫做菱形.2.性质:(1)具有平行四边形的一切性质;( 2)四条相等;( 3)两条对角线互相平分且( 4)中心对称图形,,并且每一条对角线平分一组对称图形 .;3.面积:4.判定:(1)一组邻边相等的是菱形;(2)对角线互相垂直的是菱形;(3)四边相等的是菱形.要点六、正方形1. 定义:四条边都2.性质:(1)( 3)四条边都,四个角都是的四边形叫做正方形.平行;( 2)四个角都是;;(4)对角线互相垂直平分且相等,对角线平分;( 5)两条对角线把正方形分成四个全等的三角形;( 6)对称图形,3.判定:(1)有一个角是直角的对称图形 .是正方形;( 2)一组邻边相等的是正方形;(3)对角线相等的是正方形;(4)对角线互相垂直的是正方形;(5)对角线互相垂直平分且相等的(6)四条边都相等,四个角都是直角的是正方形;是正方形 .典型例题——自主学习认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完类型一、旋转与中心对称图形A 旋转到△AB′C的′位置,例 1、如图,在△ ABC中,∠CAB=75°,在同一平面内,将△ ABC绕点使得CC′∥ AB,则∠BAB′=()A . 30 °B . 35 °C. 40 °D. 50 °【总结升华】_________________________________________________________________________.类型二、平行四边形例 2.如图,△ ABC中 AB=AC,点 D 从点 B 出发沿射线BA 移动,同时,点 E 从点 C出发沿线段AC 的延长线移动,已点知D、 E 移动的速度相同,DE 与直线 BC相交于点F.(1)如图 1,当点 D 在线段 AB 上时,过点 D 作 AC 的平行线交 BC于点 G,连接 CD、GE,判定四边形CDGE的形状,并证明你的结论;( 2)过点 D 作直线 BC的垂线垂足为M,当点 D、 E 在移动的过程中,线段BM、 MF、CF 有何数量关系请直接写出你的结论.【总结升华】_________________________________________________________________.举一反三:【变式】已知△ ABC中,AB=3,AC= 4,BC=5,分别以 AB、AC、BC 为一边在 BC 边同侧作正△ ABD、正△ ACE和正△ BCF,求以 A、 E、 F、D 四点为顶点围成的四边形的面积.类型三、矩形例3、如图, O 是矩形 ABCD的对角线的交点, E、F、G、H 分别是 OA、OB、OC、OD 上的点,且 AE =B F=CG=DH.( 1)求证:四边形EFGH是矩形;(2)若 E、F、G、H 分别是 OA、OB、OC、OD 的中点,且DG⊥AC,OF= 2 cm,求矩形 ABCD 的面积.【总结升华】________________________________________________________________.举一反三:【变式】如图, M 是△ABC的边 BC 的中点, AN 平分∠BAC,且 BN⊥ AN,垂足为 N,且 AB=6,BC=10,MN=,求△ ABC的周长.例4、在 Rt△ ABC中,∠ACB=90°,BC=4.过点 A 作 AE⊥ AB 且 AB=AE,过点 E 分别作 EF⊥ AC,ED⊥ BC,分别交 AC 和 BC的延长线与点 F, D.若 FC=5,求四边形 ABDE的周长.【总结升华】________________________________________________________________.类型四、菱形例 5、如图,平行四边形ABCD中, AB⊥AC,AB=1,BC= 5 .对角线AC,BD相交于点O,将直线 AC 绕点 O 顺时针旋转,分别交BC, AD 于点 E, F.(1)证明:当旋转角为 90°时,四边形 ABEF是平行四边形;(2)试说明在旋转过程中,线段 AF 与 EC总保持相等;(3)在旋转过程中,四边形 BEDF可能是菱形吗如果不能,请说明理由;如果能,说明理由并求出此时 AC 绕点 O 顺时针旋转的度数.【总结升华】__________________________________________________________.举一反三:AB 于 E,交BC于【变式】已知 :如图所示, BD 是△ ABC的角平分线, EF 是 BD 的垂直平分线,且交点 F.求证 :四边形 BFDE是菱形 .例 6、在口 ABCD中,对角线AC、BD 相交于点 O, BD=2AB,点 E、F 分别是 OA、BC的中点.连接BE、 EF.(1)求证: EF=BF;(2)在上述条件下,若 AC=BD,G 是 BD 上一点,且 BG: GD=3:1,连接 EG、 FG,试判断四边形EBFG的形状,并证明你的结论.【总结升华】____________________________________________________________.类型五、正方形例7、正方形 ABCD的边长为 3,E、 F分别是 AB、 BC边上的点,且∠ EDF=45°.将△ DAE绕点 D 逆时针旋转 90°,得到△ DCM.(1)求证: EF= FM;(2)当 AE= 1 时,求 EF 的长.【总结升华】______________________________________________________________.举一反三:【变式】如图(1),正方形ABCD 和正方形CEFG有一公共顶点C,且 B、C、 E 在一直线上,连接BG、 DE.(1)请你猜测BG、DE 的位置关系和数量关系并说明理由.(2)若正方形CEFG绕 C 点向顺时针方向旋转一个角度后,如图(2), BG 和 DE 是否还存在上述关系若存在,试说明理由;若不存在,也请你给出理由.学生: _______________家长:______________指导教师:_________________。
新苏教版八年级下数学教案第九章中心对称图形--平行四边形复习课

第九章中心对称图形-平行四边形单元复习课【知识梳理】9.1 图形的旋转1.概念:在平面内,将一个图形绕一个定点转动一定的角度,这样的图形运动称为图形的旋转,这个定点称为旋转中心,旋转的角度称为旋转角.2.图形旋转的性质:(1)旋转前后的图形全等;(2)对应点到旋转中心的距离相等;(3)每一对对应点与旋转中心的连线所成的角彼此相等.3.练习:(1)如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是()A. B.2 C.3 D.2(2)如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为.(3)如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.(1)求证:△BCF≌△BA1D.(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由.(4).如图1,在△ABC 中,AB=AC ,∠BAC=90°,D 、E 分别是AB 、AC 边的中点.将△ABC 绕点A 顺时针旋转α角(0°<α<180°),得到△AB ′C ′(如图2). (1)探究DB ′与EC ′的数量关系,并给予证明; (2)当DB ′∥AE 时,试求旋转角α的度数.9.2 中心对称与中心对称图形1.一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称.这个点叫做对称中心.2.成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.3.把一个图形绕 旋转 ,如果旋转后的图形能够与 ,那么这个图形叫做 ,这个点就是 。
中心对称图形的复习1(简易)
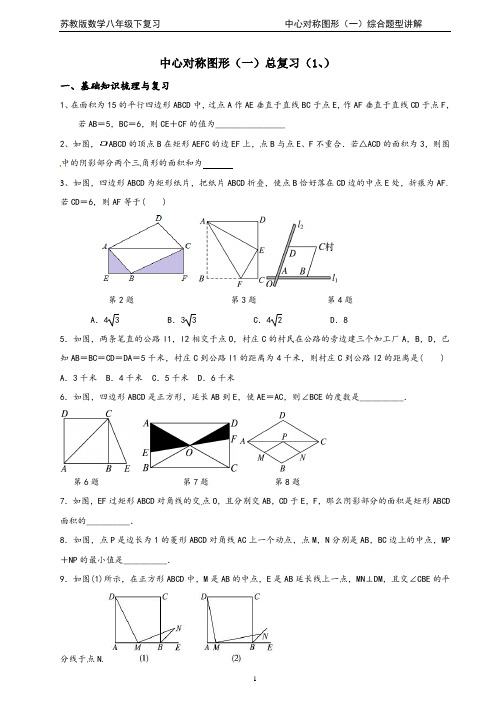
中心对称图形(一)总复习(1、)一、基础知识梳理与复习1、在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为________________2、如图,ABCD的顶点B在矩形AEFC的边EF上,点B与点E、F不重合.若△ACD的面积为3,则图中的阴影部分两个三角形的面积和为3、如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于( )第2题第3题第4题A.4 3 B.3 3 C.4 2 D.85.如图,两条笔直的公路l1,l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A,B,D,已知AB=BC=CD=DA=5千米,村庄C到公路l1的距离为4千米,则村庄C到公路l2的距离是( ) A.3千米 B.4千米 C.5千米 D.6千米6.如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是__________.第6题第7题第8题7.如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于E,F,那么阴影部分的面积是矩形ABCD 面积的__________.8.如图,点P是边长为1的菱形ABCD对角线AC上一个动点,点M,N分别是AB,BC边上的中点,MP +NP的最小值是__________.9.如图(1)所示,在正方形ABCD中,M是AB的中点,E是AB延长线上一点,MN⊥DM,且交∠CBE的平分线于点N.(1)求证:MD=MN.(2)若将上述条件中“M是AB的中点”改为“M是AB上任意一点”,其余条件不变,如图(2)所示,则结论“MD=MN”还成立吗?若成立,给出证明;若不成立,请说明理由.二、综合题分类1、在口ABCD中,对角线AC,BD交于点E,AC⊥BC,AB=8,∠ABC=30°,求BD的长。
若点P从点B出发沿B-A-D的路线以2cm/s的速度向点D移动,同时点Q从点C出发沿C-D的路线以1cm/s的速度向点D移动,当一点到达C时,另一点也停止移动。
2020-2021学年 苏科版八年级数学下册第九章 中心对称图形—平行四边形 压轴题提优复习(一)

八年级数学苏科版下册《中心对称图形—平行四边形》压轴题提优复习(一)1.如图,▱ABCD的对角线AC、BD相交于点O,过点O作EF⊥AC,分别交AB、DC 于点E、F,连接AF、CE.(1)若OE=,求EF的长;(2)判断四边形AECF的形状,并说明理由.2.如图,在矩形ABCD中,BD的垂直平分线交AD于E,交BC于F,连接BE、DF.(1)判断四边形BEDF的形状,并说明理由;(2)若AB=8,AD=16,求BE的长.3.已知:如图,在正方形ABCD中,E是对角线AC上一点,EF⊥AC,交AD,AB于点F,H.求证:CF=CH.4.如图,正方形ABCD的对角线AC、BD相交于点O,E、F分别在OB、OC上,OE =OF.求证:AE=BF.5.如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.(1)求证:△ADE≌△CBF;(2)连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.6.如图,已知四边形ABCD是平行四边形,E是AB延长线上一点且BE=AB,连接CE,BD.(1)求证:四边形BECD是平行四边形;(2)连接DE,若AB=BD=4,DE=2,求平行四边形BECD的面积.7.已知:如图,AC是▱ABCD的一条对角线,延长AC至F,反向延长AC至E,使AE =CF.求证:四边形EBFD是平行四边形.8.如图,矩形ABCD中,对角线AC与BD相交于点,过点A作AN∥BD,过点B作BN∥AC,两线相交于点N.(1)求证:AN=BN;(2)连接DN,交AC于点F,若DN⊥NB于点N,求∠DOC的度数.9.如图,已知▱ABCD中,对角线AC、BD相交于点O.点E、F在对角线BD上,且EB=FD.求证:四边形AECF是平行四边形.10.如图,在平行四边形ABCD中,线段AC的垂直平分线交AC于O,分别交BC,AD 于E,F,连接AE,CF.(1)证明:四边形AECF是菱形;(2)在(1)的条件下,如果AC⊥AB,∠B=30°,AE=2,求四边形AECF的面积.11.如图,边长为6的正方形ABCD中,E,F分别是AD,AB上的点,AP⊥BE,P为垂足.(1)如图1,AF=BF,AE=2,点T是射线PF上的一个动点,当△ABT为直角三角形时,求AT的长;(2)如图2,若AE=AF,连接CP,求证:CP⊥FP.12.如图,以Rt△ABC的斜边BC为边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6,求AC.13.如图,已知点C为线段AB上一点,四边形ACMF、BCNE是两个正方形.求证:AN=BM.14.如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.(1)求证:AB=AF;(2)若BC=2AB,∠BCD=100°,求∠ABE的度数.15.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC、BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.(1)求证:四边形ABCD是菱形;(2)若AB=5,BD=6,求CE的长.参考答案1.解:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AO=CO,∴∠FCO=∠EAO,又∵∠AOE=∠COF,∴△AOE≌△COF(ASA),∴OE=OF=,∴EF=2OE=3;(2)四边形AECF是菱形,理由:∵△AOE≌△COF,∴AE=CF,又∵AE∥CF,∴四边形AECF是平行四边形,又∵EF⊥AC,∴四边形AECF是菱形.2.解:(1)四边形BEDF是菱形;理由如下:∵EF是BD的垂直平分线,∴BE=DE,BF=DF,∴∠EBD=∠EDB,∵四边形ABCD是矩形,∴AD∥BC,∴∠DBF=∠EDB,∴∠EBD=∠DBF,∵BD⊥EF,∴BE=BF,∴BE=DE=DF=BF,∴四边形BEDF是菱形;(2)∵四边形ABCD是矩形,∴∠A=90°,由(1)知:BE=DE设BE=DE=x,则AE=AD﹣x=16﹣x,在Rt△ABE中,AB2+AE2=BE2,即82+(16﹣x)2=x2,解得:x=10,∴BE的长为10.3.证明:∵正方形ABCD中,E是对角线AC上一点,∴∠FAE=∠HAE=45°,∵EF⊥AC,∴∠FEA=∠HEA=90°,∴∠AFE=∠FAE=45°,∴AE=FE,同理可证:AE=HE,∴EF=EH,∴AC是FH的垂直平分线,∴CF=CH.4.证明:∵四边形ABCD为正方形,∴OA=OB,AC⊥BD,在△AOE和△BOF中,,∴△AOE≌△BOF(SAS)∴AE=BF.5.(1)证明:∵四边形ABCD是平行四边形,∴AD=CB,AD∥BC,∴∠ADB=∠CBD,∴∠ADE=∠CBF,在△ADE和△CBF中,,∴△ADE≌△CBF(SAS);(2)当BD平分∠ABC时,四边形AFCE是菱形,理由:∵BD平分∠ABC,∴∠ABD=∠CBD,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,AD∥BC,∴∠ADB=∠CBD,∴∠ABD=∠ADB,∴AB=AD,∴平行四边形ABCD是菱形,∴AC⊥BD,∴AC⊥EF,∵DE=BF,∴OE=OF,又∵OA=OC,∴四边形AFCE是平行四边形,∵AC⊥EF,∴四边形AFCE是菱形.6.(1)证明:∵四边形ABCD是平行四边形,∴CD=AB,CD∥AE,∵AB=BE,∴CD=BE,CD∥BE,∴四边形BECD是平行四边形;(2)解:过D作DH⊥AE于H,∵AB=BD=4,∴BE=AB=4,∴BD2﹣BH2=DE2﹣EH2=DH2,∴42﹣BH2=(2)2﹣(4﹣BH)2,∴BH=3,∴DH===,∴平行四边形BECD的面积=BE•DH=4×=4.7.证明:∵四边形ABCD是平行四边形,∴AD=BC,且AD∥BC,∴∠DAC=∠BCA,∴∠DAE=∠BCF,在△ADE和△CBF中,∵,∴△ADE≌△CBF(SAS),∴DE=BF,∠AED=∠CFB,∴DE∥BF,∴四边形EBFD是平行四边形.8.解:(1)证明:∵矩形ABCD中,对角线AC与BD相交于点O,∴OA=OB,∵AN∥BD,BN∥AC,∴四边形OANB是平行四边形,∵OA=OB,∴▱OANB是菱形,∴AN=BN,(2)由(1)可知:BN=OB=OD,∴BD=2BN,∵DN⊥NB,∴∠DNB=90°,∴∠BDN=30°,∵BN∥AC,∴∠DFO=∠DNB=90°,∴∠DOF=90°﹣30°=60°,∴∠DOC=180°﹣60°=120°.答:∠DOC的度数为120°.9.证明:∵平行四边形ABCD,∴AO=CO,BO=DO,∵BE=DF,∴BO﹣BE=DO﹣DF,∴EO=FO,∴四边形AECF是平行四边形.10.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠OAF=∠OCE,∵EF是线段AC的垂直平分线,∴OA=OC,EF⊥AC,在△AOF和△COE中,,∴△AOF≌△COE(ASA),∴AF=CE,∴四边形AECF是平行四边形,又∵EF⊥AC,∴四边形AECF是菱形;(2)解:由(1)得:四边形AECF是菱形,EF⊥AC,∴CE=AE=2,OA=OC,OB=OD,∵AC⊥AB,∴EF∥AB,∴∠OEC=∠B=30°,∴OC=CE=1,OE=OC=,∴AC=2OC=2,EF=2OE=2,∴四边形AECF的面积=AC×EF=×2×2=2.11.(1)解:在正方形ABCD中,可得∠DAB=90°.∵在Rt△BAE中,tan∠ABE===,∴∠ABE=30°.点T是射线PF上的一个动点,当△ABT为直角三角形时,分三种情况:①当点T在AB的上方,∠ATB=90°,显然此时点T和点P重合,即AT=AP=AB=3;②当点T在AB的下方,∠ATB =90°,如图①所示.在Rt△APB中,由AF=BF,可得:AF=BF=PF=3,∴∠BPF=∠FBP=30°,∴∠BFT=60°.在Rt△ATB中,TF=BF=AF=3,∴△FTB是等边三角形,∴TB=3,AT==3;③当点T在AB的下方,∠ABT=90°时,如图②所示.在Rt△FBT中,∠BFT=60°,BF=3,BT=BF•tan60°=3.在Rt△ATB中:AT==3.综上所述:当△ABT为直角三角形时,AT的长为3或3或3;(2)证明:如图③所示,∵四边形ABCD是正方形,∴AB=AD=BC,AD∥BC,∠DAB=90°,∴∠3=∠4.∵在Rt△EAB中,AP⊥BE,∴∠1+∠2=90°,∠3+∠2=90°,∴∠1=∠3,∴∠1=∠3=∠4,∵tan∠1=,tan∠3=,∴=,∵AE=AF,AB=BC,∴=,∴△PBC∽△PAF,∴∠5=∠6.∵∠6+∠7=90°,∴∠5+∠7=90°,即∠CPF=90°,∴CP⊥FP.12.解:在AC上截取CG=AB=4,连接OG,∵四边形BCEF是正方形,∠BAC=90°,∴OB=OC,∠BAC=∠BOC=90°,∵∠AHB=∠OHC,∴∠ABO=∠ACO,在△BAO和△CGO中,∴△BAO≌△CGO(SAS),∴OA=OG=6,∠AOB=∠COG,∵∠BOC=∠COG+∠BOG=90°,∴∠AOG=∠AOB+∠BOG=90°,即△AOG是等腰直角三角形,由勾股定理得:AG==12,即AC=12+4=16.13.证明:∵四边形ACMF和四边形CBEN都是正方形,∴AC=CM,NC=BC,∠ACN=∠BCM=90°,∴△ACN≌△MCB(SAS),∴AN=BM.14.证明:(1)∵四边形ABCD是平行四边形,∴CD=AB,CD∥AB,∴∠DCE=∠F,∠FBC+∠BCD=180°,∵E为AD的中点,∴DE=AE.在△DEC和△AEF中,,∴△DEC≌△AEF(AAS).∴DC=AF.∴AB=AF;(2)由(1)可知BF=2AB,EF=EC,∵∠BCD=100°,∴∠FBC=180°﹣100°=80°,∵BC=2AB,∴BF=BC,∴BE平分∠CBF,∴∠ABE=∠FBC=×80°=40°15.(1)证明:∵AB∥CD,∴∠OAB=∠DCA,∵AC为∠DAB的平分线,∴∠OAB=∠DAC,∴∠DCA=∠DAC,∴CD=AD,∵AB∥CD,∴四边形ABCD是平行四边形,∵AD=AB,∴▱ABCD是菱形;(2)解:∵四边形ABCD是菱形,∴OA=OC,BD⊥AC,OB=OD=BD=3,∴OA===4,∴AC=2OA=8,∴菱形ABCD的面积=AC×BD=×8×6=24,∵CE⊥AB,∴菱形ABCD的面积=AB×CE=5CE=24,∴CE=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9章复习讲义
1、图形旋转的性质:旋转前后的图形 ,对应点到 ,每一对对应点与 。
2、中心对称图形:把一个平面图形绕某一点旋转 ,如果旋转后的图形能够和原来的图形互相 ,那么这个图形叫做中心对称图形。
3、Ⅰ、平行四边形的性质:(1)平行四边形的 ;(2)平行四边形的 ;(3)平行四边形的 。
Ⅱ、平行四边形的判定:
(1)两组对边分别 的四边形是平行四边形; (2)两组对边分别 的四边形是平行四边形。
(3)一组对边 的四边形是平行四边形; (4)两条 的四边形是平行四边形; 【课前热身】 1、下列图形中,中心对称图形有(
).
2、如图,在平行四边形ABCD 中,E 是AD 边上的中点.若∠ABE=∠EBC ,AB=2,则平行四边形ABCD 的周长是 .
3、在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,ABC △的三个顶点都在格点上(每个小方格的顶点叫格点).画出ABC △绕点O 逆时针旋转90°后的A B C '''△.
4、如图,分别以Rt △ABC 的直角边AC 及斜边AB 向外作等边△ACD 、等边△ABE .已知∠BAC =30°,EF ⊥AB ,垂足为F ,边结DF .⑴试说明AC =EF ;⑵求证:四边形ADFE 是平行四边形.
5、如图,□ABCD 的对角线相交于点O ,直线EF 经过点O,分别与AB,CD 的延长线交于点E,F. 求证:四边形AECF 是平行四边形.
【练习】
1、下列图形中,是中心对称图形但不是轴对称图形的是(
)
2、如图, 在平面直角坐标系中, 若△ABC 与△A 1B 1C 1关于E 点成中心对称, 则对称中心E
点的坐标是
.
3、如图,已知,在□ABCD 中,AE=CF ,M 、N 分别是DE 、BF 的中点.求证:四边形MFNE 是平行四边形 .
4、国家级历史文化名城——金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB EF DC ∥∥,BC GH AD ∥∥,那么下列说法中错误的是( )
A .红花、绿花种植面积一定相等
B .紫花、橙花种植面积一定相等
C .红花、蓝花种植面积一定相等
D .蓝花、黄花种植面积一定相等
5、如图,在□ABCD 中,已知∠ODA =90°,AC =10cm ,BD =6cm ,则AD 的长为 ;
第5题
6、如图,在边长为1的小正方形组成的网格中,AOB ∆ 的三个顶点均在格点上,点A.B 的坐标分别为A (-2,3).B (-3,1).
(1)画出 AOB ∆绕点O 顺时针旋转0
90 后的11AOB ∆;
(2)点1A 的坐标为 ;
(3)四边形11AOA B 的面积为 .
7、如图,请在下列四个关系中,选出两个恰当....
的关系作为条件,推出四边形
ABCD 是平行四边形,并予以证明.(写出一种即可)关系:①AD ∥BC ,②CD AB =,③C A ∠=∠,④︒=∠+∠180C B .
已知:在四边形ABCD 中, , ;
求证:四边形ABCD 是平行四边形.
【例题讲解】
【例1】 如图,在平行四边形ABCD 中,EF BC GH AB EF ∥,
∥,与GH 相交于点O ,图中共有 个平行四边形 O H
G
F E
D
C B
A (1)
D
B
A
黄
蓝
紫 橙
红 绿 A G
E
H C B
A
B C
D
P
F
E
D B
A 【巩固】 以三角形的三个顶点作平行四边形,最多可以作( ) A .2个
B .3个
C .4个
D .5个
【例2】 如图,平行四边形ABCD 中,AB AC ⊥.对角线AC ,BD 相交于点O ,将直线AC 绕点O 顺时针旋转,分
别交BC ,AD 于点E ,F .⑴ 证明:当旋转角为90︒时,四边形ABEF 是平行四边形;⑵ 试说明在旋转过程中,线段AF 与EC 总保持相等.
【例3】 在平行四边形ABCD 中,点1A 、2A 、3A 、4A 和1C 、2C 、3C 、4C 分别为AB 和CD 的五等分点,点1B 、2B 和1D 、2D 分别是BC 和DA 的三等分点,已知四边形4242A B C D 的面积为1,则平行四边形ABCD 面积为( )
A .2
B .35
C .5
3
D .15
【巩固】 如图,在平行四边ABCD 中,AC 、BD 为对角线,6BC =,BC 边上的高为4,则阴影部分的面积为( ).
A .3
B .6
C .12
D .24
【巩固】 如图,已知:在平行四边形ABCD 中,BCD ∠的平分线CE 交边AD 于E ,ABC ∠的平分线BG 交CE 于F ,
交AD 于G .求证:AE DG =.
F
G
E
D
C
B
A
【例5】 ⑴如图,已知等边三角形的边长为10,P 是ABC ∆内一点,PD AC ∥,PE AB PF BC ∥,
∥,点D E F ,,分别在AB BC AC ,
,上,则PD PE PF ++= ⑵如图1,在平行四边ABCD 中,120A ∠=︒,则D ∠= ︒.
P
F
E
D
C
B
A E
E
A
B
C
D
图
A
B
C
D
图图1
D
C
B
A
O D B
A
(3)已知四边形的四条边长分别是a b c d ,
,,,其中a b ,为对边,并且满足222222a b c d ab cd +++=+则这个四边形是( ) A .任意四边形 B .平行四边形 C .对角线相等的四边形 D .对角线垂直的四边形 (4)已知平行四边形ABCD 的周长为60cm ,对角线AC 、BD 相交于O 点,AO B ∆的周长比BOC ∆ 的周长多8cm ,则AB 的长度为 cm .
(5)已知平行四边形ABCD 中,BC 边上的高为4,AB=5,AC=2 √5,则平行四边形ABCD 的周长等于___ 【巩固】 一个平行四边形的两条对角线的长分别为5和7,则它的一条边长a 的取值范围是 .
O
D C
B
A
【例6】 如图,四边形ABCD 的对角线AC 、BD 交于点P ,过点P 作直线交AD 于点E ,交BC 于点F .若PE PF =,
且AP AE CP CF +=+.求证:四边形ABCD 是平行四边形.
【巩固】 等边ABC ∆中,点D 在BC 上,点E 在AB 上,且CD BE =,所以AD 为边作等边ADF ∆.求证:四边形CDFE
是平行四边形.
F
E
D
C
B
A
【巩固】 如图,ABC ∆中,D 是AB 的中点,E 是AC 上任意一点,EF ∥AB ,DF ∥BE .求证:DF 与AE 互相
平分.
F
E
D
C
B A
【例7】 如图,田村有一口呈四边形的池塘,在它的四个角A B C D ,
,,处均种有一颗大核桃树,田村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想让核桃树不动,并要求扩建后的池塘成平行四边形的形状,请问田村能否实现这一设想?若能,请你设计并画出图形,若不能,请说明理由
D
B
A
【巩固】 如图,在ABC ∆中,90ACB ∠=︒,点E 为AB 中点,连结CE ,过点E 作ED BC ⊥于点D ,在DE 的延长
线上取一点F ,使AF CE =.求证:四边形ACEF 是平行四边形.
F
E
D
B
C
A
已知:如图,平行四边形ABCD 的对角线AC 、BD 相交于点O ,M 、N 分别是OA 、OC 的中点,求证: 四边形MBND 是平行四边形。
