气体分子动理论
分子动理论气体分子平均动能
32 103 26 m 5 . 31 10 kg 23 N A 6.02 10 (3)
3 3 k kT 1.38 10 23 ( 27 273) 6.21 10 21 J 2 2
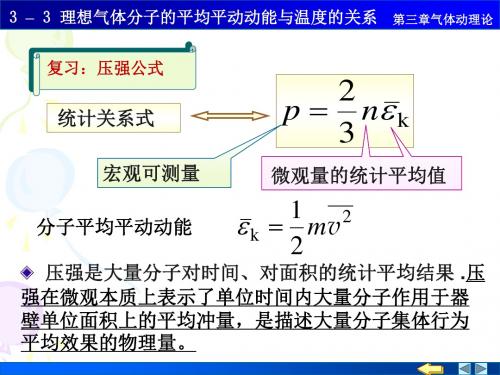
3 – 3 理想气体分子的平均平动动能与温度的关系
第三章气体动理论
子数相等。
分子数 密度
k=R/NA=1.38×10-23J· K-1
称为玻耳斯曼常量
3 – 3 理想气体分子的平均平动动能与温度的关系
第三章气体动理论
二、理想气体分子的平均平动动能与温度的关系
阿伏加德罗定律:
p nkT
2 1 2 理想气体压强公式 p n mv 3 2 1 3 2 k m v kT 分子平均平动动能 2 2
容器内不同气体的温度相同分子的平均平动动能也相同即kknkk?????????????????21而分子数密度满足????inn故压强为??????????????????????????????????????????????ikiikikikpnnnnp????????32323232即容器中混合气体的压强等于在同样温度体积条件下组成混合气体的各成分单独存在时的分压强之和
例 利用理想气体的温度公式说明Dalton 分压定律。
解:容器内不同气体的温度相同,分子的平均平动动能也 相同,即
k1 k 2 kn k
而分子数密度满足
n ni
故压强为 2 2 2 2 P n k ni k ni k ni ki Pi 3 3 3 3 即容器中混合气体的压强等于在同样温度、体积条件下组成 混合气体的各成分单独存在时的分压强之和。这就是Dalton 分压定律。
分子动理论与理想气体状态方程

分子动理论与理想气体状态方程分子动理论是研究气体微观粒子(即气体分子)的运动和相互作用规律的一门物理学理论。
它的提出对于理解和解释理想气体状态方程具有重要的意义。
一、分子动理论的基本假设分子动理论建立在以下几个基本假设之上:1. 气体是由大量微小无限可分的粒子——分子组成的;2. 分子之间的距离相比于分子的尺寸很大,分子之间几乎没有相互作用;3. 分子具有质量和速度,并且在运动过程中会发生碰撞。
二、理想气体状态方程是描述理想气体性质的基本方程,它与分子动理论之间有密切的联系。
根据分子动理论的基本假设,我们可以得到理想气体状态方程的推导。
1. PV=nRT理想气体状态方程可以表示为PV=nRT,其中P表示气体的压强,V表示气体的体积,n表示气体的物质量,R为气体常数,T为气体的绝对温度。
根据分子动理论,气体的压强与分子碰撞所产生的冲击力有关。
气体分子的速度与温度成正比,温度越高,分子速度越快,分子碰撞所产生的冲击力越大,从而压强也就越大。
因此,PV=nRT中的P、V和T是具有直接的物理意义的。
2. 分子速度与温度的关系根据分子动理论,分子的平均速率与温度呈正比关系。
具体而言,根据麦克斯韦速率分布定律,速度的平均值与温度的开平方成正比。
即v_avg=√(8RT/πM),其中v_avg表示分子的平均速率,R为气体常数,T为气体的绝对温度,M为气体分子的摩尔质量。
3. 分子速度与分子质量的关系根据分子动理论,分子速度与分子质量成反比关系。
分子的速度与质量无关,只与温度有关。
因此,气体分子的平均速率与分子的质量无关,只与气体的温度有关。
三、理想气体状态方程的适用范围尽管理想气体状态方程在很多情况下可以较好地描述气体的行为,但它也有一定的适用范围限制。
理想气体状态方程假设气体分子之间没有相互作用,但在高压、低温等极端条件下,气体分子之间的相互作用就变得不可忽略,因此理想气体状态方程在这些情况下的适用性就降低。
气体分子动理论的基本概念

F rs rt
s t
r :两个分子的中心距离 、、 s、t :正数,由实验确定。
1.第一项是正的,代表斥力; 2.第二项是负的,代表引力; 3.s,t都比较大,所以随着分子间距r的增大,分子力急剧减小。 4.有一定的有效作用距离,超出此距离,作用力可忽略。 5.s>t,所以斥力的有效作用距离比引力小。
第二章 气体分子动理论的基本概念
2.1 物质的微观模型
一、物质由大量分子所组成的论点是指宏观物体是不连续 的,它由大量分子或原子(离子)所组成的。
利用扫描隧道显微镜技术 把一个个原子排列成 IBM 字 母的照片.
分子的数密度和线度
NA 6.0221367(36) 1023 mol1
分子数密度( n ):单位体积内的分子数目.
二、物体内的分子在不停地做着无规则热运动,其剧烈程度 与物体的温度有关
由于分子之间的相互碰撞,每个 分子的运动方向和速率都在不断 地改变;任何时刻,在液体或 气体内部,沿各个方向运动的分 子都有,而且分子运动的速率有 大有小。
与物体的温度有关,温度越高,分子 的无规则运动越剧烈
扩散现象说明:一切物体(气 体、液体、固体)的分子都在不
停地运动着。
布朗运动并非分子的运动, 但它能间接反映出液体(或 气体)内分子运动的无规则 性。
为什么?
1. 为什么固体和液体的分子不会散开而能保持一定的体积? 2. 为什么固体和液体的分子不会散开而能保持一定的体积?铅 柱被切成两段,然后把两个断面对上,在两头加上不大的压力就 能使两段铅柱重新接合起来。
N NA
m
RT
RT
1 m
R M
T
大学物理课件气体分子运动论

等离子体物理
等离子体类似于气体的物质状 态,气体分子运动论为其研究 提供了理论基础。
生物学
气体分子运动论在生物学领域 的应用包括呼吸、扩散和渗透
等方面。
02
CATALOGUE
气体分子热运动的描述
气体分子的平均动能
平均动能的概念
气体分子在热运动中具有的平均动能是指气体分子在单位时间内 所做的平均动能的平均值。
大学物理课件气体 分子运动论
contents
目录
• 气体分子运动论概述 • 气体分子热运动的描述 • 气体分子之间的相互作用 • 气体分子运动论中的重要定律和公式 • 气体分子运动论中的重要实验和现象 • 气体分子运动论的未来发展与挑战
01
CATALOGUE
气体分子运动论概述
气体分子运动论的基本概念
碰撞频率与平均自由程
气体分子在单位时间内与其他分子碰撞的次数称为碰撞频 率,而分子在两次碰撞之间运动的距离称为平均自由程。
弹性碰撞与非弹性碰撞
根据碰撞过程中能量的传递情况,碰撞可分为弹性碰撞和 非弹性碰撞,弹性碰撞只改变分子的运动方向而不改变其 能量,而非弹性碰撞则会损失能量。
03
CATALOGUE
速率分布函数
描述气体分子速率分布情况的函数称为速率分布函 数,其值越大表示该速率下的分子数越多。
实验验证
通过实验可以验证气体分子的速率分布情况 ,如通过测量分子速度的分布情况来验证麦 克斯韦速度分布律。
气体分子的碰撞过程
碰撞过程的基本概念
气体分子之间的碰撞是指一个分子通过与另一个分子相互 作用而改变其运动状态的过程。
温度与平均动能的关系
温度是气体分子平均动能的量度,温度越高,气体分子的平均动能 越大。
热力学-3.气体分子动理论速率与能量

1.59 RT M
一般用于计算分子运动的平均距离;
同理,方均根速率
v2 v2 f (v)dv
3kT
3RT 1.73 RT
0
m
M
M
方均根速率用来计算分子平均动能。
最概然速率
2kT 2RT
RT
vp
m
1.41
M
M
最概然速率用在讨论分子速率分布。
f(v)
O
vp v v2
•在气体动理论方面,他提出气体分子按 速率分布的统计规律。
1。由于分子受到频繁的碰撞,每个分子热运动的速率是变化的, 要某一分子具有多大的运动速率没有意义,所以只能估计在某 个速率间隔内出现的概率;
2。哪怕是相同的速率间隔,但是不同的速率附近,其概率是不 等的。
速率接近为0的可能性很小,速率非常大的可能性也很小, 而居中速率的可能性则较大。
f (v) dN Ndv
速率分布函数
理解分布函数的几个要点: 1.条件:一定温度(平衡态)和确定的气体系统,T和m是一定的;
2.范围:(速率v附近的)单位速率间隔,所以要除以dv; 3.数学形式:(分子数的)比例,局域分子数与总分子数之比。
f (v)dv dN N
N v1 v2
v2
f (v)dv
第三章 气体分子热运动 速率和能量的统计分布律
内容回顾
第一章 平衡态和温度 第二章 压强和温度的微观本质
平均效果
气体分子按速率分布的统计规律最早是由麦克斯韦于
1859年在概率论的基础上导出的,1877年玻耳兹曼由经典统 计力学中导出,1920年斯特恩从实验中证实了麦克斯韦分子 按速率分布的统计规律。
第四章 气体动理论

§4-1
分子动理论的基本观点
一、物质微观结构的物理图象 1、物质是由大量的微观粒子——原子或分子组 成的; 2、分子在作永不停息的无规则运动; 3、分子之间有相互作用力。 综上所述,一切宏观物体(不论它是气体、 液体、还是固体)都是由大量的原子或分子组 成的;所有分子都在不停的、无规则运动中; 分子之间有相互作用力。这就是关于物质微观 结构的三个基本观点。
(s t )
C2 引力: f1 t , C2、t均 0 r 斥力: f C 1 , C 、s均 0 2 1 s r t:4 ~ 7 s : 9 ~ 13
2、图线
(f—r图线)
三、分子间的势能曲线(Ep—r图线)
1、分子间的势能: dE p fdr
C1 C2 E p fdr ( s t )dr r r C1 C2 s 1 t 1 ( s 1)r (t 1)r
N pV RT NA
p nkT
温度 T 的物理意义
1 2 3 平 m v kT 2 2
1) 温度是分子平均平动动能的量度 平 T (反映热运动的剧烈程度).
2)温度是大量分子的集体表现,个别分子无意义.
3)在同一温度下,各种气体分子平均平动动能均 相等。 注意 热运动与宏观运动的区别:温度所反 映的是分子的无规则运动,它和物体的整 体运动无关,物体的整体运动是其中所有 分子的一种有规则运动的表现.
由于热力学方法的局限性,我们对平衡态下系统内 部的情况不了解,从而对温度和理想 气体的理解 也很肤浅,对气体的压强更是一无所知,因此,为 了全面了解平衡态下的基本热学信息,我们必须用 分子物理学的方法从微观本质上加以认识。
• 气体动理论是统计物理学的基础; • 气体动理论是从微观的观点来研究气体的热学 性质; • 解释气体的温度、压强、热容、内能等的微观 本质; • 建立统计的概念。
气体动理论公式总结

气体动理论公式总结气体动理论是研究气体运动的基本理论,涉及到气体的压力、体积、温度等性质。
在研究气态物质的行为和性质时,气体动理论公式是非常重要的工具。
本文将对一些常用的气体动理论公式进行总结和解析。
1. 状态方程公式状态方程是描述气体状态的物理方程,常见的状态方程包括理想气体状态方程和范德华方程。
理想气体状态方程:PV = nRT其中,P表示气体的压力,V表示气体的体积,n表示气体的摩尔数,R为气体常数,T表示气体的绝对温度。
范德华方程:(P + an^2/V^2)(V - nb) = nRT其中,a和b为范德华常数,和实际气体分子之间的作用有关。
2. 理想气体状态方程的推导理想气体状态方程可以通过气体分子的平均动能推导得到。
根据气体分子的平均运动能量定理,可得到以下公式:KE = (3/2)kT其中,KE表示气体分子的平均动能,k为玻尔兹曼常数,T表示气体的绝对温度。
另外,气体分子的动能与气体分子的速度和质量有关:KE = (1/2)mv^2其中,m为气体分子的质量,v为气体分子的速度。
将上述两个公式相等,可以得到:(1/2)mv^2 = (3/2)kT由此,可以推导出理想气体状态方程:PV = (1/3)Nm<v^2>其中,N为气体分子的个数,<v^2>表示气体分子速度的平方的平均值。
3. 分子平均自由程公式分子平均自由程是指气体分子在碰撞间隔期间所飞过的平均距离。
分子平均自由程与气体分子的摩尔数、体积和气体分子直径有关。
分子平均自由程的公式为:λ = (1/√2) * (V/nπd^2)其中,λ表示分子平均自由程,V表示气体的体积,n表示气体的摩尔数,d表示气体分子的直径。
4. 均方根速度公式气体分子的运动速度可以用均方根速度来描述,均方根速度是指所有气体分子速度平方的平均值的平方根。
均方根速度的公式为:v(rms) = √(3kT/m)其中,v(rms)表示气体分子的均方根速度。
理想气体的状态方程与分子动理论

理想气体的状态方程与分子动理论理想气体是研究热力学和物理学中常用的一个模型。
在许多实际应用中,理想气体被用作参考点,以便更好地了解真实气体的特性和行为。
本文将探讨理想气体的状态方程以及与之相关的分子动理论。
一、状态方程理想气体的状态方程描述了压力、体积和温度之间的关系。
根据分子动理论模型,理想气体的状态方程可表示为:PV = nRT其中,P表示气体的压力,V表示气体的体积,n表示气体的物质的量,R为气体常数,T为气体的温度。
这个状态方程可以帮助我们计算气体的状态变化。
比如,当我们知道气体的压力、体积和温度时,可以使用状态方程来计算气体的物质的量。
同样地,当我们知道气体的物质的量、压力和体积时,也可以使用状态方程来计算气体的温度。
状态方程的应用范围十分广泛。
无论是在工程应用中计算气体的体积,还是在科学研究中探究气体的性质,状态方程都发挥着重要的作用。
二、分子动理论分子动理论提供了对理想气体性质的微观解释。
根据分子动理论,气体是由大量微小的分子组成的,它们在不断运动,相互之间存在弹性碰撞。
分子动理论可以帮助我们解释理想气体的一些性质,比如温度、压力和体积之间的关系。
根据分子动理论,当温度升高时,气体分子的平均动能也会增加,从而增加气体分子的运动速度和频率。
这会导致气体的压力增加。
分子动理论还可以解释理想气体的体积与其分子的运动有关。
当气体分子的平均运动速度增加时,它们在给定时间内所占据的空间也会增加,从而使得气体的体积扩大。
值得注意的是,分子动理论只适用于理想气体的情况。
在实际气体中,分子之间的相互作用和体积排斥等因素会导致实际气体的行为与理想气体有所不同。
三、理想气体与实际气体的区别虽然理想气体模型在许多情况下都能提供准确的结果,但在某些情况下,它与实际气体的行为存在一些差异。
首先,理想气体模型假设气体分子之间没有相互作用力,而实际气体中,分子之间存在一定的相互作用力,比如范德华力等。
这种相互作用力会导致气体的压力小于理想气体的压力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
气体分子动理论
气体分子动理论是指根据分子动力学原理来描述气体分子的运
动和行为的理论。
它的提出和发展对于解释气体的物理性质和行
为具有重要的意义。
本文将就气体分子动理论的起源、基本假设
和应用等方面进行探讨。
一、气体分子动理论的起源
气体分子动理论的起源可以追溯到19世纪。
在那个时候,科
学家们对气体的行为和性质提出了许多疑问。
为了解释这些现象,克劳修斯和麦克斯韦等科学家开始研究气体分子的运动规律,并
提出了气体分子动理论。
二、气体分子动理论的基本假设
气体分子动理论的基本假设有以下几点:
1. 气体分子是微小的无质量的粒子,它们之间没有相互作用。
2. 气体分子的运动是完全混乱的,没有任何规律性。
3. 气体分子之间的碰撞是弹性碰撞,即在碰撞过程中能量守恒、动量守恒。
4. 气体分子之间的平均距离远大于分子本身的大小。
这些假设为描述气体的性质和行为提供了基础。
三、气体分子动理论的应用
气体分子动理论在许多方面都有广泛的应用,下面将就几个重
要的应用领域进行介绍。
1. 描述气体的物态变化:根据气体分子动理论,当气体受到加
热时,分子的平均动能增加,分子之间的碰撞频率和力量都会增加,从而导致气体的压强增加。
当气体受到冷却时,则相反。
2. 热力学理论的基础:气体分子动理论为热力学的发展提供了
理论基础。
根据理论的推导,可以得到诸如理想气体状态方程和
分子平均动能与温度的关系等重要的热力学性质。
3. 涨落理论:根据气体分子动理论,气体分子的运动是混乱的,因此气体在微观尺度上会存在一定的涨落。
这种涨落现象不仅在
气体中存在,在固体和液体中也同样适用。
4. 扩散和输运现象:气体分子动理论对于扩散和输运现象的研究有很大的帮助。
通过分析气体分子的速度和运动方式,可以更好地理解扩散和输运的原理和机制。
总结:
气体分子动理论是对气体分子运动和行为进行描述的理论。
它的起源可以追溯到19世纪,科学家们根据气体的性质和行为提出了基本假设,并在许多领域中得到了应用。
气体分子动理论的研究对于深入理解气体的物理性质和行为具有重要的意义。
