五年级下册奥数小综合思维训练
五年级下册小学数学思维训练题及答案【最新】

五年级下册小学数学思维训练题1.新民小学133个少先队员担任卫生宣传,把他们分成几个人数相等的小组,有()种分法。
2.三根钢筋的长分别是18米、24米、36米。
现在要把它们截成同样长的小段而没有剩余,每段最长可截成()米。
3.把110个桔子分装在10全篮子里,每个篮子里所装的桔子数正好是10个连续偶数,是怎样分装的?4、99个连续的自然数相加,它们的和是奇数还是偶数?()99个连续的奇数相加,它们的和是奇数还是偶数?()99个连续的偶数相加的和是奇数还是偶数?()5.四个连续自然数的乘积是3024,这四个数分别是()。
6.一个长方体沿着高的方向截去2cm,表面积就减少48cm²,剩下的部分成为一个正方体,求原长方体的体积是()。
7.已知60 = 2×2×3×5,,知道60除了有因数1以外,还有因数()。
8.从2、3、5、7、11这五个数中,任取两个不同的数分别当作一个分数的分子和分母,这样的分数有()个。
9.把一些橙和柑分装入袋,如果每袋6个橙、5个柑,橙分完了还剩3个柑;如果每袋8个柑、6个橙,柑分完了还剩18个橙。
橙和柑一共有()个。
10.有一筐苹果每次按2个、3个、4个、5个地数,数到最后都是多一个,如果按每次数6个,最后篮子里还剩1个。
这个篮子里至少有()个苹果。
11. 一个两位数十位上的数字是个位上数字的3倍,这个两位数减9,则个位上的数字与十位上的数字相等。
这个两位数是()。
12.计算22+42+62+……+402=()13.五年级数学竞赛,小明获得的名次与他的年龄和竞赛的成绩相乘之积是2134,小明获得的名次()名,成绩是()分。
14、把三个长5dm、宽4dm、高3dm的长方体礼品盒包装在一起,怎样包装用的包装纸最少?(请画出图)要用()平方分米的包装纸。
15、把210个零件分装在几个盒子里,要使每个盒子的零件数相等,有()种装法。
16、迎宾仪仗队由男生48人、女生32人组成,要分成若干小组,每组男、女生人数分别相等,有()种分法。
五六年级奥数思维训练100题

五六年级奥数思维训练100题姓名:__________ 班级:__________ 得分:__________ 一、计算问题(15 题)1.25.6×4.2×0.252.2999+999×9993.(3.6×6+4×5)÷(6+5)4.1002×998-998×9975.4.8×(3.2÷0.6)6.890×102-8907.(5.5×8+3.5×6)÷(8+6)8.1345×8+1345 9.3.5×(4.8÷1.6)10.990×90+9011.18.5×3.6×0.12512.3999+999×99813.(4.8×7+3.2×5)÷(7+5)14.1003×997-997×99615.5.2×(4.5÷1.5)二、图形问题(15 题)16.一个平行四边形的底是 18 厘米,高是 14 厘米,求它的面积。
17.一个三角形的底是 25 厘米,高是 20 厘米,求它的面积。
18.一个梯形的上底是 10 厘米,下底是 14 厘米,高是 12 厘米,求它的面积。
19.一个正方形的边长是 15 厘米,求它的周长和面积。
20.一个长方形的长是 22 厘米,宽是 16 厘米,求它的周长和面积。
21.一个圆形的半径是 8 厘米,求它的周长和面积。
22.一个等腰梯形的上底是 8 厘米,下底是 12 厘米,高是 10 厘米,求它的面积。
23.一个直角三角形的两条直角边分别是 12 厘米和 16 厘米,求它的面积。
24.一个长方体的长、宽、高分别是 10 厘米、8 厘米、6 厘米,求它的表面积和体积。
25.一个正方体的棱长是 12 厘米,求它的表面积和体积。
五年级下册奥数思维训练:问题解决 全国通用
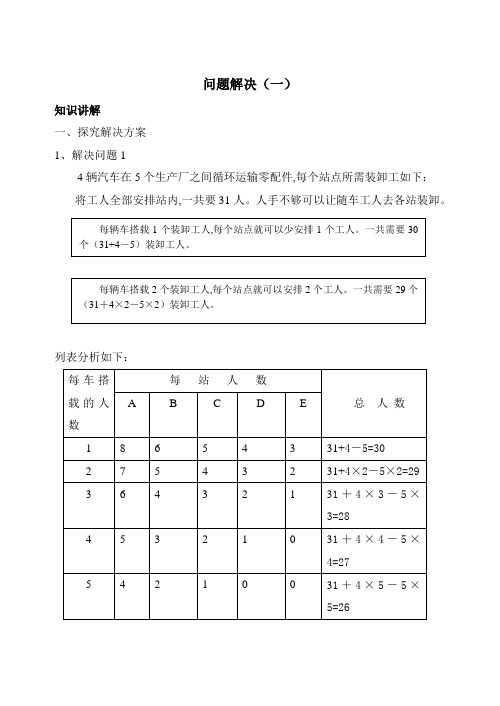
问题解决(一)知识讲解一、探究解决方案1、解决问题14辆汽车在5个生产厂之间循环运输零配件,每个站点所需装卸工如下:将工人全部安排站内,一共要31人。
人手不够可以让随车工人去各站装卸。
列表分析如下:解决这道题的过程中,你还想到了什么?选择下面的问题或自己编出类似的问题进行研究。
并在小组内交流自己的想法。
(1)如果在线路上增加一个需要10名装卸工人的站点,车的辆数保持不变,最少需要多少名工人。
(2)如果线路上的站点不变,车的辆数减少1辆,最少需要多少名工人? 学生互相讨论、交流出示交流结果,并说出解题思路。
2、模仿练习五辆汽车在7个站点之间循环运输,每个站点所需装卸工人如图所示。
怎样安排可以使运输工人人数最少?最少需要多少人?A B CGFE D 3、解决问题2AB 两地相距4a 千米,中间是荒无人烟的戈壁,只有一条公路连接,现有50辆卡车要从A 地到B 地,然后再返回A 地,已知卡车自身携带的汽油只能走3a 千米,为完成任务配备了运油车(耗油量与卡车相同),保证供油。
运油车一次● ● ● ●●●能运送一辆卡车行150a千米的汽车。
请你设计一个方案,用若干辆运油车保证任务完成?解题方案:卡车自身携带的汽油可以行3a千米,卡车从A地到B地,然后再返回A地,一共需要行8a千米的汽油,还需要性5a千米的汽油,50辆卡车一共需要行5a×50=250a千米的汽油。
要使整个任务的耗油量最少,必须使运油车的耗油量最少;要使运油车的耗油量最少,必须使运油车行尽可能少的路,尽可能利用卡车的载油量,使加油地点到B地往返的距离等于3a,因此加油地点在离B地1.5a处。
运油车携带能行150a千米的汽车,运到从A地到B地2.5a千米处停下,它为维持自身往返需要行5a千米的汽油,能为卡车提供145a千米的汽油。
一共需要行250a千米的汽油,因此,至少需要2辆运油车:一辆满载,另一辆至少载行250a -145a+5a=110a千米汽油。
五年级下册奥数思维训练:竞赛试题三 全国通用

(希望杯5年级2试第8题)如果一个自然数的各位数字中有偶数个偶数,则称之为“希望数”.例如,26,201,533是希望数,8,36,208不是希望数,那么,把所有的希望数从小到大排列,第2010个希望数是_______.(希望杯)一艘客轮在静水中的航行速度是26千米/时.往返于A 、B 两港之间,河水的流速是6千米/时,如果客轮在河中往返4趟共用13小时,那么A 、B 两港之间相距 ____千米.(客轮掉头时间不计)例1竞 赛 例2(希望 杯)试 题选 编 一例3(希望杯5年级1试)夜里下了一场大雪,早上,小龙和爸爸一起步测花园里一条环形小路的长度,他们从同一点同向行走,小龙每步长54厘米,爸爸每步长72厘米,两人各走完一圈后又都回到出发点,这时雪地上只留下60个脚印.那么这条小路长____米.例4(希望杯5年级1试)有三个自然数a,b,c,已知b除以a,得商3余3;c除以a,得商9余11.则c除以b,得到的余数是_______.例5(希望杯六年级二试)某小学的六年级有一百多名学生,若按三人一行排队,则多出一人;若按五人一行排队,则多出二人;若按七人一行排队,则多出一人.该年级的人数是_____.例6(希望杯六年级二试)如图,三角形ABC和三角形DEC都是等腰三角形,A和E是直角顶点,阴影部分是正方形.如果三角形DEC的面积是24平方米,那么三角形ABC的面积是______平方米.例7(希望杯五年级二试)如图7,梯形ABCD与正方形DEFC拼在一起,AF与DE交于点G.已知BC=CD=4,三角形AGD的面积是三角形DGF面积的2倍.⑴求梯形ABCD的面积;⑵比较三角形GEF和三角形AGD的面积大小.例8(希望杯五年级二试第7题)如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_____平方厘米.例9(希望杯六年级二试)如图,已知长方形长是宽的2倍,对角线的长是9,则长方形的面积是_______.例10(希望杯6年级2试)两个顽皮的孩子逆着自动扶梯行驶的方向行走,从扶梯的一端到达另一端,男孩走了100秒,女孩走了300秒.已知在电梯静止时,男孩每秒走3米,女孩每秒走2米,则该自动扶梯长_____米.。
五年级下册数学奥数试题 思维训练综合卷(3) 全国通用

五年级奥数阶段检测卷(3)姓名一、计算(5分×2)1、7.8×10.1-0.782、2005×20062006-2004×20052005二、应用题(10分×14)1、甲、乙两人一共有269.5元,甲的钱数的小数点向右移动一位,他的钱数就和乙的钱数相等。
甲、乙各有钱多少元?2、两个数相除,商39余58,如果被除数、除数、商及余数相加,和是3275,求被除数和除数?3、3筐苹果和5筐梨共重138千克,9筐同样的苹果和4筐同样的梨共重216千克,每筐苹果和梨各重多少?4、甲有5盒糖,乙有4盒糕共值22元,如果甲乙两人对换一盒,则每人所有的物品价钱相等,求一盒糖,一盒糕分别值多少钱?5、小刚从家到学校,去时每分钟走40米,回来时每分钟走60米,小刚往返的平均速度是多少?6、某校安排学生住宿,若每间6人,则有20人没位置,若每间住8人,则空出一间半宿舍,求宿舍几间?学生几人?7、站在桥上用绳子测桥的高度,把绳子对折垂到水面尚余3米,把绳子三折后垂到水面,尚余1米,求桥的高度和绳长?8、小明读书,第一天读83页,第二天读74页,第三天读71页,第四天读64页,第五天读的页数比五天中平均读的页数还多3.2页,小明第五天读了多少页?9、5头牛,6匹马,2只羊每天吃草143千克;6头牛,5匹马,4只羊每天吃草133千克;3头牛,2匹马,1只羊每天吃草55千克,求1头牛,1匹马,1只羊每天各吃草多少千克?10、某校招生考试,所有考生的平均分是65分,从考生中录取了15,这些学生的平均分比录取分数线高9分,其他没被录取的学生的平均分比录取分数线低21分,那么录取分数线是多少分?11、有4个数,每次选取其中3个数,算出它们的平均数,再加上另外一个数,用这样的方法计算了4次,分别得到以下四个数:26、30、36、40,那么原来四个数分别是多少?12、小红早上步行去上学,她以每分钟60米的速度先走了2分钟,然后发现,如果照这个速度走下去,要迟到5分钟;如果每分钟多走15米,则可提前2分钟到校。
小学五年级数学思维训练(奥数)《长方体和正方体巧算表面积》讲解及练习题(含答案)

长方体和正方体巧算表面积专题简析:学了长方体和正方体后,同学们都只知道,长方体和正方体都有6个面,长方体相对的两个面的大小、形状完全一样,正方体6个面的大小、形状都完全一样。
例1 两个棱长是2厘米的小正方体可以拼成一个长方体,这个长方体的表面积是多少?分析与解答先根据题意画图:从图上可以清楚地看出:两个正方体原先各有6个正方形的面,当把它们拼起来时就少了2个正方形的面。
这时,求长方体的表面积只相当于求(12-2=)10个正方形的面积;还可以这样想:当两个正方体拼成一个长方体时,求长方体的表面积,我们可以先分别求出这个长方体的长、宽、高,再求出它的表面积。
方法总结:1.当物体拼合时表面积之和少了,可以根据用原来的面去掉减少了的面,从而求出拼合后物体的面积数量,然后求出表面积。
2.还可以求出拼成后大物体的长、宽、高,再根据物体形状直接求表面积。
随堂练习:把底面积是36平方厘米的两个正方体木块拼成一个长方体,长方体的表面积是多少?例2把一个长、宽、高分别是7厘米、6厘米、5厘米的长方体截成两个长方体,使这两个长方体表面积之和最大,这时表面积之和是多少平方厘米?分析与解答:把长方体截成两个长方体后,两个长方体表面积之和等于原长方体表面积再加上两个截面的面积。
这个长方体几个面中,上、下面的面积最大,所以要看哪个面的面积最大,于是本题就按平行于上、下面的方式去截,才使表面积之和最大。
方法总结:长方体截成两个长方体有三种截法,如图:随堂练习:把两个长3厘米、宽2厘米、高1厘米的长方体拼成一个表面积最大的长方体,这个长方体的表面积是多少平方厘米?例3求出下面立体图形的表面积。
(单位:厘米)分析与解答:从图上看出,这个图形是由一个长方体和一个正方体组成的,求它的表面积时,可以把正方体的右侧面平移到长方体上,这方体的上、下、前、后四个面的面积。
随堂练习:1.在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体(如图),求这个立体图形的表面积。
小学生奥数思维训练及答案
小学生奥数思维训练及答案奥数(即奥林匹克数学竞赛)是许多小学生参与的一种数学比赛,它旨在培养学生的数学思维和解题能力。
在这里,我们将讨论一些奥数思维训练的方法,并提供一些答案以帮助小学生更好地应对这种竞赛。
一、理解问题在参加奥数比赛时,理解问题是解题的第一步。
许多竞赛问题都有一定的难度,所以正确理解问题是至关重要的。
以下是一些训练学生理解问题的方法:1. 仔细阅读问题:在阅读问题时,学生应该将注意力集中在每个细节上。
他们应该注意问题中给出的条件、要求和约束。
如果可能,学生可以在问题旁边做一些标记,以便更好地理解。
2. 弄清问题的关键点:学生应该确定问题中关键的信息和目标。
他们可以用自己的话来概括问题,以确保完全理解。
3. 解析问题:通过解析问题,学生可以从中提取有用的信息并排除不必要的内容。
他们可以使用图表、图像或其他方法来帮助他们组织思维。
二、解决问题解答奥数问题需要一定的技巧和策略。
以下是一些帮助学生解决问题的方法:1. 建立数学模型:将问题抽象为数学模型是解决问题的关键。
学生应该将问题转化为适当的数学形式,例如方程式、不等式等。
这样可以使问题更具结构性,更容易应用数学知识来解决。
2. 使用已学数学知识:奥数问题往往需要学生运用已学的数学知识来解决。
学生应该根据问题的要求来运用所学的数学概念、公式和定理。
他们也可以参考课本或在线资源以获得更多的知识。
3. 尝试不同的解题方法:对于复杂的问题,学生可以尝试不同的解题方法。
有时候,直接计算可能不是最有效的方法,使用逆向思维或试错法可能更加高效。
三、示例答案这里给出两个奥数问题的示例及其答案:问题1:某班级有30名学生,男生所占比例为3:7,女生有多少名字?解答1:设男生有3x人,女生有7x人。
根据题目条件,3x + 7x = 30,求解得到x = 3。
因此,女生共有7x = 7 * 3 = 21名。
问题2:从1到100的所有整数中,有多少个整数的个位数字是5?解答2:一共有10个个位数,分别是0, 1, 2, 3, 4, 5, 6, 7, 8, 9。
【精品奥数】五年级下册数学思维训练讲义-第二讲 盈亏问题 人教版(含答案)
第2讲盈亏问题第一部分:趣味数学盈亏问题《九章算术》第七章介绍了盈亏问题,这一类问题是把一定数量的物品平均分给若干对象,每个对象少分,则物品有余;如果每个对象多分,则物品不足。
所以分物时经常出现盈(有余)、亏(不足)、尽(恰好分完)的情况,所以古人把这类问题称为盈不足问题。
盈亏问题情况多样,解法巧妙,倍受古人重视,在许多古代算书上留下了不少好题。
下面选取其中的一个给同学欣赏:题目今有人共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?题意:有一群人凑钱买一件物品。
如果每人出8枚钱币,就比物价多出3个钱币。
如果每人出7枚钱币,就比物价少4个钱币。
求人数和钱数各是多少?分析:这是属于“一盈一亏”类的问题。
当第一次每人出8枚钱币时多3枚,当第二次每人出7枚钱币时不但不多,还要少4枚,即第二次比第一次共少了4+3=7枚。
这是由于第二次比第一次每人少出了8-7=1枚钱币。
相差7枚,就说明有7÷1=7人。
这样物价也就可以算出来了。
解答:4+3=7(枚)8-7=1(枚)7÷1=7(人)7×8 – 3 = 53(枚)答:一共有7人,物价为53枚。
事实上,古代数学家发现,在计算人数(即分物对象的个数)时,还有一个简单易记、琅琅上口的口诀:“有余加不足,大减小来除”。
这种算法的绝妙之处在于它几乎可以不动脑筋,只要把几个数按口诀对号入座,马上可以得出答案。
同学们如果你学会了,有兴趣就试试下面这个题目吧!钱几何今有散钱不知其数,作七十七陌穿之,欠五十凑穿;第二部分:奥数小练盈亏问题的基本数量关系是:(盈+亏)÷两次所分之差=人数;还有一些非标准的盈亏问题,它们被分为四类:1.两盈:两次分配都有多余;2.两不足:两次分配都不够;3.盈适足:一次分配有余,一次分配够分;4,不足适足:一次分配不够,一次分配正好。
一些非标准的盈亏问题都是由标准的盈亏问题演变过来的。
解题时我们可以记住:1.“两亏”问题的数量关系是:两次亏数的差÷两次分得的差=参与分配对象总数;2.“两盈”问题的数量关系是:两次盈数的差÷两次分得的差=参与分配对象总数;3.“一盈一亏”问题的数量关系是:盈与亏的和÷两次分得的差=参与分配对象总数。
小学五年级数学思维训练(奥数)《最大公因数》专题训练(含答案)
最大公因数专题简析:几个数公有的因数叫做这几个数的公因数,其中最大的一个就是这几个数的最大公因数。
课本向我们介绍了用列举法来求几个数的最大公因数。
本讲我们一起来探讨用短除法、辗转相除法等几个方法求几个数的最大公因数。
自然数a、b的最大公因数可以记作(a,b)。
例1用短除法求36和54的最大公因数。
分析与解答:人们常常用短除法求两个数的最大公因数,短除法的形式如下:2 36 54 ……先同时除以公因数2;3 18 27 ……再同时除以公因数3;3 6 9 ……再同时除以公因数3;2 3 ……除到两个商为互质数为止。
把上式中所有的除数相乘所得的积即为36和54的最大公因数,即(36,54)=2×3×3=18.随堂练习:用短除法求40和32的最大公因数。
例2求45、60、90这三个数的最大公因数。
分析与解答:与前面的例1不同的是这道题要求三个数的最大公因数。
方法1:可以用列举法。
45的因数有:1,3,4,5,9,15,45;60的因数有:1,2,3,4,5,6,10,12,15,20,30,60;90的因数有:1,2,3,4,5,6,10,15,18,30,45,90.45,60和90的公因数有:1,3,5,15;所以(45,60,90)=15.方法2:也可以用短除法。
345 60 90 ……先同时除以公因数3;5 15 20 30 ……再同时除以公因数5;3 4 6 ……除到三个商只有公因数1为止。
把上式的除数3和5相乘所得的积即为45,60,和90的最大公因数,即(45,60,90)=3×5=15.随堂练习:用短除法求36、48和60的最大公因数。
例3求319和377的最大公因数。
分析与解答:求这两个数的最大公因数如果用短除法很难找出它们的公因数,我们可以用下面这种新的方法:用较大的数377除以较小的数319;377÷319=1 (58)上面的算式中有余数58,用上式中的除数319除以余数58:319÷58=5 (29)上面的算式中仍有余数,再用上式中的除数58除以余数29:58÷29=2上式中没有余数了,这时算式中的除数29就是想319和377的最大公因数,即(319,377)=29上面这张求最大公因数的方法被古希腊的大数学家欧几里德命名为“辗转相除法”。
小学五年级下册数学思维训练(奥数) 《列方程解应用题(行程问题)》(含答案)
列方程解应用题(行程问题)专题解析相遇是行程问题的基本类型,在相遇问题中可以这样求全程:速度×时间=路程。
今天,我们学习此类问题。
例1 AB两地相距352千米.甲乙两辆汽车从A、B两地相对开出.甲车每小时行36千米,乙车每小时行44千米.乙车因有事,在甲车开出32千米后才出发,再出多少小时两车相遇?分析解答:要想求出两车的相遇时间,必须找到速度和、时间和总路程的数量关系式。
速度和×时间+甲先行的路程=总路程,其中甲车的速度,乙车的速度,甲先行的路和总路程已知,所以只要设时间为X小时,就可以列出方程。
解:设X小时两车相遇。
(36+44)×x+32=35280x+32=35280x=320x=4答:4小时后两车相遇。
随堂练习:甲乙两地相距300千米,客车从甲地开往乙地,每小时行40千米。
1小时后,货车从乙地开往甲地,每小时行60千米。
货车出发几小时后与客车相遇?例2 甲乙两人从A、B两地相向而行,甲乙两人从AB两地同时出发相向而行,甲每分钟行52米,乙每分钟行48米,两人走了10分钟后交叉而过,且相距64米,甲从A地到B地需多少分钟?分析解答:这道题目要求甲从A地到B地需要的时间,就发必须知道A、B两地相距的路程和甲的速度,现在甲的速度已知,所以这道题目的键就在于通过列方程求出A、B两地的相距的路程。
解:设A、B两会相距x米(52+48)×10-x=641000-x=64x=936936÷52=18(分)答:甲从A地到B地需18分钟。
随堂练习从A地到B地,水路比公路近40千米。
上午8时,一艘轮船从A地驶向B地,3小时后一辆汽车从A地到B地,它们同时到达B 地,轮船的速度是每小时24千米,汽车的速度是每小时40千米,求A地到B地水路、公路是多少千米?例3 小明和小童分别从一座桥的两端同时相向出发,往返于两端之间小明每分钟走60米,小童每分钟走75米,经过6分钟两人第二次相遇,这座桥长多少米?分析解答:第一次相遇就是行了一个全程,第二次相遇就是行了三个全程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级下册奥数小综合思维训练(1)(找规律、包含与排除)1:18÷11的商的小数点后面第2008位数字是几?2:有一列数字402140214021……问第31个数字是多少?前面30个数字的和是多少?3、17÷6的商的小数点后第123位和第124位上的数字的和是多少?4、5÷7的商的小数部分后面第100位上的数字是几?5、13.258小数部分第1000位上的数字是几?小数点后面前300个数字的和是多少?6、不用计算,直接写得数1÷7=0.142857142857…… 2÷7=0.285714285714…… 3÷7=0.428571428571……4÷7= 5÷7= 6÷7=7、23÷7的商的小数点后面2000个数字之和是多少?8、15÷52的商的小数点右边第200个数字是多少?小数点后面前200个数字的和是多少?9、9÷7的商的小数点后第2005位数字是几?10、18÷13的商的小数点后第2010位的数字是几?11:五年级有96名学生都订了刊物,有64人订了少年报,有48人订了小学生报,问两种刊物都订的有多少人?12:学校开展课外活动,共有250人参加,其中参加象棋组和乒乓球组的同学不同时活动,参加象棋组的有83人,参加乒乓球组的有86人,这两个小组都参加的有25人,问250名同学中,象棋组、乒乓球组都不参加的有多少人?13、一个班的52人都在做语文和数学作业,有32人做完了语文作业,有35人做完了数学作业。
这个班语文,数学作业都做完的有多少人?14、某班有50名学生,在一次测验中有26人满分,在第二次测验中有21人满分。
如果两次测验都没有过满分的学生有17人,那么两次测验都获满分的有多少人?15、某班的在一次测验中有26人语文获优,有30人数学获优。
其中语,数双优的有12人,另外还有8人语,数均未获优。
这个班共有多少个学生?16、第一小组的同学们都在做两道数学思考题,做对第一题的有15人,做对第二题的有10人,两道题都做对的有7人,两道题都做错的有2人,第一小组共有多少人?17、有122名同学参加语文,数学考试,每人至少有一门得优,已知语文65人得优,数学78人得优,求只有语文一门得优的有多少人?18、在100位旅客中,有70人懂英语,65人懂日语,既懂英语又懂日语的有45人,那么,既不懂英语又不懂日语的有多少人?19、老师在统计考试成绩,数学得分90分以上的有25人,语文得90分以上的有21人,两科中有一科的在90分以上有38人,问:两样都得90分以上的有多少人?20、少年乐团学生中有170人不是五年级的,有135人不是六年级的,已知五,六年级的共有205人,小年乐团中,五,六年级以外的学生共有多少人?五年级下册奥数小综合思维训练(2)(长方体和正方体、解决问题、分解质因数)1:在一个长15分米,宽12分米的长方体水箱中,有10分米深的水。
如果在水中沉入一个棱长为10厘米的正方体铁块,那么,水箱中水深多少分米?2:一个长方体棱长的总和是48厘米,已知长是宽的1.5倍,宽是高的2倍,求这个长方体的体积。
3:有一个棱长是3厘米的正方体,先从它的每个顶点处挖去一个棱长是1厘米的小正方体,再在它每个面的中央粘上一个棱长是1厘米的小正方体。
所得物体的表面积是多少平方厘米?体积是多少立方厘米?5、18个边长为2厘米的小正方体堆成如图的形状, 求它的表面积。
6、把8个同样大小的小正方体拼成一个大正方体。
已知小正方体的表面积是150平方厘米,大正方体的表面积是多少平方厘米?7、图中A 的面积是25平方米,B 的面积是15平方米,h 是4米。
现在把A 处的土堆到B 处,使A 、B 两处同样高,这时B 处比原来升高了多少米?8、在一个棱长为2厘米的正方体上面的正中间向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面再向下挖一个棱长为0.5厘米的小洞。
第三个小洞的棱长为0.25厘米挖法与前两个小洞的挖法相同。
现在这个立方体图形的表面积是多少?9、用2100个棱长是1厘米的正方体木块堆成一个实心的长方体。
已知长方体的高是10厘米,并且长和宽都大于高。
这个长方体的长和宽各是多少厘米?10、在一个长20分米,宽15分米的长方体容器中,有20分米深的水。
现在在水中沉入一个棱长20厘米的正方体铁块,这时容器中水深多少分米?11、把一个长9厘米,宽7厘米,高3厘米的长方体铁块和一块棱长5厘米的正方体铁块熔铸成一个底面积是20平方厘米的长方体。
求这个长方体的高。
12、有一块长方形的铁皮,长32厘米。
在这块铁皮的四角各剪下一个边长为4厘米的小正方形,然后制成一个无盖的长方体盒子。
已知这个盒子的容积是768厘米,求原来长方形铁皮的面积。
13:一个长方体玻璃缸,长8分米,宽6分米,高4分米,玻璃缸内水深2.8分米。
把一块棱长为4分米的正方体铁块放入玻璃缸内后,水会溢出多少升?14把一个底面积为正方形且边长是3分米,高是5分米的长方体石料尽量加工为体积最大的正方体,那么凿去的石料体积是多少立方分米?(不计损耗)15、一个长方体的玻璃缸,最多可装水120升,已知玻璃缸里面长6分米,宽4分米,现有水深3分米。
如果在玻璃缸内放入体积为15立方分米的玻璃球,里面的水会不会溢出,为什么?16、一个棱长8分米的正方体水槽里装了490升水,把这些水倒入一个长10分米,宽7分米,高8分米的长方体水槽里,水槽里的水深是多少?17、把一块棱长8厘米的正方体钢坯,锻造成长16厘米,宽5厘米的长方体钢板,这钢板有多厚?(损耗不计)18、一个长方体油桶,底面积是18平方分米,它可装43.2千克油,如果每升油重0.8千克,油桶内油高是多少?19、一个长方形铁皮长30cm,宽25cm,从四个角各切掉一个长为5cm的正方形,然后做成一个无盖的盒子,这个盒子用了多少铁皮?它的容积是多少?20、把一块长26dm的长方形木板,在四个角上分别剪去边长为3dm的正方形,将它制成容积为840立方分米的长方体无盖容器,这块木板原来的宽是多少?21、一个长方体游泳池长60米,宽30米,深2米,游泳池占地多少平方米?沿游泳池的内壁1.5米处用红漆划一条水位线,这条线的长度是多少?现在游泳池内的水正好到达水位线,求池内水的体积?22、一个长方体玻璃缸,从里面量长40厘米,宽25厘米,水深12厘米,把一块石头浸入水中后,水面上升到16厘米,求石块的体积?23:李老师带领一班学生去植树,学生恰好分成4组,如果老师和每个学生植树棵数一样多,那么他们共植树539棵。
这个班共有多少名学生?每人植多少颗树?24:把40,44,45,63,65,78,99,105这8个数字分成两组,使这两组4个数的乘积相等。
25、下面的算式里“□”里的数字各不相同,求这四个数字之和□□×□□=199525、3月12日是植树节,李老师带领同学排成两路人数相等的纵队去植树。
已知李老师和同学们每人植树的棵数相等,一共植了111棵。
叁加植树的同学有多少名?26、王老师和同学们去植树,全班同学刚好可以平均分成4个小组。
如果老师与学生每人植树的棵数相等,一共植了520棵,参加植树的一共有多少个学生?平均每人植多少棵?27、有三个学生,他们的年龄一个比一个大3岁,他们三人年龄的乘积是1620,这三个学生的年龄和是多少?28、将下面八个数分成两组,使这两组数的乘积相等2、5、14、24、27、55、56、9929、把30、33、42、52、65、66、77、78、105九个数字分为三组,使每组数的乘积相等。
30、将0.09、0.15、0.3、0.34、0.28、0.77、0.55、0.85八个数分成两组,使这两组数的乘积相等。
31、将下面8个数分成个数相等的两组,怎样分才能保证两组数的乘积相等?1.4、0.33、0.35、16.9、14.3、0.75、0.39、0.3五年级下册奥数小综合思维训练(3)(最小公倍数与最大公因数、数的整除特征)1:一块长48cm,宽42cm的布,不浪费边角料,能剪出最大的正方形布片多少块?2:用长16cm,宽14cm的长方形木板来拼成一个正方形,最少需要用这样的木板多少块?3、一个两位数,用它除58余1,除73余3,除85余1,这个两位数是多少?4、幼儿园有糖115颗,饼干148块,桔子74个,都分给大班小朋友,结果糖果多出7颗,饼干多出4块,桔子多出2个。
这个大班的小朋友最多有多少个小朋友?5、一个数能被3、5、7整除,若用11去除则余1,这个数最小是多少?6、五年级两个班的学生一起排队出操,如果9人排一行,多出1个人。
如果10人排一行,同样多出一个人,这个班最少共有多少人?7、有一盒乒乓球,每次8个8个地数,10个10个地数,12个12个地数,最后总是剩下3个,这盒乒乓球至少有多少个?8、把几十个苹果平均分成若干份,每份9个余8个,每份8个余7个,每份4个余3个,这堆苹果共有多少个?9、一个长180cm,宽45cm,高18cm的木料,能锯成尽可能大的正方体木块多少块?10、两个自然数的和是50,它们的最大公因数是5,则这两个数的差是多少?11:在五位数15□8□的□内填什么数字,才能使它既能被3整除,又含有约数5?12:在568后面补上三个数字,组成一个六位数,使它分别能被3,4,5整除。
符合这些条件的六位数中,最小的一个是多少?13、在235后面补上三个数字,组成一个六位数,使它分别能被3、4、5整除。
这个六位数最小是多少?14、有一个四位数13AA,它能被9整除。
A代表的数字是几?15、用0,1,3,5,7这五个数字中的四个数字,可以组成许多能被11整除的四位数,其中最小的一个四位数是多少?16、如果六位数1993□□能被105整除,那么,它的最后两位数是多少?17、六位数ABABA3是6的倍数,这样的六位数有多少个?18、已知87654321□□这个十位数能被36整除,那么,这个数个位上的数最小是几?19、一个六位数12□34□是88的倍数,这个数除以88所得的商是多少?20、商店有三种油漆,牌子和颜色都不同,红色的每桶1.5千克,黄色的每桶2千克,白色的每桶2.5千克。
为了方便顾客,商店把这三种油漆改装成每桶0.5千克油漆的小桶。
结果“球光牌”装了280桶,“江海牌”装了255桶,“前进牌”装了292桶。
请问:每种牌子的油漆各是什么颜色?五年级下册奥数大综合思维训练一.我会填:1、计算3.58×67+35.8×3.7-0.358×40=▁▁▁▁▁▁▁2、计算: =▁▁▁▁▁3、买一些0.8元和1元的邮票,共花了74元.已知1元邮票的张数比0.8元邮票多20张.问1元的邮票共有________张。
