周艳英全等三角形练习
全等三角形全套练习题

全等三角形全套练习题全等三角形一、全等三角形1、定义:能够完全重合的两个三角形叫做全等三角形。
特征:形状相同、大小相等、完全重合。
一个三角形经过平移、翻折、旋转可以得到它的全等形。
平移、翻折、旋转前后的图形全等。
2、全等三角形的表示:“全等”用“今”表示,“s”表示两图形的形状相同, “=”表示大小相等,读作“全等于”。
注意:记两三角形全等时,通常把表示对应顶点的字母写在对应位置上。
全等三角形的对应元素:对应顶点,对应边,对应角3、全等三角形的性质(1)全等三角形的对应边相等、对应角相等。
(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
4、全等三角形的判定(1)边边边:三边对应相等的两个三角形全等(可简写成“SSS”)(2)边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)(3)角边角:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”)(4) 角角边:两角和其中一角的对边对应相等的两个三 角形全等(可简写成“AAS”)(5) 斜边、直角边:斜边和一条直角边对应相等的两个 直角三角形全等(可简写成“HL”)5、证明两个三角形全等的基本思路:找第三边(SSS) 找夹角(匹) 找是否有直角(HL)找这边的另一个邻角亦)找这个角的另一个边迈 找这边的对角(AAS)找一角吐) 已知角是直角,找一边(HL)⑶:已知两角4找两角的夹边驱)-找夹边外的任意边吐)二、 角的平分线1、 (性质)角的平分线上的点到角的两边的距离相等。
2、 (判定)角的内部到角的两边的距离相等的点在角的平 分线上。
三、 学习全等三角形应注意的问题(1) 要正确区分“对应边”与“对边”,“对应角”与“对 角”的不同含义;(2) 表示两个三角形全等时,表示对应顶点的字母要写 在对应的位置上;(3) “有三个角对应相等”或“有两边及其中一边的对角 对应相等”的两个三角形不一定全等;(4) 时刻注意图形中的隐含条件,如“公共角”、“公共(1):已知两边一 已知一边和它的邻角 (2):已知一边一角・已知一边和它的对角.边”、“对顶角”。
(完整版)全等三角形基础练习题
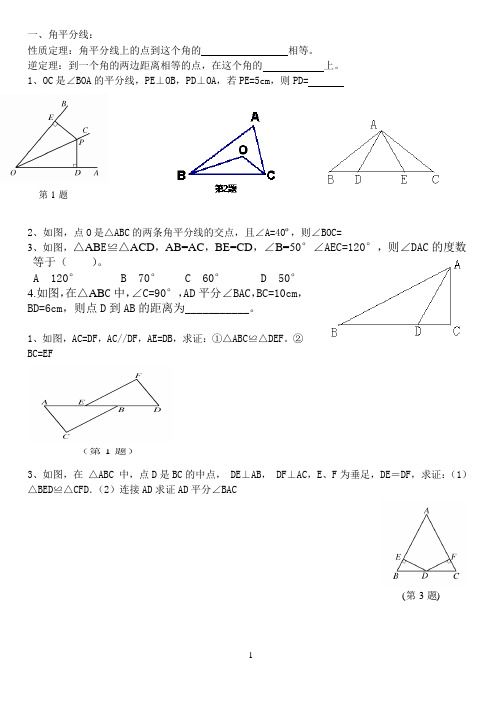
一、角平分线:性质定理:角平分线上的点到这个角的相等。
逆定理:到一个角的两边距离相等的点,在这个角的上。
1、OC是∠BOA的平分线,PE⊥OB,PD⊥OA,若PE=5cm,则PD=第1题2、如图,点O是△ABC的两条角平分线的交点,且∠A=40º,则∠BOC=3、如图,△AB E≌△ACD,AB=AC,BE=CD,∠B=50°∠AEC=120°,则∠DAC的度数等于()。
A 120°B 70°C 60°D 50°4.如图,在△AB C中,∠C=90°,AD平分∠BAC,BC=10cm,BD=6cm,则点D到AB的距离为___________。
1、如图,AC=DF,AC//DF,AE=DB,求证:①△ABC≌△DEF。
②BC=EF(第1题)3、如图,在△ABC 中,点D是BC的中点, DE⊥AB, DF⊥AC,E、F为垂足,DE=DF,求证:(1)△BED≌△CFD.(2)连接AD求证AD平分∠BAC(第3题)第1题A第2题A1、如图,已知AB=AD ,要使△ABC ≌△ADC ,可增加条件 ,理由是 定理。
2、下列说法中正确的是( )A 、两个直角三角形全等B 、两个等腰三角形全等C 、两个等边三角形全等D 、两条直角边对应相等的直角三角形全等3、如图,△ABC 中,∠C=90º,AD 平分∠CAB 交BC 于点D ,DE ⊥AB ,垂足为E ,且CD=6cm ,则DE 的长为( )A 、4cmB 、6cmC 、8cmD 、10cm4、三角形内到三条边的距离相等的点是( )A 、三角形的三条角平分线的交点B 、三角形的三条高的交点C 、三角形的三条中线的交点D 、三角形的三边的垂直平分线的交点 5、三角形内到三个顶点的距离相等的点是( )A 、三角形的三条角平分线的交点B 、三角形的三条高的交点C 、三角形的三条中线的交点D 、三角形的三边的垂直平分线的交点 6、在△ABC 中,∠A=70º,∠B=40º,则△ABC 是( )A 、钝角三角形B 、等腰三角形C 、等边三角形D 、等腰直角三角形 7、如图,AE=BE ,∠C=∠D ,求证:△ABC ≌△BAD 。
全等三角形及判定练习题

全等三角形(1)一.知识点:1.能够完全重合的两个三角形叫做全等三角形含义:形状相同,大小相等.2.符号:“≌”3.对应(边、角、顶点):重合的边、重合的角,重合的顶点4.全等三角形的性质:⑴全等三角形的对应边相等. ⑵全等三角形的对应角相等. ⑶全等三角形的周长、面积相等.二、基础习题1如图,≌,,求的度数.2、如图,≌,且、、、在同一条直线上,试找出图中互相平行的线段,并说明理由.3、如图,≌,,.求证:4.如图,≌,、、在同一条直线上,且,,.求的长和的度数.5.如图,长方形沿折叠,使得点落在边上的点处,且.求的度数.6、如图,点、、、在同一条直线上,≌.⑴判断与的位置关系,并说明理由;⑵判断与的数量关系,并说明理由.全等三角形(2)一.全等三角形的判定1:三边对应相等的两个三角形全等.简写成“边边边”或“”几何符号语言:在和中∵∴≌()二、基础习题1如图,点、、、在同一直线上,,,.求证:2、如图,点、、、在同一直线上,,,求证:3、如图,在四边形中,,.求证:①;②.4、如图,与交于点,,、是上两点,且,.求证:⑴;⑵全等三角形(3)一.全等三角形的判定2:两边和它们的夹角对应相等的两个三角形全等.简写为“边角边”或“”几何符号语言:在和中∵∴≌()二、基础习题1、如图,是中边的中点,,且. 求证:⑴≌⑵2、点、、、在同一直线上,,且.求证:⑴≌⑵3、如图,于,于,,.求证:4、如图,和都是等边三角形,连接、交于.求证:⑴⑵全等三角形(4)一.全等三角形的判定3:有两角和其夹边对应相等的两个三角形全等.简写成“角边角”或“”全等三角形的判定4:有两角和其一角对边对应相等的两个三角形全等.简写成“角角边”或“”几何符号语言:在和中∵∴≌()或:在和中∵∴≌()二、基础习题1.已知,,,则≌的根据是()A. B. C. D.2.和中,,,要使≌,则下列补充的条件中错误的是()A. B. C. D.3.如图,平分,,则图中全等三角形的对数是()A.2对 B.3对 C.4对 D.5对4.如图,已知,欲证明≌,可补充条件________.(填写一个适合的条件即可)5.如图,,,,欲得到,•可先利用_______,证明≌,得到______=______,再根据___________•证明________•≌________,即可得到.6.如图,平分和,欲证明,•可先利用___________,证明≌,得到______=_______,再根据________,证明______≌________,即可得到.7.如图,,,.求证:≌.8.如图,已知,,那么,你知道这是为什么吗?全等三角形(5)一.全等三角形的判定5:斜边和一条直角边对应相等的两个直角三角形全等.简写为“斜边、直角边”或“”几何符号语言:∵∴在和中∵∴≌二、基础习题1.如图,,于.求证:平分,2.如图,,,于,于.求证:3.在中,,,是过点的一条直线,且于,于.⑴当直线处于如图1的位置时,猜想、、之间的数量关系,并证明.⑵请你在图2选择与⑴不同位置进行操作,并猜想⑴中的结论是否还成立?加以证明;⑶归纳⑴、⑵,请你用简洁的语言表达、、之间的数量关系.4.如图,在和中,、、、在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明.①,②,③,④.5.如图,,,. 猜想线段、的关系,并说明理由.。
全等三角形的性质及判定练习题

全等三角形的性质及判定练习题(1)1:下列说法,正确的是( )A.全等图形的面积相等B.面积相等的两个图形是全等形C.形状相同的两个图形是全等形D.周长相等的两个图形是全等形2:如图1,折叠长方形ABCD ,使顶点D 与BC 边上的N 点重合,如果AD=7cm ,DM=5cm ,∠DAM=39°,则AN =____cm ,NM =____cm ,NAB ∠= .3:如图2,已知ABC ADE ∆≅∆,AB AD =,BC DE =,那么与BAE ∠相等的角是 .4:如图3,ABC ADE ∆≅∆,则AB= ,∠E= _.若∠BAE=120°,∠BAD=40°,则∠BAC= .5:如图,在ABC ∆中,::2:5:11A B ACB ∠∠∠=,若将ACB ∆绕点C 逆时针旋转,使旋转前后的//A B C ∆中的顶点/B 在原三角形的边AC 的延长线上,求/BCA ∠的度数.图4EDCBA图2 图3MDAN BC图1BFADCE6:如图1,,,AE DB BC EF BC ==∥EF .求证:ABC DEF ∆≅∆7:已知.,,AB DF AC DE BE CF ===,求证:AB ∥DF图1ADCFBEAED B8:如图,AC=DF ,AC//DF ,AE=DB ,求证:BC//EF9:如图, AD=EB,AC ∥DF ,BC ∥EF .求证:ABC DEF ∆≅∆10:如图,在△ABC 中, M 在BC 上, D 在AM 上, AB AC =,DB DC =.问BM CM =吗?说明理由.11:如图, △ABC, AD 是它的角平分线,且BD CD =,ED 、DF 分别垂直于AB 、AC ,垂足为E 、F ,请说明BE CF =.12:已知:如图 , CE ∞AB 于E , BF ∞CD 于F , 且BF=CE13:已知:如图,∠A=∠D=90°,AC ,BD 交于O ,AC=BD.求证:OB=OC .14:如图,AB AC =,AD AE =,EAD BAC ∠=∠.求证:△ABD ≌△ACE15:已知如图,AE =AC,AB =AD,∠EAB =∠CAD,试说明:∠B =∠D16:如图,BDA CEA ∠=∠,AE AD =.求证:AB AC =17:如图, △ABC 是等腰三角形,,AD BE 分别是,BAC ABC ∠∠的角平分线, △ABD 和△BAE 全等吗?请说明你的理由.18:已知:如图 , AB=AC , AD=AE , 求证:△OBD ≌△OCE全等三角形的性质及判定练习题(2)第一部分:选择题2.如图,已知AC和BD相交于O,且BO=DO,AO=CO,下列判断正确的是()A.只能证明△AOB≌△COD B.只能证明△AOD≌△COBC.只能证明△AOB≌△COB D.能证明△AOB≌△COD和△AOD≌△COB2题4.如图,已知MB=ND,∠MBA=∠NDC,下列不能判定△ABM≌△CDN的条件是()A.∠M=∠N B.AB=CD C.AM=CN D.AM∥CN5.如图,已知0A=OB,OC=0D,下列结论中:①∠A=∠B;②DE=CE;③连OE,则0E平分∠0,正确的是( )A.①② B.②③C.①③D.①②③6.已知△ABC的六个元素,下面甲、乙、丙三个三角形中和△ABC全等的图形是()A.甲和乙B.乙和丙C.只有乙D.只有丙第三部分:填空题1.如图,△ABC ≌△AED ,∠BAC=25°,∠B=35°,AB=3cm ,BC=1cm ,则∠E= , ∠ ADE= ;线段DE= cm ,AE= cm .2.已知ABC DEF ∆≅∆,若ABC ∆的周长为32,8AB =,12BC =,则DE = ,DF = . 第四部分:解答题1.如图,已知ABC AED ∆≅∆,AE AB =,AD AC =,20D E ︒∠-∠=,60BAC ︒∠=.求C ∠的度数.2.如图,已知AB=DE ,AF=DC ,BE=CF ,求证:∠A=∠D.3.已知:AB=CD ,AD=BC.试说明∠A=∠C.(公共边)ED CBABEDCAADB EFC DAO4.如图,在四边形ABCD中,已知BD平分∠ABC,∠A+∠C=180o,试说明AD=CD.。
七年级数学全等三角形练习题

七年级数学全等三角形练习题班级: 姓名: 一、知识要点 一般三角形 直角三角形 判定边角边(SAS )、角边角(ASA )角角边(AAS )、边边边(SSS )具备一般三角形的判定方法斜边和一条直角边对应相等(HL )性质 对应边相等,对应角相等对应中线相等,对应高相等,对应角平分线相等② 全等三角形面积相等. 二、练习题1、如图,已知AB=AC ,AD=AE,∠BAD =∠EAC ,求证:BD=CE.2、如图,在ABC △中,AB=AC ,∠BAC=120分别以AB AC ,为边作两个等腰直角三角形ABE 和ACD ,使∠BAE =∠DAC . (1)求DBC ∠的度数;(2)求证:BD CE =.3、如图,在△ABE 中,AB =AE,AD =AC,∠BAD =∠EAC, BC 、DE 交于点O. 求证:(1) △ABC ≌△AED ; (2) OB =OE .4、如图,四边形ABCD 的对角线AC 与BD 相交于O 点,12∠=∠,34∠=∠. 求证:(1)ABC ADC △≌△;(2)BO DO =.OC EBD ADCBAO123 4 AAO D C B AF D C B EA DC B 21C E DB A 2143CO B A5、如图,直线AD 与BC 相交于点O ,且AC=BD ,AD=BC .求证:CO=DO .6、已知:如图16,AB=AE ,BC=ED ,点F 是CD 的中点,AF ⊥CD .求证:∠B=∠E .7、如图,在△ABD 和△ACD 中,AB=AC ,∠B=∠C .求证:△ABD ≌△ACD .8、如图,已知AB=AD ,∠1=∠2,AC=AD,求证:△ABC ≌△ADE ,9、已知:如图,AB=AC ,∠1=∠2.求证:AO 平分∠BAC .。
全等三角形练习题及答案

全等三角形练习题及答案.求证如图已知C B =BC :AC.=C A AB,=B A AC,A C AB,A B ,:.1''''⊥'⊥'2.已知:如图,△ABC 中,点E 、F 分别在AB 、AC 边上,点D 是BC 边中点,且EF ∥BC,DE=DF . 求证:∠B=∠C3. 已知:如图,AC=AB,AE=AD,∠1=∠2.求证:∠3=∠44. 已知:如图 , AB=DC ,AD=BC , O 是BD 中点 ,过O 的直线分别与DA 、BC 的延长线交于E 、F . 求证:OE=OF5. 已知:如图,AB=AC,AE 平分∠BAC.求证:∠DBE=∠DCE .6. 已知:如图:AB=CD , BE=CF , AF=DE.求证:△ABE≌△DCF7. 已知:如图,∠1=∠2,BD=CD,求证:AD是∠BAC的平分线.8. 已知:如图,AD是BC上的中线,且DF=DE.求证:BE∥CF.9. 如图,已知:AC=DF,AC∥FD,AE=DB,求证:△ABC≌△DEF10. 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC∥DF.答案1. C B =BC C A B BAC C A B =BAC AC B +C CA =AC B +B BA 90=C CA =B BA AC A C AB,A B :''''''''''''⊥'⊥'∴≌△∴△∠∠即∠∠∠∠∴°∠∠∴∵证明 2. 证:∵BD=CD,EF ∥BC∴∠1=∠2,∠3=∠4∵DE=DF,∴∠2=∠4∴∠1=∠3∵D 是BC 的中点,∴BD=DC,又∠1=∠3,DE=DF ∴△BED ≌△CFD(SAS)∴∠B=∠C3. 证明:∵∠1=∠2∴∠1+∠5=∠2+∠5,即∠EAC=∠DAB 在△EAC 和△DAB 中∵∠∠AC ABEAC DABAE AD ===⎡⎣⎢⎢⎢⎢∴△EAC ≌△DAB(SAS)∴∠3=∠44. 提示:先证△ABD ≌△CDB , 再证△DOE ≌△BOF .5. 证明:在△ABE 和△ACE 中 ∵∠∠平分∠AB ACABE BAC AE AE ===⎡⎣⎢⎢⎢⎢12()∴△ABE ≌△ACE(SAS)∴BE=CE ∠3=∠ 4在△EBD 和△ECD 中∵∠∠BE CEDE ED ===⎡⎣⎢⎢⎢⎢34∴△EBD ≌△ECD(SAS) ∴∠DBE=∠DCE6. 证 明:∵AF=DE , ∴AF+FE=DE+EF .即AE=DF 在△ABE 和△DCF 中AB=CD , BE=CF , AE=DF , ∴△ABE ≌△DCF(SSS).7. 证明:∵BD=CD,∠1=∠2, ∴∠ADB=∠ADCAD=AD∴△ADB ≌△ADC(SAS) ∴∠BAD=∠CAD .即AD 平分∠BAC .8. 证:∵D 是BC 的中点,∴BD=CD ∵∠1=∠2,DF=DE,∴△BED ≌△CFD(SAS) ∴∠E=∠CFD∴BE ∥CF9. 证明:∵AE=BD∴AB=DE∵AC=DF AC ∥DF∴∠1=∠2∴△ABC ≌△DEF(SAS)10. 证明:∵BE=CF∴BE+EC=CF+EC 即BC=EF 又 AB ∥DE∴∠B=∠DEF∵AB=DE∴△ABC ≌△DEF∴∠ACB=∠F∴AC ∥DF。
三角形(全等SSS,SAS,AAS,ASA)练习
三角形全等的判定练习一、三角形的全等性质:1 如图:△ ABC^A A B',则有:AB= —, BC= —, CA =—/ A= ___ , / B= _ , / C= _ ,二、“SSS”判定的应用:1•完成下面的推理:如图,(1 )在厶ABC与厶A' B'中,AB A'B',2.如图:△ ADF ◎△ CBE,问AD 会平行CB吗?AE会等于CF吗?AC AC,• △ ABC^A A' B' (SSS・5 .如图,在△ ABC中,AB=AC , CD是厶ABC的中线,说明①厶ABD◎△ ACD。
②AD丄CB。
C 解: △A DF ◎△ CBE ( ____ )•I / A= __ (___••• AD// BC ( _______________ )△A DF ◎△ CBE ( ____ )•- AF=—( ____________________ )• AF-EF= B CA 2.女口图,AB=CD , AD=BC ,全等吗?AD会平行CB吗?解:在△ ADC与厶CBA中AD ,问:△ ADC与厶CBA ArB C6 .如图,△ ABD 和厶ABC , AC=AD , BC = BD , 那么△ ABD和厶ABC全等吗?即AE =—3.如图:△ ADB ◎△ ADC ,解: •/ △ ADB ADCAC AC,•=90•AD 丄CB=180问AD会垂直CB吗?4.如图:△ ABC ADE,问/ BAD= / CAE 吗?5.如图:△ ADF ◎△ CBE会等于CF吗?AE问AD会平行CB吗?A D•△ ADC ◎△ CBA( __ )•- / ____ = / _____ ( ___•AD// BC ( _______________________ )3.如图,C是BD和EF的中点,且BE=DF说明△BEC◎△ DFC。
4.女口图,在厶ADF 与厶BCE 中,AD=BC , DF=BE ,AE=CF,说明①厶ADF ◎△ CBE ,②AD // BC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形全等练习题
一
、填空题
1、如图1,在△ABC中,AC>BC>AB,且△ABC≌△DEF,则在△DEF
中,______<______<_______(填边)。
2、已知:△ABC≌△A′B′C′,∠A=∠A′,∠B=∠B′,∠C=70°,
AB=15cm,则∠C′=_________,A′B′=__________。
3、如图2,△ABD≌△BAC,若AD=BC,则∠BAD的对应角是________。
4、如图3,在△ABC和△FED,AD=FC,AB=FE,当添加条件__________
时,就可得到△ABC≌△FED。(只需填写一个你认为正确的条件)
5、如图4,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、
DC的中点,则图中共有全等三角形________对。
6、如图5,若BD⊥AE于B,DC⊥AF于C,且DC=DC,∠BAC=40°,
∠ADG=130°,则∠DGF=________。
7、三角形两外角平分线和第三个角的内角平分线_____一点,
且该点在三角形______部。
8、如图6,△ABC中,∠C=90°,CD⊥AB于
点D,AE是∠BAC的平分线,点E到AB的距离等
于3cm,则CF=_____cm。
9、如图7,两平面镜α、β的夹角 θ,入射光
线AO平行于β,入射到α上,经两 次反射后的出射
光线CB平行于α,则角θ等于________。
10、如图8,P是∠AOB平分线上一点,CD⊥OP
于F,并分别交OA、OB于CD,则CD_____P点到
∠AOB两边距离之和。
11.如图,在△ABC中,AD=DE,AB=BE,∠A=80°,
则∠CED=_____.
12.已知△DEF≌△ABC,AB=AC,且△ABC的周长为23cm,BC=4 cm,
则△DEF的边中必有一条边等于___
A
B
C
D
E
13.地基在同一水平面上,高度相同的两幢楼上分别住着甲、乙两位同学,有
一天,甲对乙说:“从我住的这幢楼的底部到你住的那幢楼的顶部的直线距离,
等于从你住的那幢楼的底部到我住的这幢楼的顶部的直线距离.”你认为甲的话
正确吗?答:______.
二、选择题:
14、下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,
相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及
对应角平分线分别相等,其中真命题的个数有( )
A、3个 B、2个 C、1个 D、0个
15、如图9:已知点E在△ABC的外部,点D在BC
边上,
DE交AC于F,若∠1=∠2=∠3,AC=AE,则有( )
A、△ABD≌△AFD B、△AFE≌△ADC
C、△AEF≌△DFC D、△ABC≌△ADE
16、如图10,在△ABC中,AD平分∠BAC,过B作 17.下列命题中正确的是( ) 18. 如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条
BE⊥
AD于E,过E作EF∥AC交AB于F,则( )
A、AF=2BF B、AF=BF
C、AF>BF D、AF
A.全等三角形的高相等 B.全等三角形的中线相等
C.全等三角形的角平分线相等 D.全等三角形对应角的平分线相等
角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )
A.1︰1︰1 B.1︰2︰3 C.2︰3︰4 D.3︰4︰5
