《应用回归分析 》---多元线性回归分析实验报告
应用回归分析实验报告
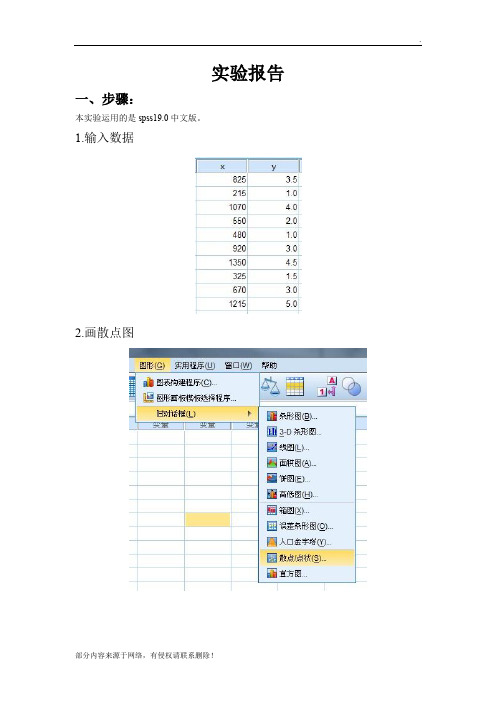
实验报告一、步骤:本实验运用的是spss19.0中文版。
1.输入数据2.画散点图输出结果为:3.回归分析二、输出结果:表一描述性统计量均值 标准 偏差Ny 2.850 1.4347 10 x762.00379.74610表二相关性y xPearson 相关性y 1.000 .949x .949 1.000Sig. (单侧)y . .000x .000 .N y 10 10x 10 10由上表可得x与y的相关系数为0.949,在置性水平为0.05下,y与x显著相关。
表三输入/移去的变量b模型输入的变量移去的变量方法1 x a. 输入a. 已输入所有请求的变量。
b. 因变量: y表四模型汇总模型R R 方调整 R 方标准估计的误差1 .949a.900 .888 .4800a. 预测变量: (常量), x。
由上图知该回归方程的标准误差是0.4800由图中的R 方知决定系数是0.900表五Anova b模型平方和df 均方 F Sig.1 回归16.682 1 16.682 72.396 .000a残差 1.843 8 .230总计18.525 9a. 预测变量: (常量), x。
b. 因变量: y由ANOVA方差分析图知,此模型的回归平方和是16.682,残差平方和是1.843,总平方和是18.525;三者自由度分别为:1,8,9;回归平方和与残差平方和的平均平方和依次为16.682,0.23;此模型的F 检验值为72.396.表六系数a模型 非标准化系数标准系数 t Sig. B 的 95.0% 置信区间 B 标准 误差试用版下限 上限 1(常量) .118 .355.333.748 -.701 .937 x.004.000.9498.509.000.003.005a. 因变量: y由上图知(1).回归方程为0.1180.004y x ∧∧=+(2).回归系数的区间估计,在置信度为95%下,01ββ∧∧和的置信区间分别为(-0.701,0.937),(0.003,0.005)。
应用回归分析实验报告

重庆交通大学学生实验报告实验课程名称应用回归分析开课实验室数学实验室学院理学院年级09专业班信息2班学生姓名zhouhoufei 学号开课时间2011 至2012 学年第1 学期2.15 一家保险公司十分关心其总公司营业部加班的程度,决定认真调查一下现状。
经过10周时间,收集了每周加班工作时间的数据和签发新保单数目,x 为每周签发的新保单数目,y 为每周加班工作时间(小时)。
(1)画散点图;(2)x 与y 之间是否大致呈线性关系? (3)用最小二乘估计求出回归方程;(4)求回归标准误差ˆσ; (5)给出0ˆβ、1ˆβ的置信度为95%的区间估计; (6)计算x 与y 的决定系数;(7)对回归方程做方差分析;(8)做回归系数1ˆβ显著性检验; (9)做相关系数的显著性检验;(10)对回归方程做残差图并作相应的分析;(11)该公司预计下一周签发新保单01000x =张,需要的加班时间是多少? (12)给出0y 的置信水平为95%的精确预测区间和近视预测区间。
(13)给出0()E y 置信水平为95%的区间估计。
(1)将数据输入到SPSS 中,画出散点图如下:(2)由下表可知x与y的相关系数高达0.949,大于0.8,所以x与y之间线性相关性显著。
相关性y xPearson 相关性y 1.000 .949x .949 1.000Sig. (单侧)y . .000x .000 .N y 10 10x 10 10由上表可知0β、1β的参数估计值0ˆβ、1ˆβ分别为0.118和0.004,所以y 对x 的线性回归方程为0.1180.004x y ∧=+(4)由SPSS 得到如下模型汇总表:模型汇总模型RR 方调整 R 方标准 估计的误差1.949a.900.888.4800a. 预测变量: (常量), x 。
由模型汇总表可知回归标准误差σ∧=0.4800(5)由以下系数表可知0ˆβ、1ˆβ的置信度为95%的区间估计分别为: (-0.701,0.937)和(0.003,0.005)。
多元线性回归实验报告模板

和广告费之间的关系可用(3)近似表示出.
实验过程:(含解决方法和基本步骤,主要程序清单及异常情况记录等)a=[1 -0.05
5.5 30.25
1 0.25 6.75 45.5625
1 0.6 7.25 52.5625
1 0 5.5 30.25
1 0.25 7 49
1 0.2 6.5 42.25
1 0.15 6.75 45.5625
实验目的: 1. 学习和掌握 Excel 及 MATLAB 的有关命令. 2. 自已收集数据(可以利用统计年鉴或其它公开的数据),利用你的数据建立模型. 3. 说明模型的意义
数学模型:
y = β0 + β1x1 + β2x2 + β3x22 + ε
实验所用软件及版本: Microsoft Word 2003 Excel MATLAB 6.5.1
三.模型评价: 从表 2 显示, r2 = 0.9194 指因变量 y 的 91.94%可由模型确定, F 的值远远超过 F 检验的临界值, p
也小于α ,因此模型(3)从整体上看是可用的。 表 ( 2 ) 的 回 归 系 数 给 出 了 模 型 三 中 的 β0, β1, β2, β3 的 估 计 值 , 即
Stats 是用于检验回归模型的统计量,有三个数值,第一个是相关系数 r2 , r2 越接近 1,说明
回归模型越显著;第二个是 F 值,F > F1−α (k, n − k −1) 时拒绝 H0 ,F 越大,说明回归方程越显著;第三
个是对应的概率 p , p < α 时拒绝 H0 ,回归模型成立。
求解步骤为:
收入
x1 电视广告费用 x2 报纸广告费用
从图 1 中发现,随着 x1 的增加, y 值有较明显的线形增长趋势,图中的直线是用线形模型
多元线性回归模型实验报告
多元线性回归模型一、实验目的通过上机实验,使学生能够使用Eviews 软件估计可化为线性回归模型的非线性模型,并对线性回归模型的参数线性约束条件进行检验。
二、实验内容(一)根据中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y,资产合计K及职工人数L进行回归分析。
(二)掌握可化为线性多元非线性回归模型的估计和多元线性回归模型的线性约束条件的检验方法(三)根据实验结果判断中国该年制造业总体的规模报酬状态如何?三、实验步骤(一)收集数据下表列示出来中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y,资产合计K及职工人数L。
序号工业总产值Y(亿元)资产合计K(亿元)职工人数L(万人)序号工业总产值Y(亿元)资产合计K(亿元)职工人数L(万人)1 3722.7 3078.22 113 17 812.7 1118.81 432 1442.52 1684.43 67 18 1899.7 2052.16 613 1752.37 2742.77 84 19 3692.85 6113.11 2404 1451.29 1973.82 27 20 4732.9 9228.25 2225 5149.3 5917.01 327 21 2180.23 2866.65 806 2291.16 1758.77 120 22 2539.76 2545.63 967 1345.17 939.1 58 23 3046.95 4787.9 2228 656.77 694.94 31 24 2192.63 3255.29 1639 370.18 363.48 16 25 5364.83 8129.68 24410 1590.36 2511.99 66 26 4834.68 5260.2 14511 616.71 973.73 58 27 7549.58 7518.79 13812 617.94 516.01 28 28 867.91 984.52 4613 4429.19 3785.91 61 29 4611.39 18626.94 21814 5749.02 8688.03 254 30 170.3 610.91 1915 1781.37 2798.9 83 31 325.53 1523.19 4516 1243.07 1808.44 33表1(二)创建工作文件(Workfile)。
多元线性回归实例分析报告

SP SS--回归-多元线性回归模型案例解析!( 一)多元线性回归,主要是研究一个因变量与多个自变量之间的相关关系,跟一元回归原理差不多,区别在于影响因素(自变量)更多些而已,例如:一元线性回归方程为:Y = 00 十 十 E毫无疑问,多元线性回归方程应该为:上图中的x1, x2, xp 分别代表“自变量” Xp 截止,代表有P 个自变量,如果有“ N 组样本,那么这个多元线性回归,将会组成一个矩阵,如下图所示:记n 俎样本分别是(兀那么,多元线性回归方程矩阵形式为:'"" + £1的误差,随机误差必须满足以下四个条件,多元线性方程才有意义(一元线性方程也一样)2:无偏性假设,即指:期望值为 3:同共方差性假设,即指,所有的4:独立性假设,即指:所有的随机误差变量都相互独立,可以用协方差解释。
今天跟大家一起讨论一下, SPSS---多元线性回归的具体操作过程, 下面以教程教程数据为例,分析汽车特征与汽车销售量之间的关系。
通过分析汽车特征跟汽车销售量的关系,建立拟合多元线性回归模型。
数据如下图所示:V = B Q +02] +角工2 + -…+y =>'2*a A1X"1儿丿,0 二卩\■■■ ■丿 /鞋丿其中:代表随机误差,其中随机误差分为:可解释的误差和不可解释1服成正太分布,即指:随机误差必须是服成正太分别的随机变量。
随机误差变量方差都相等“分析”一一回归一一线性一一进入如下图所示的界面:1 salesnesaletyp&priceengiriE 」horse pow , wheelbaswidth ] length1S.919' 16 360 0 21.500!1.8140 101.2 67.3 172.4 39 364 19S75 0 2B4003 2225 108 1 70 3 192 3 14.114 18225 0 - 3.2 225 106.9 70.5 192.0 8 588 29 725 0 42 000 3-S' 210 114 6 71 4 1966 20 397 2225S 0 33.990 1.8 150 1O2?6 63 2 178.0 1378023i'S5'5 033 9&0 28 200 108 7 76 1 192 O' 138039 00062 000 第 310 113 0 74 Q 1982 19 747 -0 26.9902.5 170 107.3 63.4 1176.01 9_231 2Se75 0 33 400 I2.8133 107 3 63 5 17'6 O' 17.537 3& 13S 0| 3S.900 ; 2-8 1931114 70.9 188.0 91 561 12-475 0 21 9751 ! 31 175 1i0'9 0 72 7194.6 39.3£0 13.740 0 25.300 , 3.3 240 109 0 72 7 196^2 27 861 20 190' 0 31.965j : 3.3 205 1138 747 206.8 S326Z 13 360'0 27 635 1 30 205 1122 73 5 200 0 63.72&22525 0 39.E95 ; 壮 275 115.3 74.5 2072 15 94327 100' O '44-475 1 46 275 112 2 75 0 201 0 e.53G 25725 0 39.G&5 , 4.6 275 108.0 75 S 200.G 11 IBS IS 2250 31 CIO i30 2C0 107 4 70 3 194呂 14.785 - 1 46.225;! 5 7 355 117.5 77.0 201.2 US. 519' 9.250' 0 13 2S0 2.2, 115 104.1 67 9 ieo'9 135 12611 22516 6351 ; 3 1 170 107 0 69 4 1904 24.62& 10.3110'0| 1S.S90 1 3.1 175 110I7.& 72 S200.9 42 593 11 525O '19 390134180110 572 7197 9curt点击蛆厂逛[manuracl]Mod si [mo'del I 炉新车售价(单位=... 茨拜肯二手车售价… £| Vehicle 射pg [typ 鬪 捞'Price in thousand... 炉 Engine size [engi... 袴 Horsep'OW'erlhor... 夕'jVlieelba3€ |whe…, 拧车宽[WFdlhl 務军衽[lergtA] 少车净垂[curb.wgt] 少 Fuel capacity 拐耗油量辺硏Inpgj @ Cooks Dfstance [... 少 95铀 LCI forinsa... 撐95«i4UCliforInsa...LCI kr Insa...将“销售量”作为“因变量”拖入因变量框内,将“车长,车宽,耗油率,车净重等个自变量 拖入自变量框内,如上图所示,在“方法”旁边,选择“逐步”,当然,你也可 以选择其它的方式,如果你选择“进入”默认的方式,在分析结果中,将会得到如下图所示 的结果:(所有的自变量,都会强行进入)輸入/窿去的吏量h移去的娈量左法 1油量迎册, 车稳 Price in tnoLJsands,Vehicle type, 车毘Engine size, Fuel capacity, Wheelbase, 军淨重, Horsepower输入a. 已输入斯肓诸號的吏量•b. 因变呈:Log-transformecJ sales如果你选择“逐步”这个方法,将会得到如下图所示的结果:(将会根据预先设定的“ 计量的概率值进行筛选,最先进入回归方程的“自变量”应该是跟“因变量”关系最为密切,J [,牯贴£川重置迟)]〔取消j [ M Ja 篷择变>(E >:! J一个对签Q* I 护 Pneo 需thousands [price]VVLS 权重®:10块1的1 ijj Veliicleb'peltyipeJPrice inthodsandslprice] $ Engine siz&Iergine^s]贡献最大的,如下图可以看出,车的价格和车轴跟因变量关系最为密切,符合判断条件的概率值必须小于,当概率值大于等于时将会被剔除)“选择变量(E)"框内,我并没有输入数据,如果你需要对某个“自变量”进行条件筛选, 可以将那个自变量,移入“选择变量框”内,有一个前提就是:该变量从未在另一个目标列表中出现!,再点击“规则”设定相应的“筛选条件”即可,如下图所示:定义琏弃规则sales 値W:....... k.i. J .產壬一二不等于小于小于等于丸于大于等于thousands h点击“统计量”弹出如下所示的框,如下所示:□ Ddrbin*Watson(U) n 个就诊断©在“回归系数”下面勾选“估计,在右侧勾选” 模型拟合度“和”共线性诊断“两个选项, 再勾选“个案诊断”再点击“离群值”一般默认值为“3”,(设定异常值的依据,只有当残差超过3倍标准差的观测才会被当做异常值) 点击继续。
回归分析 实验报告

回归分析实验报告1. 引言回归分析是一种用于探索变量之间关系的统计方法。
它通过建立一个数学模型来预测一个变量(因变量)与一个或多个其他变量(自变量)之间的关系。
本实验报告旨在介绍回归分析的基本原理,并通过一个实际案例来展示其应用。
2. 回归分析的基本原理回归分析的基本原理是基于最小二乘法。
最小二乘法通过寻找一条最佳拟合直线(或曲线),使得所有数据点到该直线的距离之和最小。
这条拟合直线被称为回归线,可以用来预测因变量的值。
3. 实验设计本实验选择了一个实际数据集进行回归分析。
数据集包含了一个公司的广告投入和销售额的数据,共有200个观测值。
目标是通过广告投入来预测销售额。
4. 数据预处理在进行回归分析之前,首先需要对数据进行预处理。
这包括了缺失值处理、异常值处理和数据标准化等步骤。
4.1 缺失值处理查看数据集,发现没有缺失值,因此无需进行缺失值处理。
4.2 异常值处理通过绘制箱线图,发现了一个销售额的异常值。
根据业务经验,判断该异常值是由于数据采集错误造成的。
因此,将该观测值从数据集中删除。
4.3 数据标准化为了消除不同变量之间的量纲差异,将广告投入和销售额两个变量进行标准化处理。
标准化后的数据具有零均值和单位方差,方便进行回归分析。
5. 回归模型选择在本实验中,我们选择了线性回归模型来建立广告投入与销售额之间的关系。
线性回归模型假设因变量和自变量之间存在一个线性关系。
6. 回归模型拟合通过最小二乘法,拟合了线性回归模型。
回归方程为:销售额 = 0.7 * 广告投入 + 0.3回归方程表明,每增加1单位的广告投入,销售额平均增加0.7单位。
7. 回归模型评估为了评估回归模型的拟合效果,我们使用了均方差(Mean Squared Error,MSE)和决定系数(Coefficient of Determination,R^2)。
7.1 均方差均方差度量了观测值与回归线之间的平均差距。
在本实验中,均方差为10.5,说明模型的拟合效果相对较好。
(实验2)多元回归分析实验报告.doc
⑩陕&科技丈嗲实验报告成绩一、实验预习:1.多元回归模型。
2.多元回归模型参数的检验。
3.多元回归模型整体的检验。
二、实验的目的和要求:通过案例分析掌握多元回归模型的建立方法和检验的标准;并掌握分析解决实际金融问题的能力。
三、实验过程:(实验步骤、原理和实验数据记录等)软件:Eviews3.1数据:给定美国机动车汽油消费量研究数据。
1.实验步骤1)在Eviews7.0中,新建文件,并将给定的数据输入新建的文件中;2)分析变量间的相关关系;3)进行时间序列的平稳性检验,根据序列趋势图,对原序列进行ADF平稳性检验,再对时间序列数据的一阶差分进行ADF检验,并对结果进行分析讨论。
2.实验原理对于只有一个解释变量的模型,其参数估计方法是最简单的,一般形式如下:y t= A)+ +其中&称为被解释变量,人称为解释变量,%称为随机误差项。
模型可分为两部分:1)回归方程部分,2)随机误差部分,义㈣归分析就是根据样本观察值寻求从和成的估计值。
图一0 Series: S Torkfile: ADF::Adf\| VeA- J Proc: Object Properties ^nnt Name {Freeze J Default-n x| Options | Sample [Gerr j图二2)建立回归模型如卜:四、实验总结:(实验数据处理和实验结果讨论等)1.实验数据处理1)数据的预处理:通过绘制动态曲线、绘制散点图、计算变量之间的相关 关系为正式建模做准备。
可以画出美国汽车各项研究数据的趋势图如下:QMG = c(l) + c(2) * MOB + c(3) * PMG + c(4) * POP + c(5) * GNP 回归结果如下:Dependent Variable: QMG Method: LeastSquares Date: 06/10/14 Time: 16:19 Sample:1950 1987 Included observations: 38QMG=C(1)+C(2)*MOB+C(3)*PMG+C(4)*POP+C(5)*GNP由表中数据带入公式可写出线性回归表达式为:QMG = 24553723 + 1.418520 * MOB- 27995762 * PMG- 59.8748 * POP- 30540.88 * GNP3)进行模型检验从表Prob列的数据中发现c(0)与c(4)的值T检验未通过,可以考虑删除相应的自变量。
回归分析实验报告总结
回归分析实验报告总结引言回归分析是一种用于研究变量之间关系的统计方法,广泛应用于社会科学、经济学、医学等领域。
本实验旨在通过回归分析来探究自变量与因变量之间的关系,并建立可靠的模型。
本报告总结了实验的方法、结果和讨论,并提出了改进的建议。
方法实验采用了从某公司收集到的500个样本数据,其中包括了自变量X和因变量Y。
首先,对数据进行了清洗和预处理,包括删除缺失值、处理异常值等。
然后,通过散点图、相关性分析等方法对数据进行初步探索。
接下来,选择了合适的回归模型进行建模,通过最小二乘法估计模型的参数。
最后,对模型进行了评估,并进行了显著性检验。
结果经过分析,我们建立了一个多元线性回归模型来描述自变量X对因变量Y的影响。
模型的方程为:Y = 0.5X1 + 0.3X2 + 0.2X3 + ε其中,X1、X2、X3分别表示自变量的三个分量,ε表示误差项。
模型的回归系数表明,X1对Y的影响最大,其次是X2,X3的影响最小。
通过回归系数的显著性检验,我们发现模型的拟合度良好,P值均小于0.05,表明自变量与因变量之间的关系是显著的。
讨论通过本次实验,我们得到了一个可靠的回归模型,描述了自变量与因变量之间的关系。
然而,我们也发现实验中存在一些不足之处。
首先,数据的样本量较小,可能会影响模型的准确度和推广能力。
其次,模型中可能存在未观测到的影响因素,并未考虑到它们对因变量的影响。
此外,由于数据的收集方式和样本来源的局限性,模型的适用性有待进一步验证。
为了提高实验的可靠性和推广能力,我们提出以下改进建议:首先,扩大样本量,以提高模型的稳定性和准确度。
其次,进一步深入分析数据,探索可能存在的其他影响因素,并加入模型中进行综合分析。
最后,通过多个来源的数据收集,提高模型的适用性和泛化能力。
结论通过本次实验,我们成功建立了一个多元线性回归模型来描述自变量与因变量之间的关系,并对模型进行了评估和显著性检验。
结果表明,自变量对因变量的影响是显著的。
应用回归分析实验报告7
实验报告实验课程应用回归分析第7 次实验实验日期2012.12.6 指导教师王振羽班级10统计学号1007402068 姓名刘晓静成绩一、实验目的掌握SPSS中找出并消除数据共线性方法.掌握SPSS中的岭回归分析方法.二、实验内容1.在训练中氧气消耗能力问题的研究中,我们想要建立一个关系式,以便根据训练测试的数据来预报肺活量,而不必进行昂贵和笨重的氧气消耗测试。
考察的因变量y为OXY(氧气消耗能力),自变量有x1(age,年龄)、x2(weight,体重)、x3(RunTime,1.5英里跑的时间)、x4(RstPulse, 休息时脉博)、x5(RunPulse,跑步时脉博)、x6(RunPulse, 跑步时最大脉博)。
(数据在“回归人大数据12_学生.xls的第2题”中),利用统计软件计算(1) 用方差扩大因子法分析数据的多重共线性;(2) 用特征根法分析数据的多重共线性;(3) 本题是否适用剔除变量的方法消除共线性,如果适用,进行变量剔除(要求写出回归方程,及主要的统计量);(4) 对此问题作岭回归分析(写明你所用的确定k的原则);注: 要求写出回归方程,及主要的统计量。
三、实验结果与分析(包括运行结果及其数据分析、解释等)(1)用方差扩大因子法分析数据的多重共线性;由上表可以看出,所有变量的方差扩大因子都不大,都小于10,由此可以看出该回归方程的多重共线性不严重,从方差扩大因子的平均数来度量多重共线性,方差扩大因子的平均数为=3.8并没有远远大于1。
综上可得出结论,用方差扩大因子法诊断该回归方程,并不存在多重共线性。
(2) 用特征根法分析数据的多重共线性;从条件数看到,最大的条件数k7=196.786,说明自变量间存在严重的多重共线性,从表中第七行x5、x6的系数分别为0.91、0.98,说明x5、x6存在较强的多重共线性。
(3) 本题是否适用剔除变量的方法消除共线性,如果适用,进行变量剔除(要求写出回归方程,及主要的统计量);从上题特征值判定法中可以知道,x5、x6存在较强的多重共线性;从上表系数矩阵中可以看出,x5、x6的相关系数为0.93,即两个变量之间的相关性很大,其中x5为跑步时的脉搏,x6为跑步时的最大脉搏,其中跑步时的脉搏包含了x6跑步时的最大脉搏,即两个变量可去其一。
回归分析实验报告
回归分析实验报告目录一、内容概括 (2)1.1 实验目的 (2)1.2 背景知识介绍 (3)二、数据收集与处理 (4)2.1 数据来源 (4)2.2 数据预处理 (5)2.3 数据描述与分析 (7)三、回归分析模型建立 (8)3.1 模型选择依据 (9)3.2 模型参数估计 (9)3.3 模型检验与修正 (10)四、实验结果分析 (11)4.1 实验结果概述 (13)4.2 参数分析 (14)4.3 模型拟合度分析 (15)4.4 预测结果分析 (16)五、实验讨论与结论 (17)5.1 实验结果讨论 (18)5.2 实验结论 (19)5.3 研究的局限性与未来研究方向 (20)六、代码实现与数据展示 (20)6.1 使用的编程语言和工具介绍 (22)6.2 代码展示与说明 (23)6.3 数据展示与解释 (24)一、内容概括本实验报告主要围绕回归分析展开,通过对数据进行深入分析和探讨,旨在探究自变量与因变量之间的关系,并建立合适的数学模型以预测未来趋势。
实验过程中,我们采用了多种统计方法和软件工具,以确保结果的准确性和可靠性。
我们首先对数据进行描述性统计分析,包括计算均值、方差、标准差等指标,以便了解数据的分布特征和离散程度。
我们进行了相关性分析,通过计算皮尔逊相关系数等方法,探究了自变量与因变量之间的相关关系强度。
我们运用回归分析中的多元线性回归模型,对数据进行了拟合优度检验、回归方程显著性检验以及残差分析。
这些分析帮助我们评估模型的拟合效果,以及自变量对因变量的解释能力。
我们得出了回归分析的结果,并据此提出了相应的结论和建议。
1.1 实验目的本回归分析实验旨在通过对给定数据集进行回归分析,探讨自变量与因变量之间的关系。
我们将学习如何使用统计软件(如Python的StatsModels库或R语言)进行回归分析,以及如何解读回归结果。
我们还将了解回归分析在实际问题中的应用,例如预测房价、股票价格等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《应用回归分析》---多元线性回归分析实验报告
二、实验步骤:
1、计算出增广的样本相关矩阵
2、给出回归方程
Y=-65.074+2.689*腰围+(-0.078*体重)3、对所得回归方程做拟合优度检验
4、对回归方程做显著性检验
5、对回归系数做显著性检验
三、实验结果分析:
1、计算出增广的样本相关矩阵相关矩阵
2、给出回归方程
回归方程:Y=-65.074+2.689*腰围+(-0.078*体重)
3、对所得回归方程做拟合优度检验
由表可知x与y的决定性系数为r2=0.800,说明模型的你和效果一般,x与y 线性相关系数为R=0.894,说明x与y有较显著的线性关系,当F=33.931,显著性Sig.p=0.000,说明回归方程显著
4、对回归方程做显著性检验
5、对回归系数做显著性检验
Beta的t检验统计量t=-6.254,对应p的值接近0,说明体重和体内脂肪比重对腰围数据有显著影响
6、结合回归方程对该问题做一些基本分析
从上面的分析过程中可以看出腰围和脂肪比重以及腰围和体重的相关性都是很大的,通过检验可以看出回归方程、回归系数也很显著。
其次可以观察到腰围、脂肪比重、体重的数据都是服从正态分布的。
