电阻应变式传感器实验报告
测试实验二 称重

实验一 应变片单臂电桥性能实验一、实验目的:了解电阻应变片的工作原理与应用并掌握应变片测量电路。
二、基本原理:电阻应变式传感器是在弹性元件上通过特定工艺粘贴电阻应变片来组成。
一种利用电阻材料的应变效应将工程结构件的内部变形转换为电阻变化的传感器。
此类传感 器主要是通过一定的机械装置将被测量转化成弹性元件的变形,然后由电阻应变片将弹性元 件的变形转换成电阻的变化,再通过测量电路将电阻的变化转换成电压或电流变化信号输 出。
它可用于能转化成变形的各种非电物理量的检测,如力、压力、加速度、力矩、重量等, 在机械加工、计量、建筑测量等行业应用十分广泛。
1、应变片的电阻应变效应所谓电阻应变效应是指具有规则外形的金属导体或半导体材料在外力作用下产生应变 而其电阻值也会产生相应地改变,这一物理现象称为“电阻应变效应”。
以圆柱形导体为例: 设其长为:L 、半径为r 、材料的电阻率为ρ时,根据电阻的定义式得2rLA L R ⋅==πρρ(1—1) 当导体因某种原因产生应变时,其长度L 、截面积A 和电阻率ρ的变化为dL 、dA 、d ρ相应的电阻变化为dR 。
对式(1—1)全微分得电阻变化率 dR/R 为:ρρd r dr L dL R dR +-=2 (1—2) 式中:dL/L 为导体的轴向应变量εL ; dr/r 为导体的横向应变量εr 由材料力学得: εL = - μεr (1—3)式中:μ为材料的泊松比,大多数金属材料的泊松比为0.3~0.5 左右;负号表示两者的变 化方向相反。
将式(1—3)代入式(1—2)得:ρρεμd R dR ++=)21( (1—4) 式(1—4)说明电阻应变效应主要取决于它的几何应变(几何效应)和本身特有的导电性能 (压阻效应)。
2、应变灵敏度它是指电阻应变片在单位应变作用下所产生的电阻的相对变化量。
(1)、金属导体的应变灵敏度K :主要取决于其几何效应;可取l RdRεμ)21(+≈ (1—5) 其灵敏度系数为:K=)21(με+=RdRl 金属导体在受到应变作用时将产生电阻的变化,拉伸时电阻增大,压缩时电阻减小,且与其 轴向应变成正比。
传感器实验报告1

传感器实验报告实验一Pt100铂电阻测温特性实验一、实验目的1.通过自行设计热电阻测温实验方案,加深对温度传感器工作原理的理解。
2.掌握测量温度的电路设计和误差分析方法。
二、实验内容1.设计PT100铂热电阻测温实验电路方案;2.测量PT100的温度与电压关系,要求测温范围为:室温~65℃;温度测量精度:±2℃;输出电压≤4V,输出以电压V方式记录。
3.通过测量值进行误差分析。
三、实验仪器、设备、材料主机箱、温度源、Pt100热电阻(2支)、温度传感器实验模板、万用表。
四、实验原理利用导体电阻随温度变化的特性,可以制成热电阻,要求其材料电阻温度系数大,稳定性好,电阻率高,电阻与温度之间最好有线性关系。
常用的热电阻有铂电阻(650℃以内)和铜电阻(150℃以内)。
铂电阻是将~mm的铂丝绕在线圈骨架上封装在玻璃或陶瓷管等保护管内构成。
在0-650℃以内,它的电阻Rt与温度t的关系为:Rt=Ro(1+At+Bt2),式中:Ro系温度为0℃时的电阻值(本实验的铂电阻Ro=100Ω)。
A=×10-3/℃,B=-×10-7/℃2。
铂电阻一般是三线制,其中一端接一根引线另一端接二根引线,主要为远距离测量消除引线电阻对桥臂的影响(近距离可用二线制,导线电阻忽略不计。
)。
实际测量时将铂电阻随温度变化的阻值通过电桥转换成电压的变化量输出,再经放大器放大后直接用电压表显示。
五、实验步骤1、用万用表欧姆档测出Pt100三根线中其中短接的二根线(同种颜色的线)设为1、2,另一根设为3,并测出它在室温时的大致电阻值。
2、在主机箱总电源、调节仪电源都关闭的状态下,再根据图1示意图接线,温度传感器实验模板中a、b(Rt)两端接传感器,这样传感器(Rt)与R3、R1、Rw1、R4组成直流电桥,是一种单臂电桥工作形式。
3、放大器调零:将图的温度传感器实验模板的放大器的两输入端引线(一根传感器引线、另一根桥路输出即Rw1活动触点输出)暂时不要引入,而用导线直接将放大器的两输入端相连(短接);将主机箱上的电压表量程(显示选择)切换开关打到2V档,合上主机箱电源开关,调节温度传感器实验模板中的RW2(逆时针转到底)增益电位器,使放大器增益最小;再调节RW3(调零电位器)使主机箱的电压表显示为0。
2.1 电阻应变式传感器

r r0
(a) 拉伸
(b) 压缩
绝对伸长 Δl 0
绝对压缩 Δl 0
Δr 0
Δr 0
传感器及检测技术
轴向应变 径向应变 泊松系数
y
Δl F l0 AE E
x
r r0 Δr F r0 r0 AE
y x
反映物质形变程度, 反映物质弹性特征(0.2 ~ 0.4), E是材料的弹性模量. E钢=2.0*1011N/m2 E铝=0.7*1011N/m2
在AB,BC两个臂上分别接上工作片,温度影响将互相抵消。
4
3
U
BD
E R1 4 R1
R R
3
3
EK 4
1 2
对臂测量
传感器及检测技术
在AB,CD两个臂上接工作片,BC,DA接温度补偿 片。四个臂的电阻同处一个温度场,温度影响相互抵消。
传感器及检测技术
电阻相对变化量为:
l
dR dL d dA R L A
2r 2(r-dr)
F 若电阻丝是圆形的, 则A=πr ²,对r 微分 得dA=2πr dr,则: l+ dl
金属丝的应变效应
dA 2rdr dr 2 2 A r r
传感器及检测技术
令
dL y — —金属的轴向应变 L dr x — —金属的径向应变 r
E R1 R2 R3 R4 EK U DB ( ) U DB 4 1 2 3 4 4 R1 R2 R3 R4
读
1
2
3
4
式中: 1、 2、 3、 4分别代表四个应变片所感受的应变值,
生物医学传感器实验报告.

综合实验报告学院医学工程学院实验名称生物医学测量与传感器综合实验专业班级学生姓名学号指导教师成绩实验一应变片单臂特性实验一、实验目的:了解电阻应变片的工作原理与应用并掌握应变片测量电路。
二、基本原理:电阻丝在外力作用下发生机械变形时,其电阻值发生变化,这就是电阻应变效应,描述电阻应变效应的关系式为:ΔR/R=Kε;式中ΔR/R为电阻丝的电阻相对变化值,K为应变灵敏系数,ε=ΔL/L为电阻丝长度相对变化。
金属箔式应变片是通过光刻、腐蚀等工艺制成的应变敏感元件,用它来转换被测部位的受力大小及状态,通过电桥原理完成电阻到电压的比例变化,对单臂电桥而言,电桥输出电压,U01=EKε/4。
(E为供桥电压)。
三、实验步骤:1位数显万用表2kΩ电阻档测量所有1、在应变梁自然状态(不受力)的情况下,用42应变片阻值;在应变梁受力状态(用手压、提振动台)的情况下,测应变片阻值,观察一下应变片阻值变化情况(标有上下箭头的4片应变片纵向受力阻值有变化;标有左右箭头的2片应变片横向不受力阻值无变化,是温度补偿片)。
如下图1—6所示。
2、差动放大器调零点:按图1—7示意接线。
将F/V表的量程切换开关切换到2V档,合上实验箱主电源开关,将差动放大器的拨动开关拨到“开”位置,将差动放大器的增益电位器按顺时针方向轻轻转到底后再逆向回转半圈,调节调零电位器,使电压表显示电压为零。
差动放大器的零点调节完成,关闭主电源。
图1—7 差放调零接线图3、应变片单臂电桥特性实验:⑴将主板上传感器输出单元中的箔式应变片(标有上下箭头的4片应变片中任意一片为工作片)与电桥单元中R1、R2、R3组成电桥电路,电桥的一对角接±4V直流电源,另一对角作为电桥的输出接差动放大器的二输入端,将W1电位器、r电阻直流调节平衡网络接入电桥中(W1电位器二固定端接电桥的±4V电源端、W1的活动端r电阻接电桥的输出端),如图1—8示意接线(粗细曲线为连接线)。
电阻应变式传感器的应用
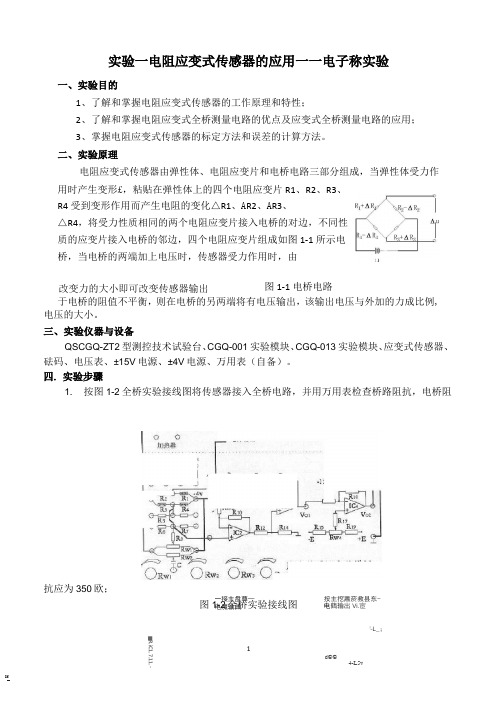
改变力的大小即可改变传感器输出图1-1电桥电路 IRJ3 *IXnxB.S应支传感器实验模枫liw实验一电阻应变式传感器的应用一一电子称实验一、实验目的1、了解和掌握电阻应变式传感器的工作原理和特性;2、了解和掌握电阻应变式全桥测量电路的优点及应变式全桥测量电路的应用;3、掌握电阻应变式传感器的标定方法和误差的计算方法。
二、实验原理电阻应变式传感器由弹性体、电阻应变片和电桥电路三部分组成,当弹性体受力作 用时产生变形£,粘贴在弹性体上的四个电阻应变片R1、R2、R3、R4受到变形作用而产生电阻的变化△R1、A R2、A R3、△R4,将受力性质相同的两个电阻应变片接入电桥的对边,不同性质的应变片接入电桥的邻边,四个电阻应变片组成如图1-1所示电桥,当电桥的两端加上电压时,传感器受力作用时,由于电桥的阻值不平衡,则在电桥的另两端将有电压输出,该输出电压与外加的力成比例, 电压的大小。
三、实验仪器与设备QSCGQ-ZT2型测控技术试验台、CGQ-001实验模块、CGQ-013实验模块、应变式传感器、砝码、电压表、±15V 电源、±4V 电源、万用表(自备)。
四. 实验步骤1. 按图1-2全桥实验接线图将传感器接入全桥电路,并用万用表检查桥路阻抗,电桥阻抗应为350欧;图1-2全桥实验接线图 一接主盘尊—电魔输曲按主挖蕭菸救县东-电鶴输出Vi.宦!-L_;■2、从QSCGQ-ZT2型测控技术试验台中可调电源部分调整±4V电源接入CGQ-013实验模块上;3、从QSCGQ-ZT2型测控技术试验台中引入电源±15V接CGQ-001实验模块,检查无误后,合上主控箱电源开关。
4、将CGQ-001实验模块输出端V02与主控箱面板上的电压表电压输入端Vi相连,电压表的切换开关打到2V档;5、放大器调零:将CGQ-001实验模块中调节增益电位器Rw1顺时针调节到中间位置,然后进行差动放大器调零,使电压表显示0.00V。
检测实验一实验报告

实验一传感器实验班号:机械91班学号:姓名:戴振亚同组同学:裴文斐、林奕峰、冯荣宇1、电阻应变片传感器一、实验目的(1) 了解金属箔式应变片的应变效应,单臂电桥工作原理和性能。
(2) 了解半桥的工作原理,比较半桥与单臂电桥的不同性能、了解其特点(3) 了解全桥测量电路的原理及优点。
(4) 了解应变直流全桥的应用及电路的标定二、实验数据三、实验结果与分析1、性能曲线A、单臂电桥性能实验由实验数据记录可以计算出的系统的灵敏度S=ΔU/ΔW=0.21(mV/g),所以运用直线拟合可以得到特性曲线如下图所示。
B、半桥性能实验由实验记录的数据我们可以得到半桥系统的灵敏度为S=ΔU/ΔW=0.41(mV/g),所以我们可以运用直线拟合实验数据得到性能曲线如下图所示。
C、全桥性能实验由实验记录的数据我们可以得到全桥系统的灵敏度为S=ΔU/ΔW=0.78(mV/g),所以我们可以运用直线拟合实验数据得到性能曲线如下图所示。
检测实验报告戴振亚D、电子称实验由实验记录的数据我们可以得到全桥系统的灵敏度为S=ΔU/ΔW=-1(mV/g),所以我们可以运用直线拟合实验数据得到性能曲线如下图所示。
2、分析a、从理论上分析产生非线性误差的原因由实验原理我们可以知道,运用应变片来测量,主要是通过外界条件的变化来引起应变片上的应变,从而可以引起电阻的变化,而电阻的变化则可以通过电压来测得。
而实际中,电阻的变化与应变片的应变的变化不是成正比的,而是存在着“压阻效应”,从而在实验的测量中必然会引起非线性误差。
b、分析为什么半桥的输出灵敏度比单臂时高了一倍,而且非线性误差也得到改善。
首先我们由原理分析可以知道,单臂电桥的灵敏度为e0=(ΔR/4R0)*e x,而半桥的灵敏度为e0=(ΔR/2R0)*e x,所以可以知道半桥的灵敏度是单臂时的两倍,而由实验数据中我们也可以看出,而由于半桥选用的是同侧的电阻,为相邻两桥臂,所以可以知道e0=(ΔR1/R0-ΔR2/R0)*e x/4,而ΔR1、ΔR2的符号是相反的,同时由于是同时作用,减号也可以将温度等其他因素引起的电阻变化的误差减去而使得非线性误差得到改善。
传感器实验报告
传感器实验报告传感器实验实验⼀、电阻应变⽚传感器1.实验⽬的(1) 了解⾦属箔式应变⽚的应变效应,单臂电桥⼯作原理和性能。
(2) 了解半桥的⼯作原理,⽐较半桥与单臂电桥的不同性能、了解其特点(3) 了解全桥测量电路的原理及优点。
(4) 了解应变直流全桥的应⽤及电路的标定。
2.实验数据整理与分析由以上两趋势图可以看出,其中⼀个20.9997R =,另⼀个20.9999R =,两个的线性都较好。
其中产⽣⾮线性的原因主要有:(1)04x R e e R R ?=+?,0e 和R ?并不成严格的线性关系,只有当0R R ?<<才有04x Re e R=,所以理论上并不是绝对线性的,总会出现⼀些⾮线性。
(2)应变⽚与材料的性能有关,这也可能产⽣⾮线性。
(3)实验中外界因素的影响,包括外界温度之类的影响。
为什么半桥的输出灵敏度⽐单臂时⾼出⼀倍,且⾮线性误差也得到改善?答:单臂:04x R e e R ?=半桥:1201()2x R R e e R R ??=-灵敏度公式:U S W=;所以半桥测量时是单臂测量的灵敏度的两倍。
0k 受电阻变化影响变得很⼩改善了⾮线性误差。
3.思考题a .半桥测量时两⽚不同受⼒状态的电阻应变⽚接⼊电桥时,应放在:(1)对边(2)邻边。
解:邻边 b .桥路(差动电桥)测量时存在⾮线性误差,是因为:(1)电桥测量原理上存在⾮线性(2)应变⽚应变效应是⾮线性的(3)调零值不是真正为零。
解:(1)(2)(3)。
c .全桥测量中,当两组对边(R1、R3为对边)值R 相同时,即R1=R3,R2=R4,⽽R1≠R2时,是否可以组成全桥:(1)可以(2)不可以。
解:(1)d .某⼯程技术⼈员在进⾏材料拉⼒测试时在棒材上贴了两组应变⽚,如何利⽤这四⽚电阻应变⽚组成电桥,是否需要外加电阻。
解:可组成全路电桥实验⼆差动变压器1.实验⽬的(1)了解差动变压器的⼯作原理和特性(2)了解三段式差动变压器的结构(3)了解差动变压零点残余电压组成及其补偿⽅法(4)了解激励频率低差动变压器输出的影响2.实验数据整理与分析实验A中产⽣⾮线性误差的原因:(1)存在零点残余电压(2)零点附近波动较⼤(3)读数时的⼈为误差分析产⽣零点残余电压的原因,对差动变压器的性能有哪些不利影响。
应变测量_实验报告
一、实验目的1. 理解应变测量的基本原理和实验方法。
2. 掌握电阻应变片的工作原理及其在应变测量中的应用。
3. 学习电桥电路在应变测量中的作用和调试方法。
4. 培养实验操作能力和数据分析能力。
二、实验原理应变测量是研究材料在受力后产生的变形程度的重要方法。
本实验主要利用电阻应变片和电桥电路进行应变测量。
电阻应变片是一种将机械应变转换为电阻变化的传感器,其基本原理是电阻应变效应。
当电阻应变片受到拉伸或压缩时,其电阻值会发生变化,从而将应变信号转换为电阻信号。
电桥电路是一种常用的测量电路,其基本原理是将电阻应变片接入电桥电路中,通过测量电桥的输出电压来反映应变片电阻的变化。
本实验采用半桥接法,即只将一个应变片接入电桥电路中。
三、实验仪器1. 电阻应变片:将应变片粘贴在被测物体表面,用于感受物体的应变。
2. 电桥电路:由四个电阻组成,用于将应变片的电阻变化转换为电压信号。
3. 数字多用表:用于测量电桥的输出电压。
4. 拉伸装置:用于施加拉伸力,使被测物体产生应变。
5. 计算机及数据采集软件:用于实时采集和记录实验数据。
四、实验步骤1. 将电阻应变片粘贴在被测物体表面,确保粘贴牢固且无气泡。
2. 将电阻应变片接入电桥电路中,采用半桥接法。
3. 连接好电桥电路,并连接数字多用表。
4. 打开计算机,启动数据采集软件,设置采样频率和采集时间。
5. 在拉伸装置上施加拉伸力,使被测物体产生应变。
6. 观察数字多用表的读数,记录电桥的输出电压。
7. 改变拉伸力的大小,重复步骤5和6,记录不同拉伸力下的电桥输出电压。
8. 利用数据采集软件分析实验数据,绘制应变-电压曲线。
五、实验结果与分析1. 实验结果如图所示,显示了不同拉伸力下电桥的输出电压。
2. 根据实验数据,绘制应变-电压曲线,分析应变与电压之间的关系。
3. 通过比较不同拉伸力下的应变-电压曲线,可以发现应变与电压之间存在线性关系。
六、实验结论1. 电阻应变片能够有效地将应变转换为电阻信号,实现应变测量。
传感器实验报告sc
实验一:金属箔式应变片单臂电桥性能实验一、实验目的:了解金属箔式应变片的应变效应,单臂电桥工作原理和性能。
二、基本原理:电阻丝在外力作用下发生机械变形时,其电阻值发生变化,这就是电阻应变效应,描述电阻应变效应的关系式为:ΔR/R=Kε式中ΔR/R为电阻丝的电阻相对变化值,K为应变灵敏系数,ε=Δl/l为电阻丝长度相对变化。
金属箔式应变片是通过光刻、腐蚀等工艺制成的应变敏感元件,用它来转换被测部位的受力大小及状态,通过电桥原理完成电阻到电压的比例变化,输出电压U0=EKε(E为供桥电压),对单臂电桥而言,电桥输出电压,U01=EKε/4。
(E为供桥电压)。
三、器件与单元:应变式传感器实验模板、应变式传感器、砝码(每只约20g)、数显表、±15V电源、±4V电源、万用表(自备)。
四、实验步骤:实验(一)1、根据图(1-1),应变式传感器已装于应变传感器模板上。
传感器中各应变片已接入模板左上方的R1、R2、R3、R4标志端。
加热丝也接于模板上,可用万用表进行测量判别,R1=R2=R3=R4=350Ω,加热丝阻值约为50Ω左右。
图1-1 应变式传感器安装示意图2、实验模板差动放大器调零,方法为:①接入模板电源±15V(从主控箱引入),检查无误后合上主控箱电源开关,将实验模板增益调节电位器Rw3顺时针调节到大致中间位置,②将差放的正、负输入端与地短接,输出端与主控箱面板上数显电压表输入端Vi相连,调节实验模板上调零电位器RW4,使数显表显示为零(数显表的切换开关打到2V档),完毕关闭主控箱电源。
3、参考图(1-2)接入传感器,将应变式传感器的其中一个应变片R1(即模板左上方的R1)接入电桥作为一个桥臂,它与R5、R6、R7接成直流电桥(R5、R6、R7在模块内已连接好),接好电桥调零电位器Rw1,接上桥路电源±4V(从主控箱引入),检查接线无误后,合上主控箱电源开关,先粗调节Rw1,再细调RW4使数显表显示为零。
工程测试技术实验报告
姓名:学号:班级:成绩:实验一 电阻式传感器的单臂电桥性能实验一、实验目的1、了解电阻应变式传感器的基本结构与使用方法。
2、掌握电阻应变式传感器放大电路的调试方法。
3、掌握单臂电桥电路的工作原理和性能。
二、实验所用单元电阻应变式传感器、调零电桥、差动放大器板、直流稳压电源、数字电压表、位移台架。
三、实验原理及电路1、电阻丝在外力作用下发生机械变形时,其阻值发生变化,这就是电阻应变效应,其关系为:ΔR/ R =K ε,ΔR 为电阻丝变化值,K 为应变灵敏系数,ε为电阻丝长度的相对变化量ΔL/ L 。
通过测量电路将电阻变化转换为电流或电压输出。
2、电阻应变式传感如图1-1所示。
传感器的主要部分是下、下两个悬臂梁,四个电阻应变片贴在梁的根部,可组成单臂、半桥与全桥电路,最大测量范围为±3mm 。
1342+5VR RR5R1─外壳 2─电阻应变片 3─测杆 4─等截面悬臂梁 5─面板接线图图1-1 电阻应变式传感器3、电阻应变式传感的单臂电桥电路如图1-2所示,图中R 1、R 2、R 3为固定,R 为电阻应变片,输出电压U O =EK ε,E 为电桥转换系数。
+5V R 2rR 1R R 1R 2R 4RP 2OP07R 3R 4RP 1R 5+15V-15V 调零电桥电 阻传感器差动放大器4321876RPR 3VA DB CE 图1-2 电阻式传感器单臂电桥实验电路图四、实验步骤1、固定好位移台架,将电阻应变式传感器置于位移台架上,调节测微器使其指示15mm 左右。
将测微器装入位移台架上部的开口处,旋转测微器测杆使其与电阻应变式传感器的测杆适度旋紧,然后调节两个滚花螺母使电阻式应变传感器上的两个悬梁处于水平状态,两个滚花螺母固定在开口处上下两侧。
2、将放大器放大倍数电位器RP 1旋钮(实验台为增益旋钮)逆时针旋到终端位置。
3、用导线将差动放大器的正负输入端连接,再将其输出端接到数字电压表的输入端;按下面板上电压量程转换开关的20V 档按键(实验台为将电压量程拨到20V 档);接通电源开关,旋动放大器的调零电位器RP 2旋钮,使电压表指示向零趋近,然后换到2V 量程,旋动调零电位器RP 2旋钮使电压表指示为零;此后调零电位器RP 2旋钮不再调节,根据实验适当调节增益电位器RP 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 1 - 大连理工大学 大 学 物 理 实 验 报 告
院(系) 材料学院 专业 材料物理 班级 0705 姓 名 童凌炜 学号 200767025 实验台号 实验时间 2009 年 03 月 06 日,第 二 周,星期 五 第 5-6 节
实验名称 电阻应变式传感器 教师评语
实验目的与要求: 1. 学习电阻应变式传感器的基本原理、 结构、 特性和使用方法 2. 测量比较几种应变式转换电路的输出特性和灵敏度 3. 了解温度变化对应变测试系统的影响和温度补偿方法
主要仪器设备: CSY10A型传感器系统实验仪
实验原理和内容: 1. 应变效应 导体或半导体在外力的作用下发生机械变形时, 其阻值也会发生相应的变化, 成为应变效应。 电阻应变片的工作原理即是基于这种效应, 将本身受力形变时发生的阻值变化通过测量电路转换为可使用的电压变化等以提供相关力的大小。 金属丝的电阻应变量可由以下算式表达: 金属丝的原始电阻值为SLR, 收到轴向拉力时, 发生电阻值变化R, 变化比例的表达式为:
SSLLRR
, 根据金属丝在力学和材料学上的相关性质, 在弹性范围内可以对公式进
行改写, 得到LLkLLLLRR)21(, 其中系数k称为电阻应变片的灵敏系数, 表示单位应变量引起的电阻值变化, 它与金属丝的几何尺寸变化和本身的材料特性有关; 一般半
成 绩 教师签字 - 2 - 导体的灵敏系数要远大于金属的灵敏系数。 (由于受力会影响到半导体内部的载流子运动, 固可以非常灵敏地反映细微的变化)
2. 电阻式应变传感器的测量电路 转换电路的作用是将电阻变化转换成电压或电流输出, 电阻应变式传感器中常用的是桥式电路, 本实验使用直流电桥。 驳接阻抗极高的仪器时, 认为电桥的输出端断路, 只输出电压信号; 根据电桥的平衡原理, 只有当电桥上的应变电阻发生阻值变化时, 电压信号即发生变化; 电桥的灵敏度定义为
RRVkv/ 根据电阻变化输入电桥的方法不同, 可以分为单臂、 半桥和全桥输入三种方式:
2.1 单臂电桥 只接入一个应变电阻片, 其余为固定电阻。 设电桥的桥臂比为nRRRR2314, 根据电桥的工作
原理, 并忽略一些极小的无影响的量, 可以得到输出电压的表达式为11)1(2RRnnUV, 同
时得到单臂电桥灵敏度表达式2)1(/nnURRVkv 单臂电桥的实际输出电压与电阻变化的关系是非线性的, 存在非线性误差, 故不常使用。
2.2 半桥 如图, 接入两个应变电阻和固定电阻, 设初始状态为R1=R2=R3=R4=R, ΔR1=ΔR2=ΔR, 可以得到电压表达式URRV21, 半桥灵敏度表达式Ukv21, 可见输出电压与电阻的变化严格呈线性关系, 不存在线性误差, 灵敏度比单臂电桥提高了一倍。
2.3 全桥 全部电阻都使用应变电阻, 且相邻的两个臂的受力方向相反, 根据电桥性质可以得到电压及灵敏 - 3 -
度的表达式URRV, URRVS/, 可见差动电桥的灵敏度比单臂电桥提高了4倍, 故广泛被使用。 补偿片的方法消除温度带来的漂移误差: 在单臂电桥中, 将与工作电阻同侧的固定电阻更换成相同受力方向的补偿片, 且原始电阻值相等; 这样在实际使用中, 由于温度造成的电阻值变化被抵消, 且补偿片不受力, 故可以消除电压的漂移输出。
步骤与操作方法: 1. 箔式单臂电桥的性能 1.1 差动放大器调零, 打开所用单元的电源开关, 差放器增益置于100倍, 并进行相关的其他调零处置。之后关闭电源 1.2 按照右侧的电路图连接实验所需的元件, 组成箔式单臂电桥电路。 1.3 调节悬臂梁头部铁心吸合的测微头, 使应变梁处以基本水平状态。 1.4 确定连线无误以后, 启动仪器电源并预热数分钟; 调整电桥Wd电位器, 使测试系统的输出为零。 1.5 旋动测微头, 带动悬臂梁分别向上和向下运动各5mm, 其中测微头每移动0.5mm记录一次差动放大器输出的电压值; 然后画出x-V曲线, 并计算桥路的灵敏度kv=ΔV/Δx
2. 箔式单臂、 半桥、 全桥电路的性能比较 基本操作过程与实验1相同, 其中连接电路部分分别使用上下梁的两个应变片, 以构成半桥; 或者全部使用应变片以构成全桥。 并进行实验, 记录数据。 在同一坐标上画出三种桥路的x-V曲线, 并进行灵敏度的比较。
3. 箔式应变片的温度效应及应变电路的温度补偿 3.1 参照实验1的步骤, 将差动器的部件调零 3.2 参照实验1的电路连接所用的元件, 并将差分放大器的输出端接毫伏表, 将P-N结温度传感器接入传感端, Vt接数字电压表。 数字电压表置于2V档, 显示环境的绝对温度。 3.3 开启仪器的电源并预热数分钟。 调整电桥的Wd电位器, 使测试系统的输出为零, 并记录此 - 4 -
时的温度T。 3.4 开启加热器电源, 观察输出电压随温度上升所发生的变化, 并记录多组数据, 计算温度漂移ΔV/ΔT。 3.5 将R4换成与应变片处于同一个应变梁上的补偿片, 重复以上实验数据, 计算新的温度漂移并与之前的进行比较。
4. 半导体单臂和半桥电路性能的比较 4.1 调零仪器, 并按照电路图连接电路, R’是半导体应变片, R’’是电桥上的固定电阻, 直流激励电源为±2V; 开启电源后预热数分钟。 4.2 调节应变梁处于基本水平状态, 调整电桥Wd电位器, 使测试系统输出为零。 4.3 旋动测微头, 以向上向下各5mm为限, 0.5mm为间隔记录数据x,V, 并作x-V曲线, 计算灵敏度 4.4 重新调整应变梁处于基本水平状态, 并重新调整输出为零。 用P-N结温度传感器测出系统的温漂。 4.5 按照电路图连接半导体半桥双臂电路, 半导体应变片处于同一桥侧, 重复以上实验步骤, 比较两种半导体桥路的灵敏度和温度漂移。
5. 相关注意事项 5.1 在进行先向上再向下的位移操作中, 易产生零点漂移; 计算式可以将正负两个方向的Δx分开计算灵敏度以后再取平均得到。 - 5 -
数据记录与处理: 单臂电桥数据 起始位置 X0=10.950mm ΔX1(mm) 0 -0.5 -1.0 -1.5 -2.0 -2.5 -3.0 -3.5 -4.0 -4.5 -5.0 U(V) 0.000 -0.007 -0.011 -0.014 -0.022 -0.029 -0.032 -0.038 -0.043 -0.049 -0.053 ΔX2(mm) 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 U(V) -0.016 -0.010 -0.009 -0.004 -0.000 0.003 0.009 0.013 0.018 0.023 0.028
半桥数据 起始位置 X0=10.950mm ΔX1(mm) 0 -0.5 -1.0 -1.5 -2.0 -2.5 -3.0 -3.5 -4.0 -4.5 -5.0 U(V) 0.000 -0.008 -0.016 -0.030 -0.042 -0.050 -0.062 -0.072 -0.082 -0.095 -0.102 ΔX2(mm) 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 U(V) 0.003 0.016 0.026 0.036 0.049 0.060 0.074 0.091 0.102 0.116 0.125 - 6 -
电压-位移关系
-0.15-0.1-0.0500.050.10.15
-6-4-20246X(mm)
U(V)单臂电桥电压(V)半桥电压(V) - 7 -
结果与分析: 将单臂电桥和半桥的数据绘制成坐标散点图, 并且拟合出直线, 如上图所示: 根据图中所添加的拟合直线, 在直线上取样计算斜率, 可以得到以下四个斜率, 表现为各自的灵敏度:
使用MLS, 测量电路的灵敏度kv=ΔV/Δx=2)()(xxyxxiii, 负向形变, 单臂电桥 ΔX1(mm) 0 -0.5 -1 -1.5 -2 -2.5 -3 -3.5 -4 -4.5 -5
U(V) 0 -0.007 -0.011 -0.014 -0.022 -0.029 -0.032 -0.038 -0.043 -0.049 -0.053
Xavg= -2.5 Xi-Xavg= 2.5 2 1.5 1 0.5 0 -0.5 -1 -1.5 -2 -2.5 Δxi*yi= 0 -0.014 -0.0165 -0.014 -0.011 0 0.016 0.038 0.0645 0.098 0.1325 SUMΔxy 0.2935 (Xi-Xavg)^2 6.25 4 2.25 1 0.25 0 0.25 1 2.25 4 6.25 SUMΔx^2 27.5 k= 0.0106
正向形变, 单臂电桥 ΔX2(mm) 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
U(V) -0.016 -0.01 -0.009 -0.004 0 0.003 0.009 0.013 0.018 0.023 0.028
Xavg= 2.5 Xi-Xavg= -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 Δxi*yi= 0.04 0.02 0.0135 0.004 0 0 0.0045 0.013 0.027 0.046 0.07 SUMΔxy 0.238 (Xi-Xavg)^2 6.25 4 2.25 1 0.25 0 0.25 1 2.25 4 6.25 SUMΔx^2 27.5 k= 0.00865
负向形变, 半桥 ΔX1(mm) 0 -0.5 -1 -1.5 -2 -2.5 -3 -3.5 -4 -4.5 -5
U(V) 0 -0.008 -0.016 -0.03 -0.042 -0.05 -0.062 -0.072 -0.082 -0.095 -0.102
Xavg= -2.5 Xi-Xavg= 2.5 2 1.5 1 0.5 0 -0.5 -1 -1.5 -2 -2.5 Δxi*yi= 0 -0.016 -0.024 -0.03 -0.021 0 0.031 0.072 0.123 0.19 0.255 SUMΔxy 0.58 (Xi-Xavg)^2 6.25 4 2.25 1 0.25 0 0.25 1 2.25 4 6.25 SUMΔx^2 27.5 k= 0.0210
