山东省龙口市兰高镇中考数学模拟试题九
山东省烟台市龙口市兰高学校九年级(上)第二次段考数学试卷(五四学制)

山东省烟台市龙口市兰高学校九年级(上)第二次段考数学试卷(五四学制)一、选择题(共13小题,每小题3分,满分39分)1.(3分)当你乘车沿一条平坦的大道向前行驶时,你会发现,前方那些高一些的建筑物好像“沉”到了位于它们前面那些矮一些的建筑物后面去了,这是因为()A.汽车开的很快B.盲区减小C.盲区增大D.无法确定2.(3分)若⊙O的直径为10,圆心O为坐标原点,点P的坐标为(4,3),则点P与⊙O 的位置关系是()A.点P在⊙O上B.点P在⊙O内C.点P在⊙O外D.以上都有可能3.(3分)下列等式:①sin30°+sin30°=sin60°;②sin25°=cos65°;③cos45°=sin45°;④cos62°=sin18°.其中正确的个数是()A.1个B.2个C.3个D.4个4.(3分)如图,抛物线的函数表达式是()A.y=x2﹣x+2B.y=x2+x+2C.y=﹣x2﹣x+2D.y=﹣x2+x+2 5.(3分)在一个晴朗的上午,小丽拿着一块矩形木板在阳光下做投影实验,矩形木板在地面上形成的投影不可能是()A.B.C.D.6.(3分)如图,抛物线y=x2﹣2x与直线y=3相交于点A、B,P是x轴上一点,若P A+PB 最小,则点P的坐标为()A.(﹣l,0)B.(0,0)C.(1,0)D.(3,0)7.(3分)在△ABC中,∠C=90°,∠BAC=30°,AD是中线,则tan∠CDA的值为()A.B.C.D.8.(3分)如图是一个水管的三叉接头,它的左视图是()A.B.C.D.9.(3分)一个长方形的周长为8cm,一边长是xcm,则这个长方形的面积y与边长x的函数关系用图象表示大致为()A.B.C.D.10.(3分)如图,在矩形ABCD中,AB=4,DE⊥AC,垂足为E,设∠ADE=α,且,则AD的长为()A.B.C.5D.11.(3分)如图,△ABC内接于⊙O,⊙O的半径为1,BC=,则∠A的度数为()A.30°B.45°C.60°D.75°12.(3分)如图,开口向下的抛物线y=ax2+bx+c交y轴的正半轴于点A,对称轴是直线x =1,则下列结论正确的是()A.a+2b+4c<0B.c<0C.2a+b﹣c=0D.b=﹣2a13.(3分)二次函数y=﹣ax2+a与反比例函数的图象大致是()A.B.C.D.二、填空题(共12小题,每小题3分,满分36分)14.(3分)已知△ABC中,∠C=90°,AB=13,AC=5,则tan A=.15.(3分)小华在距离路灯6米的地方,发现自己在地面上的影长是2米,若小华的身高为1.6米,那么路灯离地面的高度是米.16.(3分)抛物线y=2x2不动,把x轴、y轴分别向上、向左平移3个单位,则在新坐标系下,此抛物线的解析式为(可不化成一般形式).17.(3分)如图,在半径为6cm的⊙O中,弦AB⊥CD,垂足为E,若CE=3cm,DE=7cm,则AB=cm.18.(3分)如图,正方体的棱长为1米,平行光线垂直于AB,且与BC成45°角,则图中阴影部分(四边形EFGH)的面积为平方米.19.(3分)如图,已知△ABC内接于⊙O,∠C=∠OAB,OA=4cm,则AB=cm.20.(3分)一张桌子上重叠摆放了若干枚面值1元的硬币,它的三种视图如下图所示,则桌子上共有1元硬币枚.21.(3分)如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为.22.(3分)一船向东航行,上午8时到达B处,看到有一灯塔在它的南偏东60°距离为72海里的A处,上午10时到达C处,看到灯塔在它的正南方向,则这艘船航行的速度为.23.(3分)在距离地面2m高的某处把一物体以初速度v0(m/s)竖直向上抛物出,在不计空气阻力的情况下,其上升高度s(m)与抛出时间t(s)满足:s=v0t﹣gt2(其中g 是常数,通常取10m/s2).若v0=10m/s,则该物体在运动过程中最高点距地面m.24.(3分)已知二次函数y=﹣2x2+2kx﹣3的顶点在x轴的负半轴上,则k的值等于.25.(3分)计算:sin30°+cos45°﹣2tan30°﹣tan60°.三、解答题(共5小题,满分0分)26.如图,小明家(点A处)和公路(L)之间竖立着一块35米长且平行于公路的巨型广告牌(DE),广告牌挡住了小明的视线(1)请在图中画出视点A的盲区,并将盲区的那段公路记为BC;(2)若一辆以60公里/小时匀速行驶的汽车经过公路BC段的时间为3秒,已知广告牌和公路的距离为40米,求小明家到公路的距离(精确到1米)27.如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:≈1.73,≈1.41).28.某商店以每件20元的价格购进一批商品,如果以每件30元销售,那么半月内可售出400件.根据销售经验,销售单价每提高1元,半月内的销售量相应减少20件如何提高销售单价,才能在半月内获得最大利润?最大利润是多少?29.已知二次函数y=ax2+bx+c的图象如图所示,x=是该抛物线的对称轴,根据图中所提供的信息,请写出有关a,b,c的四条结论,并简要说明理由.30.某校数学研究小组在研究有关二次函数及其图象性质时,发现了一个重要结论:抛物线y=ax2+2x+3(a≠0),当实数a变化时,它们的顶点都在某条直线上.(1)请你协助探求出这条直线的表达式;(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它吗?并说明理由.山东省烟台市龙口市兰高学校九年级(上)第二次段考数学试卷(五四学制)参考答案一、选择题(共13小题,每小题3分,满分39分)1.C;2.A;3.B;4.D;5.A;6.C;7.B;8.A;9.A;10.B;11.C;12.D;13.A;二、填空题(共12小题,每小题3分,满分36分)14.;15.6.4;16.y=2(x﹣3)2﹣3;17.8;18.1;19.;20.11;21.;22.18海里/时;23.7;24.﹣;25.;三、解答题(共5小题,满分0分)26.;27.;28.;29.;30.;。
山东省龙口市兰高镇中考数学模拟试题八-人教版初中九年级全册数学试题
word 1 / 13 2018年中考数学模拟试卷八 一、选择题 1、5的相反数是( ) A. B. ﹣ C. 5 D. ﹣5 2、下列四个图案中,属于中心对称图形的是( ) A. B. C. D.
3、下列计算正确的是( ) A. a2•a=a2 B. a2÷a=a C. a2+a=a3 D. a2﹣a=a 4、轨道交通1号线、2号线建设总投资253.7亿元,其中253.7亿用科学记数法表示为( ) A. 253.7×108 B. 25.37×109 C. 2.537×1010 D. 2.537×1011 5.一个几何体的三视图如图,那么这个几何体是( )
6.一个布袋里装有5个球,其中3个红球,2个白球,每个球除颜色外其他完全相同,从中任意摸出一个球,是红球的概率是( ) A. B. C. D.
7.在式子,,,中,x可以取2和3的是( ) A. B. C. D. 8.如图,在平面直角坐标系中,反比例函数y1=的图象与一次函数y2=kx=b的图象交于A、B两点.若y1<y2,则x的取值X围是( )
A. 1<x<3 B. x<0或1<x<3 C. 0<x<1 D. x>3或0<x<1
A. B. C. D. 学校______________ 某某_______
______ 学科______________ 考号__________
密 封 线 word
2 / 13 9.把代数式2x2﹣18分解因式,结果正确的是( ) A. 2(x2﹣9) B. 2(x﹣3)2 C. 2(x+3)(x﹣3) D. 2(x+9)(x﹣9) 10、已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论: ①abc<0;②b2﹣4ac>0;③3a+c>0;④(a+c)2<b2, 其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个 11.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )
山东省烟台市龙口市兰高学校九年级(上)第一次段考数学试卷(五四学制)

参考答案
一、选择题(共 8 小题,每小题 3 分,满分 24 分) 1.D; 2.A; 3.B; 4.B; 5.A; 6.C; 7.B; 8.D; 二、填空题(每小题 3 分,共 18 分) 9. ; 10.25; 11.30; 12. ; 13.二; 14.>;
三、综合题
15.
; 16.
; 17.
二、填空题(每小题 3 分,共 18 分)
9.(3 分)若△ABC 三边长度之比为 a:b:c=3:4:5,则 sinB=
.
10.(3 分)某人沿着坡度 i=1: 的山坡走了 50 米,则他离地面
米高.
11.(3 分)等腰三角形的周长为 2+ ,腰长为 1,则底角等于
度.
12.(3 分)函数 y=(x﹣2)(3﹣x)取得最大值时,x=
A.不变
B.扩大 5 倍
C.缩小 5 倍
D.不能确定
3.(3 分)在△ABC 中,若|sinA﹣1|+( ﹣cosB)2=0,则∠C=( )
A.75°
B.60°
C.45°
D.30°
4.(3 分)设 α 是锐角,则 sinα+cosα 的值一定( )
A.小于 1
B.大于 1
C.等于 1
山东省龙口市兰高镇中考数学专题复习 一次函数(正比例
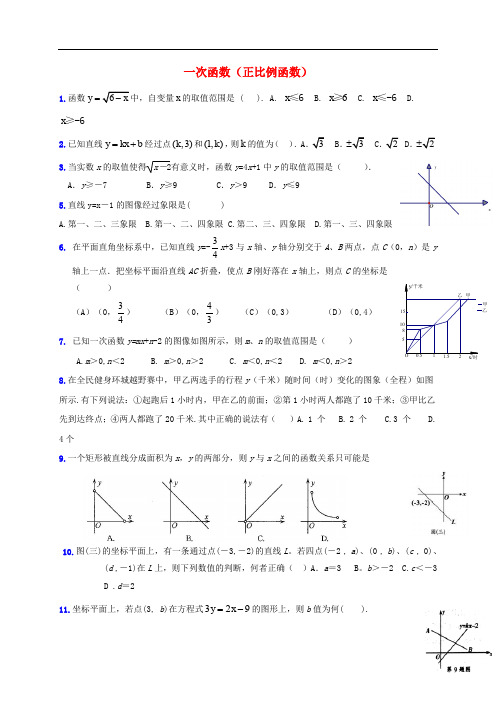
一次函数(正比例函数)1.函数y =x 的取值范围是 ( ). A. x ≤6 B. 6x ≥ C. x ≤-6 D.x ≥-62.已知直线y kx b =+经过点(,3)k 和(1,)k ,则k 的值为( ). AB..3.当实数x 的取值使得x -2有意义时,函数y =4x +1中y 的取值范围是( ).A .y ≥-7B .y ≥9C .y >9D .y ≤95.直线y=x -1的图像经过象限是( )A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象限6. 在平面直角坐标系中,已知直线y =-43x +3与x 轴、y 轴分别交于A 、B 两点,点C (0,n )是y 轴上一点.把坐标平面沿直线AC 折叠,使点B 刚好落在x 轴上,则点C 的坐标是( ) (A )(0,43) (B )(0,34) (C )(0,3) (D )(0,4) 7. 已知一次函数y=mx +n -2的图像如图所示,则m 、n 的取值范围是( ) A.m >0,n <2 B. m >0,n >2 C. m <0,n <2 D. m <0,n >2 8.在全民健身环城越野赛中,甲乙两选手的行程y (千米)随时间(时)变化的图象(全程)如图所示.有下列说法:①起跑后1小时内,甲在乙的前面;②第1小时两人都跑了10千米;③甲比乙先到达终点;④两人都跑了20千米.其中正确的说法有( )A. 1 个 B. 2 个 C.3 个 D.4个9.一个矩形被直线分成面积为x ,y 的两部分,则y 与x 之间的函数关系只可能是10.图(三)的坐标平面上,有一条通过点(-3,-2)的直线L 。
若四点(-2 , a )、(0 , b )、(c , 0)、(d ,-1)在L 上,则下列数值的判断,何者正确( )A .a =3 B 。
b >-2 C.c <-3D .d =211.坐标平面上,若点(3, b )在方程式923-=x y 的图形上,则b 值为何( ).A .-1B . 2C .3D . 912.如图,在平面直角坐标系中,线段AB 的端点坐标为A (-2,4),B (4,2),直线y=kx-2与线段AB 有交点,则k 的值不可能是( )A.-5 B.-2 C.3 D. 514.如图,已知A 点坐标为(5,0),直线y=x +b (b>0)与y 轴交于点B ,连接AB ,∠α=75°,则b 的值为 A.3 B.335 C.4 D.43515.如图所示,函数x y =1和34312+=x y 的图象相交于(-1,1),(2,2)两点. 当21y y >时,x 的取值范围是( ) A .x <-1 B .—1<x <2 C .x >2 D . x <-1或x >16.在平面直角坐标系中,把直线y=x 向左平移一个单位长度后,其直线解析式为( ). A .y=x+1 B.y=x-1 C.y=x D. y=x-2 18. 已知一次函数y ax b =+的图象过第一、二、四象限,且与x 轴交于点(2,0),则关于x 的不等式(1)0a x b -->的解集为( ). A .x<-1 B .x> -1 C . x>1 D .x<119.已知梯形ABCD 的四个顶点的坐标分别为A (-1,0),B (5,0),C (2,2),D (0,2),直线y=kx +2将梯形分成面积相等的两部分,则k 的值为( )A. -32 B. -92 C. -74 D. -72 20.y =中自变量x 的取值范围是( )A .x ≥-3 B .x ≥-3且1x ≠ C .1x ≠ D .3x ≠-且1x ≠ 21. 函数1--=x x y 中自变量x 的取值范围是( )A .x ≥0 B.x <0且x ≠l C.x <0 D .x ≥0且x ≠l 22.一次函数y=6x+1的图象不经过( )A .第一象限 B .第二象限 C .第三象限 D .第四象限23.如图,直线1l x ⊥轴于点(1,0),直线2l x ⊥轴于点(2,0),直线3l x ⊥轴于点(3,0),…直线n l x ⊥轴于点(,0)n .函数y x =的图象与直线1l ,2l ,3l ,…n l 分别交于点1A ,2A ,3A ,…n A ;函数2y x =的图象与直线1l ,2l ,3l ,…n l 分别交于点1B ,2B ,3B ,…n B .如果11OA B ∆的面积记作1S ,四边形1221A A B B 的面积记作2S ,四边形2332A A B B 的面积记作3S ,…四边形11n n n n A A B B --的面积记作n S ,那么2011S = .24.一次函数y =2x -1的图象经过点(a ,3),则a = .25.将完全相同的平行四边形和完全相同的菱形镶嵌成如图所示的图案。
教育最新K12山东省龙口市兰高镇九年级数学上册 第一章 反比例函数单元练习三(无答案) 鲁教版五四制
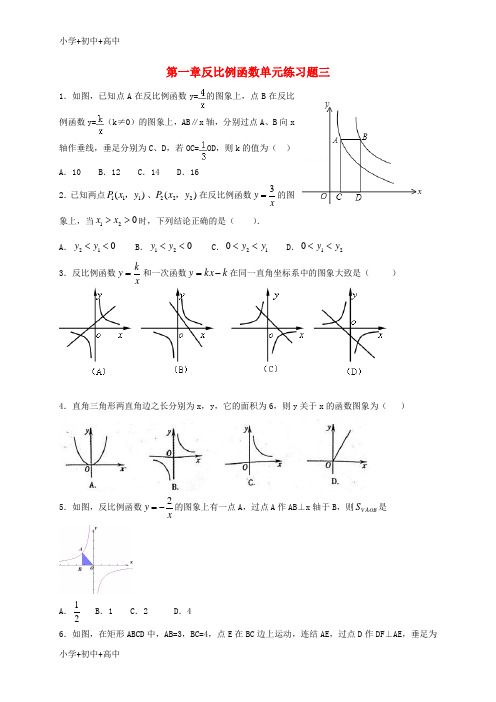
第一章反比例函数单元练习题三1.如图,已知点A 在反比例函数y=的图象上,点B 在反比例函数y=(k ≠0)的图象上,AB ∥x 轴,分别过点A 、B 向x轴作垂线,垂足分别为C 、D ,若OC=OD ,则k 的值为( )A .10B .12C .14D .162.已知两点111()P x y ,、222()P x y ,在反比例函数3y x=的图象上,当120x x >>时,下列结论正确的是( ).A .210y y <<B .120y y <<C .210y y <<D .120y y <<3.反比例函数xk y =和一次函数k kx y -=在同一直角坐标系中的图象大致是( )4.直角三角形两直角边之长分别为x ,y ,它的面积为6,则y 关于x 的函数图象为( )5.如图,反比例函数2y x=-的图象上有一点A ,过点A 作AB ⊥x 轴于B ,则AOB S V 是A .12B .1C .2D .4 6.如图,在矩形ABCD 中,AB=3,BC=4,点E 在BC 边上运动,连结AE ,过点D 作DF⊥AE,垂足为F ,设AE=x ,DF=y ,则能反映y 与x 之间函数关系的大致图象是( )A .B .C .D .7.若反比例函数图象经过点(﹣1,6),则此函数图象也经过的点是( )A .(6,1)B .(3,2)C .(2,3)D .(﹣3,2)8.如果等腰三角形的面积为10,底边长为x ,底边上的高为y ,则y 与x 的函数关系式为( )A .y=B .y=C .y=D .y=9.下列四个点,在反比例函数y=6x的图象上的是( ) A .(1,-6) B .(2,4) C .(3,-2) D .(-6,-1)10.点A ,C 是反比例函数y=(k >0)的图象上两点,AB ⊥x 轴于B ,CD ⊥x 轴于D .记Rt △AOB 和Rt △COD 的面积分别为S 1、S 2,则( )A .S 1>S 2B .S 1<S 2C .S 1=S 2D .不能确定11.我们知道,在反比例函数2y x =的图象上任取一点,过该点分别向两条坐标轴画垂线,这两条垂线与坐标轴围成的矩形面积始终是2.如果在某个函数的图象上任取一点,按同样的方式得到的矩形的周长始终是2,这个函数是 .12.已知反比例函数y =k x (k≠0)的图象经过点(3,-1),则当1<y <3时,自变量x 的取值范围是__________.13.反比例函数3k y x-=的图象,当x >0时,y 随x 的增大而增大,则k 的取值范围是 . 14.如果函数22(1)m y m x -=-是反比例函数,那么m 的值是 .15.若点A(-2,3)、B(m ,-6)都在反比例函数y =k x(k≠0)的图象上,则m 的值是________.16.如图,Rt △AOB 的一条直角边OB 在x 轴上,双曲线y=(x >0)经过斜边OA 的中点C ,与另一直角边交于点D ,若S △OCD =3,则k 的值为 .17.京沪高速公路全长约为1262km ,汽车沿京沪高速公路从上海驶往北京,汽车行驶完全程所需的时间t (h )与行驶的平均速度v (km/h )之间的函数关系式是t= .18.如图,正比例函数y=ax 的图象与反比例函数y=的图象相交于点A ,B ,若点A 的坐标为(﹣2,3),则点B 的坐标为 .19.如图, 如果函数y=-x 与y=x4的图像交于A 、B 两点, 过点A 作AC 垂直于y 轴, 垂足为点C , 则△BOC 的面积为_______.20.如图,在直角坐标系中,点 A 在y 轴正半轴上,AC ∥x 轴,点B 、C 的横坐标都是3,且BC =2,点D 在AC 上,且横坐标为1,若反比例函数y =(x >0)的图象经过点B 、D ,求k 的值.21.如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2,反比例函数y=(x>0)的图象经过OA的中点C,交AB于点D.(1)求反比例函数的关系式;(2)连接CD,求四边形CDBO的面积.22.码头工人每天往一艘轮船50吨货物,装载完毕恰好用了8天时间.(1)轮船到达目的地后开始卸货,平均卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?(2)由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?(3)若原有码头工人10名,在(2)的条件下,至少需要增加多少名工人才能完成任务?23.在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B,C两点重合),过点F的反比例函数y= (k>0)的图象与AC 边交于点E.(1)请用含k的代数式表示点E,F的坐标;(2)若△OEF的面积为9,求反比例函数的解析式.24.如图,点A(1,6)和点M(m,n)都在反比例函数y=kx(x>0)的图象上,(1)k的值为;(2)当m=3,求直线AM的解析式;(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.26.如图,在平面直角坐标系中,点A(,1)、B(2,0)、O(0,0),反比例函数y=图象经过点A.(1)求k的值;(2)将△AOB绕点O逆时针旋转60°,得到△COD,其中点A与点C对应,试判断点D是否在该反比例函数的图象上?27.如图:Rt△ACB中,∠C=90°;△ACB的边AC在x轴正半轴上,AC=2OA.已知Rt△ACB面积是4.求经过点B反比例函数的解析式.。
山东省烟台市龙口市兰高学校九年级(上)期中数学试卷(五四学制)
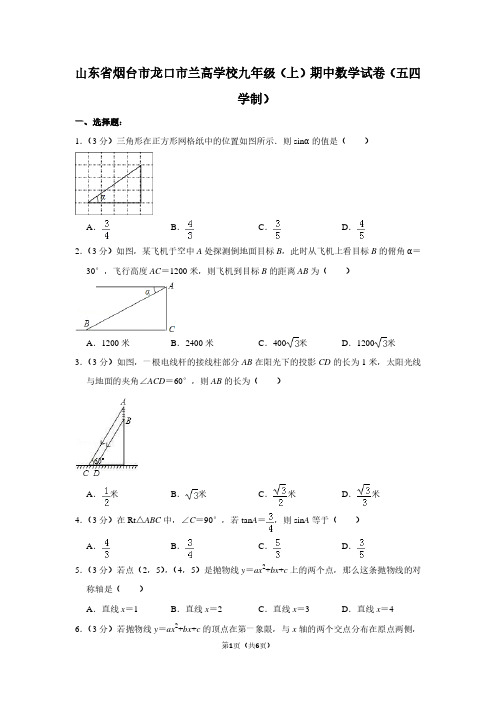
长线上的点 D′处,那么 tan∠BAD′=
.
14.(3 分)如图,在△ABC 中,∠C=90°,∠B=30°,AD 平分∠BAC,已知 AB=4 ,
那么 AD=
.
15.(3 分)顶点为(﹣2,﹣5)且过点(1,﹣14)的抛物线的解析式为
.
16.(3 分)抛物线 y=﹣2x2+4x+1 在 x 轴上截得的线段长度是
日期:2019/1/19 10:26:10; 用户:qgjyus er10 077;邮箱:q gjyus er10077.219 57750;学号 :21985083
第6页(共6页)
解析式;若不存在,请说明理由. 26.在某次数字变换游戏中,我们把整数 O,1,2.…,100 称为“旧数”,游戏的变换规
则是:将旧数先平方,再除以 100,所得到的数称为“新数”. (1)请把旧数 80 利 26 按照上述规则变换为新数; (2)经过上述规则变换后,我们发现许多旧数变小了.有人断言:“按照上述变换规则,所
.
17.(3 分)已知二次函数 y=(m﹣1)x2+2mx+3m﹣2,则当 m=
时,其最大值为 0.
18.(3 分)已知抛物线 y=ax2+2x+c 与 x 轴的交点都在原点的右侧,则点 M(a,c)在第
象限.
19.(3 分)二次函数 y=x2﹣6x+c﹣2 的顶点到 x 轴的距离是 3,则 c 的值为
24.某商人如果将进货价为 8 元的商品按每件 10 元出售,每天可销售 100 件,现采用提高 售出价,减少进货量的办法增加利润,已知这种商品每涨价 1 元其销售量就要减少 10 件, 问他将售出价(x)定为多少元时,才能使每天所赚的利润(y)最大并求出最大利润.
山东省龙口市兰高镇九年级数学上册 第一章 反比例函数单元练习二(无答案) 鲁教版五四制
第一章反比例函数单元练习题二1.已知反比例函数y A (-3,2),则k 的值为( )A . 3B . 6C . -6D . -32.当a 取何值时,反比例函数3a y x-=的图象的一个分支上满足y 随x 的增大而增大( ) A . 3a > B . 3a < C . 3a ≥ D . 3a ≤ 3.在同一直角坐标系中,一次函数y x b =+的图象与反比例函数4y x =-的图象有且只有一个交点,则b 的值为 ( )A . 4B . 2C . 4±D . 2±4.当k >0时,反比例函数y=k x和一次函数y=kx+2的图象大致是( )A .B .C .D . 5.在双曲线1k y x-=的任一支上,y 都随x 的增大而增大,则k 的值可以是( ) A . 2 B . 0 C . ﹣2 D . 1 6.如图,点P 是y kx =轴正半轴上的一个动点,过点P 作PQ ⊥4y ax =+轴交双曲线1y x =(x >0)于点Q ,连结OQ . 当点P 沿0k ≠轴的正方向运动时,Rt △QOP 的面积( ).A . 保持不变B . 逐渐减小C . 逐渐增大D . 无法确定7.若直线()110y k x k =≠和双曲线()220k y k x=≠在同一坐标系内无交点,则k 1和k 2的关系是( )A . 互为倒数B . 绝对值相等C . 符号相反D . 符号相同8.如图,△ABO 的面积为3,且AO=AB ,双曲线y=k x经过点A ,则k 的值为( )A .32B . 3C . 6D . 9 9.反比例函数y=x k 2-的图象,当x >0时,y 随x 的增大而减小,则k 的取值范围是( ) A .k <2 B .k ≤2 C .k >2 D .k ≥210.如图,两双曲线y=k x 与y=﹣3x 分别位于第一、四象限,A 是y 轴上任意一点,B 是y=﹣3x上的点,C 是y=k x 上的点,线段BC ⊥x 轴于点 D ,且4B D=3CD ,则下列说法:①双曲线y=k x在每个象限内,y 随x 的增大而减小;②若点B 的横坐标为3,则点C 的坐标为(3,﹣43);③k=4;④△ABC 的面积为定值7,正确的有( )A .B .C .D . ④11.如图,已知点A 是反比例函数2y x=-的图象上的一个动点,连接OA ,若将线段O A 绕点O 顺时针旋转90°得到线段OB ,则点B 所在图象的函数表达式为______.12.如图,▱ABCD 放置在平面直角坐标系中,已知点A (2,0),B (6,0),D (0,3).反比例函数的图象经过点C ,则反比例函数的解析式是_____.13.已知关于x 的一次函数y =kx +1和反比例函数y =6x 的图象都经过点(2,m ),则一次函数的解析式是________.14.点A (a ,b )是一次函数y=x ﹣1与反比例函数y=4x的交点,则a 2b ﹣ab 2=_____.15.直线y =kx(k >0)与双曲线y A(x 1,y 1)和B(x 2,y 2)两点,则3x 1y 2-9x 2y 1的值为________.16.若A ()11,x y ,B ()22,x y ,C ()33,x y 都是反比例函数1y x=-的图象上的点,且1230x x x <<<,则123,,y y y 由小到大的顺序是 ____________ 17.如图,直线122y x =-与x 轴、y 轴分别交于点A 和点B ,点C 在直线AB 上,且点C 的纵坐标为一1 ,点D 在反比例函数y=k x 的图象上 ,CD 平行于y 轴,△OCD 的面积S=72,则k 的值为_____.18.如图,已知反比例函数y=k x(k 为常数,k≠0)的图象经过点A ,过A 点作AB ⊥x 轴,垂足为B .若△AOB 的面积为1,则k=_____.19.如图, A 、B 是双曲线k y x=上的两点,过A 点作AC x ⊥轴,交OB 于D 点,垂足为C .若ADO 的面积为3,点D 为OB 的中点,则k 的值为__________.20.如图,已知反比例函数12y x=的图象与一次函数4y kx =+的图象相交于P 、Q 两点,并且P 点的纵坐标是6,则Q 点的坐标为__________.21.如图,已知直线y=﹣2x 经过点P (﹣2,a ),点P 关于y 轴的对称点(k≠0)的图象上.(1)求a 的值;(2)直接写出点P′的坐标;(3)求反比例函数的解析式.22.如图,直线y =k 1x (x ≥0)与双曲线y =2k x(x >0)相交于点P (2,4).已知点A (4,0),B (0,3),连接AB ,将Rt △AOB 沿OP 方向平移,使点O 移动到点P ,得到△A ′PB ′.过点A ′作A ′C ∥y 轴交双曲线于点C ,连接CP .(1)求k 1与k 2的值;(2)求直线PC 的解析式;(3)直接写出线段AB 扫过的面积.23.已知函数11y x =-和26y x=. (1)如图所示的坐标系中画出这两个函数的图象.(2)求这两个函数交点坐标.(3)观察图象,当x 在什么范围内, 12y y >?24.(本题满分8分)码头工人以每天40吨的速度往一艘轮船上装卸货物,装载完毕恰好用8天时间。
山东省烟台市龙口市兰高学校九年级(上)第一次段考数学试卷(五四学制)无答案
山东省烟台市龙口市兰高学校九年级(上)第一次段考数学试卷(五四学制)无答案
与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
23.(10分)如图抛物线y=ax2﹣5ax+4a与x轴相交于点A、B,且过点C(5,4).(1)求a的值和该抛物线顶点P的坐标.
(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的解析式.
24.(12分)如图所示.某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF 在边BC上.其余两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,每平方米投资6元;在△BHE、△FCG上都种花,每平方米投资10元;在矩形EFGH上兴建爱心鱼池,每平方米投资4元.
(1)当FG长为多少米时,种草的面积与种花的面积相等?
(2)当矩形EFGH的边FG为多少米时,△ABC空地改造总投资最小,最小值为多少?。
山东省龙口市兰高镇兰高学校2018届九年级中考复习专项训练:相似三角形(选择题)
鲁教版2018中考复习相似三角形专项训练一(选择题)1、如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD 相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.其中正确的结论有()个A.5B.4C.3D.22、如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为()A. 2B. 2.5或3.5C.3.5或4.5D. 2或3.5或4.53、如图,△ABC中,DE∥BC,DE=1,AD=2,DB=3,则BC的长是()4、如图,在▱ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=()A. 2:5 B . 2:3 C. 3:5 D.3:25、如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=,则△EFC的周长为()A. 11B. 10C. 9D. 86.如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△CEF:S四边形BCED的值为()7.如图,D 是△ABC 的边BC 上一点,已知AB=4,AD=2.∠DAC=∠B ,若△ABD 的面积为a ,则△ACD 的面积为( )A .aB .C .D .8.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S 1,S 2,则S 1+S 2的值为( )A .16B .17C .18D .199.如图,在△ABC 中,AB=AC=a ,BC=b (a >b ).在△ABC 内依次作∠CBD=∠A ,∠DCE=∠CBD ,∠EDF=∠DCE .则EF 等于( )10如图,点A ,B ,C ,D 的坐标分别是(1,7),(1,1),(4,1),(6,1),以C ,D ,E 为顶点的三角形与△ABC 相似,则点E 的坐标不可能是( )11.如图,正方形ABCD 是一块绿化带,其中阴影部分EOFB ,GHMN 都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( ) . .D .. . C . D .12..如图所示,在平行四边形ABCD 中,AC 与BD 相交于点O ,E 为OD 的中点,连接AE 并延长交DC 于点F ,则DF :FC=( )13.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x ,那么x 的值( )A. 只有1个B. 可以有2个C. 可以有3个D. 有无数个14.如图,Rt △ABC 中,∠A=90°,AD ⊥BC 于点D ,若BD :CD=3:2,则tanB=( ) 15.如图,点A ,B ,C ,D 为⊙O 上的四个点,AC 平分∠BAD ,AC 交BD 于点E ,CE=4,CD=6,则AE 的长为( )16.如图,在△ABC 中∠A=60°,BM ⊥AC 于点M ,CN ⊥AB 于点N ,P 为BC 边的中点,连接PM ,PN ,则下列结论:①PM=PN ;②;③△PMN 为等边三角形;④当∠ABC=45°时,BN=PC .其中正确的个数是( )个A. 1 B . 2 C. 3 D.417 如图,在△ABC 中,M 、N 分别是边AB 、AC 的中点,则△AMN 的面积与四边形MBCN 的面积比为( ).. . . .(A) 12(B)13(C)14(D)2318.如图,将一张三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断何者正确?()A.甲>乙,乙>丙B.甲>乙,乙<丙C.甲<乙,乙>丙D.甲<乙,乙<丙19. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上。
山东省龙口市兰高镇中考数学专题复习 全国各地反比例函数试题归类训练 鲁教版
yACP全国各地反比例函数试题归类练习考点1 正确理解反比例函数的概念,会求反比例函数的解析式 类型一、根据解析式求字母的值 1、若22)1(-+=a xa y 是反比例函数,则a 的取值为( )A .1B .-1C .±1D .任意实数 解:∵此函数是反比例函数,∴,解得a=1.规律方法:本题考查的是反比例函数的定义,先根据反比例函数的定义列出关于a 的不等式组,求出a 的值即可.本题易错点是:解答时易把系数a+1≠0漏掉而错得a=±1.类型二、根据一个点的坐标求解析式2.如图,菱形OABC 的顶点O 是原点,顶点B 在y 轴上,菱形的对角线长分别是6和4,反比例函数y=kx (x<0)图象经过点C ,则k 的值为______-6_____考点:反比例函数图象上点的坐标特征分析:先根据菱形的性质求出C 点的坐标特征,再把C 点坐标代入反比例函数的解析式中类型三、根据面积直接求解析式3.如图,矩形AOBC 的面积为4,反比例函数ky x =的图象的一支经过矩形对角线的交点P ,则该反比例函数的解析式是( ) (A )4y x =(B )2y x =(C )1y x = (D )12y x =类型四、根据面积转换求解析式 4.如图,反比例函数(x >0)的图象经过矩形OABC 对角线的交点M ,分别于AB 、BC 交于点D 、E ,若四边形ODBE 的面积为9,则k 的值为( )分析:本题可从反比例函数图象上的点E 、M 、D 入手,分别找出△OCE 、△OAD 、□OABC 的面积与|k|的关系,列出等式求出k 值.解:由题意得:E 、M 、D 位于反比例函数图象上,则S △OCE=,S △OAD=,过点M 作MG ⊥y 轴于点G ,作MN ⊥x 轴于点N ,则S□ONMG=|k|, 又∵M 为矩形ABCO 对角线的交点, ∴S 矩形ABCO=4S□ONMG=4|k|, 由于函数图象在第一象限,k >0,则 ++9=4k ,解得:k=3. 故选C .点评:本题考查反比例函数系数k 的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.本知识点是中考的重要考点,老师们应高度关注. 考点二、灵活运用反比例函数的图象和性质解决问题 类型一、比较函数值的大小1、已知点A (1,1y )、B (2,2y )、C (-3,3y )都在反比例函数x y 6=的图象上,则的大小关系是( ) A.213y y y << B.321y y y << C.312y y y << D.y 3<y 2<y 1【答案】:D【解析】:将A (1,1y )、B (2,2y )、C (-3,3y )代入x y 6=得到1y =6,2y =3,3y =-2变式:改为反比例函数 能用代入法吗?21k y x+=-本题易错点是:.反比例函数的增减性要强调在同一个象限内。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2018中考数学模拟试题九 一、 选择 1、在|﹣2|,20,2﹣1,2这四个数中,最大的数是( ) A. |﹣2| B. 20 C. 2﹣1 D.2 2、 我州今年参加中考的学生人数大约为5.08×104人,对于这个用科学记数法表示的近似数,下列说法正确的是( ) A. 精确到百分位,有3个有效数字 B. 精确到百分位,有5个有效数字 C. 精确到百位,有3个有效数字 D. 精确到百位,有5个有效数字 3、一个几何体的三视图如图所示,则这个几何体是( )
A. 三棱锥 B. 三棱柱 C. 圆柱 D. 长方体 4、下列运算正确的是( )
A. 4=±2 B. x2•x3=x6 C. 2+3=5 D. (x2)3=x6 5、菱形ABCD的一条对角线长为6,边AB的长为方程y2﹣7y+10=0的一个根,则菱形ABCD的周长为( ) A. 8 B. 20 C. 8或20 D. 10 6、股票每天的涨、跌幅均不超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停。已知一支股票某天跌停,之后两天时间又涨回到原价,若这两天此股票股价的平均增长率为x,则x满足的方程是( ) A. (1+x)²=1011 B.(1+x)²=910 C.1+2x=1011 D. 1+2x=910 7、如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则
下列结论: ①abc<0;②abac442>0;③ac﹣b+1=0;④OA•OB=﹣ac. 其中正确结论的个数是( )
主视图 左视图俯视图
y x O 2
A. 4 B. 3 C. 2 D. 1 8、如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=;⑤S四边形CDEF=S△ABF,其中正确的结论有( ) A. 5个 B. 4个 C. 3个 D. 2个
9、从所给出的四个选项中,选出适当的一个填入问号所在位置,使之呈现相同的特征【 】 A. B. C. D. 10、透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3 cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
A.13cm B.261cm C.61cm D.264cm
A C B A B C
D E F 3
11、若关于x的不等式的整数解共有4个,则m的取值范围是( ) A.612、四边形ABCD是边长为1 的正方形,四边形EFGH是边长为2的正方形,点D与点F重合,点B,D(F),H在同一条直线上,将正方形ABCD沿F→H方向平移至点B与点H重合时停止,设点D、F之间的距离为x,正方形ABCD与正方形EFGH重叠部分的面积为y,则能大致反映y与 x之间函数关系的图象是( )
二、填空 13、当x=m或x=n(m≠n)时,代数式x2﹣2x+3的值相等,则x=m+n时,代数式x2﹣2x+3的值为 .
14、如图,点B1在反比例函数y=(x>0)的图象上,过点B1分别作x轴和y轴的垂线,垂足为C1和A,得到第一个矩形AOC1B1,点C1的坐标为(1,0);取x轴上一点C2(,0),过点C2
作x轴的垂线交反比例函数图象于点B2,过B2作线段B2 A1⊥B1C1,,交B1C1于点A1,得到第二个矩
形A1C1C2B2;依次在x轴上取点C3(2,0),C4(,0) 按此规律作矩形,则第10个矩形A9C9C10B10
的面积为 . 4
15、如图3,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上AD=OA=1,则图中阴影部分的面积为
16、一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分(如图所示),则这串珠子被盒子遮住的部分有______颗.
17、抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:①abc>0;②a+b>0;③若点A(﹣3,y1),点B(3,y2)都在抛物线上,则y1<y2;④a(m﹣1)+b=0;⑤若c≤﹣1,则b2 ﹣4ac≤4a.其中结论错误的是 .(只填写序号) 18、如图,正六边形ABCDEF的边长为4,两顶点A、B分别在x轴和y轴上运动,则顶点D到原点O的距离的最大值和最小值的乘积为______. 5
三.计算和证明 19、先化简: ,然后从-1≤x≤2中选一个合适的整数作为x的值代入求值.
20、小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图). 月均用水量(单位:t)
(1)请根据题中已有的信息补全频数分布表和频数分布直方图; (2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户? 6
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率
21、如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,函数y=的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4). (1)求k的值; (2)连接PA,PB,若△ABP的面积为6,求直线BP的解析式.
22、海中两个灯塔A、B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这是测得灯塔A在北偏西60°方向上,求灯塔A、B间的距离.(计算结果用根号表示,不取近似值) 7
23、某商家计划从厂家采购空调和冰箱两种产品共20台,空调的采购单价y1(元/台)与采购数量x1(台)满足y1=﹣20x1+1500(0<x1≤20,x1为整数);冰箱的采购单价y2(元/台)与采购数量x2(台)满足y2=﹣10x2+1300(0<x2≤20,x2为整数). (1)经商家与厂家协商,采购空调的数量不少于冰箱数量的 ,且空调采购单价不低于1200 元,问该商家共有几种进货方案? (2)该商家分别以1760元/台和1700元/台的销售单价售出空调和冰箱,且全部售完.在(1)的条件下,问采购空调多少台时总利润最大?并求最大利润 8
24、如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心、OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE. (1)判断DE与⊙O的位置关系,并说明理由; (2)求证:BC2=CD•2OE; (3)若cos∠BAD=53,BE=6,求OE的长.
25、问题背景: 如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠D=90°.E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系,并说明理由. 拓展应用: 如图2,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西40°的A处,舰艇乙在指挥中心南偏东80°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以50海里/小时的速度,同时舰艇乙沿北偏东50°的方向以70海里/小时的速度各自前进2小时后,在指挥中心观测到甲、乙两舰艇分别到达E,F处,两舰艇与指挥中心之间的夹角为70°,试求此时两舰艇之间的距离. 9
26、如图,在平面直角坐标系中,顶点为(4,)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧). 已知A点坐标为(0,3). (1)求此抛物线的解析式; (2)过点B作线段AB的垂线交抛物线于点D, 如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明; (3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么 位置时,PAC的面积最大?并求出此时P点的坐标和PAC的最大面积. (4)在抛物线的对称轴上是否存在一点M,使△ABM成为等腰三角形?存在,求出M点的坐标;不存在,说明理由。 10 2018年中考数学模拟试题九
一、ACADBBABCABB
二、(13)3 (14)112 (15)43 (16)27 (17)③⑤ (18)323 三、 11
19 20. 解:(1)调查的总数是:2÷4%=50(户), 则6≤x<7部分调查的户数是:50×12%=6(户), 则4≤x<5的户数是:50﹣2﹣12﹣10﹣6﹣3﹣2=15(户),所占的百分比是:
5015×100%=30%
(2)中等用水量家庭大约有450×(30%+20%+12%)=279(户); (3)在2≤x<3范围的两户用a、b表示,8≤x<9这两个范围内的两户用1,2表示
