振动力学作业题解
机械振动基础作业(有答案-全版)
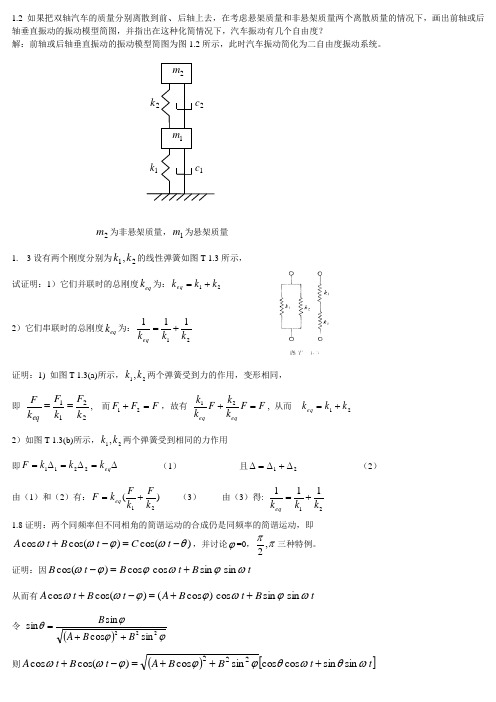
1.2 如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?解:前轴或后轴垂直振动的振动模型简图为图1.2所示,此时汽车振动简化为二自由度振动系统。
2m 为非悬架质量,1m 为悬架质量1. 3设有两个刚度分别为21,k k 的线性弹簧如图T-1.3所示, 试证明:1)它们并联时的总刚度eq k 为:21k k k eq +=2)它们串联时的总刚度eq k 为:21111k k k eq +=证明:1) 如图T-1.3(a)所示,21,k k 两个弹簧受到力的作用,变形相同, 即2211k F k F k F eq ==, 而F F F =+21,故有 F F k kF k k eq eq =+21, 从而 21k k k eq +=2)如图T-1.3(b)所示,21,k k 两个弹簧受到相同的力作用 即∆=∆=∆=eq k k k F 2211 (1)且21∆+∆=∆ (2)由(1)和(2)有:)(21k Fk F k F eq += (3) 由(3)得:21111k k k eq += 1.8证明:两个同频率但不同相角的简谐运动的合成仍是同频率的简谐运动,即)cos()cos(cos θωϕωω-=-+t C t B t A ,并讨论ϕ=0,ππ,2三种特例。
证明:因t B t B t B ωϕωϕϕωsin sin cos cos )cos(+=-从而有t B t B A t B t A ωϕωϕϕωωsin sin cos )cos ()cos(cos ++=-+令 ()ϕϕϕθ222sin cos sin sin B B A B ++=则()[]t t B B A t B t A ωθωθϕϕϕωωsin sin cos cos sin cos )cos(cos 222+++=-+=())cos(sin cos 222θωϕϕ-++t B B A令C=()ϕϕ222sin cos B B A ++,则有 )cos()cos(cos θωϕωω-=-+t C t B t A当ϕ=0时,C=A+B ;当ϕ=2π时,22B A C +=,22BA arcsin +=B θ ;当ϕ=π时,B A -=C ,0=θ1.13汽车悬架减振器机械式常规性能试验台,其结构形式之一如图T-1.13所示。
振动力学期末考试试题以及答案(很有参考价值哦)

2006《振动力学》课程本科生考试试题标准答案1. 圆筒质量m 。
质量惯性矩o J ,在平面上在弹簧k 的限制下作纯滚动,如图所示,求其固有频率。
(10分)解:令t A xt A x ωωωcos ,sin == t A xrJ m xr J m rxJ x m J x m T o o o o ωωθ22222222222cos )(21)(21)(21212121 +=+=+=+=t kA kx U ω222sin 2121==222222max max /21)(21r J m kkA A xr J m U T o o +==+∴=ωω2. 图示的弹簧质量系统,两个弹簧的连接处有一激振力t P t P ωsin )(0=的作用,求质量m 稳态响应的幅值。
(10分))(t2x xm 11x k(t P 22x k解:设m 的位移为x ,则21x x x += (1) 其中,1x 为弹簧1k 的变形,2x 为弹簧2k 的变形对m 列运动微分方程: 022=+x k xm (2) 对连接点列平衡方程: )(2211t P x k x k += (3)由(3)式可以得出:1221)(k x k t P x +=将上式代入(1)式可得出:2112)(k k xk t P x ++-=将上式代入(2)式可得出:0)(2122121=+-++t P k k k x k k k k xm令mk k k k k k e e e =+=ω,2121,有t k k k P t P k k k x k xm e ωsin )(2120212+=+=+t k P t k k k k P x eee ωωωωωωsin )(11sin )(11121022120-⋅=-⋅⋅+=∴3. 建立如图所示系统的运动微分方程并求稳态响应。
(10分)解:对物体m 列运动微分方程,有:0)(1=--+x x k x c xm 即:t kA kx x c xm ωsin =++ t Aωsin 1=xm )x -其稳态响应为:)sin()2()1(1222θωξ-+-⋅=t s s k kA x其中,20012arctan ,2,,s skmc m k s -====ξθξωωω4. 如图所示等截面悬臂梁,梁长度为L ,弹性模量为E ,横截面对中性轴的惯性矩为I ,梁材料密度为ρ。
振动物理力学答案

第九章 振动思考题9.1 什么叫作简谐振动?如某物理量x 的变化规律满足)cos(q pt A x +=,A 、p 、q 均为常数,能否说x 作简谐振动?答:物体(质点或刚体)在线性回复力或线性回复力矩作用下,围绕平衡位置的往复运动叫作简谐振动。
可由动力学方程或运动学方程加上一定的附加条件来定义:若物体相对平衡位置的位移(角位移)x 满足动力学方程 02022=+x dtx d ω,且0ω由振动系统本身性质决定时,则物体作简谐振动;若物体相对平衡位置的位移(角位移)x 满足运动学方程 )c o s (0αω+=t A x ,且0ω由振动系统本身性质决定,A 、ϕ由初始条件决定的常数时,则物体作简谐振动。
以0x 和x v 0分别表示0=t 时物体的初始位移和初始速度,则式中 20202ωxv x A +=;α可由A x 0cos =α、A v x 00sin ωα-=和000x vtg x ωα-=三式中的任意两个来决定。
上述运动学方程是动力学方程(微分方程)的解,A 、ϕ是求解时的待定积分常数。
三个定义在力学范围内是等价的,动力学方程更具普遍性。
可用三个定义中的任何一个来判断物体的运动是否简谐振动。
如某物理量x 的变化规律满足)cos(q pt A x +=,A 、p 、q 均为常数,不能说x 作简谐振动。
因为常数p 必须是由振动系统本身性质决定的固有频率,并且A 、q 是由系统初始条件决定的常数时,才可以说x 作简谐振动。
9.2 如果单摆的摆角很大,以致不能认为θθ=sin ,为什么它的摆动不是简谐振动? 答:对质量为m 的摆球,当摆角θ很大时,θθ≠sin ,其切向力θθτ⋅-≠-=mg mg f sin ,不是角位移θ的线性回复力。
由牛顿定律得:θθsin )(22mg dt l d m -=即 0sin 22=+θθl gdtd 令l g =2ω,有 0sin 2022=+θωθdtd 因此,动力学方程是非线性微分方程,其解不再为余弦函数,不满足简谐振动的定义。
第章振动作业答案

1.两个相同的弹簧,一端固定,另一端 分别悬挂质量为 m1 , m2的两个物体。若 两个物体的振动周期之比为 T1 : T2 2 : 1 则m1 : m2 =( )
A. 2 :1 C. 1: 4
B. 4 :1 D. 1: 2
2. 两个近地点各自做简谐振动,它们的 振 幅 相 同。第 一 个 质 点的振动方
振动时具有势能0.06J和动能0.02J,则振动的振
幅为0.08m;动能恰好等于势能时的位移为 ;
经过平衡位置时物体的速度±0.8m/s。
解 :(1)
E总
1 kA2 2
0.08
A 0.08(m)
(2) 1 k4
2
(3)
D. x2 A cos(t )
3. 质点作周期为T,振幅为A的谐振 动,则质点由平衡位置运动到离平 衡位置A/2处所需的最短时间是: ( )
A.T/4 B.T/6 C.T/8 D.T/12
4. 一质点在x轴上作谐振动振幅A=4cm, 周期T=2s,其平衡位置取作坐标原点, 若t=0时刻近质点第一次通过x=-2cm处, 且向x轴正方向运动,则质点第二次通过 x=-2cm,处时刻为:[]
M m T
k
(1)当振子在最大位移处时, x A, 0
物体落下,碰后振子速度 ' 0 不变,此时 x0 A,0 0
故振幅 A' A 不变。振动能量也不变。
(2) 物体是在振子到达平衡位置时落在M上
x0 0, max 0 A A
6
D.振幅等于1cm, 初相等于
6
6.一质点做简谐振动,振动方程为
x A cos(t )
振动波动作业解
x A/2
2
5 3 2 6
ቤተ መጻሕፍቲ ባይዱ
2 T t 6 5 12s 5
2
2 t t T
物理系:史彭
史彭振动波动作业解
4.一质点作简谐振动,已知振动频率为 f,则振动动能的 变化频率是: [ B ]
1 1 2 E K m m[A sin( t )] 2 2 2
3 1 2 2 sin t cos t ] 10 2 [sin sin t cos cos t ] 10 2 3 3 2 2 2 cos(t ) 10 2 3 x / 2 2 y cos(t ) 10 2 u 3 2 2x 2 y cos(t ) 10 u 3
x’ x
1 x y Acos[ (t ) ] u
物理系:史彭
史彭振动波动作业解
2.一平面简谐波沿 OX 轴传播,波函数为 y A cos[2 (t x / ) ] , 则在X1=L处,介质质点振动的初相位是 ;与X1处质点振动 状态相同的其它质点的位置是 ;与X1处质点振动速度大小 相同,但方向相反的其它各质点的位置是 。 各点初相位 2x / y X1=L
3 sin (t ) 4
2
1 2 1 E kA m 2 A2 2 2
EK 3 E 4
物理系:史彭
史彭振动波动作业解
二、填空题 1.一质点作简谐振动,其振动曲线如图所示。根据此图, 它的周期 ;用余弦函数描述时初相位 。
2
x
7 t t 12
物理系:史彭
史彭振动波动作业解
2.一质点作简谐振动,周期为 T 。质点由平衡位置向 X 轴正方向运动时,由平衡位置到二分之一最大位移这段路 所需要的时间为 [ B ]
振动系统的运动微分方程题解

习 题3-1 复摆重P ,对质心的回转半径为C ρ,质心距转动轴的距离为a ,复摆由水平位置无初速地释放,列写复摆的运动微分方程。
解:系统具有一个自由度,选复摆转角ϕ为广义坐标,原点及正方向如如题4-1图所示。
复摆在任意位置下,根据刚体绕定轴转动微分方程 O O M J =ϕ其中)(22a gP J C O +=ρ 得到复摆运动微分方程为 ϕϕρcos )(22Pa a gP C =+ 或0cos )(22=-+ϕϕρga a C3-2均质半圆柱体,质心为C ,与圆心O 1的距离为e ,柱体半径为R ,质量为m ,对质心的回转半径为C ρ,在固定平面上作无滑动滚动,如题3-2图所示,列写该系统的运动微分方程。
解:系统具有一个自由度,选θ为广义坐标。
半圆柱体在任意位置的动能为:222121ωC C J mv T +=用瞬心法求C v : 2222*2)cos 2()(θθθ Re R e CC v C -+== θω =2C C m J ρ=故2222221)cos 2(21θρθθ Cm Re R e m T +-+=系统具有理想约束,重力的元功为题3-1图题3-2图θθδd mge W sin -= 应用动能定理的微分形式W dT δ=θθθρθθd mge m Re R e m d C sin 21)cos 2(2122222-=⎥⎦⎤⎢⎣⎡+-+ θθθθθθθθθθρd mge d mRe d mRe d R e m C sin sin cos 2)(2222-=+-++ 等式两边同除dt ,θθθθθθθθθθρ sin sin cos 2)(2222mge mRe mRe R e m C -=+-++ 0≠θ ,等式两边同除θ故微分方程为0sin sin )cos 2(2222=+++-+θθθθρθmge mRe Re R e m C ①若为小摆动θθ≈sin ,1cos ≈θ,并略去二阶以上微量,上述非线性微分方程可线性化,系统微摆动的微分方程为0])[(22=++-θθρge r R C要点及讨论(1)本题也可以用平面运动微分方程求解。
振动力学课程作业
《振动力学》2015春节学期作业一、无阻尼自由振动1、如图所示,T型结构可绕水平轴O作微小摆动,已知摆动部分的质量为w,机构绕O轴的转动惯量为J,两弹簧的弹簧系数均为k,且当①=0时(即机构处于平衡位置时),两弹簧无伸缩,试求该机构的摆动频率。
2、如图所示,长度为L的刚性杆件,在O点铰支,自由端固定一质量为m的小球。
在距离铰支端a处,由两个刚度系数为k/2的弹簧将刚性杆件支持在铅垂面内。
求该系统的固有频率。
(忽略刚性杆件和弹簧的质量)(答案:①喈喘一D)(答案:①=)3、如图所示,悬臂梁长为L,截面抗弯刚度为EI,梁的自由端有质量为m 的质量块,弹簧刚 度为k ,求系统的固有频率。
4、如图所示,半径为R 的均质半圆柱体,在水平面内只作滚动而不滑动的微摆动,求其固有 角频率。
(答案:①)君篇5、如图所示,抗弯刚度为EI = 30义106(N ・m 2)的梁AB ,借弹簧支撑于A,B 两点处,弹簧系数均为k = 300(N / m )。
忽略梁的质量,试求位于B 点左边3m 处,重量为W = 1000(N )的物块自由振动的周期。
(答案:T=0.533s )借助四根端点嵌固的竖置管柱支撑着。
每根柱子的长为L,抗弯刚度为 EI 。
试求该水箱顺水平方向自由振动的周期。
(管柱的质量忽略不计) 6、一个重W 的水箱, (答案:)(答案:T = 2)1、如图所示,库伦曾用下述方法测定液体的粘性系数c ':在弹簧上悬挂一薄板A ,先测出薄板在空气中 的振动周期J 然后测出在待测粘性系数的液体中的振动周期「设液体对薄板的阻力等于2A c ′ -其 中2A 为薄板的表面面积,v 为薄板的速度。
如薄板重W ,试有测得的数据T 和T 2,求出粘性系数c 。
空 气对薄板的阻力不计。
»2 冗 W 二~~—(答案:C ’二祈口22 一 T :)12(答案:196Ns/m )3、挂在弹簧下端的物体,质量为1.96kg ,弹簧常数k=0.49N/cm,阻尼系数c=0.196Ns/cm 。
振动力学习题集
2振动力学》习题集(含答案)质量为 m 的质点由长度为 l 、质量为 m 1 的均质细杆约束在铅锤平面内作微幅摆动,如 图所示。
求系统的固有频率。
解: 系统的动能为:1 2 1 2 T m xl I x22 其中 I 为杆关于铰点的转动惯量:利用xnx 和T U 可得:3 2m m 1 g2 3m m 1 lml 1dxx 2l m 1x 2dxlm 1l31则有:系统的势能为:1 2 2 1 2 2ml x m 1l x 2 611 2 2 3m m 1 l x6U mgl 1 cosxm 1g cosx 1 2mglx14m 1glx1 2m4m 1 glx 2图质量为m、半径为R的均质柱体在水平面上作无滑动的微幅滚动,在两根弹性刚度系数为k 的水平弹簧,如图所示。
求系统的固有频率。
CA=a的A 点系有解:如图,令为柱体的转角,则系统的动能和势能分别为:利用1212 1 2 23T I B mR2mR2 2mR2B2241222U2k Ra2 k R a24k R a 23mR2R 3m图U 可得:n J k 2 k 3转动惯量为 J 的圆盘由三段抗扭刚度分别为 k 1 , k 2 和 k 3 的轴约束,如图所示。
求系统的固有频率。
k 2解:系统的动能为:12J 2k 2和 k 3相当于串联,则有:以上两式联立可得:系统的势能为:k 2k 3 k 1 k 2 k 3k 1 3,k 2k 2k 3k 3k 2k 2 k 3利用U 12k 1k 2 2212k 3 k 1 k 2 k 3 k 2k 3 2k 2 k 3n 和T U 可得:在图所示的系统中,已知 k i i 1,2,3 , m, a 和b ,横杆质量不计。
求固有频率。
答案图解:对 m 进行受力分析可得:质量 m 1在倾角为 的光滑斜面上从高 h 处滑下无反弹碰撞质量 m 2 ,如图所示。
确定mg k 3x 3 ,即 x 3mgk 3如图可得:F 1 mgb F 2 x 1, x 2k 1a b k 1k 2mga a b k 2x 0 x 1 x x 1a x 2 x 1ab a 2k 1 2b 2k 2 mga b 2 k 1k 2 x 则等效弹簧刚度为:x 0 x 3a 2k 1b 2 k 2 a b 2k 1k 21mgk 0mg2b k 1k 2k3a 2k 1k 3b 2k 2k 3 a b 2 k 1k 2则固有频率为:nk 1k 2k 3 a b 2 2 2 2 m k 1k 2 a b k 3 k 1a k 2bx 2mg系统由此产生的自由振动。
第章振动作业答案_图文
11. 固有频率为ν0的弹簧振子,在阻尼很小的情况下,受 到频率为2ν0的余弦策动力作用,做受迫振动并达到稳 定状态,振幅为A。若在振子经平衡位置时撤去策动力 ,则自由振动的振幅A’与A的关系是 A’= 2A
(1)稳定振动时振子频率即策动力频率,角频率为 ω =2π (2ν 0) ,经平衡位置时速度最大为V=ω A。
5. 一弹簧振子作简谐振动,振幅为A,周期为T ,运动方程用余弦函数表示,若t=0时, (1)振子在负的最大位移处,则初位相为_____ 。 (2)振子在平衡位置向正方向运动,则初位相为
_____。 (3)振子在位移A/2处,向负方向运动,则初位 6. 相将为复_杂__的__周。期性振动分解为一系列的简谐运
Ф-Ф1=π/6.若第一个简谐振动的振幅为
则第二个简谐振动的振幅为
( 10 )cm,第一,二个简谐振动的相位差
Ф1- Ф2为( -π/2 )
9.一简谐振动的旋转矢量如图所示,振幅矢 量长2cm,则该简谐振动的初相位为 π/4 , 振动方程为 2cos(πt+ π/4)cm
10.系统的共振角频率与系统自身性质以及阻 尼大小有关。系统的阻尼越大,共振时振 幅值越低,共振圆频率越小。
13.两个线振动合成为一个圆振动的条件是(1)同 频率;(2)同振幅;(3)两振动相互垂直;(4 )相位差为(2k+1)π /2, k=0, ±1, ±2,……
计算题
3. 一个水平面上的弹簧振子,弹簧劲度系数
为k,所系物体的质量为M,振幅为A。有一 质量为m的小物体从高度为h处自由下落。
(1)当振子在最大位移处,小物体正好落
9.两个振动方向相互垂直、频率相同的
简谐振动的合成运动的轨迹为一正椭圆 ,则这两个分振动的相位差可能为( D )
作业振动作业及答案
25-1写出本章你认为重要的知识点。
3| x 0.1cos(8 )5-2质量为10 10 kg的小球与轻弹簧组成的系统,按3求:(1) 振动的周期、振幅和初位相及速度与加速度的最大值;(2) 最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等⑶t2 5s与t1 1s两个时刻的位相差;解:(1)设谐振动的标准方程为x Acos( t 0),则知:又V m A 0.8 m s 1 2.51 m s 1(2)F m a m 0.63N当E k E p时,有E2E p ,即-kx21(1kA2)222JV2x A m220(3)(t2tj8(5 1) 325-3 一个沿x轴作简谐振动的弹簧振子,振幅为A,周期为T,其振动方程用余弦函数表示. 如果t 0 时质点的状态分别是:(1) X。
A;(2) 过平衡位置向正向运动;A⑶过x 处向负向运动;2⑷过x A2处向正向运动.试求出相应的初位相,并写出振动方程.解:因为x0 Acos 0v0Asin 0第五章作业⑸)的规律作谐振动,将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相.故有5-4 一质点同时参与两个在同一直线上的简谐振动,振动方程为2试分别用旋转矢量法和振动合成法求合振动的振动幅和初相,并写出谐振方程。
故x b 0.1cos(5 t —)m5-6 一轻弹簧的倔强系数为k,其下端悬有一质量为M的盘子•现有一质量为m的物体从离盘底h高度处自由下落到盘中并和盘子粘在一起,于是盘子开始振动.(1) 此时的振动周期与空盘子作振动时的周期有何不同?(2) 此时的振动振幅多大?(3) 取平衡位置为原点,位移以向下为正,并以弹簧开始振动时作为计时起点,求初位相并写出物体与盘子的振动方程.------------------ I解: (1)空盘的振动周期为2 ,落下重物后振动周期为2 J叫』,即增大.m 2ghV om M于是(3) tan 0V o 2kh;(M m)g(第三象限),所以振动方程为解:(专A合A A20.1m6其振动方程为5-5图为两个谐振动的X t曲线,试分别写出其谐振动方程. 题图解:由题图(a) t0 时,X0 0,V0 0,30 ,又,A 10cm,T 2s2rad s 1故由题图(b) ••• tX a 0.1cos( tA0时,X02,V0Q⑵按⑶ 所设坐标原点及计时起点,t 0时,则x0mg•碰撞时,以m,M为一系统动量守恒,k则有x。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第02章 单自由度系统的振动2.1 一根抗弯刚度72=3610Ncm EI ⨯的简支架,两支承间跨度l 1=2m ,一端伸臂l 2=1m ,略去梁的分布质量,试求悬臂端处重为Q =2548 N 的重物的自由振动频率。
【提示:22123()EJ k l l l =+,2212()3st Ql l l EI δ+=,11.77n ω=L 1/s 】 2.2 梁AB 其抗弯刚度72=910Ncm EI ⨯,A 端与B 端由弹簧支承,弹簧刚性系数均为k =52.92 kN/m ,如图所示。
略去梁的分布质量,试求位于B 端点左边1米处,重为Q =4900 N 的物块自由振动的周期。
【解法1:通过计算静变形求解。
A ,B 弹簧受力为3Q 和23Q ,压缩量为3Q k 和23Q k ,则由弹簧引起的静变形为159Qk δ=;利用材料力学挠度公式求出梁变形引起的静变形222212(321)4619Q QEI EIδ⋅⋅--==⋅。
周期为:22 1.08nT πω===s 。
解法2:通过弹簧刚度的串并联计算总等效刚度求解。
A ,B 弹簧相对Q 处的等效刚度为(产生单位变形需要的力,利用解法1中计算的静变形结果)195k k =;利用材料力学挠度公式求出梁相对Q 处的等效刚度294EI k =;总等效刚度为:12111eq k k k =+。
周期为22 1.08nT πω===s 。
】 2.4 一均质刚杆重为P ,长度为L 。
A 处为光滑铰接,在C 处由刚性系数为k 的弹簧使杆在水平位置时平衡。
弹簧质量不计,求杆在竖直面内旋转振动时的周期。
【解:利用定轴转动微分方程:21()32st P l l P k a a g ϕϕδ=--&&,2st lk a P δ=, 得:22103P l k a gϕϕ+=&&,22n T πω===题 2-1 图BAQ题 2-2 图QkkAB 题 2-4 图2.8一个重为98 N的物体,由刚性系数为k=9.8 kN/m的弹簧支承着(简化为标准m-k-c振动系统),在速度为1 cm/s时其阻力为0.98 N。
求10周振幅减小比为多少?【解:0.98980.01c==Ns/m,980031.398nk gmω===1/s,0.1572ncmξω==,11211111ln ln101nX Xn X Xδξ+==≈-,2111120416XeXξ-==】2.10 题2.10图所示振动系统,物块质量为25 kg,弹簧刚度为2 N/mm,E=210 GPa,悬臂梁长250 mm,梁横截面宽20 mm,高3 mm,求固有频率。
梁的分布质量不计。
【解:梁的参数3114.51012bhI-==⨯m4。
解法1:通过计算静变形求解。
30.2583mg mglk EIδ=+=m,固有频率 6.17ngωδ==1/s。
解法2:通过通过弹簧刚度的串并联计算总等效刚度求解。
31211113eqlk k k k EI=+=+,固有频率 6.17eqnkmω==1/s。
】2.13 求题2.13图所示系统的固有频率。
【提示:利用定轴转动微分方程或能量法。
注意重力的影响。
212nka mglmlω+=,222nka mglmlω-=,232nkamlω=】2.14 求题2.14图所示系统的固有频率。
【解法1:通过计算静变形求解。
22mg kδ=,11mgl k aδ=21stlaδδδ=+,固有频率2122212()nstk k agm k a k lωδ==+。
解法2:利用牛顿定律。
22222()mx mg k x k xδ=-+=-&&,而:111222()()k x a k x lδδ+=+利用22mg kδ=,11mgl k aδ=得1122k x a k x l=题2.13图题2.10图题2.14图又21lx x x a=+,求出:212212k al x x k a kl =+,2122212k a x x k a k l =+ 则振动方程为:21222120k k a mx x k a k l +=+&&,固有频率2122212()eq n eq k k k a m m k a k l ω==+1/s 。
解法3:利用机械能守恒。
取静平衡位置为重力势能零点,弹簧原长为弹性势能零点,212T mx =& 2211122211()()22V mgx k x k x δδ=-++++利用前面求出的1212,,,x x δδ,代入后利用()0dT V dt+=得到振动方程为: 21222120k k a mx x k a k l +=+&&,……】2.15 求题2.15图所示系统微幅振动的微分方程(m 2视为均质圆盘)。
答:12122()02k k x x m m ++=+&&2.16 求题2.16图所示系统振动的微分方程和固有频率(不计杆的质量,c 为黏滞阻尼)。
答:22220b c a k ml ml θθθ++=&&&,22422142d ma l k b c mlω=- 2.17 标准m-k-c 振动系统,弹簧刚度为32.14 kN/m ,物块质量为150 kg 。
(1)求系统的临界阻尼系数;(2)该系统的阻尼系数为0.685 kNs/m 时,问经过多少时间振幅减到10%;(3)衰减振动周期是多少。
【解:(1)14.64n kmω==1/s ,24391.4c n c m ω==Ns/m (2)0.1562n cm ξω==,12111ln ln100.9921n X n X n δξ+====- n =2.285,20.981nt nT nπω===(3)20.4351d n T ωξ==-】题2.15图题2.16图2.18 题2.18图所示系统,在空气中振动周期为T 1,在液体中振动周期为T 2,试证明液体的粘性阻尼系数为22214mc T T TT π=-。
2.19 求题 2.19图所示系统的固有频率。
【解法1:通过计算静变形求解。
21st δδδ=+,1δδ=梁,由梁的变形公式得:311111()48mg k l mg k EI k δδδδ--===梁梁而:22mg k δ=,则:2121st mg mgk k k δδδ=+=++梁固有频率321312(48)[()48]n stk k l EI gk k l EI mωδ+==++。
解法2:利用弹性元件串并联。
k 梁与1k 并联,然后与2k 串联,则:21111eq k k k k =++梁,固有频率eq n k m ω==……。
解法3:利用牛顿定律。
22222()mx mg k x k x δ=-+=-&&,利用梁的变形公式有:22211111()()k x k x x k δδδ+-++=梁又21x x x =+,求出:1122212()()k k x k x k k k δδ++-=++梁梁利用前面求出的12,δδ最后得到振动方程为:2112()0k k k mx x k k k ++=++&&梁梁,固有频率321312(48)[()48]eqn eq k k k l EI m k k l EI mω+==++。
解法4:利用机械能守恒。
取静平衡位置为重力势能零点,弹簧原长为弹性势能零点,212T mx =& 2211122211()()()22V mgx k k x k x δδ=-+++++梁利用前面求出的1212,,,x x δδ,代入后利用()0dT V dt+=得到振动方程……】题2.19图题2.18图第3章 单自由度系统强迫振动3.8 图3-8所示简支梁中间放一台重为2 kN 的电机,其中转子重0.4 kN ,偏心距e =0.02 cm ,电机静作用时的挠度δst =2 cm ,若电机的转速为1450 rpm ,试求:电机稳态强迫振动的振幅(略去梁的质量)。
【解:固有频率22.14n stgωδ==,等效弹性系数2100000n k m ω==,振动方程22000400sin 93030n n x kx e t g ππ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭&&,即:()204.1188sin 152x kx t +=&& 振幅为50022 4.09101n F X k ωω-==⨯⎛⎫- ⎪⎝⎭m 。
】3.22 题3.22图所示系统,m =9800 kg ,k =966280 N/m ,在质量块上作用有激振力4900sin 2Q t π= N ,在弹簧固定端有支撑位移0.3sin4B x t π= cm ,求系统的稳态响应。
【解:振动方程()B mx Q k x x =--&&,即4900sin0.003sin 24B mx kx Q kx t k t ππ+=+=+&&,固有频率9.93n k m ω==,频率比10.1582n r πω==,20.0794nr πω==, 响应为12221249000.003sin sin (1)2(1)4k x x x t t k r k r ππ=+=+--0.52sin 0.302sin 24t t ππ=+cm 】3.23 机器重4410N ,支撑在弹簧隔振器上,弹簧静变形为0.5 cm ,机器有一偏心重,产生偏心激振力22.254Q g ω= N ,ω为激振力频率,g 为重力加速度,不计阻尼。
求(1)在机器转速为1200 r/min时传入地基的力;(2)机器的振幅。
【解:振动方程242.254sin mx kx t g ωω+=&&,44108820000.005k ==,固有频率44.27n kmω==。
(1)偏心激振力22.254Q g ω=22.254363030n g π⎛⎫== ⎪⎝⎭,频率比12.84nr ωω==, 传入地基的力为max 23630514.4(1)F kx k k r ===-N(2)20236305.8310(1)X k r -==⨯-cm 】 3.24 弹簧质量系统,m =196 kg ,k =1.96×105 N/m ,作用在质量上的激振力为156.8sin10Q t =,阻尼系数为627.2 Ns/m 。
求(1)质量块的振幅及放大因子;(2)如果把激振频率调整为5 Hz ,放大因子为多少;(3)如果把激振频率调整为15 Hz ,放大因子为多少;(4)若忽略阻尼,上面3种情况A 题 3-8图ABQl/2l/2ωt 题3.22图的放大因子又是多少,由此说明阻尼对振幅的影响。
