几何证明专题
专题三 几何证明

专题三 几何证明【专题分析】几何证明题重在训练学生运用数学语言合情推理的能力,在数学学习中占有非常重要的地位。
此类题目经常出现在解答题的第二题,属于中低难度的题,比较基础;最后两题中也有涉及,属于中高难度的综合题.【考点解析】考点一:证明线段相等例1.如图,E 、F 是□ABCD 对角线AC 上的两点,BE ∥DF .求证:BE =DF .考点二:证明线段平行或垂直例2. 如图,点A 、F 、C 、D 在同一直线上,点B 和点E 分别在直线AD 的两侧,且AB=DE ,∠A=∠D ,AF=DC .求证:BC ∥EF .例3. 如图,△ABC 中,以BC 为直径的圆交AB 于点D ,∠ACD =∠ABC .求证:CA 是圆的切线.A B C D E FA EBC FD 考点三:证明角相等例4.如图,在梯形ABCD 中,AD ∥BC ,AD =AB ,过点A 作AE ∥DB 交CB 的延长线于点E .(1)求证:∠ABD =∠CBD ; (2)若∠C =2∠E ,求证:AB =DC .考点四:证明三角形全等或特殊四边形例5.在□ABCD 中,E 、F 分别是AB 、CD 的中点,连接AF 、CE .(1)求证:△BEC ≌△DF A ;(2)连接AC ,当CA =CB 时,判断四边形AECF 是什么特殊四边形?并证明你的结论.【基础演练】1.如图,Rt △ABC 中,∠ACB=-90°,CD ⊥AB ,垂足为D .AF 平分∠CAB ,交CD 于点E ,交CB 于点F求证:CE=CF .2.如图,一张矩形纸片ABCD ,其中AD =8cm ,AB =6cm ,先沿对角线BD 对折, 点C 落在点C ′的位置,BC ′交AD 于点G 。
求证:AG =C ′G .(第21题)CA B O C D 3.(11清远)如图,在矩形ABCD 中,E 是BC 边上的点,AE =BC ,DF ⊥AE ,垂足为F ,连接DE .求证:AB =DF .4.已知四边形ABCD 是平行四边形.(1)求证:△MEF ∽△MBA ;(2)若AF 、BE 分别是∠DAB 、∠CBA 的平分线,求证:DF=EC .5.如图,已知,△ABC 为等边三角形,点D 为边BC 上一动点(点D 不与B 、C 重合).以AD 为边作菱形ADEF ,使∠DAF=60°,连接CF .求证:∠ADB =∠AFC .6.(11漳州)如图,AB 是⊙O 的直径,⌒AC =⌒CD ,∠COD =60°.(1)△AOC 是等边三角形吗?请说明理由;(2)求证:OC ∥BD .A D EB FC 7.(2011河南)如图,在梯形ABCD 中,AD ∥BC ,延长CB 到点E ,使BE =AD ,连接DE 交AB 于点M .求证:△AMD ≌△BM E ;8.如图,在直角梯形ABCD 中,AD ∥BC ,BC ⊥CD ,∠B =60º,BC =2AD ,E 、F 分别为AB 、BC 的中点.(1)求证:四边形AFCD 是矩形; (2)求证:DE ⊥EF .【综合提升】(2011泰州)如图,四边形ABCD 是矩形,直线l 垂直平分线段AC ,垂足为O ,直线l 分别与线段AD 、CB 的延长线交于点E 、F 。
【中考数学专题】10 与翻折或轴对称作图有关的几何证明题解析-

专题十:与翻折或轴对称作图有关的几何证明题解析专题导例如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为6,则线段CF的最小值是.【分析】:先判断出Rt△ADM≌Rt△BCN(HL),得出∠DAM=∠CBN,进而判断出△DCE≌△BCE (SAS),得出∠CDE=∠CBE,即可判断出∠AFD=90°,根据直角三角形斜边上的中线等于斜边的一半可得OF=AD=3,利用勾股定理列式求出OC,然后根据三角形的三边关系可知当O、F、C 三点共线时,CF的长度最小.方法剖析轴对称的性质(1)对应线段相等,对应角相等;对称点的连线被对称轴垂直平分;(2)轴对称图形变换的特征是不改变图形的形状和大小,只改变图形的位置,新旧图形具有对称性;(3)轴对称的两个图形,它们对应线段或延长线相交,交点在对称轴上.轴对称(折叠)的思考层次全等变换:对应边相等,对应角相等;对称轴性质:对应点所连线段被对称轴(折痕)垂直平分,对称轴(折痕)上的点到对应点的距离相等;指出:(1)在翻折下,前后的图形关于折痕成轴对称,注意前后的图形成镜面对称,即前后的图形的左右位置互换;(2)翻折或对称中建构勾股方程来求取线段长及对最值类问题进行探究;(3)轴对称常见的结构,折叠会产生垂直平分,等腰三形.导例答案:解:如图,在正方形ABC D中,AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE,在Rt△ADM和Rt△BCN中,,∴Rt△ADM≌Rt△BCN(HL),∴∠DAM=∠CBN,在△DCE和△BCE中,,∴△DCE≌△BCE(SAS),∴∠CDE=∠CBE∴∠DAM=∠CDE,∵∠ADF+∠CDE=∠ADC=90°,∴∠DAM+∠ADF=90°,∴∠AFD=180°﹣90°=90°,取AD的中点O,连接OF、OC,则OF=DO =AD=3,在Rt△OD C中,OC ==3根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC﹣OF=3﹣3.故答案为:3﹣3.典型例题类型一:利用已知直线作对称图形进行证明例1、在等边△AB C中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1).(1)求证:∠BAD=∠EDC;(2)点E关于直线BC的对称点为M,连接DM,AM.①依题意将图2补全;②证明:在点D运动的过程中,始终有DA=AM.【分析】(1)先判断出∠BAD+∠CAD=60°,进而得出∠BAD+∠E=60°,即可得出结论;(2)①由对称性即可补全图形;②由对称性判断出DM=DE,∠MDC=∠EDC,再用三角形的外角的性质,判断出∠ADC=∠B+∠BAD=∠B+∠MDC,进而判断出△ADM是等边三角形,即可得出结论.类型二:对已知图形进行翻折进行证明例2.如图,矩形ABC D中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.(1)求证:△DEC≌△EDA;(2)求DF的值;(3)在线段AB上找一点P,连结FP使FP⊥AC,连结PC,试判定四边形APCF的形状,并说明理由,直接写出此时线段PF的大小.【分析】(1)根据矩形的性质、轴对称的性质可得到AD=EC,AE=DC,即可证到△DEC≌△EDA (SSS);(2)易证AF=CF,设DF=x,则有AF=4﹣x,然后在Rt△ADF中运用勾股定理就可求出DF的长.(3)根据三角形的内角和定理求得∠APF=∠AFP根据等角对等边得出AF=AP进而得出FC=AP,从而证得四边形APCF是平行四边形,又因为FP⊥AC证得四边形APCF为菱形,然后根据菱形的面积S菱形=PF•AC=AP•AD,即可求得.专项突破1.如图,在Rt△AB C中,∠C=90°,点D、E分别是BC、AB上一个动点,连接DE.将点B沿直线DE折叠,点B的对应点为F,若AC=3,BC=4,当点F落在AC的三等分点上时,BD的长为.2.如图,正方形ABC D中,点E是BC延长线上一点,连接DE,过点B作BF⊥DE于点F,连接F C.(1)求证:∠FBC=∠CDF;(2)作点C关于直线DE的对称点G,连接CG,FG,猜想线段DF,BF,CG之间的数量关系,并证明你的结论.3.已知矩形ABCD,其中AD>AB,依题意先画出图形,然后解答问题.(1)F为DC边上一点,把△ADF沿AF折叠,使点D恰好落在BC上的点E处.在图1中先画出点E,再画出点F,若AB=8,AD=10,直接写出EF的长为;(2)把△ADC沿对角线AC折叠,点D落在点E处,在图2先画出点E,AE交CB于点F,连接BE.求证:△BEF是等腰三角形.4.如图,Rt△AB C中,∠ACB=90°,AC=BC,点D为AB边上的一个动点(不与点A,B及A B中点重合),连接CD,点A关于直线CD的对称点为点E,直线BE,CD交于点F.(1)如图1,当∠ACD=15°时,根据题意将图形补充完整,并直接写出∠BFC的度数;(2)如图2,当45°<∠ACD<90°时,用等式表示线段AC,EF,BF之间的数量关系,并加以证明.5.在Rt△AB C中,∠ACB=90°,CA=C B.点D为线段BC上一个动点(点D不与点B,C重合),连接AD,点E在射线AB上,连接DE,使得DE=D A.作点E关于直线BC的对称点F,连接BF,DF.(1)依题意补全图形;(2)求证:∠CAD=∠BDF;(3)用等式表示线段AB,BD,BF之间的数量关系,并证明.6.如图①,在等腰三角形AB C中,AB=AC=8,BC=14.如图②,在底边BC上取一点D,连结AD,使得∠DAC=∠AC D.如图③,将△ACD沿着AD所在直线折叠,使得点C落在点E处,连结BE,得到四边形ABE D.则BE的长是.7.在等边三角形ABC外侧作射线AP,∠BAP=α,点B关于射线AP的对称点为点D,连接CD交AP于点E.(1)依据题意补全图形;(2)当α=20°时,∠ADC= ;∠AEC= ;(3)连接BE,求证:∠AEC=∠BEC;(4)当0°<α<60°时,用等式表示线段AE,CD,DE之间的数量关系,并证明.8.在等边△ABC外侧作直线AP,点B关于直线AP的对称点为D,连结BD,CD,其中CD交直线AP与点E.(1)如图1,若∠P AB=30°,则∠ACE=;(2)如图2,若60°<∠P AB<120°,请补全图形,判断由线段AB,CE,ED可以构成一个含有多少度角的三角形,并说明理由.9.如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.(1)求证:△BDF是等腰三角形;(2)如图2,过点D作DG∥BE,交BC于点G,连结FG交BD于点O.①判断四边形BFDG的形状,并说明理由;②若AB=6,AD=8,求FG的长.10.【问题情境】如图①,在Rt△AB C中,∠ACB=90°,AC=BC,点D为A B中点,连结CD,点E为CB上一点,过点E且垂直于DE的直线交AC于点F.易知:BE=CF.(不需要证明)【探索发现】如图②,在Rt△AB C中,∠ACB=90°,AC=BC,点D为A B中点,连结CD,点E为CB的延长线上一点,过点E且垂直于DE的直线交AC的延长线于点F.【问题情境】中的结论还成立吗?请说明理由.【类比迁移】如图③,在等边△AB C中,AB=4,点D是A B中点,点E是射线AC上一点(不与点A、C重合),将射线DE绕点D逆时针旋转60°交BC于点F.当CF=2CE时,CE=.11.在△AB C中,∠ACB=90°,AC<BC,点D在AC的延长线上,点E在BC边上,且BE=AD,(1)如图1,连接AE,DE,当∠AEB=110°时,求∠DAE的度数;(2)在图2中,点D是AC延长线上的一个动点,点E在BC边上(不与点C重合),且BE=AD,连接AE,DE,将线段AE绕点E顺时针旋转90°得到线段EF,连接BF,DE.①依题意补全图形;②求证:BF=DE.专题十:与翻折或轴对称作图有关的几何证明题解析例1.解:(1)∵△ABC是等边三角形,∴∠BAC=∠ACB=60°,∴∠BAD+∠CAD=60°,∵DE=DA,∴∠CAD=∠E,∴∠BAD+∠E=60°,∵∠EDC+∠E=∠ACB=60°,∴∠BAD=∠EDC;(2)①补全图形如图2所示;②∵△ABC是等边三角形,∴∠B=60°,由对称性得,∠EDC=∠MDC,由(1)知,∠EDC=∠BAD,∴∠MDC=∠BAD,∵∠ADC=∠B+∠BAD=∠B+∠MD C.∴∠ADM=∠B=60°,由对称性得,DM=DE,∵DE=DA,∴DA=DM,∴△ADM是等边三角形,∴DA=DM,即:在点D运动的过程中,始终有DA=AM.例2.(1)证明:∵四边形ABCD是矩形,∴AD=BC,AB=CD,AB∥CD,∴∠ACD=∠CAB,∵△AEC由△ABC翻折得到,∴AB=AE,BC=EC,∠CAE=∠CAB,∴AD=CE,DC=EA,∠ACD=∠CAE,在△ADE与△CE D中,,∴△DEC≌△EDA(SSS);(2)解:如图1,∵∠ACD=∠CAE,∴AF=CF,设DF=x,则AF=CF=4﹣x,在RT△ADF中,AD2+DF2=AF2,即32+x2=(4﹣x)2,解得;x=,即DF=.(3)解:四边形APCF为菱形,设AC、FP相较于点O∵FP⊥AC∴∠AOF=∠AOP又∵∠CAE=∠CAB,∴∠APF=∠AFP∴AF=AP∴FC=AP又∵AB∥CD∴四边形APCF是平行四边形又∵FP⊥AC∴四边形APCF为菱形,在矩形ABC D中,AB=4,AD=3,∴AC=5,∵S菱形=PF•AC=AP•AD,∵AP=AF=4﹣=∴PF==.专项突破1.解:∵折叠∴BD=DF,∵点F落在AC的三等分点上∴CF=1或CF=2,若CF=1时,在Rt△CDF中,DF2=CD2+CF2,∴BD2=(4﹣BD)2+1∴BD=当CF=2时,在Rt△CDF中,DF2=CD2+CF2,∴BD2=(4﹣BD)2+4∴BD=故答案为:或2.解:(1)∵ABCD为正方形,∴∠DCE=90°.∴∠CDF+∠E=90°,又∵BF⊥DE,∴∠FBC+∠E=90°,∴∠FBC=∠CDF(2)如图所示:在线段FB上截取FM,使得FM=F D.∵∠BDC=∠MDF=45°,∴∠BDM=∠CDF,∵==,∴△BDM∽△CDF,∴==,∠DBM=∠DCF,∴BM=CF,∴∠CFE=∠FCD+∠CDF=∠DBM+∠BDM=∠DMF=45°,∴∠EFG=∠EFC=45°,∴∠CFG=90°,∵CF=FG,∴CG=CF,∴BM=CG,∴BF=BM+FM=CG+DF.补充方法:连接GM,证明四边形BMGC是平行四边形即可.3.解:(1)如图1,在BC上截取AE=AD得点E,作AF垂直DE交CD于点F(或作∠AED的平分线AF交CD于点F,或作EF垂直AE交CD于点F等等),∵四边形ABCD是矩形,∴AB=CD=8,AD=BC=10,∠B=∠C=90°,在Rt△ABE中,BE==6,∴EC=10﹣6=4,设EF=DF=x,在Rt△EF C中,则有x2=(8﹣x)2+42,解得x=5,∴EF=5.故答案为:5;(2)证明:如图2,作DH垂直AC于点H,延长DH至点E,使HE=DH.方法1:∵△ADC≌△AEC,∴AD=AE=BC,AB=DC=EC,在△ABE与△CE B中,,∴△ABE≌△CEB(SSS),∴∠AEB=∠CBE,∴BF=EF,∴△BEF是等腰三角形.方法2:∵△ADC≌△AEC,∴AD=AE=BC,∠DAC=∠EAC,又∴AD∥BC,∴∠DAC=∠ACB,∴∠EAC=∠ACB,∴F A=FC,∴FE=FB,∴△BEF是等腰三角形.4.(1)如图1中,连接E C.∵A,E关于CD对称,∴∠DCA=∠DCE=15°,CA=CE=C B.∵∠ACB=90°,∴∠ECB=60°,∴△ECB是等边三角形,∴∠CEB=60°,∵∠CEB=∠BFC+∠DCE,∴∠BFC=60°-15°=45°.(2)结论:EF2+BF2=2AC2.理由:如图2,连接CE,AF,延长AC交FE的延长线于点G.∵A,E关于CD对称,∴AC=CE,AF=EF,又∵CF=CF,∴△ACF≌△ECF(SSS),∴∠CAF=∠1,∵AC=BC,∴BC=CE,∴∠1=∠2,∴∠CAF=∠2,∵∠ACB=90°,∴∠G+∠2=90°,∴∠CAF+∠G=90°,∴∠AFG=90°,在Rt△AF B中,AB2=AF2+BF2,在Rt△AB C中,AB2=AC2+BC2=2AC2,∴BF2+AF2=2AC2,∴BF2+EF2=2AC2.5.(1)如图所示:(2)∵∠ACB=90°,CA=CB,∴∠BAC=∠CBA=45°,∴∠CAD+∠DAB=45°,∵DA=DE,∴∠DAE=∠DEB,∵∠DBA是△DBE的一个外角,∴∠EDB+∠DEB=∠DBA=45°,∴∠EDB=∠CAD,∵点E关于直线BC的对称点F,∴∠EDB=∠FDB,∴∠CAD=∠FDB;(3)线段AB,BD,BF之间的数量关系是AB﹣BF=√2BD,证明:过点D作AC的平行线交AB于M点,∴∠C=∠MDB=90°,∠CAB=∠DMB=45°,∴∠DMB=∠DBM,∴DM=DB,∴MB=√2BD,∵点E关于直线BC的对称点F,∴DE=DF,∵AD=DE,∴AD=DF,∵AC∥MD,∴∠CAD=∠ADM,∵∠CAD=∠FDB,∴∠ADM=∠FDB,∴△ADM≌△FDB(SAS),∴AM=BF,∴AB﹣BF=AB﹣AM=MB,又∵MB=√2BD,∴AB﹣BF=√2B D.6.解:∵AB=AC,∴∠ABC=∠C,∵∠DAC=∠ACD,∴∠DAC=∠ABC,∵∠C=∠C,∴△CAD∽△CBA,∴=,∴=,∴CD=,BD=BC﹣CD=,∵∠DAM=∠DAC=∠DBA,∠ADM=∠ADB,∴△ADM∽△BDA,∴=,即=,∴DM=,MB=BD﹣DM=,∵∠ABM=∠C=∠MED,∴A、B、E、D四点共圆,∴∠ADB=∠BEM,∠EBM=∠EAD=∠ABD,∴△ABD∽△MBE,∴=,∴BE ===.故答案为:.7.(1)如图;EDP(2)40°;60 °;(3)证明:∵点B关于射线AP的对称点为点D,∴△BAE≌△DAE.∴∠BAE=∠DAE=α.∵AD=AB=AC,∴∠ADC=()1806022α︒-︒+=60°-α.∴∠AEC=60°.∵∠ACB=60°,∠ACD=∠ADC=60°-α,∴∠BCE=α.∵∠ABC=60°,∠ABE=∠ADC=60°-α,∴∠BEC=60°.(4)证明:法一:在CD上截取AF=AE.F EDAB C P∵∠AEF =60°,∴△AEF 是等边三角形.∴∠AFC =∠AED =120°.∵∠ACD =∠ADC =60°-α,∴△ADE ≌△ACF .∴DE =CF .∴CD =2DE +EF .∵AE =EF ,∴CD =2DE +AE .法二:在CD 上截取BG =BE .GEDAB C P∵∠BEC =60°,∴△BEG 是等边三角形.∴∠BGC =∠AED =120°.∵∠BCE =∠DAE =α,∴△BCG ≌△DAE .∴AE =CG .∵EG =BE =DE ,∴CD =2DE +CG .∴CD =2DE +AE .8.解:(1)连接AD ,如图1.∵点D 与点B 关于直线AP 对称,∴AD =AB ,∠DAP =∠BAP =30°,∵AB =AC ,∠BAC =60°,∴AD =AC ,∠DAC =120°,∴2∠ACE +60°+60°=180°,∴∠ACE =30°,故答案为:30°;(3)线段AB ,CE ,ED 可以构成一个含有60°角的三角形.证明:连接AD ,EB ,如图2.∵点D 与点B 关于直线AP 对称,∴AD =AB ,DE =BE ,∴∠EDA =∠EBA ,∵AB =AC ,AB =AD ,∴AD =AC ,∴∠ADE =∠ACE ,∴∠ABE =∠ACE .设AC ,BE 交于点F ,又∵∠AFB =∠CFE ,∴∠BAC =∠BEC =60°,∴线段AB ,CE ,ED 可以构成一个含有60°角的三角形.9.(1)根据折叠,∠DBC =∠DBE ,又AD ∥BC ,∴∠DBC =∠ADB ,∴∠DBE =∠ADB ,∴DF =BF ,∴△BDF 是等腰三角形(2)①菱形,理由:∵四边形ABCD 是矩形,∴AD ∥BC ,∴FD ∥BG ,又∵FD ∥BG ,∴四边形BFDG 是平行四边形,∵DF =BF ,∴四边形BFDG 是菱形②∵AB =6,AD =8,∴BD =10.∴OB =12BD =5.设DF =BF =x ,∴AF =AD -DF =8-x .∴在Rt △ABF 中,AB 2+AF 2=BF 2,即62+(8-x )2=x 2,解得x =254,即BF =254,∴FO =BF 2-OB 2=(254)2-52=154,∴FG =2FO =152 10.解:【问题情境】证明:∵在Rt △AB C 中,∠ACB =90°,AC =BC ,点D 为A B 中点, ∴CD ⊥AB ,CD =BD =AD =AB ,∠BCD =∠B =45°,∴∠BDC =90°,∵∠EDF =90°,∴∠CDF=∠BDE,在△BDE与△CDF中,,∴△BDE≌△CDF(ASA),∴BE=CF;【探索发现】成立,理由:∵在Rt△AB C中,D为A B中点,∴CD=BD,又∵AC=BC,∴DC⊥AB,∴∠DBC=∠DCB=45°,∵DE⊥DF,∴∠EDF=90°,∴∠EDB+∠BDF=∠CDF+∠BDF=90°,∴∠CDF=∠BDE,∴∠ADF=∠CDE,∴AF=CE,∴CF=BE;【类比迁移】∵△ABC是等边三角形,∴∠A=∠B=60°,∵∠FDE=60°,∴∠BDF=120°﹣∠ADE,∠AED=120°﹣∠ADE,∴∠BDF=∠AED,∴△ADE∽△BDF,∴,∵点D为A B中点,AB=4,∴AD=BD=2,AC=BC=4,∵CF=2CE,∴设CE=x,则CF=2x,当点E在线段AC上时,∴AE=4﹣x,BF=4﹣2x,∴=,解得:x=3﹣,x=3+(不合题意,舍去),∴CE=3﹣,如图④,当点E在AC的延长线上时,∵AE=4+x,BF=4﹣2x,∴=,解得:x=﹣1+,(负值舍去),∴CE=﹣1+.综上所述,CE=3﹣或﹣1+,故答案为:3﹣或﹣1+.11.解:(1)∵∠AEB=110°,∠ACB=90°,∴∠DAE=∠AEB﹣∠ACB=20°;(2)①补全图形,如图所示.②证明:由题意可知∠AEF=90°,EF=AE.∵∠ACB=90°,∴∠AEC+∠BEF=∠AEC+∠DAE=90°.∴∠BEF=∠DAE.∵在△EBF和△ADE中,,∴△EBF≌△ADE(SAS).∴DE=BF.。
高考数学专题几何证明选讲

编写说明:考虑到复习实际,本书将选修4-5不等式选讲与前面第六章不等式、推理与证明整合编写。
选修4-1几何证明选讲第一节相似三角形的判定及有关性质1.平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.推论1:经过三角形一边的中点与另一边平行的直线必平分第三边.推论2:经过梯形一腰的中点,且与底边平行的直线平分另一腰.2.平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例.推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.3.相似三角形的判定与性质(1)判定定理:(2)1.在使用平行线截割定理时易出现对应线段、对应边对应顺序混乱,导致错误. 2.在解决相似三角形的判定或应用时易出现对应边和对应角对应失误. [试一试]1.如图,F 为▱ABCD 的边AD 延长线上的一点,DF =AD ,BF 分别交DC ,AC 于G ,E 两点,EF =16,GF =12,则BE 的长为________.解析:由DF =AD ,AB ∥CD 知BG =GF =12,又EF =16知EG =4,故BE =8.答案:82.在△ABC 中,点D 在线段BC 上,∠BAC =∠ADC ,AC =8,BC =16,则CD =________. 解析:∵∠BAC =∠ADC ,∠C =∠C ,∴△ABC ∽△DAC ,∴BC AC =AC CD ,∴CD =AC 2BC =8216=4.答案:41.判定两个三角形相似的常规思路 (1)先找两对对应角相等;(2)若只能找到一对对应角相等,则判断相等的角的两夹边是否对应成比例;(3)若找不到角相等,就判断三边是否对应成比例,否则考虑平行线分线段成比例定理及相似三角形的“传递性”.2.借助图形判断三角形相似的方法 (1)有平行线的可围绕平行线找相似;(2)有公共角或相等角的可围绕角做文章,再找其他相等的角或对应边成比例; (3)有公共边的可将图形旋转,观察其特征,找出相等的角或成比例的对应边. [练一练]1.如图,D ,E 分别是△ABC 的边AB ,AC 上的点,DE ∥BC 且ADDB =2,那么△ADE 与四边形DBCE 的面积比是________.解析:∵DE ∥BC ,∴△ADE ∽△ABC ,∴S △ADE S △ABC =AD 2AB 2. ∵AD DB =2,∴AD AB =23,∴S △ADE S △ABC =49, ∴S △ADES 四边形DBCE =45.答案:452.如图,已知在△ABC 中,CD ⊥AB 于D 点,BC 2=BD ·AB ,则∠ACB =______.解析:在△ABC 与△CBD 中, 由BC 2=BD ·AB , 得BC BD =ABBC,且∠B =∠B , 所以△ABC ∽△CBD .则∠ACB =∠CDB =90°. 答案:90°平行线分线段成比例定理的应用,AE 交BD 于F ,则BF ∶FD =________.解析:∵AD =BC ,BE ∶EC =2∶3, ∴BE ∶AD =2∶5. ∵AD ∥BC ,∴BF ∶FD =BE ∶AD =2∶5.即BF ∶FD =25.答案:2∶52.(2013·惠州调研)如图,在△ABC 中,DE ∥BC ,DF ∥AC ,AE ∶AC =3∶5,DE =6,则BF =________.解析:由DE ∥BC 得DE BC =AE AC =35,∵DE =6,∴BC =10. 又因为DF ∥AC ,所以BF BC =BD AB =CE AC =25,即BF =4.答案:43.如图,在四边形ABCD 中,EF ∥BC ,FG ∥AD ,则EF BC +FGAD =________.解析:由平行线分线段成比例定理得 EF BC =AF AC ,FG AD =FC AC , 故EF BC +FG AD =AF AC +FC AC =AC AC=1. 答案:1 [类题通法]比例线段常用平行线产生,利用平行线转移比例是常用的证题技巧,当题中没有平行线条件而有必要转移比例时,也常添加辅助平行线,从而达到转移比例的目的.相似三角形的判定及性质[典例] O 内一点E ,过E 作BC 的平行线与AD 的延长线交于点P .已知PD =2DA =2,则PE =________.[解析] 由PE ∥BC 知,∠A =∠C =∠PED .在△PDE 和△PEA 中,∠APE =∠EPD ,∠A =∠PED ,故△PDE ∽△PEA ,则PD PE =PEP A,于是PE 2=P A ·PD =3×2=6,所以PE = 6.[答案]6[类题通法]1.判定两个三角形相似要注意结合图形特征灵活选择判定定理,特别要注意对应角和对应边.2.相似三角形的性质可用来证明线段成比例、角相等;也可间接证明线段相等. [针对训练](2013·佛山质检)如图,∠B =∠D ,AE ⊥BC ,∠ACD =90°,且AB =6,AC =4,AD =12,则BE =________.解析:由于∠B =∠D ,∠AEB =∠ACD ,所以△ABE ∽△ADC ,从而得AB AD =AEAC,解得AE =2,故BE =AB 2-AE 2=4 2.答案:4 2射影定理的应用[典例] AD ⊥BC 于D∠ABC 的平分线,交AD 于F ,求证:DF AF =AE EC.[证明] 由三角形的内角平分线定理得,在△ABD 中,DF AF =BDAB ,① 在△ABC 中,AE EC =ABBC,②在Rt △ABC 中,由射影定理知,AB 2=BD ·BC , 即BD AB =ABBC. ③ 由①③得:DF AF =ABBC ,④由②④得:DF AF =AEEC .[类题通法]1.在使用直角三角形射影定理时,要学会将“乘积式”转化为相似三角形中的“比例式”.2.证题时,要注意作垂线构造直角三角形是解直角三角形时常用的方法. [针对训练]在Rt △ACB 中,∠C =90°,CD ⊥AB 于D ,若BD ∶AD =1∶9,则tan ∠BCD =________. 解析:由射影定理得CD 2=AD ·BD ,又BD ∶AD =1∶9, 令BD =x ,则AD =9x (x >0).∴CD 2=9x 2,∴CD =3x . Rt △CDB 中,tan ∠BCD =BD CD =x 3x =13.答案:13第二节直线与圆的位置关系1.圆周角定理 (1)圆周角定理圆上一条弧所对的圆周角等于它所对的圆心角的一半. (2)圆心角定理圆心角的度数等于它所对弧的度数.推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.2.圆内接四边形的性质与判定定理(1)性质定理1:圆内接四边形的对角互补.定理2:圆内接四边形的外角等于它的内角的对角.(2)判定判定定理:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.推论:如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.3.圆的切线性质及判定定理(1)性质:性质定理:圆的切线垂直于经过切点的半径.推论1:经过圆心且垂直于切线的直线必经过切点.推论2:经过切点且垂直于切线的直线必经过圆心.(2)判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.(3)弦切角定理:弦切角等于它所夹的弧所对的圆周角.4.与圆有关的比例线段(1)相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.(2)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.(4)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.1.易混圆心角与圆周角,在使用时注意结合图形作出判断.2.在使用相交弦定理、割线定理、切割线定理时易出现比例线段对应不成比例而失误.[试一试]1.如图,P是圆O外一点,过P引圆O的两条割线PB、PD,P A=AB=5,CD=3,则PC=________.解析:设PC=x,由割线定理知P A·PB=PC·PD.即5×25=x(x+3),解得x=2或x=-5(舍去).故PC=2.答案:22.如图,EB ,EC 是⊙O 的两条切线,B ,C 是切点,A ,D 是⊙O 上两点,如果∠E =46°,∠DCF =32°,则∠BAD =________.解析:由已知,显然△EBC 为等腰三角形, 因此有∠ECB =180°-∠E 2=67°,因此∠BCD =180°-∠ECB -∠DCF =81°. 而由A ,B ,C ,D 四点共圆, 得∠BAD =180°-∠BCD =99°. 答案:99°1.与圆有关的辅助线的五种作法 (1)有弦,作弦心距.(2)有直径,作直径所对的圆周角. (3)有切点,作过切点的半径. (4)两圆相交,作公共弦. (5)两圆相切,作公切线. 2.证明四点共圆的常用方法(1)利用圆内接四边形的判定定理,证明四点组成的四边形的对角互补; (2)证明它的一个外角等于它的内对角; (3)证明四点到同一点的距离相等.当证明四点共圆以后,圆的各种性质都可以得到应用. 3.圆幂定理与圆周角、弦切角联合应用时,要注意找相等的角,找相似三角形,从而得出线段的比,由于圆幂定理涉及圆中线段的数量计算,所以应注意代数法在解题中的应用.[练一练]1.(2013·荆州模拟)如图,P A 是⊙O 的切线,切点为A ,过P A的中点M 作割线交⊙O 于点B 和C ,若∠BMP =110°,∠BPC =30°,则∠MPB =________.解析:由切割线定理得,MA 2=MB ·MC ,又MA =MP ,故MP 2=MB ·MC ,即MB MP =MP MC ,又∠BMP =∠PMC .故△BMP ∽△PMC ,所以∠MPB =∠MCP ,所以30°+∠MPB +∠MCP =∠AMB =180°-110°=70°,所以∠MPB =20°.答案:20°2.(2013·长沙一模)如图,过圆O 外一点P 分别作圆的切线和割线交圆于点A ,点B ,且PB =7,C 是圆上一点,使得BC =5,∠BAC =∠APB ,则AB =________.解析:由P A 为圆O 的切线可得,∠P AB =∠ACB ,又∠BAC =∠APB ,于是△APB ∽△CAB ,所以PB AB =ABBC,而PB =7,BC =5,故AB 2=PB ·BC =7×5=35,即AB =35. 答案:35圆周角、弦切角和圆的切线问题1.(2013·天津高考)如图, △ABC 为圆的内接三角形, BD 为圆的弦, 且BD ∥AC . 过点A 作圆的切线与DB 的延长线交于点E ,AD 与BC 交于点F .若AB =AC ,AE =6,BD = 5,则线段CF 的长为________.解析:因为AE 是圆的切线,且AE =6,BD =5,由切割线定理可得EA 2=EB ·ED ,即36=EB ·(EB +5),解得EB =4.又∠BAE =∠ADB =∠ACB =∠ABC ,所以AE ∥BC .又AC ∥BD ,所以四边形AEBC 是平行四边形,所以AE =BC =6,AC =EB =4.又由题意可得△CAF ∽△CBA ,所以CA CB =CFCA ,CF=CA 2CB =166=83. 答案:832.(2013·广东高考)如图,AB 是圆O 的直径,点C 在圆O 上.延长BC 到D 使BC =CD ,过C 作圆O 的切线交AD 于E .若AB =6,ED =2,则BC =________.解析:连接OC ,则OC ⊥CE ,∠OCA +∠ACE =90°,∵∠OAC =∠OCA ,∴∠OAC +∠ACE =90°.易知Rt △ACB ≌Rt △ACD ,则∠OAC =∠EAC .∴∠EAC +∠ACE =90°,∴∠AEC =90°,在Rt △ACD 中,由射影定理得:CD 2=ED ·AD ①,又CD =BC ,AD =AB ,将AB =6,ED =2代入①式,得CD = 12=2 3,∴BC =2 3.答案:2 33.(2014·岳阳模拟)如图所示,⊙O 的两条切线P A 和PB 相交于点P ,与⊙O 相切于A ,B 两点,C 是⊙O 上的一点,若∠P =70°,则∠ACB =________.解析:如图所示,连接OA ,OB , 则OA ⊥P A ,OB ⊥PB .故∠AOB =110°, ∴∠ACB =12∠AOB =55°.答案:55° [类题通法]1.圆周角定理及其推论与弦切角定理及其推论多用于推出角的关系,从而证明三角形全等或相似,可求线段或角的大小.2.涉及圆的切线问题时要注意弦切角的转化;关于圆周上的点,常作直径(或半径)或向弦(弧)两端作圆周角或弦切角.圆内接四边形的性质及判定[典例]是AB 延长线上的一点,GCD 是⊙O 的割线,过点G 作AG 的垂线,交直线AC 于点E ,交直线AD 于点F ,过点G 作⊙O 的切线,切点为H .(1)求证:C ,D ,E ,F 四点共圆; (2)若GH =6,GE =4,求EF 的长.[解] (1)证明:连接DB , ∵AB 是⊙O 的直径, ∴∠ADB =90°,在Rt △ABD 与Rt △AFG 中,∠ABD =∠AFE , 又∠ABD =∠ACD , ∴∠ACD =∠AFE , ∴C ,D ,E ,F 四点共圆.(2)⎭⎪⎬⎪⎫C ,D ,E ,F 四点共圆⇒GE ·GF =GC ·GD GH 切⊙O 于点H ⇒GH 2=GC ·GD ⇒GH 2=GE ·GF , 又GH =6,GE =4,∴GF =9,EF =GF -GE =5. [类题通法]证明多点共圆,当它们在一条线段同侧时,可证它们对此线段张角相等,也可以证明它们与某一定点距离相等;如两点在一条线段异侧,则证明它们与线段两端点连成的凸四边形对角互补.[针对训练]如图所示,在四边形ABCP 中,线段AP 与BC 的延长线交于点D ,已知AB =AC 且A ,B ,C ,P 四点共圆.(1)求证:PC AC =PDBD;(2)若AC =4,求AP ·AD 的值.解:(1)证明:因为点A ,B ,C ,P 四点共圆,所以∠ABC +∠APC =180°,又因为∠DPC +∠APC =180°,所以∠DPC =∠ABC ,又因为∠D =∠D ,所以△DPC ∽△DBA ,所以PC AB =PD BD ,又因为AB =AC ,所以PC AC =PD BD. (2)因为AB =AC ,所以∠ACB =∠ABC ,又∠ACD +∠ACB =180°,所以∠ACD +∠ABC =180°.由于∠ABC +∠APC =180°,所以∠ACD =∠APC ,又∠CAP =∠DAC ,所以△APC ∽△ACD ,所以AP AC =ACAD ,所以AP ·AD =AC 2=16. 与圆有关的比例线段[典例] 是∠ACB 的平分线,△ACD 的外接圆交BC 于点E ,AB =2AC .(1)求证:BE =2AD ;(2)当AC =1,EC =2时,求AD 的长.[解] (1)证明:连接DE ,因为四边形ACED 是圆的内接四边形,所以∠BDE =∠BCA , 又∠DBE =∠CBA ,所以△BDE ∽△BCA , 所以BE BA =DE CA ,而AB =2AC , 所以BE =2DE .又CD 是∠ACB 的平分线,所以AD =DE ,从而BE =2AD . (2)由已知得AB =2AC =2,设AD =t (0<t <2),根据割线定理得, BD ·BA =BE ·BC ,即(AB -AD )·BA =2AD ·(2AD +CE ),11 所以(2-t )×2=2t (2t +2),即2t 2+3t -2=0,解得t =12,即AD =12. [类题通法]1.应用相交弦定理、切割线定理要抓住几个关键内容:如线段成比例与相似三角形、圆的切线及其性质、与圆有关的相似三角形等.2.相交弦定理、切割线定理主要用于与圆有关的比例线段的计算与证明.解决问题时要注意相似三角形知识与圆周角、弦切角、圆的切线等相关知识的综合应用.[针对训练](2014·郑州模拟)如图,已知⊙O 和⊙M 相交于A ,B 两点,AD 为⊙M 的直径,直线BD 交⊙O 于点C ,点G 为弧BD 的中点,连接AG 分别交⊙O ,BD 于点E ,F ,连接CE.求证:(1)AG ·EF =CE ·GD ;(2)GF AG =EF 2CE 2. 证明:(1)连接AB ,AC ,∵AD 为⊙M 的直径,∴∠ABD =90°,∴AC 为⊙O 的直径,∴∠CEF =∠AGD =90°.∵G 为弧BD 的中点,∴∠DAG =∠GAB =∠ECF .∴△CEF ∽△AGD ,∴CE AG =EF GD,∴AG ·EF =CE ·GD . (2)由(1)知∠DAG =∠GAB =∠FDG ,又∠G =∠G ,∴△DFG ∽△ADG ,∴DG 2=AG ·GF .由(1)知EF 2CE 2=GD 2AG 2,∴GF AG =EF 2CE 2.。
2019届中考数学复习《几何证明与计算》专题训练含答案
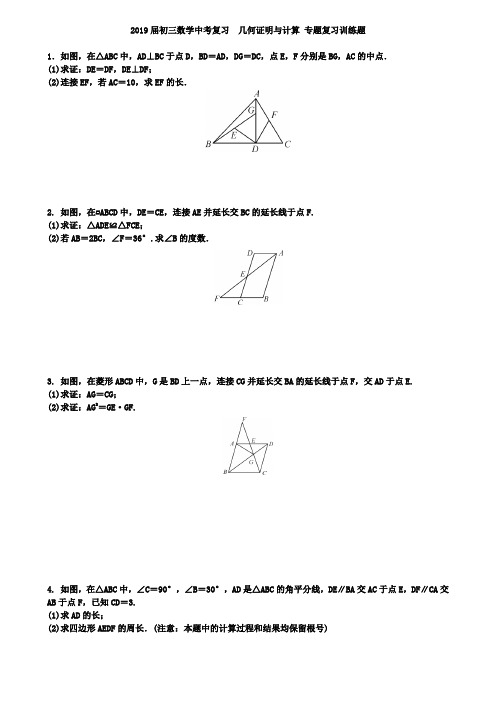
2019届初三数学中考复习几何证明与计算专题复习训练题1.如图,在△ABC中,AD⊥BC于点D,BD=AD,DG=DC,点E,F分别是BG,AC的中点.(1)求证:DE=DF,DE⊥DF;(2)连接EF,若AC=10,求EF的长.2. 如图,在▱ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.(1)求证:△ADE≌△FCE;(2)若AB=2BC,∠F=36°.求∠B的度数.3. 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.(1)求证:AG=CG;(2)求证:AG2=GE·GF.4. 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.(1)求AD的长;(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)5. 如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.6. 如图,点E是正方形ABCD的边BC延长线上一点,连接DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于点H,交CD于点G.(1)求证:BG=DE;(2)若点G为CD的中点,求HGGF的值.7. 如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.8. 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.(1)求证:△ACD∽△BFD;(2)当tan∠ABD=1,AC=3时,求BF的长.9. 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.(1)求证:AG=CG;(2)求证:AG2=GE·GF.10. 如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF,延长DB交EF于点N.(1)求证:AD=AF;(2)求证:BD=EF;(3)试判断四边形ABNE的形状,并说明理由.11. 在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.(1)如图①,若AB=32,BC=5,求AC的长;(2)如图②,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.12. 如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.(1)求证:△ABM∽△EFA;(2)若AB=12,BM=5,求DE的长.参考答案:1. 解:(1)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°.在△BDG和△ADC中,⎩⎪⎨⎪⎧BD =AD ,∠BDG =∠ADC DG =DC ,,∴△BDG ≌△ADC. ∴BG =AC ,∠BGD =∠C.∵∠ADB=∠ADC=90°, E ,F 分别是BG ,AC 的中点,∴DE =12BG =EG ,DF =12AC =AF.∴DE=DF ,∠EDG =∠EGD,∠FDA =∠FAD.∴∠EDG+∠FDA=90°,∴DE ⊥DF.(2)∵AC=10,∴DE =DF =5,由勾股定理,得EF =DE 2+DF 2=5 2. 2. 解:(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC.∴∠D=∠ECF.在△ADE 和△FCE 中,⎩⎪⎨⎪⎧∠D=∠ECF,DE =CE ,∠AED =∠FEC,∴△ADE ≌△FCE(ASA).(2)∵△ADE≌△FCE,∴AD=FC.∵AD=BC ,AB =2BC ,∴AB=FB.∴∠BAF=∠F=36°.∴∠B=180°-2×36°=108°. 3. 证明:(1)∵四边形ABCD 是菱形,∴AB ∥CD ,AD =CD ,∠ADB =∠CDB.又GD 为公共边,∴△ADG ≌△CDG(SAS),∴AG =CG. (2)∵△ADG≌△CDG,∴∠EAG =∠DCG.∵AB∥CD,∴∠DCG =∠F.∴∠EAG=∠F.∵∠AGE=∠AGE,∴△AGE ∽△FGA.∴AG FG =EG AG.∴AG 2=GE·GF. 4. 解:(1)∵∠C=90°,∠B =30°,∴∠CAB =60°.∵AD 平分∠CAB ,∴∠CAD =12∠CAB=30°.在Rt △ACD 中,∵∠ACD =90°,∠CAD =30°,∴AD =2CD =6. (2)∵DE∥BA 交AC 于点E ,DF ∥CA 交AB 于点F , ∴四边形AEDF 是平行四边形,∠EAD =∠ADF=∠DAF. ∴AF=DF.∴四边形AEDF 是菱形.∴AE=DE =DF =AF. 在Rt △CED 中,∵DE ∥AB ,∴∠CDE =∠B=30°. ∴DE =CDcos30°=2 3.∴四边形AEDF 的周长为8 3.5. 解:(1)证明:∵四边形ABCD 是菱形,∴∠B =∠D,AB =BC =DC =AD.∵点E ,O ,F 分别为AB ,AC ,AD 的中点,∴AE =BE =DF =AF ,OF =12DC ,OE =12BC ,OE ∥BC.在△BCE 和△DCF 中,⎩⎪⎨⎪⎧BE =DF ,∠B =∠D,BC =DC ,∴△BCE ≌△DCF(SAS). (2)当AB⊥BC 时,四边形AEOF 是正方形, 理由如下:由(1)得AE =OE =OF =AF ,∴四边形AEOF 是菱形.∵AB⊥BC,OE∥BC,∴OE⊥AB.∴∠AEO=90°.∴四边形AEOF 是正方形.6. 解:(1)证明:∵BF⊥DE,∴∠GFD =90°.∵∠BCG =90°,∠BGC =∠DGF,∴∠CBG =∠CDE. 在△BCG 与△DCE 中.⎩⎪⎨⎪⎧∠CBG=∠CDE,BC =CD ,∠BCG =∠DCE,∴△BCG ≌△DCE(ASA),∴BG =DE.(2)设CG =x ,∵G 为CD 的中点,∴GD =CG =x , 由(1)可知△BCG≌△DCE(ASA),∴CG =CE =x.由勾股定理可知DE =BG =5x ,∵sin ∠CDE =CE DE =GFGD ,∴GF=55x.∵AB∥CG,∴△ABH ∽△CGH.∴AB CG =BH GH =21. ∴BH=253x ,GH =53x.∴HG GF =53.7. 解:(1)结论:AG 2=GE 2+GF 2.理由:连接CG.∵四边形ABCD 是正方形,∴点A ,C 关于对角线BD 对称. ∵点G 在BD 上,∴GA=GC.∵GE⊥DC 于点E ,GF⊥BC 于点F , ∴∠GEC=∠ECF=∠CFG=90°.∴四边形EGFC 是矩形.∴CF=GE.在Rt △GFC 中,∵CG 2=GF 2+CF 2,∴AG 2=GF 2+GE 2.(2)过点B 作BN⊥AG 于点N ,在BN 上取一点M ,使得AM =BM.设AN =x.∵∠AGF=105°,∠FBG =∠FGB=∠ABG=45°, ∴∠AGB =60°,∠GBN =30°,∠ABM =∠MAB=15°.∴∠AMN =30°.∴AM =BM =2x ,MN =3x.在Rt △ABN 中,∵AB 2=AN 2+BN 2,∴1=x 2+(2x +3x)2,解得x =6-24,∴BN =6+24.∴BG=BN cos30°=32+66. 8. 解:(1)∵AD⊥BC,BE ⊥AC ,∴∠BDF =∠ADC=∠BEC=90°,∴∠C +∠DBF=90°,∠C +∠DAC=90°,∴∠DBF =∠DAC,∴△ACD ∽△BFD(2)∵tan ∠ABD =1,∠ADB =90°,∴AD BD =1,∵△ACD ∽△BFD ,∴AC BF =ADBD=1,∴BF =AC =39. 解:(1)∵四边形ABCD 是菱形,∴AB ∥CD ,AD =CD ,∠ADB =∠CDB,可证△ADG≌△CDG(SAS),∴AG =CG(2)∵△ADG≌△CDG,∴∠EAG =∠DCG,∵AB ∥CD ,∴∠DCG =∠F,∴∠EAG =∠F,∵∠AGE =∠AGE,∴△AGE ∽△FGA ,∴AG FG =EG AG,∴AG 2=GE·GF10. 解:(1)∵AB=AC ,∠BAC =90°,∴∠ABC =∠ACB =45°,∴∠ABF =135°,∵∠BCD =90°,∴∠ACD =∠ACB+∠BCD=135°,∴∠ABF =∠ACD,∵CB =CD ,CB =BF ,∴BF =CD ,可证△ABF≌△ACD(SAS),∴AD =AF(2)由(1)知AF =AD ,△ABF ≌△ACD ,∴∠FAB =∠DAC,∵∠BAC =90°,∴∠EAB =∠BAC=90°,∴∠EAF =∠BAD,可证△AEF≌△ABD(SAS),∴BD =EF(3)四边形ABNE 是正方形.理由如下:∵CD=CB ,∠BCD =90°,∴∠CBD =45°,又∵∠ABC=45°,∴∠ABD =∠ABC+∠CBD=90°,由(2)知∠EAB=90°,△AEF ≌△ABD ,∴∠AEF =∠ABD=90°,∴四边形ABNE 是矩形,又∵AE=AB ,∴四边形ABNE 是正方形 11. 解:(1)∵∠ABM=45°,AM ⊥BM ,∴AM =BM =ABcos45°=32×22=3. 则CM =BC -BM =5-3=2,∴AC =AM 2+CM 2=22+32=13.(2)证明:延长EF 到点G ,使得FG =EF ,连接BG.∵DM =MC ,∠BMD =∠AMC ,BM =AM ,∴△BMD≌△AMC(SAS).∴AC =BD.又CE =AC ,∴BD =CE.∵BF =FC ,∠BFG =∠EFC ,FG =FE ,∴△BFG≌△CFE.∴BG=CE ,∠G=∠E.∴BD=CE =BG ,∴∠BDG=∠G=∠E. 12. 解:(1)证明:∵四边形ABCD 是正方形, ∴AB=AD ,∠B=90°,AD∥BC.∴∠AMB=∠EA F.又∵EF⊥AM,∴∠AFE=90°.∴∠B=∠AFE.∴△ABM∽△EFA. (2)∵∠B=90°,AB =AD =12,BM =5,∴AM =122+52=13.∵F 是AM 的中点,∴AF =12AM =6.5.∵△ABM∽△EFA,∴BM AF =AM AE ,即56.5=13AE.∴AE =16.9,∴DE =AE -AD =4.9.2019-2020学年数学中考模拟试卷一、选择题1.已知二次函数y =ax 2+bx+c (a≠0),过(1,y 1)、(2,y 2).下列结论:①若y 1>0时,则a+b+c >0; ②若a =2b 时,则y 1<y 2;③若y 1<0,y 2>0,且a+b <0,则a >0.其中正确的结论个数为( ) A .0个B .1个C .2个D .3个2.已知直线a ∥b ,将一块含45o角的直角三角板(∠C=90o)按如图所示的位置摆放,若∠1=55o,则∠2 的度数为( )A .85oB .70oC .80oD .75o3.如图,⊙O 与BC 相切于点B ,弦AB ∥OC ,若∠C =40°,则∠AOB 的度数是( )A.60B.70°C.80°D.90°4.如图,点P(-a,2a)是反比例函数与的一个交点,图中阴影部分的面积为5π,则反比例函数的解析是为( )A. B. C. D.5.如图,等边三角形ABC ,B 点在坐标原点,C 点的坐标为(4,0),则点A 的坐标为( )A .(2,3)B .(2,)C .(,2)D .(2,6.如图,在平面直角坐标系中,四边形OABC 是菱形,点C 的坐标为(4,0),60AOC ∠=︒,垂直于x 轴的直线l 从y 轴出发,沿x 轴正方向以每秒1个单位长度的速度向右平移,设直线l 与菱形OABC 的两边分别交于点M ,N(点M 在点N 的上方),若OMN ∆的面积为S ,直线l 的运动时间为t 秒(04)t ≤≤,则能大致反映S 与t 的函数关系的图象是( )A. B.C. D.7.如果a+b =12,那么a b a b b a+--22的值是( ) A .12B .14C .2D .48.《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十.问甲乙持钱各几何?”其大意是:今有甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半,那么甲共有钱;如果乙得到甲所有钱的三分之二,那么乙也共有.问甲、乙两人各带了多少钱?设甲带钱为,乙带钱为,根据题意,可列方程组为( )A.B.C.D.9.如图,在矩形ABCD 中,AB=8,BC=6,点E 在边AB 上,点F 在边CD 上,点G ,H 在对角线AC 上,若四边形GEHF 是菱形,则AE 的长是( )A.5B.254C. D.10.正比例函数y =kx(k≠0)的图象上一点A 到x 轴的距离与到y 轴的距离之比为2 : 3,且y 随x 的增大而减小,则k 的值是 ( ) A .23B .32C .32-D .23-11.如图,在四边形ABCD 中,AC 与BD 相交于点O ,∠BAD =90°,BO =DO ,那么添加下列一个条件后,仍不能判定四边形ABCD 是矩形的是( )A .∠ABC =90°B .∠BCD =90°C .AB =CD D .AB ∥CD12.如图,在矩形ABCD 中,6AB =,4BC =,动点E 从点A 出发,沿A B C →→的路线运动,当点E 到达点C 时停止运动,过点E 作FE AE ⊥,交CD 于点F ,设点E 运动的路程为x ,FC y =.则y 关于x 的图象大致为( )A .B .C .D .二、填空题13.如图,将边长为3的正方形纸片ABCD 对折,使AB 与DC 重合,折痕为EF ,展平后,再将点B 折到边CD 上,使边AB 经过点E ,折痕为GH ,点B 的对应点为M ,点A 的对应点为N ,那么折痕GH 的长为_____.14.计算:①232n m ⎛⎫= ⎪⎝⎭_____;②b a a b a b -=-- _____. 15.如图是23名射击运动员的一次测试成绩的频数分布折线图,则射击成绩的中位数_____。
专题05几何证明选择填空之压轴题训练1沪教版解析版

专题05 几何证明选择填空之压轴题训练(1)一、选择题(本大题共12题)1.(浦东四署2019期中6)下列命题中,真命题的序号为()①相等的角是对顶角;②在同一平面内,若a//b,b//c,则a//c;③同旁内角互补;④互为邻补角的两角的平分线互相垂直.A.①②;B.①③;C.①②④;D.②④.【答案】D;【解析】解:相等的角不一定是对顶角,还要考虑位置关系,故①错误;若a//b,b//c,则a//c,故②正确;两直线平行,同旁内角互补,故③错误;互为邻补角的两角的平分线互相垂直,故④正确;因此答案选D.2.(松江区2020期末6)下列说法错误的是( )A.在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线;B.到点P距离等于1 cm的点的轨迹是以点P为圆心,半径长为1cm的圆;C.到直线l距离等于2 cm的点的轨迹是两条平行于l且与l的距离等于2cm的直线;D.等腰△ABC的底边BC固定,顶点A的轨迹是线段BC的垂直平分线.【答案】D;【解析】解:在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线,A正确;到点P距离等于1 cm的点的轨迹是以点P为圆心,半径长为1cm的圆,B正确;到直线l距离等于2 cm的点的轨迹是两条平行于l且与l的距离等于2cm 的直线,C正确;等腰△ABC的底边BC固定,顶点A的轨迹是线段BC的垂直平分线(BC的中点除外),D错误,故答案选D.3.(2019位育10月5)下列命题正确的是()A.到角的两边距离相等的点在这个角的平分线上;B.线段的垂直平分线上的点与该线段的两端点均能构成等腰三角形;C.三角形一边的两端到这边中线所在的直线的距离相等;D.两边及第三边上的高对应相等的两个三角形全等.【答案】C;【解析】解:到角的两边距离相等的点可以在这个角平分线的反向延长线上,故A错误;当点在线段的中点时,不能构成等腰三角形,故B错误;三角形一边的两端到这边中线所在的直线的距离相等,根据等面积法可知C正确;如图所示的两个三角形不全等,故D错误;因此答案选C.4.(浦东部分校2020期末5)下列命题中,逆命题是假命题的是()A.全等三角形的对应边相等;B.全等三角形的对应角相等;C.直角三角形的两个锐角互余;D.直角三角形斜边上的中线等于斜边的一半.【答案】B ;【解析】解:对应边相等的两个三角形全等,故A 正确;对应角相等的两个三角形不一定全等,故B 错误;两个锐角互余的三角形是直角三角形,故C 正确;一条边上的中线等于这条边的一半,那么这个三角形是直角三角形,可以证明这个结论正确,故D 正确;因此答案B.5.(金山教育局2020期末6)下列四个命题:①有两边及其中一边的对角对应相等的两个三角形全等;②三角形的一条中线把三角形分成面积相等的两部分:a =,则a>0:④点P(1,2)关于原点的对称点坐标为P(-1,-2);其中真命题的是( )A. ①、②;B. ②、④;C. ③、④;D. ①、③【答案】B ;【解析】解:①有两边及其中一边的对角对应相等的两个三角形不一定全等,故①错误;a =,则a≥0,故③错误;④点P(1,2)关于原点的对称点坐标为P(-1,-2),故④正确.其中真命题的是②④.故答案选B.6.(2019华理附10月6)如图,在四边形ABCD 中,如果AD//CD ,AE//CF, BE=DF ,那么下列等式中错误的是()A.∠DAE=∠BCF ;B. AB=CD ;C. ∠BAE=∠DCF ;D. ∠ABE=∠EBC ;【答案】D ;【解析】解:∵AD//CD ,∴∠ADB=∠CBD ,∵AE//CF ,∴∠AED=∠CFB ,∵BE=DF ,∴BF=DE ,∴△ADE ≌△CBF ,∴∠DAE=∠BCF ,故A 正确;∴AD=BC ,故四边形ABCD 为平行四边形,∴AB=CD ,故B 正确;∴BAD=∠BCD ,∴∠BAE=∠b a h ha bA B CD A'B'C'D'FE D CB ADCF ;故C 正确;此时四边形ABCD 不一定是菱形,故∠ABE=∠EBC 不一定成立,故D 错误;因此答案选D.7.(浦东南联合2019期中6)如图所示,在△ABC 中,点D 、E 分别在AB 、AC 边上,且AD :BD =3:4,AE :CE =2:1 .联结DE ,那么:ADE BCED S S D =四边形() (A )12 (B )25 (C )37 (D )49【答案】B ;【解析】解:联结BE ,设6ADE S S D =,∵AD :BD=3:4,∴8BDE S S D =,∴14ABE S S D =,又∵AE :CE =2:1,∴:2:1ABE BCE S S D =四边形,∴7BCE S S D =,∴15BCED S S =四边形,∴:6:15ADE BCED S S S S D =四边形=25,故答案选B.8.(建平实验2019期中6)如图,在△ABC 中,AB=AC ,∠A=40°,点D 在△ABC 内,且∠DBC=∠DCA ,则∠BDC 的度数为( )A.120°B.115°C.110°D.105°【答案】C ;【解析】解:∵AB=AC ,∠A=40°,∴∠ABC=∠ACB=70°,又设∠DBC=∠DCA=x ,则∠DCB=70°- x ,∴∠BDC=180°-(x+70°-x )=110°,故答案选C.9.(浦东四署2020期末6)如图,在ABC D 中,点D 在BC 边上,DE 垂直平分AC 边,垂足为点E ,若70B Ð=°,且AB+BD=BC ,则BAC Ð的度数是()A.40°;B. 65°;C. 70°;D. 75°.A CB D【答案】D ;【解析】如图,联结AD ,因为AB+BD=BC ,所以AB=CD ,又DE 垂直平分AC 边,所以AD=CD ,故AB=AD=CD ,所以,,B ADB DAC C Ð=ÐÐ=Ð所以1802BAD B Ð=°-Ð=40°,1352DAC ADB Ð=Ð=°,故403575BAC BAD DAC Ð=Ð+Ð=°+°=°,因此选D.10.(浦东新区2020期末6)如图,在Rt ABC D 中,90BCA Ð=°,CD 是高,BE 平分∠ABC 交CD 于点E ,EF ∥AC 交AB 于点F ,交BC 于点G .在结论:(1) EFD Ð=BCD Ð;(2) AD CD =;(3)CG EG =;(4) BF BC =中,一定成立的有()A. 1个;B. 2个;C. 3个;D. 4个.【答案】B;【解析】解:∵EF ∥AC ,∠BCA=90°,∴∠CGE=∠BCA=90°,∴∠BCD+∠CEG=90°,又∵CD 是高,∴∠EFD+∠FED=90°,∵∠CEG=∠FED (对顶角相等),∴∠EFD=∠BCD ,故(1)正确;只有∠A=45°,即△ABC 是等腰直角三角形时,AD=CD ,CG=EG 而立,故(2)(3)不一定成立,错误;∵BE 平分∠ABC ,∴∠EBC=∠EBF ,在△BCE 和△BFE 中,EFD BCD EBC EBF BE BE ÐÐìïÐÐíïî===,∴△BCE ≌△BFE (AAS ),∴BF=BC ,故(4)正确,综上所述,正确的有(1)(4)共2个.故选:B .11.(浦东新区2021期末6) 在ABC V 中,A Ð、B Ð、C Ð的对应边分别是a 、b 、c ,下列条件中不能说明ABC V 是直角三角形的是()A. 222b ac =- B. C A B Ð=Ð+ÐC. ::3:4:5A B C ÐÐÐ= D. ::5:12:13a b c =【答案】C ;EAB D CGA ECD F B【解析】解:A .222b a c =-,即222b c a +=,根据勾股定理逆定理可知△ABC 是直角三角形,故A 不符合题意.B .根据三角形内角和180A B C Ð+Ð+Ð=°与C A B Ð=Ð+Ð,得出2180C Ð=°,即90C Ð=°,所以△ABC 是直角三角形,故B 不符合题意.C .设3A x Ð=,则4B x Ð=,5C x Ð=,根据三角形内角和180A B C Ð+Ð+Ð=°,即345180x x x ++=°,解得15x =°,即45A Ð=°、60B Ð=°、75C Ð=°.所以△ABC 不是直角三角形,故C 符合题意.D .设5a x =,则12b x =,13c x =,由222(5)(12)(13)x x x +=可知222a b c +=,根据勾股定理逆定理可知△ABC 是直角三角形,故D 不符合题意.故选:C .12.(2019徐汇南模12月6) 如图,将边长2cm 的正方形ABCD 沿其对角线AC 剪开,再把ABC V 沿着AD 方向平移,得到A B C ¢¢¢V ,若两个三角形重叠部分的面积为21cm ,则它移动的距离AA ¢等于( )A. 0.5cm ;B. 1cm ;C. 1.5cm ;D. 2cm .【答案】B ;【解析】解:设AC 交A′B′于H ,∵AC 是正方形ABCD 的对角线,∴∠A=45°,∠D=90°,∴△A′HA 是等腰直角三角形,设AA′=x ,则阴影部分的底A′H=x ,高A′D=2-x ,∴x•(2-x)=1,即2210x x -+=,解得:121x x ==,即AA′=1cm .故选:B .二、填空题(本大题共12题)13.(2019浦东一署10月18)如果一个等腰三角形的一个外角是110°,那么它的底角为 °.【答案】70°或55°;【解析】解:如果110°是顶角的外角,则此等腰三角形的底角为11102´°=55°;如果110°是底角的外角,则此等腰三角形的底角为180°-110°=70°;故它的底角为55°或70°.14.(2019复旦附中10月14)如图,在△ABC 中,已知点O 是边AB 、AC 垂直平分线的交点,点E 是∠ABC 、∠ACB 角平分线的交点,若∠O+∠E=180°,则∠A= 度.【答案】36;【解析】解:联结OA ,∵点O 是边AB 、AC 垂直平分线的交点,∴OA=OB=OC ,∴∠OAB=∠OBA ,∠OAC=∠OCA ,∴∠BOC=∠OAB+∠OBA+∠OAC+∠OCA=2∠BAC , 即∠BOC=2∠BAC ;又∵点E 是∠ABC 、∠ACB 角平分线的交点,∴∠E=90°+12BAC Ð;∵∠O+∠E=180°,∴2∠BAC+90°+12BAC Ð=180°,∴∠BAC=36°.15.(2019上宝15)如图,在平面直角坐标系xOy 中,O 为原点,点A 、C 的坐标分别为(2,0)、. 将△AOC 绕AC 的中点旋转180°,点O 落到点B 的位置,D 的坐标为(1,. 若点P 是x 轴上一点,以P 、A 、D 为顶点作平行四边形,该平行四边形的另一顶点在y 轴上,则点P 的坐标为 .【答案】P(-1,0)或P(1,0)或 P(3,0);【解析】解:设(,0)P a ,另一个顶点为(0,)Q b . ①当AP 与DQ 为对角线时,∵A(2,0),(1,D ,∵平行四边形对角线互相平分与中点坐标公式得:a+2=1+0,解得a=-1,∴P(-1,0); ②当AQ 与PD 为对角线时,同理可得:2+0=a+1,解得a=1,∴P(1,0); ③当AD 与PQ 为对角线时,可得:2+1=a+0,a=3,∴P(3,0);综上述:P(-1,0)或P(1,0)或 P(3,0).16.(川中南2019期中18)如图,在Rt △ABC 中,∠ACB=90°,AB=5,AC=3,BC=4,将点C 折叠到点E 处,折痕为BD ,则DE 的长度为 .EOC B A O E C BA【答案】43;【解析】解:∵折叠,∴CD=DE ,∠C=∠DEB=90°,故ABC BCD ABD S S S D D D =+,即111222BC AC BC CD AB DE =+g g g ,∴()BC AC BC AB DE =+g ,∴43(45)DE ´=+×,∴43DE =.17.(建平实验2019期中18)如图,正方形ABCD 中,点E 是DC 边上一点,DE=6,EC=3,点F 在直线AB 上,当线段CF 的长为时,把线段AE 绕点A 旋转,使点E 恰好落在点F 处.【答案】或;【解析】解:∵DE=6,EC=3,∴AD=AB=9,∴;若点F 在BA 延长线上时,AF=AE=,∴BF=9+,BC=9,∴=;当点F 在AB 延长线上时,BF=-9,∴;综上述CF=.18.(浦东新区2020期末18)正方形ABCD 的边长为4,E 为BC 边上一点,BE=3,M 为线段AE 上一点,射线BM 交正方形的一边于点F ,且BF=AE,则BM 的长为____.【答案】51225或;【解析】解:如图,当BF 如图位置时,∵AB=AB ,∠BAF=∠ABE=90°,AE=BF ,∴△ABE ≌△BAF (HL ),∴∠ABM=∠BAM ,∴AM=BM ,AF=BE=3,∵AB=4,BE=3,∴AE= 5==,过点M 作MS ⊥AB ,由等腰三角形的性质知,EDC B AA B DCE点S 是AB 的中点,BS=2,SM 是△ABE 的中位线,∴BM=12AE=12×5=52,当BF 为BG 位置时,易得Rt △BCG ≌Rt △ABE ,∴BG=AE=5,∠AEB=∠BGC ,∴△BHE ∽△BCG ,∴BH :BC=BE :BG ,∴BH=125.故答案是:51225或.19.(松江区2020期末18)如图,在Rt △ABC 中,已知∠C =90°,∠B =55°,点D 在边BC 上,BD =2CD .把△ABC 绕着点D 逆时针旋转m (0<m <180)度后,如果点B 恰好落在初始Rt △ABC 的边上,那么m = .【答案】70°或120°;【解答】解:①当点B 落在AB 边上时,∵DB =DB 1,∴∠B =∠DB 1B =55°,∴m =∠BDB 1=180°﹣2×55°=70°,②当点B 落在AC 上时,在RT △DCB 2中,∵∠C =90°,DB 2=DB =2CD ,∴∠CB 2D =30°,∴m =∠C +∠CB 2D =120°,故答案为70°或120°.20.(静安附校2020期末14)在△ABC 中,∠B=15°,△ABC 的面积为3,过点A 作AD ⊥AB 交边BC 边于点D. 设BC=x ,BD=y. 那么y 与x 之间的函数解析式 .(不写函数定义域).【答案】24y x=;【解析】解:过A 作AH ⊥BC 于点H ,由132ABC S BC AH D ==g ,得6AH x=;又AH=AB•sin15°,AB=BD•cos15°,∴AH=y•sin15°cos15°=1sin 302y °,∴61sin 302y x =°,解得24y x =.(或用cos15°=,sin15°=21.(普陀区2020期末18)在Rt △ABC 中,∠ACB=90°,BC=3,如图所示. 如果将△ABC 绕点C 顺时针旋转60°得到△DEC ,其中点A 、B 的对应点分别为点D 、E ,联结BD ,那么BD 的长等于 .【解析】解:如图,过D 做DH ⊥BC 交BC 延长线于H ,依题可知∠BCE=60°,∴∠ACE=30°,∴∠DCH =∠ACE=30°,∵CD=DH=CH =6,∴BH =9,∴BD.22.(闵行区2020期中18)如图,三角形纸片ABC 中,∠A =75°,∠B =72°.将三角形纸片的一角折叠,使点C 落在△ABC 内,如果∠1=32°,那么∠2= 度.【答案】34;【解答】解:如图延长AE 、BF 交于点C ′,连接CC ′.在△ABC ′中,∠AC ′B =180°﹣72°﹣75°=33°,∵∠ECF =∠AC ′B =40°,∠1=∠ECC ′+∠EC ′C ,∠2=∠FCC ′+∠FC ′C ,∴∠1+∠2=∠ECC ′+∠EC ′C +∠FCC ′+∠FC ′C =2∠AC ′B =66°,∵∠1=32°,∴∠2=34°,故答案为:34.23.(浦东新区2021期末18)如图,已知正方形ABCD 的面积为4,正方形FHIJ 的面积为3,点D 、C 、G 、J 、I 在同一水平面上,则正方形BEFG 的面积为__________.C B A A B C HED。
第8章立体几何专题4 垂直的证明-人教A版(2019)高中数学必修(第二册)常考题型专题练习

垂直的证明【方法总结】1、证明线面垂直的方法:①利用线面垂直定义:如果一条直线垂直于平面内任一条直线,则这条直线垂直于该平面;②用线面垂直判定定理:如果一条直线与平面内的两条相交直线都垂直,则这条直线与平面垂直;③用线面垂直性质:两条平行线中的一条垂直于一个平面,则另一条也必垂直于这个平面.2、证明线线(或线面)垂直有时需多次运用线面垂直的定义和线面垂直的判定定理,实现线线垂直与线面垂直的相互转化.3、证明面面垂直一般要先找到两个面的交线,然后再在两个面内找能与交线垂直的直线,最后通过证明线面垂直证明面面垂直。
【分类练习】考向一线面垂直例1、在四棱锥P ABCD -中,PA ⊥底面ABCD ,//AB CD ,AB BC ⊥,1AB BC ==,2DC =,点E 在PB 上求证:CA ⊥平面PAD ;【答案】(1)证明见解析;(2)2.【解析】(1)过A 作AF ⊥DC 于F ,则CF =DF =AF ,所以∠DAC =90°,即AC ⊥DA ,又PA ⊥底面ABCD ,AC ⊂面ABCD ,所以AC ⊥PA ,因为PA 、AD ⊂面PAD ,且PA ∩AD =A ,所以AC ⊥平面PAD .例2、如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;解析:(1)由已知得,11B C ⊥平面11ABB A ,BE ⊂平面11ABB A ,故11B C ⊥BE .又1BE EC ⊥,所以BE ⊥平面11EB C .例3、如图,在三棱柱111ABC A B C -中,1CC ⊥平面ABC ,D ,E ,F ,G 分别为1AA ,AC ,11A C ,1BB 的中点求证:AC ⊥平面BEF ;【解析】(1)在三棱柱111ABC A B C -中,∵1CC ⊥平面ABC ,∴四边形11A ACC 为矩形.又E ,F 分别为AC ,11A C 的中点,∴AC ⊥EF .∵AB BC =.∴AC ⊥BE ,∴AC ⊥平面BEF .例4、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,CD ⊥AD ,BC ∥AD ,12BC CD AD ==.(Ⅰ)求证:BD ⊥平面PAB ;【解析】因为PA ⊥平面ABCD ,BD ⊂平面ABCD ,所以BD ⊥PA .所以222AD AB BD =+,所以BD AB ⊥.因为PA AB A = ,所以BD ⊥平面PAB .【巩固练习】1、如图,在三棱柱ABC-A 1B 1C 1中,AB=AC,A 1在底面ABC 的射影为BC 的中点,D 是B 1C 1的中点.证明:A 1D⊥平面A 1BC;【答案】见解析【解析】证明:设E 为BC 的中点,连接A 1E,AE.由题意得A 1E⊥平面ABC,所以A 1E⊥AE.因为AB=AC,所以AE⊥BC.故AE⊥平面A 1BC.连接DE,由D,E 分别为B 1C 1,BC 的中点,得DE∥B 1B 且DE=B 1B,从而DE∥A 1A 且DE =A 1A,所以AA 1DE 为平行四边形.于是A 1D∥AE.因为AE⊥平面A 1BC,所以A 1D⊥平面A 1BC.2.(2019·上海格致中学高三月考)如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD DC =,E 是PC 的中点,作EF PB ⊥交PB 于点F .(1)证明:PA ∥平面EDB ;(2)证明:PB ⊥平面EFD .【答案】(1)详见解析;(2)详见解析.【解析】(1)设AC 与BD 相交于O ,连接OE ,由于O 是AC 中点,E 是PC 中点,所所以PA ∥平面EDB .(2)由于PD ⊥底面ABCD ,所以PD BC ⊥,由于,BC CD PD CD D ⊥⋂=,所以BC ⊥平面PCD ,所以BC DE ⊥.由于DP DC =且E 是PC 中点,所以DE PC ⊥,而PC BC C ⋂=,所以DE ⊥平面PBC ,所以DE PB ⊥.依题意EF PB ⊥,DE EF E = ,所以PB ⊥平面EFD .3.(2019·江苏高三月考)如图,在四棱锥P ABCD -中,四边形ABCD 是平行四边形,AC ,BD 相交于点O ,OP OC =,E 为PC 的中点,PA PD ⊥.(1)求证://PA 平面BDE ;(2)求证:PA ⊥平面PCD【答案】(1)详见解析(2)详见解析【解析】(1)连结OE .因为四边形ABCD 是平行四边形,AC ,BD 相交于点O ,所以O 为AC 的中点.因为E 为PC 的中点,所以//OE PA .因为OE ⊂平面BDE ,PA ⊄平面BDE ,所以//PA 平面BDE .(2)因为OP OC =,E 为PC 的中点,所以OE PC ⊥.由(1)知,//OE PA ,所以PA PC ⊥.因为PA PD ⊥,PC ,PD ⊂平面PCD ,PC PD P ⋂=,所以PA ⊥平面PCD .考向二面面垂直例1、如图,在四棱锥P ABCD -中,已知底面ABCD 为矩形,且AB =,1BC =,E ,F 分别是AB ,PC 的中点,PA DE ⊥.(1)求证://EF 平面PAD ;(2)求证:平面PAC ⊥平面PDE .【答案】(1)详见解析(2)详见解析【解析】证明:(1)取PD 中点G ,连AG ,FG ,F ,G 分别是PC ,PD 的中点又E 为AB 中点//AE FG ∴,AE FG=四边形AEFG 为平行四边形//EF AG ∴,又EF ⊄平面PAD ,AG ⊂平面PAD//EF ∴平面PAD(2)设AC DE H= 由AEH CDH ∆∆ 及E 为AB 中点又BAD ∠为公共角GAE BAC∴∆∆ 90AHE ABC ∴∠=∠=︒即DE AC ⊥又DE PA ⊥,PA AC A= DE ⊥平面PAC ,又DE ⊂平面PDE∴平面PAC ⊥平面PDE例2、如图,边长为2的正方形ABCD 所在的平面与半圆弧 CD所在平面垂直,M 是 CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;【解析】(1)由题设知,平面CMD ⊥平面ABCD ,交线为CD .因为BC ⊥CD ,BC ⊂平面ABCD ,所以BC ⊥平面CMD ,故BC ⊥DM .因为M 为 CD上异于C ,D 的点,且DC 为直径,所以DM ⊥CM .又BC CM =C ,所以DM ⊥平面BMC .而DM ⊂平面AMD ,故平面AMD ⊥平面BMC .例3、如图,在梯形ABCD 中,AB ∥CD ,AD=DC=CB=a ,∠ABC=3π,平面ACFE ⊥平面ABCD ,四边形ACFE 是矩形,AE=AD ,点M 在线段EF 上。
八年级数学下册期末几何题证明题专题
1.(10分)如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP 的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.(1)求证:△AEG是等腰直角三角形;(2)求证:AG+CG=DG.2.(8分)如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.3.(9分)如图,在梯形ABCD中,M、N分别为AD、BC的中点,E、F分别为BM、CM的中点.(1)求证:四边形MENF是平行四边形;(2)若四边形MENF的面积是梯形ABCD面积的,问AD、BC满足什么关系?4.如图,在四边形 ABCD 中,AD=12,DO=OB=5,AC=26,∠ADB=90°.(1)求证:四边形 ABCD 为平行四边形;(2)求四边形 ABCD 的面积.5、四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:△ADE≌△CBF;(2)若AC与BD相交于点O,求证:AO=CO.6、如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.(1)求证:BF=2AE;(2)若CD=,求AD的长.7、如图,E是▱ABCD的边CD的中点,延长AE交BC的延长线于点F.(1)求证:△ADE≌△FCE.(2)若∠BAF=90°,BC=5,EF=3,求CD的长.8、如图,在菱形ABCD中,AB=2,∠DAB=60°。
点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD、AN。
(1)求证:四边形AMDN是平行四边形。
(2)当AM为何值时,四边形AMDN是矩形?请说明理由。
9.(6 分)如图,菱形ABCD 的对角线AC、BD 相交于点O,且DE∥AC,AE∥B D.求证:四边形AODE 是矩形.10(9 分)如图,在△ABC 中,D 是BC 边上的中点,E 是AD 边上的中点,过A 点作BC的平行线交CE 的延长线于点F,连结BF.(1)求证:四边形AFBD 是平行四边形.(2)当△ABC 满足什么条件时,四边形AFBD 是矩形?请说明理由.10.(7 分)如图,在△ABC 中,AB=AC,AD 平分∠BAC 交BC 于点D,分别过点A、D作AE∥BC、DE∥AB,AE 与DE 相交于点E,连结CE.(1)求证:BD =CD.(2)求证:四边形ADCE 是矩形.11.(9 分)如图,E、F 分别是矩形ABCD 的边BC、AD 上的点,且BE =DF.(1)求证:四边形AECF 是平行四边形.(2)若四边形AECF 是菱形,且CE = 10,AB = 8,求线段BE 的长.12.(7 分)如图,在△ABC 中,AD 是∠BAC 的平分线,AD 的垂直平分线交AB 于点E,交AC 于点F,连结DE、DF.(1)求证:∠ADE=∠DAF.(2)求证:四边形AEDF 是菱形.13.【感知】如图①,四边形ABCD、AEFG 都是正方形,可知BE =DG .【探究】当正方形AEFG 绕点A 旋转到图②的位置时,连结BE、DG.求证:BE =DG .【应用】当正方形AEFG 绕点A 旋转到图③的位置时,点F 在边AB 上,连结BE、D G.若DG =13 ,AF = 10 ,则AB 的长为.14. (10 分)如图,以△ABC 的三边为边分别作等边△ACD、△BCE、△ABF.(1)求证:四边形ADEF 是平行四边形(2)△ABC 满足什么条件时,四边形ADEF 是矩形?(3)△ABC 满足什么条件时,四边形ADEF 是菱形?20.如图,将▱ABCD 的边 DC 延长到点 E ,使 CE=DC ,连接 AE ,交 BC 于点 F . (1)求证:△ABF ≌△ECF ;(2)若∠AFC=2∠D ,连接 AC 、BE ,求证:四边形 ABEC 是矩形.18.(本题8分)如图,□ABCD 的对角线AC 、BD 相交于点O ,过点D 作DE ∥AC ,且DE =21AC ,连接CE 、OE(1) 求证:四边形OCED 是平行四边形; (2) 若AD =DC =3,求OE 的长.21.(本题8分)如图,在四边形ABCD 中,AD ∥BC ,AB =3,BC =5,连接BD ,∠BAD 的平分线分别交BD 、BC 于点E 、F ,且AE ∥CD (1) 求AD 的长;(2) 若∠C =30°,求CD 的长.27.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE 的延长线于点F,且AF=BD,连接BF.(1)证明:BD=CD;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.28.如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2,,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.(1)求证:△APP′是等腰直角三角形;(2)求∠BPQ的大小.18. (本题满分12分)如图,DB∥AC,且DB=12AC,E是AC的中点。
专题五几何证明人教版八年级数学(上册)-【完整版】
∴△DAB≌△CBA(AAS). ∴BD=AC. ∴AD=BC. 在△ADC和△BCD中,
∴△ADC≌△BCD(SSS). ∴∠CDA=∠DCB.
四、 证明线段垂直
15. 如图,点 C 在线段 AB 上,AD∥EB,AC=BE,
AD=BC,CF 平分∠DCE.求证:CF⊥DE.
∵F为CE的中点, ∴AF平分∠EAC. ∴AF⊥CE.即∠AFC=90°. 又∠FAC+∠ACE=180°-∠AFC=90°, ∠DAC=∠ACE, ∴∠DAC+∠FAC=90°. 即∠DAF=90°. ∴AF⊥AD.
五、 证明等边三角形
20. 如图,在△ABC 中,D 为 AC 边上一点,DE⊥AB
专题五 几何证明人教版八年级数学上册-精 品课件p pt(实 用版)
专题五 几何证明人教版八年级数学上册-精 品课件p pt(实 用版)
在△ACM和△DCN中,
∴△ACM≌△DCN(ASA). ∴CM=CN. 又∠DCN=60°, ∴△CMN为等边三角形.
专题五 几何证明人教版八年级数学上册-精 品课件p pt(实 用版)
证明:∵△ABC≌△EDC, ∴BC=DC,∠ACB=∠DCE.
在△BCF和△DCH中,
∴△BCF≌△DCH(SAS). ∴∠FBC=∠HDC. 在△FBC和△FDK中, ∵∠FBC=∠HDC,∠BFC=∠DFK, ∴∠DKF=∠ACB.
14. 如图,AC 与 BD 相交于点 O,∠DBA=∠CAB, ∠1=∠2. 求证:∠CDA=∠DCB.
点 F,连接 BE. 求证:BE⊥AF.
证明:∵AD∥BC, ∴∠DAE=∠F,∠ADE=∠FCE.
在△ADE和△FCE中,
几何证明专题练习一
第1题BDa第3题CD第4题AE 第4题AB C 几何证明专题练习一班级_________姓名_________1、如图,已知062ABC ∠=,12∠=∠,求C ∠的度数;2、如图,已知直线,a b 被直线l 所截,//a b ,且01(316)x ∠=+,02(211)x ∠=-,求1,2∠∠的度数;3、如图,已知0032,68AEC B ∠=∠=,AEC A ∠=∠,求BEF ∠的度数;4、(1)如图,已知//AB CD ,那么B BED D ∠+∠+∠等于多少度?证明;(2)如图,已知//AB CD ,证明B D BED ∠+∠=∠;ab BDC第7题A D EF第8题A 第9题B5、如图,001140,240∠=∠=,03120∠=,求4∠6、如图,已知//AB CD ,012180∠+∠=,说明//EF CD ;7、如图,//AB CD ,BE ,CF 分别平分ABC ∠,BCD ∠,说明//BE CF ;8、如图,已知,A D C F ∠=∠∠=∠,说明//CE BF ;9、如图,已知//,12CD GF ∠=∠,说明//DE BC ;第10题EC第11题CE第13题DE第14题B 10、如图,已知//AB CD ,0065,115C DAE ∠=∠=,说明//AD BC ;11、如图,已知,//BAD CAD AD BE ∠=∠,说明ABE E ∠=∠12、如图,已知直线AB ,CD 被直线AE 所截,且//AE CD ,若01115∠=,求2,3,4∠∠∠的度数;13、如图,直线DE 经过点A ,00//,42,57DE BC B C ∠=∠=,求,D A B C A D ∠∠的度数;14、如图,已知//DE BC ,如果12∠=∠,说明B C ∠=∠;。
反证法之几何证明专题
反证法之几何证明专题例1.已知:AB、CD是⊙O内非直径的两弦(如图1),求证AB与CD不能互相平分。
(1)证明:假设AB与CD互相平分于点M、则由已知条件AB、CD均非⊙O直径,可判定M不是圆心O,连结OA、OB、OM。
∵OA=OB,M是AB中点∴OM⊥AB(等腰三角形底边上的中线垂直于底边)同理可得:OM⊥CD,从而过点M有两条直线AB、CD都垂直于OM这与已知的定理相矛盾。
故AB与CD不能互相平分。
例2.已知:在四边形ABCD中,M、N分别是AB、DC的中点,且MN=(AD+BC)。
求证:AD∥BC(2)证明:假设AD BC,连结ABD,并设P是BD的中点,再连结MP、PN。
在△ABD中∵BM=MA,BP=PD∴MP AD,同理可证PN BC从而MP+PN=(AD+BC)①这时,BD的中点不在MN上若不然,则由MN∥AD,MN∥BC,得AD∥BC与假设AD BC矛盾,于是M、P、N三点不共线。
从而MP+PN>MN②由①、②得(AD+BC)>MN,这与已知条件MN=(AD+BC)相矛盾,故假设AD BC不成立,所以AD∥BC。
练习1.求证:三角形中至少有一个角不大于60°。
2.求证:一直线的垂线与斜线必相交。
3. 已知:设m,n分别为直线l的垂线和斜线(如图),垂足为A,斜足为B求证:m和n必相交。
3.在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于H,求证:AD 与BE不能被点H互相平分。
4.求证:直线与圆最多只有两个交点。
5.求证:等腰三角形的底角必为锐角。
已知:△ABC中,AB=AC求证:∠B、∠C必为锐角。
参考答案:1.证明:假设△ABC中的∠A、∠B、∠C都大于60°则∠A+∠B+∠C>3×60°=180°这与三角形内角和定义矛盾,所以假设不能成立。
故三角形中至少有一个角不大于60°。
2.证明:假设m和n不相交则m∥n∵m⊥l ∴n⊥l这与n是l的斜线相矛盾,所以假设不能成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何证明专题
1、如图,在直角梯形ABCD中,AB∥CD,∠A=90°,CD>AD,
将纸片沿过点D的直线折叠,使点A落在边CD上的点E处,折痕为DF.
(1)求证:四边形ADEF是正方形;
(2)取线段AF的中点G,联结EG,若BG=CD,试说明四边形GBCE是等腰梯形.
2、 如图,在Rt△ABC中,∠BAC = 90°,AD =CD, 点E是边AC的中点,联结DE,
DE的延长线与边BC相交于点F,
AG // BC,交DE于点G,联结AF、CG.
(1)求证:AF = BF;
(2)如果AB = AC,求证:四边形AFCG是正方形.
3、如图,四边形ABCD 是平行四边形,在边 AB的延长线上截取BE=AB ,点 F在AE 的
延长线上, CE和 DF交于点M , BC和DF 交于点 N.
(1)求证:四边形 DBEC是平行四边形;
(2)如果 AD(^2)=AB•AF, 求证:CM•AB=DM•CN .
4、如图(1),在△ABC和△EDC中,AC=CE=CB=CD,
∠ACB=∠ECD=90° ,AB与CE交于F,ED与AB、BC分别交于M、H.
(1)求证:CF=CH;
(2)如图(2),△ABC不动,将△EDC绕点C旋转到∠BCE=45° 时,试判断四边形ACDM
是什么四边形?并证明你的结论.
