4.2 代数式y
浙教版初中数学七年级上册4.2 代数式 课件

(4)a与b的和的平方 变式:a与b的平方的和
a与b两数的平方和
列代数式的步骤:
(1)理解每个关系语 (2)弄清用什么运算 (3)辨清运算顺序 (4)书写代数式
那我们在列代数式的时候又应该注意什么呢?
列代数式注意点:
(1)数字与字母相乘,乘号用“·”代替或省略不 写数字应写在字母前面. (2)1或-1与字母相乘时通常把1省略 (3)代数式中出现加减运算,且后面有单位的, 要添上括号. (4)带分数与字母相乘时,带分数应化成假分数. (5)除号用分数线代替
为5米,如果车子速度为 v米/秒,那么
汽车通过大桥的时间是___l_v_5___秒.
2a 3a
a
2. 我们来到了动物园,看到了一 个五彩花圃,它的形状如图,则
花圃的面积为__2_a_2__.
s
l5
前面所填式子:300a ,t ,50a 60b,v ,2a2来自分别表示了某种数量关系
由数、表示数的字母和运算符号组成数学表达式 称为代数式.
指加、减、乘、除、 乘方和开方
注意:单独一个数或者一个字母也称为代数式!
下列算式是不是代数式?
2m
(1√)3x (2√) 1(×3)a 3(×4)b a 1(√5)n
例1.用代数式表示:
(1)x的121倍与3的和 3
(2)2a的立方根
带分数与字母相 乘时,带分数应
化成假分数
(3)m的3倍除以n的商
为 a ,则25年前的大象头数是 多1少9a0%.
我们来动物园汽车以60千米/时的速度行驶,花了t 时,
现在为了尽快赶回学校,汽车速度增加了v 千米/时.
(1)学校与动物园的路程是多少千米? (2)回到学校的时间是多少呢?
4.2《代数式》参考教案2

然后进展相应的课堂练习,加强理解
例2、一辆汽车以80千米/时的速度行驶,从城A到城B需t时.如果该车的行驶速度增加v千米/时,那么从A城到B城需多少时间?
分析:对此实际应用题进展分析,指导学生独立解决,让学生自主判断解决的对错.
用代数式表示用语言表达的数量关系要注意:①弄清代数式中括号的使用;②字母与数字做乘积时,习惯上数字要写在字母的前面.
(1)加法交换律a+b=b+a;
(2)乘法交换律a·b=b·a;
(3)加法结合律(a+b)+c=a+(b+c);
(4)乘法结合律(ab)c=a(bc);
(5)乘法分配律a(b+c)=ab+ac.
1.指出:(1)“×〞也可以写成“·〞号或者省略不写,但数与数之间相乘,一般仍用“×〞;
2.上面各种运算律中,所用到的字母a,b,c都是表示数的字母,它代表我们过去学过的一切数.
四、课堂练习
通过练习,回忆本届内容,强化记忆,再进展思维
课堂
小结
1.本节课学习了哪些内容?2.用字母表示数的意义是什么?
3.什么叫代数式?
课后作业
课本92页A组
教
学
过
程
设
计
那么终究什么叫代数式呢?代数式的意义又是什么呢?这正是本节课我们将要学习的内容.
二、讲授新课
1.代数式
单独的一个数字或单独的一个字母以及用运算符号把数或表示数的字母连接而成的式子叫代数式.
学习代数,首先要学习用代数式表示数量关系,明确代数式的意义.
2பைடு நூலகம்举例说明
例1.用代数式表示:
(1)x的3倍与3的差;(2)x的2倍与y的1/2的和;
浙教版七年级数学上册4.2 代数式公开课优质教案(2)

数、表示数的字母和运算符号
2、单独的一个数或者一个字母也称代数式。
3,做一做
在x,1,x-2,s=ab, v=sh中代数式的个数是()
A.5 B. 4C. 3D. 2
4例1用代数式表示:
⑴3倍与3的差; ⑵x的2倍与y的的和
⑶a与 b的和的平方; ⑷a与b的平方的和;
3、日平 均气温是指一天中2:00,8:00,14:00,20:00
四个时刻气温的平均值,若上述四个时刻的摄氏度数
分别为a、b、c、d,则日平均气温的摄氏度数是
4、一隧道长a米,一列火车长180米,如果该列火车
穿过隧道所花的时间为t分,则列车的速度为
二新课展开
像10x+5y, , , ,a
这样 含有字母的数学表达式称为代数式
⑸a、b两数的平方和; ⑹比a除以b小2的数
⑺2a的立方根
5练一练:
1、用代数式表 示“a与-2的差的3倍”,
正确的是( )
A.a-2B. 3[a-(-2)] C.a-(-2)×3 D.3(a-2)
2、说出下列代数式的意义:
⑴2a-b⑵2(a-b)⑶a-2b
6.例2一辆汽车以80 千米/小时的速度行 驶,从A城到B城需t小时,如果该车的行驶速 度增加v千米 /小时,则从A城到B城需多少时间?
教学
重点
理解代数式的意义,会正确书写代数式 。
教学
难点
用代数式表示数量关系。
教学
方法
教学
用具
多媒体
教
学
过
程
集体备课稿
个案补充
一合作学习
1)成人2名,小孩3名,购买门票应付多少元?
2) 成人x名,小孩y名,购买门票应付 多 少元?
七年级数学上册 4.2 代数式 用代数式解图形问题素材 (新版)浙教版
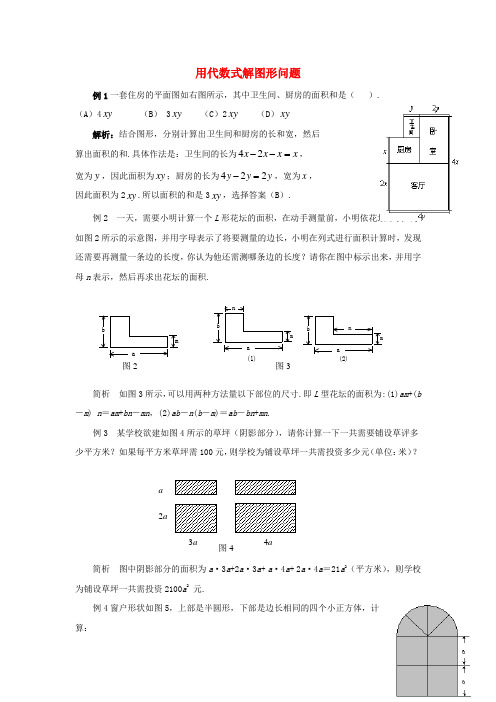
用代数式解图形问题例1一套住房的平面图如右图所示,其中卫生间、厨房的面积和是( ).(A )4xy (B ) 3xy (C )2xy (D )xy解析:结合图形,分别计算出卫生间和厨房的长和宽,然后算出面积的和.具体作法是:卫生间的长为x x x x =--24,宽为y ,因此面积为xy ;厨房的长为y y y 224=-,宽为x ,因此面积为2xy .所以面积的和是3xy ,选择答案(B ).例2 一天,需要小明计算一个L 形花坛的面积,在动手测量前,小明依花坛形状画了如图2所示的示意图,并用字母表示了将要测量的边长,小明在列式进行面积计算时,发现还需要再测量一条边的长度,你认为他还需测哪条边的长度?请你在图中标示出来,并用字母n 表示,然后再求出花坛的面积.简析 如图3所示,可以用两种方法量以下部位的尺寸.即L 型花坛的面积为:(1)am +(b -m ) n =am +bn -mn ,(2)ab -n (b -m )=ab -bn +mn .例3 某学校欲建如图4所示的草坪(阴影部分),请你计算一下一共需要铺设草评多少平方米?如果每平方米草坪需100元,则学校为铺设草坪一共需投资多少元(单位:米)?简析 图中阴影部分的面积为a ·3a +2a ·3a + a ·4a + 2a ·4a =21a 2(平方米),则学校为铺设草坪一共需投资2100a 2 元.例4窗户形状如图5,上部是半圆形,下部是边长相同的四个小正方体,计算:b m a 图2 nb m a (1)b m a n (2)图3(1)窗户的面积及窗框的总长.(2)当a=50厘米时,窗户的面积及窗框的总长的值分别是多少?(结果精确到0.1厘米) 分析:窗户的面积包括两大部分,上面的半圆的面积和下面四个正方形的面积,半圆的半径是a ,而窗框的总长应包括所有框架的长.解:(1)面积为:4a 2+221a π,窗框的总长为15a+πa. (2)当a=50厘米,窗户的面积是4a 2+221a π=4×502+25014.321⨯⨯=13925.0平方厘米;窗框的总长为15a +πa=15×50+3.14×50=907.0厘米.。
初中数学浙教版七年级上册4.2 代数式

游程3:参观
鲁迅生平事迹陈列厅呈长方形,长 m米,宽n米,共展出鲁迅展品2p件.
陈列厅占地面积有多少平方米呢? 【mn 平方米】
平均每平方米展出了多少件展品呢?【
2p mn
平方米】
...
三味书屋是鲁迅小时候读书的地方, 刻有“早”字的课桌就摆放在边长为a 米的正方形大堂内。
此大堂的面积为多少?【 a2 平方米】
...
象山丹城第二中学 沈敏亚
...
游程1:出发
象山距绍兴s千米,小汽车的s 平均速度 为40千米/小时,到达绍兴需__4_0__小时.
...
象山
绍兴
游程2:买票
鲁迅纪念馆门票价格 大人:每人60元 小孩:每人40元
售票处 ……...
我们有a个大人, b
个小孩,买门票需
付
_
__(_6_0_a__+_4元0b钱) .
利用含n的代数式... 表示:
(1) 任意一个偶数____2_n_____; (2)任意一个奇数_2_n_+__1_或__2_n_-1__; (3)任意一个能被5整除的整数__5_n_____
请结合生活实... 际,编写
一个问题,使得问题Байду номын сангаас 答案可以用 m 表示。
n
数学来源于生活,应用于生 活,而最终是为... 生活服务的。
4.2 代数式
s ,60a 40b, mm, 2 p , a2
40
mn
思考:
它们与我们以前学过的算.式.. 有什么区别和联系呢?
像 s ,60a 40b, mm, 2 p , a2 这样由数、表示 数的40字母和运算符m号n 组成的数学表达式称为 代数式.(algebraic expression).
七年级数学上册 4.2 代数式教案 (新版)浙教版

4. 2代数式教学目标 1、在具体情境中让学生观察、分析归纳得出代数式的概念。
理解代数式的意义。
2、能根据代数式和具体问题说出一个代数式表示的数量关系。
3.进一步让学生理解字母表示数的意义,并能解释代数式的实际背景或几何意义,发展符号感4使学生初步认识数学与人类的密切关系,体验数学活动充满着探索与创造。
教学重点理解代数式的意义,会正确书写代数式。
教学难点用代数式表示数量关系。
教学方法教学用具多媒体教学过程集体备课稿个案补充一合作学习1)成人 2 名,小孩 3 名,购买门票应付多少元?2)成人 x 名,小孩 y 名,购买门票应付多少元?2.小芳三分钟能打m个汉字,平均每分钟打_____个;小丽每分钟能打n个汉字,小芳和小丽两人一小时共打___________________个;3、日平均气温是指一天中2:00,8:00,14:00,20:00四个时刻气温的平均值,若上述四个时刻的摄氏度数分别为a、b、c、d,则日平均气温的摄氏度数是4、一隧道长a米,一列火车长180米,如果该列火车穿过隧道所花的时间为t分,则列车的速度为二新课展开售票处成人票价 10元小孩票价 5元像10x+5y,,,, a这样含有字母的数学表达式称为代数式1、一个代数式由什么组成呢?数、表示数的字母和运算符号2、单独的一个数或者一个字母也称代数式。
3,做一做在x,1,x -2,s=ab, v=sh中代数式的个数是( )A. 5B. 4C. 3D. 24例1 用代数式表示:⑴ x的3倍与3的差;⑵ x的2倍与y的的和⑶ a与b的和的平方;⑷ a与b的平方的和;⑸ a、b两数的平方和;⑹比a除以b小2的数⑺ 2a的立方根5练一练:1、用代数式表示“a与-2的差的3倍”,正确的是( )A.a-2B. 3[a-(-2)]C.a-(-2)×3D.3(a-2)2、说出下列代数式的意义:⑴ 2a-b ⑵ 2(a-b) ⑶ a-2b6.例2 一辆汽车以80千米/小时的速度行驶,从A城到B城需t小时,如果该车的行驶速度增加v千米/小时,则从A城到B城需多少时间?解:由题意得,A,B两城之间的路程为80t千米,如果该车的行驶速度增加v千米/小时,则汽车的速度为(80+v)千米/小时,此时从A城到B城需答:当该车行驶速度增加v千米/小时,从A城到B城需小时。
4.2 代数式
4.2 代数式(第1课时)一、教学目标:知识目标:了解代数式的概念,使学生认识用字母表示数的意义,并能说出一个代数式所表示的数量关系;能力目标:培养学生基本的分析、比较能力和抽象思维能力。
情感目标:鼓励学生积极主动参与教学过程,激发求知欲,体验成功,增强学习的兴趣和信心。
二、教学重难点:重点:代数式的概念和根据数量关系列代数式难点:代数式变化以及例2三、教学过程:(一)导入新课:一隧道长l米,一列火车长180米,如果该列火车穿过隧道所花的时间为t分,则列车的速度怎么表示呢?师生共同讨论完成此问题,从而引入本节课我们将要学习的内容------代数式。
(二)探究新知:1.代数式的概念请解答下面的问题:(1)大米的单价为每千克a元,食油的单价为每千克b元,买10千克大米,2千克食油共需__________元。
(2)日平均气温是指一天中2:00,8:00,14:00,20:00四个时刻气温的平均值。
若上述四个时刻气温的摄氏度数分别是a,b,c,d,则日平均气温的摄氏度数是________.(3)一个五彩花圃的形状如图4-1(P91图),花圃的面积是_______.师生共同讨论完成此问题上面的问题,观察比较后得出代数式的概念:由数、表示数的字母和运算符合组成的数学表达式称为代数式.注意:代数式的概念中的运算是指加、减、乘、除、乘方和开方。
单独一个数或者一个字母也称代数式。
2.例题讲解例1 用代数式表示:(1)x的3倍与3的差; (2)x的2倍与y的1/2的和;(3)a与b的和的平方; (4)2a的立方根.教师讲解:(1)先理解题目中表示运算关系的词,理清关系;(2)分清运算顺序.补充书写规范:(1)带分数与字母相乘时,应把带分数化为假分数;(2)实际问题中含有单位时,如果运算结果是加或减时,用括号把代数式整个括起来,再写单位.(三)课内小结:1.本节课用字母表示数时应该注意哪些问题?2.通过本节课的学习你还有什么疑惑?让学生先口答,然后师生共同完善,形成相应的知识体系.(四)课堂练习:P92课内练习1,3题(五)作业布置:P92作业题1,2题4.2 代数式(第2课时)一、教学目标:知识目标:掌握如何利用代数式来表示简单的数量关系。
新浙教版数学七年级上册§4.2代数式师生共用讲学稿
碧莲镇中学师生共用讲学稿年级:初一年级学科:数学执笔:啊潘审核:初一备课组内容:§4.2 代数式课型:新授讲学时间:2009年10月30日学习目标:1、在具体情境中,体会字母表示数的意义,发展符号感。
2、能解释一些简单代数式的实际背景或几何意义。
3、根据具体情境,列代数式、求出代数式的值。
重点分析问题中的数量关系,列出代数式。
难点用语言叙述代数式的意义。
一、学前准备1、知识回顾(1)已知矿泉水的单价为1.5元/瓶, 牛奶的单价为3.5元/瓶,买4瓶矿泉水和5瓶牛奶共需要______元,若买了a瓶矿泉水和b瓶牛奶,共需要______元?(2)日平均气温是指一天中2:00,8:00,14:00,20:00四个时刻气温的平均值,若上述四个时刻气温的摄氏度数分别是a,b,c,d,则北京日平均气温的摄氏度数是。
(3)一隧道长a米,一列火车长180米,如果该列火车穿过隧道所花的时间为t 分,则火车的速度为米/分。
(4)有一个五彩花圃(如图所示),“你知道五彩花圃的面积吗?”以上所得的式子与以前数学算式有什么区别?2、新课预习代数式的概念3、预习疑问二、探索、交流1、判断下列算式是不是代数式:(1)x 2-1 (2)1 (3) x (4)1-x(5) n m2 (6)t=12-x (7)π+1 (8)3x>02、用代数式表示:(1) x 的3倍与3的差; (2) x 的2倍与y 的 1/2 的和;(3) 2a 的立方根; (4) a 与b 的和的平方.a 与b 的平方和,a 与b 的平方的和用代数式又该怎么表示?3、汽车以80千米/小时的速度行驶,从北京到场口需 t 小时.如果该车的行驶速度增加v 千米/小时,那么从北京到场口需多少时间?三、学习体会1.什么是代数式,代数式的组成要素。
2.用代数式表示数量关系时,要正确理解语句的含义,搞清楚数与字母的运算关系,及运算顺序!四、自我检测1、学以致用(1)比a除以b小2的数(2)a与b的平方的差(3)a与b的平方差(4)a与b的差的平方(5)x的相反数与x的绝对值的和(6)x与1的差的平方根(7)v1 与 v2 的和除S所得的商(8)x的3倍与y的4倍的比2、牛刀小试(1)已知甲数比乙数的2倍多1.设乙数为χ,用关于χ的代数式表示甲数. (2)已知甲数是乙数的倒数的2倍多1.设乙数为χ,用关于χ的代数式表示甲数.(3)甲乙两品牌上衣的单价分别为x元、y元. 在换季时,甲品牌上衣按4折(即原价的40%)销售,乙品牌上衣按6折销售.这时购买两种品牌的上衣各一件,共需元?五、应用拓展1、已知12头大象1天的食品可供1000只老鼠吃600天.假定每只老鼠吃的食量都相等,那么t头大象1天的食品可供100只老鼠吃多少天?2、1)一个两位数的个位数字是a ,十位数字是2,请用代数式表示这个两位数。
4.2 代数式 课件
代数式的组成:
① 一个代数式由数,表示数的字母和运算符号组成;
② 单独一个数或者一个字母也称为代数式.
式子不含“=”、“>”、“<”、“≤”、
“代≥”。(1) a×b
数
式 (2) 1÷a
通常写作 aቤተ መጻሕፍቲ ባይዱb 通常写作 1
或 ab ;
;
的
a
规 (3) 数字通常写在字母前面;
范
写 法 :
(4)带分数一般写成假分数.
S 180
列车的速度为 s 180
t
s+180
看下面的问题,填空:
(2)日平均气温是指一天中2:00,8:00,14:00,20:00四个时刻 气温的平均值.若上述四个时刻气温的摄氏度数分别 是a,b,c,d,则日平均气温的摄氏度数_a___b___c__d____。
(3)一五彩花圃的形状
要正确写出代数式要注意 (1)审清题,弄懂一些术语 (2)抓住关键词,弄清运算顺序 (3)一般先读的先写
(4)用代数式表示应用问题时,还弄清题中的 数量关系。
同时一个代数式可表示不同的意义。
在代数式中同一意义的量应用同一个字母表示, 不同意义的量应用不同的字母表示。
1.一隧道长 s 米,一列火 车长180米,如果该列火车 穿过隧道所花的时间为 t 分, 则列车的速度怎么表示?
问题1 什么火车叫做穿过隧道? 你能得出表示列车 速度的算式吗?
从车头进洞开始到车尾离洞结束。
问题2 火车穿过隧道需经过多少路程?
一隧道长 s 米,一列火车长180米,如果 该列火车穿过隧道所花的时间为 t 分,则 列车的速度怎么表示?
(3)10x+5y可以怎样解释?
七年级数学上册 第四章 代数式 4.2 代数式导学课件浙教级上册数学课件
4.2 代数式
解:(1)3x-3. 1
(2)2x+3y. (3)(a+b)2. (4)a2+b2.
12/10/2021
第七页,共十四页。
4.2 代数式
【归纳总结】 代数式的书写格式: (1)数与字母相乘或字母与字母相乘,乘号可以省略不写,也 可以写成“·”;数与字母相乘,在省略乘号时,要把数写在字母 前面. (2)带分数与字母相乘,带分数要写成假分数; (3)除法运算写成分数的形式; (4)式子后面有单位时,和差形式的代数式要用括号括起来. 注意:数与数相乘,仍用“×”号.
(1)如果小红家每月用水 8 吨,那么水费是________元;如果小 红家每月用水 20 吨,那么水费是________元.
(2)如果用字母 x 表示小红家每月用水的吨数,那么小红家每月 的水费该如何用含 12/10/2021 x 的代数式表示呢?
第九页,共十四页。
4.2 代数式
解:(1)每月用水 8 吨时,水费为 8×2=16(元), 每月用水 20 吨时,水费为 2.5×(20-10)+20=45(元). (2)如果 x≤10,那么水费为 2x 元; 如果 x>10,那么水费为[2.5(x-10)+20]元.
第4章 代数式
12/10/2021
Hale Waihona Puke 第一页,共十四页。第4章 代数式
4.2 代数式
学知识 筑方法 勤反思
12/10/2021
第二页,共十四页。
4.2 代数式
学知识
知识点 代数式
由数、表示数的字母和运算符号组成的数学表达式称为代数 式.单独一个___数___或者一个__字_母__(z_ìm也ǔ) 称代数式,注意代数式不含 等号或不等号.
12/10/2021
