双曲线与抛物线认识双曲线与抛物线的特征
高中数学有关圆-椭圆-双曲线-抛物线的详细知识点

<一>圆的方程(x-a)^2+(y-b)^2=r^2,圆心O(a,b),半径r。
(1)圆的一般式方程:x^2+y^2+Dx+Ey+F=0此方程可用于解决两圆的位置关系:配方化为标准方程:(x+D/2)^2.+(y+E/2)^2=(D^2+E^2-4F)/4其圆心坐标:(-D/2,-E/2)半径为r=√[(D^2+E^2-4F)]/2此方程满足为圆的方程的条件是:D^2+E^2-4F>0若不满足,则不可表示为圆的方程(2)点与圆的位置关系点P(X1,Y1) 与圆(x-a)^2+(y-b) ^2=r^2的位置关系:⑴当(x1-a)^2+(y1-b) ^2>r^2时,则点P在圆外。
⑵当(x1-a)^2+(y1-b) ^2=r^2时,则点P在圆上。
⑶当(x1-a)^2+(y1-b) ^2<r^2时,则点P在圆内。
圆与直线的位置关系判断平面内,直线Ax+By+C=0与圆x^2+y^2+Dx+Ey+F=0的位置关系判断一般方法是:1.由Ax+By+C=0,可得y=(-C-Ax)/B,(其中B不等于0),代入x^2+y^2+Dx+Ey+F=0,即成为一个关于x的一元二次方程f(x)=0。
利用判别式b^2-4ac的符号可确定圆与直线的位置关系如下:如果b^2-4ac>0,则圆与直线有2交点,即圆与直线相交。
如果b^2-4ac=0,则圆与直线有1交点,即圆与直线相切。
如果b^2-4ac<0,则圆与直线有0交点,即圆与直线相离。
2.如果B=0即直线为Ax+C=0,即x=-C/A,它平行于y轴(或垂直于x 轴),将x^2+y^2+Dx+Ey+F=0化为 (x-a)^2+(y-b) ^2=r^2。
令y=b,求出此时的两个x值x1、x2,并且规定x1<x2,那么:当x=-C/A<x1或x=-C/A>x2时,直线与圆相离;当x1<x=-C/A<x2时,直线与圆相交;半径r,直径d在直角坐标系中,圆的解析式为:(x-a)^2+(y-b)^2=r^2;x^2+y^2+Dx+Ey+F=0=> (x+D/2)^2+(y+E/2)^2=(D^2+E^2-4F)/4=> 圆心坐标为(-D/2,-E/2)其实只要保证X方Y方前系数都是1就可以直接判断出圆心坐标为(-D/2,-E/2)这可以作为一个结论运用的且r=根号(圆心坐标的平方和-F)<二>椭圆的标准方程椭圆的标准方程分两种情况:当焦点在x轴时,椭圆的标准方程是:x^2/a^2+y^2/b^2=1,(a>b>0);当焦点在y轴时,椭圆的标准方程是:y^2/a^2+x^2/b^2=1,(a>b>0);其中a>0,b>0。
椭圆双曲线抛物线通径

椭圆、双曲线和抛物线是常见的二次曲线,它们在数学和几何中具有重要的性质和特点。
下面简要介绍一下这些曲线的通径(焦点之间的距离):
椭圆(Ellipse):
对于一个椭圆,它具有两个焦点(F1和F2)。
椭圆的通径是通过椭圆的中心点,并且与两个焦点相交的线段。
通径的长度等于两个焦点之间的距离。
双曲线(Hyperbola):
对于一个双曲线,它也有两个焦点(F1和F2)。
双曲线的通径是通过双曲线的中心点,并且与两个焦点相交的线段。
通径的长度等于两个焦点之间的距离。
抛物线(Parabola):
抛物线只有一个焦点(F)和一个顶点。
对于抛物线,通径是通过顶点,并且垂直于抛物线的对称轴。
通径的长度等于焦点到对称轴的距离的两倍。
需要注意的是,通径是曲线的一个重要性质,它与曲线的形状和焦点位置相关。
在数学和物理学中,通径在解决问题和分析曲线性质时具有重要的应用价值。
(完整版)椭圆,双曲线,抛物线知识点
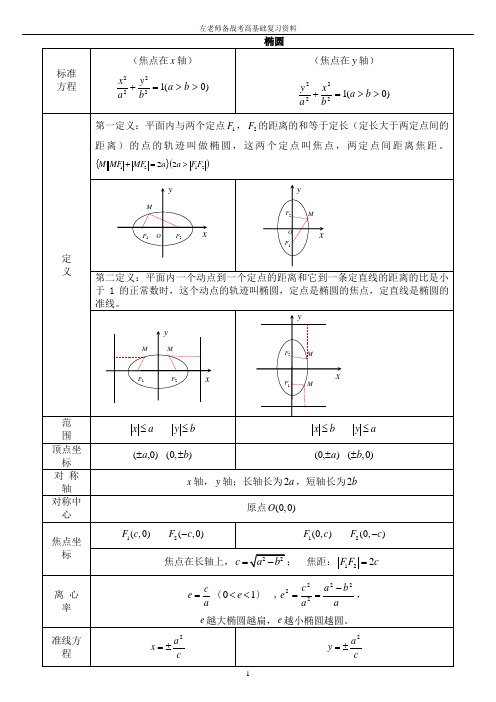
标准
方程
(焦点在 轴)
(焦点在 轴)
定 义
第一定义:平面内与两个定点 , 的距离的和等于定长(定长大于两定点间的距离)的点的轨迹叫做椭圆,这两个定点叫焦点,两定点间距离焦距。
第二定义:平面内一个动点到一个定点的距离和它到一条定直线的距离的比是小于1的正常数时,这个动点的轨迹叫椭圆,定点是椭圆的焦点,定直线是椭圆的准线。
顶点到准线的距离
焦点到准线的距离
焦点弦的几条性质
设直线过焦点F与抛物线 >0)交于 ,
则:(1) =
(2)
(3)通径长:
(4)焦点弦长
直线与抛物线的位置
抛物线 与直线 的位置关系:
利用 转化为一元二次方程用判别式确定。
切线
方程
焦点 ( )到准线 ( )的距离为
焦点 ( )到准线 ( )的距离为
椭圆上到焦点的最大(小)距离
最大距离为:
最小距离为:
相关应用题:远日距离
近日距离
椭圆的参数方程
( 为参数)
( 为参数)
椭圆上的点到给定直线的距离
利用参数方程简便:椭圆 ( 为参数)上一点到直线 的距离为:
直线和椭圆的位置
椭圆 与直线 的位置关系:
焦点 ( )到准线 ( )的距离为
焦点 ( )到准线 ( )的距离为
渐近线
方程
( )
( )
共渐近线的双曲线系方程
( )
( )
直线和双曲线的位置
双曲线 与直线 的位置关系:
利用 转化为一元二次方程用判别式确定。
二次方程二次项系数为零直线与渐近线平行。
相交弦AB的弦长
通径:
过双曲线上一点的切线
双曲线抛物线知识点总结

标准图
参数p几何意义
参数p表示焦点到准线的距离,p越大,开口越阔.
几何性质
开口方向
右
左
上
下
焦点位置
X正
X负
Y正
Y负
焦点坐标
准线方程
范围
对称轴
X轴
X轴
Y轴
Y轴
离心率
通 径
2p
焦半径
焦点弦长
引申
焦点弦长 的补充,
以 为直径的圆必与准线 相切
若 的倾斜角为 ,
若 的倾斜角为 ,则
双曲线知识点总结
定义
在平面内到两定点F1、F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫双曲线
标准方程
焦点在x轴
焦点在y轴
- =1(a>0,b>0)
- =1(a>0,b>0)
标准图
几
何
性
质
1.范围
x≥a或x≤-a
y∈R
x∈R
y≤-a或y≥a
2.对称性
对称轴:坐标轴对称中心:原点
3.顶点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
4.渐近线
y=± x
y=± x
5.离心率
6.实虚轴
线段A1A2叫做双曲线的实轴,它的长|A1A2|=2a;
线段B1B2叫做双曲线的虚轴,它的长|B1B2|=2b;
a叫做双曲线的实半轴长,b叫做双曲线的虚半轴长
a、b、c的关系
c2=a2+b2(c>a>0,c>b>0)
焦点三角形
1.余弦定理:∣F1F2∣2=∣PF1∣2+∣PF2∣2-2∣PF1∣∣PF2∣cosθ
椭圆、双曲线、抛物线分类比较
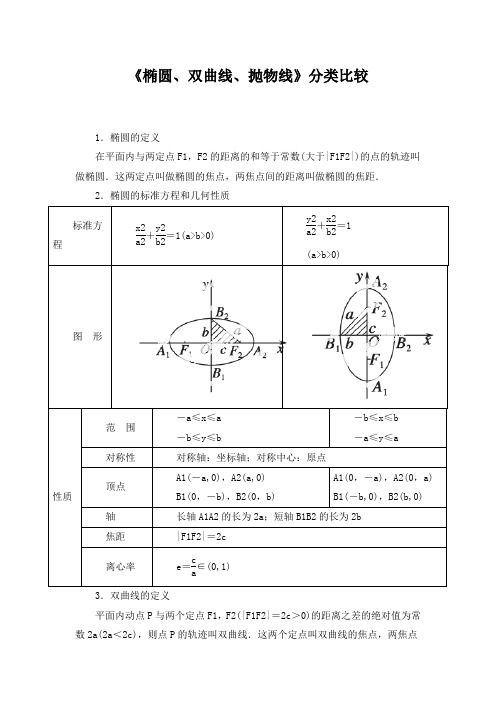
《椭圆、双曲线、抛物线》分类比较1.椭圆的定义在平面内与两定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.2.椭圆的标准方程和几何性质标准方程x2a2+y2b2=1(a>b>0)y2a2+x2b2=1(a>b>0)图形性质范围-a≤x≤a-b≤y≤b-b≤x≤b-a≤y≤a 对称性对称轴:坐标轴;对称中心:原点顶点A1(-a,0),A2(a,0)B1(0,-b),B2(0,b)A1(0,-a),A2(0,a)B1(-b,0),B2(b,0) 轴长轴A1A2的长为2a;短轴B1B2的长为2b焦距|F1F2|=2c离心率e=ca∈(0,1)3.双曲线的定义平面内动点P与两个定点F1,F2(|F1F2|=2c>0)的距离之差的绝对值为常数2a(2a<2c),则点P的轨迹叫双曲线.这两个定点叫双曲线的焦点,两焦点间的距离叫焦距.4.双曲线的标准方程和几何性质标准方程x2a2-y2b2=1(a>0,b>0)y2a2-x2b2=1(a>0,b>0)性质范围x≥a或x≤-a,y∈R x∈R,y≤-a或y≥a 对称性对称轴:坐标轴;对称中心:原点顶点A1(-a,0),A2(a,0)A1 (0,-a),A2(0,a)渐近线y=±bax y=±abx 离心率e=ca,e∈(1,+∞),其中c=a2+b2实虚轴线段A1A2叫做双曲线的实轴,它的长|A1A2|=2a;线段B1B2叫做双曲线的虚轴,它的长|B1B2|=2b;a叫做双曲线的半实轴长,b叫做双曲线的半虚轴长a,b,c的关系c2=a2+b2(c>a>0,c>b>0)5.抛物线的定义(1)平面内与一个定点F和一条定直线l(F∉l)的距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.(2)其数学表达式:|MF|=d(其中d为点M到准线的距离).6.抛物线的标准方程与几何性质图形标准方程y2=2px (p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)续表。
椭圆、双曲线、抛物线的统一定义以及动画演示

双曲线的定义 :
平面内与两定点F1、F2的距离的差的绝对 值是常数(小于|F1F2|)的点的轨迹叫做双 曲线.这两个定点F1、F2叫做双曲线的 焦点,两个焦点之间的距离叫做焦距.
说明:若动点M到两定点的距离之差的 绝对值为2a ,| F1 F2| = 2c 当c > a >0时,动点M的轨迹是双曲线; 当a = c>0时,动点M的轨迹是两条射线; 当 0 < c < a时,动点M无轨迹
关于椭圆、双曲线、抛物线你了解多少? 在我们的实际生活中有这些曲线吗? 它们分别给我们什么印象?
椭圆?
汽车贮油罐的横截面的外轮廓线 的形状像椭圆.
北京摩天大楼
巴西利亚大教堂
法拉利主题公园
花瓶
椭圆定点 F1 ,F2的距离之和 为常数(大于F1 F2 距离)的点的轨迹 叫椭圆,两个定点 叫椭圆的焦点,两 焦点的距离叫做椭 圆的焦距.
的点的轨迹叫做抛物线.
· N M
定点F叫做抛物线的焦点.
·F
定直线l 叫做抛物线的准线.
即:
若
︳MF ︳MN
︳ ︳ 1,
则 点M的
轨迹
是
抛物线
。
椭圆的定义:
平面内到两定点F1、F2的距离之和等于 常数(大于|F1F2|)的点的轨迹叫做椭圆. 这两个定点叫做椭圆的焦点,两焦点 间的距离叫做焦距.
说明: 若动点M到的距离之和为2a , | F1 F2| = 2c 则当a>c>0时,动点M的轨迹是椭圆; 当a = c>0时,动点M的轨迹是线段F1 F2 ; 当 0 < a < c时,动点M无轨迹
抛物线的定义 :
平面内到一个定点F和一条定直线L(F不在L 上)的距离相等的点轨迹叫做抛物线,定点F叫做 抛物线的焦点,定直线L叫做抛物线的准线.
高一数学《认识双曲线》知识点总结

高一数学《认识双曲线》知识点总结认识双曲线双曲线是高一数学中重要的曲线之一,它在几何图形和函数图像的研究中有着广泛的应用。
本文将对认识双曲线的相关知识点进行总结和讲解。
一、双曲线的定义和基本性质双曲线是平面上一种特殊的曲线,它与椭圆和抛物线类似,也是由一条弯曲的曲线组成。
但与椭圆和抛物线不同的是,双曲线的两支曲线分离并且无限延长。
双曲线的数学定义为平面上满足以下方程的点的集合:(x^2/a^2) - (y^2/b^2) = 1 或者 (y^2/b^2) - (x^2/a^2) = 1其中,a和b是正实数,表示曲线在x轴和y轴上的截距。
双曲线有许多基本性质,包括:两支曲线分离且无限延长、有着对称轴和对称中心、双曲线的离心率大于1等等。
这些性质是我们认识双曲线的基础,也是我们进一步探索其特性和应用的前提。
二、双曲线的标准方程及图像双曲线可以通过标准方程来描述,标准方程分别为:(x^2/a^2) - (y^2/b^2) = 1 和 (y^2/b^2) - (x^2/a^2) = 1其中,a和b是双曲线的参数,决定了双曲线的形状和大小。
当a>b时,双曲线的主轴与x轴平行;当a<b时,双曲线的主轴与y轴平行。
根据双曲线的标准方程,我们可以使用数值计算或绘图软件来画出双曲线的图像。
通过观察图像,我们可以更直观地理解双曲线的特性和性质。
三、双曲线的焦点和准线与椭圆和抛物线类似,双曲线也有着焦点和准线。
在双曲线的定义中,焦点和准线是与双曲线的离心率密切相关的概念。
对于双曲线方程(x^2/a^2) - (y^2/b^2) = 1,焦点的坐标为(±c, 0),其中c = √(a^2 + b^2)。
而准线是曲线的两支与离心率所确定的直线。
根据准线与离心率的关系,我们可以进一步求解双曲线的离心率。
四、双曲线的渐近线双曲线还具有渐近线,即无限远处曲线趋近的直线。
对于双曲线方程 (x^2/a^2) - (y^2/b^2) = 1,它的渐近线有两条,分别是与曲线相交于两个交点的直线。
热点18 双曲线与抛物线-2017年高考数学二轮核心考点总

2017届高考数学考点总动员【二轮精品】第一篇热点18 双曲线与抛物线【热点考法】本热点双曲线考题形式为选择填空题、抛物线为选择填空题或解答题,与向量、函数、不等式结合主要考查双曲线的定义、标准方程、几何性质与抛物线的定义、方程、几何性质及直线与抛物线的位置关系,考查运算求解能力、数形结合思想与转化与化归思想,是中档题或难题,分值为10至15分. 【热点考向】考向一 双曲线定义及其标准方程【解决法宝】1.涉及双曲线上的点到两焦点的距离问题时,要灵活运用双曲线的定义; 求解双曲线的标准方程的求法是“先定型,后计算”.所谓“定型”,就是指确定类型,所谓“计算”,就是指利用待定系数法求出方程中的22,b a 的值,最后代入写出双曲线的标准方程.例1.【河北唐山市2017届上学期高三摸底考,5】已知12,F F 是双曲线2214x y -=的两个焦点,P 在双曲线上,且满足01290F PF ∠=,则12FPF ∆的面积为( )A .1B .2 D 【分析】首先设出n PF m PF ==21,并由定义可得等式421=-=-n m PF PF ,然后结合已知条件可得出另一个等式,再联立两个等式即可求出mn 的值,最后由三角形的面积计算公式即可得出所求的结果.考向二 抛物线的定义与标准方程【解决法宝】1.涉及抛物线上的点到焦点的距离时,常利用定义转化为到抛物线的准线的距离;2.抛物线的标准方程的求法是“先定型,后计算”.所谓“定型”,就是指确定类型,所谓“计算”,就是指利用待定系数法求出方程中的p 的值,最后代入写出抛物线的标准方程.例2 【广东海珠区2017届上学期高三综合测试(一),11】过抛物线22(0)y px p =>的焦点F 且倾斜角为60的直线l 与抛物线在第一、四象限分别交于,A B 两点,则||||AF BF 的值等于( )A .5B .4C .3D .2【分析】设出直线l 方程,将直线l 方程代入抛物线,化为关于x 的一元二次方程,将B A ,横坐标用p 表示出来,再利用抛物线定义将AF 、BF 用p 表示出来,即可求出||||AF BF 的值.考向三 双曲线、抛物线的几何性质【解决法宝】1.双曲线的离心率是双曲线的主要性质,是反映双曲线的开口大小的一个量,在求解有关离心率的问题时,一般不是直接求出a 和c 的值,而是根据题目给出的双曲线的几何特征,建立关于参数c b a ,,的方程或不等式,通过解方程或不等式求得离心率的值或范围;2.抛物线的几何性质的特点:有一个顶点,一个焦点,一条准线,一条对称轴,无对称中心,无渐近线,p 的几何意义是焦点到准线的距离.例3. 【河北石家庄2017届高三上学期第一次质检,16】已知F 为双曲线()222210,0x y a b a b-=>>的右焦点,过原点的直线l 与双曲线交于,M N 两点,且0,MF NF MNF =∆的面积为ab ,则该双曲线的离心率为 .【分析】由已知即双曲线的对称性知四边形F MFN '为矩形,利用双曲线的定义||||2MF NF a -=,由三角形面积公式,||||MF NF =2ab ,在Rt MNF ∆中利用勾股定理即可的c b a ,,的关系式,从而求出离心率.【解析】因为0MF NF ⋅=,所以MF NF ⊥.设双曲线的左焦点为F ',则由双曲线的对称性知四边形F MFN '为矩形,则有||||,||2MF NF MN c '==.由双曲线的定义知,||NF '-||NF =2a ,所以||||2MF NF a -=.因为1||||2MNF S MF NF ab ∆==,所以||||MF NF =2ab .在Rt MNF ∆中,222||||||MF NF MN +=,即2(||||)2||||MF NF MF NF -+=2||MN ,所以22(2)22(2)a ab c +⋅=,把222c a b =+代入,并整理,得1b a =,所以c e a===考向四 直线与抛物线的位置关系【解决法宝】解决直线与抛物线的位置关系问题,常采用“设而不求”的方法,步骤如下: (1)先根据条件设出直线方程或抛物线方程,联立两个方程,消去x 或y ,整理成关于x 的二次方程;(2)设直线与椭圆的交点坐标为),(),,(2211y x B y x A ,根据根与系数的关系,写出两根和与两根积的表达式;(3)将题中的条件用B A ,的坐标表示,然后化简整理.但要注意的是,对于直线与抛物线的位置关系的判定时,联立方程后首先要看二次项系数是否为0.例4【云南省、四川省、贵州省2017届高三上学期百校大联考数学,20】(本小题满分12分) 已知抛物线2:2(0)E y px p =>,直线3x my =+与E 交于A ,B 两点,且6OA OB =,其中O 为坐标原点. (1)求抛物线E 的方程;(2)已知点C 的坐标为(-3,0),记直线CA 、CB 的斜率分别为1k ,2k ,证明:22212112m k k +-为定值.【分析】设11(,)A x y ,22(,)B x y ,联立方程组223y pxx my ⎧=⎨=+⎩,消元得2260y pmy p --=,所以122y y pm +=,126y y p =-.又2121212122()4y y OA OB x x y y y y p⋅=+=+,所以12p =,从而求出结果.(2)因为1111136y y k x my ==++,2222236y y k x my ==++,因此222222121211662()()2m m m m k k y y +-=+++- 222121212221212()2212362y y y y y y m m m y y y y ++-=++-,又122y y pm m +==,1263y y p =-=-,代入即可求出定值.【解析】(1)解:设11(,)A x y ,22(,)B x y ,联立方程组223y pxx my ⎧=⎨=+⎩,消元得2260y p m y p --=, 所以122y y pm +=,126y y p =-.……………………………………………………………………………2分又2121212122()9664y y OA OB x x y y y y p p=+=+=-=,……………………………………………………6分 所以12p =,从而2y x =.………………………………………………………………………………………5分(2)因为1111136y y k x my ==++,2222236y y k x my ==++,所以1116m k y =+,2216m k y =+,……………………………………………………………………………6分 因此222222121211662()()2m m m m k k y y +-=+++- 222212121111212()36()2m m m y y y y =++++-………………………………………………………………8分222121212221212()2212362y y y y y y m m m y y y y ++-=++- 又122y y pm m +==,1263y y p =-=-,…………………………………………………………………9分所以2222221211622123622439m m m m m m k k -++-==+⨯+⨯-=.……………………………………11分 即22212112m k k +-为定值.………………………………………………………………12分 【热点集训】1.【湖北省黄石市2017届高三年级九月份调研,6】过抛物线24y x =的焦点F 的直线l 与抛物线交于A B 、两点,若A B 、两点的横坐标之和为103,则AB =( ) A .133 B .143 C .5 D .163【答案】D【解析】由抛物线定义得1016233A B AB x x p =++=+=,选D. 2.【长春市普通高中2016届高三质量监测(二)】过双曲线22115y x -=的右支上一点P ,分别向圆221:(4)4C x y ++=和圆2:C 22(4)1x y -+=作切线,切点分别为,M N ,则22||||PM PN -的最小值为( )A. 10B. 13C. 16D. 19【答案】B 【解析】3.【江西南昌市2017届摸底考试,10】若圆22((1)3x y +-=与双曲线22221(0,0)x y a b a b -=>>的一条渐近线相切,则此双曲线的离心率为( )A B C .2 D 【答案】A2c a c b e a =⇒=⇒=⇒==,选A. 4.【云南省、四川省、贵州省2017届高三上学期百校大联考数学,5】已知双曲线2222:1(0,0)x y C a b a b-=>>的渐近线方程为34y x =±,且其右焦点为(5,0),则双曲线C 的方程为( )A .221916x y -= B .221169x y -= C .22134x y -= D .22143x y -= 【答案】B 【解析】由题意得34b a =,22225c a b =+=,所以4a =,3b =,所求双曲线方程为221169x y -=. 5.【河北邯郸市2017届高三9月联考,4】设抛物线2:4C y x =的焦点为F ,准线l 与x 轴的交点为R ,过抛物线C 上一点P 作准线l 的垂线,垂足为Q ,若Q R F ∆的面积为2,则点P 的坐标为( )A .(1,2)或(1,-2)B .(1,4)或(1,-4) C.(1,2) D .(1,4) 【答案】A .【解析】设点P 的坐标为),(00y x , 则因为QRF ∆的面积为2,所以22210=⨯⨯y ,即20=y ,所以14410=⨯=x ,所以点P 的坐标为(1,2)或(1,-2),故应选A . 6.【广西南宁二中、柳州高中、玉林高中2017届高三8月联考,9】若双曲线22221x y a b-=(0,0a b >>)的左、右焦点分别为12,F F ,且线段12F F 被抛物线24y bx =的焦点分成5:3的两段,则双曲线的离心率为( ) A.15B.3 C【答案】A7.【甘肃省河西五市部分普通高中2016年1月高三第一次联考】已知点A 是抛物线214y x =的对称轴与准线的交点,点F 为该抛物线的焦点,点P 在抛物线上且满足||||PF m PA =,当m 取最小值时,点P 恰好在以A ,F 为焦点的双曲线上,则该双曲线的离心率为( ) AB.12C1 D1【答案】C.【解析】如下图所示,(0,1)A -,(0,1)F ,过P 作准线的垂线,垂足是H ,由对称性,不妨令P 在第一象限,∴||||sin ||||PF PH m PAH PA PA ===∠,∴问题等价于求PAH ∠的最小值,而21111144tan 14y x PAH x x x x ++∠===+≥=,当且仅当1124x x x =⇒=时等号成立,此时||||221PA PF a a -==⇒,∴1c e a ===,故选C .8.【广东珠海市2017届上学期调研测试(1),6】设点P 是双曲线22221(0,0)x y a b a b-=>>上的一点,12,F F 分别为双曲线的左、右焦点,已知12PF PF ⊥,且12||2||PF PF =,则双曲线的离心率为( )A .2D 【答案】D【解析】由双曲线的定义可得12||||2PF PF a -=,又 12||2||PF PF =,得21||2,||4PF a PF a ==,在12,RT F F ∆中,2222221212,,4164F F PF PF c a a =+∴=+, 即225c a =,则ce a==,故选D. 9.【甘肃省张掖市2016届高三第一次诊断考试】过抛物线x y 42=的焦点的直线l 交抛物线于()()1122,,,P x y Q x y 两点,如果126x x +=,则PQ = ( )A .9B .8C .7D .6【答案】B10. 【广东郴州市2017届高三第二次教学质量监测试卷,10】已知F 为双曲线22221(0,0)x y a b a b -=>>的左焦点,点A 为双曲线虚轴的一个顶点,过,F A 的直线与双曲线的一条渐近线在y 轴右侧的交点为B ,若(21)FA AB =-,则此双曲线的离心率是( )A .【答案】A【解析】FA 的方程为1x yc b +=-,即0bx cy bc -+=,联立00bx cy bc bx ay -+=⎧⎨-=⎩得(,),(21)ca bc B FA AB c a c a =---,所以1)cac c a=⋅-,解得e = A. 11.【河北唐山市2017届高三年级期末,11】已知O 为坐标原点,F 是双曲线()2222:10,0x y a b a b Γ-=>>的左焦点,,A B 分别为Γ的左、右顶点,P 为Γ上一点,且PF x ⊥轴, 过点A 的直线l 与线段PF 交于点M ,与y 轴交于点E ,直线 BM 与y 轴交于点N ,若2OE ON =,则 Γ的离心率为 ( ) A .3 B .2 C.32 D .43【答案】A12.【黑龙江省哈尔滨六中2016届高三上学期期末】若抛物线y 2=2px (p >0)的焦点为F ,其准线经过双曲线的左焦点,点M 为这两条曲线的一个交点,且|MF|=p ,则双曲线的离心率为( ) A .B .C .D .【答案】C【解析】抛物线y 2=2px (p >0)的焦点为F (,0),其准线方程为x=﹣,∵准线经过双曲线的左焦点,∴c=;∵点M 为这两条曲线的一个交点,且|MF|=p ,∴M 的横坐标为, 代入抛物线方程,可得M 的纵坐标为±p,将M 的坐标代入双曲线方程,可得﹣=1,∴a=p ,∴e==1+.故选:C .13.【山东省肥城市2017届高三上学期升级统测,14】在平面直角坐标系xOy 中, 若双曲线22214x y m m -=+则m 的值为 . 【答案】2【解析】由题意得m >= 2.m =14.【山东省实验中学2017届高三第一次诊,15】过双曲线22221x y a b-=(0a >,0b >)的右焦点F 作渐进线的垂线,设垂足为P (P 为第一象限的点),延长FP 交抛物线22y px =(0p >)于点Q ,其中该双曲线与抛物线有一个共同的焦点,若1()2OP OF OQ =+,则双曲线的离心率的平方为 .【解析】1()2OP OF OQ =+⇒P 为FQ 的中点,所以22,2,Q Q a b FQ b x b c y c ⋅==-=,因此22222()(2)1,a b b c c a b ⋅--=解得2e =15.【河南百校联考2017届高三9月质检,16】已知双曲线()2222:10,0x y C a b a b -=>>的左、右焦点分别为()()12,0,,0F c F c -,,A B 是圆()2224x c y c ++=与C 位于x 轴上方的两个交点,且12//F A F B ,则双曲线C 的离心率为______________.16.【河南省广东省佛山市2017届高三教学质量检测(一),16】已知双曲线()2222:10x y C b a a b-=>>的右焦点为F ,O 为坐标原点,若存在直线l 过点F 交双曲线C 的右支于A ,B 两点,使0OA OB ⋅=,则双曲线离心率的取值范围是 .e ≤<【解析】设1122(,),(,)A x y B x y ,直线l 的方程为x my c =+(0)am b≤<,联立双曲线方程,消去x ,得22222()2b m a y b mcy -++40b =,所以2122222b mcy y b m a +=--①,412222b y y b m a =-②.因为OA OB ⋅=12120x x y y +=,即22121212()0m y y mc y y c y y ++++=,代入①②整理,得422222222b m b m c c b m -+-2240a c b +=,4222222420b a c a m b c b b-≤=<-.由4220b a b -≥,得22222()0c a a c --≥,即422430c a c a -+≥,42310e e -+≥,解得e ≥;由42222242b a c a b c b b -<-,得44220b a a c --<,即222422()0c a a a c ---<,42230c a c -<,所以ca<综上所述,e ∈.17.【广西南宁二中、柳州高中、玉林高中2017届高三8月联考,20】(本小题满分12分)已知抛物线24y x =的焦点为F ,过点F 的直线交抛物线于,A B 两点. (1)若3AF FB =,求直线AB 的斜率;(2)设点M 在线段AB 上运动,原点O 关于点M 的对称点为C ,求四边形OACB 面积的最小值.【答案】(1(2)4.【解析】(1)依题意可设直线:1AB x my =+, 将直线AB 与抛物线联立214x my y x=+⎧⎨=⎩⇒2440y my --=,设11(,)A x y ,22(,)B x y , 由韦达定理得121244y y my y +=⎧⎨=-⎩,∵1233AF FB y y =⇒=-213m ⇒= (2)121212242OACB AOB S S OF y y y y ∆==⋅-=-=≥, 当0m =时,四边形OACB 的面积最小,最小值为4.18.【湖南永州市2017届高三第一次模拟,20】(本题满分12分)已知曲线C 上的任一点到点(0,1)F 的距离减去它到x 轴的距离的差都是1. (1)求曲线C 的方程;(2)设直线(0)y kx m m =+>与曲线C 交于A ,B 两点,若对于任意k R ∈都有0FA FB <,求m 的取值范围.【答案】(1)24x y =;(2)33m -<<+【解析】(1)设曲线C 上的任一点为(,)P x y ,则||1y =,……………………………3分化简得24x y =, 即曲线C 的方程为:24x y =.…………………………………………………………………………………5分(2)将y kx m =+,代入24x y =得2440x kx m --=.当0m >时,216160k m ∆=+>, 设11(,)A x y ,22(,)B x y ,则124x x k +=,124x x m =-.……………………………………………………7分11(,1)FA x y =-,22(,1)FB x y -,12121212(1)(1)(1)(1)FA FB x x y y x x kx m kx m =+--=++-+-221212(1)(1)()(1)k x x k m x x m =++-++-2224(1)4(1)(1)m k k m m =-++-+-224(1)4k m m =-+--.………………………………………………………………………………9分∵对于任意k R ∈都有0FA FB <,∴224(1)40k m m -+--<对任意的k R ∈恒成立.则2(1)40m m --<,解得33m -<<+所以m的取值范围是33m -<+………………………………………………………………12分19.【河南百校联盟2017届9月质检,21】(本小题满分12分)如图所示,抛物线()2:20C x py p =>,其焦点为,F C 上的一点()4,M m 满足4MF =.(1)求抛物线C 的标准方程;(2)过点()1,0E -作不经过原点的两条直线,EA EB 分别与抛物线C 和圆()22:24F x y +-=相切于点,A B ,试判断直线AB 是否经过焦点F .【答案】(1)28x y =(2)经过【解析】(1)抛物线C 的准线方程为2py =-, 所以42pMF m =+=,又因为162pm =,所以28160p p -+=,得4p =, 所以抛物线C 的标准方程为28x y =........................4分(2)设:1EA x ky =-,联立218x ky x y=-⎧⎨=⎩,消去x 得:()222810k y k y -++=,因为EA 与C 相切,所以()222840k k ∆=+-=,即2k =-,所以1,22A A y x ==-,得12,2A ⎛⎫- ⎪⎝⎭,.................................7分设:1EB x ty =-,联立()22124x ty x y =-⎧⎪⎨+-=⎪⎩,消去x 得:()()2212410t y t y +-++=, 因为EB 与圆F 相切,所以()()2224410t t ∆=+-+=,即34t =-,所以48,55B B y x ==-,得84,55B ⎛⎫- ⎪⎝⎭,................................. 10分 所以直线AB 的斜率34AB k =, 可得直线AB 的方程为324y x =+,经过焦点()0,2F .................12分20.【广东珠海市2017届上学期调研测试(1),20】(本小题满分12分)已知点F 为抛物线E :22(0)y px p =>的焦点,点(2,)A m 在抛物线E 上,且到原点的距离为(1)求抛物线E 的方程;(2)已知点(1,0)G -,延长AF 交抛物线E 于点B ,证明:以点F 为圆心且与直线GA 相切的圆,必与 直线GB 相切.【答案】(1)24y x =;(2)证明见解析.【解析】(1)由题意可得:24m p⎧=⎪=解得2p =,所以抛物线E 的方程为24y x =.(2)设以点F 为圆心且与直线GA 相切的圆的半径为r . 因为点(2,)A m 在抛物线:E 24y x =上,所以m =±由抛物线的对称性,不妨设A .由A ,(1,0)F 可得直线AF的方程为1)y x =-.由21)4y x y x⎧=-⎪⎨=⎪⎩,得22520x x -+=,解得2x =或12x =,从而1(,2B . 又(1,0)G -,故直线GA的方程为30y -+=,从而r ==又直线GB的方程为30y ++=, 所以点F 到直线GB的距离为d r ===.这表明以点F 为圆心且与直线GA 相切的圆必与直线GB 相切.21.【广西南宁二中、柳州高中、玉林高中2017届高三8月联考,20】(本小题满分12分)已知抛物线24y x =的焦点为F ,过点F 的直线交抛物线于,A B 两点. (1)若3AF FB =,求直线AB 的斜率;(2)设点M 在线段AB 上运动,原点O 关于点M 的对称点为C ,求四边形OACB 面积的最小值.【答案】(1(2)4.【解析】(1)依题意可设直线:1AB x my =+, 将直线AB 与抛物线联立214x my y x=+⎧⎨=⎩⇒2440y my --=,设11(,)A x y ,22(,)B x y , 由韦达定理得121244y y my y +=⎧⎨=-⎩,∵1233AF FB y y =⇒=-213m ⇒=(2)121212242OACB AOB S S OF y y y y ∆==⋅-=-=≥,当0m =时,四边形OACB 的面积最小,最小值为4.22.【河北衡水中学2017届高三摸底联考,20】(本小题满分12分)在平面直角坐标系xOy 中, 过点()2,0C 的直线与抛物线24y x =相交于,A B 两点,()()1122,,,A x y B x y . (1)求证:12y y 为定值;(2)是否存在平行于y 轴的定直线被以AC 为直径的圆截得的弦长为定值?如果存在,求该直线方程和弦长;如果不存在,说明理由.【答案】(1)见解析;(2) 存在平行于y 轴的定直线1x =被以AC 为直径的圆截得的弦长为定值.(解法2)设直线AB 的方程为2-=x my由⎩⎨⎧=-=xy x my 422得0842=--my y 821-=∴y y 因此有821-=y y 为定值 . (Ⅱ)设存在直线l :a x =满足条件,则AC 的中点)2,22(11y x E +,2121)2(y x AC +-= 因此以AC 为直径的圆的半径421)2(2121212121+=+-==x y x AC r又E 点到直线a x =的距离|22|1a x d -+= 所以所截弦长为212122)22()4(4122a x x dr -+-+=- 2121)22(4a x x -+-+=2148)1(4a a x a -+--=当01=-a 即1=a 时,弦长为定值2,这时直线方程为1=x .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双曲线与抛物线认识双曲线与抛物线的特征双曲线与抛物线:认识双曲线与抛物线的特征
双曲线和抛物线是数学中两种常见的曲线形状。
它们在几何、物理、工程等领域中都有广泛的应用。
本文将介绍双曲线与抛物线的基本定义、特征以及它们在实际中的应用。
一、双曲线的定义和特征
双曲线是一种由一个平面上的点P到两个定点F1和F2的距离之差
的绝对值等于常数d的点集。
这两个定点称为双曲线的焦点,常数d
称为离心率。
根据焦点的位置,双曲线可以分为椭圆双曲线和双曲双
曲线。
1.1 椭圆双曲线的特征
椭圆双曲线有以下特征:
a) 中心对称性:椭圆双曲线关于原点O对称。
b) 焦点和顶点:椭圆双曲线有两个焦点F1和F2,以及两个顶点
V1和V2。
c) 主轴和次轴:椭圆双曲线有两个轴,其中长的轴称为主轴,短的
轴称为次轴。
d) 焦点与顶点之间的距离:每个椭圆双曲线都满足焦点与顶点之间
的距离之和等于常数2a,其中a为离心率。
1.2 双曲双曲线的特征
双曲双曲线与椭圆双曲线相似,但有以下特征:
a) 中心对称性:双曲双曲线关于原点O对称。
b) 焦点和顶点:双曲双曲线有两个焦点F1和F2,以及两个顶点
V1和V2。
c) 主轴和次轴:双曲双曲线有两个轴,其中长的轴称为主轴,短的轴称为次轴。
d) 焦点与顶点之间的距离:每个双曲双曲线满足焦点与顶点之间的距离之差等于常数2a,其中a为离心率。
二、抛物线的定义和特征
抛物线是一个平面上到一定点(F)的距离等于到一条直线(L)的距离的点的集合。
抛物线具有以下特征:
2.1 中心对称性
抛物线关于直线ax = 0对称,其中a为实数。
2.2 焦点和准线
抛物线有一个焦点F和一条准线L(也称为焦准距),焦点F位于抛物线的焦线上,准线L位于抛物线的准线上。
2.3 顶点
抛物线的顶点是抛物线曲线的最高点或最低点。
2.4 对称轴
抛物线的对称轴是通过焦点和顶点的直线。
2.5 焦点和顶点之间的距离
每个抛物线满足焦点到顶点的距离等于焦点到准线的距离。
三、双曲线与抛物线的应用
双曲线和抛物线在现实生活中有着广泛的应用。
以下是它们的一些
应用领域:
3.1 双曲线的应用
a) 物理学:双曲线可以描述粒子在万有引力场中的运动轨迹。
b) 工程学:双曲线可以应用于抛物面天线的设计和管道的布置。
c) 经济学:双曲线可以应用于描述成本、需求和价格等的变化关系。
3.2 抛物线的应用
a) 物理学:抛物线可以描述物体在只受重力作用下的自由落体运动
轨迹。
b) 工程学:抛物线可以用于设计桥梁、卫星接收器的轨迹和抛物面
反射器等。
c) 电子学:抛物线可以应用于天线的设计和聚光器的设计。
总结起来,双曲线和抛物线是两种常见的数学曲线,它们在几何学、物理学、工程学和经济学等领域中都有着重要的应用。
通过了解双曲
线和抛物线的定义和特征,我们可以更好地理解并应用它们在不同领
域中的实际问题中。
