上海市七宝中学2019-2020学年高三上学期10月月考数学试题(教师版)
2020届上海市七宝中学高三高考押题卷数学试卷(1)及答案解析
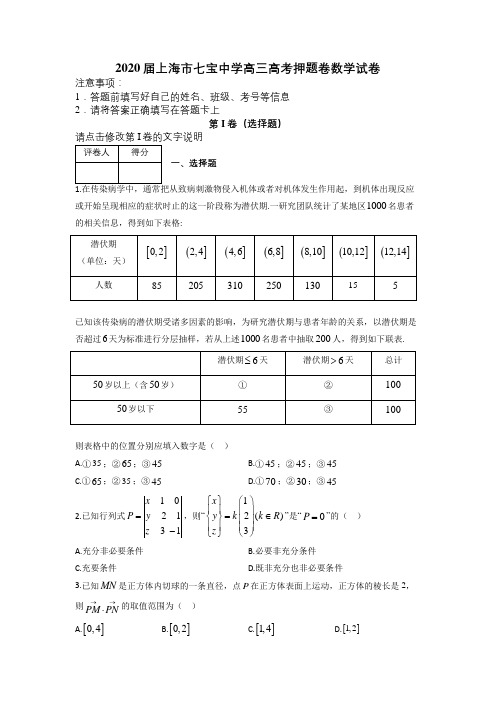
2020届上海市七宝中学高三高考押题卷数学试卷注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题或开始呈现相应的症状时止的这一阶段称为潜伏期.一研究团队统计了某地区1000名患者的相关信息,得到如下表格:已知该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,若从上述1000名患者中抽取200人,得到如下联表.则表格中的位置分别应填入数字是( ) A.①35;②65;③45 B.①45;②45;③45 C.①65;②35;③45D.①70;②30;③452.已知行列式102131x P y z =-,则“12()3x y k k R z ⎧⎫⎛⎫⎪⎪ ⎪=∈⎨⎬ ⎪⎪⎪ ⎪⎩⎭⎝⎭”是“0P =”的( )A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件3.已知MN 是正方体内切球的一条直径,点P 在正方体表面上运动,正方体的棱长是2,则PM PN →→⋅的取值范围为( ) A.[]0,4B.[]0,2C.[]1,4D.[]1,24.如图,已知函数()y f x =与y x =的图象有唯一交点()1,1,无穷数列{}()*n a n N ∈满足点()1,n n n P a a +()*n N∈均落在()y f x =的图象上,已知()13,0P ,()20,2P ,有下列两个命题:(1)lim 1n n a →∞=;(2){}21n a -单调递减,{}2n a 单调递增;以下选项正确的是( )A.(1)是真命题,(2)是假命题B.两个都是真命题C.(1)是假命题,(2)是真命题D.两个都是假命题第II 卷(非选择题)二、填空题(题型注释)5.已知集合}41,A x x k k Z ==±∈,{}2,B y y n n Z ==∈,则AB =________.6.已知圆225x y +=和点()2,1A -,则过点A 的圆的切线方程为._________7.满足()12log 24x x -+=的实数x =________.8.已知复数13z i =-+(i 是虚数单位)是实系数一元二次方程20ax bx c ++=的一个虚根,则::a b c =________.9.已知向量()1,2AB =,()4,2AC =-,则ABC 的面积为_____________ .10.为了支持“新冠肺炎”的湖北抗疫工作,上海市某医院某科室拟从2名男性,3名女性医务人员中抽调两人前往湖北支援,则抽调的两人刚好为一男一女的概率为________.11.已知函数()2,021,0x x f x x x ⎧<=⎨+≥⎩的反函数是()1f x -,则()112f f --⎡⎤=⎣⎦________. 12.已知O 是ABC 内部一点,20OA OB OC ++=,4BA BC ⋅=,且6ABC π∠=,则OAC 的面积为________.13.音乐与数学有着密切的联系,我国春秋时期有个著名的“三分损益法”:以“宫”为基本音,“宫”经过一次“损”频率变为原来的32,得到“徵”;“徵”经过一次“益”,频率变为原来的34,得到“商”;……依次损益交替变化,获得了“宫、徵、商、羽、角”五个音阶,设“宫”的频率为1,则“角”的频率为________.14.过双曲线221168x y -=的左焦点1F 作倾斜角为α的直线与y 轴交于点A ,与双曲线的右支位于第四象限的部分交于点B ,若()112OA OB OF =+,则α=________. 15.若0>ω,函数()f x 3sin 4cos 03x x x πωω⎛⎫=+≤≤ ⎪⎝⎭的值域为[]4,5,则cos 3πω⎛⎫⎪⎝⎭的取值范围是________.16.已知x R ∈,[]x 表示小于x 的最大整数,{}[]x x x =-,令{}{}M x 0x 100,1x =≤≤=,则M 中元素之和为________.三、解答题(题型注释)17.如图,一智能扫地机器人在A 处发现位于它正西方向的B 处和北偏东6π方向上的C 处分别有需要清扫的垃圾,红外线感应测量发现机器人到B 的距离比到C 的距离少0.4米,于是选择沿A B C →→路线清扫,已知智能扫地机器人的直线行走速度为0.2米/秒,10秒钟完成了清扫任务(忽略机器人吸入垃圾及在B 处旋转所用时间)(1)B 、C 两处垃圾的距离是多少?(2)求智能扫地机器人此次清扫过程中旋转角的最小值?请指出旋转方向. 18.将函数()2sin 2f x x =的图象向右平移()0ϕϕ>个长度单位,得到()2sin 23g x x π⎛⎫=- ⎪⎝⎭的图象,再把()g x 的图象上各点的横坐标缩小到原来的23(纵坐标不变),得到函数()h x 的图象.(1)求ϕ的最小值和()h x 的解析式; (2)当0,2x π⎡⎤∈⎢⎥⎣⎦时,求函数()h x 的单调递减区间. 19.如图,四边形11ABB A 是圆柱1OO 的轴载面,4AB =,12OO =,以圆柱上底面为底面作高为2的圆锥1PO ,C 、1C 分别在AB 、11A B 上,2AOC π∠=,1113AO C π∠=.(1)求这个几何体的表面积和体积; (2)求二面角111O AC C --的余弦值.20.已知椭圆C :22221x y a b+=(0a b >>)经过1,0A ,()0,B b 两点.O 为坐标原点,且AOB的面积为4.过点()0,1P 且斜率为k (0k >)的直线l 与椭圆C 有两个不同的交点M ,N ,且直线AM ,AN 分别与y 轴交于点S ,T . (Ⅰ)求椭圆C 的方程;(Ⅱ)求直线l 的斜率k 的取值范围;(Ⅲ)设PS PO λ=,PT PO μ=,求λμ+的取值范围. 21.对于数列{}n a 、{}n b 、{}()*n d n N∈,若()()2211nn n n n n da b d a d ++-=对任意的*n N ∈恒成立,则称数列{}n a 、{}n b 、{}n d 具有性质P .设121nk n k a a a a ==+++∑;(1)证明:数列{}n a 、{}n b 、{}n d 具有性质P 的一个充分条件为:1n n n nn n a b d b a d +=⎧⎨=⎩;(2)若()*tan3n n d n N π=∈,{}n a 、{}n b 、{}n d 满足(1)的充分条件,求()2020221nn n ab =+∑;(3)若{}n a 、{}n b 、{}3n d 的每一项均为有理数,但{}n d 每一项均为无理数,试给出数列{}n a 、{}n b 、{}n d 具有性质P 的充要条件.若在此条件下令13332n nd =⨯,试探究数列{}n b 的一些性质(如单调性,极限,{}n b 的最大项等).参考答案1.C【解析】1.计算出200人中潜伏期6≤天的人数,结合表格中的数据可计算出①②③处应填入的数字. 由分层抽样可知,从上述1000名患者中抽取200人,其中潜伏期6≤天的人数为852053102001201000++⨯=,所以,①处应填的数字为1205565-=,②处应填的数字为1006535-=,③处应填的数字为1005545-=. 故选:C. 2.A【解析】2.利用行列式展开法则推导出“12()3x y k k R z ⎧⎫⎛⎫⎪⎪ ⎪=∈⎨⎬ ⎪⎪⎪ ⎪⎩⎭⎝⎭”是“0P =”的充分条件,举反例说明“12()3x y k k R z ⎧⎫⎛⎫⎪⎪ ⎪=∈⎨⎬ ⎪⎪⎪ ⎪⎩⎭⎝⎭”不是“0P =”的必要条件,由此能求出结果. 行列式102131x P y z =-,“12()3x y k k R z ⎧⎫⎛⎫⎪⎪ ⎪=∈⎨⎬ ⎪⎪⎪ ⎪⎩⎭⎝⎭”,2355230P x z x y x y z k k k ∴=-+-+=-++=-++=, ∴ “12()3x y k k R z ⎧⎫⎛⎫⎪⎪ ⎪=∈⎨⎬ ⎪⎪⎪ ⎪⎩⎭⎝⎭”是“0P =”的充分条件,当50P x y z =-++=时,有可能52y z x ==, ∴ “12()3x y k k R z ⎧⎫⎛⎫⎪⎪ ⎪=∈⎨⎬ ⎪⎪⎪ ⎪⎩⎭⎝⎭”不是“0P =”的必要条件,∴ “12()3x y k k R z ⎧⎫⎛⎫⎪⎪ ⎪=∈⎨⎬ ⎪⎪⎪ ⎪⎩⎭⎝⎭”是“0P =”的充分不必要条件.故选:A .3.B【解析】3.利用向量的线性运算和数量积运算律可将所求数量积化为21PO →-,根据正方体的特点可确定PO →的最大值和最小值,代入即可得到所求范围. 设正方体内切球的球心为O ,则1OM ON ==,2PM PN PO OM PO ON PO PO OM ON OM ON →→→→→→→→→→→→⎛⎫⎛⎫⎛⎫⋅=+⋅+=+⋅++⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,MN 为球O 的直径,0OM ON →→∴+=,1OM ON →→⋅=-,21PM PN PO →→→∴⋅=-,又P 在正方体表面上移动,∴当P 为正方体顶点时,PO →P 为内切球与正方体的切点时,PO →最小,最小值为1,[]210,2PO →∴-∈,即PM PN →→⋅的取值范围为[]0,2.故选:B . 4.B【解析】4.根据函数()y f x =的图象和()11f =可得出n a 的取值范围,再根据函数()y f x =的单调性判断{}21n a -和{}2n a 的单调性,结合数列各项的取值范围和单调性可得数列的极限值.()1n n a f a +=,当01n a <<时,由图象可知,112n a +<<;当13n a <<时,101n a +<<.13a =,20a =,32a =,401a ∴<<,512a <<,601a <<,712a <<,,因为函数()y f x =在区间()0,3上单调递减,因为5302a a <<=,()()53f a f a ∴>,即64a a >,()()64f a f a <,即75a a <,()()75f a f a >,即86a a >,,以此类推,可得1357a a a a >>>>,数列{}21n a -单调递减,2468a a a a <<<<,数列{}2n a 单调递增,命题(2)正确;当2n ≥时,2112n a -<≤,201n a <<,且数列{}21n a -单调递减,{}2n a 单调递增,所以,lim 1n n a →∞=,命题(1)正确. 故选:B. 5.Z【解析】5.分析出集合A 为奇数集,集合B 为偶数集,由此可计算得出AB .{}{}41,41,A x x k k Z x x k k Z ==+∈⋃=-∈{}(){}{}221,2211,21,x x k k Z x x k k Z x x m m Z ==⋅+∈⋃=⋅-+∈==+∈,则集合A 为奇数集,{}2,B y y n n Z ==∈为偶数集, 因此,Z AB =.故答案为:Z . 6.250x y --=【解析】6.经分析不存在切线斜率不存在的情况,设出切线方程:()21y k x =--,根据相切时圆心到直线的距离为圆的半径求解出k 的值,即可写出切线方程. 设切线方程为:()21y k x =--,=2k =,所以切线方程为:()221y x =--,即250x y --=. 故答案为:250x y --=. 7.3【解析】7.本题可通过对数与指数的运算得出结果.()12log 24x x -+=,1242x x -+=,1224x x --=,112224x x --⨯-=, 124x -=,解得3x =,故答案为:3. 8.1:2:10【解析】8.利用求根公式可知,一个根为13i -+,另一个根为13i --,利用韦达定理即可求出a 、b 、c 的关系,从而可得 ::a b c利用求根公式可知,一个根为13i -+,另一个根为13i --,由韦达定理可得()()()13131313b i i ac i i a ⎧-++--=-⎪⎪⎨⎪-+--=⎪⎩ ,整理得:210ba c a⎧=⎪⎪⎨⎪=⎪⎩ 所以2b a =,10c a =,所以:::2:101:2:10a b c a a a == 故答案为:1:2:10 9.5【解析】9.根据向量的坐标可得向量垂直,从而得到三角形为直角三角形,求出向量的模长,即可得答案;因为AB AC ==0AB AC ⋅=,所以90BAC ∠=︒,所以152ABCS==. 故答案为:5. 10.35【解析】10.本题首先可以令2名男性分别为A 、B ,3名女性分别为a 、b 、c ,然后列出抽调两人的所有可能情况,再然后列出刚好为一男一女的所有可能情况,最后根据古典概型的概率计算公式即可得出结果.令2名男性分别为A 、B ,3名女性分别为a 、b 、c ,从中抽调两人的所有可能情况为:AB 、Aa 、Ab 、Ac 、Ba 、Bb 、Bc 、ab 、ac 、bc 共十种,满足刚好为一男一女的所有可能情况:Aa 、Ab 、Ac 、Ba 、Bb 、Bc 共六种, 则抽调的两人刚好为一男一女的概率63105P ==,故答案为:35. 11.1-【解析】11. 先求出()1fx -,再计算1(2)f - ,即可得()112f f --⎡⎤⎣⎦的值.当0x <时()20,1x y =∈,可得2log x y =,即()12log f x x -=,()0,1x ∈,当0x ≥时,[)211,y x =+∈+∞,可得12y x -=,即11()2x f x --=,[)1,x ∈+∞, 所以函数()2,021,0x x f x x x ⎧<=⎨+≥⎩的反函数是()21log ,011,12x x f x x x -<<⎧⎪=⎨-≥⎪⎩,1211(2)22f --==, ()1112112log 122f f f ---⎛⎫⎛⎫⎡⎤===- ⎪ ⎪⎣⎦⎝⎭⎝⎭, 故答案为:1-【解析】12.由20OA OB OC ++=可得()12BO OA OC =+,设D 为AC 中点,则()12OD OA OC =+,可得BO OD =,从而可得O 为BD 的中点,进而可得12AOC ABC S S =△△,由4BA BC ⋅=可得83BA BC ⋅=12||||sin ABC BA AB S BC C ⋅⋅=∠△即可求出. 在ABC 中,由20OA OB OC ++=可得()12BO OA OC =+, 设D 为AC 中点,则()12OD OA OC =+, BO OD ∴=,∴O 为BD 的中点,12AOCABCSS ∴=,4BA BC ⋅=,3cos 42BA BC BA BC ABC BA BC ∴⋅=⋅⋅∠=⋅⋅=, 83BA BC ∴⋅=111||||sin 22323ABCS BA BC ABC ∠∴=⋅⋅=⨯⨯=12AOCS==.故答案为:3. 13.8164【解析】13.根据已知条件经过一次“损”频率变为原来的32,经过一次“益”,频率变为原来的34,依次损益交替变化求概率即可.由“宫”的频率为1,“宫”经过一次“损”得到“徵”的频率变为32, “徵”经过一次“益”,得到商的频率为339248⨯=, “商”经过一次“损”,得到“羽”的频率为93278216⨯=, “羽”经过一次“益”,得到“角”的频率为2738116464⨯=, 所以“角”的频率为8164, 故答案为:816414.απ=-【解析】14.由双曲线方程求得左焦点坐标,由直线的倾斜角可得直线的斜率,写出直线方程,得到直线在y 轴上的截距,由向量等式可知A 为1F B 的中点,由中点坐标公式求得B 点坐标,代入双曲线方程可得tan α,再由反三角函数求得角α值.如图,由双曲线221168x y -=,得1(F -,直线AB 的斜率为tan (αα为钝角),直线方程为tan (y x α=+, 取0x =,得y α=,则)A α, 由11()2OA OB OF =+,可得A 为1F B 的中点,设(,)B x y ,则00x y α⎧-=⎪⎨+=⎪⎩,B ∴)α. B 在双曲线上,∴224961168tan α-=,即tan 12α=-. α为钝角,απ∴=-.故答案为:απ=- 15.74,255⎡⎤⎢⎥⎣⎦【解析】15.首先利用辅助角公式对()f x 化简,可得()()5sin f x x ωϕ=+,再利用()f x 的值域,可求出23ππωϕπϕ≤+≤-的范围,即得0223ππϕωπϕπ<-≤≤-<,再结合余弦函数的单调性,4sin 5ϕ=,3cos 5ϕ=,即可求出cos 3πω⎛⎫⎪⎝⎭的取值范围. ()34f 3sin 4cos =5sin cos 55x x x x x ωωωω⎡⎤=++⎢⎥⎣⎦()5sin x ωϕ=+,其中4sin 5ϕ=,3cos 5ϕ=, 因为03x π≤≤,所以3x πϕωϕωϕ≤+≤+,令x t ωϕ+=,则5sin y t =的值域为[]4,5,可得sin y t =的值域为4,15⎡⎤⎢⎥⎣⎦又因为4sin 5ϕ=,所以23ππωϕπϕ≤+≤-, 即0223ππϕωπϕπ<-≤≤-<,且cos y x =单调递减,因为4cos sin 25πϕϕ⎛⎫-==⎪⎝⎭,()221697cos 2cos 2sin cos 252525πϕϕϕϕ-=-=-=-=, 所以cos 3πω⎛⎫⎪⎝⎭的取值范围是74,255⎡⎤⎢⎥⎣⎦故答案为:74,255⎡⎤⎢⎥⎣⎦16.5050【解析】16.本题首先可根据题意确定集合{}0,1,2,3,4,,100M =,然后根据等差数列求和公式即可得出结果.因为{}[]x x x =-,0x 100≤≤,{}1x =, 所以集合{}0,1,2,3,4,,100M =,则M 中元素之和为010001210010150502, 故答案为:5050.17.(1)1.4m (2)11cos 14arc π-,方向见解析.【解析】17.(1)利用余弦定理,结合a c +列方程组,解方程组求得BC .(2)利用余弦定理求得cos B 的值,由此求得旋转角的最小值,并判断出旋转方向.(1)依题意可知2263A πππ∠=+=,设,,A B C 的对边分别为,,a b c ,则 2222220.21020.40.42cos a c a c b c b c a b c bc A a b c bc +=⨯+=⎧⎧⎪⎪-=⇒-=⎨⎨⎪⎪=+-=++⎩⎩, 将2,0.4 2.4c a b c a =-=+=-代入222a b c bc =++化简得2 6.67.280a a -+=,即()()1.4 5.20a a --=,由于0.2102a <⨯=,所以()()1.4 5.20a a --=解得 1.4m a =. 且20.6m, 2.41m c a b a =-==-=.(2)由余弦定理得222 1.960.361 1.3211cos 22 1.40.6 1.6814a cb B ac +-+-====⨯⨯,由于23A π=,所以B 为锐角. 所以旋转角的最小值为11cos 14arc π-,方向沿顺时针方向旋转. 18.(1)ϕ的最小值为6π,()2sin 33h x x π⎛⎫=- ⎪⎝⎭;(2)5,182ππ⎡⎤⎢⎥⎣⎦.【解析】18.(1)利用三角函数的图象变换可得出关于ϕ的表达式,进而可求得正数ϕ的最小值,再利用正弦型函数的伸缩变换可求得函数()y h x =的解析式; (2)求得函数()y h x =在R 上的单调递减区间,与区间0,2π⎡⎤⎢⎥⎣⎦取交集可得出结果. (1)将函数()2sin 2f x x =的图象向右平移()0ϕϕ>个长度单位, 可得到函数()()()2sin 22sin 22g x x x ϕϕ=-=-⎡⎤⎣⎦的图象,又()2sin 23g x x π⎛⎫=- ⎪⎝⎭,()223k k Z πϕπ∴-=-+∈,可得()6k k Z πϕπ=-∈,0ϕ>,当0k =时,ϕ取最小值6π,将函数()2sin 23g x x π⎛⎫=-⎪⎝⎭的图象上各点的横坐标缩小到原来的23(纵坐标不变), 可得到函数()2sin 33h x x π⎛⎫=-⎪⎝⎭的图象,因此,()2sin 33h x x π⎛⎫=-⎪⎝⎭;(2)令()3232232k x k k Z πππππ+≤-≤+∈,解得()52112183183k k x k Z ππππ+≤≤+∈, 所以,函数()y h x =在R 上的单调递减区间为()52112,183183k k A k Z ππππ⎡⎤=++∈⎢⎥⎣⎦,50,,2182A πππ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦.因此,当0,2x π⎡⎤∈⎢⎥⎣⎦时,函数()y h x =的单调递减区间为5,182ππ⎡⎤⎢⎥⎣⎦. 19.(1)表面积为(12π+,体积为323π;(2.【解析】19.(1)计算出圆锥的母线长,利用圆锥的侧面积公式和圆柱的侧面积、底面积公式可计算出几何体的表面积,结合柱体和锥体的体积公式可求得几何体的体积;(2)以点O 为坐标原点,OA 、OC 、OP 所在直线分别为x 、y 、z 轴建立空间直角坐标系O xyz -,利用空间向量法可求得二面角111O AC C --的余弦值. (1)由题意可知,圆柱的底面半径为22ABr ==, 因为1PO 为圆锥的高,且12PO =,所以,圆锥的母线长为1PA==,又12OO =,因此,该几何体的表面积为(22+222212S ππππ=⨯⨯⨯+⨯=+.该几何体的体积为22132222233V πππ=⨯⨯+⨯⨯⨯=; (2)以点O 为坐标原点,OA 、OC 、OP 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系O xyz -,则点()10,0,2O ,()12,0,2A,()1C ,()0,2,0C ,设平面11A CC 的一个法向量为(),,m x y z =,()11AC =-,()12,2,2AC =--, 由11100m AC m AC ⎧⋅=⎪⎨⋅=⎪⎩,得02220x x y z ⎧-+=⎪⎨-+-=⎪⎩,令x =1y =,1z =,所以,平面11A CC的一个法向量为(3,1,1m =,易知平面111O AC 的一个法向量为()0,0,1n =,(cos ,m n m nm n⋅<>===⋅,由图象可知,二面角111O AC C --20.(Ⅰ)2221x y +=(Ⅱ)2⎛⎫+∞ ⎪ ⎪⎝⎭(Ⅲ))2【解析】20.(Ⅰ)把点A 坐标代入椭圆的方程得1a =.由AOB 12ab =得b ,进而得椭圆C 的方程.(Ⅱ)设直线l 的方程为1y kx=+,()11,M x y ,()22,N x y .联立直线l 与椭圆C 的方程可得关于x 的一元二次方程.>0∆,进而解得k 的取值范围.(Ⅲ)因为1,0A ,()0,1P ,()11,M x y ,()22,N x y ,写出直线AM 的方程,令0x =,解得111y y x -=-.点S 的坐标为110,1y x ⎛⎫- ⎪-⎝⎭.同理可得:点T 的坐标为220,1y x ⎛⎫- ⎪-⎝⎭.用坐标表示PS ,PT ,PQ ,代入PS PO λ=,PT PO μ=,得111111111y kx x x λ+=+=+--.同理22111kx x μ+=+-.由(Ⅱ)得122421kx x k +=-+,122121x x k =+,代入λμ+,化简再求取值范围.(Ⅰ)因为椭圆C :22221x y a b+=经过点1,0A ,所以21a =解得1a =. 由AOB124ab =,解得2b =所以椭圆C 的方程为2221x y +=.(Ⅱ)设直线l 的方程为1y kx =+,()11,M x y ,()22,N x y .联立22211x y y kx ⎧+=⎨=+⎩,消y 整理可得:()2221410k x kx +++=.因为直线与椭圆有两个不同的交点,所以()22164210k k ∆=-+>,解得212k >. 因为0k >,所以k的取值范围是⎫+∞⎪⎪⎝⎭.(Ⅲ)因为1,0A ,()0,1P ,()11,M x y ,()22,N x y . 所以直线AM 的方程是:()1111y y x x =--. 令0x =,解得111y y x -=-. 所以点S 的坐标为110,1y x ⎛⎫- ⎪-⎝⎭. 同理可得:点T 的坐标为220,1y x ⎛⎫- ⎪-⎝⎭.所以110,11y PS x ⎛⎫-=- ⎪-⎝⎭,220,11y PT x ⎛⎫-=- ⎪-⎝⎭,()0,1PO =-. 由PS PO λ=,PT PO μ=,可得:1111y x λ--=--,2211y x μ--=--, 所以111111111y kx x x λ+=+=+--. 同理22111kx x μ+=+-. 由(Ⅱ)得122421kx x k +=-+,122121x x k =+, 所以()()()1212121212122121122111kx x k x x kx kx x x x x x x λμ+-+-+++=++=+---++ ()222214212212121412121k k k k k k k k ⎛⎫⋅+--- ⎪++⎝⎭=+⎛⎫++ ⎪++⎝⎭()22224422121421k k k k k k -+-+=++++()()2121k k -+=++)12221k k ⎛⎫=-+∈> ⎪ ⎪+⎝⎭ 所以λμ+的范围是)2.21.(1)证明见解析;(2)40394;(3)单调递减,lim 0n n b →∞=,()max637n b =.【解析】21.(1)将1n n n n n na b d b a d +=⎧⎨=⎩代入验证等式()()2211n n n n n n d a b d a d ++-=即可证得结论成立;(2)根据条件1n n n n n na b d b a d +=⎧⎨=⎩求得22n n a b +关于n 的表达式,进而可求得()2020221n n n a b =+∑的值;(3)根据题意求得数列{}n a 、{}n b 、{}n d 具有性质P 的充要条件为636111n nnn n a d d b d ⎧=⎪+⎪⎨⎪=⎪+⎩,由结合13332nn d =⨯可推导出数列{}n b 的单调性、极限以及最大项.(1)1n n n a b d +=,n n n b a d =,所以,()()()()()22222211111n n n n n n n n n n n n n d a b d a d d a d d a d a ++-=+-=--+()()223111n n n n n n n n n d b d a d d b a d =-+=-+=,因此,数列{}n a 、{}n b 、{}n d 具有性质P 的一个充分条件为:1n n n nn n a b d b a d +=⎧⎨=⎩;(2)1n n n n n n a b d b a d +=⎧⎨=⎩,且tan 3n n d π=,可得tan 13tan3n n n n n a b n b a ππ⎧+=⎪⎪⎨⎪=⎪⎩,所以,222211cos 31tan sin 331cos 3n n a n n n ππππ===++,tansin cos 333n n n n n b a πππ==, 所以,224222222cossin cos cos cos sin cos 3333333n n n n n n n n n a b πππππππ⎛⎫+=+=+= ⎪⎝⎭121cos 23n π⎛⎫=+ ⎪⎝⎭, ()()()2222122123cos cos cos 2333n k k k nn n n a b πππ+=++⎡⎤+=+++⎢⎥⎣⎦∑12222224243cos cos cos sin sin cos cos sin sin 2333333333n n n n n πππππππππ⎛⎫=+++++ ⎪⎝⎭1212212233cos cos cos 23232323232n n n n n πππππ⎛⎫=+-+--= ⎪ ⎪⎝⎭, 202036731=⨯+,因此,()2020222211131220191201940396731cos 2232424nn n ab a b π=⎛⎫+=++⨯=++=+= ⎪⎝⎭∑; (3)()()2211nn n n n n da b d a d ++-=,23421n n n n n n n n n n n a d a b d b d a d a d ∴+++--=,()331n n n n n n n a b d d b a d ∴++-=,{}n a 、{}n b 、{}3n d 为有理数列,{}n d 为无理数列,3310n n n n n n a b d b a d ⎧+=⎨-=⎩,所以636111n nnn n a d d b d ⎧=⎪+⎪⎨⎪=⎪+⎩, 当13332n nd =⨯时,则332nn d =⨯,则32111943232nn nn nb ⨯==+⨯+⨯⨯,令326n t =⨯≥,由双勾函数的单调性可知,函数1y t t=+在区间[)6,+∞上单调递增,所以,数列{}n b 单调递减,1lim lim13232n n n n nb →∞→∞==+⨯⨯,数列{}n b 的最大项为12661637b ==+.。
上海市七宝中学2020-2021学年高二上学期10月月考数学试题(教师版)

2020-2021年上海市七宝中学高二上10月月考一、填空题(1-6题每题4分,7-12题每题5分,共54分)1. 二元一次方程组3121x y x y +=⎧⎨-=-⎩的增广矩阵是________.【答案】131121⎛⎫⎪--⎝⎭【解析】 【分析】本题可通过增广矩阵的概念进行求解,即可得出结果.【详解】由增广矩阵概念,可知二元一次方程组所对应的增广矩阵为131121A ⎛⎫⎪--⎝⎭=,故答案为:131121⎛⎫⎪--⎝⎭.【点睛】本题考查二元一次方程组的矩阵形式,解题时要认真审题,注意熟练掌握增广矩阵的概念,属于基础题. 2. 已知1tan tan 1tan tan A αβαβ⎛⎫= ⎪+-⎝⎭,117B ⎫=⎪-⎝⎭,若A B =,则tan()αβ+=________. 【答案】17- 【解析】 【分析】根据矩阵相等得到117tan tan tan tan αβαβ+=-⎧⎨-=⎩,利用两角和的正切公式即可求解.【详解】11=tan tan 1tan tan 17A B αβαβ⎛⎫⎫== ⎪⎪+--⎝⎭⎝⎭,∴ 117tan tan tan tan αβαβ+=-⎧⎨-=⎩,tan tan 1tan()=1tan tan 7αβαβαβ+∴+=--故答案为:17-【点睛】本题考查了相等矩阵,两角和的正切公式,意在考查学生的计算能力和综合应用能力,属于中档题. 3. 已知||2a =,||1b =,a 与b 的夹角为4π,若()a b a λ-⊥,则λ=________. 【答案】12【解析】 【分析】由平面向量数量积的定义可得1a b ⋅=,再由平面向量垂直的性质可得()0a b a λ-⋅=,运算即可得解. 【详解】因为||2a =,||1b =,a 与b 的夹角为4π,所以cos 14a b a b π⋅=⋅=,又()a b a λ-⊥,所以2()210a b a a a b λλλ-⋅=-⋅=-=,解得12λ=.故答案为:12. 4. 计算两矩阵的积:132102131250-⎛⎫-⎛⎫ ⎪= ⎪ ⎪-⎝⎭ ⎪-⎝⎭________. 【答案】07158-⎛⎫⎪-⎝⎭【解析】 【分析】由矩阵乘法的运算法则运算即可得解.【详解】由题意,13210072131215850-⎛⎫--⎛⎫⎛⎫⎪= ⎪ ⎪ ⎪--⎝⎭⎝⎭ ⎪-⎝⎭. 故答案为:07158-⎛⎫⎪-⎝⎭.5. 若()2,3a =,()4,7b =-,则a 在b 方向上的投影为________ 5【解析】 【分析】用坐标表示平面向量的数量积和模,即可得结果.【详解】a在b方向上的投影为(24374a bb⨯-+⨯⋅===-故答案为:5【点睛】本题考查了平面向量的数量积运算和平面向量的模,考查了运算求解能力,属于基础题目.6. 记等差数列{a n}的前n项和为S n,若1OB a=200OA a OC+,且A、B、C三点共线(该直线不过原点O),则S200=_________.【答案】100【解析】试题分析:依题意,12001a a+=,故()12002002001002a aS+==.考点:等差数列的前n项和公式.【方法点晴】本题主要考查了等差数列的前n项和公式以及共线向量定理的应用,属于基础题.解答本题时部分考生找不到解题思路,根本原因是对题目条件的挖掘不够,“1OB a=200OA a OC+且,,A B C三点共线”,由共线向量定理的推论可知12001a a+=,再由等差数列的前n项和公式即可求出200S的值.7. 已知向量序列123,,na a a a⋅⋅⋅⋅⋅⋅,满足如下条件:12a=,2||4d=,121a d⋅=-,且1(2)n na a d n--=≥,若1ka a⋅=,则k=________.【答案】9【解析】【分析】由题意知{na→}是以1a为首项,d→为公差的等差数列,则1(1)ka a k d→→→=+-,计算1ka a→→⋅=即可求解.【详解】因为1n na a d→→→--=,所以1(1)ka a k d→→→=+-,因为121a d→→⋅=-,所以112a d→→⋅=-,所以2111111(1)(1)402kka a a a k d a k a d→→→→→→→→-⎡⎤⋅=⋅+-=+-⋅=-=⎢⎥⎣⎦,解得9k =. 故答案为:9【点睛】本题考查了等差数列的通项公式及向量的数量积,属中档题.8. 设点O 在ABC 内部,且5370OA OB OC ++=,则ABC 与AOC △的面积之比为________. 【答案】5:1 【解析】 【分析】本题可根据奔驰定理以及5370OA OB OC ++=得出结果. 【详解】因为点O 在ABC 内部,满足奔驰定理0BOC AOC AOB S OA S OB S OC △△△⋅+⋅+⋅=,且5370OA OB OC ++=,所以ABC 与AOC △的面积之比为(537):35:1++=, 故答案为:5:1.【点睛】本题考查奔驰定理在解决向量问题中的应用,奔驰定理可用来解决三角形中的面积比值问题,考查计算能力,是简单题.9. 平面直角坐标系中,已知点0(3,1)P ,1(4,2)P ,且()1112n n n n P P P P n N ++-=-∈,当n →+∞时,点P 无限趋近于点M ,则点M 的坐标是________. 【答案】115,33⎛⎫⎪⎝⎭【解析】 【分析】由平面向量及其数乘运算的坐标表示结合等比数列的前n 项和公式可得11111141,213232n n n P --⎛⎫⎡⎤⎡⎤⎛⎫⎛⎫------ ⎪⎢⎥⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭,再由极限的知识即可得解. 【详解】因为2112101111222nn n n n n n P P P P P P P P +---⎛⎫⎛⎫=-=-⋅⋅⋅=- ⎪ ⎪⎝⎭⎝⎭()10112,122nn n OP OP ⎛⎫⎛⎫⎛⎫=--=-- ⎪ ⎪ ⎛⎫⎪⎝⎭⎝⎭⎝⎭ ⎪ ⎪⎝⎭, 所以22231111114,2,4,2,,222222P P ⎛⎫⎛⎫⎛⎫⎛⎫---+--+-⋅⋅⋅ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭21211111114,2222222n n n P --⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+-+⋅⋅⋅+--+-+⋅⋅⋅+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭, 所以1111111122224,2111122n n n P --⎛⎫⎡⎤⎡⎤⎛⎫⎛⎫------⎪⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭ ⎪⎢⎥⎢⎥⎣⎦⎣⎦++ ⎪++ ⎪ ⎪⎝⎭, 即11111141,213232n n n P --⎛⎫⎡⎤⎡⎤⎛⎫⎛⎫------ ⎪⎢⎥⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭,所以点115,33M ⎛⎫⎪⎝⎭. 故答案为:115,33⎛⎫⎪⎝⎭.10. 已知点(1,1)A -,(3,0)B ,(2,1)C ,若平面区域D 由所有满足AP AB AC λμ=+(12λ≤≤,01μ≤≤)的点P 组成,则D 的面积为__________.【答案】3 【解析】()2,1AB =,()1,2AC =,()()()2,11,22,2AP AB AC λμλμλμλμ=+=+=++,设(),P x y ,则()1,1AP x y =-+,所以12,{12,x y λμλμ-=++=+即23,3{23.3y x x y μλ-+=--= 因为12λ≤≤,01μ≤≤,所以23013y x -+≤≤且23123x y --≤≤,即画出平面区域,如下图所示,5CD =E 到直线230x y --=5BDCE 的面积为3.【考点定位】本题考查两条直线的位置关系、考查了点到直线的距离、平面向量的线性运算、坐标运算,线性规划问题.难度较大.11. 在ABC 中,2AB =,10BC =3AC =,若点O 为三角形外心,则满足关系式:AO m AB n AC →→→=+的有序实数对(,)m n =________.【答案】14,39⎛⎫⎪⎝⎭【解析】 【分析】根据题意,作出图形,先根据BC AC AB →→→=-,结合模的公式 可得32AB AC →→=⋅,进而得342AO AB m n →→⋅=+,392AO AC m n →→⋅=+,另一方面,延长AO 与三角形的外接圆交于点D ,则2AO AB →→⋅=,92AO AC →→⋅=,再联立方程即可得答案. 【详解】解:根据题意,作出图形如图,延长AO 与三角形的外接圆交于点D ,因为BC AC AB →→→=-,所以2222()()()()2BC AC AB AC AB AC AB →→→→→→→=-=+-⋅, 即10942AC AB →→=+-⋅,所以32AB AC →→=⋅, 所以23()()42AO AB m AB n AC AB m AB n AC AB m n →→→→→→→→⋅=+⋅=+⋅=+, 同理392AO AC m n →→⋅=+, 又2111()()2222AO AB AD AB AB BD AB AB →→→→→→→→⋅=⋅=+⋅==,同理92 AO AC→→⋅=,所以342239922m nm n⎧+=⎪⎪⎨⎪+=⎪⎩,解得1349mn⎧=⎪⎪⎨⎪=⎪⎩,所以有序实数对14(,),39m n⎛⎫= ⎪⎝⎭.故答案为:14,39⎛⎫⎪⎝⎭【点睛】本题考查平面向量在几何中的应用,考查运算能力,化归转化思想,方程思想,是中档题. 12. 在ABC中,AB AC→→⊥,点P在线段BC上,且4AP AC AP AB→→→→⋅=⋅=,则||AB AC AP→→→++的最小值为________.【答案】6【解析】【分析】根据数量积公式直接求向量长度,利用基本不等式求向量长度的最值.【详解】因为4AP AC AP AB→→→→⋅=⋅=,所以()0AP AC AB AP BC→→→→→-=⋅=所以24AP→=,解得2AP=,所以2||()AB AC AP AB AC AP→→→→→→++=++222222AB AC AP AB AP AC AP AB AC→→→→→→→→→=+++⋅+⋅+⋅==设BP m =,CP n =,则BC m n =+,由射影定理得2BP CP AP ⋅=,即4mn =,所以22()416BC m n mn =+≥=,当且仅当2m n ==时等号成立,所以||6AB AC AP →→→++=,即最小值为6. 故答案为:6【点睛】本题主要考查平面向量数量积的应用,要求熟练掌握向量的数量积公式,考查学生的计算能力.二、选择题(每小题5分,共20分)13. 已知命题甲:非零向量a ,b ,c 满足0a b c ++=;命题乙:a ,b ,c 可以构成三角形,则甲是乙的( )条件 A. 充分非必要 B. 必要非充分C. 充要D. 非充分非必要【答案】D 【解析】 【分析】由充分条件,必要条件的定义,判断即可得解.【详解】若0a b c ++=且a ,b ,c 共线,则a ,b ,c 不可以构成三角形,故甲不能推出乙; 在ABC 中,若a AB =,b BC =,c AC =,则a ,b ,c 可以构成三角形, 但20AB BC AC A a C b c ++=+=≠+, 故a ,b ,c 可以构成三角形推不出0a b c ++=; 所以甲是乙的非充分非必要条件. 故选:D.14. 下面给出矩阵的一些性质中正确的是( ) A. AB BA =B. AB O A O =⇒=或B O =C. AC BC A B =⇒=D. ()()AB C A BC =【答案】D 【解析】由矩阵的运算法则可判断A 、D ,举出反例可判断B 、C ,即可得解. 【详解】对于A ,矩阵乘法运算没有交换律,故A 错误; 对于B ,令0100A ⎛⎫=⎪⎝⎭,1000B ⎛⎫= ⎪⎝⎭,则0000AB O ⎛⎫== ⎪⎝⎭,此时A O ≠且B O ≠,故B 错误; 对于C ,若0100A ⎛⎫=⎪⎝⎭,1000B ⎛⎫= ⎪⎝⎭,0000C ⎛⎫= ⎪⎝⎭,满足AC BC =,但是A B ≠,故C 错误;对于D ,矩阵乘法运算有结合律,故()()AB C A BC =,故D 正确. 故选:D.15. 在直角三角形ABC 中,点D 是斜边AB 的中点,点P 为线段CD 的中点,则222||||PA PB PC +=A. 2B. 4C. 5D. 10【答案】 D【解析】【详解】试题分析:将直角三角形的直角顶点C 与原点重合,设(,0)B a ,(0,)A b ,那么,22a b D ⎛⎫⎪⎝⎭,,44a b P ⎛⎫⎪⎝⎭那么22222222299||||1616161610||1616a b b a PA PB a b PC ++++==+,故选D . 考点:1.坐标系;2.两点间距离.【方法点睛】本题考查了向量法解决平面几何的问题,属于中档题型,而向量法又分是用向量代数表示,还是用坐标表示,经分析用坐标表示,那如何建坐标系?题设只说是直角三角形,所以就以直角顶点为原点建立坐标系,两条直角边落在坐标轴上,这样就可以设各点的坐标,转化为两点间距离求值.坐标法解决平面几何的问题,很多时候会事半功倍.16. 已知点O 是ABC 所在平面上的一点,ABC 的三边为,,a b c ,若0aOA bOB cOC →→→→++=,则点O 是ABC 的( ) A. 外心B. 内心C. 重心D. 垂心【解析】【分析】在AB,AC上分别取单位向量,AD AE→→,作AF AD AE→→→=+,则AF平分BAC∠,用,,OA AB AC→→→表示出,OB OC→→代入条件式,用,AB AC→→表示出AO→,则可证明A,F,O三点共线,即AO平分BAC∠.【详解】在AB,AC上分别取点D,E,使得ABADc→→=,ACAEb→→=,则||||1AD AE→→==.以AD,AE为邻边作平行四边形ADFE,如图,则四边形ADFE是菱形,且AB ACAF AD AEc b→→→→→=+=+.AF∴为BAC∠的平分线.aOA bOB cOC→→→→++=()()0a OAb OA ABc OA AC→→→→→→∴⋅+⋅++⋅+=,即()0a b c OA b AB c AC→→→→++++=,∴()b c bc AB AC bcAO AB AC AFa b c a b c a b c c b a b c→→→→→→=+=+=++++++++.A∴,O,F三点共线,即O在BAC∠的平分线上.同理可得O在其他两角的平分线上,O∴是ABC的内心.故选:B.【点睛】本题考查了三角形内心的向量表示,向量的线性运算,属于中档题.三、解答题(本题共76分)17. 已知||4a =,||2b =,且a 与b 夹角为120︒, 求:(1)(2)()a b a b -⋅+; (2)|2|a b -; (3)a 与a b +的夹角.【答案】(1)12;(2)|2|221a b -=;(3)6π. 【解析】 【分析】(1)先计算a b ⋅,再把(2)()a b a b -⋅+展开,代入已知计算可得答案; (2)先对2a b -进行平方运算,再开方可得答案;(3)先对a b +进行平方运算,再开方求其模长,再计算()a a b ⋅+,最后代入夹角公式可得答案. 【详解】(1)42cos1204a b ⋅=⨯⨯︒=-所以22(2)()2164812a b a b a a b b -⋅+=-⋅-=+-=; (2)因为222(2)446416484a b a a b b -=-⋅+=++=, 所以|2|221a b -=;(3)因为222()2168412a b a a b b +=+⋅+=-+=, 所以||23a b +=,又2()16412a a b a a b ⋅+=+⋅=-=,所以()cos ,||||42a a b a a b a a b ⋅+<+>===+⨯,所以a 与a b +的夹角为6π. 【点睛】本题考查了向量的数量积、模长的计算,考查了向量的夹角公式,属于基础题.18. (1)设向量(3,1)OA =,(1,2)OB =-,向量OC 垂直于向量OB ,向量BC 平行于OA ,试求OD OA OC +=时,OD 的坐标;(2)用行列式解方程组()2251(1)(1)1x m y m x m y ⎧--=-⎪⎨+-+=⎪⎩(m 为常数)【答案】(1)(11,6)OD =;(2)答案见解析.【分析】(1)设(,)OC x y =,由平面向量垂直、平行的坐标表示可得147x y =⎧⎨=⎩,再由平面向量线性运算的坐标表示即可得解;(2)分别求出系数行列式D 及x D 、y D ,运算即可得解.【详解】(1)设(,)OC x y =,因为OC OB ⊥,所以20OC OB x y ⋅+=-=, 又(1,2)BC OC OB x y =-=+-,且//BC OA ,(3,1)OA =,所以3(2)(1)0y x --+=,即370y x --=,所以147x y =⎧⎨=⎩,所以(14,7)OC =,所以(11,6)OD OC OA =-=; (2)由题意,系数行列式()()22215(1)151(1)m D m m m m m --==+--+-+-+(1)(3)(2)m m m =+-+,()()()22152121(1)x m D m m m ---=-+-+=,11211y D m m -=++=,当1m ≠-且3m ≠且2m ≠-时,0D ≠,原方程组有唯一解()21(3)(1)1(3)(1)xy m D x D m m D y D m m ⎧-==⎪-+⎪⎨⎪==⎪-+⎩;当2m =-时,0x y D D D ===,原方程组有无数组解; 当3m =或1m =-时,0D =,0x D ≠,0y D ≠,原方程组无解.19. (1)已知ABC 的三边长8AB =,7BC =,3AC =,求AB BC BC CA CA AB ⋅+⋅+⋅; (2)在Rt ABC 中,已知斜边BC a =,若长为2a 的线段PQ 以点A 为中点,求BP CQ ⋅的最大值? 【答案】(1)61-;(2)0. 【解析】(1)由余弦定理可得cos A 、cos B 、cos C ,再由平面向量数量积的定义即可得解;(2)由平面向量的线性运算法则结合数量积的运算可得22cos ,BP CQ a a PQ BC ⋅=-+,即可得解.【详解】(1)由余弦定理得222649491cos 22832AB AC BC A AB AC +-+-===⋅⨯⨯,同理13cos 14B =,1cos 7C =-, 所以AB BC BC CA CA AB ⋅+⋅+⋅cos()cos()cos()AB BC B BC CA C CA AB A πππ=⋅-+⋅-+⋅-1311877338611472⎛⎫⎛⎫=⨯⨯-+⨯⨯+⨯⨯-=- ⎪ ⎪⎝⎭⎝⎭;(2)由题意作出图形,如图,因为AP AQ =-,BP AP AB =-,CQ AQ AC =-,所以()()()()BP CQ AP AB AQ AC AQ AB AQ AC ⋅=-⋅-=--⋅-()22AQ AQ AC AB AQ AB AC a AQ AC AB AB AC =-+⋅-⋅+⋅=-⋅-++⋅2212a AQ BC a PQ BC =-⋅=-++⋅22cos ,a a PQ BC =-+,故当cos ,1PQ BC =,即PQ 与BC 同向时,BP CQ ⋅取得最大值0. 20. 已知向量(,)u x y =与向量(,2)v y y x =-的对应关系用()v f u =表示. (1)设(1,1)a =,(1,0)b =,求向量()f a 与()f b 的坐标; (2)求使()(),f c p q =(p ,q 为常数)的向量c 的坐标;(3)证明:对任意的向量a ,b 及常数m ,n ,恒有()()()f ma nb mf a nf b +=+成立. 【答案】(1)()(1,1),()(0,1)f a f b ==-. (2)(2,)c p q p =- (3)证明见解析 【解析】 【分析】(1)根据向量(,)u x y =与向量(,2)v y y x =-的对应关系用()v f u =表示,可求得;(2)设()00,c x y =,根据对应关系()v f u =计算可得()000(),2(,)f c y y x p q =-=,由此解得; (3)根据对应关系()v f u =计算()f ma nb +,()()mf a nf b +可证. 【详解】(1)解:∵(1,1)a =,(1,0)b =,∴()(1,211)(1,1),()(0,201)(0,1)f a f b =⨯-==⨯-=-. (2)解:设()00,c x y =,则()000(),2(,)f c y y x p q =-=,∴000,2,y p y x q =⎧⎨-=⎩∴002,,x p q y p =-⎧⎨=⎩∴(2,)c p q p =-.(3)证明:设()12,a a a =,()12,b b b =, 则()2211,ma nb ma nb ma nb +=++,∴()222211(),22f ma nb ma nb ma nb ma nb +=++--. ∵()()221221(),2,(),2mf a m a a a nf b n b b b =-=-,∴()()221221()(),2,2mf a nf b m a a a n b b b +=-+-()222211,22ma nb ma nb ma nb =++--. 故对任意的向量a ,b 及常数m ,n ,恒有()()()f ma nb mf a nf b +=+成立. 【点睛】本题考查向量的坐标运算以及平面向量基本定理,属于中档题.21. 一个三角形数表按如下方式构成(如图:其中项数5n ≥):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:()()()2,11,11,2f f f =+;(),f i j 为数表中第i 行的第j 个数.()1,1f ()1,2f …()1,1f n - ()1,f n ()2,1f ()2,2f …()2,1f n - ()3,1f …()3,2f n -……(),1f n(1)求第2行和第3行的通项公式()2,f j 和()3,f j ;(2)证明:数表中除最后2行外每一行的数都依次成等差数列,并求(),1f i 关于()1,2,,i i n =的表达式;(3)若()()(),111i f i i a =+-,11i i i b a a +=,试求一个等比数列()()1,2,,g i i n =,使得()()()121123n n S b g b g b g n =+++<,且对于任意的11,43m ⎛⎫∈ ⎪⎝⎭,均存在实数λ,当n λ>时,都有n S m >.【答案】(1)()()2,841,2,,1f j j j n =+=-.()()3,16161,2,2f j j j n =+=-.(2)见证明;(3)()2ig i =.【解析】 【分析】(1)根据等差数列和等比数列的定义即可求出相应的通项公式,(2)根据条件建立方程关系即可求出f (i ,1)的表达式.(3)根据条件寻找等比数列g (i ),即可得到结论.【详解】(1)()()()()()()f 3,j f 2,j f 2,j 12f 2,j 828j 4816j 16j 1,2,n 2=++=+=++=+=-()i 1i n 3≤≤-.(2)由已知,第一行是等差数列,假设第i d 行是以()()()()()()f i 1,j 1f i 1,j f i,j 1f i,j 2f i,j +f i,j 1⎡⎤⎡⎤++-+=+++-+⎣⎦⎣⎦为公差的等差数列,则由()()i f i,j 2f i,j 2d =+-= ()i 11i n 3+≤≤-(常数)知第i 2d 行的数也依次成等差数列,且其公差为i d 4=.综上可得,数表中除最后2行以外每一行都成等差数列;由于()i i 1d 2d i 2-=≥,i 1i 1i d 422-+=⋅=,所以()()()()i 1f i,1f i 1,1f i 1,22f i 1,1d -=-+-=-+,所以i i 1d 2-=,由()()i f i,12f i 1,12=-+,得()()ii 1f i,1f i 1,1122--=+,于是()()ii 1f i,1f i 1,1122---=,即()1f 1,14222==,又因为()i f i,12⎧⎫⎨⎬⎩⎭, 所以,数列()()if i,12i 1i 12=+-=+是以2为首项,1为公差的等差数列,所以,()()()if i,1i 12i 1,2,,n =+⋅=,所以()()()()i i i f i,1f i,1i 1a 1a 121i 1=+-⇒=+=++.(3)()()i i i i 1i 1i i i 111111b a a 221212121+++⎛⎫⇒===- ⎪++++⎝⎭, ()()i i i i i i 1i i 111111g i 2b g i 2221212121++⎛⎫=⇒=-⨯=- ⎪++++⎝⎭, 令n 223n n 1n 1111111111S 2121212121213213++⎛⎫⎛⎫⎛⎫⇒=-+-++-=-<⎪ ⎪ ⎪+++++++⎝⎭⎝⎭⎝⎭, n n 1n 1111113mS m m m 3212133++->⇔->⇔<-=++.111m ,013m 434⎛⎫∈⇒<-< ⎪⎝⎭,n 123321n log 1113m 13m +⎛⎫⇒+>⇒>-- ⎪--⎝⎭,23λlog 113m ⎛⎫=- ⎪-⎝⎭,令n λ>,则当n S m >时,都有()ig i 2=,∴适合题设的一个等比数列为()ig i 2=.【点睛】本题主要考查等差数列和等比数列的综合应用,裂项相消求和,考查学生的运算能力,综合性较强,运算量较大,是难题。
上海市七宝中学2020届高三三模考试数学试题 Word版含解析

七宝中学高三三模数学试卷一.填空题1.已知集合{|2,}A x x k k ==∈Z ,{|22}B x x =-≤≤,则A B =________【答案】{2,0,2}- 【解析】 【分析】利用集合的交运算即可求解.【详解】由集合{|2,}A x x k k ==∈Z ,{|22}B x x =-≤≤, 则AB ={2,0,2}-.故答案为:{2,0,2}-【点睛】本题考查了集合的基本运算,解题的关键是理解集合中的元素特征,属于基础题. 2.若直线方程0ax by c 的一个法向量为3,1)-,则此直线的倾斜角为________【答案】3π 【解析】 【分析】根据题意首先求出直线的一个方向向量,然后再求出直线的斜率,根据直线的斜率与倾斜角的关系即可求解.【详解】设直线的一个方向向量为(),a x y = 由直线方程0ax by c的一个法向量为3,1)-,30x y -=,令1x =,则3y =所以直线的一个方向向量为3),33k ==,设直线的倾斜角为α, 由tan k α=,所以直线的倾斜角为:3πα=.故答案:3π 【点睛】本题考查了直线的法向量、方向向量、直线的斜率与倾斜角的关系,属于基础题. 3.已知复数z 满足1i z i ⋅=+(i 为虚数单位),则Im z =__________. 【答案】1- 【解析】 【分析】把已知等式变形,再由复数代数形式的乘除运算化简得答案. 【详解】解:由1i z i ⋅=+,得21(1)()1i i i z i i i ++-===--, ∴Im 1z =-. 故答案为:1-.【点睛】本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.4.已知a 、b 、c 是任意实数,能够说明“若a b c >>,则a b c +>”是假命题的一个有序整数组(,,)a b c 可以是________ 【答案】1,2)3(,---(答案不唯一) 【解析】 【分析】根据题意,适当的进行赋值验算即可求解【详解】根据题意,要说明其为假命题,可以令1a =-,2b =-,3c =-,此时满足a b c >>,但33a b c +=->=-不成立,故原命题为假命题. 故答案为:1,2)3(,---(答案不唯一)【点睛】本题主要考查命题及其关系,属于基础题.5.函数|2|=+y xi (x ∈R ,i 是虚数单位)的图象与直线y a =有且仅有一个交点,则实数a =________【答案】2 【解析】 【分析】先通过复数模的求法得到函数24+y x ,再利用数形结合法求解.【详解】函数2224242y x y xi x y ⎧-==+=+⇔⎨≥⎩,∴函数图象为双曲线224y x -=的一支, 如图所示:又因为函数图象与y a =有且仅有一个交点, 则2a =. 故答案为:2【点睛】本题主要考查复数的模的几何意义以及函数图象的交点问题,还考查了数形结合的思想方法,属于基础题.6.直角坐标系xOy 内有点()()()()2,1,2,2,0,2,0,1A B C D ,将四边形ABCD 绕直线1y =旋转一周,所得到的几何体的体积为____ 【答案】2π 【解析】 【分析】四边形ABCD 是矩形,边AD 在直线1y =上,旋转一周后得一圆柱,AD 是圆柱的高,AB 是底面半径,由此可计算体积。
2018-2019学年上海市七宝中学高一上学期10月月考数学试题(解析版)

2018-2019学年上海市七宝中学高一上学期10月月考数学试题一、单选题1.已知,a b 为非零实数,且a b <,则下列命题成立的是 A .22a b < B .22ab a b <C .2211ab a b< D .b aa b< 【答案】C 【解析】【详解】若a <b <0,则a 2>b 2,A 不成立;若220{,ab a b ab a b>⇒<<B 不成立;若a =1,b=2,则12,2b a b aa b a b==⇒>,所以D 不成立 ,故选C. 2.设集合A={}{}|1,,2,.x x a x R B x x b x R -<∈=-∈若A ⊆B,则实数a,b 必满足A .3a b +≤B .3a b +≥C .3a b -≤D .3a b -≥【答案】D【解析】试题分析:{}{}|1,|11A x x a x R x a x a =-<∈=-<<+,{}{}222B x x b x x b x b =-=+<-或,若A ⊆B ,则有21b a +≤-或21b a -≥+3a b ∴-≥【考点】1.绝对值不等式解法;2.集合的子集关系3.已知函数2()f x ax bx c =++,且a b c >>,0a b c ++=,集合{|()0}A x f x =<,则下列结论中正确的是( ) A .任意x A ∈,都有(3)0f x +> B .任意x A ∈,都有(3)0f x +< C .存在x A ∈,都有(3)0f x += D .存在x A ∈,都有(3)0f x +<【答案】A【解析】由题意可得 0a >,且0c <,122c a -<<-,1x =为()f x 的一个零点,再由根与系数的关系可得,另一零点为c a.可得{|1}cA x x a =<<,31x +>,有(3)0f x +>恒成立,从而得出结论.【详解】解:Q 函数2()f x ax bx c =++,且a b c >>,0a b c ++=,故有0a >,且0c <, 02a a c a c ∴<++=+,即2ca>-,且02a c c a c >++=+, 即12c a <-,因此有122c a -<<-, 又(1)0f a b c =++=,故1x =为()f x 的一个零点, 由根与系数的关系可得,另一零点为0c a<,所以有:{|1}cA x x a =<<,所以,331cx a+>+>,所以有(3)0f x +>恒成立, 故选:A . 【点睛】本题主要考查二次函数的性质,一元二次方程根的分布与系数的关系,体现了转化的数学思想,属于中档题.4.设,,,a b c d R ∈,32()()()f x x a x bx cx d =++++,32()(1)(1)g x ax dx cx bx =++++.记集合{|()0,}Sx f x x R ==∈,{|()0,}T x g x x R ==∈,若Card()S 、Card()T 分别表示集合S ,T 的元素个数,则下列结论不可能的是( ) A .Card()1S =,Card()0T = B .Card()1S =,Card()1T = C .Card()2S =,Card()2T = D .Card()2S =,Card()3T =【答案】D【解析】给a ,b ,c ,d 取特值,可排除A ,B ,C ,再根据()()f x g x ,解析式关系,确定对应根的关系,即可判断D . 【详解】当a =b =c =d =0时,f (x )=x 3,g (x )=1,此时Crad (S )=1,Card (T )=0,排除A ;当a =b =c =d =1时,f (x )=(x +1)(x 3+x 2+x +1)=(x +1)2(x 2+1),g (x )=x 3+x 2+x +1=(x +1)(x 2+1),此时Card (S )=1,Card (T )=1,排除B ; 当a =2,b =c =d =1时,f (x )(x +2)(x +1)(x 2+1),此时Card (S )=2,g (x )=(2x +1)(x +1)(x 2+1),此时Card (T )=2,排除C ;当0x ≠时32411()(1)(1)()a d c b g f x x x x x x x=++++=又当0ad =时(0)0f ad ==,而(0)1g =,所以Card()S Card()T ≥,因此结论不可能的是D . 故选:D . 【点睛】本题考查函数解析式以及函数零点,考查综合分析判断能力,属中档题.二、填空题5.不等式||1x >的解集为________; 【答案】(,1)(1,)-∞-+∞U 【解析】根据绝对值定义化简求解 【详解】||111x x x >∴><-Q 或故答案为:(,1)(1,)-∞-+∞U 【点睛】本题考查解含绝对值不等式,考查基本求解能力,属基础题.6.已知集合{}02A x x =<<,{}11B x x =-<<,则A B =I _________. 【答案】()0,1【解析】根据交集的定义即可写出答案。
上海市闵行区七宝中学2019_2020学年高一数学上学期9月月考试题(含解析)

如果您喜欢这份文档,欢迎下载!祝您成绩进步,学习愉快! 上海市闵行区七宝中学2019-2020学年高一数学上学期9月月考试题(含解析)一:填空题。
1.点(2,3)P -关于y 轴对称的点的坐标为________ 【答案】(2,3) 【解析】 【分析】根据点关于y 轴对称点的特征,求得P 点关于y 轴的对称点.【详解】点关于y 轴对称,横坐标相反,纵坐标相同,故()2,3P -关于y 轴对称点的坐标为()2,3.故填:()2,3.【点睛】本小题主要考查点关于y 轴对称点的特征,属于基础题.2.函数y =x 的取值范围是________ 【答案】35x <≤ 【解析】 【分析】根据分母不为零,偶次方根被开方数为非负数列不等式组,解不等式组求得函数定义域. 【详解】依题意3050x x ->⎧⎨-≥⎩,解得35x <≤.故填:35x <≤.【点睛】本小题主要考查函数定义域的求法,主要考虑分式的分母、偶次方根的被开方数,属于基础题.3.已知反比例函数ky x=(0k ≠),当0x <时,y 随x 的增大而增大,那么一次函数y kx k=-的图像不经过第________象限 【答案】三 【解析】 【分析】根据反比例函数的单调性求得k 的范围,由此判断出一次函数不经过的象限. 【详解】由于函数k y x=0x <时递增,故k 0<,由()1y kx k k x =-=-可知,直线过()1,0,且斜率小于零,由此可判断一次函数y kx k =-不经过第三象限.故填:三.【点睛】本小题主要考查反比例函数的单调性,考查一次函数过定点以及一次函数经过的象限,属于基础题.4.x =-的解的集合为________ 【答案】{}1- 【解析】 【分析】先求得x 的范围,然后两边平方求得方程的解的集合.【详解】依题意0x -≥,解得0x ≤x =-两边平方得22x x +=,解得1x =-或2x =,由于0x ≤,故1x =-,所以方程的解的集合为{}1-.故填:{}1-.【点睛】本小题主要考查含有根式的方程的解法,解题过程中要注意x 的取值范围,属于基础题.5.反比例函数2y x=的图像与一次函数y x b =-+的图像在第一象限内有交点,则b 的最小值为________【答案】22【解析】【分析】联立一次函数和反比例函数的解析式,利用判别式为非负数且0b>列不等式组,解不等式组求得b的最小值.【详解】由于反比例函数2yx=过第一、三象限,一次函数y x b=-+斜率为10-<,两个函数公共点在第一象限,故0b>,由2yxy x b⎧=⎪⎨⎪=-+⎩,消去y得220x bx-+=,其判别式280b-≥,结合0b>解得22b≥,故b的最小值为22.故填:22.【点睛】本小题主要考查反比例函数、一次函数的图像交点问题,考查一元二次方程有解的条件,属于基础题.6.如图,过△ABC的重心G作BC的平行线,分别交AB、AC于点E、F,若4EF=,则BC=_______【答案】6【解析】【分析】根据三角形重心的性质列方程,解方程求得BC的长.【详解】由于G是三角形ABC的重心,且//EF BC,所以23EFBC=,所以362EFBC==. 故填:6.【点睛】本小题主要考查三角形重心的性质,考查平行线的性质,属于基础题.7.已知0x y z ++≠,a 、b 、c 均不为0,且x a y z =+,yb x z=+,z c x y =+,则111a b ca b c++=+++_______ 【答案】1 【解析】 【分析】化简已知条件,由此求得表达式的化简结果. 【详解】由xa y z=+,yb x z=+,zc x y=+得1,1,1x y z x y z x y za b c y z x z x y ++++++=+=+=++++,所以111,,111y z x z x y a x y z b x y z c x y z +++===+++++++++,所以111a b ca b c ++=+++1x y z x y z x y z x y z++=++++++. 故填:1.【点睛】本小题主要考查代数式的运算,属于中档题.8.已知点(1,1)A 和点(3,2)B ,在直线y x =-上有一个点P ,满足PA PB +最小,则PA PB +的最小值是________ 【答案】5 【解析】 【分析】根据对称性求得A 关于直线y x =-对称点的坐标'A ,由'A B 求得PA PB +的最小值.【详解】由于()1,1A 在y x =上,所以点A 关于直线y x =-的对称点为()'1,1A --,所以PA PB +的最小值为'5A B ==.故填:5.【点睛】本小题主要考查点关于直线对称点问题,考查类似将军饮马的最短距离和问题,考查数形结合的数学思想方法,属于基础题.9.已知方程|53||54|7x x ++-=,则x 的取值范围是_______ 【答案】3455x -≤≤ 【解析】 【分析】化简原方程,利用绝对值的几何意义,求得x 的取值范围. 【详解】由|53||54|7x x ++-=得347555x x ++-=,方程表示数轴上到35-和45的距离和为75的点,而35-和45的距离是75,故符合题意的x 的范围是3455x -≤≤.故填:3455x -≤≤. 【点睛】本小题主要考查利用绝对值的几何意义解方程,属于基础题.10.关于x 方程221(43|43|)2x x x x k -+--+=有两个不同的根,则k 的取值范围是_____ 【答案】(1,0)- 【解析】 【分析】根据x 的取值范围去绝对值,求得方程左边的表达式,根据方程根的个数,结合图像,求得k 的取值范围.【详解】当1x ≤或3x ≥时,方程为0k =,不符合题意.当13x <<时,方程为()()2431,3x x k x -+=∈,画出()()2431,3y x x x =-+∈的图像如下图所示,由图可知,要使方程()()2431,3x x k x -+=∈有两个不相同的根,则需()1,0k ∈-. 故填:(1,0)-.【点睛】本小题主要考查含有绝对值的方程的求解策略,考查数形结合的数学思想方法,属于中档题.11.已知集合{1,2,3,,}M n =⋅⋅⋅(1n >,*n ∈N ),则M 的所有非空子集的元素和为_______(只需写出数学表达式)【答案】22()2n n n -+⋅【解析】 【分析】求得含1个元素的子集的元素和、求得含2个元素的子集的元素和、以此类推,求得含n 个元素的子集的元素和,然后相加,求得M 所有非空子集的元素和. 【详解】含1个元素的子集的元素和为()()11112n n n C C -+++⋅-L ,含2个元素的子集的元素和为()()22112n n n C C -+++⋅-L ,……以此类推含1n -个元素的子集的元素和为()()11112n n n n n C C ---+++⋅-L ,含n 个元素的子集的元素和为()12nn n C +++⋅L .上述n 个式子相加得()()()1212111112n n n n n n n n n n C C C C C C ----+⎡⎤+++++++⎣⎦L L ()2122222n n n n n n --+=⋅=+⋅. 故填:()222n n n -+⋅.【点睛】本小题主要考查集合非空子集元素和的计算,考查等差数列前n 项和公式,考查二项式展开式的二项式系数和公式,属于中档题.12.当一个非空数集F 满足条件“若,a b F ∈,则+a b ,-a b ,ab F ∈,且当0b ≠时,aF b∈”时,称F 为一个数域,以下四个关于数域的命题: (1)0是任何数域的元素;(2)若数域F 有非零元素,则2019F ∈; (3)集合{|3,}P x x k k ==∈Z 为数域; (4)有理数集为数域;其中,真命题的编号为________(写出所有真命题的编号) 【答案】(1)(2)(4) 【解析】根据新定义数域的概念,对四个命题逐一分析,由此得出真命题的编号. 【详解】对于(1),当a b =时,0a b F -=∈,故(1)正确. 对于(2),当a b =时,1aF b=∈,所以11,21,,20181+++L 都是F 的元素,故(2)正确. 对于(3)由于33,3P P ∈∉,故P 不是数域.对于(4)有理数集满足,a b F ∈,则+a b ,-a b ,ab F ∈,且当0b ≠时,aF b∈.故(4)正确.综上所述,正确的命题编号为:(1)(2)(4). 故填:(1)(2)(4).【点睛】本小题主要考查新定义集合的理解,考查分析问题与解决问题的能力,属于中档题.二.选择题13.已知关于x 的一次函数27y mx m =+-在15x -≤≤上的函数值总是正的,则m 的取值范围是( ) A. 7m > B. 1m >C. 17m ≤≤D. 以上都不对 【答案】A 【解析】 【分析】根据一次函数的单调性列不等式组,解不等式组求得m 的取值范围.【详解】由于一次函数是单调函数,依题意有2705270m m m m -+->⎧⎨+->⎩,解得7m >,故选A.【点睛】本小题主要考查一次函数的性质,考查一元一次不等式组的解法,属于基础题.14.m 是一个完全平方数,则( ) A. 1m -一定是完全平方数 B. 1m -一定不是完全平方数 C. 2m +一定是完全平方数 D. 2m +一定不是完全平方数【答案】D【分析】对m 取特殊值,排除错误选项,从而得出正确结论.【详解】当4m =时,13m -=不是完全平方数,26m +=不是完全平方数,由此排除A,C 两个选项.当1m =时,10m -=是完全平方数,由此排除B 选项.故本小题选D. 【点睛】本小题主要考查完全平方数的特点,考查特殊值解选择题的方法,属于基础题.15.如图,反比例函数3y x=-(0x >)图像经过矩形OABC 边AB 的中点E ,交边BC 于F 点,连结EF 、OE 、OF ,则△OEF 的面积是( )A.32B.94C.73D.52【答案】B 【解析】 【分析】设出A 点坐标,求得,,B E F 的坐标,利用矩形面积减去三个直角三角形的面积,求得三角形OEF 的面积.【详解】设(),0,0A a a >,则366,,,,,2a E a B a F a a a ⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,矩形OABC 的面积为66a a ⋅=,三个直角三角形的面积为131********222222424a a a a a a ⋅⋅+⋅⋅+⋅⋅=++=,所以三角形OEF 的面积为159644-=,故选B. 【点睛】本小题主要考查反比例函数上点的坐标的特点,考查利用割补法求三角形面积,属于基础题.16.如果不等式组9080x a x b -≥⎧⎨-<⎩的整数解有n (*n ∈N )个,那么适合这个不等式组的整数a 、b 的有序数对(,)a b 共有( )个A. 17个B. 64个C. 81个D. 72个【答案】D 【解析】 【分析】先解不等式组求得x 的取值范围,根据整数解的情况,确定有序对的个数. 【详解】由9080x a x b -≥⎧⎨-<⎩得98a bx ≤<,不妨设1n =,故a 可取1,2,3,4,5,6,7,8,9共9种可能,b 可取9,10,11,12,13,14,15,16共8种可能,可以满足整数解有1个,为1.所以有序数对(),a b 共有9872⨯=个,故选D.【点睛】本小题主要考查一元一次不等式组的解法,考查分步计数原理,考查整数的性质,考查分析与思考的能力,属于基础题.三.解答题17.求3232x x x ++-除以2x -的商式与余数. 【答案】商式23715x x =++,余式28=. 【解析】 【分析】设商为2ax bx c ++,利用()()22x ax bx c -++的展开式与3232x x x ++-比较,求得,,a b c的值,进而求得商式和余式.【详解】设商为2ax bx c ++,()()22x ax bx c -++()()32222ax b a x c b x c =+-+--,所以32121a b a c b =⎧⎪-=⎨⎪-=⎩,解得3,7,15a b c ===,()()223715x x x -++22330x x x =++-,由()32223233028x x x x x x ++--++-=可知,余式为28.【点睛】本小题主要考查多项式除法,考查化归与转化的数学思想方法,属于基础题.18.如图所示为圆柱形大型储油罐固定在U 型槽上的横截面图,已知图中ABCD 为等腰梯形(AB ∥DC ),支点A 与B 相距8m ,罐底最低点到地面CD 距离为1m ,设油罐横截面圆心为O ,半径为5m ,56D ∠=︒,求:U 型槽的横截面(阴影部分)的面积.【参考数据:sin530.8︒≈,tan56 1.5︒≈,3π≈,结果保留整数】【答案】202m【解析】【分析】利用梯形面积,减去弓形面积,求得阴影部分面积.【详解】连接,,OA OB AB ,过O 作OG CD ⊥交AB 于E ,交劣弧»AB 于F .过A 作AH CD ⊥交CD 于H ,过B 作BI CD ⊥交CD 于I .由于228AB AE BE ===,5OB OA ==,所以3,2,3OE FE OF OE EG EF FG ==-==+=,所以3AH BI ==,在直角三角形ADH 中,3tan ,tan 56,2AH D DH DH DH===o ,同理求得2CI =,所以28212CD =++=,故梯形ABCD 的面积为8123302+⨯=.在直角三角形OAE 中4sin 0.85AOE ∠==,故53,106AOE AOB ∠≈∠=o o ,所以扇形OAFB 的面积为1063522360⨯⨯≈,而三角形AOB 的面积为183122⨯⨯=,所以弓形AFB 的面积为221210-=,故阴影部分面积为2301020m -=.【点睛】本小题主要考查与圆有关的面积计算,考查梯形面积公式、扇形面积公式,考查分析与思考、解决问题的能力,属于中档题.19.如图,在边长为6的正方形ABCD 中,弧AC 的圆心为B ,过弧AC 上的点P 作弧AC 的切线,与AD 、CD 分别相交于点E 、F ,BP 的延长线交AD 边于点G .(1)设AE x =,CF y =,求y 与x 之间的函数解析式,并写出函数定义域;(2)当2AE =时,求EG 的长.【答案】(1)3666x y x -=+,(0,6)x ∈;(2)52. 【解析】【分析】(1)根据切线长定理求得,PE PF 的长,在直角三角形DEF 中利用勾股定理求得y 与x 的关系式.(2)以B 为平面直角坐标系原点,BC BA 分别为,x y 轴建立平面直角坐标系,又,E F 坐标,求得直线EF 的斜率,进而求得直线BP 的斜率,由此求得AG 长,进而求得EG 的长.【详解】(1)根据切线长定理得,PE AE x PF CF y ====,且6,6DE x DF y =-=-,直角三角形DEF 中由勾股定理得()()()22266x y x y +=-+-,化简得3666x y x -=+,由066x <-<,解得06x <<,也即函数定义域为()0,6.所以函数解析式为()()3660,66x y x x-=∈+.(2)当2AE =时,由(1)知3CF =.以B 为平面直角坐标系原点,BC BA 分别为,x y 轴建立平面直角坐标系,则()()()()0,6,6,0,2,6,6,3A C E F ,所以直线EF 的斜率为633264-=--,所以与EF 垂直的直线BG 的斜率为43,而4tan tan 3AB AGB GBC AG ∠=∠==,所以3942AB AG ==,所以95222EG AG AE =-=-=.即EG 长为52.【点睛】本小题主要考查圆的切线长定理,考查勾股定理,考查坐标法求解几何问题,属于中档题.20.对于函数()f x ,若存在0x ∈R ,使00()f x x =成立,则称点00(,)x x 为函数()f x 的不动点.(1)已知函数2()f x ax bx b =+-(0a ≠)有不动点(1,1)和(3,3)--,求a 、b ;(2)若对于任意的实数b ,函数2()f x ax bx b =+-总有两个相异的不动点,求实数a 的取值范围.【答案】(1)1a =,3b =;(2)(0,1).【解析】【分析】(1)根据不动点的定义列方程组,解方程组求得,a b 的值.(2)根据不动点的概念列式,利用一元二次方程根的个数与判别式的关系列不等式,解不等式求得a 的取值范围.【详解】(1)依题意()()11393943f a b b a f a b b a b ⎧=+-==⎪⎨-=--=-=-⎪⎩,解得1,3a b ==. (2)首先0a ≠,依题意20000()f x ax bx b x =+-=有两个不同的解,即()20010ax b x b +--=有两个不同的解,所以()2140b ab ∆=-+>,即()24210b a b +-+>对任意b R ∈都成立,所以()24240a ∆=--<,即216160a a -<,()10a a -<,解得01a <<.所以实数a 的取值范围是()0,1.【点睛】本小题主要考查新定义概念的理解和运用,考查一元二次不等式根的个数与判别式的关系,考查一元二次不等式恒成立问题的求解策略,属于中档题.21.设n 为正整数,集合12{|(,,,),{0,1}}n k A t t t t αα==⋅⋅⋅∈(1,2,,k n =⋅⋅⋅),对于集合A 中的任意元素12(,,,)n x x x α=⋅⋅⋅和12(,,,)n y y y β=⋅⋅⋅,记111122221(,)[(||)(||)(||)]2n n n n M x y x y x y x y x y x y αβ=+--++--+⋅⋅⋅++--. (1)当3n =时,若(1,1,0)α=,(0,1,1)β=,求(,)M αα和(,)M αβ的值;(2)当4n =时,设B 是A 的子集,且满足:对于B 中的任意元素α、β,当α、β相同时,(,)M αβ是奇数,当α、β不同时,(,)M αβ是偶数,求集合B 中元素个数的最大值.【答案】(1)(,)2M αα=,(,)1M αβ=;(2)4.【解析】【分析】(1)利用(,)M αβ的定义,求得(,)M αα和(,)M αβ的值.(2)当4n =时,根据α、β相同时,(,)M αβ是奇数,求得此时集合B 中元素所有可能取值,然后验证α、β不同时,(,)M αβ是偶数,由此确定集合B 中元素个数的最大值.【详解】(1)依题意(,)M αα()()()111011000022=+-++-++-=⎡⎤⎣⎦; (,)M αβ()()()110111001112=+-++-++-=⎡⎤⎣⎦. (2)当4n =时,依题意当α、β相同时,(,)M αβ()()()()1122334412x x x x x x x x =+++++++⎡⎤⎣⎦1234x x x x =+++为奇数,则1234,,,x x x x 中有“3个1和1个0”或者“1个1和3个0”.当α、β不同时:①当1234,,,x x x x 中有“3个1和1个0”时,元素为()()()()1,1,1,0,1,1,0,1,1,0,1,1,0,1,1,1,经验证可知(,)M αβ是偶数,符合题意,集合B 最多有4个元素()()()()1,1,1,0,1,1,0,1,1,0,1,1,0,1,1,1.②当1234,,,x x x x 中有“1个1和3个0”时,元素为()()()()1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,经验证可知(,)Mαβ是偶数,符合题意,集合B 1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1.最多有4个元素()()()()综上所述,不管是①还是②,集合B中元素个数的最大值为4.【点睛】本小题主要考查新定义概念的理解和运用,考查分析、思考与解决问题的能力,属于中档题.。
上海2020-2021学年七宝中学高三上学期期中仿真密卷(数学学科)参考答案

上海2021-2021学年七宝中学高三上学期期中仿真密卷 数学学科参考答案一. 填空题1. (,3][1,0)-∞--2. 79-3. 24. 3log 1x +〔1(0,)3x ∈〕 5. 312n n a n n =⎧=⎨≥⎩6. 507.10109.110. 1}-11.(3---12.1288二. 选择题13. B 14.C15.C 16. B 17.如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1. 〔1〕证明:BE ⊥平面EB 1C 1;〔2〕假设AE =A 1E ,求二面角B –EC –C 1的正弦值.【答案】〔1〕证明见解析;〔2【解析】 【分析】〔1〕利用长方体的性质,可以知道11B C ⊥侧面11A B BA ,利用线面垂直的性质可以证明出11B C EB ⊥,这样可以利用线面垂直的判定定理,证明出BE ⊥平面11EB C ;〔2〕以点B 坐标原点,以1,,BC BA BB 分别为,,x y z 轴,建立空间直角坐标系,设正方形ABCD 的边长为a ,1B B b =,求出相应点的坐标,利用1BE EC ⊥,可以求出,a b 之间的关系,分别求出平面EBC 、平面1ECC 的法向量,利用空间向量的数量积公式求出二面角1B EC C --的余弦值的绝对值,最后利用同角的三角函数关系,求出二面角1B EC C --的正弦值. 【详解】证明〔1〕因为1111ABCD A B C D -是长方体,所以11B C ⊥侧面11A B BA ,而BE ⊂平面11A B BA ,所以11BE B C ⊥又1BE EC ⊥,1111B C EC C ⋂=,111,B C EC ⊂平面11EB C ,因此BE ⊥平面11EB C ;〔2〕以点B 坐标原点,以1,,BC BA BB 分别为,,x y z 轴,建立如以下图所示的空间直角坐标系,1(0,0,0),(,0,0),(,0,),(0,,)2bB C a C a b E a ,因为1BE EC ⊥,所以2210(0,,)(,,)002224b b b BE EC a a a a b a ⋅=⇒⋅-=⇒-+=⇒=,所以(0,,)E a a ,1(,,),(0,0,2),(0,,)EC a a a CC a BE a a =--==, 设111(,,)m x y z =是平面BEC 的法向量,所以111110,0,(0,1,1)0.0.ay az m BE m ax ay az m EC +=⎧⎧⋅=⇒⇒=-⎨⎨--=⋅=⎩⎩,设222(,,)n x y z =是平面1ECC 的法向量,所以2122220,0,(1,1,0)0.0.az n CC n ax ay az n EC =⎧⎧⋅=⇒⇒=⎨⎨--=⋅=⎩⎩,二面角1B EC C --的余弦值的绝对值为122m n m n⋅==⋅,所以二面角1B EC C --=【点睛】此题考查了利用线面垂直的性质定理证明线线垂直,考查了利用空间向量求二角角的余弦值,以及同角的三角函数关系,考查了数学运算能力.18.在ABC ∆在在在在A在B ,C 所对的边分别为a ,b ,c.sin cos 6b A a B π⎛⎫=-⎪⎝⎭. ,1〕求角B 的大小;,2〕设a =2,c =3,求b 和()sin 2A B -的值.【答案】(Ⅰ)3πⅠ(Ⅰ)b =【解析】分析:ⅠⅠⅠ由题意结合正弦定理边化角结合同角三角函数根本关系可得tanB =B =π3Ⅰ ⅠⅡ〕在△ABC 中,由余弦定理可得b Ⅰ结合二倍角公式和两角差的正弦公式可得()214sin A B -=详解:ⅠⅠ〕在△ABC 中,由正弦定理a b sinA sinB=,可得bsinA asinB =Ⅰ 又由π6bsinA acos B ⎛⎫=-⎪⎝⎭,得π6asinB acos B ⎛⎫=- ⎪⎝⎭Ⅰ即π6sinB cos B ⎛⎫=- ⎪⎝⎭,可得tanB =又因为()0πB ∈,,可得B =π3Ⅰ ⅠⅡ〕在△ABC 中,由余弦定理及a =2Ⅰc =3ⅠB =π3Ⅰ 有22227b a c accosB =+-=,故b Ⅰ由π6bsinA acos B⎛⎫=-⎪⎝⎭,可得sinA =a <c,故cosA =Ⅰ 因此22sin A sinAcosA ==Ⅰ212217cos A cos A =-=.所以,()222sin A B sin AcosB cosAsinB -=-=1127-= 点睛:在处理三角形中的边角关系时,一般全部化为角的关系,或全部化为边的关系.题中假设出现边的一次式一般采用到正弦定理,出现边的二次式一般采用到余弦定理.应用正、余弦定理时,注意公式变式的应用.解决三角形问题时,注意角的限制范围.19.华为董事会决定投资开发新款软件,估计能获得10万元到1000万元的投资收益,讨论了一个对课题组的奖励方案:奖金y (单位:万元)随投资收益x (单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.〔1〕请分析函数11005x y =-是否符合华为要求的奖励函数模型,并说明原因; 〔2〕假设华为公司采用模型函数110100100510100100010x x y x a x x ⎧-≤≤⎪⎪=⎨-⎪<≤⎪+⎩作为奖励函数模型,试确定正整数a 的取值集合.【答案】〔1〕不符合,原因见解析〔2〕a 的取值集合为{}910911912,, 【解析】【分析】〔1〕根据题意,总结奖励模型需要满足的条件①()f x 在定义域[10,1000]上是增函数;②()9f x ≤恒成立;③()5xf x ≤恒成立;判断单调性及最值,即可求解;〔2〕由题意,依此判断分段函数的单调性,最大值和()5xf x ≤,即可求解参数范围,由a 为正整数,即可确定取值集合. 【详解】〔1〕设奖励函数模型为()y f x =,按公司对函数模型的根本要求,函数()y f x =满足:当[10,1000]x ∈时,①()f x 在定义域[10,1000]上是增函数;②()9f x ≤恒成立;③()5x f x ≤11005x y =-.当[10,1000]x ∈时,11005x y =-是增函数,max 1000149()(1000)910055f x f ==-=>所以()9f x ≤不恒成立.故该函数模型不符合公司要求.〔2〕对于函数模型110100100510100100010x x y x a x x ⎧-≤≤⎪⎪=⎨-⎪<≤⎪+⎩,当10100x ≤≤时,()f x 在定义域[10,100]上是增函数,且()9f x ≤恒成立;当1001000x <≤时,10100()101010x a a f x x x ---==+++,只有1000410005110a a --<⎧⎪-⎨≤⎪⎩时,()f x 在定义域[10,1000]上是增函数;要使()9f x ≤在[10,1000]x ∈恒成立,(1000)9f ≤,即100041000[100,912]5110(1000)9a aa f --<⎧⎪-⎪≤⇒∈⎨⎪≤⎪⎩;要使()5x f x ≤恒成立对[10,1000]x ∈恒成立,即11010010055101001000105x xx x a x x x ⎧-<≤≤⎪⎪⎨-⎪<<≤⎪+⎩,即24050x x a -+≥恒成立,所以910a ≥; 综上所述,910a ≥,所以满足条件的正整数a 的取值集合为{}910911912,, 【点睛】此题结合实际问题,考查了〔1〕函数的单调性,最值和恒成立问题;〔2〕由函数的单调性最值和不等式确定参数的取值范围;考查计算能力,考查数学建模思想,属于中等题型.20.椭圆2222:1x y C a b +=(0)a b >>经过点(2,1)A,离心率为2,过点(3,0)B 的直线l 与椭圆C 交于不同的两点M N 、, 〔1〕求椭圆C 的方程; 〔2〕求BM BN ⋅的取值范围;〔3〕设直线AM 和AN 的斜率分别为AM k 和AN k ,求证:AM AN k k +为定值.【答案】〔1〕22163x y +=〔2〕(2,3]〔3〕证明见解析【解析】【分析】〔1〕根据离心率和(2,1)A 代入椭圆方程可求得a 和c ,进而求得b ,方程可得;〔2〕由题意显然直线l 方程为()3y k x =-,联立直线与椭圆的方程22(3)163y k x x y =-⎧⎪⎨+=⎪⎩消去y 得()222212121860k xk x k +-+-=.因为直线l 与椭圆C 交于不同的两点M ,N ,∴>0∆,可得11k -<<,再用坐标表示出BM BN ⋅,即可求取值范围. 〔3〕由〔2〕用坐标表示出AM AN k k +化简即可. 【详解】〔1〕由题意得22222411a b a b c c a⎧+=⎪⎪⎪=+⎨⎪⎪=⎪⎩,解得a =b =∴椭圆C 的方程为22163x y +=.〔2〕由题意显然直线l 的斜率存在,设直线l 的方程为()3y k x =-,由22(3)163y k x x y =-⎧⎪⎨+=⎪⎩得()222212121860k x k x k +-+-=.∵直线l 与椭圆C 交于不同的两点M ,N ,∴()()()42221444121862410k kkk ∆=-+-=->,解得11k -<<.设M ,N 的坐标分别为()11,x y ,()22,x y ,那么21221212k x x k +=+,212218612k x x k-=+, 又()113y k x =-,()223y k x =-,()2223333122212k k k +==+++, ∵11k -<<,∴()233232212k <+≤+, ∴BM BN ⋅的范围为(]2,3. 〔3〕由〔2〕得所以AM AN k k +为定值,=2AM AN k k +- 【点睛】此题考查主要考查椭圆的标准方程求解,运用韦达定理解决直线与椭圆相交问题,椭圆定点问题,考查逻辑推理能力和计算求解能力,综合性较强,有一定难度.21.定义在R 上的函数()f x 和数列{}n a 满足以下条件:121,a a a a =≠,当n *∈N 且2n ≥时,1()n n a f a -=且11()()()n n n n f a f a k a a ---=-,其中a k 、均为非零常数. 〔1〕数列{}n a 是等差数列,求k 的值;〔2〕令1()n n n b a a n N *+=-∈,假设11b =,求数列{}n b 的通项公式;〔3〕证明:{}n a 数列是等比数列的充要条件是()(1)f x kx k =≠. 【答案】〔1〕1〔2〕n b ()1210n k a a -=-≠〔3〕证明见解析【解析】【分析】〔1〕由题意知1()n n a f a -=,11()()()n n n n f a f a k a a ---=-()2n ≥,得()()112n n n n a a k a n a --=-≥-,再由等差数列,即可求解k 值;〔2〕由1210b a a =-≠,可得()()()23221210b a a f a f a k a a =-=-=-≠,因此()()()1111n n n n n n n n b a a f a f a k a a kb +---=-=-=-=,由此可知,数列{}n b 是一个公比为k 的等比数列.〔3〕先进行充分性证明:假设()(1)f x kx k =≠那么{}n a 数列是等比数列;再进行必要性证明:假设{}n a 数列是等比数列,那么()(1)f x kx k =≠.【详解】〔1〕由()1n n a f a -=,()()()()112,3,4,n n n n f a f a k a a n ---=-=⋅⋅⋅, 得()()()()1112,3,4,n n n n n n a a f a f a k a a n +---=-=-=⋅⋅⋅, 由数列{}n a 是等差数列,得()112,3,4,n n n n a a a n a +-=-=-⋅⋅⋅,所以,()11n n n n a a k a a ---=-,()2,3,4,n =⋅⋅⋅, 得1k =.〔2〕由1210b a a =-≠,可得()()()23221210b a a f a f a k a a =-=-=-≠, 且当2n >时,()()()111n n n n n n n b a a f a f a k a a +--=-=-=-()1210n ka a -==-≠,所以,当2n ≥时,()()()1111111n n n n n n n n n n n n n n f a f a k a a b a a k b a a a a a a --+-------====---, 因此,数列{}n b 是一个公比为k 的等比数列.故通项公式为()1210n n b ka a -=-≠〔3〕{}n a 是等比数列的充要条件是()()1f x kx k =≠,充分性证明:假设()()1f x kx k =≠,那么由10a a =≠,()()12,3,4,n n a f a n -==⋅⋅⋅ 得()12,3,4,n n n a ka -==⋅⋅⋅,所以,{}n a 是等比数列. 必要性证明:假设{}n a 是等比数列,由〔2〕知,()()1*21n n b ka a n N -=-∈,()()()12121211n n n b b b a a a a a a --++⋅⋅⋅+=-+-+⋅⋅⋅+-()12n a a n =-≥, ()1121n n a a b b b -=+++⋅⋅⋅+.当1k =时,()()()12112n a a a a n n =+--≥.上式对1n =也成立, 所以,数列{}n a 的通项公式为:()()()()*1n a a f a an n N =+--∈.所以,当1k =时,数列{}n a 是以a 为首项,()f a a -为公差的等差数列.所以,1k ≠.当1k ≠时,()()1121121n n k a a a a n k --=+-≥-. 上式对1n =也成立,所以,()11()1n n k a a f a a k --=+--1()(())11n f a a f a a k a k k---=+---. 所以,()0()1f a aa f a ka k-+=⇒=-.Ⅰ,等式()(1)f x kx k =≠对于任意实数a 均成立.所以()(1)f x kx k =≠.【点睛】此题考查等差数列的定义,利用等比数列定义证明,求解等比数列通项公式及证明,考查分类讨论思想,考查计算能力,属于难题.。
上海市七宝中学2019-2020学年高三下学期数学综合基础强化练习卷5(word,含答案)
七宝中学高三数学综合基础强化052020.04一.填空题1.已知集合A=[a,+∞), B={-1,0,1}, 若B ⊆A,则实数a 的最大值为____2.若lim(1)nn x →∞-存在,则实数x 的取值范围为___ 3.满足不等式|x-A|<B ( B>0, A ∈R )与实数x 的集合叫做A 的B 邻域,若a+b-2的a+ b 邻域是一个关于原点对称的区间,则14a b +的取值范围是____ 4.已知函数f(x)=|2x-a|+a, g(x)=|2x-1|, 若f(x)+ g(x)≥3对任意x ∈R 恒成立,则实数a 的取值范围是____5.若f(x)是奇函数,当x>0时, f(x)=π-arccos(sinx), 则当x<0时,f(x)的解析式是f(x)=____6.设a ∈(-∞,0)内变化时,若经过O(0,0)、 A(4,0)、 B(1,a)三点的圆的圆心在△AOB 的内部或三角形的上,则a 的最大值是_____7.设集合A 共有6个元素,用这全部的6个元素组成的不同矩阵的个数为_____8.已知,,a b c r r r 是平面内三个单位向量,若,a b ⊥r r 则||2||32|a c a b c +++-r r r r r 的最小值是_____9.已知3sin cos 1(x x ωωω+=>0)在x ∈(0,2π)有且仅有一个实数根,则实数ω的取值范围____10.从双曲线22221x y a b-=上任意一点P 引实轴平行线交两渐近线于Q 、R 两点,则|PQ|:|PR|=_____ 11.如图,某几何体的三视图是由三个边长为2的正方形和其内部的一些虚线构成的,则该几何体的体积为____12.在图中的三角形数阵的,用*(,,)i a i j i j ≥∈N 表示第i 行第j 个数,且,1112i na =-且当i≥3时,每行中的其他各数均等于其“肩膀”上的两个数之和,即,1,11,i j i j i j a a a ---=+(2≤j≤i -1),若,22020,m a >则正整数m 的最小值为____二.选择题13.已知点P(a,b),曲线1C 的方程1,y x =-曲线2C 的方程221,x y +=则“点P(a,b)在曲线1C 上”是“点P(a,b)在曲线2C 上”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件14.曲线22:(0,45x y Γ--=要使直线y=m (m ∈R )与曲线r 有四个不同的交点,则实数m 的取值范围是( )55.(,)33A - B.(-3,3)55.(3,)(,3)33C --⋃ 5555.(3,)(,)(,3)3333D --⋃-⋃ 15.已知函数()sin(2019)cos(2019)44f x x x ππ=++-的最大值为M ,若存在实数m 、n,使得对任意实数x 总有f(m)≤f(x)≤f(n)成立,则M·|m-n|的最小值为( ).2019A π 2.2019B π 4.2019C π .4038D π16. 记f(x)=x-[x],其中[x]表示不大于x 的最大整数,0(),10kx x g x x x≥⎧⎪=⎨-<⎪⎩若方程f(x)= g(x)在[-5,5]上有7个不同的实数根,则实数k 的取值范围( ) 11.[,]65A 11.(,]65B 11.(,]54C 11.[,)54D 三.解答题 17.已知等差数列{}n a 中,255,14,a a ==数列{}n b 的前n 项和2 1.n n S b =-(1)求,n n a b (2)若(1),n n n n c a b =-+求{}n c 的前n 项和.n T18.如图所示,四棱锥P- ABCD 的底面是菱形,PO ⊥底面ABCD, O 、E 分别是AD 、AB 的中点,AB=6, AP=5,∠BAD= 60°.(1)求直线PB 与平面POE 所成角的正弦值;(2)在DC 边上是否存在点F ,使BF 与PA所成角的余弦值为若存在,确定点F 位置,如不存在,说明理由.19. 设a 为实数,函数2()||1()f x x x a a =+-+∈R(1)若函数y= f(x)是偶函数,求实数a 的值;(2) 若a=2,求f(x)的最小值;(3)对于函数y= m(x)和给定区间[a,b],若存在00()x a x b <<,满足0()()(),m b m a m x b a -=-则称函数m(x)是区间[a,b]上的“平均值函数”,0x 是它的一个“均值点”,如函数2y x =是[-1,1] 上的平均值函数, 0就是它的均值点,现有函数2()g x x mx =-++1是区间[-1,1]上的平均值函数,求实数m 的取值范围.。
上海市七宝中学2020-2021学年高三上学期期中数学试题
5.设函数 ,则函数 的定义域是________
6.已知函数 和 的定义如下表:
x
2016
2017
2018
f(x)
2017
2018
2016
x
2016
2017Байду номын сангаас
2018
g(x)
2016
2018
11.若关于 的不等式 的解集恰好是 ,则 .
12.定义在 上的函数 满足对任意 , 成立,当 时, ,则在 内,函数 的所有零点之和为________
二、单选题
13.下列图形表示数集D到C的对应法则,其中表示定义域是D,值域是C的函数的是()
A. B.
C. D.
14.若圆弧长度等于圆内接正方形的边长,则该圆弧所对圆心角的弧度数为( )
故答案为:{x|2≤x<3}.
【点睛】
本题考查交集的求法,考查交集、补集的定义等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.
5.
【分析】
由对数式的真数大于0求得f(x)的定义域,再由﹣1 1,即可得到函数 的定义域.
【详解】
解:由1﹣x2>0,可得﹣1<x<1.
∴f(x)的定义域为(﹣1,1),
4.
【分析】
求出集合A={x|1<x<3},B={x||x﹣1|<1}={x|0<x<2}.由文氏图得到P=A∩(∁RB),由此能求出集合P.
【详解】
解:集合 {x|1<x<3},
B={x||x﹣1|<1}={x|0<x<2}.
由文氏图得到P=A∩(∁RB)={x|1<x<3}∩{x|x≤0或x≥2}={x|2≤x<3}.
2019-2020学年上海中学高三(上)期中数学试卷(解析版)
2019-2020学年上海中学高三(上)期中数学试卷一.填空题1.已知集合{|42}M x x =-<<,2{|60}N x x x =--<,则M N = .2.函数y = .3.等比数列{}n a 中,公比4q =,且前3项之和是21,则数列的通项公式n a = . 4.设奇函数()f x 在(0,)+∞上为增函数,且f (1)0=,则不等式()()0f x f x x --<的解集是 .5.设0x >,0y >,25x y +=的最小值为 .6.若不等式20px qx r -+…的解集为{|2x x -…或3}x …,则不等式2()(1)0qx px r x ++->的解集为 .7.已知等差数列{}n a 的首项及公差均为正数,令*n b n N =∈,2020)n <,当k b 是数列{}n b 的最大项时,k = .8.若不存在整数x 使不等式2(4)(4)0kx k x ---<成立,则实数k 的取值范围是 . 9.定义:数集的容量是集合中所有元素的和.例如,数集{1,2,3}的容量为1236++=.则满足条件“{1A ⊆,2,3,4,5,6,7},且若a A ∈时,必有8a A -∈”的所有非空集合A 的容量的总和是 .10.a 是实数,函数2()223f x ax x a =+--.如果函数()y f x =在区间[1-,1]上有零点,则a 的取值范围是 .11.若一个整数数列的首项和末项都是1,且任意相邻两项之差的绝对值不大于1,则我们称这个数列为“好数列”,例如:1,2,2,3,4,3,2,1,1是一个好数列,若一个好数列的各项之和是2019,则这个数列至少有 项.12.设220()|||1|0x ax x f x x a x x ⎧-+=⎨++->⎩…,若()f x 的最小值为1a +,则实数a 的取值范围为 .二.选择题13.王昌龄《从军行》中两句诗为“黄沙百战穿金甲,不破楼兰终不还”,其中后一句中“攻破楼兰”是“返回家乡”的( ) A .充分条件 B .必要条件C .充要条件D .既不充分也不必要条件14.在等比数列{}n a 中,11a =,公比||1q ≠.若12345m a a a a a a =,则(m = ) A .9B .10C .11D .1215.若存在[1x ∈,2],使得|21|20x a -->成立,则实数a 的取值范围是( ) A .13(,)24-B .13(,)(,)22-∞-+∞ C .13(,)44-D .13(,)(,)44-∞-+∞ 16.给定函数()f x 和()g x ,令(){()h x max f x =,()}g x ,对以下三个论断:(1)若()f x 和()g x 都是奇函数,则()h x 也是奇函数;(2)若()f x 和()g x 都是非奇非偶函数,则()h x 也是非奇非偶函数;(3)()f x 和()g x 之一与()h x 有相同的奇偶性; 其中正确论断的个数为( ) A .0个 B .1个 C .2个 D .3个三.解答题17.已知实数a 、b 满足01a <<,01b <<. (1)若1a b +=,求11(1)(1)a b++的最小值;(2)若14ab =,求1111a b+--的最小值. 18.已知()|1|()f x ax a R =-∈,()1||g x x =-. (1)解关于x 的不等式()1f x …;(2)若()()f x g x …的解集为R ,求a 的取值范围.19.若函数()y f x =与()y g x =在给定的区间上满足()()0f x g x …恒成立,则称这两个函数在该区间上“和谐”.(1)若函数2()(1)22f x x a x a =+--+与2()22g x x ax a =+-在R 上和谐,求实数a 的取值范围;(2)若函数30()f x a x =-与()()xg x lg a=在*N 上和谐,求实数a 的取值范围. 20.在数列{}n a 中,10a =,21n na a m +=+,其中m R ∈,*n N ∈.(1)若2a 、3a 、4a 依次成公差不为0的等差数列,求m ; (2)证明:“14m >”是“*11()4n a n N +>∈恒成立”的充要条件; (3)若14m >,求证:存在*k N ∈,使得2019k a >. 21.已知2()||f x x a x b =--,其中0a >,0b >. (1)若2a =,1b =,写出()f x 的单调区间;(2)若函数()f x 恰有三个不同的零点,且这些零点之和为2-,求a 、b 的值;(3)若函数()f x 在[2-,2]上有四个不同零点1x 、2x 、3x 、4x ,求1234||||||||x x x x +++的最大值.2019-2020学年上海中学高三(上)期中数学试卷参考答案与试题解析一.填空题1.已知集合{|42}M x x =-<<,2{|60}N x x x =--<,则M N = {|22}x x -<< .【解答】解:集合{|42}M x x =-<<,2{|60}{|23}N x x x x x =--<=-<<,{|22}MN x x ∴=-<<.故答案为:{|22}x x -<<.2.函数y = [4.)+∞ . 【解答】解:由已知可得2log 20x x ⎧⎨>⎩…,解不等式可得{|4}x x …故答案为:[4,)+∞3.等比数列{}n a 中,公比4q =,且前3项之和是21,则数列的通项公式n a = 14n - . 【解答】解:因为公比4q =,且前3项之和是21, 所以31(14)2114a -=-,解得11a =,所以11144n n n a a --==, 故答案为:14n -.4.设奇函数()f x 在(0,)+∞上为增函数,且f (1)0=,则不等式()()0f x f x x--<的解集是 (1-,0)(0⋃,1) . 【解答】解:函数()f x 是奇函数 ()()f x f x ∴-=- ∴不等式()()0f x f x x--<可转化为:()0f x x <根据条件可作一函数图象: ∴不等式()()0f x f x x--<的解集是(1-,0)(0⋃,1)故答案为:(1-,0)(0⋃,1)5.设0x >,0y >,25x y +=的最小值为【解答】解:0x >,0y >,25x y +=,==+;由基本不等式有:64xyxy=;当且仅当=时,即:3xy =,25x y +=时,即:31x y =⎧⎨=⎩或232x y =⎧⎪⎨=⎪⎩时;等号成立,;故答案为:6.若不等式20px qx r -+…的解集为{|2x x -…或3}x …,则不等式2()(1)0qx px r x ++->的解集为 (3-,1)(2⋃,)+∞ .【解答】解:20px qx r -+…的解集为{|2x x -…或3}x …,所以其对应的方程20px qx r -+=有两个根2-,3,且0p >,22(2)(3)6px qx r p x x px px p -+=+-=--,所以q p =,6r p =-. 2()(1)0qx px r x ++->,即2(6)(1)0p x x x +-->,即(3)(2)(1)0x x x +-->,由穿针引线法,得(3x ∈-,1)(2⋃,)+∞. 故答案为:(3-,1)(2⋃,)+∞.7.已知等差数列{}n a 的首项及公差均为正数,令*n b n N =∈,2020)n <,当k b 是数列{}n b 的最大项时,k = 1010 .【解答】x =y =,*n b n N =∈,2020)n <,∴根据基本不等式222222222()22()x y x y xy x y x y x y +=+++++=+…,得222020*********()2(2)4n n n b a a a a -=+==…,当且仅当2020n n a a -=时,n b 取到最大值, 此时1010n =,1010k ∴=. 故答案为:1010.8.若不存在整数x 使不等式2(4)(4)0kx k x ---<成立,则实数k 的取值范围是 14k 剟 .【解答】解:设原不等式的解集为A , 当0k =时,则4x >,不合题意,当0k >且2k ≠时,原不等式化为[(x -4)](4)0k x k +-<,44k k+>, ∴4(4,)A k k =+,要使不存在整数x 使不等式2(4)(4)0kx k x ---<成立,须45k k+…,解得:14k 剟; 当2k =时,A =∅,合题意,当0k <时,原不等式化为[(x -4)](4)0k x k +->,(A ∴=-∞,4)(4k k+⋃,)+∞,不合题意,故答案为:14k 剟. 9.定义:数集的容量是集合中所有元素的和.例如,数集{1,2,3}的容量为1236++=.则满足条件“{1A ⊆,2,3,4,5,6,7},且若a A ∈时,必有8a A -∈”的所有非空集合A 的容量的总和是 224 .【解答】解:若满足条件则下列同一括号里的数,同时属于或不属于A ,即(1,7)、(2,6)、(3,5),4又(1,7)属于集合是一种情况,不属于集合又是一种情况,共两种情况,同理(2,6),(3,5),4同(1,7)类似各有两种情况,∴利用乘法原理,可得满足条件的集合个数为42(1,7)、(2,6)、(3,5),4出现和不出现的次数是相等的, (1,7)∴、(2,6)、(3,5),4出现的次数均为8, ∴总容量为:8(8884)224⨯+++=,故答案为:22410.a 是实数,函数2()223f x ax x a =+--.如果函数()y f x =在区间[1-,1]上有零点,则a 的取值范围是 ([1,)+∞ . 【解答】解:0a =时,不符合题意,所以0a ≠,2()2230f x ax x a =+--=在[1-,1]上有解,2(21)32x a x ∴-=-在[1-,1]上有解∴212132x a x-=-在[1-,1]上有解, 问题转化为求函数22132x y x -=-在[1-,1]上的值域.设32t x =-,[1x ∈-,1],则23x t =-,[1t ∈,5], 17(6)2y t t∴=+-,设7()g t t t =+,27()1g t t∴'=-,[1t ∈时,()0g t '<,此函数()g t 单调递减,t ∈,5]时,()0g t '>,此函数()g t 单调递增,y ∴的取值范围是3-,1],∴13a∈-,1],1a ∴…或a ….故答案为(-∞[1,)+∞. 11.若一个整数数列的首项和末项都是1,且任意相邻两项之差的绝对值不大于1,则我们称这个数列为“好数列”,例如:1,2,2,3,4,3,2,1,1是一个好数列,若一个好数列的各项之和是2019,则这个数列至少有 89 项.【解答】解:由题可知,数列要想项数最少,需要各项最大;又因为数列首项和末项都是1,且任意相邻两项之差的绝对值不大于1, 所以需要数列前面递增,后面对称递减; 又各项之和是2019,中间可能存在相等的项,设除去相等项后的各项为:1,2,3⋯,(1)n -,n ,(1)n -,3⋯,2,1; ∴令各项和:2(1)[1(1)]123(1)(1)212[123(1)]2(1)20192n n n n n n n n n n n n -+-+++⋯+-++-+⋯++=+++⋯+-+=⨯+=-+=…, 得44n …,当n 为44时,项数为432187⨯+=项, 220194483-=,将83分成小于或等于44的项,最少可以分成两项, 故这个数列至少有87289+=项, 故答案为:89.12.设220()|||1|0x ax x f x x a x x ⎧-+=⎨++->⎩…,若()f x 的最小值为1a +,则实数a 的取值范围为{2[1---,1] .【解答】解:(1)若0a -…,即0a …时,22,0()1,0121,1x ax x f x a x x a x ⎧-+⎪=+<⎨⎪+->⎩……, ()f x ∴在(-∞,0]上单调递减,最小值为(0)2f =,在(0,)+∞上最小值为1a +,故只需21a +…即可,解得01a 剟; (2)若01a <-…,即10a -<…时,则22,021,0()1,121,1x ax x x a x af x a a x x a x ⎧-+⎪--+<-⎪=⎨+-<<⎪⎪+-⎩………,()f x ∴在(-∞,0]上先减后增,最小值为2()224a a f =-,在(0,)+∞上最小值为1a +,故只需2214a a -+…即可,解得22a ---+, 又10a -<…,10a ∴-<…;(3)若1a ->,即1a <-时,22,021,01()1,121,x ax x x a x f x a x a x a x a⎧-+⎪--+<⎪=⎨--<<-⎪⎪+--⎩………,()f x ∴在(-∞,0]上先减后增,最小值为2()224a a f =-,()f x 在(0,)+∞上的最小值为10a -->,而()f x 的最小值为10a +<,故只需令2214a a -=+即可,解得2a =--2a =-+(舍),综上,a的取值范围是{2[1---,1].故答案为:{2[1---,1]. 二.选择题13.王昌龄《从军行》中两句诗为“黄沙百战穿金甲,不破楼兰终不还”,其中后一句中“攻破楼兰”是“返回家乡”的( ) A .充分条件 B .必要条件C .充要条件D .既不充分也不必要条件【解答】解:“攻破楼兰”是“返回家乡”的必要非充分条件. 故选:B .14.在等比数列{}n a 中,11a =,公比||1q ≠.若12345m a a a a a a =,则(m = ) A .9B .10C .11D .12【解答】解:根据等比数列的性质得,215243a a a a a ==, 又12345m a a a a a a =,所以53m a a =, 因为111m m m a a q q --==,2231a a q q ==, 所以125()m q q -=,所以110m -=,即11m =, 故选:C .15.若存在[1x ∈,2],使得|21|20x a -->成立,则实数a 的取值范围是( ) A .13(,)24-B .13(,)(,)22-∞-+∞C .13(,)44-D .13(,)(,)44-∞-+∞ 【解答】解:命题存在[1x ∈,2],使得|21|20x a -->成立的否定为[1x ∀∈,2],使得|21|20x a --…成立.由[1x ∀∈,2],使得|21|20x a --…成立,得2212x a --剟,即1322x xa -剟, 当[1x ∈,2]时,12x -的最大值为14-,32x 的最小值为34. ∴命题[1x ∀∈,2],使得|21|20x a --…成立为真命题的a 的取值范围为1[4-,3]4, 则命题[1x ∀∈,2],使得|21|20x a --…成立为假命题的a 的取值范围为13(,)(,)44-∞-+∞,即存在[1x ∈,2],使得|21|20x a -->成立的实数a 的取值范围是13(,)(,)44-∞-+∞. 故选:D .16.给定函数()f x 和()g x ,令(){()h x max f x =,()}g x ,对以下三个论断:(1)若()f x 和()g x 都是奇函数,则()h x 也是奇函数;(2)若()f x 和()g x 都是非奇非偶函数,则()h x 也是非奇非偶函数;(3)()f x 和()g x 之一与()h x 有相同的奇偶性; 其中正确论断的个数为( ) A .0个B .1个C .2个D .3个【解答】解:(1)若()f x x =-,3()g x x =,则3,0(),0x x h x x x -<⎧=⎨⎩…,则()h x 为非奇非偶函数,故(1)错误,(2)若()2xf x =,()2xg x -=,则2,0()2,0x x x h x x -⎧=⎨<⎩…,则()h x 为偶函数,故(2)错误,(3)由(1)(2)知,()f x 和()g x 与()h x 的奇偶性没有关系,故(3)错误, 故正确的个数为0个, 故选:A . 三.解答题17.已知实数a 、b 满足01a <<,01b <<. (1)若1a b +=,求11(1)(1)a b++的最小值;(2)若14ab =,求1111a b+--的最小值.【解答】解:已知实数a 、b 满足01a <<,01b <<.(1)若1a b +=,11(1)(1)(1)(1)(2)(2)4419a b a b a ba b a b b a ++++=++=++++=…,当且仅当a b =成立,故最小值为9,(2)令11x a =-,11y b =-,所以1x a x-=,1y b y -=,1x >,1y >,所以2x y +>,由14ab =,得1114x y x y --=,化简得234()34()44x y xy x y +=+++…,当且仅当x y =时成立, 解得4x y +…,或者43x y +…(不成立) 故x y +的最小值为4.18.已知()|1|()f x ax a R =-∈,()1||g x x =-. (1)解关于x 的不等式()1f x …;(2)若()()f x g x …的解集为R ,求a 的取值范围. 【解答】解:(1)()1f x …,|1|1ax ∴-…,111ax ∴--剟,02ax ∴剟,∴当0a >时,20xa 剟;当0a =时,x R ∈;当0a <时,20x a剟, ∴当0a >时,不等式的解集为2[0,]a;当0a =时,不等式的解集为R ; 当0a <时,不等式的解集为2[,0]a;(2)不等式()()f x g x …的解集为R , 即|1|1||ax x --…的解集为R . |1|y ax =-经过定点(0,1), ∴当0a =时,||0x …,满足题意; 当0a ≠时,关于x 的不等式|1|1||ax x --…的解集为R , 则11a …或11a-…,11a ∴-剟且0a ≠, a ∴的取值范围为[1-,1].19.若函数()y f x =与()y g x =在给定的区间上满足()()0f x g x …恒成立,则称这两个函数在该区间上“和谐”.(1)若函数2()(1)22f x x a x a =+--+与2()22g x x ax a =+-在R 上和谐,求实数a 的取值范围;(2)若函数30()f x a x =-与()()xg x lg a=在*N 上和谐,求实数a 的取值范围. 【解答】解:(1)由2()(1)22f x x a x a =+--+与2()22g x x ax a =+-是公共区间上的“和谐函数”,可得在公共定义域上()()0f x g x …, 若()f x ,()g x 对应的方程是同解方程, 则1222a a a a⎧-=⎪⎨⎪-+=-⎩,解得2a =; 此时22(2)(224)0x x x x +-+-…. 若()f x ,()g x 对应的方程不是同解方程,要保证对于定义域内的任意实数x ,函数值乘积均为正, 则需要两个二次函数的判别式均小于或等于0, 即22(1)4(22)042(2)0a a a a ⎧---+⎨-⨯⨯-⎩……, 解得70a -剟, 即a 的取值范围是70a -剟. 当0a =时,函数化为2()2f x x x =-+与2()2g x x =,()g x 大于等于0,()f x 的判别式小于0,()f x 大于0恒成立,函数值乘积恒非负,也满足条件.综上知,实数a 的取值范围是70a -剟或2a =; (2)由定义域可得0xa>,由题意可得0a >, 由()0f x =,可得30x a=,由()0g x =,可得x a =, 由题意可得两零点之间无正整数, 由于5630⨯=,所以当05a <<时,306a>,不满足题意; 当6a >时,3005a<<,不满足题意; 当56a 剟时,3056a剟,满足题意.所以a 的取值范围是[5,6].20.在数列{}n a 中,10a =,21n na a m +=+,其中m R ∈,*n N ∈. (1)若2a 、3a 、4a 依次成公差不为0的等差数列,求m ; (2)证明:“14m >”是“*11()4n a n N +>∈恒成立”的充要条件; (3)若14m >,求证:存在*k N ∈,使得2019k a >. 【解答】解:(1)10a =,21n na a m +=+,其中m R ∈,*n N ∈. 当1n =时,20a m m =+=, 当2n =时,23a m m =+,当3n =时,224()a m m m m =++=,∴若2a 、3a 、4a 依次成公差不为0的等差数列,3242a a a ∴=+,得1m =-± (2)证明: 充分性:21n n a a m +=+,其中m R ∈,*n N ∈.1n a m +∴…,14m >, *11()4n a n N +∴>∈恒成立.∴ “14m >” ⇒ “*11()4n a n N +>∈恒成立”. 必要性:21n n a a m +=+,其中m R ∈,*n N ∈,1n a m +∴…,又*11()4n a n N +>∈恒成立,14m ∴>, ∴ “*11()4n a n N +>∈恒成立” ⇒ “14m >” (3)221111()()244n n n n n a a a m a a m m +-=+-=-+--…,又14m >,∴令104d m =->, 由1n n a a d --…, 12n n a a d ---…,⋯21a a d -…,将上述不等式相加,得: 1(1)n a a n d --…,即(1)n a n d -…,取正整数20191k d>+,就有 2019(1)()2019k a k d d d->=…. 21.已知2()||f x x a x b =--,其中0a >,0b >. (1)若2a =,1b =,写出()f x 的单调区间;(2)若函数()f x 恰有三个不同的零点,且这些零点之和为2-,求a 、b 的值;(3)若函数()f x 在[2-,2]上有四个不同零点1x 、2x 、3x 、4x ,求1234||||||||x x x x +++的最大值.【解答】解:(1)2a =,1b =时,2222222,1(1)1,1()2|1|22,1(1)3,1x x x x x f x x x x x x x x ⎧⎧-+-+=--==⎨⎨+-<+-<⎩⎩厖, ()f x ∴在(-∞,1]-单调递减,在(1,1)-上单调递增,在[1,)+∞单调递增;(2)由题意2()||0f x x a x b =--=有三个解,且他们的和为2-,x b <时,2()0f x x ax ab =+-=必有两个解,x =,x b ∴>时,2()0f x x ax ab =-+=只有一解,△240a ab =-=,4a b =①,2x b =②,联立①②解得4a =,1b =,综上所述4a =,1b =;(3)2()||0f x x a x b =--=即20x ax ab -+=或20x ax ab +-=,设20x ax ab -+=的两根为1x ,2x ,则12x x a +=,10x >,20x >;设20x ax ab +-=的两根为3x ,4x ,则34x x a +=-,340x x ab =-<,23434||||||4x x x x a ab ∴+=-==+,1x ,2x ,3x ,4x 均在区间[2-,2]内,20x ax ab ∴+-=在区间[2-,2]内,∴2-,4a ∴+,1234||||||||4x x x x a ∴+++=+,综上所述1234||||||||x x x x a +++=+的最大值为4;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年七宝中学高三上10月月考
一.填空题 1.已知复数z满足117izi(i是虚数单位),则z . 【答案】5 【解析】 【分析】 把已知等式变形,然后利用复数代数形式的乘除运算化简,再由复数求模公式计算得答案. 【详解】由(1+i)z=1﹣7i,
得1711768341112iiiiziiii, 则|z|=22(3)(4)5. 故答案为:5. 【点睛】本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.
2.设{|}Mxxa,{2,0,1}N,若{2,0}MNI,则实数a的范围是________ 【答案】[0,1) 【解析】 【分析】 由已知集合M,N,以及M交N,可得到实数a的取值范围. 【详解】解:∵集合M={x|x≤a},N={﹣2,0,1}, 又M∩N={﹣2,0}, ∴实数a的取值范围是:0≤a<1. 故答案为:[0,1). 【点睛】本题考查了交集及其运算,利用好数轴是解题的关键,是基础题.
3.已知定义域在[-1,1]上的函数y=f(x)的值域为[-2,0],则函数y=f(cosx)的值域是______.
【答案】[-2,0] 【解析】 【分析】 可以看出-1cos1x,从而对应的函数值cos2,0fx,这便得出了该函数的值域. 【详解】解:∵cosx∈[-1,1]; ∴cos2,0fx; 即y∈[-2,0]; ∴该函数的值域为[-2,0]. 故答案为:[-2,0]. 【点睛】考查函数定义域、值域的概念,本题可换元求值域:令cosx=t,-1≤t≤1,从而得出f(t)∈[-2,0].
4.若3sin()45,则cos()4的值是________ 【答案】35-
【解析】 【分析】 利用诱导公式即可得到结果. 【详解】∵3sin()45,
∴cos()=cos()4423sin()45 故答案为:35- 【点睛】本题考查诱导公式的应用,考查学生恒等变形的能力,属于常考题型.
5.设6()axx(0a)展开式中3x的系数为A,常数项为B,若4BA,则a________ 【答案】2 【解析】 【分析】 首先写出二项展开式的通项,化简后按照要求确定字母的指数,得到特征项.
【详解】解:二项式6()axx(a>0)的展开式,通项为366266()()kkkkkkaCxCaxx, 令632k3,得到k=2,所以x3系数为A226Ca15a2; 令632k=0,k=4,所以常数项为B446()Ca15a4, 又B=4A,所以15a4=4×15a2,a>0,解得a=2; 故答案为:2 【点睛】本题考查了二项展开式的特征项的求法,关键是正确写出通项,考查学生的计算能力.
6.向量(3,4)a在向量(1,1)br 方向上的投影为________. 【答案】22
【解析】 【分析】 根据向量在向量方向上的投影公式计算即可.
【详解】依题意得·1,2abb,因此向量a在向量b方向上的投影为·22abb.
【点睛】本题主要考查了向量在向量方向上的投影及其计算,属于中档题.
7.已知函数224,0(){4,0xxxfxxxx若2(2)(),fafa则实数a的取值范围是 _____________. 【答案】 【解析】 解:因为根据函数图像可知,分段函数在整个定义域上单调递增,因此原不等式等价于2-a2>a,解得a的范围是-28.设21{|10}Pxxax,22{|20}Pxxax,有下列命题:①对任意实数a,1P是2P的子集;
②对任意实数a,1P不是2P的子集;③存在实数a,使1P不是2P的子集;④存在实数a,使1P是2P的子集;其中正确的有________ 【答案】①④ 【解析】 【分析】 运用集合的子集的概念,令m∈P1,推得m∈P2,可得对任意a,P1是P2的子集,从而作出判断. 【详解】对于集合P1={x|x2+ax+1>0},P2={x|x2+ax+2>0}, 可得当m∈P1,即m2+am+1>0,可得m2+am+2>0, 即有m∈P2, 可得对任意a,P1是P2的子集; 显然①④正确 故答案为:①④ 【点睛】本题考查集合的关系的判断,注意运用二次不等式的解法,以及任意和存在性问题的解法,考查判断和推理能力,属于基础题.
9.已知常数0a,函数2()2xxfxax的图像经过点6(,)5Pp、1(,)5Qq,若216pqpq,则a________ 【答案】4 【解析】 【分析】 直接利用函数的关系式,利用恒等变换求出相应的a值.
【详解】函数f(x)=22xxax的图象经过点P(p,65),Q(q,15).
则:226112255pqpqapaq, 整理得:22222222pqpqpqpqpqaqapaqapapq=1, 解得:2p+q=a2pq, 由于:2p+q=16pq, 所以:a2=16, 由于a>0, 故:a=4. 故答案为:4 【点睛】本题主要考查函数的性质和指数幂的运算,意在考查学生对这些知识的掌握水平和分析推理计算能力.
10.已知函数211()521xxxfxxx,若方程()fxm有两个不等实根1x、2x,且121xx,则实数
m的取值范围为________
【答案】(3,13) 【解析】 【分析】 作出函数f(x)的图象,根据分段函数的关系,结合一元二次函数的对称性,利用数形结合进行求解即可. 【详解】解:作出函数f(x)的图象如图: 由x2+x+1=5x﹣2得x2﹣4x+3=0得x=1或x=3, 即y=x2+x+1与y=5x﹣2的交点坐标为(1,3),(3,12), 当x≤1时,y=x2+x+1=(x12)234,抛物线的对称轴为x12, 若方程f(x)=m有两个不相等的实数根x1、x2, 则m34>, 若x1+x2<﹣1, 则12122xx<, 即两个函数的交点(x1、f(x1)),(x2、f(x2))的中点在x12的左侧, 即当x>1时,x2+x+1<5x﹣2,即1<x<3, 此时3<f(x)<13, 即3<m<13, 故答案为:(3,13)
【点睛】本题主要考查分段函数的应用,利用一元二次函数的对称性,利用数形结合是解决本题的关键. 11.若()fx是R上单调函数,且对任意x都有21[()]222xffx,则2(log5)f_____ 【答案】57
【解析】 【分析】 设f(x)222xt,(t为常数),则f(x)=t222x,f(t)12,从而t21222t, 令g(x)=x222x,推导出f(x)=1222x,由此能求出f(log25). 【详解】∵函数f(x)是R上的单调函数,且对任意实数x,都有f[f(x)222x]12, ∴可设f(x)222xt,(t为常数),∴f(x)=t222x, ∴f(t)12,∴t21222t,令g(x)=x222x, ∵g(x)在R上单调递增,且g(1)12,∴t=1, f(x)=1222x,f(log25)=12525227log
.
故答案为:57. 【点睛】本题考查函数值的求法,考查函数性质等基础知识,考查运算求解能力,是中档题.
12.已知两定点(3,2)E和(3,2)F,若对于实数,函数|2||2|4yxx(44x)的图像上有
且仅有6个不同的点P,使得PEPF成立,则的取值范围是________ 【答案】9(,1)5
【解析】
【分析】 画出函数y=|x+2|+|x﹣2|﹣4在[﹣4,4]的图象,讨论若P在AB上,设P(x,﹣2x﹣4);若P在BC上,设P(x,0);若P在CD上,设P(x,2x﹣4).求得向量PE,PF的坐标,求得数量积,由二次函数的最值
的求法,求得取值范围,讨论交点个数,即可得到所求范围. 【详解】解:函数y=|x+2|+|x﹣2|﹣4 42420222424xxxxx,,<,<,
(1)若P在AB上,设P(x,﹣2x﹣4),﹣4≤x≤﹣2. ∴PE(3﹣x,6+2x),PF(﹣3﹣x,6+2x). ∴PEPFx2﹣9+(6+2x)2=5x2+24x+27, ∵x∈[﹣4,﹣2],∴由二次函数的性质可得:当9λ15时有两解; (2)若P在BC上,设P(x,0),﹣2<x≤2. ∴PE(3﹣x,2),PF(﹣3﹣x,2). ∴PEPFx2﹣9+4=x2﹣5, ∵﹣2<x≤2,∴﹣5≤λ≤﹣1. ∴当λ=﹣5或﹣1时有一解,当﹣5<λ<﹣1时有两解; (3)若P在CD上,设P(x,2x﹣4),2<x≤4. PE(3﹣x,6﹣2x),PF(﹣3﹣x,6﹣2x), ∴PEPFx2﹣9+(6﹣2x)2=5x2﹣24x+27, ∵2<x≤4, ∴∴由二次函数的性质可得:当9λ15时有两解; 综上,可得有且只有6个不同的点P的情况是9λ15. 故答案为:9(,1)5.
