六年级奥数综合训练题七
六年级奥数训练第7讲几何综合一
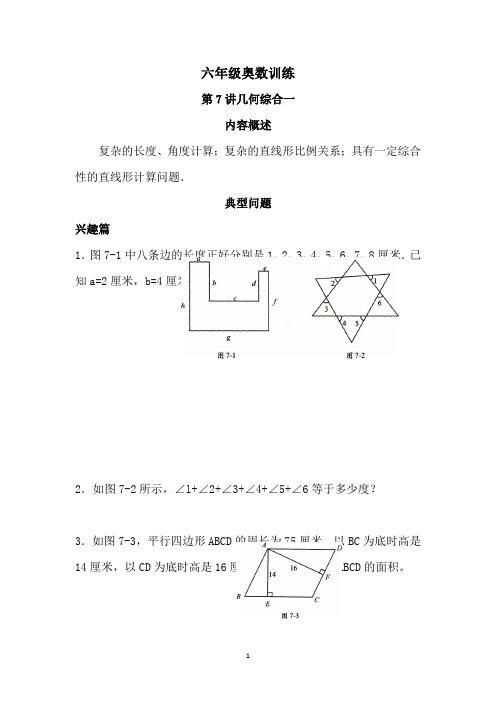
六年级奥数训练第7讲几何综合一内容概述复杂的长度、角度计算;复杂的直线形比例关系;具有一定综合性的直线形计算问题.典型问题兴趣篇1.图7-1中八条边的长度正好分别是1、2、3、4、5、6、7、8厘米.已知a=2厘米,b=4厘米,c=5厘米,求图形的面积.2.如图7-2所示,∠l+∠2+∠3+∠4+∠5+∠6等于多少度?3.如图7-3,平行四边形ABCD的周长为75厘米,以BC为底时高是14厘米,以CD为底时高是16厘米.求平行四边形ABCD的面积。
4.如图7-4,一个边长为1米的正方形被分成4个小长方形,它们的面积分别是103平方米、52平方米、51平方米和101平方米.已知图中的阴影部分是正方形,那么它的面积是多少平方米?5.如图7-5,红、黄、绿三块大小一样的正方形纸片,放在一个正方体盒内,它们之间相互重叠,已知露在外面的部分中,红色的面积是20,黄色的面积是14,绿色的面积是10.那么,正方体盒子的底面积是多少?6.如图7-6,在三角形ABC 中,IF 和BC 平行,GD 和AB 平行,HE 和AC 平行.已知AG :GF :FC =4:3:2,那么AH: HI: IB 和BD: DE: EC 分别是多少?7.如图7-7,已知三角形ABC的面积为1平方厘米,D、E分别是AB、AC边的中点,求三角形OBC的面积.8.在图7-8的正方形中,A、B、C分别是ED、EG、GF的中点.请问:三角形CDO的面积是三角形ABO面积的几倍?9.如图7-9,ABCD是平行四边形,面积为72平方厘米,E、F分别为边AB、BC的中点,则阴影部分的面积为多少平方厘米?10.如图7-10,在三角形ABC中,CE=2AE,F是AD的中点,三角形ABC的面积是1,那么阴影部分的面积是多少?拓展篇1.如图7-11,A、B是两个大小完全一样的长方形,已知这两个长方形的长比宽长8厘米,图7-11中的字母表示相应部分的长度,问:A、B中阴影部分的周长哪个长?长多少?2.如图7-12.ABCDE是正五边形,CDF是正三角形,∠BFE等于多少度?3.一个各条边分别为5厘米、12厘米、13厘米的直角三角形,将它的短直角边对折到斜边上去与斜边相重合,如图7-13所示,问:图中的阴影部分(即折叠的部分)的面积是多少平方厘米?4.在图7-14中大长方形被分为四个小长方形,面积分别为12、24、36、48.请问:图中阴影部分的面积是多少?5.三个面积都是12的正方形放在一个长方形的盒子里面,如图7-15,盒中空白部分的面积已经标出,求图中大长方形的面积.6.如图7-16,三角形ABC的面积为1.D、E分别为AB、AC的中点.F、G是BC边上的三等分点.请问:三角形DEF的面积是多少?三角形DOE的面积是多少?7.如图7-17,梯形ABCD的上底AD长10厘米,下底BC长15厘米.如果EF与上、下底平行,那么EF的长度为多少?8.如图7-18,正六边形的面积为6,那么阴影部分的面积是多少?9.两盏4米高的路灯相距10米,有一个身高1.5米的同学行走在这两盏路灯之间,那么他的两个影子总长度是多少米?10.如图7-19,D是长方形ABCD一条对角线的中点,图中已经标出两个三角形的面积为3和4,那么阴影直角三角形的面积是多少?11.如图7-20,在三角形ABC中,AE= ED,D点是BC的四等分点,阴影部分的面积占三角形ABC面积的几分之几?12.如图7-21,在三角形ABC中,三角形AEO的面积是1,三角形ABO 的面积是2,三角形BOD的面积是3,则四边形DCEO的面积是多少?超越篇1.如图7 - 22,长方形的面积是60平方厘米,其内3条长度相等且两两夹角为120°的线段将长方形分成了两个梯形和一个三角形.请问:一个梯形的面积是多少平方厘米?2.如图7-23,P是三角形ABC内一点,DE平行于AB,FG平行于BC,HI平行于CA,四边形AIPD的面积是12,四边形PGCH的面积是15,四边形BEPF的面积是20.请问:三角形ABC的面积是多少?3.如图7 -24所示,正方形ABCD的面积为1.E、F分别是BC和DF 的中点,DE与BF交于M点,DE与AF交于Ⅳ点,那么阴影三角形MFN 的面积为多少?4.如图7 -25,三角形ABC的面积为1,D、E、F分别是三条边上的三等分点,求阴影三角形的面积.5.如图7-26,小悦测出家里瓷砖的长为24厘米,宽为10厘米,而且还测出了边上的中间线段均为4厘米,那么中间菱形的面积是多少平方厘米?6.如图7-27,ED垂直于等腰梯形ABCD的上底AD,并交BC于G,AE 平行于BD,∠DCB =45°,且三角形ABD和三角形EDC的面积分别为75、45,那么三角形AED的面积是多少?7.在长方形ABCD中,E、F、G、H分别是边AB、BC、CD、DA上的点,将长方形的四个角分别沿着HE、EF、FG、GH对折后,A点与B点重合,C点与D点重合.已知EH =3,EF =4,求线段AD与AB的长度比.8.如图7-28,在长方形ABCD中,AE: ED= AF:AB= BG: GC.已知△EFC 的面积为20,△FGD的面积为16,那么长方形ABCD的面积是多少?。
六年级数学下册试题-小升初奥数高频考点历年真题总汇(七) 人教版

小升初奥数高频考点历年真题总汇(七)1 、某单位租赁了两辆同样的大巴车运送员工外出活动,从出发地到目的地的车程是2个小时,两车以相同速度同时出发,但甲车刚出发10分钟即发生故障,只能以原速的匀速较慢行驶,乙车将本车员工送到目的地后,原路返回与甲车相遇,载上甲车员工驶往目的地,当所有员工到达目的地时,在途用时总计为()。
(上下车时间不计)A.3小时50分钟B.4小时C.4小时20分钟D.4小时40分钟2 、一个木制正方体在表面涂上颜色,将它的每条棱三等分,然后从等分点将正方体展开,得到27个小正方体,将这些小正方体充分混合后,装入一个口袋,从这个口袋中随机取出两个小正方体,其中一个正方体只有一个面涂有颜色,另一个至少2个面涂有颜色的概率约为:A.0.05B.0.17C.0.34D.0.673、大型体育竞赛开幕式需要列队,共10排。
导演安排演员总数的一半多一个在第一排,安排剩下演员人数的一半多一个在第2排……..依次类推。
如果在第10排拍好将演员排完,那么参与排队列的演员共有()名。
A.2000B.2008C.2012D.20464 、小王早上看到挂钟显示8点多,急忙赶时间上班,但是到了公司却发现时间和自己出门看到的挂钟时间一样,才明白是自己出门前误把挂钟的时针看成分针,分针看成时针。
已知小王平时上班路程不超过1.5小时,今天上班他花费了()。
A.48分钟B.55分钟C.1小时D.1小时3分钟5 、某羽毛球赛共有23支队伍报名参赛,赛事安排23支队伍抽签两两争夺下一轮的出线权,没有抽到对手的队伍轮空,直接进入下一轮。
那么,本次羽毛球赛最后共会遇到多少次轮空的情况?A.2B.3C.4D.56 、甲乙两人需托运行李,托运收费标准为10kg以下6元/kg,超出10kg部分每公斤收费略微低一些。
已知甲乙两人托运费分别为109.5元、78元,甲的行李比乙重了50%。
那么,超出10kg部分每公斤收费标准比10kg以内的低了()元。
六年级综合练习七及答案

Powered by
8.
在 4 × 4 的方格表中将一些方格染成黑色,使得任意两个黑格都没有公共顶点。请问:最多可以将 多少个方格染成黑色?
【分析】第一行可染 1 格或 2 格; 染 1 格时,相邻行只能染 1 格; 染 2 格时,相邻行只能染 0 格; 可见,相邻两行最多共染 2 格,则 4×4 的方格表最多可染 4 格,下图为示例.
5 说明这样的五位数有 3 A5 = 360 个
3.
用 10 个 1× 3 的长方形纸片覆盖一个 10 × 3 的方格表,共有多少种覆盖方法?
【分析】设 × 3 的覆盖方式有 f (n) 观察 10×3 的“尾部” ,要么是一竖要么是三横; 显然一竖有 f (9) 种覆盖方式,三横有 f (7) 种覆盖方式; 可见 f (10) = f (9) + f (7) ,推广得递推式 f (n) = f (n − 1) + f (n − 3) 相应的递推数列为: 1,1, 2,3, 4, 6,9,13,19, 28 ;可见 f (10) = 28 4. 如图(1) ,讲一个梯形分成四个三角形,其中两个三角形的面积分别为 10 与 12. 已知梯形的上底 长度是下底的 2/3 请问:阴影部分的总面积是多少?
ab ⇒ ab = 10 2 平行四边形的面积 ah = 22 − 10 = 12
6. 如图(3) ,一张边长为 18 厘米的正方形纸片,从距离四角 5 厘米处,用剪刀剪出 45°的角度, 纸 片中间会形成一个小正方形。这个小正方形的面积是多少平方厘米?
【分析】如图进行分割,显然两块阴影的面积一样大; 中间正方形面积为: 7. 5× 5 × 4 = 50 . 2
9.
古希腊有一位久负盛名的学者,名叫海伦。他精通数学、物理,聪慧过人。有一天,一位将军向 他请教一个问题:如图(5) ,将军从甲地骑马出发,要到河边上让马饮水,然后再回到乙地的马 棚,为了使走的路线最短,应该让马在什么地方饮水?
六年级下册奥数第七讲整数的分拆 例题 习题 通用版(例题含答案)

第七讲整数的分拆整数分拆是数论中一个既古老又活跃的问题、把自然数n分成为不计顺序的若干个自然数之与n=n1+n2+…+nm(n1≥n2≥…≥nm≥1)的一种表示法,叫做n的一种分拆、对被加项及项数m加以一些限制条件,就得到某种特别类型的分拆、早在中世纪,就有关于特别的整数分拆问题的研究。
1742年德国的哥德巴赫提出“每个不小于6的偶数都能够写成两个奇质数的与”,这就是著名的哥德巴赫猜想,中国数学家陈景润在研究中取得了突出的成果、下面我们通过一些例题,简单介绍有关整数分拆的基本知识、一、整数分拆中的计数问题例1有多少种方法能够把6表示为若干个自然数之与?解:依照分拆的项数分别讨论如下:①把6分拆成一个自然数之与只有1种方式;②把6分拆成两个自然数之与有3种方式6=5+1=4+2=3+3;③把6分拆成3个自然数之与有3种方式6=4+1+1=3+2+1=2+2+2;④把6分拆成4个自然数之与有2种方式6=3+1+1+1=2+2+1+1;⑤把6分拆成5个自然数之与只有1种方式6=2+1+1+1+1;⑥把6分拆成6个自然数之与只有1种方式6=1+1+1+1+1+1、因此,把6分拆成若干个自然数之与共有1+3+3+2+1+1=11种不同的方法。
说明:本例是不加限制条件的分拆,称为无限制分拆,它是一类重要的分拆、例2有多少种方法能够把1994表示为两个自然数之与?解法1:采纳有限穷举法并考虑到加法交换律:1994=1993+1=1+1993=1992+2=2+1992=998+996=996+998=997+997因此,一共有997种方法能够把1994写成两个自然数之与。
解法2:构造加法算式:因此,只须考虑从上式右边的1993个加号“+”中每次确定一个,并把其前、后的1分别相加,就能够得到一种分拆方法;再考虑到加法交换律,因此共有997种不同的分拆方式。
说明:应用本例的解法,能够得到一般性结论:把自然数n≥2表示为两个自然数之与,一共有k种不同的方式,其中例3有多少种方法能够把100表示为(有顺序的)3个自然数之与?(例如,把3+5+92与5+3+92看作为100的不同的表示法)分析本题仍可运用例1的解法2中的处理方法、解:构造加法算式因此,考虑从上式右边的99个加号“+”中每次选定两个,并把它们所隔开的前、中、后三段的1分别相加,就能够得到一种分拆方法、因此,把100表示为3个自然数之与有种不同的方式。
小学六年级奥数题及答案

小学六年级奥数题及答案精选小学六年级奥数题及答案9篇六年级的奥数学习,是巩固加强的阶段,这个时候要多做奥数题,进行训练。
要提高做奥数的速度和正确率。
以下是店铺整理的小学六年级奥数题及答案,希望对大家有所帮助。
小学六年级奥数题及答案篇1六年级的同学们马上就要面临小升初的考试了,所以一定要在这段时间不能松懈,把每天的练习坚持到底你才能有更大的收获。
两地相距900米,甲、乙二人同时、同地向同一方向行走,甲每分钟走80米,乙每分钟走100米,当乙到达目标后,立即返回,与甲相遇,从出发到相遇共经过多少分钟?答案与解析:甲、乙二人开始是同向行走,乙走得快,先到达目标.当乙返回时运动的方向变成了相向而行,把相同方向行走时乙用的时间和返回时相向而行的时间相加,就是共同经过的时间.乙到达目标时所用时间:900100=9(分钟),甲9分钟走的路程:80x9=720(米),甲距目标还有:900-720=180(米),相遇时间:180(100+80)=1(分钟),共用时间:9+1=10(分钟).另解:观察整个行程,相当于乙走了一个全程,又与甲合走了一个全程,所以两个人共走了两个全程,所以从出发到相遇用的时间为:900x2(100+80)=10分钟.小学六年级奥数题及答案篇2内容概述较为复杂的以成本与利润、溶液的浓度等为内容的分数与百分数应用题.要利用整数知识,或进行分类讨论的综合性和差倍分问题.典型问题1.某店原来将一批苹果按100%的利润(即利润是成本的100%)定价出售.由于定价过高,无人购买.后来不得不按38%的利润重新定价,这样出售了其中的40%.此时,因害怕剩余水果腐烂变质,不得不再次降价,售出了剩余的全部水果.结果,实际获得的总利润是原定利润的30.2%.那么第二次降价后的价格是原定价的百分之多少?【答案解析】第二次降价的利润是:(30.2%-40%×38%)÷(1-40%)=25%,价格是原定价的(1+25%)÷(1+100%)=62.5%.2.某商品76件,出售给33位顾客,每位顾客最多买三件.如果买一件按原定价,买两件降价10%,买三件降价20%,最后结算,平均每件恰好按原定价的85%出售.那么买三件的顾客有多少人?【答案解析】3×(1-20%)+1×100%=340%=4×85%,所以1个买一件的与1个买三件的平均,正好每件是原定价的85%.由于买2件的,每件价格是原定价的1-10%=90%,所以将买一件的与买三件的一一配对后,仍剩下一些买三件的人,由于3×(2×90%)+2×(3×80%)=12×85%.所以剩下的买三件的人数与买两件的人数的比是2:3。
【6年级奥数详解(下)】第07讲_计算综合练习

小学奥数创新体系6年级 (下册授课课本) 最
新 讲 义
小学奥数 第七讲 计算综合练习 1. 答案:312032.解答:原式=11111312345620248163232. 2. 答案:4019.解答:原式=2010201020102010201020102010201014019. 3. 答案:7.58.解答:原式=1231338625.587.585558.
4. 答案:2976.解答:原式=111129361876762232292929296.
5. 答案:29.解答:原式=111111112344589399
L.
6. 答案:2.解答:原式=2342009201023452010L. 7. 答案:12345678887654321.解答: 原式=12345678910000000001123456789000000000123456789123456788876543211.
8. 答案:2051.解答:原式=355713151517355713151517
L
11111111112035571315151731751
L.
9. 答案:100. 解答:原式=22.017.992.017.992.017.997.992.012.017.997.992.017.99 102.017.99100
.
10. 答案:672345.解答: 原式=123456200820092010362007672345LL.
11. 答案:0.2.解答:分子=2513757152251071151424712810815471042; 分母=19121415192251681519751575355152575255722;所以,原式=15751225.
小学六年级奥数试题
小学六年级奥数试题 小学六年级奥数试题 在日常学习和工作中,我们都要用到试题,借助试题可以检测考试者对某方面知识或技能的掌握程度。什么样的试题才是科学规范的试题呢?以下是小编精心整理的小学六年级奥数试题,欢迎大家分享。 小学六年级奥数试题 篇1 1、(归一问题)工程队计划用60人5天修好一条长4800米的公路,实际上增加了20人,每人每天比计划多修了4米,实际修完这条路少用了几天? 2、(相遇问题)甲、乙两辆汽车同时从东西两地相向开出,甲车每小时行56千米,乙车每小时行48千米。两车距中点40千米处相遇。东西两地相距多少千米? 3、(追及问题)大客车和小轿车同地、同方向开出,大客车每小时行60千米,小轿车每小时行84千米,大客车出发2小时后小轿车才出发,几小时后小轿车追上大客车? 4、(过桥问题)列车通过一座长2700米的大桥,从车头上桥到车尾离桥共用了3分钟。已知列车的速度是每分钟1000米,列车车身长多少米? 5、(错车问题)一列客车车长280米,一列货车车长200米,在平行的轨道上相向而行,从两个车头相遇到车尾相离经过20秒。如果两车同向而行,货车在前,客车在后,从客车头遇到货车尾再到客车尾离开货车头经过120秒。客车的速度和货车的速度分别是多少? 6、(行船问题)客轮和货轮从甲、乙两港同时相向开出,6小时后客轮与货轮相遇,但离两港中点还有6千米。已知客轮在静水中的速度是每小时30千米,货轮在静水中的速度是每小时24千米。求水流速度是多少? 7、(和倍问题)小李有邮票30枚,小刘有邮票15枚,小刘把邮票给小李多少枚后,小李的邮票枚数是小刘的8倍? 8、(差倍问题)同学们为希望工程捐款,六年级捐款数是二年级的3倍,如果从六年级捐款钱数中取出160元放入二年级,那么六年级的捐款钱数比二年级多40元,两个年级分别捐款多少元? 9、(和差问题)一只两层书架共放书72本,若从上层中拿出9本给下层,上层还比下层多4本,上下层各放书多少本? 10、(周期问题)20xx年7月1日是星期六,求10月1日是星期几? 小学六年级奥数试题 篇2 一、知识要点 定义新运算是指运用某种特殊符号来表示特定的意义,从而解答某些算式的一种运算。 解答定义新运算,关键是要正确地理解新定义的算式含义,然后严格按照新定义的计算程序,将数值代入,转化为常规的四则运算算式进行计算。 定义新运算是一种人为的、临时性的运算形式,它使用的是一些特殊的运算符号,如:*、△、⊙等,这是与四则运算中的“+、-、×、÷”不同的。 新定义的算式中有括号的,要先算括号里面的。但它在没有转化前,是不适合于各种运算定律的。 二、精讲精练 【例题1】假设a*b=(a+b)+(a—b),求13*5和13*(5*4)。 【思路导航】这题的新运算被定义为:a*b等于a和b两数之和加上两数之差。这里的“*”就代表一种新运算。在定义新运算中同样规定了要先算小括号里的。因此,在13*(5*4) 中,就要先算小括号里的 (5*4)。 练习1: 1。将新运算“*”定义为:a*b=(a+b)×(a—b)。。求27*9。 2。设a*b=a2+2b,那么求10*6和5*(2*8)。 3。设a*b=3a-b×1/2,求(25*12)*(10*5)。 【例题2】设p、q是两个数,规定:p△q=4×q—(p+q)÷2。求3△(4△6)。 【思路导航】根据定义先算4△6。在 这里“△”是新的运算符号。 练习2: 1.设p、q是两个数,规定p△q=4×q-(p+q)÷2,求5△(6△4)。 2.设p、q是两个数,规定p△q=p2+(p-q)×2。求30△(5△3)。 3.设M、N是两个数,规定M*N=M/N+N/M,求10*20-1/4。 【例题3】如果1*5=1+11+111+1111+11111,2*4=2+22+222+2222, 3*3=3+33+333,4*2=4+44,那么7*4=________;210*2=________。 【思路导航】经过观察,可以发现本题的新运算“*”被定义为。因此 练习3: 1.如果1*5=1+11+111+1111+11111,2*4=2+22+222+2222, 3*3=3+33+333,……那么4*4=________。 2.规定, 那么8*5=________。 3.如果2*1=1/2,3*2=1/33,4*3=1/444,那么(6*3)÷(2*6)=________。 【例题4】规定②=1×2×3,③=2×3×4 ,④=3×4×5,⑤=4×5×6,……如果1/⑥-1/⑦ =1/⑦×A,那么,A是几? 【思路导航】这题的新运算被定义为: @ = (a-1)×a×(a+1),据此,可以 求出1/⑥-1/⑦ =1/(5×6×7)-1/(6 ×7×8),这里的分母都比较大,不易直接 求出结果。根据1/⑥-1/⑦ =1/⑦×A,可 得出A = (1/⑥-1/⑦)÷1/⑦ = (1/ ⑥- 1/⑦)×⑦ = ⑦/⑥ -1。即 练习4: 1.规定:②=1×2×3,③=2×3×4,④=3×4×5,⑤=4×5×6,……如果1/⑧-1/⑨=1/⑨×A,那么A=________。 2.规定:③=2×3×4,④=3×4×5,⑤=4×5×6,⑥=5×6×7,……如果1/⑩+1/⑾=1/⑾×□,那么□=________。 3.如果1※2=1+2,2※3=2+3+4,……5※6=5+6+7+8+9+10,那么x※3=54中,x=________。 【例题5】设a⊙b=4a-2b+1/2ab, 求z⊙(4⊙1)=34中的未知数x。 【思路导航】先求出小括号中的4⊙1=4×4—2×1+1/2×4×1=16,再根据x⊙16=4x-2×16+1/2×x×16 = 12x-32,然后解方程12x-32 = 34,求出x的值。列算式为 练习5: 1. 2.对两个整数a和b定义新运算“△”:a△b= △8。 3.对任意两个整数x和y定于新运算,“*”:x*y= 个确定的整数)。如果1*2=1,那么3*12=________。 设a⊙b=3a-2b,已知x⊙(4⊙1)=7求x。 ,求6△4+9(其中m是一 小学六年级奥数试题 篇3 1.甲乙两地相距6千米.陈宇从甲地步行去乙地,前一半时间每分钟走80米,后一半的时间每分钟走70米.这样他在前一半的时间比后一半的时间多走()米. 考点: 简单的行程问题. 分析: 解:设陈宇从甲地步行去乙地所用时间为2X分钟,根据题意,前一半时间和后一半的时间共走(0.07+0.08)X千米,已知甲乙两地相距6千米,由此列出方程(0.07+0.08)X=6,解方程求出一半的时间,因此前一半比后一半时间多走:(80-70)×40米,解决问题. 解答: 解:设陈宇从甲地步行去乙地所用时间为X分钟,根据题意得: (0.07+0.08)X=6, 0.15X=6, X=40; 前一半比后一半时间多走: (80-70)×40, =10×40, =400(米). 答: 前一半比后一半的时间多走400米. 故答案为:400. 点评: 根据题目特点,巧妙灵活地设出未知数,是解题的关键. 小学六年级奥数试题 篇4 1、(鸡兔同笼问题)小丽买回0.8元一本和0.4元一本的练习本共50本,付出人民币32元。0.8元一本的练习本有多少本? 2、(年龄问题)5年前父亲的年龄是儿子的7倍。15年后父亲的年龄是儿子的二倍,父亲和儿子今年各是多少岁? 3、(盈亏问题)王老师发笔记本给学生们,每人6本则剩下41本,每人8本则差29本。求有多少个学生?有多少个笔记本? 4、(还原问题)便民水果店卖芒果,第一次卖掉总数的一半多2个,第二次卖掉剩下的一半多1个,第三次卖掉第二次卖后剩下的一半少1个,这时只剩下11个芒果。求水果店里原来一共有多少个芒果? 5、(置换问题)学校买回6张桌子和6把椅子共用去192元。已知3张桌子的价钱和5把椅子的价钱相等,每张桌子和每把椅子各是多少元? 6、(安排)烤面包的架子上一次最多只能烤两个面包,烤一个面包每面需要2分钟,那么烤三个面包最少需要多少分钟? 7、(油和桶问题)一桶油连桶共重18千克,用去油的一半后,连桶还重9.75千克,原有油多少千克?桶重多少千克? 8、(和倍)青青农场一共养鸡、鸭、鹅共12100只,鸭的只数是鸡的2倍,鹅的只数是鸭的4倍,问鸡、鸭、鹅各有多少只? 9、(鸡兔同笼)实验小学举行数学竞赛,每做对一题得9分,做错一题倒扣3分,共有12道题,小旺得了84分,小旺做错了几道题? 10、(相遇问题)甲、乙两人同时从相距20xx米的两地相向而行,甲每分钟行55米,乙每分钟行45米,如果一只狗与甲同时同向而行,每分钟行120米,遇到乙后,立即回头向甲跑去,遇到甲再向乙跑去。这样不断来回,直到甲和乙相遇为止,狗共行了多少米? 小学六年级奥数试题 篇5 甲、乙、丙三人行路,甲每分钟走60米,乙每分钟走67.5米,丙每分钟走75米,甲乙从东镇去西镇,丙从西镇去东镇,三人同时出发,丙与乙相遇后,又经过2分钟与甲相遇,求东西两镇间的路程有多少米? 解:那2分钟是甲和丙相遇,所以距离是(60+75)×2=270米,这距离是乙丙相遇时间里甲乙的路程差, 所以乙丙相遇时间=270÷(67.5-60)=36分钟,所以路程=36×(60+75)=4860米。 小学六年级奥数试题 篇6 现在的奥数,其难度和深度远远超过了同级的义务教育教学大纲。而相对于这门课程,一般学校的数学课应该称为“普通基础数学”。特此为大家准备了关于某工厂的六年级奥数专题强化。 某工厂11月份工作忙,星期日不休息,而且从第一天开始,每天都从总厂陆续派相同人数的工人到分厂工作,直到月底,总厂还剩工人240人。如果月底统计总厂工人的工作量是8070个工作日(一人工
六年级上册数学奥数试题-全国168所名牌小学小考必做的600道奥数题(七)人教版
全国168所名牌小学小考必做的600道奥数题(七)1、有1997根火柴,甲、乙两人轮流取火柴,每人每次可取1至10根,谁能取到最后一根谁为胜利者,甲先取,乙后取。
甲有获胜的可能吗?取胜的策略是什么?2、盒子里有47粒珠子,两人轮流取,每次最多取5粒,最少取1粒,谁最先把盒子的珠子取完,谁就胜利,小明和小红来玩这个取珠子的游戏,先名先、小红后,谁胜?取胜的策略是什么?3、在黑板上写有999个数:2,3,4,……,1000。
甲、乙两人轮流擦去黑板上的一个数(甲先擦,乙后擦),如果最后剩下的两个数互质,则甲胜,否则乙胜。
谁必胜?必胜的策略是什么?4、甲、乙两人轮流从分别写有1,2,3,……,99的99张卡片中任意取走一张,先取卡的人能否保证在他取走的第97张卡片时,使剩下的两张卡片上的数一个是奇数,一个是偶数?5、两个人进行如下游戏,即两个人轮流从数列1,2,3,……,100,101勾去九个数。
经过这样的11次删除后,还剩下两个数。
如果这两个数的差是55,这时判第一个勾数的人获胜。
问第一个勾数的人能否获胜?获胜的策略是什么?6、甲、乙两人轮流在黑板上写下不超过10的自然数,规定禁止在黑板上写已写过的数的约数,最后不能写的人为失败者。
如果甲第一个写,谁一定获胜?写出一种获胜的方法。
7、甲、乙两人轮流在黑板上写上不超过14的自然数。
书写规则是:不允许写黑板上已写过的数的约数,轮到书写人无法再写时就是输者。
现甲先写,乙后写,谁能获胜?应采取什么对策?8、一片松树林里有很多种树,有1500棵树不是松树,1200棵树不是杨树,松树、杨树共700棵,杨树有多少棵?9、爸爸今年43岁,儿子今年11岁,几年后爸爸的年龄是儿子的3倍?10、妈妈今年的年龄是女儿的4倍,3年前,妈妈和女儿的年龄和是39岁,问妈妈、女儿今年各是多少岁?11、两个数相除,商4余1,被除数、除数、商和余数的和是156,被除数、除数各是多少?12、两个数的和是94,有人计算时将其中一个加数个位上的0漏掉了,结果算出的和是31,求这两个数。
小学六年级奥数综合训练试题
小学六年级奥数综合训练试题
Revised by Chen Zhen in 2021 模拟试卷.4 姓名 得分
一、填空题: 1.41.2×8.1+11×9.25+537×0.19=______. 2.在下边乘法算式中,被乘数是______. 3.小惠今年6岁,爸爸今年年龄是她的5倍,______年后,爸爸年龄是小惠的3倍. 4.图中多边形的周长是______厘米. 5.甲、乙两数的最大公约数是75,最小公倍数是450.若它们的差最小,则两个数为______和______. 6.鸡与兔共有60只,鸡的脚数比兔的脚数多30只,则鸡有______只,兔有______只. 7.师徒加工同一种零件,各人把产品放在自己的筐中,师傅产量是徒弟的2倍,师傅的产品放在4只筐中.徒弟产品放在2只筐中,每只筐都标明了产品数量:78,94,86,77,92,80.其中数量为______和______2只筐的产品是徒弟制造的. 8.一条街上,一个骑车人与一个步行人同向而行,骑车人的速度是步行人速度的3倍,每隔10分钟有一辆公共汽车超过行人,每隔20分钟有一辆公共汽车超过骑车人.如果公共汽车
从始发站每次间隔同样的时间发一辆车,那么间隔______分发一辆公共汽车. 9.一本书的页码是连续的自然数,1,2,3,…,当将这些页码加起来的时候,某个页码被加了两次,得到不正确的结果1997,则这个被加了两次的页码是______. 10.四个不同的真分数的分子都是1,它们的分母有两个是奇数,两个是偶数,而且两个分母是奇数的分数之和等于两个分母是偶数的分数之和.这样的两个偶数之和至少为______. 二、解答题: 1. 把任意三角形分成三个小三角形,使它们的面积的比是2∶3∶5. 2.如图,把四边形ABCD的各边延长,使得AB=BA′,BC=CB′CD=DC′,DAAD′,得到一个大的四边形A′B′C′D′,若四边形ABCD的面积是1,求四边形A′B′C′D′的面积. 3.如图,甲、乙、丙三个互相咬合的齿轮,若使甲轮转5圈时,乙轮转7圈,丙轮转2圈,这三个齿轮齿数最少应分别是多少齿? 4.(1)图(1)是一个表面涂满了红颜色的立方体,在它的面上等距离地横竖各切两刀,共得到27个相等的小立方块.问:在这27个小立方块中,三面红色、两面红色、一面红色,各面都没有颜色的立方块各有多少?
小学六年级奥数年龄问题专项强化训练题(高难度)
小学六年级奥数年龄问题专项强化训练题(高难度)例题1:某公司的平均年龄是40岁,其中男性占总员工数的1/4,女性占总员工数的3/4。
如果男性员工的平均年龄是35岁,那么女性员工的平均年龄是多少岁?解析:设男性员工数为x,女性员工数为y。
已知男性员工的平均年龄是35岁,那么男性员工的总年龄就是35x。
公司的平均年龄是40岁,所以总年龄是40(x+y)。
女性员工占总员工数的3/4,所以女性员工的总年龄就是40y。
根据题意,得到以下等式:35x + 40y = 40(x+y)35x + 40y = 40x + 40y35x = 40x5x = 0x = 0根据男性员工数为0,可以得到女性员工数为总员工数。
所以女性员工的平均年龄就是公司的平均年龄40岁。
专项训练题:1. 某班级男生和女生的人数比为2:3。
男生的平均年龄是10岁,女生的平均年龄是12岁。
这个班级的平均年龄是多少岁?2. 一所小学的学生总数是120人,其中男生占总人数的1/3,女生占总人数的2/5。
男生的平均年龄是9岁,女生的平均年龄是10岁。
这所小学的平均年龄是多少岁?3. 某公司的员工总数是80人,其中男员工占总人数的1/4,女员工平均年龄是35岁,男员工平均年龄是40岁。
这个公司的平均年龄是多少岁?平均年龄是多少岁?5. 某家庭兄妹四人,他们的平均年龄是20岁。
老大比老二大2岁,老二比老三大5岁,老三比老四大3岁。
老大的年龄是多少岁?6. 一个班级有40名男生,男生的平均年龄是14岁;有30名女生,女生的平均年龄是12岁。
这个班级的平均年龄是多少岁?7. 某学校的学生总数是1600人,其中男生占总人数的3/4,女生的平均年龄是14岁,男生的平均年龄是12岁。
这所学校的平均年龄是多少岁?8. 某公司的员工总数是200人,其中男员工占总人数的1/5,女员工的平均年龄是30岁,男员工的平均年龄是35岁。
这个公司的平均年龄是多少岁?9. 一个班级的男女生人数比为5:6,男生的平均年龄是13岁,女生的平均年龄是14岁。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级综合训练题七
1、 一枝钢笔,如果售价8元,可赚60%如果降价到6.4元出售,可赚
( )%
2、 小明和小亮分别从甲、乙两地同时出发相向而行,他们分别到达乙、甲两地
后立即返回。第一次相遇处离甲地 680米,第二次相遇离乙地340米,则甲、 乙
两地相距( )米。
3、 小军行走的路程比小红多 -,而小红行走的时间却比小军多 丄,小军与小
4 10
红速度的比是( )
O
4、 有甲、乙两大瓶牛奶,甲瓶牛奶比乙瓶多 100克。如果从两瓶中各取出 5
克,则甲瓶的1等于乙瓶的原来两瓶共有( )克牛奶。
3 2
5、 一个长方形的长增加
1、宽增加1
后得到一个新长方形,新长方形的面积比
2 3
原长方形增加多少?
6、 把一个圆形纸片剪开后,拼成一个宽等于半径、面积相等的近似长方形,这 个
长方形的周长是24.84厘米,原来这个圆形纸片的面积是( )平方厘米。
7、一个正方形的周长和一个圆的周长相等,这个正方形的面积是圆面积的一<
&有一分数,若分子加上1,就等于4 ;若分母加上1,就等于3 ;原分数是
5 4
()。
二、应用题
1、一辆客车和一辆卡车同时从甲、乙两站相对开出,4小时后两车在途中相遇, 客
车行完全部路程需用9小时,卡车每小时行40千米。问甲、乙两站相距 多少千
米?
2、客车和货车同时从A、B两地相对开出,客车每小时行驶50千米,货车的速 度
是客车速度的80%相遇后客车继续行3.2小时到达B地,A,B两地相距 多少
千米?
3、一个圆柱形水桶高4分米,侧面积是50.24平方分米,如果1升水重1千克, 这
个水桶能装水多少千米?
4、师徒两人生产一批零件,
师傅计划完成这批零件个数的右,他完成任务后,
又替徒弟生产了 24个,这时师傅实际生产的个数是徒弟的1-倍。问:徒弟
3
计划生产多少个?
5、甲、乙两班学生共118人,已知甲班中男生占 -,乙班中女生占
5
,两班
11 9
女生共有多少人?
6、一个胶水瓶,它的瓶身呈圆柱形(不包括瓶颈),容积为31.4立方厘米。当 瓶
子正放时,瓶内胶水液面高 8厘米;瓶子倒放时,空余部分高为 2厘米。瓶 内胶
水的体积是多少?
7 •求边长是整数厘米,周长是 20厘米的不同的等腰三角形有多少个?
8. —个六面都涂满红色的长方体,恰好能切成若干个棱长为1分米的正方
体。现切得的正方体中有8个每个面都没有红色,那么,长方体的体积是多少?
9•两个相同的直角三角形如图1所示(单位:厘米)重叠在一起,BO=3
EO=2 EF=1Q求阴影部分的面积。
10•图2中三角形AOB面积为15平方厘米,线段OB的长度是OD的3倍,
梯形ABCD5积是多少?
11. 一个正方形被分成四个长方形,它们的面积分别是 1/10平方米、丨/
5平方米、3/10平方米和2/5平方米。图3中的阴影部分是一个正方形,那 么它的
面积是多少。
3
1
10
1
1
2
1
S
~ III
C
liv "To"
图3
12•将表面积为54平方厘米、96平方厘米、150平方厘米的三个铁质正方 体
熔成一个大正方体(不计损耗),求这个大正方位的表面积。
13. —块方木料,横截面是正方形,这个正方形的边长为 1. 8分米,木料 长5
分米。现在要把它加工成尽可能大的圆柱体, 求这块木料的利用率?(取 3. 14)
14. 将一个长9厘米、宽8厘米、高3厘米的长方体锯成若干个小长方体 (损
耗不计),然后拼成一个大正方体,求这个大正方体的表面积。
15. 如
图4所示,正方形边长为4厘米,以边长为半径,以相对的两个顶 点为圆心,在正
方形内画弧,组成图中的阴影部分,求阴影部分的面积( 取
3. 14)。
16. —个长方体的长是宽的1. 5倍,宽是高的2倍,边长总和为96厘米, 求
它的体积。
17. 把一块长19厘米、宽5厘米、高3厘米的长方体铝块和一棱长为7厘 米的
正方体铝块熔铸成一个底面周长为 31. 4厘米的圆柱形铝块,求铝块的高 是多少
厘米(取3. 14)?
参考答案
【能力训练】
1 •解:
由于三角形两边之和大于第三边,因而该等腰三角形的最长边不能大于 9
厘米,它们的边长可以是 9、9、2厘米,或8、8、4厘米,或7、7、6厘米, 还可
以是6、& 8厘米,所以所求三角形有4个。
2•解:
首先要搞清以下问题:第一,这 8个每面都没有颜色的正方体都分布在长 方体
的里面,否则切成正方体后有的面会有颜色。第二,这 8个正方体在长方
体里面是怎样排列的。第三,这些不同排列的8个正方体要用多少正方体盖住。
3X4X4=48 (立方分米)
答:长方体的体积是48立方分米。
3•解:
因为阴影部分的面积不能直接求出, 而
S ABC S
DEF
,都减去△ DOC勺面积 后,根据
差不变的性质,应有直角梯形ABOD勺面积=直角梯形EOCF勺面积,即
(10-3+10 )X 2-2= 17 (平方厘米)。
答:阴影部分的面积是17平方厘米。
4•解:
由于 OD OB= 1: 3
S
AOD — S AOB
所以 3
S AOD 15 — 5
即 3 (平方厘米)
又因为
S BAD S
CAD
所以S COD S AOB 15平方厘米
而0B=30,那么S BOC 3 S DOC 3 15 45(平方厘米),因此梯形ABCD 的面积是5+15
X
2+45=80 (平方厘米)。
答:梯形ABCD勺面积是80平方厘米。
5•解:
由已知条件知S正方形1平方米,得正方形边长为1米。在长方形I和U中,
^23 3
它们面积之比是10 : 5 4,可知AB BD=3 4, AB占边长的7 , BD占边长的
4 2 1
7。同理在长方形川和W中,AC占边长的3 , CD占边长的3
。因此BC占边长
2 3 2 1 A A
的 3 7 21,即 21 21 (米)。
25
答:小正方形的面积是441平方米。
6•解:
三个正方体的棱长
54=6X 9=6X( 3X 3),棱长为 3 厘米
所以小正方形面积为
21 21
25
441
(平方
米)
96=6X 16=6X( 4X 4),棱长为 4 厘米
150= 6X 25=6X( 5X 5),棱长为 5 厘米
三个正方体的体积:
3X 3X 3=27,体积为27立方厘米
4X4X4 = 64,体积为64立方厘米
5X 5X 5=125,体积为125立方厘米
大正方体的体积为:
27+64+125=216 (立方厘米)
216=6X 6X 6,棱长为6厘米
大正方体的表面积为:
6X( 6X 6)= 216 (平方厘米)
答:大正方体的表面积为216平方厘米。
7•解:
要使加工成的圆柱体尽可能大。必须使圆柱的底面直径为正方形的边长
2
1. 8分米,高为5分米,其体积为 0・9 5 (立方分米)。
0.92 5 0.9 0.9 3.14
2
3.14 78.5%
1.8 5 1.8 1.8 4
答:利用率是78. 5%
8.解:
锯法:把长 3等分,宽 4等分,将长方体锯成 12块,每一块长 3厘米,宽
2 厘米,高 3 厘米。把 12块长方体木块摆成两层,使长宽高均为 6 厘米,组成 一
个大正方体。因此,大正方体的表面积为:
6X6X6=216 (平方厘米)
答:这个大正方体的表面积为 2 1 6平方厘米。
9.解: 可把阴影部分的面积看成两扇形面积的重叠,只要将两扇形面积之和减
去
一个正方形面积,所得差就是我们要求的阴影部分的面积。面积是 9.12 平方
厘米。
10 .解:
只需求出该长方体的长、 宽、高。设高为 x 厘米,则宽为 2x 厘米.长为
1 .5 X 2x=3x 厘米,根据题意得:
4X( 3x+2x+x) =96
24x= 96
x = 4
2x=8,3x=12
4X 8X 12=384
答:长方体的体积为 384 立方厘米。
11 .解:
设圆柱的高为x厘米,底面半径为r
2n r=31.4 r = 5
根据熔铸前后铝块的体积不变列方程:
52 x 19 5 3 73
19 5 3 343
x -----------------------
3.14 25
x=8
答:圆柱形铝块的高是8厘米。
