Lukasiewicz三值命题逻辑在非均匀概率空间下命题的真度理论

合集下载

n值lukasiewicz命题逻辑系统中理论的相容度

n值lukasiewicz命题逻辑系统中理论的相容度Lukasiewicz命题逻辑系统的相容度定义了在这些信息系统中表示的概念。

它是一种在基本命题逻辑系统（PCS）中表示知识表示的可能方式。

Lukasiewicz命题逻辑系统中定义的和比较的相容性，涉及定义和比较具有不同程度的不同类型的表示：实例和概念。

PCS背后的思想是，它把概念的表示和实例的表示成为等效的，从而允许在一个系统中定义和比较它们。

PSC提供了一种范式，允许实例和概念在不同的情境中被彼此表达。

它也提供了实际的建议，以理解概念和实例的表示，以及它们之间的关系。

在Lukasiewicz命题逻辑系统中，概念的表达可以通过一定范围内的不同等级来表示。

表示概念的等级可以从单个实例到概念的完备描述，也就是“定义”模型。

另一方面，实例可以通过不同等级的表示来表示，如：命题逻辑中的“实例”模型，这是一种在概念表示中表明当实例属于概念时，它必须满足的条件。

在Lukasiewicz命题逻辑系统中，相容度旨在使概念和实例的表示成为一致的，从而为实现概念的表示提供有用的指导。

Lukasiewicz的概念相容度提供了一种架构，以允许用户在不同的命题逻辑系统中定义和测量概念的深度，以及实例的范围和准确性。

它可以被用来构建系统，这些系统可以使用更有力的能力来对概念和实例进行表示和分析。

Lukasiewicz命题逻辑系统中的相容度有助于确保用户在使用和理解表示层次概念时，有一致的方式来定义和表达它们。

它为使用统一的信息表示提供了坚实的基础，因此，它有助于构建数据的准确性和可靠性。

在面对不断增长的大数据时代，Lukasiewicz命题逻辑系统的相容性可以为大数据分析提供帮助，以抽取和识别有用的模式。

Lukasiewicz三值命题逻辑系统中公式的概率真度理论

ＣｍｕｎｅｎｇａｄＡｐｉｔｎ计算机工程与应用ｏｐ￣ｒＥ￣ｎｅｎｎｐｌａｉｓｃｏBiblioteka ２１，６６００４（）
３７
Ｌｋｓｗｃ三值命题逻辑系统中公式的概率真度理论ｕａｉｉｚｅ
关晓红，刘晓
ＧＵＡＮａ — ｎｇ，ＩＸｉｏｈｏＬＵＸｉｏａ
ＧＵＡＮａ－ｏｇ，Ｕａ．ｅｒｆｐｏａｉｔｒｔｅｒｅｉｋｓｅｃ－ａｕｄｌｇｃｓｓｅＣｏｕｅｇｎｅｉｇＸｉｏｈｎＬＩＸｉｏＴｈｏｙｏｒｂｂｌｙｔｕｈｄｇｅｎＬｕａｉｗｉｚ３ｖｌｅｏｉｙｔｍ．ｍｐｔｒＥｎｉｅｒｎｉ
ｎｓｌｅｏｔｉ［，】ｈｏｃｐｉｓｏｒｂｂｌｙｓｌｔｄｇｅｎｓｕｏｍｔｃｏｗｏｕａｒｄｆｅｙｏｉａｄｐｉｎ０ｌ．ｅｃｎｅｔｎｆｐｏａｉｔｉａｙｅｒｅａｄｐｅｄ — ｅｒｎｔｏｆｒｌａｅｅｎｄｂｏｔｎＴｏｉｍｉｒｉｉｍｓｉ
ｍｅｎｏｈｃｎｅｔｏｒｂｂｌｙｒｔｅｒｅｆｐｏｏｉｏｓＭｏｅｖｒｔｅｐｏａｉｔｏｉｔｃｐｃｉｕｌＩｉｒｖｄａｓｆｔｅｏｃｐｆｐｏａｉｔｔｈｄｇｅｏｒｐｓｔｎ．ｒｏｅ，ｒｂｂｌｙｌｇｃｍｅｒｓａｅｓｉｕｉｈｉｉｂｉ．ｓｐｏｅｔｔｈｔｔｉｐｃａｏｉａｅｏｎ．ｎｉａｒｖｄｏｓｅｆｔａｈｓｓａｅｈｓｎｓｌｔｄｐｉｔｅｔｃｎｐｏｉｅａｐｓｉｌｒｍｅｒｏｐｒｘｍａｅｒａｏｉｇｔｅｒ．ｏｈＴｂａｗｏｋｆｒａｐｏｉｔｅｓｎｎｈｏｙＫｅｒｓｐｏａｉｔａｕｅｐｏａｉｔｒｔｅｒｅｓｌｒｔｅｒｅｐｅｄ — ｔｃｉｏａｅｏｎｙｗｏｄ：ｒｂｂｌｙｍｅｓｒ；ｒｂｂｌｙｔｕｈｄｇｅ；ｉａｉｄｇｅ；ｓｕｏｍｅｒ；ｓｌｔｄｐｉｔｉｉｍｉｙｉ

【国家自然科学基金】_lukasiewicz系统_基金支持热词逐年推荐_【万方软件创新助手】_20140730

2008年序号 1 2 3 4 5 6 7 8 9 10 11 12 13
科研热词推荐指数真度 2 闭集 1 闭逻辑理论 1 逻辑系统■ 1 逻辑度量空间 1 近似推理 1 相容性 1 相容度 1 相似度 1 条件真度 1 数理逻辑 1 发散度 1 三值lukasiewicz命题逻辑 1
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
2011年科研热词推荐指数模糊逻辑 2 lukasiewicz系统 2 计量逻辑学 1 紧致性定理 1 积分真度 1 真度 1 满足性定理 1 正则双stone代数 1 概率逻辑学基本定理 1 概率 1 极大相容理论 1 有限理论 1 度量空间 1 公理 1 不可靠度 1 γ -真度 1 γ -伪距离 1 rough集 1 rough逻辑 1 rough蕴涵 1 r0系统 1 lukasiewicz模糊命题逻辑 1 g(o)del系统 1
2013年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
科研热词 lukasiewicz命题逻辑随机逻辑度量空间随机真度随机发散度逻辑等价类计量逻辑学计数问题等价形式真度定义概率计量逻辑推理规则准析(合)取范式 shannon展开式 n值mcnaughton函数 borel型概率真度
科研热词非均匀概率空间逻辑系统nmg 逻辑系统'luk 紧致性等式稠密积分真度真度满足性模糊逻辑模糊赋值极大相容理论强蕴涵算子伪距离不等式 mv-代数 lukasiewicz三角模和三角余模 cantor空间
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

逻辑系统G3在非均匀概率空间下命题的真度理论

学者从不同的角度提出了公式的程度化真确度的方法【３．献【还就格值逻辑的情形基于２］文４］公式的多种不同的被知值概念展开了知识状态的研究文献【，］５６中利用积分方法建立了公式
逻辑系统Ｇ在非均匀概率空间下命题的真度理论３
左卫兵
（华北水利水电学院，数学与信息科学学院，河南郑州４０１）５１０
摘要在离散概率测度空间下定义了三值逻辑ｇｒ测度，ｊ）并相应地定义了命题逻辑系统中公式的真度概
念在值辑（ｉ）度 ÷ ）度证了题辑统Ｇ中体式真值集０］；三逻１测和（．测下明命逻系３全公的度之在【．．．１
（１）Ｐ（）一ｑ，（ｏ）＜）．｛）．｛）一ｒ（ｔ佗一１２…）其中０≤Ｐ ‘ ．＋ｑ ‘ ．ｘ — ｎ：．．：＜１ｐ＋７一１令Ｘ
设为上的关于，２… 的无穷乘积测度，称为三值逻辑（，．）度．ｎ，Ｐｑｒ测
注文献【］ｌ中讨论的三值逻辑测度即为本文的三值逻辑（１测度，故本文是文献【】Ｏ．）１０
的推广．，当ｑ另＝０，三值逻辑（）度即退化为二值逻辑ｐ时弘ｑ测一测度【】１．２
一
设Ｓ＝｛１ｐ．｝，（是由Ｓ生成的（．型自由代数，这里 “一 ”与 “一 ”分别是ｐ，２… ，～一）元与二元运算，称ｓ中的元为原子命题（原子公式）称Ｆ（）中的元为命题（或，Ｓ或公式）．设

【国家自然科学基金】_lukasiewicz命题逻辑_基金支持热词逐年推荐_【万方软件创新助手】_20140801

科研热词真度非均匀概率空间逻辑系统nmg 逻辑系统'luk 紧致性等式稠密积分真度满足性模糊逻辑极大相容理论导出函数函数f:{0,1/2,1}n→{0,1/2,1} 充要条件伪距离代数不等式三元三值lukasiewicz 命题逻辑l3* mv代数 mv lukasiewicz命题逻辑 cantor空间
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010辑度量空间真度函数相似度伪距离
推荐指数 1 1 1 1
2011年序号 1 2 3 4 5 6 7 8 9
2011年科研热词推荐指数计量逻辑学 1 紧致性定理 1 满足性定理 1 概率逻辑学基本定理 1 概率 1 极大相容理论 1 度量空间 1 不可靠度 1 lukasiewicz模糊命题逻辑 1
2012年序号 1 2 3 4 5 6 7 8
科研热词推荐指数概率真度 1 极限定理 1 probability truth degree 1 lukasiewicz命题逻辑 1 lukasiewicz propositional logic 1 limit theorem 1 borel概率测度 1 borel probability measure 1
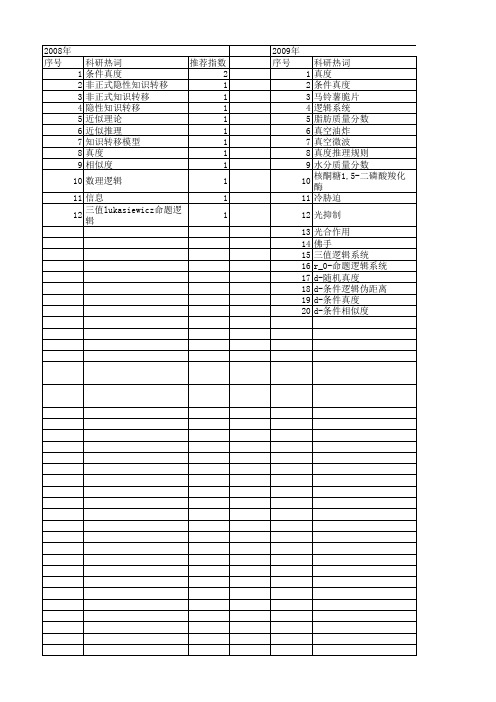
2008年序号 1 2 3 4 5 6 7 8 9 10 11 12 13
科研热词推荐指数真度 2 闭集 1 闭逻辑理论 1 逻辑系统■ 1 逻辑度量空间 1 近似推理 1 相容性 1 相容度 1 相似度 1 条件真度 1 数理逻辑 1 发散度 1 三值lukasiewicz命题逻辑 1
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

区间值模糊Lukasiewicz蕴涵的研究

区间值模糊Lukasiewicz蕴涵的研究杜浩翠;薛占熬;肖运花【摘要】The Lukasiewicz implication is a common and significant implication.Some operations are defined in the interval-valued fuzzy sets.＜I[0,1],≤＞ is proved bounded,distributive,completed and complemented lattice,and ＜I[0,1],∩,∪,c＞ is derivational algebras system by complemented lattice ＜I[0,1],≤＞.A new Lukasiewicz implication is reconstructed in the interval-valued fuzzy sets,and itsregularities,monotonicities and algebraic properties are discussed.%Lukasiewicz蕴涵是一个常用的重要蕴涵.在区间值模糊集合上给出了交并等几个运算的概念,证明了<I[0,1],≤>是有界格、分配格、完备格和有余格,其中,<I[0,1],∩,∪,c>是有余格<I[0,1],≤>诱导的代数系统.重新构造了一种区间值模糊Lukasiewicz蕴涵,讨论了该蕴涵的正则、单调和代数等重要性质.【期刊名称】《计算机工程与应用》【年(卷),期】2011(047)033【总页数】4页(P149-152)【关键词】区间值模糊集;Lukasiewicz蕴涵;模糊集;有余格【作者】杜浩翠;薛占熬;肖运花【作者单位】河南师范大学计算机与信息技术学院,河南新乡453007;河南师范大学计算机与信息技术学院,河南新乡453007;河南师范大学计算机与信息技术学院,河南新乡453007【正文语种】中文【中图分类】TP181 引言Lukasiewicz逻辑系统是一种较为具体且有用的多值逻辑系统，是人脑处理模糊信息的一种有效的方法，符合人类的思维推理过程，是逻辑学研究的热点[1-5]。

Lukasiewicz区间值命题逻辑的a-真度理论

ｔｅｐｏａｉｔｓａｅｒｅｐｎｅｔｔｅｎｅｖｌａｕｄＯｎｈｓａｉ，ｈｆｉｉｔｒａ— ａｕｄｍｅｓｒｉｅｎｄ，ｎｔｅｈｒｂｂｌｙｐｃａｅｘａｄｄｏｈｉｔｒａ — ｌｅ．ｔｉｌｖｂｓｓｔｅｉｔｎｅｖｌｌｅｎｅｖａｕｅｓｄｆｅａｄｈｉｃｎｅｔｏｈｉｆｉｐｏｕｔｉｉｅｏｈｉｔｒａ — ａｕｄｐｏａｉｔｓａｅＴｅｏｃｐｆｔｅｏｃｐｆｔｅｎｎｔｒｄｃｓｇｖｎｎｔｅｎｅｌｖｌｅｒｂｂｌｙｐｃ．ｈｃｎｅｔｏｈｉｅｖｉ－ｒｔｄｇｅｓｓｎｒ ‘ ｔｕｈｅｒｅｉｉｔｏ
区分公式可靠程度的思想早在１５年就由ＲｓｒＴｒ９２ｏｓ和ｕ．ｅ
概念如Ｆ：
ｑｅｅｕｔ提出。王国俊教授于均匀概率的思想在二值命ｔ］。等基题逻辑中引入公式的真度理论，后来，俊等对Ｌｋｓ — 李ｕａｉｅｗｃｉｚ三值，ｕａｉｗｃ值和Ｇｏｅ值命题逻辑中的真度Ｌｋｓｉｅｚｄｌ理论进行了研究，文献［］而８是在非均匀概率空间下对二值逻
Ｅｍａ：ｕｚａａ＠１３ｏ — ｉｘｅｈｎｏ６．ｍｌｔ
ＸＵＥＺｈａ．ｏ。ＥＩＬｉｐｎＣＥＮｎ，ｔａ．ｅｒｆａｔｕｈｄｇｅｓｉＬｕａｉｗｉｚｉｔｒａ－ａｕｄｐｏｏｉｏａｏ。ｎａＷ－ｉｇ，Ｆｅｇｅ１Ｔｈｏｙｏ－ｒｔｅｒｅｎｋｓｅｃｎｅｖｌｖｌｅｒｐｓｎｌｌｇｉｔ

【国家自然科学基金】_条件真度_基金支持热词逐年推荐_【万方软件创新助手】_20140801

2010年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
科研热词蕴涵算子公式的条件真度伴随对三角模算子 d-条件真度逻辑系统g3 近似推理浮游动物
推荐指数 2 2 2 2 2 1 1 1 1 模糊命题系统g(o)del和l* 1 小黄鱼 1 吕泗渔场 1 d-真度 1 d-条件逻辑度量空间 1 d-条件发散度 1 d-条件伪距离 1 d-发散度 1
科研热词真度条件真度马铃薯脆片逻辑系统脂肪质量分数真空油炸真空微波真度推理规则水分质量分数核酮糖1,5-二磷酸羧化酶冷胁迫光抑制光合作用佛手三值逻辑系统 r_0-命题逻辑系统 d-随机真度 d-条件逻辑伪距离 d-条件真度 d-条件相似度
推荐指数 3 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 11 12
科研热词推荐指数条件真度 2 非正式隐性知识转移 1 非正式知识转移 1 隐性知识转移 1 近似理论 1 近似推理 1 知识转移模型 1 真度 1 相似度 1 数理逻辑 1 信息 1 三值lukasiewicz命题逻辑 1
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2012年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
科研热词推荐指数近似推理 2 高羊茅 1 计量逻辑 1 草坪质量 1 育种 1 综合抗性 1 磁化率 1 真度 1 理论和谐度 1 沉积物 1 条件随机逻辑度量空间 1 条件随机真度 1 条件随机相似度 1 条件真度 1 条件实验 1 有机碳同位素 1 无性系 1 孢粉 1 子一代 1 地球化学 1 古气候 1 华南 1 二叠纪-三叠纪之交 1 sedimentary rock 1 organic carbon isotopes 1 conditional experiments 1

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ＺＵＯｅ — ｎＷｉｂｉｇ
（ｅｔｏａｈ．ａｄｌｏｃ，ｏｔＣｉａｌｓｆａｒＣｎｅａｃｎｙｒｌｔｃＰｗｒＺｅｚｏ０１，ｈ）Ｏｐ．ｆＭｔｅｎｆｒｉＮｒｈｎｔＷｔｏｓｒｎｙａｄＨｄｏｅｒｏｅ，ｈｎｈｕ５０１Ｃ／ｎ．Ｓ．ｈｎ．ｏｅｖｅｃｉｇ４ａｎ
摘要：离散概率测度空间下定义了三值逻辑（ｑ）在Ｐ，，ｒ测度，并相应地定义了命题逻辑系统中公式
的度概在值逻，，测证明了Ｌ中体公式的值之集在［，］是稠密真念；三辑Ｉ寺）度下ｉｉ，全真度０１上
、 … ，
，１
维普资讯
第２３卷第１期
２００８年２月
郑州轻工业学院学报（自然科学版）
ＪＵＮＬＦＨＮＺＯＮＶＲＩＹＯＨＤＳＲ（ａｒｃｎｅＯＲＡＥＧＨＵＵＩＥＳＦ０ＺＴＨＧＴＩＵＴＹＮｔａＳｉｃ｝Ｎｕｌｅ
Ｒｓｅ和Ｔｒｕｔ提出，国俊等基于均匀概ｏｓｒｕｑｅｅｔ王
率的思想在经典二值命题逻辑中引入了公式的真
度概念，提出了一种近似推理的框架．来，骏并后李
等提出三值命题逻辑中的真度理论，使得赋值域
离散情形下对公式的可靠程度有了判定的理论和
ＯｎＬｕｓｅｃＳｔｅ－ａｕｅｒｔｇｅｈｅｒｎｔｐｃｆｋａｉｗｉｚ’ ｈｒｅｖｌｄｔｕｈｄｅｒｅｔｏｙｉｈｅｓａｅｏ
ｕｅｅｉｃｅｅｐｏａｉｔｎｖｎｄｓｒｔｒｂｂｌｙｉ
Ｋｅｏｄ：ｎｖｎｐｏａｉｔｓａｅ（ｑｒｙｗｒｓｕｅｅｒｂｌｙｐｃ；Ｐ，，）ｍｅｓｒ；ｕｈｄｇｅ；ｉｉｒｙｄｇｅｂｉａｕｅｔｔｅｒｅｓｌｉｅｒｅｒｍａｔ
０引言
区分公式可靠程度的思想早在１５９２年就由
第１期
左卫兵：ｕａｉｉＬｋｓｗｃｅｚ三值命题逻辑在非均匀概率空间下命题的真度理论
ｄｇｅｎｔｅｔｕｈｄｅｅｏｕｌｓｏｅｔｐｆｐｅｄ — ｉｔｎｅｉｈｅｆａｌｆｒｕａｓｉｔｏｃｄ，ｅｒｅｉｈｒｔｇｅｆｒａ，ｎｙｅｏｓｕｏｄｓａｃｎｔｅｓｔｏｏｒｍｌｍｌｗａｎｒｄｕｅｓＳｏｓｂｅｓｒｃｕｅｏｒｘｍｉｅｓｎｎｈｏｙｗａｏｉｅＯａｐｓｉｌｔｕｔｒｆｐｏｉｔｒａｏｉｇｔｅｒｓｐｒ１Ｆｂ０８ｅ．２０
文章编号：０４—１７（０８０ — ｌ８— ４１０４８２０）１０１０
Ｌｋｓｗｃ三值命题逻辑在非均匀概率ｕａｉｉｅｚ空间下命题的真度理论
左卫兵
（华北水利水电学院数学与信息科学学院，河南郑州４０１）５０１
收稿１期：０７— ５—１３２０００基金项目：河南省自然科学基金项目（６１５６００１０２０）作者简介：左卫兵（９６）男，南省内黄县人，１７一，河华北水利水电学院讲师，主要研究方向：应用数学与概率统计．
维普资讯
ｔ６ｔｔｔｅｌ（，，ｍｓｔｅｅｆｕｈｎ。０］ｅｅｈｉｅｒｖｅｅｒｅｈｇ。ｌｌｎｅｇｆ，ｓｄａｅａｄｔｔｎｈ．ｕ）ａｅｔｒｆａｅ［１ｉｈｕｔｒｄｅａｏｓｔｍｈｕｌｒｉｍ
ｗｓｄｎｅａｄｔｅｅｐｅｓｎｅｅ￣ｅｐｅｓｎｏｒｕａｔｔｅｅａｉｅ．ａｅｎｔｅｓｌｒｔａｅｓｎｈｘｒｓｉｇｇｎｒｘｒｓｉｆｏｏｆｍｌｒｈｄｇｅｗｓｇｖｎＢｓｄｏｉａｉｕｒｈｍｉｙ
ＡｓａｔＴｅｔｅ—￣ｅＰ，ｒｏｉｍａｕｅｉｔｅｓａｅｏｎｖｎｄｃｅｒｂｂｌｙｗｓｄ— ｂｔｃ：ｈｒｅｖｕｄ（，ｑ）ｌｃｅｓｒｎｈｐｃｆｅｅｉｒｔｐｏａｉｔａｅｒｈｇｕｓｅｉ
ｉｅｆｎｄ，ａｄｔｅｔｕｈｄｅｒｅｏｏｍｕａｉｒｐｓｔｎｌｇｃｓｓｅｗａｏｒｓｏｄｉｇｙｄｆｅｉｓａｓｎｈｒｔｇｅｆｆｒｌｎｐｏｏｉｉｏｉｙｔｍｓｃｒｅｐｎｎｌｅｎｄ；ｔｗａｌｏｏｉ
１
１、
的，并给出真度的表达式；利用真度定义公式的相似度和一种伪距离，为一般离散概率空间下三值命
题的近似推理理论提供了一种可能的框架．
关键词：均匀概率空间；Ｐ，，）非（ｑｒ测度；真度；相似度中图分类号：４。０１１１文献标识码：Ａ