电动力学常用数学公式
电动力学常用数学公式

垐,,AA AAA A A A===(单位矢量)在坐标系中 31i ii A Ae ==∑ 直角系 z yz A A i Aj A k =++方向余弦:cos ,cos cos cos cos x y z Ax Ay Az Ae e e A Aβγαβγ===++321(A A =+二.矢量运算加法: A B B A +=+ 交换律 ()()A B C A B C ++=++ 结合律 31()iiii A B A B e =+=+∑ 满足平行四边形法则标量积:31cos i ii A B A BAB θ=⋅==∑A B B A ⋅=⋅ 交换律()A B C A B A C ⋅+=⋅+⋅ 分配律123123123sin n e e e A B AB e A A A B B B θ⨯== ()A B C A B A C ⨯+=⨯+⨯ 分配律A B B A ⨯=-⨯ 不满足交换律 123123123()()()A A A A B C B C A C A B B B B C C C ⋅⨯=⋅⨯=⋅⨯=3乘2,点2乘3)()()A B C A B C ⨯⨯≠⨯⨯三.矢量微分ˆˆdA dA dAA A dt dt dt=+ ()A B dB dAA B dt dt dt ⋅=⋅+⋅ ()A B dB dAA B dt dt dt⨯=⨯+⨯ 四.并矢与张量并矢: AB (一般 AB BA ≠),有九个分量。
若某个量有九个分量,它被称为张量33,1,i i ijij i ji j i jT AB A B e e T e e====∑∑ i j e e 为单位并矢,矢量与张量的矩阵表示:123,i iA A Ae A A A ⎛ == ⎝∑1211223(,B AB A A A B A B A B ⎛⎫==++T AB = T T T T ⎛ = ⎝单位张量:31i j i e e ==∑0100 = ⎝,i j()()()()AB C A B C A C B AC BC B A C BAB C A B CA⋅=⋅=⋅=⋅=⋅=⋅=⋅=⋅()()()C AB C A B B C A B A C BA C ⋅=⋅=⋅=⋅=⋅与矢量叉乘:()()AB C A B C C AB C A B ⎧⨯=⨯⎪⎨⨯=⨯⎪⎩并矢并矢两并矢点乘:()()()AB CD A B C D A B C AD CD AB ⋅=⋅=⋅≠⋅ (并矢) 两并矢二次点乘: ()():AB CD B C A D =⋅⋅ 标量与单位张量点乘:C C C ⋅=⋅=AB AB AB ⋅=⋅=:AB A B =⋅15-20分钟))()A B A B +⨯- ()()2B A =⨯ ()()M b a c a b c =⋅-⋅与矢量C 垂直。
电动力学公式
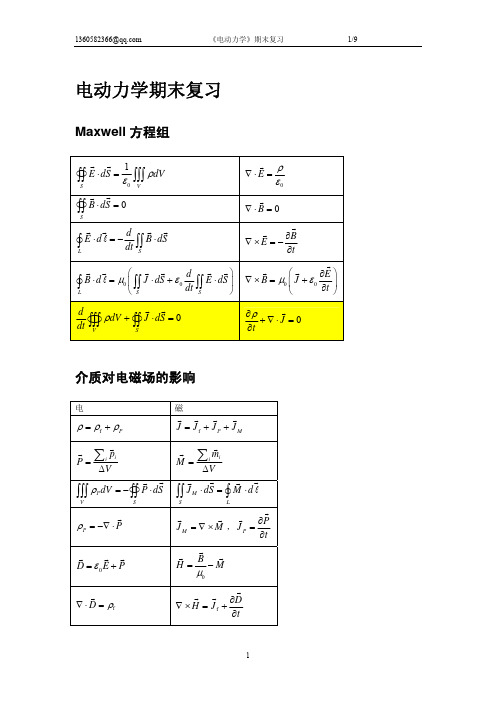
电动力学期末复习Maxwell方程组介质对电磁场的影响简单介质的电磁性质电磁场的能量和动量电磁势电磁辐射的推迟势电磁场的边值关系静电场D E ε=G G2f,ρϕε∇=−分离变量法20ϕ∇=2222222111sin sin sin r r r r r r θ2θθθθ∂∂∂∂∂⎛⎞⎛⎞∇=++⎜⎟⎜⎟∂∂∂∂∂⎝⎠⎝⎠φ 11,,(,,)(cos )cos (cos )sin n m nm nm nm nm n nm nn n n m n m b d r a r P m c r P r r m ϕθφθφθφ++⎛⎞⎛⎞=+++⎜⎟⎜⎟⎝⎠⎝⎠∑∑ ˆˆˆsin R e e e R R R φθθθφ∂∂∇=++∂∂∂∂镜像法2,,RQ R q b a a=−=电多极矩3001()111():446V Q p D x dV R x r RR ρϕπεπεR ⎡⎤′′⋅⎛⎞=⇒++∇∇⎢⎥⎜⎟⎝⎠⎣⎦∫∫∫GG G G G()V x dV Q i ρ′′=∫∫∫G,()i Vx x dV ρp ′′′=∫∫∫G,()23()3()i j ij i j ij VVx .ij x x dV D x x r x dV ρδρ′′′′′′′′′=⇒=−∫∫∫∫∫∫G GE DW p =−⋅GG , , ()e F p E =⋅∇G G G e M p E =×G G G .磁多极矩03()()44VJ x dV m R A x r R μμππ′′×=⇒∫∫∫G GG G G G 1()2Vm x J x dV ′′′=×⇒∫∫∫G G G G GIS BW m =−⋅G G , , ()e F m B =⋅∇G G Ge M m B =×G G G时谐电磁波模简谐平面电磁波简谐平面电磁波的能量和动量0(,)cos()E x t E k x t ω=⋅−G G GG G0(,)cos()B x t B k x t ω=⋅−G G GG G简谐平面电磁波的反射和折射狭义相对论 光速不变原理22222222()()0ct x y z ct x y z ′′′′−−−=−−−=狭义相对性原理协变量 Einstein 约定 矩阵形式 标量U U ′=四维矢量 V a V μμνν′=V A V′=⋅二阶张量 F a a F μνμλντ′=λτ F AFA ′=3231211230000i 123B B E ci B B E c F F iB B E c i i i E E E cccμν⎡⎤−−⎢⎥⎢⎥⎢⎥−−⎢⎥⎡⎤==⎢⎥⎣⎦⎢⎥−−⎢⎥⎢⎥⎢⎥⎣⎦。
电动力学总结

c) 给定边界条件
a)做替代时,所研究空间的泊松方程不能被改变(即自由 点电荷位置、Q 大小不能变)。所以假想电荷必须放在 所求区域之外。
b)不能改变原有边界条件(实际是通过边界条件来确定假 想电荷的大小和位置)。
c)一旦用了假想(等效)电荷,不再考虑原来的电荷分布。 d)坐标系选择仍然根据边界形状来定。
2、在所求区域的介质中若有自由电荷分布,则要求 自由电荷分布在真空中产生的势为已知。 一般所求区域为分区均匀介质,则不同介质分界
面上有束缚面电荷。区域V中电势可表示为两部分
的和,即 0, 0 为已知自由电荷产生
的电势, 不满足 20 , 为束缚电荷产生 的电势,满足拉普拉斯方程 20
但注意,边值关系还要用 而不能用
Z
0
0
Y(y) Cek2y Dek2y Z(z) Esinkz Fcoskz
2. 柱坐标
2 1 (r) 1 2 2 0 r r r r22 z 2
讨论 (r,) ,令 ( r , ) f( r )g ()
d2g() d2
2g()
0
1 r
d (r dr
df)2
dr r2
面或导体表面上的电荷一般 点电荷时,可以将导体面上感
非均匀分布的,造成电场缺 应电荷分布等效地看作一个或
乏对称性。
几个点电荷来给出尝试解。
3. 电象法概念、适用情况
电象法:
用假想点电荷来等效地 代替导体边界面上的面 电荷分布,然后用空间 点电荷和等效点电荷迭 加给出空间电势分布。
注意:
适用情况:
a) 所求区域有少许几个点电荷, 它产生的感应电荷一般可以 用假想点电荷代替。
电动力学知识的总结

第一章 电磁现象的普遍规律§1.1 电荷与电场1、库仑定律(1)库仑定律如图1-1-1所示,真空中静止电荷'Q 对另一个静止电荷Q 的作用力F 为()'3''041r r rr Q Q F --=πε (1.1.1)式中0ε是真空介电常数。
(2)电场强度E静止的点电荷'Q 在真空中所产生的电场强度E为()'3''41r r r r Q E --=πε (1.1.2)(3)电场的叠加原理N 个分立的点电荷在r 处产生的场强为()'13'0'4iNi i i r r r r Q E --=∑=πε (1.1.3)体积V 内的体电荷分布()'rρ所产生的场强为()()'3'''041r r r r dV r E V--=⎰ρπε (1.1.4)式中'r 为源点的坐标,r为场点的坐标。
2、高斯定理和电场的散度高斯定理:电场强度E穿出封闭曲面S 的总电通量等于S 内的电荷的代数和)(∑ii Q 除以0ε。
用公式表示为∑⎰=⋅iiSQS d E 01ε (分离电荷情形) (1.1.5)或⎰⎰=⋅VSdV S d E ρε01(电荷连续分布情形) (1.1.6)其中V 为S 所包住的体积,S d为S 上的面元,其方向是外法线方向。
应用积分变换的高斯公式⎰⎰⋅∇=⋅VSdV E S d E(1.1.7)由(1.1.6)式可得静电场的散度为ρε01=⋅∇E 3. 静电场的旋度由库仑定律可推得静电场E的环量为0=⋅⎰Ll d E(1.1.8)应用积分变换的斯托克斯公式⎰⎰⋅⨯∇=⋅SLS d E l d E从(1.1.8)式得出静电场的旋度为0=⨯∇E(1.1.9)§1.2 电流和磁场1、电荷守恒定律不与外界交换电荷的系统,其电荷的代数和不随时间变化。
对于体积为V ,边界面为S 的有限区域内,有⎰⎰-=⋅V S dV dtdS d J ρ (1.2.1) 或0=∂∂+⋅∇tJ ρ(1.2.2)这就是电荷守恒定律的数学表达式。
电动力学公式总结

电动力学公式总结电动力学是物理学中的一个重要分支,研究电荷在电场和磁场中的行为规律。
本文将对电动力学中常见的几个重要公式进行总结和介绍。
库仑定律库仑定律是电动力学中最基本的定律之一,描述了两个电荷之间的相互作用力的大小。
库仑定律公式如下:F=k⋅q1⋅q2 r2其中,F表示电荷间的作用力,q1和q2分别表示两个电荷的大小,r表示它们之间的距离,k是库仑常数。
电场强度电场强度描述了单位正电荷在电场中所受到的力,电场强度的大小与电场中的电荷量有关。
电场强度E与电场中的电荷q之间的关系可以用如下公式表示:E=F q其中,F为电荷所受力,q为电荷量。
高斯定律高斯定律是描述电场的一项基本定律,它规定了电场通过一个封闭曲面的电场通量与内部电荷量的比值。
高斯定律可以用如下公式表示:Φ=Q enc ε0其中,Φ表示电场通过曲面的电场通量,Q enc表示曲面内的电荷量,ε0是真空介电常数。
安培环路定理安培环路定理描述了电流在产生的磁场中所受的力。
根据安培环路定理,磁场力与电流及它们之间的关系可以用如下公式表示:F=B⋅l⋅I⋅sin(θ)其中,F表示力的大小,B表示磁场强度,l表示电流元长度,I表示电流强度,θ表示磁场与电流元之间的夹角。
洛伦兹力洛伦兹力是描述带电粒子在电场和磁场中所受合力的物理定律。
洛伦兹力F对带电粒子的加速度a描述如下:F=q(E+v×B)其中,q为电荷量,E为电场强度,v为带电粒子的速度,B为磁场强度。
以上就是电动力学中的几个重要公式的简要总结,这些公式在电场和磁场的研究中具有重要作用,有助于我们理解电荷之间、电流与磁场之间的相互作用规律。
电动力学公式总结

电动力学公式总结电动力学是物理学中研究电荷间相互作用及其相关现象的分支学科。
电动力学公式是描述电场、电势、电流、电荷等电动力学量之间关系的数学表达式。
本文将总结常见的电动力学公式,并进行简要解释。
1. 库仑定律(Coulomb's Law)库仑定律用于描述两个电荷之间的相互作用力。
假设两个电荷分别为q1和q2,它们之间的作用力F由以下公式给出:F = k * (q1 * q2) / r^2其中,k为库仑常数,r为两个电荷间的距离。
2. 电场强度(Electric Field Strength)电场强度描述在给定点附近单位正电荷所受到的力的大小和方向。
电场强度E由以下公式给出:E =F / q其中,F为单位正电荷所受的力,q为正电荷的大小。
3. 电势差(Electric Potential Difference)电势差描述电场对电荷进行的功所引起的状态变化。
电势差V由以下公式给出:V = W / q其中,W为电场对电荷进行的功,q为电荷的大小。
4. 高斯定理(Gauss's Law)高斯定理是一个描写电场线分布和电荷分布之间关系的重要定理。
它表示电场的流出和流入电荷的总和等于电荷总量除以真空介电常数ε0。
该定理由以下公式给出:∮E · dA = (1 / ε0) * Q_enclosed其中,E为电场强度,dA为微元的面积矢量,Q_enclosed为电荷的总量。
5. 法拉第电磁感应定律(Faraday's Law of Electromagnetic Induction)法拉第电磁感应定律描述通过磁场的变化引起的电场变化。
它由以下公式给出:ε = -dΦ/dt其中,ε代表感应电动势,dΦ/dt为磁通量的变化率。
6. 奥姆定律(Ohm's Law)奥姆定律描述了电流、电压和电阻之间的关系。
根据奥姆定律,电流I等于电压V与电阻R的比值,即:I = V / R其中,I为电流,V为电压,R为电阻。
电动力学必背公式

电动力学必背公式第一章 第1节1.高斯公式、格林公式、散度公式⎰⎰⋅=⋅∇v s s d A dV A )(2.斯托克斯定理l d A s d A l ⋅=⋅⨯∇⎰⎰)(s3.静电场的散度公式微分形式)(0ερ=⋅∇E 4.静电场的旋度公式积分形式)(微分形式).......(0..........0=⋅=⋅∇⎰l d E E l第一章 第2节电流和磁场1.磁场的旋度(积分形式)(微分形式)⎰=⋅=⨯⋅∇l I l d B J B .......................00μμ2.磁场的散度⎰=⋅=⋅∇l s d B B 积分形式)(微分形式)(..........0. 03.电流连续性方程=⋅∇∂∂-⋅∂∂-=⋅∇⎰⎰J dv t s d J tJ s V ρρ第一章 第3节 麦克斯韦方程组⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⋅∇=⋅∇∂∂+=⨯∇∂∂-=⨯∇磁场的高斯定律电场的高斯定理安培环路定律法拉第电磁感应定律....................................................................................000.ρερεμμD B t E J H t B E 第一章 第4节 介质的电磁性质1.麦克斯韦方程组⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⋅∇=⋅∇∂∂+=⨯∇∂∂-=⨯∇.’定律Savart -揃iot 实验规律是.相关),磁单单极子不存(描述磁场述磁场是.........0.”定律揅oulomb 关实验规律是描述电述电荷激发电场...........”定律Savart -揃iot 律是激发发磁场,相关实验描述电述电流和变化的.......”电磁感应定律Faraday?场,相关实验规律是描述变述变化的磁场激...............0B B t D J B t B B f ερM B H PE D -=+=001με2.辅助方程第一章 第5节 边值关系⎪⎪⎪⎩⎪⎪⎪⎨⎧=-⨯=-⨯=-⨯=-⨯0)(ˆ)(ˆ)(ˆ0)(ˆ12121212B B eD D e H H eE E e n n n nσα 第一章 第6节 电磁场的能量和能流1.能量守恒⎪⎪⎩⎪⎪⎨⎧⋅-=∂∂+⋅∇+⋅=⋅∇-⎰⎰⎰v f t w s wdV dt d dV v f dV s V V V 微分形式:积分形式:)( 第二章 第1节 静电场 1.电势)称为静电场标势(简称ϕϕ..........-∇=E 2.σϕεϕε-=∂∂-∂∂nn 1122 3.边值关系:21ϕϕ= 4.ερϕ-=∇25.电场能量公式静电场条件静电场条件普遍适用......)()(81.............................21.. (2)1''dVdV r x x W dV W dV D E W ⎰⎰⎰⎰==⋅=∞∞ρρπεϕρ 第二章 第2节 唯一性定理1.泊松方程:ερϕ-=∇22.边值关系:sij sij j n n ∂∂=∂∂=j ji i i ϕεϕεϕϕ或者3.边界条件:sn ∂∂ϕϕ或者s 第二章 第3节 拉普拉斯方程 分离量法1.拉普拉斯方程:ερϕϕ-=∇⇐=∇220 2.球坐标下轴对称拉普拉斯方程通解:)(cos )(n 1θϕn n n nn P R b R a ∑++= 3.球坐标下球对称拉普拉斯方程通解:Rb a +=ϕ 第二章 第6节 电多极矩点多极矩⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧↔∂⋅∂∂=⋅==∑个独立分量个分量,但只有有)()()(561614144,2j i,0230100R y x D R R P R Q j i j i πεϕπεϕπεϕ 第三章 第1节 矢势及微分方程矢势:s d B l d A s L ⋅=⋅⎰⎰第三章 第2节 磁标势 磁标势:⎰⋅=-∇=V m dV J A H 21ϕ。
电动力学_知识点总结

电动力学_知识点总结电动力学是物理学的一个重要分支,研究电荷、电场、电流、磁场等现象和它们之间的相互作用。
下面是电动力学的一些重要知识点的总结。
1.库仑定律:库仑定律描述了两个点电荷之间的力,它与它们之间的距离成反比,与它们的电荷量成正比。
该定律为电场的基础,用数学公式表示为F=k(q1*q2)/r^2,其中F是电荷之间的力,k是库仑常数,q1和q2是电荷量,r是两个电荷之间的距离。
2.电场:电场是指任何点周围的电荷所受到的力的效果。
电场可以通过电场线来表示,电场线从正电荷出发,指向负电荷。
电场线的密度表示了电场的强度,而电场线的形状表示了电场的方向。
3.电势能:电势能是指一个电荷在电场中具有的能量。
电荷在电场中移动时,会因电场做功而改变其势能。
电势能可以表示为U=qV,其中U是电势能,q是电荷量,V是电势。
4.电势:电势是一种描述电场中电场强度的物理量。
电势可以通过电势差来表示,电势差是指两个点之间的电势差异。
电势差可以表示为ΔV=W/q,其中ΔV是电势差,W是从一个点到另一个点所做的功,q是电荷量。
5.高斯定理:高斯定理是描述电场和电荷之间关系的一个重要定律。
它表明,穿过一个闭合曲面的电场通量等于该曲面内部的总电荷除以真空介电常数。
数学表达式为Φ=∮E*dA=Q/ε0,其中Φ是电场通量,E是电场强度,dA是曲面的微元面积,Q是曲面内的电荷,ε0是真空介电常数。
6. 安培定律:安培定律是描述电流和磁场之间关系的一个重要定律。
它表明,通过一个闭合回路的磁场强度等于该回路内部的总电流除以真空中的磁导率。
数学表达式为∮B * dl = μ0I,其中∮B * dl是磁通量,B是磁场强度,dl是回路的微元长度,I是回路内的电流,μ0是真空中的磁导率。
7. 法拉第定律:法拉第定律描述了电磁感应现象。
它表明,当一个导体中的磁通量发生变化时,该导体内产生的电动势与磁通量的变化率成正比。
数学表达式为ε = -dΦ/dt,其中ε是产生的电动势,dΦ是磁通量的变化量,dt是时间的微元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
垐,,AA AAA A A A===(单位矢量)在坐标系中 31i ii A Ae ==∑ 直角系 z yz A A i Aj A k =++方向余弦:cos ,cos cos cos cos x y z Ax Ay Az Ae e e A Aβγαβγ===++321(A A =+二.矢量运算加法: A B B A +=+ 交换律 ()()A B C A B C ++=++ 结合律 31()iiii A B A B e =+=+∑ 满足平行四边形法则标量积:31cos i ii A B A BAB θ=⋅==∑A B B A ⋅=⋅ 交换律()A B C A B A C ⋅+=⋅+⋅ 分配律123123123sin n e e e A B AB e A A A B B B θ⨯== ()A B C A B A C ⨯+=⨯+⨯ 分配律A B B A ⨯=-⨯ 不满足交换律 123123123()()()A A A A B C B C A C A B B B B C C C ⋅⨯=⋅⨯=⋅⨯=3乘2,点2乘3)()()A B C A B C ⨯⨯≠⨯⨯三.矢量微分ˆˆdA dA dAA A dt dt dt=+ ()A B dB dAA B dt dt dt ⋅=⋅+⋅ ()A B dB dAA B dt dt dt⨯=⨯+⨯ 四.并矢与张量并矢: AB (一般 AB BA ≠),有九个分量。
若某个量有九个分量,它被称为张量33,1,i i ijij i ji j i jT AB A B e e T e e====∑∑ i j e e 为单位并矢,矢量与张量的矩阵表示:123,i iA A Ae A A A ⎛ == ⎝∑1211223(,B AB A A A B A B A B ⎛⎫==++T AB = T T T T ⎛ = ⎝单位张量:31i j i e e ==∑0100 = ⎝,i j()()()()AB C A B C A C B AC BC B A C BAB C A B CA⋅=⋅=⋅=⋅=⋅=⋅=⋅=⋅()()()C AB C A B B C A B A C BA C ⋅=⋅=⋅=⋅=⋅与矢量叉乘:()()AB C A B C C AB C A B ⎧⨯=⨯⎪⎨⨯=⨯⎪⎩并矢并矢两并矢点乘:()()()AB CD A B C D A B C AD CD AB ⋅=⋅=⋅≠⋅ (并矢) 两并矢二次点乘: ()():AB CD B C A D =⋅⋅ 标量与单位张量点乘:C C C ⋅=⋅=AB AB AB ⋅=⋅=:AB A B =⋅15-20分钟))()A B A B +⨯- ()()2B A =⨯ ()()M b a c a b c =⋅-⋅与矢量C 垂直。
(求M C ⋅)。
计算下列各式:()a a b ⋅⨯ ⑵ ()a b a ⨯⨯ ⑶ ()j i k ⨯⋅ ⑷ ()k i j ⨯⋅, 2()a b a a b -⋅, -1, 1)证明下列各式:()()()()()()a b c d a c b d a d b c ⨯⋅⋅=⨯⋅-⨯⋅()()()0a b c b c a c a b ⨯⨯+⨯⨯+⨯⨯=证: ⑴ ()()[()]a b c d c d a b ⨯⋅⋅=⨯⨯ [()()]()()()()()()()()c d b a d ab b c a d b c b d a a c b d b c a d=⋅⋅-⋅=⋅⋅-⋅⋅=⋅⋅-⋅⋅⑵ ()()()a b c b c a c a b ⨯⨯+⨯⨯+⨯⨯()()()()()()0a cb a bc b a c b c a c b a c a b =⋅-⋅+⋅-⋅+⋅-⋅=描述场用一个空间中和时间坐标的函数:(,,,)(,)(,,,)(,)x y z t x t A x y z t A x t ϕϕ==⎪⎩矢量场 A 与t 无关时称为稳恒场(稳定场、静场),有关则称为变化场(时变场)。
当已知场函数则可以了解场的各种性质:A 随时空的变化关系(梯、散、旋度)。
同样已知梯、散、旋度场函数可以确定场函数(以后主要讨论的问题)。
二、标量场的梯度dz zϕx y z dxe dye dze =++x y z e e e d d xy z ϕϕϕ⎡⎤∂∂∂=++⋅=∇⋅⎢⎥∂∂∂⎣⎦l d e dϕϕ=∇⋅ (d e d =,d 方向上的单位矢量) cos ϕθ=∇ (θ为ϕ∇与d 之间的夹角)在M 点方向上导致有无穷多个,其中有一个最大,即max0,d d ϕθϕ⎛⎫==∇⎪⎝⎭, 定义梯度 grad ϕ=意义:空间某点上标量场函数的最大变化率,刻画了标量场的空间分布特征。
已知梯度即可求出沿任一方向的方向导致。
()x =常数的曲面称为等值面。
xy z e e e x y z ∂∂∂++∂∂∂ 具有矢量性质,分量是微分符号。
xy z e e e x y zϕϕϕ∂∂∂=++∂∂∂ , ∇它可以作用在矢量上,可以作点乘、叉乘。
()x x y z x x y y z z A A e e e e A e A e A xy z x ⎛⎫∂∂∂∂=++⋅++=+ ⎪∂∂∂∂⎝⎭y y x x z z x y z A A A A A A A e e e y z z x x y ∂∂⎛⎫⎛⎫∂∂∂∂⎛⎫∇⨯=-+-+-⎪ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭ x y z xyze e e x y z A A A ∂∂∂=∂∂∂ r 的数值(r r x x ⎡==-⎣点均可变动。
一般称P '为源点(一后电场中电荷所在点)为场点(观测点)。
解:固有两个变量(),x y 和(,,x y z ''112()2r x x x x x r'∂-'=⋅-∂ 而r z ∂xy z x x y y z z rr e e e r r r r'''---∴∇++= (2)求 )ϕψ∇。
解:(x ϕψ∂∂(ϕψ∂∂)x y z x y z e e e e e e x y z x y z ψψψϕϕϕϕψϕψϕ⎛⎫⎛⎫∂∂∂∂∂∂=+++++=∇ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭§3. 高斯定理与矢量场的散度矢量场的通量矢量族:在矢量场中对于给定的一点,有一个方向,它沿某一曲线的无穷多条这样的曲线构成一个矢量族。
A ds ⋅称为A 通过面元ds 的通量,记作A ds ⋅,记作A ds ⋅,有限面积S ,通量上SA ds Φ=⋅⎰,闭合曲面S ,通量上SA ds ⋅⎰,ds 方向,由面内指向面外。
>0Φ, 场线进入的少,穿出得多,称S 面内有源。
=0Φ, 场线进入的与穿出得同样多,称S 面内无源。
<0Φ, 场线进入的少,穿出得少,称S 面内有负源。
意义: 用来描述空间某一范围内场的发散或会聚,它只具有局域性质,不能反映空间一点的情况。
二、高斯定理 S V V A A ds AdV ⎛⎛∂⋅=∇⋅= ∂⎝⎝⎰⎰⎰⎰⎰一种面积分与体积分的变换关系,有时称为高斯公式(证明略)三、矢量场的散度为了反映空间某一点发散与会聚的情况,可以将面缩小到体元体元仅包围一个点,此时,高斯定理可以改为SA ds A V ⋅=∇⋅∆⎰SA ds A V⋅=∆⎰,取0limSV A ds A V∆→⋅=∆⎰称为矢量A 的散度。
(>0, 有源;=0,无源,<0,源)。
有时表示成divA (divergence )。
若空间各点处处0A ∇⋅=,则称A 为无源场。
例题:1. 求r ∇⋅,其中()()()x y z r x x e y y e z z e '''=-+-+- 3xr x∂∇⋅=-=∂3r r,()()()12222(0)r x x y y z z r ⎡⎤'''=-+-+-≠⎣⎦333r x x y y z z r x r y r '''∂-∂-∂-⎛⎫⎛⎫⎛⎫=+ ⎪ ∂∂⎝⎭⎝(330x x r r r r+-=⎣⎦⎣()A A A ϕϕϕ=∇⋅+∇⋅。
)()()(xyA A A A x y zϕϕϕ∂∂∂=++∂∂∂y z x y A A A A A y z x y z ϕϕϕ∂⎤∂∂∂∂++++⎥∂∂∂∂∂⎦A A ϕ+∇⋅矢量场的环量(环流)A 沿任一闭合曲线LA dl ⋅⎰0Γ=表明在区域内无涡旋状态,不闭合, 0Γ≠表明在区域内有涡旋状态存在,闭合,意义:用来刻画矢量场在空间某一范围内是否有涡旋存在,二、斯托克斯公式(定理)()LSA dl A dS ⋅=∇⨯⋅⎰⎰ (证明略)三、矢量场的旋度当L 无限缩小,它用的面积化为S ∆时,()()LnA dl A S A S ⋅=∇⨯⋅∆=∇⨯∆⎰, (∇⨯()limLnS A dl A S∆→⋅∇⨯=∆⎰S Sn ∆=∆,n 为法线上单位矢。
定义A ∇⨯为矢量场的旋度,它在S ∆法线方向上的分量为单位面积上的环量。
刻画矢量场场线在空间某点上的环流特征。
若空间各点0A ≡,则A 称为无旋场。
1. 3rr ∇⨯它的x 分量为z z y y r '∂-∂⎛⎫⎛- ⎪ ∂⎝(3z z '-⎫=-⎪⎭x ⎦y r ⎣⎦)A A A ϕϕ=∇⨯+∇)()()z y xA A A y zϕϕ∂∂⎤=-⎦∂∂ y z y A A A y z zϕϕϕ∂∂∂+--∂∂∂ )xAA y ϕ∂+∂()x A e ϕ∇⨯A A ϕ+∇⨯§5. 常用的运算公式复合函数的“三度”运算公式()dA A u u du =⋅∇, ()A u u ∇⨯=∇SVVA ds AdV dV A ⋅=∇⋅=∇⋅⎰⎰⎰斯托克斯公式:()()LSSA dl A dS dS A ⋅=∇⨯⋅=⨯∇⋅⎰⎰⎰)2SdV dS ψϕϕψψϕ∇+∇⋅∇=∇⋅⎰)()22SdV dS ψϕϕψψϕϕψ∇-∇=∇-∇⋅⎰SL dV dSdS dl ∇↔⨯∇↔⎰⎰T T S S S dV dSdV A dS A dV dS ϕϕ∇=∇⨯=⨯∇⋅=⋅⎰⎰⎰()()T V S SdS A dS ⎧⎪⎪⨯∇⨯=⎨⎪⨯∇⋅=⎪⎩⎰⎰⎰T T SdS =⨯⎰()T SdS ⨯∇⨯=⎰一般变换规则证明: SA dS A =⨯⎰任取常矢量C 点乘上式两端 ()()V C A dV A C ⎤⎡⎤⋅∇⨯=∇⋅⨯⎦⎣⎦⎰ 用)()()A B A B A B ⨯=∇⨯⋅-⋅∇⨯()()SS dS A C C dS A ⋅⨯=⋅⨯⎰⎰ 用混合积公式()SLdS A dl A ⨯∇⨯=⨯⎰⎰证: 左()()()SSC dS A dS A C ⎡⎤=⋅⨯∇⨯=⨯∇⋅⨯⎣⎦⎰⎰ ()()LLA C dl C dl A =⨯⋅=⋅⨯⎰⎰三.∇算符常用公式()()ϕψϕψϕψ∇=∇+∇()A A A ϕϕϕ∇⋅=∇⋅+∇⋅()A A A ϕϕϕ=∇⨯+∇⨯)()()A B A B B A ⨯=∇⨯⋅-∇⨯⋅ )()()AB A B A B =∇⋅-⋅∇()()()()()A B B A B A A B A B ⨯=∇⋅+⋅∇-∇⋅-⋅∇()()()(A B A B A B B ∇⋅=⨯∇⨯+⋅∇+⨯∇⨯()()212A A A A A ⨯∇⨯=∇-⋅∇()()2A A A ∇⨯∇⨯=∇∇⋅-∇ 10. ()0,0A ϕ∇⨯∇=∇⋅∇⨯=证:()()()C C A B A B A B ∇⨯⨯=∇⨯⨯+∇⨯⨯ 微分运算()()()C C A B A B A B ∇⨯⨯=∇⨯⨯+∇⨯⨯ 去掉角标。
