14种布拉菲格子
14种布拉维格子和球体紧密堆积

实验一14种布拉维格子和球体紧密堆积一、实验目的加深对14种布拉维格子和球体紧密堆积原理的理解。
二、基本原理1、布拉维格子只在单位平行六面体的八个角顶上分布有结点的空间格子,称为原始格子(Primitive lattice,符号P),在单位平行六面体的体中心还有一个结点时,则构成体心格子(Body-centered lattice,,符号I)。
如果在某一对面的中心上各有一个结点时,称为单面心格子(One-face-centered lattice)(001)面上有心的格子为底心格子或称为C心格子(End-centered , Based-centered lattice or C-centered lattice,符号C)当(100)面或(010)面上有心是,分别称为A心格子(A-centered lattice,符号A)和B心格子(B-centered lattice,符号B)如果在所有的三对面的中心都有结点时,称为面心格子或全面心格子(Face-centered lattice or All-faced-centered lattice,符号F)。
符合对称特点和选择原则的格子共有7种类型,共计14种不同形式的空间格子,即通常所称的14种布拉维格子(The fourteen Bravais space lattices),如下图所示。
布拉维格子是空间格子的基本组成单位,只要知道了格子形式和单位平行六面体参数后,就能确定整个空间格子的一切特征。
2、球体紧密堆积原子核离子都具有一定的有效半径,可以看作是具有一定大小的球体。
金属晶体和离子晶体中的金属键和离子键没有方向性和饱和性,因此金属原子之间或离子之间相互结合,再形式上可以看作是球体间的相互堆积。
由于晶体具有最小的内能性,原子核离子相互结合时,彼此间的引力和斥力达到平衡状态,相当于要求球体间做紧密堆积。
最紧密堆积的方式有两种,一种是六方最紧密堆积(Cubic closest packing,缩写为CCP),最紧密排列层平行于{0001},可以用ABABAB……顺序来表示,如下图所示:另一种是立方最紧密堆积(Hexagonal closest packing,缩写为HCP),最紧密排列层平行于{111},可以用ABCABCABC……顺序表示,如下图所示:自然铜、自然金、自然铂等矿物的晶体结构属于立方最紧密堆积方式。
14种布拉维格子
14种布拉维格子之十:正交C心 oC(或 oA, oB)
请 点 击 按 钮 打 开 晶 格 模 型
14种布拉维格子之十一:正交面心(oF)
请 点 击 按 钮 打 开 晶 格 模 型
14种布拉维格子之十二:单斜简单(mP)
请点击按钮打开晶格模型
14种布拉维格子之十三:单斜C心(mC)
请点击按钮打开晶格模型
14种布拉维格子二:立方体心(cI)
请点击按钮打开晶格模型
14种布拉维格子三:立方面心(cF)
请点击按钮打开晶格模型
14种布拉维格子之四:
四方简单(tP)
请点击按钮打开晶格模型
14种布拉维格子之五: 四方体心(tI)
请点击按钮打开晶格模型
14种布拉维格子之六:六方简单(hP)
黑色与灰白色点 都是点阵点.黑点 与蓝线表示一个 正当格子
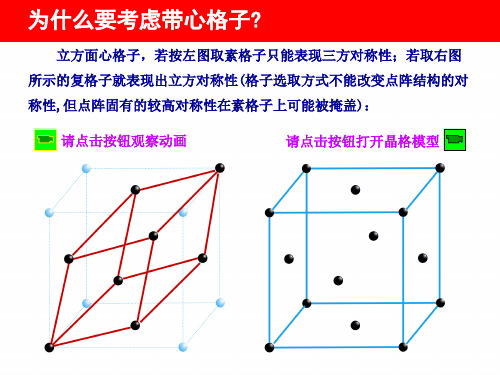
为什么要考虑带心格子?
立方面心格子,若按左图取素格子只能表现三方对称性;若取右图
所示的复格子就表现出立方对称性(格子选取方式不能改变点阵结构的对 称性,但点阵固有的较高对称性在素格子上可能被掩盖): 请点击按钮观察动画
请点击按钮打开晶格模型
14种布拉维格子之一:立பைடு நூலகம்简单(cP)
请点击按钮打开晶格模型
14种布拉维格子之十四:三斜简单 (aP)
请点击按钮打开晶格模型
晶系的六方简单 (hP)格子相同(即hR是两个晶系共用的), 但真实的三方晶体中只
有三次对称轴而没有六次对称轴, 六方晶体才有六次对称轴.
14种布拉维格子之八:正交简单(oP)
请 点 击 按 钮 打 开 晶 格 模 型
14种布拉维格子之九:正交体心(oI)
请 点 击 按 钮 打 开 晶 格 模 型
空间点阵

-空间点阵空间点阵到底有多少种排列形式?按照“每个阵点的周围环境相同”的要求,在这样一个限定条件下,法国晶体学家布拉菲(A. Bravais)曾在1848年首先用数学方法证明,空间点阵只有14种类型。
这14种空间点阵以后就被称为布拉菲点阵。
空间点阵是一个三维空间的无限图形,为了研究方便,可以在空间点阵中取一个具有代表性的基本小单元,这个基本小单元通常是一个平行六面体,整个点阵可以看作是由这样一个平行六面体在空间堆砌而成,我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时,只需选取其中一个单胞来研究即可。
在同一空间点阵中,可以选取多种不同形状和大小的平行六面体作为单胞,如图1-8所示。
一般情况下单胞的选取有以图1-8 空间点阵及晶胞的不同取法图1-9面心立方阵胞中的固体物理原胞图1-10晶体学选取晶胞的原则下两种选取方式:1.固体物理选法在固体物理学中,一般选取空间点阵中体积最小的平行六面体作为单胞,这样的单胞只能反映其空间点阵的周期性,但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征,如图1-9所示。
2.晶体学选法由于固体物理单胞只能反映晶体结构的周期性,不能反映其对称性,所以在晶体学中,规定了选取单胞要满足以下几点原则(如图1-10所示):①要能充分反映整个空间点阵的周期性和对称性;②在满足①的基础上,单胞要具有尽可能多的直角;③在满足①、②的基础上,所选取单胞的体积要最小。
根据以上原则,所选出的14种布拉菲点阵的单胞(见图1-12)可以分为两大类。
一类为简单单胞,即只在平行六面体的 8个顶点上有结点,而每个顶点处的结点又分属于 8个相邻单胞,故一个简单单胞只含有一个结点。
另一类为复合单胞(或称复杂单胞),除在平行六面体顶点位置含有结点之外,尚在体心、面心、底心等位置上存在结点,整个单胞含有一个以上的结点。
14种布拉菲点阵中包括7个简单单胞,7个复合单胞。
图1-11 单晶胞及晶格常数根据单胞所反映出的对称性,可以选定合适的坐标系,一般以单胞中某一顶点为坐标原点,相交于原点的三个棱边为X、Y、Z三个坐标轴,定义X、Y轴之间夹角为γ,Y、Z之间夹角为α,Z、X轴之间夹角为β,如图1-11所示。
十四种不拉维格子

正交体心格子(P)
属于正交晶系,单位平行六面体为长、宽、高都不等的长方体,单位平行六面体参数为:a0 ≠ b0 ≠ c0 α=β=γ=90°
下载
正交底心格子(Q)
属于正交晶系,单位平行六面体为长、宽、高都不等的长方体,单位平行六面体参数为:a0 ≠ b0 ≠ c0 α=β=γ=90°
下载
正交面心格子(S)
下载
四方原始格子(T)
属于四方晶系,单位平行六面体为横截面为正方形的四方柱。规定柱面相交的棱c0,单位平行六面体参数为:a0 = b0 = c0 α=β=γ= 90°
下载
四方体心格子(U)
属于四方晶系单位平行六面体为横截面为正方形的四方柱。规定柱面相交的棱c0,单位平行六面体参数为:a0 = b0 = c0 α=β=γ= 90°
下载
三斜原是格子(Z)
单斜平行六面体是三条棱不相等,三对面互相间不垂直的斜平行六面体。单位平行六面体参数为:a0 ≠ b0 ≠ c0,α≠β≠γ≠900
下载
单斜原始格子(M)
单位平行六面体的三对面中有两对是矩形,另一对是非矩形。两对矩形平面都垂直于非矩形平面,而它们之间的夹角为β,但∠β≠90°。a0≠b0≠c0,α=γ=90°,β≠90°
下载
立方和三方原始格子(H)
对应于六方晶系的空间六方格子。单位平行六面体底面为菱形的柱体。菱形交角为60o和120 o,如果把三个单位平行六面体拼起来,底面就成六边形,柱面的交棱就是六次轴方向。单位平行六面体参数为:a0≠b0≠c0,α=β=90 o,γ=120 o
下载
三方菱面体格子(R)
属于三方晶系,单位平行六面体相当于立方体在4L3中的一个L3方向被拉长或压缩,使立方体变成菱面体。单位平行六面体参数为:a0 = b0 = c0 α=β=γ≠90°、60°、109°28′16″
布拉菲点阵

关于奥古斯特·布拉菲及布拉菲点阵浅析奥古斯特·布拉菲(August Bravais,1811—1863),法国物理学家,于1845年推导出了三维晶体原子排列的所有14种点阵结构,首次将群的概念应用到物理学,为固体物理学做出了重大贡献。
这是非常有意义的结论,为了纪念他,后人称这14种点阵为布拉菲点阵。
除此之外,布拉菲还对磁性、极光、气象、植物地理学、天文学和水文学等方面进行过研究。
图1 奥古斯特·布拉菲在几何学以及晶体学中,布拉菲晶格(又译布拉菲点阵)是为了纪念奥古斯特·布拉维在固态物理学的贡献命名的。
法国晶体学家布拉菲(A.Bravais)于1850年用数学群论的方法推导出空间点阵只能有十四种: 简单三斜、简单单斜、底心单斜、简单正交、底心正交、体心正交、面心正交、简单六方、简单菱方、简单四方、体心四方、简单立方、体心立方、面心立方。
根据其对称特点,它们分别属于七个晶系。
空间点阵到底有多少种排列形式?按照“每个阵点的周围环境相同”的要求,在这样一个限定条件下,法国晶体学家布拉菲(A. Bravais)曾在1848年首先用数学方法证明,空间点阵只有14种类型。
这14种空间点阵以后就被称为布拉菲点阵。
空间点阵是一个三维空间的无限图形,为了研究方便,可以在空间点阵中取一个具有代表性的基本小单元,这个基本小单元通常是一个平行六面体,整个点阵可以看作是由这样一个平行六面体在空间堆砌而成,我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时,只需选取其中一个单胞来研究即可。
在同一空间点阵中,可以选取多种不同形状和大小的平行六面体作为单胞,如下图所示:其选取方式有,1.固体物理选法:在固体物理学中,一般选取空间点阵中体积最小的平行六面体作为单胞,这样的单胞只能反映其空间点阵的周期性,但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征。
2.晶体学选法:由于固体物理单胞只能反映晶体结构的周期性,不能反映其对称性,所以在晶体学中,规定了选取单胞要满足以下几点原则:①要能充分反映整个空间点阵的周期性和对称性;②在满足①的基础上,单胞要具有尽可能多的直角;③在满足①、②的基础上,所选取单胞的体积要最小。
布拉维格子
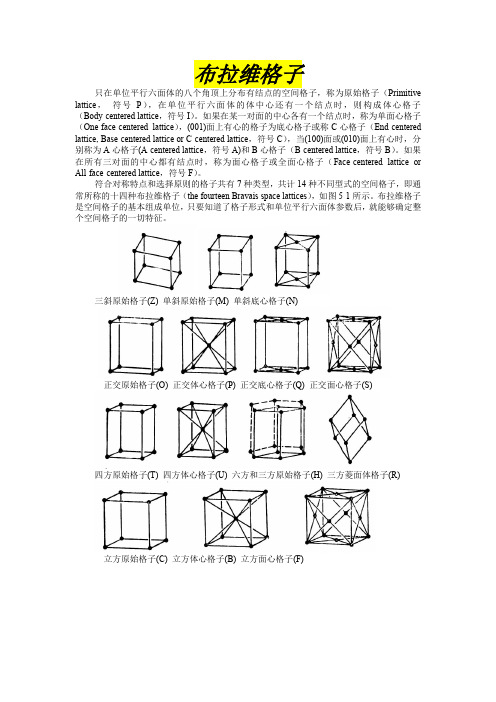
布拉维格子
只在单位平行六面体的八个角顶上分布有结点的空间格子,称为原始格子(Primitive lattice,符号P),在单位平行六面体的体中心还有一个结点时,则构成体心格子(Body-centered lattice,符号I)。
如果在某一对面的中心各有一个结点时,称为单面心格子(One-face-centered lattice),(001)面上有心的格子为底心格子或称C心格子(End-centered lattice, Base-centered lattice or C-centered lattice,符号C),当(100)面或(010)面上有心时,分别称为A心格子(A-centered lattice,符号A)和B心格子(B-centered lattice,符号B)。
如果在所有三对面的中心都有结点时,称为面心格子或全面心格子(Face-centered lattice or All-face-centered lattice,符号F)。
符合对称特点和选择原则的格子共有7种类型,共计14种不同型式的空间格子,即通常所称的十四种布拉维格子(the fourteen Bravais space lattices),如图5-1所示。
布拉维格子是空间格子的基本组成单位,只要知道了格子形式和单位平行六面体参数后,就能够确定整个空间格子的一切特征。
三斜原始格子(Z) 单斜原始格子(M) 单斜底心格子(N)
正交原始格子(O) 正交体心格子(P) 正交底心格子(Q) 正交面心格子(S)
四方原始格子(T) 四方体心格子(U) 六方和三方原始格子(H) 三方菱面体格子(R)
立方原始格子(C) 立方体心格子(B) 立方面心格子(F)。
!七大晶系十四种布喇菲格子

晶系
晶胞基矢的 特性
布喇菲 格子
所属点群
三斜晶系
简单三斜
单斜晶系
简单单斜 底心单斜
01_07_晶格的对称性 —— 晶体结构
正交晶系 三角晶系
简单正交 底心正交 体心正交 面心正交
三角
01_07_晶格的对称性 —— 晶体结构
四方晶系 六角晶系 立方晶系
简单四方 体心四方
六角
简单立方 体心立方 面心立方
01_07_晶格的对称性 —— 晶体结构
9) 简单四方(四角) 10) 体心四方(四角)
01_07_晶格的对称性 —— 晶体结构
11) 六角
01_07_晶格的对称性 —— 晶体结构
12) 简立方 13) 体心立方 14) 面心立方
01_07_晶格的对称性 —— 晶体结构
七大晶系的布喇菲格子、晶胞和所属点群
立方 三角
四方
正交
三斜
按晶胞个点分布特点分为14种布喇菲原胞 1) 简单三斜
01_07_晶格的对称性 —— 晶体结构
2) 简单单斜 3) 底心单斜
01_07_晶格的对称性 —— 晶体结构
4) 简单正交 5) 底心正交 6) 体心正交 7) 面心正交
01_07_晶格的对称性 —— —— 晶体结构
底心立方?=简单四方
底心四方=简单四方
01_07_晶格的对称性 —— 晶体结构
体心四方与面心四方等价
01_07_晶格的对称性 —— 晶体结构
§1.7 晶格的对称性
—— 32种点群描述的晶体对称性 —— 对应的只有14种布喇菲格子 —— 分为7个晶系
—— 晶胞的三个基矢
沿晶体的对称轴或对称面
的法向,在一般情况下,它们构成斜坐标系
第一章结晶学基础-1.3.1十四种布拉维点阵_6.14ZSQ

材料科学基础第1 章1.3.1 十四种布拉维点阵十四种布拉维点阵一、单位平行六面体的选取二、十四种布拉维点阵三、晶胞空间点阵的划分 空间点阵是一个由无限多结点在三维空间作有规则排列的图形。
整个空间点阵就被这些平行线分割成多个紧紧地排列在一起的平行六面体有缘学习更多驾卫星ygd3076或关注桃报:奉献教育(店铺)单位平行六面体的 选取原则 3.大小原则体积最小 1 对称性原则应能反映空间点阵对称性 2 角度原则 直角关系尽可能多4 对称性规定夹角不为直角 结点间距最小的行列做棱,夹角最接近直角的平行六面体二维平面点阵的划分(A)具有L44P的平面点阵;(B)具有L22P的平面点阵单位平行六面体在空间点阵中,选取出来的能够符合这几条原则的平行六面体称为单位平行六面体;可以用三条互不平行的棱a、b、c和棱间夹角α、β、γ来描述,如下图所示。
点阵常数棱a、b、c和棱间夹角α、β、γ的大小称为点阵常数。
晶体的点阵常数十四种布拉维点阵(格子)简单(原始)点阵(格子)(P) 结点分布在角顶,每个点阵包含一个结点体心点阵(格子)(I)结点分布在角顶和体心,每个点阵包含二个结点十四种布拉维点阵(格子)面心点阵(格子)(F) 结点分布在角顶和面心,每个点阵包含四个结点单面心点阵(格子)(A/B/C) 结点分布在角顶和一对面心,每个点阵包含2个结点根据布拉维推导,从一切晶体结构中抽象出来的空间点阵,按上述原则来选取平行六面体,只能有14种类型,称为14种布拉维点阵。
十四种空间点阵正交P(简单) C(底心) I(体心) F(面心) 点阵常数 a ≠ b ≠ cα= β= γ= 90°立方简单立方(P) 体心立方(I)面心立方(F)点阵常数 a =b =cα= β= γ= 90°如图立方为什么没有底心呢?假如有底心,将破坏立方的3L 4的对称性,只有1L 4。
立方三方(R ) 90120≠<====γβαc b a 点阵常数:六方(H )12090===≠=γβαcb a 点阵常数: 四方(P ) 四方(I )90===≠=γβαc b a 点阵常数:四方也不可能有底心,假如有,则破坏了“点阵点最少”的条件,还可画出只有一个点阵点的格子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简单正交
底心正交
体心正交
面心正交
简单六方
三方菱面体
简单四方
体心四方
简单立方
体心立方
面心立方
为什么没有面心四方?
•
1、有时候读书是一种巧妙地避开思考 的方法 。20.1 2.1020. 12.10Thursday, December 10, 2020
•
2、阅读一切好书如同和过去最杰出的 人谈话 。00:3 7:2900: 37:2900 :3712/ 10/2020 12:37:29 AM
•
3、越是没有本领的就越加自命不凡。 20.12.1 000:37: 2900:3 7Dec-20 10-Dec-20
•
4、越是无能的人,越喜欢挑剔别人的 错儿。 00:37:2 900:37: 2900:3 7Thursday, December 10, 2020
•
5、知人者智,自知者明。胜人者有力 ,自胜 者强。 20.12.1 020.12. 1000:3 7:2900: 37:29D ecembe r 10, 2020
• 13、无论才能知识多么卓著,如果缺乏热情,则无异 纸上画饼充饥,无补于事。Thursday, December 10, 202
010-Dec-2020.12.10
• 14、我只是自己不放过自己而已,现在我不会再逼自 己眷恋了。20.12.1000:37:2910 December 202000:37
2020 12:37:29 AM00:37:292020/12/10
• 11、自己要先看得起自己,别人才会看得起你。12/10/
谢 谢 大 家 2020 12:37 AM12/10/2020 12:37 AM20.12.1020.12.10
• 12、这一秒不放弃,下一秒就会有希望。10-Dec-2010 December 202020.12.10
•
8、业余生活要有意义,不要越轨。20 20年12 月10日 星期四 12时37 分29秒 00:37:2 910 December 2020
•
9、一个人即使已登上顶峰,也仍要自 强不息 。上午 12时37 分29秒 上午12 时37分 00:37:2 920.12. 10
• 10、你要做多大的事情,就该承受多大的压力。12/10/
•
6、意志坚强的人能把世界放在手中像 泥块一 样任意 揉捏。 2020年 12月10 日星期 四上午 12时37 分29秒 00:37:2 920.12. 10
•
7、最具挑战性的挑战莫过于提升自我 。。20 20年12 月上午 12时37 分20.1 2.1000: 37Dece mber 10, 2020
