专题13 圆的基本性质(解析版)
圆的基本性质知识点及典型例题
圆的基本性质知识点及典型例题辅导学案：圆的基本性质一、知识点梳理1.圆的定义及有关概念圆是平面内到定点的距离等于定长的所有点组成的图形。
圆的一些相关概念包括弦、直径、弧、等弧、优弧、劣弧、半圆、弦心距、等圆、同圆、同心圆等。
在同圆或等圆中，能够重合的两条弧叫做等弧。
2.平面内点与圆的位置关系圆的半径为r，同一平面内点到圆心的距离为d，点与圆的位置关系可以分为在圆外、在圆上和在圆内三种情况。
二、例题解析例1：如图，在Rt△ABC中，直角边AB=3，BC=4，点E，F分别是BC，AC的中点，以点A为圆心，AB的长为半径画圆，则点E在圆A的内部，点F在圆A的上方。
例2：在直角坐标平面内，圆O的半径为5，圆心O的坐标为(-1,-1)，点P(3,-4)。
判断点P与圆O的位置关系。
例3：下列说法中，正确的是：直径是弦，但弦不一定是直径；半圆是弧，但弧不一定是直径；半径相等的两个半圆是等弧；一条弦把圆分成两段弧中，至少有一段优弧。
例4：有下列四个命题：直径相等的两个圆是等圆；长度相等的两条弧是等弧；圆中最大的弦是通过圆心的弦；一条弦把圆分成两条弧，这两条弧不可能是等弧。
其中真命题是直径相等的两个圆是等圆。
三、垂径定理及应用垂径定理指出，垂直于弦的直径平分这条弦，并且平分弦所对的弧。
平分弦的直径垂直于这条弦，并且平分弦所对的弧。
垂径定理最重要的应用是通过勾股定理来解决有关弦、半径、弦心距等问题。
例1：下列语句中正确的是：相等的圆心角所对的弧相等；相等的弧所对的弦相等；平分弦的直径垂直于弦；弦的垂直平分线必过圆心。
例2：过圆内一点M的最长弦长为10cm，最短弦长为8cm，那么OM的长为9cm。
例3：如图所示，以O为圆心的两个同心圆中，小圆的弦AB的延长线XXX圆于C，若AB=6，BC=1，则与圆环的面积是π(26-3)。
例4：在半径为5厘米的圆内有两条互相平行的弦，一条弦长为8厘米，另一条弦长为6厘米，则两弦之间的距离为1厘米。
圆的基本性质(解析版)2018年数学全国中考真题-2
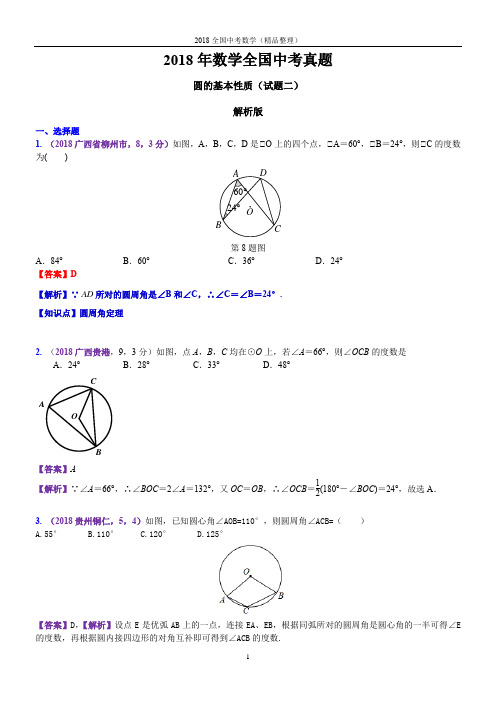
2018年数学全国中考真题圆的基本性质（试题二）解析版一、选择题1. （2018广西省柳州市，8，3分）如图，A ，B ，C ，D 是⊙O 上的四个点，⊙A ＝60°，⊙B ＝24°，则⊙C 的度数为( )第8题图 A ．84° B．60°C ．36°D ．24°【答案】D【解析】∵AD 所对的圆周角是∠B 和∠C ，∴∠C ＝∠B ＝24°.【知识点】圆周角定理2. （2018广西贵港，9，3分）如图，点A ，B ，C 均在⊙O 上，若∠A ＝66°，则∠OCB 的度数是 A ．24° B ．28° C ．33° D ．48°【答案】A【解析】∵∠A ＝66°，∴∠BOC ＝2∠A ＝132°，又OC ＝OB ，∴∠OCB ＝12(180°－∠BOC )＝24°，故选A ．3. （2018贵州铜仁，5，4）如图，已知圆心角∠AOB=110°，则圆周角∠ACB=（ ） A.55° B.110° C.120° D.125°【答案】D ，【解析】设点E 是优弧AB 上的一点，连接EA 、EB ，根据同弧所对的圆周角是圆心角的一半可得∠E 的度数，再根据圆内接四边形的对角互补即可得到∠ACB 的度数.【解答过程】设点E 是优弧AB 上的一点，连接EA 、EB ，如图， ∵∠AOB=110°，∴∠AEB=12∠AOB=55°，∴∠ACB=180°-∠E=125°.4. （2018江苏苏州，7，3分）如图，AB 是半圆的直径，O 为圆心，C 是半圆上的点，D 是AC 上的点．若∠BOC＝40°，则∠D 的度数为 A ．100° B ．110°C ．120°D ．130°【答案】B【解析】 本题解答时要利用等腰三角形的性质和圆的内接四边形的对角互补的性质进行计算.∵OC =OB ，∠BOC =40゜，∴∠B =70゜，∴∠D =180゜-70゜=110゜，故选B .5. （2018内蒙古通辽，7，3分）已知⊙O 的半径为10，圆心O 到弦AB 的距离为5，则弦AB 所对圆周角的度数是 A ．30° B ．60° C ．30°或150° D ．60°或120° 【答案】D【解析】如答图，连接OA 、OB ，∵OC ⊥AB ，∴OC ＝5，OA ＝OB ＝10，又OC ＝12OA ，∴cos ∠AOC ＝12，∴∠AOC ＝60°∴∠AOB ＝120°，∴弦AB 所对的圆周角的度数是60°或120°． 故选D ．6.（湖北省咸宁市，7，3）如图，已知⊙O 的半径为5，弦AB ，CD 所对的圆心角分别为∠AOB ，∠COD ，若∠AOB 与∠COD 互补，弦CD =6，则弦AB 的长为( )A ．6B ．8 C． D．【答案】【解析】解：作OF ⊥AB 于F ，作直径BE ，连接AE ，如图， ∵∠AOB+∠COD=180°， 而∠AOE+∠AOB=180°， ∴∠AOE=∠COD ， ∴AE DC ，∴AE=DC=6，∵OF ⊥AB ， ∴BF=AF ， 而OB=OE ，∴OF 为△ABE 的中位线， 由勾股定理可得AF=4，∴AB=8，故选择B ．【知识点】圆周角定理；垂径定理；三角形中位线性质7. (2018湖北黄石，8，3分)如图，AB 是⊙O 的直径，点D 为⊙O 上一点，且∠ABD ＝30°，BO ＝4，则BD 的长为( )第8题图A ．23πB ．43πC ．2πD ．83π FE【答案】D 【解析】连接OD ，则∠AOD ＝2∠B ＝60°，∴∠BOD ＝120°.∴l BD ＝120180π×4＝83π.8. (2018湖南邵阳，6，3分)如图(二)所示，四边形ABCD 为⊙O 的内接四边形，∠BCD ＝120°，则∠BOD 的大小是( )A ．80°B ．120°C ．100°D ．90°图(二)【答案】B ，【解析】根据“圆内接四边形的对角互补”可得∠BCD ＋∠A ＝180°，因为∠BCD ＝120°所以∠A ＝60°．又根据“在同圆中，同弧所对的圆心角等于圆周角的2倍”，所以∠BOD ＝2∠A ＝120°．故选B ．9.（2018四川眉山，6，3分）如图所示，AB 是⊙O 的直径，P A 切⊙O 于点A ，线段PO 交⊙O 于点C ，连结BC ，若∠P ＝36°，则∠B 等于（ ）A ．27°B ．32°C ．36°D ．54°【答案】A ，【解析】由P A 是⊙O 的切线，可得⊙OAP ＝90°，∴∠AOP ＝54°，根据同弧所对的圆周角等于圆心角的一半，可得∠B ＝27°10. （2018辽宁锦州，7，3分）如图：在△ABC 中，∠ACB=90°，过B 、C 两点的⊙O 交AC 于点D ，交AB 于点E ，连接EO 并延长交⊙O 于点F ，连接BF 、CF ，若∠EDC=135°，CF=22，则AE 2+BE 2的值为A 、8B 、12C 、16D 、20D【答案】C，【解析】：如图，∠EDC=1350，∠ACB=90°，得△ACB是等腰直角三角形，ECF是等腰直角三角形，得△AEC与△BFC是全等三角形，AE=BF,△EBF是直角三角形，AE2+BE2=FE2=2FC2.二、填空题100，则弧AB所对的圆周角是°.1.（2018广东省，11，3）同圆中，已知弧AB所对的圆心角是【答案】50°【解析】同弧所对的圆周角是圆心角的一半，圆心角为100°，所以圆周角为50°.【知识点】圆周角、圆心角关系2. （2018海南省，18，4分）如图，在平面直角坐标系中，点A 的坐标是（20，0），点B 的坐标是（16，0），点C ， D 在以OA 为直径的半圆M 上，且四边形OCDB 是平行四边形，则点C 的坐标为________．【答案】（2，6）【思路分析】过点M 作MN ⊥CD ，垂足为点N ，连接CM ，过点C 作CE ⊥OA ，垂足为点E ，由题意可知OB 及圆的半径长，OB =CD ，由垂径定理可求得MN 的长，CN =EM ，从而求出OE 的长，进而得到点C 的坐标．【解题过程】过点M 作MN ⊥CD ，垂足为点N ，连接CM ，过点C 作CE ⊥OA ，垂足为点E ，点A 的坐标是（20，0），所以CM =OM =10，点B 的坐标是（16，0），所以CD =OB =16，由垂径定理可知，821==CD CN ，在Rt⊙CMN 中，CM =10，CN =8，由勾股定理可知MN =6，所以CE =MN =6，OE =OM ﹣EM =10﹣8=2，所以点C 的坐标为（2，6）．【知识点】垂径定理，勾股定理，平行四边形的性质3. （2018黑龙江省龙东地区，6，3分）如图，AB 为⊙O 的直径，弦CD ⊥AB 于点E ，已知CD ＝6，EB ＝＝1，则⊙O 的半径为________．【答案】5【解析】连接OC ，∵AB 是⊙O 的直径，CD ⊥AB ，∴CE ＝12CD ，∵CD ＝6，∴CE ＝3．设⊙O 的半径为r ，则OC ＝r ，∵EB ＝1，∴OE ＝4，在Rt △OCE 中，由勾股定理得OE 2＋CE 2＝OC 2，∴（r －1）2＋32＝r 2，解得r ＝5，∴⊙O 的半径为5．D【知识点】垂径定理；勾股定理4.（2018黑龙江绥化，16，3分）如图，△ABC是半径为2的圆内接正三角形，则图中阴影部分的面积是．（结果用含π的式子表示）【答案】4π-.【解析】解：连接OA，OB，OC，过O点作OD⊥BC于点D.∵△ABC为等边三角形，∴∠OBD=30°.∵⊙O的半径为2，∴OB=2，∴OD=1，∴∴S△ABC=3S△OBC=3×12BC·OD=D∴S阴影=4π-故答案为：4π-【知识点】含30°角的直角三角形的性质，垂径定理，三角形面积计算，圆的面积计算5.（2018黑龙江绥化，20，3分）如图，一下水管道横截面为圆形，直径为100cm，下雨前水面宽为60cm，一场大雨过后，水面宽为80cm，则水位上升 cm【答案】10或70.【解析】解：作半径OD⊥AB于C，连接OB，由垂径定理得：BC=12AB=30，在Rt△OBC中，当水位上升到圆心以下时水面宽80 cm则OC′，水面上升的高度为：40-30=10cm；当水位上升到圆心以上时，水面上升的高度为：40+30=70cm，综上可得，水面上升的高度为10cm或70cm．故答案为10或70.【知识点】垂径定理，勾股定理6.7.（2018浙江嘉兴，14，4）如图，量角器的O度刻度线为AB．将一矩形直尺与量角器部分重叠，使直尺一边与量角器相切于点C，直尺另一边交量角器于点A、D，量得AD＝10cm，点D在量角器上的读数为60°．则该直尺的宽度为cm．【解析】根据题意，抽象出数学图形根据题意可知：AD ＝10，∠AOD ＝120°，由OA ＝OD ，∴∠DAO ＝30°，设OE ＝x ，则OA ＝2x ，∵OE ⊥AD ，∴AE ＝DE ＝5，在Rt △AOE 中，x 2+52＝（2x ）2，解得：xCE ＝OE8. （2018贵州省毕节市，19，3分）如图,AB 是⊙O 的直径，C 、D 为半圆的三等分点，CE ⊥AB 于点E ， ∠ACE 的度数为______.【答案】30°．【解题过程】∵AB 是⊙O 的直径,C 、D 为半圆的三等分点，∴∠A ＝∠BOD ＝13×180°＝60°，又∵CE ⊥AB ，∴∠ACE ＝90°－60°＝30°．【知识点】圆的性质；直角三角形的性质9.（2018吉林省，13, 2分）如图，A ，B ，C ，D 是⊙O 上的四个点，=⌒BC ，，若∠AOB=58°，则∠BDC=___ 度．BO【答案】29【解析】连接CO，根据同圆中，等弧所对圆心角相等，则∠COB=∠AOB=58°，∴∠BDC=29°【知识点】圆周角定理，圆心角、弧、弦之间的关系10.（2018江苏扬州，15，3）如图，已知⊙O的半径为2，△ABC内接于⊙O，∠ACB=135°，则AB= ．2【答案】2【思路分析】根据圆内接四边形对边互补和同弧所对的圆心角是圆周角的2倍，可以求得∠AOB的度数，然后根据勾股定理即可求得AB的长．【解题过程】连接AD、AE、OA、OB，∵⊙O的半径为2，△ABC内接于⊙O，∠ACB=135°，∴∠ADB=45°，∴∠AOB=90°，∵OA=OB=2，∴2，故答案为2．【知识点】三角形的外接圆和外心，圆内接四边形对边互补，圆周角的性质11.（2018青海，9，2分）如图5，A、B、C是⊙O上的三点，若∠AOC=110°,则∠ABC= . 【答案】125°．【解析】如图所示：优弧AC上任取一点D，连接AD、CD，∵∠AOC=110°，∴∠ADC=∠AOC=×110°=55°，∵四边形ABCD内接与⊙O，∴∠ABC=180°﹣∠ADC=180°﹣55°=125°．【知识点】圆内接四边形的性质，圆周角的性质12. （2018江苏镇江，9，2分）如图，AD 为△ABC 的外接圆⊙O 的直径，若∠BAD ＝50°，则∠ACD ＝________°．【答案】40°．【解析】如答图所示，连接B C ． ∵AB 是⊙O 的直径， ∴∠ACB ＝90°．∵∠BCD ＝∠BAD ＝50°，∴∠ACD ＝∠ACB －∠BCD ＝90°－50°＝40°．13. （2018内蒙古通辽，17，3分）如图，在平面直角坐标系中，反比例函数y ＝kx （k ＞0）的图象与半径为5的⊙O 相交于M 、N 两点，△MON 的面积为3.5，若动点P 在x 轴上，则PM ＋PN 的最小值是 ．【答案】52【解析】设M （a ，b ），则N （b ，a ），依题意，得：a 2＋b 2＝52……①（第9题答图）（第9题图）a 2－ab －12（a －b ）2＝3.5……②①、②联立解得a ＝572，b ＝432所以M 、N 的坐标分别为（572，432），（432，572） 作M 关于x 轴的对称点M ′，则M ′的坐标为（572，－432）， 则M ′N 的距离即为PM ＋PN 的最小值．由于M ′N 2＝（572－432）2＋（－432－572）2＝50， 所以M ′N ＝52，故应填：52．14. （2018山东莱芜，16，3分）如图，正方形ABCD 的边长为2a ，E 为BC 边的中点，⌒AE 、⌒DE 的圆心分别在边AB 、CD 上，这两段圆弧在正方形内交于点F ，则E 、F 间的距离为_______．【答案】32a【思路分析】先用勾股定理求出⌒DFE 的所在圆的半径，再由垂径定理求出EF 的长．【解题过程】解：如图，设⌒DFE 的圆心为G ，作GH ⊥EF 于H ，连接EG ．设⌒DFE 所在圆的半径为x ，在Rt △CEG 中，EG 2＝CG 2＋CE 2，则x 2＝(2a －x )2＋a 2，解得x ＝54a ；由垂径定理，得EF ＝2EH ＝2⎝ ⎛⎭⎪⎫54a 2－a 2＝32a ．故答案为32a ．【知识点】正方形的性质；勾股定理；垂径定理；15. （2018湖北随州12，3分）如图，点A ，B ，C 在⊙O 上，∠A ＝40度，∠C ＝20度，则∠B ＝______度．EEA D【答案】60．【解析】如图，连接OA ，根据“同圆的半径相等”可得OA ＝OC ＝OB ，所以∠C ＝∠OAC ，∠OAB ＝∠B ，故∠B ＝∠OAB ＝∠OAC ＋∠BAC ＝∠C ＋∠BAC ＝20°＋40°＝60°．16.（2018湖北随州16，3分）如图，在四边形ABCD 中，AB ＝AD ＝5，BC ＝CD 且BC ＞AB ，BD ＝8．给出下列判断：①AC 垂直平分BD ；②四边形ABCD 的面积S ＝AC ·BD ；③顺次连接四边形ABCD 的四边中点得到的四边形可能是正方形；④当A 、B 、C 、D 四点在同一个圆上时，该圆的半径为256； ⑤将△ABD 沿直线BD 对折，点A 落在点E 处，连接BE 并延长交CD 于点F ，当BF ⊥CD 时，点F 到直线AB 的距离为678125．其中正确的是______________．（写出所有正确判断的序号）【答案】①③④．【解析】根据“到线段两个端点的距离相等的点在这条线段的垂直平分线上”可知，A ，C 两点都在线段BD 的垂直平分线上，又“两点确定一条直线”，所以AC 垂直平分BD ，故①正确； 如图1，取AC ，BD 的交点为点O ，则由①知OB ⊥AC ，OD ⊥AC ，所以S 四边形ABCD ＝S △ABC ＋S △ADC ＝12AC ·OB ＋12AC ·OD ＝12AC ·(OB ＋OD )＝ 12AC ·BD ，故②错误； 如图2，取AB ，BC ，CD ，AD 四边的中点分别为P ，Q ，M ，N ，则由三角形的中位线定理得PQ ∥AC ∥MN ，PQ ＝MN ＝12AC ，PN ∥BD ∥QM ，PN ＝QM ＝12BD ，于是知四边形PQMN 及阴影四边形都是平行四边形．又由①知AC ⊥BC ，所以可证∠AOB ＝∠QPN ＝90°，故四边形PQMN 为矩形．若AC ＝BD ，则有PQ ＝PN ，四边O ABCCBAO ABDC形PQMN 是正方形，所以顺次连接四边形ABCD 的四边中点得到的四边形可能是正方形，故③正确；当A 、B 、C 、D 四点在同一个圆上时，四边形ABCD 是这个圆的内接四边形，则∠ABC ＋∠ADC ＝180°．根据“SSS ”可证△ABC ≌△ADC ，所以∠ABC ＝∠ADC ＝90°，则AC 是这个圆的直径．由①知BO ＝OD ＝12BD ＝4，在Rt △AOB 中，根据勾股定理，求得AO＝3．然后，证明△AOB ∽△ABC ，得到AB 2＝AO ·AC ，所以AC ＝253，该圆的半径为256，故④正确； 如图1，过点F 作FG ⊥AB 于点G ，过点E 作EH ⊥AB 于点H ，由折叠知，AE ＝2AO ＝6，BE ＝BA ＝5．由于BF ⊥CD ，AE ⊥BD ，可证得△BOE ∽△BFD ，所以BO BF ＝BE BD ，即4BF ＝58，BF ＝325．因为S △ABE ＝12AB ·EH＝12AE ·BO ，所以EH ＝645⨯＝245．又可证△BEH ∽△BFG ，所以EH FG ＝BE BF ，即245FG ＝5325，FG ＝768125，故⑤错误．17. （2018云南曲靖，10，3分）如图，四边形ABCD 内接于⊙O ，E 为BC 延长线上一点，若∠A ＝n °，则∠DCE ＝_________【答案】n °【解析】圆内接四边形的对角互补，所以∠BCD ＝180°－∠A ，而三点BCD 在一条直线上，则∠DCE ＝180°－∠BCD ，所以∠DCE ＝∠A ＝n °.18. （2018年浙江省义乌市，13，5）如图，公园内有一个半径为20米的圆形草坪，A ，B 是圆上的点，O 为圆心，∠AOB =120°，从A 到B 只有路AB ，一部分市民为走“捷径”，踩坏了花草，走出了一条小路AB ．通过计算可知，这些市民其实仅仅少B 走了_________步（假设1步为0.5米，结果保留整数）．（参考数据：图1GFEH OABDC 图21.732，π取3.142）【答案】15【解析】作OC⊥AB于C，如图，则AC=BC，∵OA=OB，∴∠A=∠B=12（180°﹣∠AOB）=12（180°﹣120°）=30°，在Rt△AOC中，OC=12OA=10，，∴69（步）；而AB的长=12020180π⨯≈84（步），AB的长与AB的长多15步．所以这些市民其实仅仅少B走了15步．故答案为15．【知识点】垂径定理；勾股定理19.（2018浙江舟山，14，4）如图，量角器的O度刻度线为AB．将一矩形直尺与量角器部分重叠，使直尺一边与量角器相切于点C，直尺另一边交量角器于点A、D，量得AD＝10cm，点D在量角器上的读数为60°．则该直尺的宽度为cm．BC【解析】根据题意，抽象出数学图形根据题意可知：AD ＝10，∠AOD ＝120°，由OA ＝OD ，∴∠DAO ＝30°，设OE ＝x ，则OA ＝2x ，∵OE ⊥AD ，∴AE ＝DE ＝5，在Rt △AOE 中，x 2+52＝（2x ）2，解得：x ，∴CE ＝OE．三、解答题1. （2018年江苏省南京市，26，8分）如图，在正方形ABCD 中，E 是AB 上一点，连接DE .过点A 作AF DE ⊥，垂足为F .⊙O 经过点C 、D 、F ，与AD 相交于点G .（1）求证AFG DFC ∽△△；（2）若正方形ABCD 的边长为4，1AE =，求O 的半径.【思路分析】（1）欲证明△AFG ∽△DFC ，只要证明∠FAG=∠FDC ，∠AGF=∠FCD ； （2）首先证明CG 是直径，求出CG 即可解决问题；【解题过程】（1）证明：在正方形ABCD 中，90ADC ∠=. ∴90CDF ADF ∠+∠=. ∵AF DE ⊥. ∴90AFD ∠=.∴90DAF ADF ∠+∠=. ∴DAF CDF ∠=∠.∵四边形GFCD 是⊙O 的内接四边形， ∴180FCD DGF ∠+∠=. 又180FGA DGF ∠+∠=，O∴FGA FCD ∠=∠. ∴AFG DFC ∽△△. （2）解：如图，连接CG .∵90EAD AFD ∠=∠=，EDA ADF ∠=∠， ∴EDA ADF ∽△△. ∴EA DA AF DF =，即EA AFDA DF=. ∵AFG DFC ∽△△， ∴AG AFDC DF =. ∴AG EADC DA=. 在正方形ABCD 中，DA DC =，∴1AG EA ==，413DG DA AG =-=-=.∴5CG ===.∵90CDG ∠=， ∴CG 是⊙O 的直径. ∴⊙O 的半径为52.【知识点】相似三角形的判定和性质 正方形的性质 圆周角定理及推论2. （2018江苏徐州，28，10分） 如图，将等腰直角三角形ABC 对折，折痕为CD ．展平后，再将点B 折叠再边AC 上，（不与A 、C 重合）折痕为EF ，点B 在AC 上的对应点为M ，设C D 与EM 交于点P ，连接PF ．已知BC ＝4．（1）若点M 为AC 的中点，求CF 的长；（2）随着点M 在边AC 上取不同的位置．①△PFM 的形状是否发生变化？请说明理由； ②求△PFM 的周长的取值范围.第28题图【解答过程】 解：（1）根据题意，设BF ＝FM ＝x ，则CF ＝4－x ，∵M 为AC 中点，AC ＝BC ＝4，∴ CM ＝12AC ＝2，∵∠ACB ＝90°，∴CF 2+CM 2＝FM 2，∴(4－x )2+22＝x 2，解得x ＝52，∴CF ＝4－52＝32； （2）①△PFM 的形状不变，始终是以PM 、PF 为腰的等腰直角三角形，理由如下：∵等腰直角三角形ABC 中，CD ⊥AB ，∴AD ＝DB ，CD ＝12AB ＝DB ，∴∠B ＝∠DCB ＝45°，由折叠可得∠PMF ＝∠B ＝45°，∴∠PMF ＝∠DCB ，∴P 、M 、F 、C 四点共圆，∴∠FPM +∠FCM ＝180°，∴∠FPM ＝180°－∠FCM ＝90°，∠PFM ＝90°－∠PMF ＝45°＝∠PMF ，∴△PFM 的形状不变，始终是以PM 、PF 为腰的等腰直角三角形； ②当M 与C 重合时，F 为BC 中点，CF ＝12BC ＝2，PM ＝PF ＝cos 45CF=︒此时△PFM 的周长为2＋当M 与A 重合时，F 于C 重合，E 与D 重合，FM ＝AC ＝4，PM ＝PF ＝ACcos45°＝，此时△PFM 的周长为4＋B 不与A 、C 重合，所以△PFM 的周长的取值范围是大于2＋且小于4＋.3. (2018辽宁葫芦岛，25，12分)在△ABC 中，AB ＝BC ，点O 是AC 的中点，点P 是AC 上的一个动点(点P 不与点A ，O ，C 重合)．过点A ，点C 作直线BP 的垂线，垂足分别为点E 和点F ，连接OE ，OF ． （1）如图1，请直接写出线段OE 与OF 的数量关系；（2）如图2，当∠ABC ＝90°时，请判断线段OE 与OF 之间的数量关系和位置关系，并说明理由； （3）若｜CF －AE ｜＝2，EF ＝POF 为等腰三角形时，请直接写出线段OP 的长．【思路分析】（1）连接OB ，则OB ⊥AC ，进而得A 、E 、O 、B 四点共圆，B 、F 、O 、C 四点共圆．由同弧所对的圆周角相等得∠OEB ＝∠OAB ，∠OFC ＝∠OBC ．又因为∠OFE ＝90°－∠OFC ，∠ACB ＝90°－∠OBC ，所以∠OFE ＝∠OCB ，又因为∠OAB ＝∠OCB ，所以∠OE B ＝∠OFE ，所以OE ＝OF ；（2）类比（1）可得OE ＝OF ；由∠ABC ＝90°，AB ＝BC ，可得∠OAB ＝∠OCB ＝∠OEB ＝∠OFE ＝45°，所以OE ⊥OF ．（3）取EF的中点为M，则EM＝FMAM并延长交CF于D，连接OM．由△AME≌△DMF，｜CF－AE｜＝2，得OM＝1．进而得OF＝2．由sin∠OFM＝12，得∠OFM＝30°．因为点P在EF上，所以OP＜OE＝OF；因为AE⊥EF，∠APE、∠OPF均为锐角，故PF≠PO．当PF＝OF＝2时，PM＝2理得OP＝【解答过程】（1）OE＝OF；（2）OE＝OF，OE⊥OF．理由：连接OB，则OB⊥AC．∵∠AEB＝∠AOB＝90°，∴进而得A、E、O、B四点共圆，∴∠OEB＝∠OAB．∵∠BFC＝∠BOC＝90°，∴B、F、O、C四点共圆．∴∠OFC＝∠OBC．又∵∠OFE＝90°－∠OFC，∠ACB＝90°－∠OBC，∴∠OFE＝∠OCB，又∵∠ABC＝90°，AB＝BC，∴∠OAB＝∠OCB＝45°．∴∠OE B＝∠OFE＝45°．∴OE＝OF，OE⊥OF．（3）OP＝223．4.（2018上海，25，14分）已知圆O的直径AB=2，弦AC与弦BD，交于点E，且OD⊥AC，垂足为点F．(1)图11，如果AC=BD，求弦AC的长；(2)如图12，如果E为BD的中点，求∠ABD的余切值(3)联结BC、CD、DA，如果BC是圆O的内接正n边形的一边，CD是的内接正(n+4)边形的一边，求△ACD的面积．【思路分析】(1)连结CB．可以证明弧AD、弧DC、弧CB相等，从而得到∠ABC=60°．在△ABC中求出AC长．(2)运用中位线及全等转化求出CB长，再把直角三角形OBE中的两个直角边求出，即可∠ABD的余切值．(3)根据“BC是圆O的内接正n边形的一边，CD是的内接正(n+4)边形的一边”求出n值，从而求出∠AOD=45°，可得各线段长，再求△ACD的面积．【解答过程】（1）连结CB．∵AC=BD，∴弧AC=弧BD，∵OD⊥AC，∴弧AD=弧DC=12弧AC，∴弧AD=弧DC=弧CB，∴∠ABC=60°在Rt△ABC中, ∠ABC=60°，AB=2，∴AC=3（2）∵OD⊥AC，∴∠AFO=90°，AF=FC∵AO=OB，∴FO∥CB，FO=12 CB∵E为BD的中点，∴DE=EB∵FO∥CB，∴△DEF≌△BEC，∴DF=CB=2FO∴FO=13，CB=23在Rt △ABC 中，AB =2，CB =23，∴AC ，∴EC ∴EB ，∵E 为BD 的中点，OD =OB ，∴∠OEB =90°，∴EO cot ∠ABD =EB EO ． （3）∵BC 是圆O 的内接正n 边形的一边，∴∠COB =360n° ∵CD 是的内接正(n +4)边形的一边，∴∠COD =3604n +° ∵弧AD =弧DC ，∴∠AOD =3604n +° ∵∠COB +∠COD +∠AOD =180°，∴360n +3604n ++3604n +=180，解得n =4 ∴∠AOD =∠COD =3604n +°=45°∵OD =OA =OC =1，∴AC ，OF ，DF =1，∴S △ACD =12×AC ×DF =2－12．5. （2018黑龙江哈尔滨，26，10）已知:⊙O 是正方形ABCD 的外接圆，点E 在弧AB 上，连接BE 、DE ，点F 在弧AD 上，连接BF 、DF 、BF 与DE 、DA 分别交于点G 、点H ，且DA 平分∠EDF ．(1)如图1，求证:∠CBE ＝∠DHG ;(2)如图2，在线段AH 上取一点N (点N 不与点A 、点H 重合)，连接BN 交DE 于点L ，过点H 作HK //BN 交DE 于点K ，过点E 作EP ⊥BN ，垂足为点P ，当BP ＝HF 时，求证:BE ＝HK ;(3)如图3，在(2)的条件下，当3HF ＝2DF 时，延长EP 交⊙O 于点R ，连接BR ，若△BER 的面积与△DHK 的面积的差为47，求线段BR 的长．图1 图2 图3【思路分析】（1）问利用同弧和等弧所对圆周角等与三角形外角性质易证的结论．（2）过H 作HM ⊥KD ，易证得HM ＝BP ，加上直角条件，可导出第三个全等条件，得到△BEP ≌△HKM ，所以BE ＝HK ．（3）连接BD 后根据条件3HF ＝2DF 可得到tan ∠ABH ＝tan ∠ADE ＝ABAH ＝32，过点H 作HS ⊥BD 后再设边计算就能求出tan ∠BDE ＝tan ∠DBF ＝BSHS ＝51，在ER 上截取ET ＝DK ，连接BT 易证得△BET ≌△HKD ，这时21BP ·ER 21-HM ·DK ＝21BP (ER －DK )＝21BP (ER －ET )＝47，易求得BP ＝1，PR ＝5，BR ＝22RP BP +＝2251+＝26【解答过程】（1）证明:∵四边形ABCD 是正方形∴∠A ＝∠ABC ＝90°∵∠F ＝∠A ＝90°∴∠F ＝∠ABC∵DA 平分∠EDF ∴∠ADE ＝∠ADF ∵∠ABE ＝∠ADE ∴∠ABE ＝∠ADF又∵∠CBE ＝∠ABC ＋∠ABE ，∠DHG ＝∠F ＋∠ADF ∴∠CBE ＝∠DHG（2）证明:过H 作HM ⊥KD 垂足为点M ∵∠F ＝90°∴HF ⊥FD 又∵DA 平分∠EDF ∴HM ＝FH∵FH ＝BP ∴HM ＝BP ∵KH ∥BN ∴∠DKH ＝∠DLN ∵∠ELP ＝∠DLN ∴∠DKH ＝∠ELP∵∠BED ＝∠A ＝90°∴∠BEP ＋∠LEP ＝90°∵EP ⊥BN ∴∠BPE ＝∠EPL ＝90°∴∠LEP ＋∠ELP ＝90°∴∠BEP ＝∠ELP ＝∠DKH ∵HM ⊥KD ∴∠KMH ＝∠BPE ＝90°∴△BEP ≌△HKM ∴BE ＝HK(3)解:连接BD ∵3HF ＝2DF ，BP ＝FH ∴设HF ＝2a ，DF ＝3a ∴BP ＝FH ＝2a由(2)得HM ＝BP ，∠HMD ＝90°∵∠F ＝∠A ＝90°∴tan ∠HDM ＝tan ∠FDH ∴DM HM ＝DF FH ＝32 ∴DM ＝3a ∴四边形ABCD 是正方形∴AB ＝AD ∴∠ABD ＝∠ADB ＝45°∵∠ABF ＝∠ADF ＝∠ADE ，∠DBF ＝45°－∠ABF ，∠BDE ＝45°－∠ADE ∴∠DBF ＝∠BDE ∵∠BED ＝∠F ，BD ＝BD ∴△BED ≌△DFB ∴BE ＝FD ＝3a 过点H 作HS ⊥BD 垂足为点S ∵tan ∠ABH ＝tan ∠ADE ＝ABAH ＝32 ∴设AB ＝32m ，AH ＝22m ∴BD ＝2AB ＝6m DH ＝AD －AH ＝2m sin ∠ADB ＝DHHS ＝22 ∴HS ＝m ∴ DS ＝22HS DH -＝m ∴BS ＝BD －DS ＝5m ∴tan ∠BDE ＝tan ∠DBF ＝BS HS ＝51 ∵∠BDE ＝∠BRE ∵tan ∠BRE ＝PR BP ＝51∵BP ＝FH ＝2a ∴RP ＝10a 在ER 上截取ET ＝DK ，连接BT 由(2)得∠BEP ＝∠HKD ∴△BET ≌△HKD ∴∠BTE ＝∠KDH ∴tan ∠BTE ＝tan ∠KDH ∴PT BP ＝32 ∴PT ＝3a ∴TR ＝RP －PT ＝7a ∵S △BER －S △KDH ＝47∴21BP ·ER 21-HM ·DK ＝47 ∴21BP (ER －DK )＝21BP (ER －ET )＝47∴21×2a ×7a ＝47 ∴a 2＝41，a 1＝21，a 2＝21-(舍去)∴BP ＝1，PR ＝5 ∴BR ＝22RP BP +＝2251+＝26。
圆的有关概念和性质-2024年中考数学考点总复习(全国通用)(解析版)
【中考高分指南】数学（选择+填空）【备战2024年中考·数学考点总复习】（全国通用）圆的有关概念和性质一、圆的有关概念弦 连接圆上任意两点的线段叫做弦。
直径经过圆心的弦叫做直径。
弧 圆上任意两点间的部分叫做圆弧，简称弧。
优弧 大于半圆的弧叫做优弧。
劣弧小于半圆的弧叫做劣弧。
常用公式：Lr r n S r n L 213601802===π，π扇形三角形扇形弓形S S S ±=三、垂径定理1．定理:垂直于弦的直径平分弦，并且平分弦所对的两条弧.2．推论1:①平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧.②弦的垂直平分线经过圆心，并且平分弦所对的两条弧.③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧.3．推论2:圆的两条平行弦所夹的弧相等.注意：轴对称性是圆的基本性质，垂径定理及其推论就是根据圆的轴对称性总结出来的，它们是证明线段相等、角相等、垂直关系、弧相等和一条弦是直径的重要依据.遇弦作弦心距是圆中常用的辅助线.二、弧、弦、圆心角、圆周角的关系定理1．弧、弦、圆心角的关系定理:在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等.推论:在同圆或等圆中，两个圆心角、两条弧、两条弦中如果有一组量相等，则它们所对应的其余各组量也分别相等.2．圆心角:顶点在圆心，角的两边和圆相交的角叫做圆心角.圆周角:顶点在圆上且角的两边和圆相交的角叫做圆周角.3．圆周角定理定理:一条弧所对的圆周角等于它所对的圆心角的一半.推论:①同弧或等弧所对的圆周角相等.②半圆(或直径)所对的圆周角是直径，90°的圆周角所对的弦是圆的直径.③圆内接四边形的对角互补.【考点1】圆的相关概念⏜上的点，连接AD并延长与OB的延长线交于点C，若CD=OA，【例1】（2023·江苏）如图，在扇形AOB中，D为AB∠O=75°，则∠A的度数为( )A. 35°B. 52.5°C. 70°D. 72°【答案】C【分析】本题考查了圆的认识：熟练掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了三角形内角和定理、等腰三角形的性质．连接OD ，如图，设∠C 的度数为n ，由于CD =OA =OD ，根据等腰三角形的性质得到∠C =∠DOC =n ，则利用三角形外角性质得到∠ADO =2n ，所以∠A =2n ，然后利用三角形内角和定理得到75°+n +2n =180°，然后解方程求出n ，从而得到∠A 的度数． 【解析】解：连接OD ，如图，设∠C 的度数为n ， ∵CD =OA =OD ， ∴∠C =∠DOC =n ，∴∠ADO =∠DOC +∠C =2n ， ∵OA =OD ， ∴∠A =∠ADO =2n ，∵∠AOC +∠C +∠A =180°，∠AOC =75°， ∴75°+n +2n =180°， 解得n =35°， ∴∠A =2n =70°． 故选：C ．【例2】（2024·全国模拟）如图，在△ABC 中，∠C =90°，AB =10.若以点C 为圆心，CA 长为半径的圆恰好经过AB 的中点D ，则⊙C 的半径为( ) A. 5√ 3 B. 8 C. 6 D. 5 【答案】D【解析】解：如图，连结CD ， ∵CD 是直角三角形斜边上的中线， ∴CD =12AB =12×10=5． 故选：D ．连结CD ，根据直角三角形斜边中线定理求解即可．本题考查了直角三角形斜边上的中线，掌握在直角三角形中，斜边上的中线等于斜边的一半是解题的关键． 【例3】（2024·江西模拟）一张直径为10cm 的半圆形卡纸，过直径的两端点剪掉一个三角形，以下四种裁剪图中，所标数据(单位：cm)长度不合理的是( )A.B.C.D.【答案】D【解析】解：A 、B 、C 图形中的三角形，满足三角形三边关系定理，且三角形三边长度合理，故A 、B 、C 不符合题意；D 、如图，过A 作AH ⊥BC 于H ，∵AB =AC ，∴BH =12BC =12×10=5(cm)， ∴AH =√ AB 2−BH 2=√ 39， ∴AH >5， ∴A 在圆外，∴三角形三边长度不合理， 故D 不符合题意． 故选：D ．由三角形三边关系定理，点和圆的位置关系即可判断．本题考查三角形三边关系，等腰三角形的性质，勾股定理，点和圆的位置关系，关键是由等腰三角形的性质，勾股定理求出AH 的长．1.（2024·湖北模拟）以下命题：(1)等弧所对的弦相等；(2)相等的圆心角所对的弧相等；(3)三点确定一个圆；(4)圆的对称轴是直径；(5)在同圆或等圆中，同一条弦所对的圆周角相等；(6)三角形三边的垂直平分线的交点到三角形三个顶点的距离相等.其中正确的命题的个数是( )A. 2个B. 3个C. 4个D. 5个【答案】A【分析】本题主要考查圆的相关概念和性质，深刻理解圆的相关性质是解题的关键．根据圆的相关概念和性质，对各个选项逐一分析判断即可得出答案．【解析】解：(1)等弧所对的弦相等；正确；(2)在同圆或等圆中，相等的圆心角所对的弧相等；故(2)错误；(3)不在同一直线上的三点确定一个圆；故(3)错误；(4)圆的对称轴是直径所在直线；故(4)错误；(5)在同圆或等圆中，同一条弦所对的弧有两条，每一条弧所对的圆心角不一定相等，则所对的圆周角也不一定相等；故(5)错误；(6)三角形三边的垂直平分线的交点即为其外接圆的圆心，外心到三角形三个顶点的距离相等.故(6)正确；综上所述，正确的有(1)(6)，故选A．2.（2024·江苏模拟）下列说法中，正确的是①对角线垂直且互相平分的四边形是菱形；②对角线相等的四边形是矩形；③同弧或等弧所对的圆周角相等；④半圆是弧，但弧不一定是半圆．( )A. ①④B. ②③C. ①③④D. ②③④【答案】A【解析】解：①、对角线互相平分的四边形是平行四边形，对角线互相垂直的平行四边形为菱形，故该项正确；②、对角线相等的平行四边形为矩形，故该选项错误；③、在同圆或等圆中，同弧或等弧所对的圆周角相等，故该选项错误；④、弧分为优弧、劣弧、半圆弧，则半圆是弧，但弧不一定是半圆，故该项正确；故选：A．根据对角线互相垂直的平行四边形为菱形，对角线相等的平行四边形为矩形，在同圆或等圆中，同弧或等弧所对的圆周角相等，弧分为优弧、劣弧、半圆弧分别判断即可．本题考查基本概念，熟记知识点是解题关键．3.（2023·全国模拟）下列说法中，不正确的是( )A. 直径是最长的弦B. 同圆中，所有的半径都相等C. 圆既是轴对称图形又是中心对称图形D. 长度相等的弧是等弧【答案】D【分析】本题主要考查了圆的基本概念，解答此题的关键是正确理解弦，弧的定义，解答此题根据圆的基本概念判断即可．【解析】解：A.直径是最长的弦，正确；B.同一个圆的半径相等，正确；C.圆既是轴对称图形，也是中心对称图形，正确；D.长度相等的弧不一定是等弧，同圆或等圆中长度相等的弧才是等弧，故该选项的说法错误．故选D．4.（2024·广东模拟）如图所示，MN为⊙O的弦，∠N=52°，则∠MON的度数为( )A. 38°B. 52°C. 76°D. 104°【答案】C【分析】本题考查了圆的认识：掌握与圆有关的概念．根据半径相等得到OM=ON，则∠M=∠N=52°，然后根据三角形内角和定理计算∠MON的度数．【解析】解：∵OM=ON，∴∠M=∠N=52°，∴∠MON=180°−2×52°=76°．故选：C．【考点2】垂径定理【例1】（2023·四川）如图，在⊙O中，OA⊥BC，∠ADB=30°，BC=2√ 3，则OC=( )A. 1B. 2C. 2√ 3D. 4【答案】B【解析】解：连接OB，设OA交BC于E，如图：∵∠ADB=30°，∴∠AOB=60°，∵OA⊥BC，BC=2√ 3，BC=√ 3，∴BE=12，在Rt△BOE中，sin∠AOB=BEOB，∴sin60°=√ 3OB∴OB=2，∴OC=2；故选：B．连接OB，设OA交BC于E，由∠ADB=30°，得∠AOB=60°，根据OA⊥BC，BC=2√ 3，得BE=1BC=√ 3，2故sin60°=√ 3，从而OC=OB=2．OB本题考查垂径定理，圆周角定理及勾股定理的应用，解题的关键是掌握含30°角的直角三角形三边关系．【例2】（2024·湖南模拟）如图，AB是⊙O的直径，弦CD⊥OA于点E，连接OC，OD.若⊙O的半径为m，∠AOD=α，则下列结论一定成立的是A. OE=m·tanαB. CD=2m·sinαC. AE=m·cosαD. S△OCD=m2·sinα【答案】B【分析】本题考查了垂径定理，解直角三角形，解决本题的关键是掌握垂径定理，解直角三角形等知识.根据垂径定理和锐角三角函数计算则可进行判断．【解析】解：A．∵AB是⊙O的直径，弦CD⊥OA于点E，CD，∴DE=12在Rt△EDO中，OD=m，∠AOD=∠α，∴tanα=DEOE，∴OE=DEtanα=CD2tanα，故选项A错误不符合题意；B.∵AB是⊙O的直径，CD⊥OA，∴CD=2DE，∵⊙O的半径为m，∠AOD=∠α，∴DE=OD⋅sinα=m⋅sinα，∴CD=2DE=2m⋅sinα，故选项B正确符合题意；C.∵cosα=OEOD，∴OE=OD⋅cosα=m⋅cosα，∵AO=DO=m，∴AE=AO−OE=m−m⋅cosα，故选项C错误不符合题意；D.∵CD=2m⋅sinα，OE=m⋅cosα，∴S△COD=12CD×OE=12×2m⋅sinα×m⋅cosα=m2sinα⋅cosα，故选项D错误不符合题意；故选B．【例3】（2024·全国模拟）如图，已知⊙O的周长等于6π，则该圆内接正六边形ABCDEF的边心距OG为．( )A. 3√ 3B. 32C. 3√ 32D. 3【答案】C【解析】连接OC、OD，如图所示，∵正六边形ABCDEF是圆的内接多边形，∴∠COD=60°．∵OC=OD，OG⊥CD，∴∠COG =30°． ∵⊙O 的周长等于6π，∴OC =3，∴CG =32，∴OG =3√ 32． 故选C ．1．垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．2．根据垂径定理构造直角三角形，一般为过圆心作已知弦的弦心距，常用于求线段的长度.1.（2024·广东模拟）已知：如图，在⊙O 中，OA ⊥BC ，∠AOB =70°，则∠ADC 的度数为( )A. 30°B. 35°C. 45°D. 70°【答案】B【分析】本题考查的是垂径定理、圆周角定理、圆心角与弧的关系定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．先根据垂径定理得出AB ⏜=AC ⏜，再由圆周角定理即可得出结论． 【解析】解：如图，连接OC ．∵OA ⊥BC ， ∴AB⏜=AC ⏜， ∴∠AOC =∠AOB =70°，∴∠ADC =12∠AOC =35°． 故选B ．2.（2024·江苏模拟）如图，AB 是⊙O 的直径，弦CD ⊥AB 于E 点，若AD =CD =2√3.则BC ⌒的长为( ) A. π3B.2π3C. √3π3D.2√3π3【答案】B【解析】解：连接AC 、OC ， ∵AB 是⊙O 的直径，CD ⊥AB ， ∴CE =ED =12CD =√3，BC ⌒=BD ⌒，∴AB 是线段CD 的垂直平分线， ∴AC =AD ， ∵AD =CD ， ∴AC =AD =CD ， ∴△ACD 为等边三角形， ∴∠CAD =60∘， ∴∠COB =60∘，在Rt △COE 中，OC =CEsin∠COE =2， ∴BC ⌒的长=60π×2180=2π3， 故选：B.连接AC 、OC ，根据垂径定理得到CE =ED =12CD =√3，BC ⌒=BD ⌒，根据线段垂直平分线的性质得到AC =AD ，根据等边三角形的性质求出∠CAD =60∘，根据正弦的定义求出OC ，根据弧长公式计算，得到答案． 本题考查的是弧长的计算、垂径定理，掌握弧长公式：l =nπr180是解题的关键． 3.（2024·陕西模拟）如图，已知AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，且∠ACD =22.5°，CD =4，则⊙O 的半径长为( ) A. 2 B. 2√ 2 C. 4 D. 10【答案】B【解析】解：连接OD ，如图所示：∵AB 是⊙O 的直径，弦CD ⊥AB ，CD =4，∴CE =DE =12CD =2，∵∠ACD =22.5°，∴∠AOD =2∠ACD =45°，∴△DOE 为等腰直角三角形，∴OD =√ 2DE =2√ 2，即⊙O 的半径为2√ 2，故选：B ．连接OD ，由圆周角定理得出∠AOD =45°，根据垂径定理可得CE =DE =2，证出△DOE 为等腰直角三角形，利用特殊角的三角函数可得答案．此题主要考查了圆周角定理、垂径定理、以及三角函数的应用；关键是掌握圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．4.（2023·江苏）如图，矩形内接于⊙O ，分别以AB 、BC 、CD 、AD 为直径向外作半圆.若AB =4，BC =5，则阴影部分的面积是( )A. 414π−20B. 412π−20C. 20πD. 20【答案】D【解析】解：如图，连接BD ，则BD 过点O ，在Rt △ABD 中，AB =4，BC =5，∴BD 2=AB 2+AD 2=41，S 阴影部分=S 以AB 为直径的圆+S 以AD 为直径的圆+S 矩形ABCD −S 以BD 为直径的圆=π×(42)2+π×(52)2+4×5−π×(BD 2)2 =41π4+20−41π4=20，故选：D ．根据矩形的性质可求出BD ，再根据图形中各个部分面积之间的关系，即S 阴影部分=S 以AB 为直径的圆+S 以AD 为直径的圆+S 矩形ABCD −S 以BD 为直径的圆进行计算即可．本题考查勾股定理，矩形的性质以及圆形面积的计算，掌握矩形的性质、勾股定理以及圆形面积的计算方法是正确解答的前提．5.（2023·内蒙古）如图，⊙O 是锐角三角形ABC 的外接圆，OD ⊥AB ，OE ⊥BC ，OF ⊥AC.垂足分别为D ，E ，F ，连接DE ，EF ，FD.若DE +DF =6.5，△ABC 的周长为21，则EF 的长为( )A. 8B. 4C. 3.5D. 3【答案】B【解析】解：∵OD ⊥AB ，OE ⊥BC ，OF ⊥AC ，∴AD =BD ，AF =CF ，BE =CE ，∴DE ，DF ，EF 是△ABC 的中位线，∴DE =12AC,DF =12BC,EF =12AB ，∴DE +DF +EF =12(AB +BC +AC)=12×21=10.5，∵DE +DF =6.5，∴EF =10.5−6.5=4，故选：B ．根据垂径定理得到AD =BD ，AF =CF ，BE =CE ，根据三角形的中位线定理得到DE +DF +EF =12(AB +BC +AC)=12×21=10.5，于是得到结论．本题考查了三角形外接圆与外心，三角形中位线定理，垂径定理，熟练掌握三角形中位线定理是解题的关键．【考点3】垂径定理的应用【例1】（2023·湖北）如图，一条公路的转弯处是一段圆弧(AC⏜)，点O 是这段弧所在圆的圆心，B 为AC ⏜上一点，OB ⊥AC 于D.若AC =300√ 3m ，BD =150m ，则AC⏜的长为( )A. 300πmB. 200πmC. 150πmD. 100√ 3πm【答案】B【解析】解：如图所示：∵OB ⊥AC ，∴AD =12AC =150√ 3m ，∠AOC =2∠AOB ，在Rt △AOD 中，∵AD 2+OD 2=OA 2，OA =OB ，∴AD 2+(OA −BD)2=OA 2，∴(150√ 3)2+(OA −150)2=OA 2解得：OA =300m ，∴sin∠AOB =AD OA =√ 32， ∴∠AOB =60°，∴∠AOC =120°，∴AC ⏜的长=120×300π180=200πm ．故选：B ．先根据垂径定理求出AD 的长，由题意得OD =OA −BD ，在Rt △AOD 中利用勾股定理即可求出OA 的值，然后再利用三角函数计算出AC⏜所对的圆心角的度数，由弧长公式求出AC ⏜的长即可． 本题考查的是垂径定理，勾股定理及弧长的计算公式，根据垂径定理得出AD 的长，再由勾股定理求出半径是解答此题的关键，同时要熟记圆弧长度的计算公式．【例2】（2024·山东模拟）唐代李皋发明了“桨轮船”，这种船是原始形态的轮船，是近代明轮航行模式之先导.如图，某桨轮船的轮子被水面截得的弦AB 长8m ，轮子的吃水深度CD 为2m ，则该桨轮船的轮子直径为( )A. 10mB. 8mC. 6mD. 5m【答案】A【解析】解：设半径为r m ，则OA =OC =r m ，∴OD =(r −2)m ，∵AB =8m ，∴AD =4m ，在Rt △ODA 中，有：OA 2=OD 2+AD 2，即：r 2=(r −2)2+42，解得r =5m ，则该桨轮船的轮子直径为10m ．故选：A ．设半径为r ，再根据圆的性质及勾股定理，可求出答案．本题考查垂径定理，勾股定理，关键在于知道OC 垂直平分AB 这个隐藏的条件．垂径定理及其推论方法技巧：1.圆中模型“知2得3”由图可得以下5点：①AB ⊥CD ；②AE=EB ；③AD 过圆心O ；④⋂⋂=BC AC ；⑤⋂⋂=BD AD ；以上5个结论，知道其中任意2个，剩余的3个都可以作为结论使用。
圆的基本性质教案含答案
DB圆的基本性质基础知识回放集合：圆：圆可以看作是到定点的距离等于定长的点的集合； 圆的外部：可以看作是到定点的距离大于定长的点的集合； 圆的部：可以看作是到定点的距离小于定长的点的集合 轨迹：1、到定点的距离等于定长的点的轨迹是：以定点为圆心，定长为半径的圆；2、到线段两端点距离相等的点的轨迹是：线段的中垂线；3、到角两边距离相等的点的轨迹是：角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线 垂径定理:垂径定理：垂直于弦的直径平分弦且平分弦所对的弧 推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧； （2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB 是直径 ②AB ⊥CD ③CE=DE ④⑤推论2：圆的两条平行弦所夹的弧相等。
即：在⊙O 中，∵AB ∥CD圆心角定理圆周角定理圆周角定理：同一条弧所对的圆周角等于它所对的圆心的角的一半即：∵∠AOB 和∠ACB 是 所对的圆心角和圆周角 ∴∠AOB=2∠ACBBC BD =AC AD =BBAOMA P圆周角定理的推论：推论1弧即：在⊙O 中，∵∠C 、∠D 都是所对的圆周角 ∴∠C=∠D推论2：半圆或直径所对的圆周角是直角；圆周角是直角所对的弧是半圆，所对的弦是直径 即：在⊙O 中，∵AB 是直径 或∵∠C=90° ∴∠C=90°∴AB 是直径推论3：三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形 即：在△ABC 中，∵OC=OA=OB ∴△ABC 是直角三角形或∠C=90°注：此推论实是初二年级几何中矩形的推论：在直角三角形中斜边上的中线等于斜边的一半的逆定理。
2024中考数学一轮复习核心知识点精讲—圆的基本性质
2024中考数学一轮复习核心知识点精讲—圆的基本性质1.理解圆心角及其所对的弧、弦之间的关系；2.理解并运用圆周角定理及其推论；3.探索并证明垂径定理会应用垂径定理解决与圆有关的问题；4.理解并运用圆内接四边形的性质.考点1：圆的定义及性质圆的定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫圆。
这个固定的端点O叫做圆心，线段OA叫做半径。
圆的表示方法：以O点为圆心的圆记作⊙O，读作圆O。
圆的特点：在一个平面内，所有到一个定点的距离等于定长的点组成的图形。
圆的对称性：1）圆是轴对称图形，经过圆心的每一条直线都是它的对称轴；2）圆是以圆心为对称中心的中心对称图形。
考点2：圆的有关概念弦的概念：连结圆上任意两点的线段叫做弦(例如：右图中的AB)。
直径的概念：经过圆心的弦叫做直径（例如：右图中的CD）。
备注：1）直径是同一圆中最长的弦。
2）直径长度等于半径长度的2倍。
，读作圆弧弧的概念：圆上任意两点间的部分叫做圆弧，简称弧。
以A、B为端点的弧记作ABAB或弧AB。
等弧的概念：在同圆或等圆中，能够互相重合的弧叫做等弧。
半圆的概念：圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆。
优弧的概念：在一个圆中大于半圆的弧叫做优弧。
劣弧的概念：小于半圆的弧叫做劣弧。
考点3：垂径定理垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。
推论1：1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；3）平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧。
推论2：圆的两条平行弦所夹的弧相等。
常见辅助线做法（考点）：1）过圆心，作垂线，连半径，造Rt △，用勾股，求长度；2）有弧中点，连中点和圆心，得垂直平分考点4：垂径定理的应用考点5：圆心角的概念圆心角概念：顶点在圆心的角叫做圆心角。
弧、弦、弦心距、圆心角之间的关系定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等。
圆的基本性质(解答题)
21．圆的基本性质（解答题）三、解答题85.（2009柳州）如图，AB是⊙O的直径，C是弧BD的中点，CE⊥AB，垂足为E，BD交CE 于点F．（1）求证：CF＝BF；（2）若AD＝2，⊙O的半径为3，求BC的长．【关键词】圆证明：（1）连结AC，如图。
∵C是弧BD的中点∴∠BDC＝∠DBC又∠BDC＝∠BAC在三角形ABC中，∠ACB＝90°，CE⊥AB∴ ∠BCE＝∠BAC∠BCE＝∠DBC∴ CF＝BF因此，CF＝BF．（2）证法一：作CG⊥AD于点G，∵C 是弧BD 的中点∴ ∠CAG＝∠BAC ， 即AC 是∠BAD 的角平分线．∴ CE＝CG ，AE ＝AG在Rt△BCE 与Rt△DCG 中，CE ＝CG ， CB ＝CD∴Rt△BCE≌Rt△DCG∴BE＝DG∴AE＝AB-BE ＝AG ＝AD+DG即 6-BE ＝2+DG∴2BE＝4，即 BE ＝2又 △BCE∽△BAC∴ 212BC BE AB ==·32±=BC （舍去负值） ∴32=BC（2）证法二：∵AB 是⊙O 的直径，CE⊥AB∴∠BEF＝︒=∠90ADB ，在Rt ADB △与Rt FEB △中，∵FBE ABD ∠=∠∴ADB △∽FEB △，则BF AB EF AD = 即BFEF 62=， ∴EF BF 3= 又∵CF BF =， ∴EF CF 3=利用勾股定理得：EF EF BF BE 2222=-=又∵△EBC∽△ECA则CE BE AE CE =，即则BE AE CE ⋅=2 ∴BE BE EF CF ⋅-=+)6()(2即EF EF EF EF 22)226()3(2⋅-=+∴22=EF ∴3222=+=CE BE BC .86.(2009年四川省内江市)如图，四边形ABCD 内接于圆，对角线AC 与BD 相交于点E 、F 在AC 上，AB ＝AD ，∠BFC ＝∠BAD ＝2∠DFC.求证：（1）CD ⊥DF ；（2）BC ＝2CD【关键词】三角形全等的判定.【答案】证：（1）设∠DFC ＝θ，则∠BAD ＝2θ在△ABD 中，∵AB ＝AD ， ∴∠ABD ＝∠ADB∠ABD ＝12（180°-∠BAD ）＝90°-θ又∠FCD ＝∠ABD ＝90°-θ∴∠FCD+∠DFC ＝90°∴CD ⊥DF（2）过F 作FG ⊥BC 于G在△FGC 和△FDC 中 ，∠FCG ＝∠ADB ＝∠ABD ＝∠FCD∠FGC ＝∠FDC ＝90°,FC ＝FC∴△FGC ≌△FDC∴GC ＝CD 且∠GFC ＝∠DFC又∠BFC ＝2∠DFC∴∠GFB ＝∠GFC∴BC ＝2GC ， ∴BC ＝2CD.87．（2009年甘肃庆阳）（10分）如图，在边长为2的圆内接正方形ABCD 中，AC 是对角线，P 为边CD 的中点，延长AP 交圆于点E ．（1）∠E ＝ 度； （2）写出图中现有的一对不全等的相似三角形，并说明理由； （3）求弦DE 的长．【关键词】圆周角和圆心角；相似三角形【答案】本小题满分10分解：（1）45．（2）△ACP∽△DEP．理由：∵∠AED＝∠ACD，∠APC＝∠DPE，∴ △ACP∽△DEP．（3）方法一： ∵ △ACP∽△DEP， ∴ .AP AC DP DE = 又 AP ＝522=+DP AD ，AC ＝2222=+DC AD ，∴ DE＝5102．方法二：如图2，过点D 作DF AE ⊥于点F ．在Rt ADP △中， AP 225,AD DP +又1122ADP S AD DP AP DF ==△， ∴ DF＝552．∴ 51022==DF DE ．88.(2009年衢州）如图，AD 是⊙O 的直径．(1) 如图①，垂直于AD 的两条弦B 1C 1，B 2C 2把圆周4等分，则∠B 1的度数是 ，∠B 2的度数是 ；(2) 如图②，垂直于AD 的三条弦B 1C 1，B 2C 2，B 3C 3把圆周6等分，分别求∠B 1，∠B 2， ∠B 3的度数；(3) 如图③，垂直于AD 的n 条弦B 1C 1，B 2C 2，B 3 C 3，…，B n C n 把圆周2n 等分，请你用含n 的代数式表示∠B n 的度数(只需直接写出答案)．【关键词】开放性试题【答案】解：(1) 22.5°，67.5°(2) ∵ 圆周被6等分，∴ 11B C ＝12C C ＝23C C ＝360°÷6＝60°．∵ 直径AD ⊥B 1C 1，∴ 1AC ＝1211B C ＝30°，∴ ∠B 1m =121AC ＝15°． ∠B 2m =122AC ＝12×(30°＋60°)＝45°， ∠B 3m =123AC ＝12×(30°＋60°＋60°)＝75°． (3) 11360360[(1)]2222n B n n n ︒︒∠=⨯+-⨯(9045)n n-︒=． (或3604590908n B n n︒︒∠=︒-=︒-)89. （2009年广州市）如图，在⊙O 中，∠ACB ＝∠BDC＝60°，AC ＝cm 32，（1）求∠BAC 的度数； （2）求⊙O 的周长【关键词】圆【答案】90.（2009年广西钦州）（2）已知：如图2，⊙O 1与坐标轴交于A （1，0）、B （5，0）两点，点O 15．求⊙O 1的半径．B A O图2 x y A BO 1O【关键词】垂径定理、勾股定理、坐标系【答案】（2）解：过点O 1作O 1C ⊥AB ，垂足为C ，则有AC ＝BC ． B A O图2 x yA BO 1O C由A （1，0）、B （5，0），得AB ＝4，∴AC ＝2．在1Rt AO C △中，∵O 15，∴O 1C 5．∴⊙O 1的半径O 1A 22221(5)2O C AC ++3．91．(2009年南充)如图8，半圆的直径10AB =，点C 在半圆上，6BC =．（1）求弦AC 的长；（2）若P 为AB 的中点，PE AB ⊥交AC 于点E ，求PE 的长．P BCE A【关键词】圆的性质，三角形相似的性质【答案】解：AB 是半圆的直径，点C 在半圆上，90ACB ∴∠=°．在Rt ABC △中，22221068AC AB BC =-=-= （2）PE AB ⊥，90APE ∴∠=°．90ACB ∠=°，APE ACB ∴∠=∠．又PAE CAB ∠=∠，AEP ABC ∴△∽△，PE AP BC AC∴= 110268PE ⨯∴= 301584PE ∴==．92．（2009年哈尔滨）如图，在⊙O 中，D 、E 分别为半径OA 、OB 上的点，且AD ＝BE ． 点C 为弧AB 上一点，连接CD 、CE 、CO ，∠AOC＝∠BOC．求证：CD ＝CE ．【关键词】圆的半径，圆心角【答案】此题证明△OCD 与△OCE 全等即可，给出了一对角相等，再利用半径相等的性质即可得证OA OB AD BE ==，，OA AD OB BE ∴-=-，即OD OE =．93．（2009年中山）（1）如图1，圆心接ABC △中，AB BC CA ==，OD 、OE 为O ⊙的半径，OD BC ⊥于点F ，OE AC ⊥于点G ，求证：阴影部分四边形OFCG 的面积是ABC △的面积的13． （2）如图2，若DOE ∠保持120°角度不变，求证：当DOE ∠绕着O 点旋转时，由两条半径和ABC △的两条边围成的图形（图中阴影部分）面积始终是ABC △的面积的13．【关键词】圆的内接三角形【答案】（1）如图1，连结OA OC ，，因为点O 是等边三角形ABC 的外心，所以Rt Rt Rt OFC OGC OGA △≌△≌△．2OFCG OFC OAC S S S ==△△，因为13OAC ABC S S =△△， 所以13OFCG ABC S S =△． （2）解法一：连结OA OB ，和OC ，则AOC COB BOA △≌△≌△，12∠=∠，不妨设OD 交BC 于点F ，OE 交AC 于点G ，3412054120AOC DOE ∠=∠+∠=∠=∠+∠=°，°，35∴∠=∠．在OAG △和OCF △中，1235OA OC ∠=∠⎧⎪=⎨⎪∠=∠⎩，，， OAG OCF ∴△≌△，13OFCG AOC ABC S S S ∴==△△．解法二：不妨设OD 交BC 于点F ，OE 交AC 于点G ，作OH BC OK AC ⊥⊥，，垂足分别为H K 、，在四边形HOKC 中，9060OHC OKC C ∠=∠=∠=°，°，360909060120HOK ∴∠=-︒-︒=︒°-?，即12120∠+∠=°．又23120GOF ∠=∠+∠=°，13∴∠=∠．AC BC =， OH OK ∴=，OGK OFH ∴△≌△，13OFCG OHCK ABC S S S ∴==△．在ODC △ 和OEC △中，OD OE DOC EOC OC OC =⎧⎪∠=∠⎨⎪=⎩ODC OEC ∴△≌△．CD CE ∴=．94.（2009年广州市）如图，在⊙O 中，∠ACB ＝∠BDC＝60°，AC ＝cm 32，（1）求∠BAC 的度数； （2）求⊙O 的周长【关键词】圆【答案】95. （2009年株洲市）（本题满分10分）如图，点A 、B 、C 是O 上的三点，//AB OC .（1）求证：AC 平分OAB ∠.（2）过点O 作OE AB ⊥于点E ，交AC 于点P . 若2AB =，30AOE ∠=︒，求PE 的长．【关键词】与圆有关的综合题【答案】（1）∵//AB OC ， ∴C BAC ∠=∠；∵OA OC =，∴C OAC ∠=∠ ∴BAC OAC ∠=∠ 即AC 平分OAB ∠.（2）∵OE AB ⊥ ∴112AE BE AB === 又30AOE ∠=︒，90PEA ∠=︒∴60OAE ∠=︒∴1302EAP OAE ∠=∠=︒， ∴12PE PA =，设PE x =，则2PA x =，根据勾股定理得2221(2)x x +=，解得3x =tan PE EAP AE ∠=） 即PE 397.(2009年潍坊)如图所示，圆O 是ABC △的外接圆，BAC ∠与ABC ∠的平分线相交于点I ，延长AI 交圆O 于点D ，连结BD DC 、．（1）求证：BD DC DI ==；（2）若圆O 的半径为10cm ，120BAC ∠=°，求BDC △的面积．（1）证明：AI 平分BAC ∠BAD DAC BD DC ∴∠=∠∴=，BI 平分ABC ABI CBI ∠∴∠=∠，BAD DAC DBC DAC ∠=∠∠=∠，BAD DBC ∴∠=∠，又DBI DBC CBI DIB ABI BAD ∠=∠+∠∠=∠+∠， DBI DIB BDI ∴∠=∠∴，△为等腰三角形 BD ID BD DC DI ∴=∴==，（2）解：当120BAC ∠=°时，ABC △为钝角三角形，∴圆心O 在ABC △外，连结OB OD OC 、、，2120DOC BOD BAD ∴∠=∠=∠=°， 60DBC DCB ∴∠=∠=°，∴BDC △为正三角形．又知10cm OB =，32sin 60210103cm BD OB ∴==⨯⨯=° 223(103)753cm BDC S ∴=⨯=△.答：BDC △的面积为7532．98.（09湖北宜昌）已知：如图，⊙O 的直径AD ＝2，BC CD DE ==，∠BAE ＝90°．(1)求△CAD的面积；(2)如果在这个圆形区域中，随机确定一个点P，那么点P落在四边形ABCD区域的概率是多少？【关键词】圆的基本性质、圆周角和圆心角【答案】解：（1）∵AD为⊙O的直径，∴∠ACD＝∠BAE＝90°．∵ BC CD DE==，∴ ∠BAC＝∠CAD＝∠DAE．∴∠BAC＝∠CAD＝∠DAE ＝30°．∵在Rt△ACD中，AD＝2，CD＝2sin30°＝1， AC＝2cos30°＝3．∴S△ACD＝1 2AC×CD ＝32．(2) 连BD，∵∠A BD＝90°，∠BAD＝＝60°，∴∠BDA＝∠BCA＝30°，∴BA＝BC.作BF⊥AC，垂足为F，（5分）∴AF＝12AC＝32，∴BF＝AFtan30°＝12，∴S△ABC＝12AC×BF ＝34，∴S ABCD＝334．∵S⊙O＝π ，∴P点落在四边形ABCD区域的概率＝334π＝334π．（2）解法2：作CM⊥AD，垂足为M．∵∠BCA＝∠CAD（证明过程见解法），∴BC∥AD．∴四边形ABCD为等腰梯形．∵CM＝ACsin30°＝32，∴S ABCD＝12(BC+AD)CM＝334．∵S⊙O＝π，∴P点落在四边形ABCD区域的概率＝334π＝334π．99.(2009年黄冈市)如图，已知AB是⊙O的直径，点C是⊙O上一点，连结BC，AC，过点C 作直线CD⊥AB于点D，点E是AB上一点，直线CE交⊙O于点F，连结BF，与直线CD交于点G．求证：BFBGBC⋅=2.【关键词】圆周角性质【答案】∵AB是⊙O的直径，∴∠ACB＝90°又∵CD⊥AB于点D，∴∠BCD＝90°－∠ABC＝∠A＝∠F∵∠BCD＝＝∠F，∠FBC＝∠CBG∴△FBC∽△CBG∴CBFBBGBC=∴BFBGBC⋅=2100. （2009襄樊市）如图12，已知：在O中，直径4AB=，点E是OA上任意一点，过E作弦CD AB⊥，点F是BC上一点，连接AF交CE于H，连接AC、CF、BD、OD．（1）求证：ACH AFC△∽△；（2）猜想：AH AF与AE AB的数量关系，并说明你的猜想；（3）探究：当点E 位于何处时，14?AEC BOD S S =△△::并加以说明．证明：（1）∵直径AB CD ⊥ ∴AC AD = ∴F ACH ∠=∠ 又CAF FAC ∠=∠ ∴ACH AFC △∽△（2）答：AH AF AE AB =,连接FB ∵AB 是直径，∴90AFB AEH ==︒∠∠ 又EAH FAB =∠∠ ∴Rt Rt AEH AFB △∽△∴AE AHAF AB =∴AH AF AE AB =（3）当32OE =（或12AE =）时，14AEC BOD S S =△△．::∵直径AB CD ⊥ ∴CE ED =∵1122AEC BOD S AE EC S OB ED ==△△，∴14AEC BOD S AE S OB ==△△∵O 的半径为2∴2124OE -= ∴32OE =101.（2009湖北省荆门市）如图，半径为25的⊙O内有互相垂直的两条弦AB、CD相交于P点．（1）求证：PA·PB＝PC·PD；（2）设BC中点为F，连接FP并延长交AD于E，求证：EF⊥AD；（3）若AB＝8，CD＝6，求OP的长．解:（1）∵∠A、∠C所对的圆弧相同，∴∠A＝∠C．∴Rt△APD∽Rt△CPB，∴AP PDCP PB=，∴PA·PB＝PC·PD；（2）∵F为BC中点，△BPC为Rt△，∴FP＝FC，∴∠C＝∠CPF．又∠C＝∠A，∠DPE＝∠CPF，∴∠A＝∠DPE．∵∠A＋∠D＝90°，∴∠DPE＋∠D＝90°．∴EF⊥AD．（3）作OM⊥AB于M，ON⊥CD于N，由垂径定理：∴OM2＝（52－42＝4，ON2＝（52－32＝11又易证四边形MONP是矩形，2215OM ON+=.102. 44.（2009年泸州）如图，在△ABC中，AB＝BC，以AB为直径的⊙O与AC交于点D，过D作DF⊥BC，交AB的延长线于E，垂足为F．(1)求证：直线DE是⊙O的切线；(2)当AB＝5，AC＝8时，求cosE的值．【关键词】三角函数及切线的判定. 【答案】(1)如图,连结OD 、BD. ∵AB 是⊙O 的直径, ∴∠ADB ＝90°,∴BD ⊥AC. ∵AB ＝BC,∴AD ＝DC. ∵OA ＝OB,∴OD ∥BC, ∵DE ⊥BC,OD ⊥DE, ∴直线DE 是⊙O 的切线.(2)作DH ⊥AB,垂足为H,则∠EDH+∠E ＝90°, 又∵DE ⊥OD,∴∠ODH+∠EDH ＝90°,∴∠E ＝∠ODH, ∵AD ＝DC,AC ＝8,∴AD ＝4. 在Rt △ADB 中,3452222=-=-=AD AB BD ,由三角形面积公式得:AB ·DH ＝DB ·DA,即5DH ＝4×3,解得512=DH , 在Rt △ODH 中,cos ∠ODH ＝5.2512＝2524,∴cosE ＝2524.103. （2009年常德市）如图，△ABC 内接于⊙O，AD 是△ABC 的边BC 上的高，AE 是⊙O 的直径，连接BE ，△ABE 与△ADC 相似吗？请证明你的结论．【关键词】圆 【答案】△ABE 与△ADC 相似．理由如下： 在△ABE 与△ADC 中∵AE 是⊙O 的直径， ∴∠ABE＝90o， ∵AD 是△ABC 的边BC 上的高， ∴∠ADC＝90o， ∴∠ABE＝∠ADC．又∵同弧所对的圆周角相等， ∴∠BEA＝∠DCA． ∴△ABE ～△ADC．104.如图，A 、P 、B 、C 是⊙O 上的四点，∠APC ＝∠BPC ＝ 60︒，AB 与PC 交于Q 点． （1）判断△ABC 的形状，并证明你的结论； （2）求证：QBAQPB AP =； （3）若∠ABP ＝ 15︒，△ABC 的面积为43，求PC 的长．解:（1） 证明:∵ ∠ABC ＝∠APC ＝ 60︒，∠BAC ＝∠BPC ＝ 60︒，∴ ∠ACB ＝ 180︒－∠ABC －∠BAC ＝ 60︒， ∴ △ABC 是等边三角形．（2）如图，过B 作BD ∥PA 交PC 于D ，则 ∠BDP ＝∠APC ＝ 60︒．又 ∵ ∠AQP ＝∠BQD ， ∴ △AQP ∽△BQD ，BDAPQB AQ =． ∵ ∠BPD ＝∠BDP ＝ 60︒， ∴ PB ＝ BD ． ∴PBAPQB AQ =． （3）设正△ABC 的高为h ，则 h ＝ BC · sin 60︒．∵21BC · h ＝ 43， 即21BC · BC · sin 60︒ ＝ 43，解得BC ＝ 4．连接OB ，OC ，OP ，作OE ⊥BC 于E ．由△ABC 是正三角形知∠BOC ＝ 120︒，从而得∠OCE ＝ 30︒， ∴ 3430cos =︒=CE OC ．由∠ABP ＝ 15︒ 得 ∠PBC ＝∠ABC +∠ABP ＝ 75︒，于是 ∠POC ＝ 2∠PBC ＝ 150︒． ∴ ∠PCO ＝（180︒－150︒）÷2 ＝ 15︒．如图，作等腰直角△RMN ，在直角边RM 上取点G ，使∠GNM ＝ 15︒，则∠RNG ＝ 30︒，作GH ⊥RN ，垂足为H ．设GH ＝ 1，则 cos ∠GNM ＝ cos15︒ ＝ MN ． ∵ 在Rt △GHN 中，NH ＝ GN · cos30︒，GH ＝ GN · sin30︒． 于是 RH ＝ GH ，MN ＝ RN · sin45︒，∴ cos15︒ ＝462+． 在图中，作OF ⊥PC 于E ，∴ PC ＝ 2FD ＝ 2 OC ·cos15︒ ＝36222+．105.(2009年福建省泉州市)已知：直线y ＝kx(k ≠0)经过点（3，-4）.(1)求k 的值；(2)将该直线向上平移m （m ＞0）个单位，若平移后得到的直线与半径为6的⊙O 相离（点O 为坐标原点）,试求m 的取值范围.【关键词】直线与⊙O 相离【答案】解：（1）依题意得：-4＝3k ，∴k ＝34-（2）由（1）及题意知，平移后得到的直线l 所对应的函数关系式为y ＝34-x+m(m ＞0) 设直线l 与x 轴、y 轴分别交于点A 、B ，（如图所示）当x ＝0时，y ＝m;当y ＝0时，x ＝43m. ∴A(43m,0),B(0,m)，即OA ＝43m ，OB ＝m 在Rt △OAB 中，AB ＝22OB OA + 2＝m m m 4516922=+ 过点O 作OD ⊥AB 于D ，∵S △ABO ＝21OD ·AB ＝21OA ·OB ∴21OD ·m 45＝21·43m ·m ∵m ＞0,解得OD ＝53m依题意得：53m ＞6，解得m ＞10即m 的取值范围为m ＞10.。
沪教版 九年级(上)数学 秋季课程 第9讲 圆的基本性质(解析版)
圆的基本性质是初中数学九年级下学期第一章第一节的内容．需要掌握点与圆的位置关系，理解圆心角、弧、弦、弦心距的概念和掌握它们之间的关系，重点是这四者关系的灵活运用，以及垂径定理及其推论的应用．1、圆的概念圆：平面上到一个定点的距离等于定长的所有点所成的图形．圆心：以上概念中的“定点”；以点O为圆心的圆称为“圆O”，记作O．半径：联结圆心和圆上任意一点的线段；以上概念中的“定长”是圆的半径长．2、点与圆的位置关系设一个圆的半径长为R，点P到圆心的距离为d，则有以下结论：当点P在圆外时，d > R；当点P在圆上时，d = R；当点P在圆内时，0d R≤<．反之亦然．3、相关定理：不在同一直线上的三个点确定一个圆．三角形的三个顶点确定一个圆．经过一个三角形各顶点的圆叫做这个三角形的外接圆，外接圆的圆心叫做这个三角形的外心；这个三角形叫做这个圆的内接三角形．如果一个圆经过一个多边形的各顶点，那么这个圆叫做这个多边形的外接圆，这个多边形叫做这个圆的内接多边形．圆的基本性质内容分析知识结构模块一：圆的确定知识精讲2 / 25ABCD O【例1】 在平面直角坐标系内，A （3-，tan30-︒），B （2a a，0），A 的半径为4，试说明点B 与A 的位置关系．【答案】点B 在A 外．【解析】由题意得333A ⎛⎫-- ⎪ ⎪⎝⎭，，()10B ，，所以()223733133AB ⎛⎫=--+-= ⎪ ⎪⎝⎭， 因为4AB >，所以点B 在A 外．【总结】本题考察了点与圆的位置关系，设一个圆的半径长为R ，点P 到圆心的距离为 d ，则有以下结论：当点P 在圆外时，d > R ；当点P 在圆上时，d = R ；当点P 在 圆内时，0d R ≤<．反之亦然．【例2】 过一个点可以画______个圆，过两个点可以画______个圆，过三个点可以画______个圆．【答案】无数；无数；一或零．【解析】不共线的三点才可以确定一个圆．【总结】本题考察了圆的确定，不共线的三点可以确定一个圆．【例3】 已知，如图，在O 中，AB 、BC 为弦，OC 交AB 于点D ．求证：（1）ODB OBD ∠>∠；（2）ODB OBC ∠>∠．【答案】详见解析．【解析】（1）∵OA OB =，∴OAB OBA ∠=∠，∵ODB OAB AOD ∠=∠+∠，∴ODB OBA AOD ∠=∠+∠，∴ODB OBD ∠>∠．（2）∵OC OB =，∴OBC OCB ∠=∠，∵ODB OCB DBC ∠=∠+∠，∴ODB OBC DBC ∠=∠+∠，∴ODB OBC ∠>∠．【总结】本题考查了圆的性质，利用外角是解决问题的关键．【例4】 如图，O 的半径为15，O 到直线l 的距离OH = 9，A 、B 、C 为直线l 上的三个点，AH = 9，BH = 12，CH = 15，请分别说明点A 、B 、C 与O 的位置关系．【答案】A 在O 内；B 在O 上；C 在O 外．例题解析HOlP【解析】连接OP ，∵15OP =，9OH =，∴2212PH OP OH =-=， ∵9AH HP =<，∴A 在O 内； ∵12BH HP ==，∴B 在O 上； ∵12CH HP =<，∴C 在O 外．【总结】本题考查了点与圆的位置关系．【例5】 若A （a ，27-）在以点B （35-，27-）为圆心，37为半径的圆上，求a 的值．【答案】2或72-．【解析】∵A 点在B 上，∴37BA =，即()()2235272737a ++-+=，解得12a =，272a =-．【总结】本题考查了点与圆的位置关系，注意此题有两种解．【例6】 如图，作出AB 所在圆的圆心，并补全整个圆． 【答案】如图所示．【解析】在AB 上任意作两条弦，分别做两条弦的垂直平分线，两垂直平分线的交点即为圆心．【总结】本题考查了不共线三点定圆的作法．【例7】 如图，CD 是半圆的直径，O 是圆心，E 是半圆上一点，且45EOD ∠=︒，A 是DC 延长线上一点，AE 与半圆交于B ，若AB = OC ，求EAD ∠的度数．【答案】15EAD ∠=︒．【解析】∵AB OC =，OC OB =，∴AB OB =，∴EAD BOA ∠=∠， ∴2OBE BOA EAD EAD ∠=∠+∠=∠，AB CDEO4 / 25∵OB OE =，∴E OBE ∠=∠，∴2OEB EAD ∠=∠， ∵345EOD OEA EAD EAD ∠=∠+∠=∠=︒， ∴15EAD ∠=︒．【总结】本题考查了同一个圆中半径处处相等及三角形外角的应用．【例8】 已知，如图，AB 是O 的直径，半径OC AB ⊥，过OC 的中点D 作EF // AB ．求证：12ABE CBE ∠=∠．【答案】详见解析． 【解析】连接OE ，∵OC AB ⊥，EF //AB ， ∴OC EF ⊥，OBE DEB ∠=∠，∵OB OE =，∴OBE OEB ∠=∠，∴OBE OEB DEB ∠=∠=∠，∵D 为OC 的中点，∴1122OD OC OE ==，∴30OED ∠=︒，∴1152ABE OED ∠=∠=︒，∴451530CBE CBO ABE ∠=∠-∠=︒-︒=︒，∴12ABE CBE ∠=∠．【总结】本题主要考查了等腰三角形的性质以及直角三角形性质的综合运用．【例9】 已知：AB 是O 的直径，点P 是OA 上任意一点，点C 是O 上任意一点．求证：PA PC PB ≤≤．【答案】详见解析．【解析】当P 与O 重合时，可得PA PC PB ==，当P 与O 不重合时，连接OC ，则OA = OC = OB ， ∴PA OA OP OC OP PC =-=-<，PB OP OB OP OC PC =+=+>，综上可知PA PC PB ≤≤．ABC D E F O【总结】本题考查了圆中半径处处相等，并利用三角形的三边关系解决问题．6 / 25A BCO1、 圆心角、弧、弦、弦心距的概念圆心角：以圆心为顶点的角叫做圆心角； 弧：圆上任意两点之间的部分叫做圆弧，简称弧；弦：连接圆上任意两点的线段叫做弦，过圆心的弦就是直径； 弦心距：圆心到弦的距离叫做弦心距． 2、 半圆、优弧、劣弧半圆：圆的任意一条直径的两个端点将圆分成两条弧，每一条弧都叫做半圆． 优弧：大于半圆的弧叫做优弧． 劣弧：小于半圆的弧叫做劣弧．如图，以A 、C 为端点的劣弧记作AC ，读作“弧AC ”； 以A 、C 为端点的优弧记作ABC ，读作“弧ABC ”． 3、 等弧和等圆能够重合的两条弧称为等弧，或者说这两条弧相等．若AB 与''A B 是等弧，记作''AB A B ．半径相等的两个圆一定能够重合，我们把半径相等的两个圆称为等圆． 4、 圆心角、弧、弦、弦心距之间关系的定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等．5、 圆心角、弧、弦、弦心距之间关系的定理的推论在同圆或等圆中，如果两个圆心角、两条劣弧（或优弧）、两条弦、两条弦的弦心距得到的四组量中有一组量相等，那么它们所对应的其余三组量也分别相等．模块二：圆心角、弧、弦、弦心距之间的关系知识精讲AB COABCDO【例10】 下列命题中真命题的个数是（ ）① 相等的圆心角所对的弧也相等；② 在同圆中，如果两条弦相等，那么所对的弧也相等； ③ A 、B 是O 上任意两点，则AO + BO 等于O 的直径长； ④ 三角形的外心到三角形三边的距离相等． A ．1个B ．2个C ．3个D ．4个【答案】A ．【解析】① 需说明是在同圆或等圆中，故①错误；② 一条弦对两条弧，所以需要说明是优弧还是劣弧，故②错误； ③ 易知AO 、BO 均为圆的半径，所以AO BO +为直径，故③正确； ④ 三角形的外心到三角形三个顶点的距离相等，故④错误．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理．【例11】 一条弦把圆分成1 : 3两部分，则弦所对的圆心角为______°． 【答案】90．【解析】∵一条弦把圆分成1 : 3两部分，∴整个圆分为四等分，则劣弧的度数为360490︒÷=︒， ∴弦所对的圆心角为90︒．【总结】本题考查了同圆中圆心角、弧、弦、弦心距之间的关系．【例12】 如图，在O 中，AB AC =，70B ∠=︒，则BAC ∠=______． 【答案】40︒．【解析】∵在O 中，AB AC =，∴C B ∠=∠，∵70B ∠=︒，∴18040BAC B C ∠=︒-∠-∠=︒．【总结】本题主要考查等腰三角形的性质以及三角形内角和定理的应用． 【例13】 如图，已知O 的半径是6，30BOD ∠=︒，BD BC =，CD =______．【答案】6．【解析】∵BD BC =，30BOD ∠=︒，∴30BOD BOC ∠=∠=︒，例题解析8 / 25OABC∴60COD ∠=︒，∵OC OD =，∴OCD ∆是等边三角形， ∴6CD =．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理的应用．【例14】 如图，1O 和2O 是等圆，P 是12O O 的中点，过点P 作直线AD 交1O 于点A 、B ，交2O 于点C 、D ．求证：AB = CD ．【答案】详见解析．【解析】作1O E AB ⊥于E ，2O F CD ⊥于F ，∵P 是12O O 的中点，∴1PEO ∆≌2PFO ∆，∴12O E O F =， ∵1O 和2O 是等圆，∴AB CD =．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理的应用．【例15】 已知，如图，AB 、CD 是O 的直径，弦AE // CD ，联结CE 、BC ．求证：BC = CE ． 【答案】详见解析．【解析】∵OA OE =，∴A OEA ∠=∠，∵AE //CD ，∴BOC A ∠=∠，EOC OEA ∠=∠， ∴BOC EOC ∠=∠，∴BC CE =．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理的应用．【例16】 如图，O 是ABC ∆的外接圆，AO 平分BAC ∠，AOB BOC ∠=∠，判断ABC∆的形状，并说明理由．【答案】等边三角形．【解析】∵AO 平分BAC ∠，∴BAO CAO ∠=∠，∵OA OC OB ==，∴ABO BAO CAO ACO ∠=∠=∠=∠， ∴AOB AOC ∠=∠，∵AOB BOC ∠=∠，∴AOB AOC BOC ∠=∠=∠，FABCDPEA BCDEO∴AB BC CA ==，∴ABC ∆是等边三角形．【总结】本题考查同圆中相等的圆心角所对的弦相等．【例17】 已知，如图，AB 是O 直径，M 、N 分别是AO 、BO 的中点，CM AB ⊥，DN AB ⊥．求证：AC BD =．【答案】详见解析．【解析】连接OC 、OD ，则OC OD =，∵M 、N 分别是AO 、BO 的中点，∴OM ON =， ∵CM AB ⊥，DN AB ⊥，∴OCM ∆≌ODN ∆， ∴COM DON ∠=∠，∴AC BD =．【总结】本题考查了同圆中相等的圆心角所对的弧相等．【例18】 如图，以点O 为圆心的圆弧上依次有四个点A 、B 、C 、D ，且AOB COD ∠=∠．求证：四边形ABCD 是等腰梯形．【答案】详见解析． 【解析】连接AC 、BD ，∵AOB COD ∠=∠，∴AB CD =，∵12ACB AOB ∠=∠，12CAD COD ∠=∠，∴ACB CAD ∠=∠，∴AD ∥BC ，∴四边形ABCD 是等腰梯形．【总结】本题综合性较强，主要考查了同一条弦所对的圆周角和圆心角的关系，老师可 以选择性的讲解．1、 垂径定理如果圆的一条直径垂直于一条弦，那么这条直径平分这条弦，并且平分这条弦所对的弧． 2、 相关结论（1）如果圆的直径平分弦（这条弦不是直径），那么这条直径垂直于这条弦，并且模块三：垂径定理知识精讲ABCDONM OAB CD10 / 25CE FO平分这条弦所对的弧．（2）如果圆的直径平分弧，那么这条直径就垂直平分这条弧所对的弦． （3）如果一条直线是弦的垂直平分线，那么这条直线经过圆心，并且平分这条弦所对的弧．（4）如果一条直线平分弦和弦所对的一条弧，那么这条直线经过圆心，并且垂直于这条弦．（5）如果一条直线垂直于弦，并且平分弦所对的一条弧，那么这条直线经过圆心，并且平分这条弦．总结：在圆中，对于某一条直线“经过圆心”、“垂直于弦”、“平分弦”、“平分弦所对的弧”这四组关系中，如果有两组关系成立，那么其余两组关系也成立．【例19】 O 的直径为10，圆心O 到弦AB 的距离OM 的长为3，则弦AB 的长为______． 【答案】8．【解析】∵O 的直径为10，∴5OB =，∵OM AB ⊥，∴OM 平分AB ， ∴224BM OB OM =-=，∴28AB BM ==． 【总结】本题考查了垂径定理的运用．【例20】 在半径为2的O 中，弦AB 的长为22，则弦AB 所对的圆心角AOB ∠=____°． 【答案】90．【解析】作OD AB ⊥于D ，则2AD BD ==，∵2OB =，∴222OD OB BD =-=，∴45BOD ∠=︒，∴90AOB ∠=︒．【总结】本题考查了垂径定理的运用．【例21】 如图，O 是ABC ∆的外接圆，圆心O 在这个三角形的高CD 上，点E 和点F分别是边AC 和BC 的中点．例题解析求证：四边形CEDF 是菱形．【答案】详见解析．【解析】∵CD AB ⊥，且CD 过圆心，∴AD BD =，∴CA CB =，∵点E 和点F 分别是边AC 和BC 的中点，∴12CE AC =，12DE AC =，12CF BC =，12DF BC =，∴CE DE DF CF ===，∴四边形CEDF 是菱形．【总结】本题考查了垂径定理的运用即菱形的判定．【例22】 如图，一根横截面为圆形的输水管道，阴影部分为有水部分，此时水面宽AB为0.6米，污水深CD 为0.1米，求圆形的下水管道的直径．【答案】1米．【解析】连接OB ，设圆半径为R ，则0.1OD R =-， 10.32BD AB ==，由222OD BD OB +=得()2220.10.3R R -+=，解得0.5R =， 所以下水管道的直径为1米．【总结】本题考查了垂径定理以及勾股定理的综合运用．【例23】 如图，在O 中，弦CD 、EF 的延长线相交于点P ，G 、H 分别是CD 、EF 的中点，GH 与PC 、PE 分别相交于Q 、R 两点，试判断PQR ∆的形状，并证明所得到的结论．【答案】等腰三角形． 【解析】连接OG 、OH ，∵G 、H 分别是CD 、EF 的中点，∴OG CD ⊥，OH EF ⊥，∵OH OG =，∴H G ∠=∠，∴GQC HRE ∠=∠，∴PQR PRQ ∠=∠， ∴PQR ∆是等腰三角形．【总结】本题考查了垂径定理的运用．ABCD O CDEFG HO PQR12 / 25B CDH O【例24】 如图，P 是O 的弦AB 的中点，PC OA ⊥，垂足为C ，求证：PA PB AC AO =． 【答案】详见解析．【解析】连接OP ，∵P 是O 的弦AB 的中点，∴OP AB ⊥，∵PC OA ⊥，∴ACP ∆∽APO ∆，∴PA AOAC PA =，∵PA PB =， ∴PA AOAC PB=，即PA PB AC AO =． 【总结】本题考查了垂径定与相似三角形的综合运用．【例25】 位于本市浦东临港新城的滴水湖是圆形人工湖．为测量该湖的半径，小智和小方沿湖边选取A 、B 、C 三根木柱，使得A 、B 之间的距离与A 、C 之间的距离相等，并测得BC 长240米，A 到BC 的距离为5米，如图所示．请你帮他们求出滴水湖的半径．【答案】1442.5米．【解析】连接OA 交BC 于D 点，连接OC ，∵A 、B 之间的距离与A 、C 之间的距离相等， ∴OA BC ⊥，BD DC =，设半径为R ，则5OD R =-，120DC =，由222OD DC OC +=，∴()2225120R R -+=，解得：1442.5R =， 所以滴水湖的半径为1442．5米．【总结】本题考查了垂径定理的运用．【例26】 如图，弦CD 垂直于O 的直径AB ，垂足为H ，且22CD =，3BD =，则OPABCBCAODAB 的长为_______．【答案】3．【解析】由题意得2DH =，221BH DB DH =-=，设半径为R ，则1OH R =-，由222OD OH HD =+，∴()()22212R R =-+，解得32R =，∴23AB R ==．【总结】本题考查了垂径定理的运用．【例27】 已知O 的半径4r =，AB 、CD 为O 的两条弦，AB 、CD 的长分别是方程()24341630x x -++=的两根，其中AB > CD ，且AB // CD ，求AB 与CD 间的距离．【答案】232+或232-．【解析】∵()24341630x x -++=，解得：143x =，24x =．∵AB >CD ，∴43AB =，4CD =，当AB 、CD 圆心同侧时，作OE AB ⊥于E ，并延长交CD 于F ，∵AB // CD ，∴OF ⊥CD ，∴222OE OB BE =-=，2223OF OD DF =-=， ∴232EF OF OE =-=-，当AB 、CD 圆心两侧时，同理可得232EF OF OE =+=+， ∴AB 与CD 间的距离是232+或232-．【总结】本题考查了垂径定理的运用，做题的关键是要分情况讨论．14 / 25【例28】 已知，如图，1O 与2O 交于A 、B ，过A 的直线分别交1O 与2O 于M 、N ，C 是MN 的中点，P 是12O O 的中点． 求证：PA PC =．【答案】详见解析．【解析】作1O E AM ⊥，2O F AN ⊥，作PH MN ⊥于H ，则12////O E PH O F ，且E 、F 分别为AM 、AN 的中点，∴12AE AF EF MN +==，∵C 是MN 的中点，∴12NC MN =，∴EF NC =，∴EC FN AF ==，∵P 是12O O 的中点，∴EH FH =， ∴HC HA =，∴PA PC =．【总结】本题考查了垂径定理的运用．【例29】 如图，已知四边形ABCD 外接圆O 的半径为2，对角线AC 与BD 的交点为E ，AE = EC ，2AB AE =，且23BD =，求四边形ABCD 的面积．【答案】23．【解析】∵AE EC =，2AB AE =，∴222AB AE AE AC ==⋅，∴AB AE AC AB=，又EAB BAC ∠=∠，∴ABE ∆∽ACB ∆， ∴ABE ACB ∠=∠，∵ADB ACB ∠=∠，∴ABE ADB ∠=∠，∴AB AD =， 连接AO 交BD 于H ，连接BO ，∵AB AD =，∴AO BD ⊥，∴3BH DH ==， ∵2OB =，∴1OH =，∴1AH =，∴132ABD S BD AH ∆=⋅⋅=，∵E 为AC 中点，∴ABE CBE S S ∆∆=，ADE CDE S S ∆∆=，即ABD CBD S S ∆∆=， ∴223ABD ABCD S S ∆==四边形， ∴四边形ABCD 的面积是23．【总结】本题考查了垂径定理的运用及图形的分割，综合性较强，解题时注意认真观察．A BCP N ME FH A BC DEOH【例30】 如图，在半径为2的扇形AOB 中，90AOB ∠=︒，点C 是弧AB 上的一个动点（不与点A 、B 重合），OD BC ⊥，OE AC ⊥，垂足分别为D 、E ．（1）在DOE ∆中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由．（2）设BD = x ，DOE ∆的面积为y ，求y 关于x 的函数关系式，并写出它的定义域．【答案】（1）DE 长度不变，2DE =；（2）()2244024x x x y x -+-=<<．【解析】（1）连接AB ，∴2222AB OA OB =+=，∵OD BC ⊥，OE AC ⊥， ∴D 、E 分别为BC 、AC 中点，∴122DE AB ==．（2）作DF OE ⊥于F ，由（1）易得1452DOE AOB ∠=∠=︒，由题意得24OD x =-，∴28222ODx DF OF -===，2222EF DE EF x =-=， ∴28222x xOE OF EF -+=+=，OABCDEF∴2214402 2x x xy DF OE x-+-=⋅⋅=<<．【总结】本题考查了垂径定理、勾股定理及中位线定理的综合运用，综合性较强．16/ 25A BC D EF OABCDE O【习题1】已知O 半径为5，若点P 不在O 上，则线段OP 的取值范围为_______________．【答案】05OP ≤<或5OP >．【解析】∵点P 不在O 上，∴当点P 在O 内时，05OP ≤<；当点P 在O 外时， 5OP >，综上可知05OP ≤<或5OP >． 【总结】本题考查了点与圆的位置关系．【习题2】如图，AB 是直径，BC CD DE ==，40BOC ∠=︒，则AOE ∠=_____．【答案】60︒．【解析】∵BC CD DE ==，∴BOC COD DOE ∠=∠=∠，∵40BOC ∠=︒，∴180360AOE BOC ∠=︒-∠=︒． 【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理．【习题3】如图，为方便三个村庄居民子女的上学问题，上级镇政府决定在A 、B 、C 三个村庄旁边造一所学校，要求它到各村庄的距离相等，请你在图中画出学校的位置．（保留作图痕迹）【答案】如图所示．【解析】作线段AB 、AC 的中垂线的交点P 即为学校位置．【总结】本题考查了不共线的三点可以确定一个圆． 【习题4】如图，AB CD =，OE AB ⊥，OF CD ⊥，25OEF ∠=︒，求EOF ∠的度数．随堂检测18 / 25AB CD EOCDE FO【答案】130︒．【解析】∵AB CD =，OE AB ⊥，OF CD ⊥，∴OE OF =，∴OEF OFE ∠=∠，∵25OEF ∠=︒， ∴1801802130EOF OEF OFE OEF ∠=︒-∠-∠=︒-∠=︒．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理．【习题5】如图，在ABC ∆中，90B ∠=︒，60A ∠=︒，以点B 为圆心，AB 为半径画圆，交AC 于点D ，交BC 于点E ．求证：（1）2AD DE =；（2）D 是AC 的中点．【答案】详见解析．【解析】（1）连接BD ，∵BA BD =，60A ∠=︒，∴ABD ∆是等边三角形，∴60ABD ∠=︒，∵90B ∠=︒，∴30DBC ∠=︒，∴2ABD DBC ∠=∠， ∴2AD DE =；（2）由（1）得60ADB ∠=︒，DB DA =，∵ADB DBC C ∠=∠+∠，∴30C ∠=︒，∴DB DC =，∴DA DC =， ∴D 是AC 的中点．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理．【习题6】如图，AB 为O 直径，E 为BC 的中点，OE 交BC 于点D ，BD = 3，AB =10，则AC =______．【答案】8．【解析】∵AB 为O 直径，E 为BC 的中点，∴OD BC ⊥，BD CD =，∴224OD OB BD =-=， ∵OA OB =，∴28AC OD ==．【总结】本题考查了垂径定理及三角形中位线． 【习题7】如图，一条公路的转弯处是一段圆弧（即图中的CD ），点O 是CD 的圆心，其中CD = 600米，E 为CD 上一点，且OE CD ⊥，垂足为F ，EF = 90米，求这段弯路的半径．【答案】545米．【解析】∵点O 是CD 的圆心，OE CD ⊥，AB CD E∴13002DF CD ==，设O 的半径为R ，则90OF R =-，由222OD OF FD =+得()22290300R R =-+，解得545R =， ∴这段弯路的半径为545米．【总结】本题考查了垂径定理的应用．【习题8】如图，在ABC ∆中，70A ∠=︒，O 截ABC ∆的三边所得的弦长都相等，求BOC ∠的度数．【答案】125︒．【解析】作OE AB ⊥、OF BC ⊥、OG AC ⊥，∵O 截ABC ∆的三边所得的弦长都相等， ∴OE OF OG ==，∴OB 平分ABC ∠，OC 平分ACB ∠， ∵70A ∠=︒，∴110ABC ACB ∠+∠=︒，∴115522OBC OCB ABC ACB ∠+∠=∠+∠=︒，∴18055125BOC ∠=︒-︒=︒．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理、角平分线的逆定理及三角形的内角和．【习题9】已知，如图，ABC ∆是等边三角形，AB 是O 的直径，AE EF FB ==，CE 、CF 交AB 于点M 、N ． 求证：AM = MN = NB ．【答案】详见解析． 【解析】连接OE 、OF ，∵AE EF FB ==，∴60AOE EOF FOB ∠=∠=∠=︒， ∵ABC ∆是等边三角形，ABCOEFG ABCE FN MO20 / 25∴CAO AOE ∠=∠，∴OE //AC ，∴OM OEMA AC=． ∵AC BC =，O 是AB 中点， ∴1302ACO ACB ∠=∠=，∴12OA AC =，∴12OE AC =．∴2AM OM =，∴23AM OA =，13OM OA =， 同理23BN OB =，13ON OB =，∵OA OB =，∴23OM ON OA +=，∴AM MN NB ==．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理及平分线分线段成比例．【习题10】 如图，AB 为O 的直径，CD 为弦，过点C 、D 分别作CN CD ⊥、DM CD ⊥，分别交AB 于点N 、M ，请问图中的AN 与BM 是否相等，说明理由．【答案】AN 与BM 相等． 【解析】作OH CD ⊥交CD 于H ，则CH DH =，∵CN CD ⊥、DM CD ⊥， ∴CN ∥OH ∥DM ，∴ON OM =， ∵OA OB =，∴OA ON OB OM -=-， ∴AB BM =．【总结】本题考查了垂径定理及梯形的中位线．【作业1】在下列命题中，正确的个数是（ ） ① 圆心角相等，则它们所对的弦必相等；② 经过线段的两个端点及线段所在直线外一点可以确定一个圆； ③ 直径平分弦，则必垂直于弦；④ 如果同圆中，两条弦互相平分，那么这两条弦都是直径． A ．0个B ．1个C ．2个D ．3个【难度】★ 【答案】B ．【解析】① 需说明是在同圆或等圆中，故①错误；课后作业ABCDON M H② 不共线的三点可以确定一个圆，故②正确； ③ 直径平分非直径的弦，则必垂直于弦，故③错误； ④ 如果同圆中，直径垂直于弦，则必然平分弦，故④错误．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理及垂径定理．【作业2】在ABC ∆中，90C ∠=︒，D 、E 分别是AB 、AC 的中点，AC = 7，BC = 4．若以点C 为圆心，BC 为半径作圆，判断点D 、E 与C 的位置关系．【答案】点D 在C 外；点E 在C 内．【解析】∵AC = 7，BC = 4，90C ∠=︒，∴2265AB AC BC =+=，∵4C R =，16522DC AB R ==>，∴点D 在C 外； 1722EC AC R ==<，∴点E 在C 内． 【总结】本题考查了点与圆的位置关系．【作业3】已知直线a 和直线外两点A 、B ，经过A 、B 作一圆，使它的圆心在直线a上．【答案】如图所示．【解析】作线段AB 的中垂线于直线a 的交点P即为圆心．【总结】本题考查了线段的垂直平分线的作法．22 / 25【作业4】已知O 外一点A 和圆上的点最大距离为23厘米，最小距离为10厘米，则O 的半径为______厘米． 【答案】132．【解析】点A 与圆心的连心线所在的直线与圆的交点即为点A 到圆上的最大距离和最小距离，所以半径()13231022R =-÷=厘米．【总结】本题考查了点与圆的位置关系．【作业5】如图，在O 中，2AB BC =，试确定AB 与2BC 的大小关系．【答案】2AB BC <．【解析】取AB 中点E ，∵2AB BC =，∴AE EB BC ==，∵AE EB AB +>， ∴2AB BC <．【总结】本题考查了圆心角、弧、弦、弦心距之间关系的定理．【作业6】如图，矩形ABCD 与圆心在AB 上的O 交于点G 、B 、F 、E ，GB = 8厘米，AG = 1厘米，DE = 2厘米，则EF = ______厘米．【答案】6．【解析】连接OE ，作OH DC ⊥于H 点，∵GB = 8厘米，AG = 1厘米，DE = 2厘米， ∴4OE =厘米，3EH =厘米， ∴26EF EH ==厘米．【总结】本题考查了垂径定理的应用．【作业7】已知点A （1，0），B （4，0），P 是经过A 、B 两点的一个动圆，当P与y 轴相交，且在y 轴上两交点的距离为3时，求圆心P 的坐标．【答案】5522⎛⎫ ⎪⎝⎭，或5522⎛⎫- ⎪⎝⎭，． OABCD EF GHAB COEOP ABC【解析】设()P x y ，∵P 是经过A 、B 两点的一个动圆，∴P 在线段AB 的中垂线上，∵A （1，0），B （4，0），∴52x =且P 在x 轴上两交点的距离为3，∵P 与y 轴相交，且在y 轴上两交点的距离为3， ∴P 在x 轴上与y 轴上截得的两条弦相等．∴x y =，∴52y =±，∴P 点坐标为5522⎛⎫ ⎪⎝⎭，或5522⎛⎫- ⎪⎝⎭，．【总结】本题考查了垂径定理的应用．【作业8】已知，如图，在O 中，弦AB 的长是半径OA 的3倍，C 为AB 的中点，AB 、OC 相交于P ．求证：四边形OACB 为菱形．【答案】详见解析．【解析】∵C 为AB 的中点，∴OC AB ⊥，AP PB =，∵弦AB 的长是半径OA 的3倍，∴32AP AO =，∴30PAO ∠=︒， ∴1122PO OA OC ==，即OP PC =，∵AP BP =，OC AB ⊥，∴四边形OACB 为菱形．【总结】本题考查了垂径定理的应用及菱形的判定．【作业9】已知：过圆O 内一点P 作弦AB 、CD ，且AB = CD ，在BD 上取两点E 、AC OPM N24 / 25F ，且BE DF =．求证：直线PO 是EF 的垂直平分线．【答案】详见解析．【解析】作OM AB ⊥，ON CD ⊥，∵AB = CD ，∴OM ON =，BM DN =， ∴POM ∆≌PON ∆，∴PM PN =，∴PB PD =，∵OB OD =，PO PO =，∴OPB ∆≌OPD ∆， ∴POB POD ∠=∠，∵BE DF =，∴BOE DOF ∠=∠， ∴POE POF ∠=∠，∴EOH FOH ∠=∠，∵OE OF =， ∴直线PO 是EF 的垂直平分线．【总结】本题考查了垂径定理及圆心角、弧、弦、弦心距之间关系的定理的综合应用．【作业10】 如图，1O 与2O 交于A 、B ，M 为12O O 的中点，过点A 作EF AM ⊥分别交1O 与2O 于点E 、F ．若1290O AO ∠=︒，1212AO AO O O m ==（2m ≥），求EF 的长．【答案】4．【解析】作1O C AE ⊥于C 点，并延长与2O A 的延长线交于G 点，作2O D AF ⊥于D 点，∵EF AM ⊥，M 为12O O 的中点，∴AC AD =，∴2O AD ∆≌GAC ∆，∴2AG AO =，∵1290O AO ∠=︒，∴1O AC ∆∽1O GA ∆，∴11O A AG O G AC ⋅=⋅， ∴121O A AO O G AC ⋅=⋅，∵1212AO AO O O m ==，∴121O O O G AC =⋅，∵1290O AO ∠=︒，2AG AO =，∴121O O O G =， ∴1AC =，∴44EF AC ==．【总结】本题考查了垂径定理及相似三角形性质的综合应用．ABEFMGC D。
圆的基本性质及应用题型
圆的基本性质及应用题型1. 圆的定义和基本术语圆是平面上所有到一个固定点的距离都相等的点的集合。
固定点称为圆心，到圆心的距离称为半径。
在圆上任意取两个点，将它们和圆心连线，得到的线段称为弦。
若弦通过圆心，则称其为直径，直径等于2倍的半径。
若弦和圆心不重合，则称其为弧。
2. 圆的基本性质2.1 圆的周长和面积圆的周长称为圆周，用C表示，圆的面积用S表示。
圆周的计算公式为：C = 2πr，其中r为圆的半径。
圆的面积计算公式为：S = πr^2，其中r为圆的半径。
2.2 弧长和扇形面积从圆上截取的弧，可以计算其长度，称为弧长。
弧长的计算公式为：L = 2πr * (θ/360°)，其中θ为弧所对的圆心角的度数。
另外，可以从圆上截取一个扇形，扇形的面积为扇形的弧长与圆周的比例乘以圆的面积。
扇形的面积计算公式为：A = (θ/360°) * πr^2，其中θ为扇形的圆心角的度数。
3. 圆的应用题型3.1 弧长和扇形面积的应用例题1：一个半径为5cm的圆，截取一个占据1/4的扇形，请计算该扇形的面积和弧长。
解答：已知半径r = 5cm，圆心角θ = 360° / 4 = 90°。
根据扇形的面积计算公式可知，A = (90°/360°) * π * 5^2 = 6.25π cm^2。
根据弧长的计算公式可知，L = 2π * 5 * (90°/360°) = 5π cm。
所以该扇形的面积为6.25π cm^2，弧长为5π cm。
3.2 圆的周长和面积的应用例题2：一个圆的周长为20cm，请计算该圆的面积。
解答：已知圆周长为20cm，根据圆周的计算公式可知，C = 2πr = 20 cm。
由此可算得圆的半径r = 10/π cm ≈ 3.18 cm。
根据圆的面积计算公式可知，S = πr^2 = π * (10/π)^2 = 100/π cm^2。
圆的基本性质知识点及典型例题
圆的基本性质一、知识点梳理★知识点一：圆的定义及有关概念1、圆的定义：平面内到定点的距离等于定长的所有点组成的图形叫做圆。
2、有关概念：弦、直径;弧、等弧、优弧、劣弧、半圆;弦心距;等圆、同圆、同心圆。
圆上任意两点间的部分叫做圆弧，简称弧。
连接圆上任意两点间的线段叫做弦，经过圆心的弦叫做直径，直径是最长的弦。
在同圆或等圆中，能够重合的两条弧叫做等弧。
★知识点二：平面内点与圆的位置关系：r表示圆的半径，d表示同一平面内点到圆心的距离，则有点在圆外；点在圆上；点在圆内。
例1、如图，在中，直角边，，点，分别是，的中点，以点为圆心，的长为半径画圆，则点在圆A的_________，点在圆A的_________．例2、在直角坐标平面内，圆的半径为5，圆心的坐标为．试判断点与圆的位置关系．例3、下列说法中，正确的是。
（1）直径是弦，但弦不一定是直径；（2）半圆是弧，但弧不一定是直径；（3）半径相等的两个半圆是等弧；（4）一条弦把圆分成两段弧中，至少有一段优弧。
例4、有下列四个命题：（1）直径相等的两个圆是等圆；（2）长度相等的两条弧是等弧；（3）圆中最大的弦是通过圆心的弦；（4）一条弦把圆分成两条弧，这两条弧不可能是等弧，其中真命题是。
★知识点三：垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。
推论：平分弦（）的直径垂直于这条弦，并且平分弦所对的弧。
平分弧的直径垂直平分弧所对的弦。
垂径定理最重要的应用是通过勾股定理来解决有关弦、半径、弦心距等问题例1：下列语句中正确的是。
（1）相等的圆心角所对的弧相等；（2）相等的弧所对的弦相等；（3）平分弦的直径垂直于弦；（4）弦的垂直平分线必过圆心。
例2、过⊙内一点M的最长弦长为10cm，最短弦长为8cm，那么OM的长为（）（A）3cm （B）6cm （C）cm （D）9cm例3、如图所示,以O为圆心的两个同心圆中,小圆的弦AB的延长线交大圆于C,若AB=6,BC=1,则与圆环的面积是例4、在半径为5厘米的圆内有两条互相平行的弦,一条弦长为8厘米,另一条弦长为6厘米,则两弦之间的距离为_______.7厘米或1厘米例5、如图，矩形ABCD与与圆心在AB上的⊙O交于点G、B、F、E，GB=8cm，AG=1cm，DE=2cm，则EF=cm.例6、如图所示，是一个直径为650mm的圆柱形输油管的横截面，若油面宽AB=600mm，求油面的最大深度。
圆的有关性质汇总
圆的面积
圆的面积是指圆所占平面的大小，计算公式为 $A = pi r^2$。
输入 标题
详细描述
这个公式是由圆的半径和π的乘积得出的。这个公式 在几何学和数学中非常重要，它可以帮助我们计算各 种与圆有关的量，如圆的周长、圆的体积等。
总结词
总结词
根据圆的面积公式和直径与半径的关系，我们可以得 出直径是半径的两倍。
如果四个点都在同一个圆上，则这四 个点之间的距离相等。
圆的基本性质
01
02
03
04
圆心性质
圆心到圆上任一点的距离都相 等，即圆的半径。
直径性质
通过圆心且两端点在圆上的线 段称为直径，直径等于半径的
两倍。
弦的性质
连接圆上任意两点的线段称为 弦，弦的长度小于直径。
弧的性质
圆上任意两点之间的曲线段称 为弧，弧的长度小于半圆周长
详细描述
通过圆的面积公式，我们可以推导出圆的半径和直径 的关系，即 $d = Nhomakorabea2r$。
圆的体积
总结词
圆的体积是指三维空间中，一个圆所占的空间大 小。
总结词
通过球的体积公式，我们可以推导出球的半径和 直径的关系，即 $d = 3r$。
详细描述
在几何学中，我们通常使用球的体积公式来计算 一个球的体积，这个公式为 $V = frac{4}{3} pi r^3$。这个公式可以帮助我们计算各种与球有关 的量，如球的表面积、球的重量等。
该方程描述了一个以原点为中心，半径为$r$的圆，圆上任一 点的极径$rho$等于半径$r$。
THANKS
感谢观看
02 对于任意一条与圆相切的直线L，
关于圆心O的对称直线L'与圆平 行，且OL=OL'。
圆的基本性质(解析版)
一、选择题9．（2020·杭州）如图，已知BC是⊙O的直径，半径OA⊥BC，点D在劣弧AC上（不与点A，点C重合），BD与OA交于点E．设∠AED=α，∠AOD=β，则（）A．3α＋β＝180°B．2α＋β＝180°C．3α－β＝90°D．2α－β＝90°{答案}D{解析}本题考查了同圆的半径相等，三角形的内角和定理以及三角形的外角．因为OA⊥BC，所以∠AOB＝90°．因为OB＝OD，所以∠B＝∠D．在△OBD中，∠B＋∠D＋∠BOD＝180°，即2∠D＋90°＋β＝180°，所以2∠D＋β＝90°．因为∠AED是△ODE的外角，所以∠D＝∠AED－∠AOD＝α－β，所以2(α－β)＋β＝90°，整理，得2α－β＝90°，因此本题选D．4．（2020·绍兴）如图．点A，B，C，D，E均在⊙O上．∠BAC=15°，∠CED=30°，则∠BOD的度数为（）A．45°B．60°C．75°D．90°{答案}D{解析}本题考查了圆周角、圆心角以及它们所对的弧的度数之间的关系．在同圆中，圆周角的度数等于它所对的弧的度数的一半，圆心角的度数等于它所对的弧的度数，因为∠BAC=15°，∠CED=30°，所以弧BC是30°，弧CD是60°，则弧BD是90°，故它所对的圆心角∠BOD的度数是90°．因此本题选D．4．（2020湖州）如图，已知四边形ABCD内接于⊙O，∠ABC＝70°，则∠ADC的度数是（）A．70°B．110°C．130°D．140°【分析】根据圆内接四边形的性质即可得到结论．【解答】解：∵四边形ABCD内接于⊙O，∠ABC＝70°，∴∠ADC＝180°﹣∠ABC＝180°﹣70°＝110°，故选：B．7．（2020·黔东南州）如图，⊙O的直径CD＝20，AB是⊙O的弦，AB⊥CD，垂足为M，OM：OC＝3：5，则AB的长为（）A．8B．12C．16D．2√91{答案}C {解析}如图，连接OA，∵⊙O的直径CD＝20，OM：OD＝3：5，∴OD＝10，OM＝6.∵AB⊥CD，∴AM=√OA2−OM2=√102−62=8，∴AB＝2AM＝16．9．（2020·安徽）已知点A，B，C在⊙O上，则下列命题为真命题的是（）A．若半径OB平分弦AC，则四边形OABC是平行四边形B．若四边形OABC是平行四边形，则∠ABC＝120°C．若∠ABC＝120°，则弦AC平分半径OBD．若弦AC平分半径OB，则半径OB平分弦AC{答案}B{解析}逐项分析如下：选项逐项分析图示真假命题AEDOC连接BD，则△D的大小（）A．55°B．65°C．60°D．75°第9题图{答案}B{解析} E是弦BC的中点，由垂径定理的逆定理可知OE△BC，连接OB、OC，由△A＝50°可知△BOC＝2△A＝100°，由等腰三角形的“三线合一”可知△BOD＝50°，在等腰△BOD中，△D＝(180°－50°)÷2＝65°．第9题答图6．（2020·青岛）如图，BD是⊙O的直径，点A，C在⊙O上，弧AB=弧AD，AC交BD于点G.若∠COD=126°，则∠AGB的度数为（）A.99°B.108°C.110°D.117°{答案}B{解析}本题考查了圆周角定理及其推论的应用，解答过程如下：∵BD是⊙O的直径，∴∠BAD=90°.∵弧AB=弧AD ，∴∠ADB=∠ABD=45°.∵∠COD=126°，∴∠CAD=12∠COD=12×126°=63°.∴∠AGB=∠ADB+∠CAD=45°+63°=108°. 因此本题选B ．8．（2020·泰安）如图，△ABC 是⊙O 的内接三角形，AB ﹦BC ，∠BAC ﹦30°，AD 是直径，AD ﹦8，则AC 的长为（ ） A ．4B ．4 3C ．833 D ．2 3{答案} B{解析}本题考查了等腰三角形的性质、直径所对的圆周角是直角以及锐角三角函数，因为△ABC 中，AB ﹦BC ，∠BAC ﹦30°，所以∠B=120°，因为四边形ABCD 内接于⊙O ，所以∠D=60°.因为AD 是⊙O 的直径，所以∠ACD=90°.因为sin ∠D=ACAD ，所以AC=AD ·sin ∠D=8×√32=4 3 ，因此本题选B ． 7. （2020·淮安）如图,点A 、B 、C 在⊙O 上,∠ACB=54°,则∠ABO 的度数是（ ）A.54°B.27°C.36°D.108°{答案} C{解析}本题考查了同弧所对的圆周角和圆心角的关系，由已知得△AOB=2∠ACB=108°，再在等腰三角形AOB 中由三角形的内角和定理求出△ABO 的度数． ∵∠ACB=54°，∴∠AOB=2∠ACB=108°， ∵OA=OB ，∴∠ABO=∠OAB=（180°-108°）÷2=36°． 故选C ．9．（2020·福建）如图，四边形ABCD 内接于⊙O ，AB =CD ，A 为BD ⏜中点，∠BDC =60°，则∠ADB 等于（ ）AD（第8题）A.40°B.50°C.60°D.70°{答案}A{解析}本题考查了弧，弦，圆周角等的关系，∵AB =CD ，A 为BD ⏜中点，∴AB ⏜=AD ⏜=CD ⏜，∵∠BDC =60°，∴优弧BAC 是240°，∴弧AB 是80°，∴∠ADB =40°，因此本题选A ．7．(2020·荆门)如图4，⊙O 中，OC ⊥AB ，∠APC ＝28°，则∠BOC 的度数为( ) A ．14° B ．28° C ．42° D ．56°{答案}D{解析}连结OA ．由垂径定理可知AC ＝BC ，∴∠BOC ＝∠AOC ．由圆周角定理可知∠AOC ＝2∠P ＝56°．∴∠BOC ＝56°．故选D ．16．（2020·镇江）如图，AB 是半圆的直径，C 、D 是半圆上的两点，∠ADC =106∘ ，则 ∠CAB 等于( )A ．10∘B ．14∘C ．16∘D ．26∘{答案}C{解析}本题考查了圆周角相关知识，连接BC ，则∠B ＋∠D ＝180°，∵∠ADC ＝106°，∴∠B ＝74°，∵AB 为⊙O 的直径，∴∠ACB ＝90°，∴∠CAB ＝16°．7．（2020·常州）如图，AB 是⊙O 的弦，点C 是优弧AB 上的动点(C 不与A 、B 重合)，CH ⊥AB ，垂足为H ，点M 是BC 的中点．若⊙O 的半径是3，则MH 长的最大值是( ) A ．3 B ．4 C ．5 D ．6(第7题)OABCDPC ABO图4{答案}A{解析}{解析}本题考查了直角三角形斜边中线等于斜边的一半，因为∠BHC ＝90°，M 为BC 的中点，所以MH ＝12BC ，而BC 的最大值是直径，所以MH 的最大值等于3．5．（2020·天水）如图所示，P A 、PB 分别与⊙O 相切于A 、B 两点，点C 为⊙O 上一点，连接AC 、BC ，若∠P ＝70°，则∠ACB 的度数为（ ） A ．50° B ．55° C ．60° D ．65°{答案}B{解析}根据切线的性质和圆周角定理可求，连接OA 、OB ，则∠ACB ＝12∠AOB ，又由P A 、PB 分别与⊙O相切于A 、B 两点，得到∠P AO ＝∠PBO ＝90°，所以∠AOB ＝180°－∠P ＝180°－70°＝110°，从而得到∠ACB ＝12×110°＝55°，因此本题选B ．5. （2020·张家界）如图，四边形ABCD 为⊙O 的内接四边形，已知∠BCD 为120°，则∠BOD 的度数为（ ）A. 100°B. 110°C. 120°D. 130°{答案}C{解析}本题考查的是圆内接四边形的性质，掌握圆内接四边形的对角互补是解题的关键． 根据圆内接四边形的性质求出∠A ，根据圆周角定理计算，得到答案． 解：∵四边形ABCD 是⊙O 内接四边形， ∴∠A ＝180°−∠BCD ＝60°，由圆周角定理得，∠BOD ＝2∠A ＝120°， 故选：C ．14．（2020·河北）有一题目:“已知:点O 为△ABC 的外心，∠BOC =130°，求∠A .”嘉嘉的解答为:画 以及它的外接圆O ，连接OB ，OC ，如图8.由∠BOC =2∠A =130°，得∠A =65°. 而淇淇说:“嘉嘉考虑的不周全， 还应有另一个不同的值.” 下列判断正确的是A.淇淇说的对，且∠A的另一个值是115°B.淇淇说的不对，∠A就得65°C.嘉嘉求的结果不对，∠A应得50°D.两人都不对，应有3个不同值{答案}A{解析}如图1，当∠A是锐角时，△ABC的外心O在其内部，∠A=65°；如图2，当∠A是钝角时，△ABC的外心O在其外部，∵∠1=2∠A，∴∠A=12∠1=12×230°=115°.故∠A=65°或115°，答案为A.7.（2020·牡丹江）如图，点A，B，S在圆上，若弦AB的长度等于圆半径的√2倍，则∠ASB的度数是（）A．22.5°B．30°C．45°D．60°{答案}C{解析}设圆心为O，连接OA，OB，如图，∵弦AB的长度等于圆半径的√2倍，即AB＝√2OA＝√2OB，∴OA2+OB2＝AB2，∴△OAB为等腰直角三角形，∠AOB＝90°，根据圆周角定理可得∠ASB＝12∠AOB＝45°，故选C．10．（2020·宜昌）如图，E,F,G为圆上的三点，△FEG=50°，P点可能是圆心的是（）.A．B．C．D．{答案}C{解析}由圆周角定理可知：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．当点P为圆心时，根据圆周角定理，可得△FPG=2△FEG．故选：C．9．（2020·凉山州）下列命题是真命题的是（）A．顶点在圆上的角叫圆周角B．三点确定一个圆C．圆的切线垂直于半径D．三角形的内心到三角形三边的距离相等{答案}D{解析}因为顶点在圆上且两边都与圆相交的角叫圆周角，不在同一条直线上的三个点确定一个圆，图8OBACA BS（第7题图）OA BS圆的切线垂直于过切点的半径，所以A 、B 、C 选项皆为假命题，故选D ． 11．（2020·凉山州）如图，等边三角形ABC 和正方形ADEF 都内接于△O ，则AD ﹕AB ＝（ ） A ．2√2﹕√3 B ．√2﹕√3 C ．√3﹕√2 D ．√3﹕2√2{答案}B{解析}如答图，连接OA 、OB 、OD ，则∠AOD ＝90°，∠AOB ＝120°．令OA ＝OB ＝OD ＝r ，则AD ＝√2r ，AB ＝√3r ，从而AD ﹕AB ＝√2﹕√3，故选B ．10.(2020·潍坊)如图，在Rt △AOB 中，∠AOB =90°,OA =3,OB =4，以点O 为圆心，2为半径的圆与OB 交于点C ，过点C 作CD ⊥OB 交AB 于点D ，点P 是边OA 上的动点．当PC +PD 最小时，OP 的长为（ ）A 12B. 34C. 1D. 32{答案}B{解析}由题意可知，点C 、D 是定点，点P 是边OA 上的动点，PC+PD 最小值时，即为将军饮马问题.点点P 为点C 关于点O 的对称点时，PC+PD 的值最小，求出OP 的长即可.延长CO 交⊙O 于点E ，连接ED ，交AO 于点P ，如图，∵CD ⊥OB ，∴∠DCB=90°,又∠AOB =90°，∴∠DCB=∠AOB ，∴CD//AO ，∴BC BO =CDAO ∵OC=2，OB=4，∴BC=2,∴24=CD3，解得，CD=32；∵CD//AO ，∴EO EC =PO DC ，即24=PO3，解得，PO=34 . 7．（2020·营口）如图，AB 是⊙O 的直径，点C ，点D 是⊙O 上的两点，连接CA ，CD ，AD ，若∠CAB =40°，DP OCBA.EDPOCBA第11题图O F ED CBA第11题答图rr r OD CBA则∠ADC 的度数是（ ）A ．110°B ．130°C ．140°D ．160° {答案}B{解析}如图，连接BC ，∵AB 是⊙O 的直径，∴∠ACB=90°，∴∠CAB+∠CBA =90°，∵∠CAB=40°，∴∠CBA =50°，∵∠ADC +∠CBA =180°，∴∠ADC=130°．9．（2020·滨州）在O 中，直径AB ＝15，弦DE △AB 于点C ．若OC ：OB ＝3：5，则DE 的长为（ ）A ．6B ．9C ．12D ．15{答案}C{解析}本题考查了垂径定理和勾股定理，直径AB=15，∴BO=7.5，∵OC ：OB=3：5，∴CO=4.5，∴DC=√OD 2−OC 2=6，∴DE=2DC=12，因此本题选C ．8．（2020·内江）如图，点A 、B 、C 、D 在⊙O 上，∠AOC =120°，点B 是AC⏜的中点，则∠D 的度数是（ ）A. 30°B. 40°C. 50°D. 60°{答案} A{解析}本题考查了圆心角、弧、弦的关系定理、圆周角定理，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解题的关键．根据圆心角、弧、弦的关系定理得到∠AOB ＝12∠AOC ，再根据圆周角定理解答．连接OB ，∵点B 是AC ⏜的中点，∴∠AOB ＝12∠AOC ＝60°， 由圆周角定理得，∠D ＝12∠AOB ＝30°，因此本题选A ．14．（2020·临沂）如图，在⊙O 中，AB 为直径，∠AOC =80°，点D 为弦AC 的中点，点E 为BC⏜上任意一点.则∠CED 的大小可能是（ ）BABAA.10°B.20° C.30° D.40°{答案}C{解析}梳理题目中的已知条件，有直径，可以相应的有90°的圆周角；∠AOC =80°，则∠OAC =∠OCA =50°；同时点D 为弦AC 的中点，则可以考虑利用垂径定理；另外，题目中具体数值较少，∠CED 的具体值不容易求，那么我们可以根据已有条件探求它的取值范围，从而确定那个值在范围内. 解：连接AE ，作过OD 的直线分别交圆周于点M 、N ，连接CM ，如下图：∵∠AOC =80°∴∠AEC =40°∴∠CED =∠AEC −∠AED <40°； 又∵点D 为弦AC 的中点∴∠COD =12∠AOC =40°∴∠CMN =12∠COD =20°∵∠CED 所对的弧大于CN⏜∴∠CED >∠CMN ，即：∠CED >20° 综上：20°<∠CED <40°，选C. 9．（2020·宜宾）如图，AB 是△O 的直径，点C 是圆上一点，连结AC 和BC ，过点C 作CD △AB 于点D ，且CD ＝4，BD ＝3，则△O 的周长是（ ）A ．253πB ．503πC ．6259π D ．62536π{答案}A{解析}根据“直径所对的圆周角为直角”，得∠ACB ＝90°，由CD ⊥AB ，根据勾股定理得BC ＝√CD 2+BD 2＝5，根据相似三角形的判定（两角对应相等的两个三角形相似）得Rt △ABC ∽Rt △CBD ，再根据相似三角形的三边对应成比例，得ABCB ＝BCBD ，即AB ＝253，∴⊙O 的周长是253π．8．（2020·广州）往直径为52cm 的圆柱形容器内装入一些水以后，截面如图4所示，若水面宽AB=48cm ，则水的最大深度为（ ）MNA ．8cmB ．10cmC ．16cmD ．20cm{答案}C{解析}本题考查了垂径定理，解答过程如下：过点O 作OC ⊥AB 于D ，交⊙O 于点C ，连接OA ．由题意，OA=OC ＝26cm ，AD=12AB=24cm ，再由勾股定理可得：OC=10cm ，所以水深CD=OC-OD=26-10=16cm.因此本题选C ．9．（2020·武汉）如图，在半径为3的⊙O 中，AB 是直径，AC 是弦，D 是弧AC 的中点，AC 与BD 交于点E ．若E 是BD 的中点，则AC 的长是 ················································ （ ）A ．52√3B ．3√3C ．3√2D ．4√2{答案}D{解析}本题考查了圆的垂径定理，弧线圆心角关系，全等判定，中位线等定理，连接OD ，交AC 于点F ，由D 是弧AC 的中点，易证出OD ⊥AC ，AF ＝CF ，又∵O 是AB 的中点，∴2OF ＝BC ，∵AB 是直径，∴∠ACB ＝90°，又∵E 是BD 的中点，∴易证出△EFD ≌△ECB （AAS ）∴DF ＝BC ，又∵半径为3，∴2OF ＝DF ＝BC ＝2，在Rt △ABC 中，AC ＝√AB 2－BC 2＝√62－22＝4√2，因此本题选D ．图4图4F10．（2020·海南）如图，已知AB 是△O 是直径，CD 是弦，若△BCD ＝36°，则∠ABD 等于( )A ．54°B ．56°C ．64°D ．66° {答案}A{解析}∵AB 是⊙O 的直径，∴∠ADB ＝90°.又由圆周角定理可知∠A ＝∠C ，∴∠ABD ＝90°－∠A ＝90°－36°＝54°.6.（2020·吉林）如图，四边形ABCD 内接于⊙O ．若∠B =108°，则∠D 的大小为（ ）A. 54°B. 62°C. 72°D. 82°【答案】C【详解】因为，四边形ABCD 内接于⊙O ，∠B =108°，所以，∠D =180°-∠B =180°−108°=72° 故选：C.9．（2020·黄石）如图，点A 、B 、C 在⊙O 上，CD ⊥OA ，CE ⊥OB ，垂足分别为D 、E ，若∠DCE ＝40°，则∠ACB 的度数为（ ）A ．140°B ．70°C ．110°D ．80°{答案} C{解析}先根据四边形的内角和为360°求∠AOB ＝360°﹣90°﹣90°﹣40°＝140°，再由同弧所对的圆周角是圆心角的一半可得∠P 的度数，最后由四点共圆的性质得结论．如图，在优弧AB 上取一点P ，连接AP ，BP ，∵CD ⊥OA ，CE ⊥OB ，∴∠ODC ＝∠OEC ＝90°，∵∠DCE ＝40°，∴∠AOB ＝360°﹣90°﹣90°﹣40°＝140°，∴∠P ＝12∠AOB ＝70°，∵A 、C 、B 、P 四点共圆，A∴∠P +∠ACB ＝180°，∴∠ACB ＝180°﹣70°＝110°，故选：C ．9．（2020·武威）如图，A 是⊙O 上一点，BC 是直径，AC ＝2，AB ＝4，点D 在⊙O 上且平分，则DC的长为（ ）A ．2B ．C ．2D ．【解析】∵点D 在⊙O 上且平分，∴，∵BC 是⊙O 的直径， ∴∠BAC ＝∠D ＝90°， ∵AC ＝2，AB ＝4， ∴BC ＝＝2，Rt △BDC 中，DC 2+BD 2＝BC 2， ∴2DC 2＝20， ∴DC ＝，故选：D ．二、填空题A13．（2020湖州）如图，已知AB 是半圆O 的直径，弦CD ∥AB ，CD ＝8，AB ＝10，则CD 与AB 之间的距离是 3 ．【分析】过点O 作OH ⊥CD 于H ，连接OC ，如图，根据垂径定理得到CH ＝DH ＝4，再利用勾股定理计算出OH ＝3，从而得到CD 与AB 之间的距离．【解答】解：过点O 作OH ⊥CD 于H ，连接OC ，如图，则CH ＝DH =12CD ＝4，在Rt △OCH 中，OH =√52−42=3，所以CD 与AB 之间的距离是3．故答案为3．16．（2020·遵义）如图，⊙O 是△ABC 的外接圆，∠BAC ＝45°，AD ⊥BC 于点D ，延长AD 交⊙O 于点E ，若BD ＝4， CD ＝1，则DE 的长是_________．{答案}{解析}本题考查圆的基本性质、相似三角形的判定与性质、全等三角形的判定与性质，利用特殊角作垂线构造全等三角形是解题的关键．如图，过点B 作BH ⊥AC 于点H ，交AE 于点F ，连接BE ，则△AHF ≌△BHC ．∴AF=BC=5． ∵∠HAF ＝∠HBC ，∠HAF ＝∠EBC ，∴∠HBC ＝∠EBC ．∵AD ⊥BC 于点D ， ∴DE=DF ． ∵∠CAE ＝∠CBE ，∠ACB ＝∠AEB ，∴△ACD ∽△BED ．∴CD DE =ADBD ,即1DE =5+DE 4．∴DE=−5+√412(舍去负值)．故答案为−5+√412.19．（2020·黔东南州）如图，AB 是半圆O 的直径，AC ＝AD ，OC ＝2，∠CAB ＝30°，则点O 到CD 的距离OE 为 ． {答案}√2 {解析}∵AC ＝AD ，∠A ＝30°，∴∠ACD ＝∠ADC ＝75°.∵AO ＝OC ，∴∠OCA ＝∠A ＝30°，∴∠OCD ＝45°，∴△OCE 是等腰直角三角形. 在等腰Rt △OCE 中，OC ＝2，∴OE =√2．19．(2020·绥化)如图5，正五边形ABCDE 内接于⊙O ，点P 为DE 上一点(点P 与点D ，点E 不重合)，连接PC 、PD ，DG ⊥PC ，垂足为G ，∠PDG 等于______度．{答案}54{解析}连结CE ．正五边形的内角∠CDE ＝15×(5－2)×180°＝108°．∵DC ＝DE ，∴∠P ＝∠DEC ＝12×(180°－108°)＝36°．∵DG ⊥PC ，∴∠PDG ＝90°－∠P ＝54°．14．（2020·聊城）如图，在⊙O 中，四边形OABC 为菱形，点D 在AmC ︵上，则∠ADC 的度数是 ．-+5412F H EAD CO B图5 O P G D E C A B D CO BA{答案}60°{解析}利用圆周角定理、圆内接四边形的性质以及菱形的对角相等构建方程求解．在菱形OABC 中，∠B＝∠O，又∵∠O ＝2∠D，∠D ＋∠B＝180°，∴∠D ＋2∠D＝180°，∴∠D＝60°．14．（2020·贵阳）（4分）如图，△ABC是△O的内接正三角形，点O是圆心，点D，E分别在边AC，AB上，若DA＝EB，则△DOE的度数是度．{答案}120．{解析}解：连接OA，OB，△△ABC是△O的内接正三角形，△△AOB＝120°，△OA＝OB，△△OAB＝△OBA＝30°，△△CAB＝60°，△△OAD＝30°，△△OAD＝△OBE，△AD＝BE，△△OAD△△OBE（SAS），△△DOA＝△BOE，△△DOE＝△DOA+△AOE＝△AOB＝△AOE+△BOD＝120°，故答案为：120．16．（2020·黑龙江龙东）如图，AD是△ABC的外接圆△O的直径，若△BCA＝50°，则△ADB＝°．{答案}50．{解析}本题考查了圆周角的性质，解：△AD是△ABC的外接圆△O的直径，△点A，B，C，D在△O上，△△BCA＝50°，△△ADB＝△BCA＝50°，故答案为：50．15．（2020·襄阳）在⊙O中，若弦BC垂直平分半径OA，则弦BC所对的圆周角等于__________°．{答案}60或120．{解析}如答图，连接OB，OC，由弦BC垂直平分半径OA，得OD＝12OA＝12OB，∠ODB＝90°，从而cos∠DOB＝12，∠DOB＝60°，于是∠DOC＝120°．∴∠BP1C＝12∠BOC＝60°．∵∠BP1C＋∠BP2C＝180°，∴∠BP2C＝120°．综上，弦BC所对的圆周角等于60°或120°，故答案为60或120．ODABCm（2020·四川甘孜州）14．如图，AB为⊙O的直径，弦CD⊥AB于点H，若AB＝10，CD＝8，则OH的长度为________．{答案}3{解析}本题考查了垂径定理和勾股定理．连接OC，∵AB为⊙O的直径，AB＝10，∴OC＝OA＝5．∵弦CD ⊥AB于点H，CD＝8，∴CH＝4．在Rt△OCH中，由勾股定理得OH＝√OC2−CH2＝√52−42＝3．故答案为3．14.（2020·盐城）如图，在⊙O中，点A在BC上，∠BOC=100°,则∠BAC=∘14．130°，解析：本题考查了同弧所对的圆周角是圆心角的一半和圆内接四边形对角互补等知识，因此在⊙O上取一点D，连接CD，BD，则∴∠BDC＝12∠BOC＝50°∵四边形ABDC为圆内接四边形∴∠BAC+∠BDC＝180°∵∠BDC＝50°∴∠BAC＝130°此本题答案为130° ．P2P1DOCB第15题答图（2020·济宁）15.如图,在四边形ABCD 中，以AB 为直径的半圆O 经过点C,D.AC 与BD 相交于点E ，CD 2=CE ·CA,分别延长AB,DC 相交于点P ，PB=BO ，CD=2√2.则BO 的长是_________.{答案}4{解析}：连结OC ，如图，∵CD 2＝CE •CA ，∴CDCE =CADC ，而∠ACD ＝∠DCE ，∴△CAD ∽△CDE ，∴∠CAD ＝∠CDE ， ∵∠CAD ＝∠CBD ，∴∠CDB ＝∠CBD ，∴BC ＝DC ； 设⊙O 的半径为r ，∵CD ＝CB ，∴CD ̂=CB ̂，∴∠BOC ＝∠BAD ，∴OC ∥AD ， ∴PCCD =POOA =2r r=2，∴PC ＝2CD ＝4√2，∵∠PCB ＝∠P AD ，∠CPB ＝∠APD ， ∴△PCB ∽△P AD ， ∴PC PA=PBPD，即4√23r=6√2，∴r ＝4， ∴OB ＝4．16． （2020·岳阳）如图，AB 为半圆O 的直径，M ，C 是半圆上的三等分点，AB ＝8，BD 与半圆O 相切于点B ，点P 为AM⏜上一动点（不与点A ，M 重合），直线PC 交BD 于点D ，BE ⊥OC 于点E ，延长BE 交PC 于点F ，则下列结论正确的是 ．（写出所有正确结论的序号） ①PB =PD ； ②BC ⏜的长为43π； ③∠DBE =45°； ④ΔBCF ∽ΔPFB ； ⑤CF ⋅CP 为定值.{答案}②⑤{解析}∵M ，C 是半圆上的三等分点，∴∠BOC ＝13×180°=60°，根据同弧所对的圆周角等于圆心角的一半，∠BPC＝12∠BOC＝12×60°=30°，∵BD与半圆O相切于点B，∴∠ABD＝90°∵P是AM⏜上一动点，∴∠PBA 角度不确定，∴∠PBD不确定，∠D也不确定，所以PB＝PD不成立，结论①错误；∵直径AB ＝8，∴半径为4，∴BC⏜=60π×4180=4π3，∴结论②正确；∵BE⊥OC，∴∠BEO＝90°，∴∠OBE＝180°－90°－60°＝30°，∴∠DBE＝∠ABD－∠OBE＝90°－30°＝60°，∴结论③错误；∵∠PFB＝∠FCB ＋∠FBC，所以∠PFB＞∠FBC，∴△BCF和△PFB不可能相似，∴结论④错误；∵OB＝OC，∠BOC＝60°，∴△BOC是等边三角形，∴∠CBO＝60°，∵BE⊥OC，所以∠CB E＝12∠CBO＝30°，∴∠CBF=∠CPB，又∵∠BCF=∠PCB，∴△BCF∽△PCB，∴CFCB=CBCP，∴CF⋅CP=CB2，∵△OBC是等边三角形，∴CB＝OB＝4，∴CF⋅CP=16，为定值，∴结论⑤正确．综上，结论正确的是②⑤.12．（2020·随州）如图，点A，B，C在⊙O上，AD是∠BAC的角平分线，若∠BOC=120°，则∠CAD的度数为 .{答案}30°{解析}本题考查了圆周角定理、角平分线的定义，解答过程如下：∵∠BOC=120°，∴∠BAC=12∠BOC=12×120°=60°.∵AD是∠BAC的角平分线，∴∠CAD=12∠BAC=12×60°=30°.12．（2020·南通）⊙O的半径为13，弦AB的长度是10，则圆心O到弦AB的距离为▲ ．{答案}12{解析}过圆心作弦AB的垂线，连接OA，由垂径定理和勾股定理可求出距离．作OC9．(2020·青海)已知⊙O的直径为10cm，AB，CD是⊙O的两条弦，AB∥CD，AB＝8cm，CD＝6cm，则AB与CD之间的距离为______cm．{答案}7或1{解析}过圆心O作OM⊥AB于M，交CD于点N，连结OB，OD．∵AB∥CD，∴MN⊥CD．由垂径定理可知MB＝4，ND＝3．∴OM＝22OB MB-＝3，ON＝22OD ND-＝4．(1)当圆心O在AB，CD之间时，如图#(1)，MN＝OM＋ON＝7；(2)当圆心O在AB，CD同侧时，如图#(2)，MN＝ON－OM＝1．⊥AB于点C，∴AC＝12AB=5，∴OC=√OA2−AC2=√132−52=12．O图#(1)DCA BMNO图#(2)DCA BMN13．(2020·成都)如图，A，B，C是△O上的三个点，△AOB＝50°，△B＝55°，则△A的度数为．{答案}30°{解析}首先根据△B的度数求得△BOC的度数，然后求得△AOC的度数，从而求得等腰三角形的底角即可．解：△OB＝OC，△B＝55°，△△BOC＝180°﹣2△B＝70°，△△AOB＝50°，△△AOC＝△AOB+△BOC＝70°+50°＝120°，△OA＝OC，△△A＝△OCA=180°−120°2=30°，故答案为：30°．14.（2020·安顺）如图，ΔABC是⊙O的内接正三角形，点O是圆心，点D，E分别在边AC，AB上，若DA=EB，则∠DOE的度数是度.{答案}120{解析}连接OA，OB.∵ΔABC是⊙O的内接正三角形，∴∠OAD=∠OBE=30°，∠AOB=120°.又∵AD=BE,OA=OB，∴△OAD≌△OBE.∴∠AOD=∠BOE.即∠DOE=120°.16．（2020·滨州）如图，O是正方形ABCD的内切圆，切点分别为E、F，G，H，ED与O相交于点M，则sin∠MFG的值为________{答案}√55{解析}本题考查了圆周角的性质及锐角三角函数的概念，设正方形的边长为a，∵⊙O是正方形ABCD的内切圆，AE=12AB=12a，AD=EG=BC=a，DE=√52a，根据圆周角的性质可得：∠MFG=∠MEG．∵sin∠MFG=sin∠MEG=DGDE=√55，∴sin∠MFG=√55，因此本题填√55．第14题图第14题答19．（2020·临沂）我们知道，两点之间线段最短，因此，连接两点间线段的长度叫做两点间的距离；同理，连接直线外一点与直线上各点的所有线段中，垂线段最短，因此，直线外一点到这条直线的垂线段的长度，叫做点到直线的距离.类似地，连接曲线外一点与曲线上各点的所有线段中．．．．．．．．．．．．．．．．．．．，最短线段的长．．．．．．度．，叫做点到曲线的距离．．．．．．．．．.依此定义，如图，在平面直角坐标系中，点A(2,1)到以原点为圆心，以1为半径的圆的距离为_________.{答案}√5−1{解析} 连接OA交圆周于点N，过点A作x轴的垂线，垂足为点M：∵点A(2,1)∴OM=2,AM=1∴OA=√OM2+AM2=√22+12=√5.∴AN=OA−ON=√5−1.14．（2020·宜宾）如图，A、B、C是△O上的三点，若△OBC是等边三角形，则cos△A＝．{答案}√32{解析}利用等边三角形的性质、圆周角定理、特殊角的三角函数值求解．∵△OBC是等边三角形，∴∠BOC＝60°，∴∠A＝30°，∴cos∠A＝cos30°＝√32．15. （2020·攀枝花）如图，已知锐角三角形ABC内接于半径为2的⊙O，OD⊥BC于点D，∠BAC=60°，则OD=.NM{答案}1{解析}如图，连接OB 、OC ，则易知∠BOC =2∠BAC =120°， 由垂径定理可知∠BOD =12∠BOD =60°，则∠OBD =30°，∴OD =12OB =1.三、解答题22．（2020·温州）如图,C ,D 为⊙O 上两点,且在直径AB 两侧,连结CD 交AB 于点E ,G 是AC ⏜上一点,∠ADC ＝∠G .(1)求证:∠1＝∠2(2)点C 关于DG 的对称点为F ,连结CF .当点F 落在直径AB 上时CF ＝10,tan ∠1＝25,求⊙O 的半径.{解析}本题考查了垂径定理及解直角三角形．（1）由∠ADC ＝∠G 得到AC⏜＝AD ⏜,从而得到CB ⏜=DB ⏜，从而∠1＝∠2；（2）根据圆是轴对称图形可知CF ＝DF ，又由点C 关于DG 的对称点为F 得到CD ＝DF ，从而求得DE ＝5，分别解Rt △AED 和Rt △BDE ，求得AE 和EB ，从而得到直径AB 。
中考数学考点29圆的基本性质总复习(解析版)
圆的基本性质【命题趋势】圆的基本性质是中考考查的重点.常以选择题.填空题和解答题考查为主；其中选择题和填空题的难度不会太大.对应用、创新、开放探究型题目.会根据当前的政治形势、新闻背景和实际生活去命题.进一步体现数学来源于生活.又应用于生活。
【中考考查重点】一、运用垂径定理及其推论进行计算二、运用圆周角定理及其推论进行计算三、垂径定理雪与圆周角定理结合考点：圆的有关概念圆的定义：在一个平面内.线段OA绕它固定的一个端点O旋转一周.另一个端点A所形成的图形叫圆。
这个固定的端点O叫做圆心.线段OA叫做半径。
圆的表示方法：以O点为圆心的圆记作⊙O.读作圆O。
圆的特点：在一个平面内.所有到一个定点的距离等于定长的点组成的图形。
确定圆的条件：1）圆心；2）半径。
备注：圆心确定圆的位置.半径长度确定圆的大小。
【补充】1）圆心相同且半径相等的圆叫做同圆；2）圆心相同.半径不相等的两个圆叫做同心圆；3）半径相等的圆叫做等圆。
圆的对称性：1）圆是轴对称图形.经过圆心的每一条直线都是它的对称轴；2）圆是以圆心为对称中心的中心对称图形。
弦的概念：连结圆上任意两点的线段叫做弦(例如：右图中的AB)。
直径的概念：经过圆心的弦叫做直径（例如：右图中的CD）。
备注：1）直径是同一圆中最长的弦。
2）直径长度等于半径长度的2倍。
⏜.读弧的概念：圆上任意两点间的部分叫做圆弧.简称弧。
以A、B为端点的弧记作AB作圆弧AB或弧AB。
等弧的概念：在同圆或等圆中.能够互相重合的弧叫做等弧。
半圆的概念：圆的任意一条直径的两个端点把圆分成两条弧.每一条弧都叫做半圆。
优弧的概念：在一个圆中大于半圆的弧叫做优弧。
劣弧的概念：小于半圆的弧叫做劣弧。
弦心距概念：从圆心到弦的距离叫做弦心距。
1．（2021秋•顺义区期末）如图.在⊙O中.如果＝2.则下列关于弦AB与弦AC之间关系正确的是（）A．AB＝AC B．AB＝2AC C．AB＞2AC D．AB＜2AC【答案】D【解答】解：如图.取弧AB的中点D.连接AD.BD.则＝2＝2.∵＝2.∴＝＝.∴AD＝BD＝AC．在△ABD中.AD+BD＞AB.∴AC+AC＞AB.即AB＜2AC．故选：D．2．（2021秋•平原县期末）下列语句.错误的是（）A．直径是弦B．相等的圆心角所对的弧相等C．弦的垂直平分线一定经过圆心D．平分弧的半径垂直于弧所对的弦【答案】B【解答】解：直径是弦.A正确.不符合题意；在同圆或等圆中.相等的圆心角所对的弧相等.B错误.符合题意；弦的垂直平分线一定经过圆心.C正确.不符合题意；平分弧的半径垂直于弧所对的弦.D正确.不符合题意；故选：B．3．（2021秋•玉林期末）如图.从A地到B地有两条路可走.一条路是大半圆.另一条路是4个小半圆．有一天.一只猫和一只老鼠同时从A地到B地．老鼠见猫沿着大半圆行走.它不敢与猫同行（怕被猫吃掉）.就沿着4个小半圆行走．假设猫和老鼠行走的速度相同.那么下列结论正确的是（）A．猫先到达B地B．老鼠先到达B地C．猫和老鼠同时到达B地D．无法确定【答案】C【解答】解：以AB为直径的半圆的长是：π•AB；设四个小半圆的直径分别是a.b.c.d.则a+b+c+d＝AB．则老鼠行走的路径长是：a+πb+πc+πd＝π（a+b+c+d）＝π•AB．故猫和老鼠行走的路径长相同．故选：C．考点：垂径定理垂径定理：垂直于弦的直径平分这条弦.并且平分弦所对的两条弧。
圆的性质精品文档
餐具：碗和盘子 通常设计成圆形， 方便盛放食物和 用餐具
井盖：为了方便 运输和安装，通 常采用圆形设计 ，同时圆形井盖 不易掉入井中
管道：圆形管道 可以保证水流顺 畅，减少阻力
圆在数学问题中的应用
圆的周长公式：C=2πr，常用于计算圆的周长和圆的面积公式中的半径r 圆的面积公式：S=πr²，常用于计算圆的面积和圆球体的体积公式中的半径r 圆弧长公式：L=θr，常用于计算圆弧的长度，其中θ为圆心角，r为半径 圆的标准方程：(x-a)²+(y-b)²=r²，常用于表示圆心在(a,b)，半径为r的圆
参数方程的优缺点
优点：能够准确地描述 圆的形状和大小，使得 计算和绘图更加方便
缺点：相对于直角坐标 系，参数方程较为复杂， 不易理解和掌握，且在 某些情况下可能存在精 度损失的问题
圆的几何应用
圆在几何作图中的应用
圆规：用于绘制圆形，是几何作图的基本工具之一。
圆弧连接：利用圆上的一段弧连接两条直线或圆，是几何作图中的重要技巧。
相切：圆与直线 相切于一点，该 点到圆心的距离 等于圆的半径
相交：圆与直线 在两点相交，该 两点到圆心的距 离小于圆的半径
相离：圆与直线 不相交，该直线 到圆心的距离大 于圆的半径
圆的参数方程
参数方程的建立
参数方程的概念 圆的参数方程的建立过程 参数方程在圆中的应用 参数方程与直角坐标方程的转换
圆的性质
汇报人：XX
汇报时间：20XX/XX/XX
YOUR LOGO
目录
CONTENTS
1 圆的几何性质 2 圆的解析性质 3 圆的参数方程 4 圆的几何应用 5 圆的解析应用
圆的几何性质
圆的基本性质
圆上三点确定一个平面
初中数学圆的专题讲解
初中数学中考复习辅导专题圆考点一：圆的基本性质【例题精讲】例题1.如图，公园的一座石拱桥是圆弧形（劣弧），其跨度为24米，拱的半径为13米，则拱高为（）A ．5米B．8米C ．7米D ．53米例题2.如图⊙O 的半径为5，弦AB=8，M 是弦AB 上的动点，则OM 不可能为（）A ．2B ．3C ．4D ．5例题3.如图⊙O 弦AB=6，M 是AB 上任意一点，且OM 最小值为4，则⊙O 半径为（）A ．5B ．4C ．3D ．2例题4.如图，⊙O 的半径为1，AB 是⊙O 的一条弦，且AB=3，则弦AB 所对圆周角的度数为（）A.30° B.60° C.30°或150° D.60°或120°例题5．AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∠CDB ＝30°,⊙O 的半径为cm 3，则弦CD 的长为（）A ．3cm 2B ．3cmC ．23cmD ．9cm例题6.如图，BC 是以线段AB 为直径的O ⊙的切线，AC 交O ⊙于点D ，过点D 作弦DE AB ⊥，垂足为点F ，连接BD BE 、．．（1）仔细观察图形并写出四个不同的正确结论：①______，②________，③______，④________（不添加其它字母和辅助线）（2）A ∠=30°，CD =233，求O ⊙的半径r ．考点二：与圆有关的位置关系【例题精讲】例1.⊙O 的半径是6，点O 到直线a 的距离为5，则直线a 与⊙O 的位置关系为（）A ．相离B ．相切C ．相交D ．内含例2.如图，⊙O 内切于ABC △，切点分别为D,E,F.∠B=50°，∠C=60°，，连结OE,OF,DE,DF ，则EDF ∠等于（）A ．40°B ．55°C ．65°D ．70°第2题第3题例3.如图，已知直线L 和直线L 外两定点A 、B ，且A 、B 到直线L 的距离相等，则经过A 、B 两点且圆心在L 上的圆有（）A ．0个B ．1个C ．无数个D ．0个或1个或无数个例4．已知⊙O 1半径为3cm ，⊙O 2半径为4cm ，并且⊙O 1与⊙O 2相切，则这两个圆的圆心距为（）A.1cm B.7cm C.10cm D.1cm 或7cm 例5．两圆内切，圆心距为3，一个圆的半径为5，另一个圆的半径为。
中考数学专项训练： 圆的基本性质(含解析)
一、选择题7．（2019·嘉兴）如图，已知⊙O 上三点A ，B ，C ，半径OC ＝1，∠ABC ＝30°，切线PA 交OC 延长线于点P ，则PA 的长为（ ）A ．2B ．C ．D ．【答案】B【解析】连接OA ，因为∠ ABC=30°，所以∠AOC=60°，又因为PA 为切线，所以∠OAP=90°，因为OC=1，所以.3.（2019·杭州）如图，P 为⊙O 外一点，PA 、PB 分别切⊙O 于A 、B 两点，若PA=3，则PB=（ ） A ．2 B.3 C.4 D.5【答案】B【解析】因为P A 和PB 与⊙O 相切，根据切线长定理，可知： P A =PB =3，故选B ．12．（2019·烟台）如图，AB 是O e 的直径，直线DE 与O e 相切于点C ，过点A ，B 分别作AD DE ⊥，BE DE ⊥，垂足为点D ，E ，连接AC ，BC．若AD =3CE =，则»AC 的长为（ ）． A．3 B．3 C．2 D．3【答案】D【解题过程】连接OC ，因为AD DE ⊥，BE DE ⊥，所以90ADC CEB ∠=∠=︒ODEBA所以90DAC ACD ∠+∠=︒ 因为AB 是O e 的直径，所以90ACB ∠=︒，所以90BCE ACD ∠+∠=︒， 所以BCE DAC ∠=∠， 在△ADC 与△CED ,因为90ADC CEB ∠=∠=︒，BCE DAC ∠=∠ 所以△ADC ∽△CED ,所以BC CE AC AD ===在Rt △ACB 中，sin BCBAC AC∠== 所以60BAC ∠=︒， 又因为OA OC =，所以△AOC 是等边三角形， 所以60ACO ∠=︒，因为直线DE 与 O e 相切于点C ， 所以OC DE ⊥，因为AD DE ⊥，OC DE ⊥， 所以AD//OC ，所以60DAC ACO ∠=∠=︒，所以9030ACD DAC ∠=︒-∠=︒，所以2AC AD ==， 所以△AOC 是等边三角形，所以OA AC ==，60AOC ∠=︒，所以»AC =．9．（2019·陕西）如图，AB 是⊙O 的直径，EF ，EB 是⊙O 的弦，且EF ＝EB ，EF 与AB 交于点C ，连接OF ，若∠AOF ＝40°，则∠F 的度数是（ ）A ．20°B ．35°C ．40°D ．55°【分析】连接FB ，得到∠FOB ＝140°，求出∠EFB ，∠OFB 即可．【解答】解：连接FB ．∵∠AOF ＝40°，∴∠FOB ＝180°﹣40°＝140°， ∴∠FEB ＝∠FOB ＝70° ∵EF ＝EB∴∠EFB ＝∠EBF ＝55°， ∵FO ＝BO ，∴∠OFB ＝∠OBF ＝20°， ∴∠EFO ＝∠EBO ，∠EFO ＝∠EFB ﹣∠OFB ＝35°， 故选：B ．【点评】本题考查圆周角定理，等腰三角形的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．12．（2019·威海）如图，⊙P 与x 轴交与点A （—5，0），B （1，0），与y 轴的正半轴交于点C ，若∠ACB ＝60°，则点C 的纵坐标为A.B. C. D .2【答案】D【解题过程】连接PA 、PB 、PC ,过点P 分别作PF ⊥AB ，PE ⊥OC ，垂足为F,E. 由题意可知：四边形PFOE 为矩形， ∴PE ＝OF ,PF ＝OE . ∵∠ACB ＝60°， ∴∠APB ＝120°. ∵P A ＝PB ，＝30°.cos 30°＝AFAP， ∴PF ,AP ＝∴OE,PC ＝在RT △PEC 中，CE ＝ ＝，∴OC ＝CE ＋EO ＝ 2.5． 如图，线段AB 经过⊙O 的圆心，AC BD 分别与⊙O 相切于点D .若AC= BD = 4,∠A =45°， 则圆弧CD 的长度为（ ）A .πB . 2πC . D.4π 【答案】B【解析】连接CO ,DO ,因为AC ,BD分别与⊙O 相切于C ,D ，所以∠ACO =∠DBO =90°, 所以∠AOC =∠A =45°, 所以CO =AC =4，因为AC =BD ,CO =DO ,所以△ACO ≌△BDO ,所以∠DOB =∠AOC =45°，所以∠DOC =180°-∠DOB -∠AOC =180°-45°-45°=90°，»CD=904180π⨯=2π，故选B . 9．（2019·益阳）如图，PA 、PB 为圆O 的切线，切点分别为A 、B ，PO 交AB 于点C ，PO 的延长线交圆O 于点D ，下列结论不一定成立的是（）A. PA=PBB.∠BPD ＝∠APDC.AB ⊥PDD.AB 平分PD第9题图【答案】D【解析】∵PA 、PB 为圆O 的切线，切点分别为A 、B ，PO 交AB 于点C ，PO 的延长线交圆O 于点D ，∴PA=PB ，∠BPD ＝∠APD ，故A 、B 正确；∵PA=PB ，∠BPD ＝∠APD ，∴PD ⊥AB ，PD 平分AB ，但AB 不一定平分PD ，故C 正确，D 错误.7．（2019·黄冈）如图，一条公路的转弯处是一段圆弧（»AB ），点O 是这段弧所在圆的圆心，AB ＝40m ，点C 是»AB 的中点，点D 是AB 的中点，且CD ＝10m .则这段弯路所在圆的半径为（） A.25mB.24mC.30mD.60m【答案】A【解析】连接OD ，由垂径定理可知O ，C ，D 在同一条直线上，OC ⊥AB ，设半径为r ，则OC ＝OA ＝r ，AD ＝20，OD ＝OA －CD ＝r －10，在Rt △ADO ，由勾股定理知：r 2＝202＋(r －10)2，解得r ＝25.9．（2019·陇南）如图，点A，B，S在圆上，若弦AB的长度等于圆半径的倍，则∠ASB的度数是（）A．22.5°B．30°C．45°D．60°【答案】C【解析】作AB的垂直平分线，交圆与点C，D，设圆心为O，CD与AB交于点E，∵OA，∴AE=，∴2sin2OEAOEOA OA∠===,∴∠AOE=45°，∴∠AOB=90°，∴∠ASB=45°，故选：C．1.（2019·滨州）如图，AB为⊙O的直径，C，D为⊙O上两点，若∠BCD＝40°，则∠ABD的大小为（）A．60°B．50°C．40°D．20°【答案】B【解析】如图，连接AD，∵AB为⊙O的直径，∴∠ADB=90°．∵∠A和∠BCD都是弧BD所对的圆周角，∴∠A=∠BCD=40°，∴∠ABD=90°－40°=50°．故选B．2. (2019·聊城)如图,BC是半圆O的直径,D,E是»BC上两点,连接BD,CE并延长交于点A,连接OD,OE,如果∠A＝70°,那么∠DOE的度数为A.35°B.38°C.40°D.42°【答案】C【解析】∵∠A＝70°,∴∠B+∠C＝110°,∴∠BOE+∠COD＝220°,∴∠DOE＝∠BOE+∠COD－180°＝40°,故选C.3.（2019·潍坊）如图，四边形ABCD内接于⊙O，AB为直径，AD=CD．过点D作DE⊥AB于点E．连接AC交DE于点F．若sin∠CAB=35，DF=5，则BC的长为（）A．8 B．10 C．12 D．16 【答案】C【解析】连接BD．∵AD=CD，∴∠DAC=∠ACD．∵AB为直径，∴∠ADB=∠ACB=90°．∴∠DAB+∠ABD=90°．∵DE⊥AB，∴∠DAB+∠ADE=90°．∴∠ADE=∠ABD．∵∠ABD=∠ACD，∴∠DAC=∠ADE．∴AF=DF=5．在Rt△AEF中，sin∠CAB=35 EFAF=∴EF=3，AE=4．∴DE=3+5=8．由DE2=AE▪EB，得228164DEBEAE===．∴AB=16+4=20．在Rt△ABC中，sin∠CAB=35 BC AB=∴BC=12．4. （2019·凉山）下列命题：①直线外一点到这条直线的垂线段，叫做点到直线的距离；②两点之间线段最短；③相等的圆心角所对的弧相等；④平分弦的直径垂直于弦．其中，真命题的个数（▲）A．1 B．2 C．3 D．4【答案】A【解析】直线外一点到这条直线的垂线段的长度，叫做点到直线的距离；两点之间线段最短；在同圆或等圆中，相等的圆心角所对的弧相等；平分弦（不是直径）的直径垂直于弦，所以只有①是对的，故选A. 5.（2019·眉山）如图，⊙O的直径AB垂直于弦CD．垂足是点E，∠CAO=22．5°，OC=6，则CD的长为A．B．．6 D．12【答案】A【解析】∵∠A=22.5°，∴∠COE=45°，∵⊙O的直径AB垂直于弦CD，OC=6，∴∠CEO=90°，∵∠COE=45°，∴OC＝CD=2CE= D.6.（2019·衢州）一块圆形宣传标志牌如图所示，点A，B，C在⊙O上，CD垂直平分AB于点D.现测得AB=8dm，DC=2dm，则圆形标志牌的半径为（A）A.6dmB.5dmC.4dmD.3dm【答案】B【解析】连接OD，OB，则O，C，D三点在一条直线上，因为CD垂直平分AB，AB=8dm，所以BD=4dm,OD=（r-2）dm，由勾股定理得42+（r-2）2=r2，r=5dm，故选B.7.(2019·泰安) 如图,△ABC是e O的内接三角形,∠A＝119°,过点C的圆的切线交BO于点P,则∠P的度数为A.32 °B.31°C.29°D.61°【答案】A【解析】连接CO,CF,∵∠A＝119°,∴∠BFC＝61°,∴∠BOC＝122°,∴∠COP＝58°,∵CP与圆相切于点C,∴OC⊥CP,∴在Rt△OCP中,∠P＝90°－∠COP＝32°,故选A.二、填空题7．（2019·嘉兴）如图，已知⊙O 上三点A ，B ，C ，半径OC ＝1，∠ABC ＝30°，切线PA 交OC 延长线于点P ，则PA 的长为（ ）A ．2B ．C ．D ．【答案】B【解析】连接OA ，因为∠ ABC=30°，所以∠AOC=60°，又因为PA 为切线，所以∠OAP=90°，因为OC=1，所以.3.（2019·杭州）如图，P 为⊙O 外一点，PA 、PB 分别切⊙O 于A 、B 两点，若PA=3，则PB=（ ） A ．2 B.3 C.4 D.5【答案】B【解析】因为P A 和PB 与⊙O 相切，根据切线长定理，可知： P A =PB =3，故选B ．12．（2019·烟台）如图，AB 是O e 的直径，直线DE 与O e 相切于点C ，过点A ，B 分别作AD DE ⊥，BE DE ⊥，垂足为点D ，E ，连接AC ，BC．若AD =3CE =，则»AC 的长为（ ）． ABCD【答案】D【解题过程】连接OC ，因为AD DE ⊥，BE DE ⊥，所以90ADC CEB ∠=∠=︒ 所以90DAC ACD ∠+∠=︒ 因为AB 是O e 的直径，所以90ACB ∠=︒，所以90BCE ACD ∠+∠=︒， 所以BCE DAC ∠=∠， 在△ADC 与△CED ,因为90ADC CEB ∠=∠=︒，BCE DAC ∠=∠ 所以△ADC ∽△CED ,所以BC CE AC AD ===在Rt △ACB中，sin BCBAC AC∠== 所以60BAC ∠=︒， 又因为OA OC =，所以△AOC 是等边三角形， 所以60ACO ∠=︒，因为直线DE 与 O e 相切于点C ， 所以OC DE ⊥，因为AD DE ⊥，OC DE ⊥， 所以AD//OC ，所以60DAC ACO ∠=∠=︒，所以9030ACD DAC ∠=︒-∠=︒，所以2AC AD ==， 所以△AOC 是等边三角形，所以OA AC ==，60AOC ∠=︒，所以»AC=．12．（2019·威海）ODEBA如图，⊙P 与x 轴交与点A （—5，0），B （1，0），与y 轴的正半轴交于点C ，若∠ACB ＝60°，则点C 的纵坐标为B.B. C. D .2【答案】D【解题过程】连接PA 、PB 、PC ,过点P 分别作PF ⊥AB ，PE ⊥OC ，垂足为F,E. 由题意可知：四边形PFOE 为矩形， ∴PE ＝OF ,PF ＝OE . ∵∠ACB ＝60°， ∴∠APB ＝120°. ∵P A ＝PB ，＝30°.cos 30°＝AFAP， ∴PF ,AP ＝∴OE,PC ＝在RT △PEC 中，CE ＝ ＝，∴OC ＝CE ＋EO ＝ 2.16．（2019·娄底）如图（9），C 、D 两点在以AB 为直径的圆上，AB＝2，∠ACD ＝30°，则AD ＝_____________．【答案】1．【解析】如图，图9－1，连结AD ，∵由AB 为⊙O 的直径， ∴∠ADB ＝90°，又∵在⊙O 中有∠ACD ＝30°, ∴∠B ＝∠ACD ＝30°，∴112122AD AB ==⨯=． 17．（2019·衡阳）已知圆的半径是6，则圆内接正三角形的边长是． 【答案】63【解析】如图，作OD ⊥BC 于D ，∵OB ＝6，∠OBD ＝30，∴BD ＝12BC ＝33，∴BC ＝63，故答案为63．13．（2019·安徽）如图，△ABC 内接于⊙O ，∠CAB=30°，∠CBA=45°，CD ⊥AB 于点D ，若⊙O 的半径为2，则CD 的长为 .DCBOA【答案】2【解析】本题考查了三角形的外接圆与外心，圆周角定理，等腰直角三角形的性质，正确的作出辅助线是解题的关键．连接CO 并延长交⊙O 于E ，连接BE ，于是得到∠E=∠A=30°，∠EBC=90°，解直角三角形即可得到结论．连接CO 并延长交⊙O 于E ，连接BE ，则∠E=∠A=30°，∠EBC=90°，∵⊙O 的半径为2，∴CE=4，∴BC=21CE=2，∵CD ⊥AB ，∠CBA=45°，∴CD=22BC=2，故答案为2．16．（2019·株洲）如图所示，AB 为⊙O 的直径，点C 在⊙O 上，且OC ⊥AB ，过点C 的弦CD 与线段OB 相交于点E ，满足∠AEC ＝65°，连接AD ，则∠BAD ＝度．第16题【答案】20°【解析】如图，连接DO ，因为CO ⊥AB,所以∠COB=90°，∵∠AEC ＝65°，∴∠C=25°，∵OD=OC,∴∠ODC=∠C=25°，△DCO 中，∠DOC=130°，∴∠DOB=40°，∴2∠BAD=∠DOB,∴∠BAD=20°。
备战中考数学分点透练真题圆的基本性质(解析版)
第二十讲圆的基本性质命题点1 圆周角定理及其推论有关的计算1．（2021•长沙）如图，点A，B，C在⊙O上，∠BAC＝54°，则∠BOC的度数为（）A．27°B．108°C．116°D．128°【答案】B【解答】解：∵∠A＝54°，∴∠BOC＝2∠A＝108°，故选：B．2．（2021•重庆）如图，AB是⊙O的直径，AC，BC是⊙O的弦，若∠A＝20°，则∠B的度数为（）A．70°B．90°C．40°D．60°【答案】A【解答】解：∵AB是⊙O的直径，∴∠C＝90°，∵∠A＝20°，∴∠B＝90°﹣∠A＝70°，故选：A．3．（2021•嘉峪关）如图，点A，B，C，D，E在⊙O上，AB＝CD，∠AOB＝42°，则∠CED ＝（）A．48°B．24°C．22°D．21°【答案】D【解答】解：连接OC、OD，∵AB＝CD，∠AOB＝42°，∴∠AOB＝∠COD＝42°，∴∠CED＝∠COD＝21°．故选：D．4．（2021•邵阳）如图，点A，B，C是⊙O上的三点．若∠AOC＝90°，∠BAC＝30°，则∠AOB的大小为（）A．25°B．30°C．35°D．40°【答案】B【解答】解：∵∠BAC与∠BOC所对弧为，由圆周角定理可知：∠BOC＝2∠BAC＝60°，又∠AOC＝90°，∴∠AOB＝∠AOC﹣∠BOC＝90°﹣60°＝30°．故选：B．5．（2021•武汉）如图，AB是⊙O的直径，BC是⊙O的弦，先将沿BC翻折交AB于点D，再将沿AB翻折交BC于点E．若＝，设∠ABC＝α，则α所在的范围是（）A．21.9°＜α＜22.3°B．22.3°＜α＜22.7°C．22.7°＜α＜23.1°D．23.1°＜α＜23.5°【答案】B【解答】解：如图，连接AC，CD，DE．∵＝，∴ED＝EB，∴∠EDB＝∠EBD＝α，∵＝＝，∴AC＝CD＝DE，∴∠DCE＝∠DEC＝∠EDB+∠EBD＝2α，∴∠CAD＝∠CDA＝∠DCE+∠EBD＝3α，∵AB是直径，∴∠ACB＝90°，∴∠CAB+∠ABC＝90°，∴4α＝90°，∴α＝22.5°，故选：B．6．（2021•宿迁）如图，在Rt△ABC中，∠ABC＝90°，∠A＝32°，点B、C在⊙O上，边AB、AC分别交⊙O于D、E两点，点B是的中点，则∠ABE＝．【答案】13°【解答】解：如图，连接DC，∵∠DBC＝90°，∴DC是⊙O的直径，∵点B是的中点，∴∠BCD＝∠BDC＝45°，在Rt△ABC中，∠ABC＝90°，∠A＝32°，∴∠ACB＝90°﹣32°＝58°，∴∠ACD＝∠ACB﹣∠BCD＝58°﹣45°＝13°＝∠ABE，故答案为：13°．7．（2021•安徽）如图，圆O的半径为1，△ABC内接于圆O．若∠A＝60°，∠B＝75°，则AB＝．【答案】【解答】解：如图，连接OA，OB，在△ABC中，∠BAC＝60°，∠ABC＝75°，∴∠ACB＝180°﹣∠A﹣∠B＝45°，∴∠AOB＝90°，∵OA＝OB，∴△OAB是等腰直角三角形，∴AB＝OA＝．故答案为：．8．（2021•烟台）如图，在正方形网格中，每个小正方形的边长都是1，⊙O是△ABC的外接圆，点A，B，O在网格线的交点上，则sin∠ACB的值是．【答案】【解答】解：如图，连接AO并延长交⊙O于D，由圆周角定理得：∠ACB＝∠ADB，由勾股定理得：AD＝＝2，∴sin∠ACB＝sin∠ADB＝＝＝，故答案为：．命题点2 垂径定理及其推论类型一垂径定理及其推论有关的计算9．（2021•丽水）如图，AB是⊙O的直径，弦CD⊥OA于点E，连结OC，OD．若⊙O的半径为m，∠AOD＝∠α，则下列结论一定成立的是（）A．OE＝m•tanαB．CD＝2m•sinαC．AE＝m•cosαD．S△COD＝m2•sinα【答案】B【解答】解：∵AB是⊙O的直径，弦CD⊥OA于点E，∴DE＝CD，在Rt△EDO中，OD＝m，∠AOD＝∠α，∴tanα＝，∴OE＝＝，故选项A不符合题意；∵AB是⊙O的直径，CD⊥OA，∴CD＝2DE，∵⊙O的半径为m，∠AOD＝∠α，∴DE＝OD•sinα＝m•sinα，∴CD＝2DE＝2m•sinα，故选项B正确，符合题意；∵cosα＝，∴OE＝OD•cosα＝m•cosα，∵AO＝DO＝m，∴AE＝AO﹣OE＝m﹣m•cosα，故选项C不符合题意；∵CD＝2m•sinα，OE＝m•cosα，∴S△COD＝CD×OE＝×2m•sinα×m•cosα＝m2sinα•cosα，故选项D不符合题意；故选：B．10．（2021•营口）如图，⊙O中，点C为弦AB中点，连接OC，OB，∠COB＝56°，点D 是上任意一点，则∠ADB度数为（）A．112°B．124°C．122°D．134°【答案】B【解答】解：作所对的圆周角∠APB，如图，∵C为AB的中点，OA＝OB，∴OC⊥AB，OC平分∠AOB，∴∠AOC＝∠BOC＝56°，∴∠APB＝∠AOB＝56°，∵∠APB+∠ADB＝180°，∴∠ADB＝180°﹣56°＝124°．故选：B．11．（2021•凉山州）点P是⊙O内一点，过点P的最长弦的长为10cm，最短弦的长为6cm，则OP的长为（）A．3cm B．4cm C．5cm D．6cm【答案】B【解答】解：如图所示，CD⊥AB于点P．根据题意，得：AB＝10cm，CD＝6cm．∵AB是直径，且CD⊥AB，∴CP＝CD＝3cm．根据勾股定理，得OP＝＝＝4（cm）．故选：B．12．（2021•黄冈）如图，⊙O是Rt△ABC的外接圆，OE⊥AB交⊙O于点E，垂足为点D，AE，CB的延长线交于点F．若OD＝3，AB＝8，则FC的长是（）A．10B．8C．6D．4【答案】A【解答】解：由题知，AC为直径，∴∠ABC＝90°，∵OE⊥AB，∴OD∥BC，∵OA＝OC，∴OD为三角形ABC的中位线，∴AD＝AB＝×8＝4，又∵OD＝3，∴OA＝＝＝5，∴OE＝OA＝5，∵OE∥CF，点O是AC中点，∴OE是三角形ACF的中位线，∴CF＝2OE＝2×5＝10，故选：A．13．（2021•广东）如图，AB是⊙O的直径，点C为圆上一点，AC＝3，∠ABC的平分线交AC于点D，CD＝1，则⊙O的直径为（）A．B．2C．1D．2【答案】B【解答】解：如图，过点D作DT⊥AB于T．∵AB是直径，∴∠ACB＝90°，∴DC⊥BC，∵DB平分∠CBA，DC⊥BC，DT⊥BA，∴DC＝DT＝1，∵AC＝3，∴AD＝AC﹣CD＝2，∴AD＝2DT，∴∠A＝30°，∴AB＝＝＝2，解法二：AD＝2DT由此处开始，可以在Rt△ADT中用勾股定理得AT＝，再由垂径定理可得AB＝2AT得解．故选：B．14．（2021•成都）如图，在平面直角坐标系xOy中，直线y＝x+与⊙O相交于A，B两点，且点A在x轴上，则弦AB的长为．【答案】2【解答】解：设直线AB交y轴于C，过O作OD⊥AB于D，如图：在y＝x+中，令x＝0得y＝,∴C(0,),OC＝,在y＝x+中令y＝0得x+＝0,解得x＝﹣2,∴A(﹣2,0),OA＝2,Rt△AOC中，tan∠CAO＝＝＝,∴∠CAO＝30°，Rt△AOD中，AD＝OA•cos30°＝2×＝，∵OD⊥AB，∴AD＝BD＝，∴AB＝2，故答案为：2．类型二垂径定理的实际应用15．（2021•青海）如图是一位同学从照片上剪切下来的海上日出时的画面，“图上”太阳与海平线交于A，B两点，他测得“图上”圆的半径为10厘米，AB＝16厘米．若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟，则“图上”太阳升起的速度为（）A．1.0厘米/分B．0.8厘米/分C．1.2厘米/分D．1.4厘米/分【答案】A【解答】解：设“图上”圆的圆心为O，连接OA，过点O作OD⊥AB于D，如图所示：∵AB＝16厘米，∴AD＝AB＝8（厘米），∵OA＝10厘米，∴OD＝＝＝6（厘米），∴海平线以下部分的高度＝OA+OD＝10+6＝16（厘米），∵太阳从所处位置到完全跳出海平面的时间为16分钟，∴“图上”太阳升起的速度＝16÷16＝1.0（厘米/分），故选：A．16．（2021•恩施州）《九章算术》被尊为古代数学“群经之首”，其卷九勾股篇记载：今有圆材埋于壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何？如图，大意是，今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深CD等于1寸，锯道AB长1尺，问圆形木材的直径是多少？（1尺＝10寸）答：圆材直径寸．【答案】26【解答】解：过圆心O作OC⊥AB于点C，延长OC交圆于点D，连接OA，如图：∵OC⊥AB，∴AC＝BC＝AB，．则CD＝1寸，AC＝BC＝AB＝5寸．设圆的半径为x寸，则OC＝（x﹣1）寸．在Rt△OAC中，由勾股定理得：52+（x﹣1）2＝x2，解得：x＝13．∴圆材直径为2×13＝26（寸）．故答案为：26．命题点3 圆内接四边形17．（2021•吉林）如图，四边形ABCD内接于⊙O，点P为边AD上任意一点（点P不与点A，D重合）连接CP．若∠B＝120°，则∠APC的度数可能为（）A．30°B．45°C．50°D．65°【答案】D【解答】解：∵四边形ABCD内接于⊙O，∴∠B+∠D＝180°，∵∠B＝120°，∴∠D＝180°﹣∠B＝60°，∵∠APC为△PCD的外角，∴∠APC＞∠D，只有D满足题意．故选：D．18．（2021•泰安）如图，四边形ABCD是⊙O的内接四边形，∠B＝90°，∠BCD＝120°，AB＝2，CD＝1，则AD的长为（）A．2﹣2B．3﹣C．4﹣D．2【答案】C【解答】解：延长AD、BC交于E，∵∠BCD＝120°，∴∠A＝60°，∵∠B＝90°，∴∠ADC＝90°，∠E＝30°，在Rt△ABE中，AE＝2AB＝4，在Rt△CDE中，DE＝＝，∴AD＝AE﹣DE＝4﹣，故选：C．19．（2021•苏州）如图，四边形ABCD内接于⊙O，∠1＝∠2，延长BC到点E，使得CE ＝AB，连接ED．（1）求证：BD＝ED；（2）若AB＝4，BC＝6，∠ABC＝60°，求tan∠DCB的值．【答案】（1）略（2）tan∠DCB＝【解答】（1）证明：∵四边形ABCD内接于⊙O，∴∠A＝∠DCE，∵∠1＝∠2，∴＝，∴AD＝DC，在△ABD和△DCE中，，∴△ABD≌△CED（SAS），∴BD＝ED；（2）解：过点D作DM⊥BE于M，∵AB＝4，BC＝6，CE＝AB，∴BE＝BC+EC＝10，∵BD＝ED，DM⊥BE，∴BM＝ME＝BE＝5，∴CM＝BC﹣BM＝1，∵∠ABC＝60°，∠1＝∠2，∴∠2＝30°，∴DM＝BM•tan∠2＝5×＝，∴tan∠DCB＝＝．20．（2021秋•越秀区校级期中）已知：在圆O内，弦AD与弦BC交于点G，AD＝CB，M，N分别是CB和AD的中点，联结MN，OG．（1）求证：OG⊥MN；（2）联结AC，AM，CN，当CN∥OG时，求证：四边形ACNM为矩形．【答案】（1）略（2）四边形AMNC是矩形．【解答】（1）证明：如图，连接OM，ON，OB，OD．∵M，N分别是CB和AD的中点∴OM⊥CB，ON⊥AD，∵AD＝BC，∴BM＝DN，在Rt△OMB和Rt△OND中，，∴Rt△OMB≌Rt△OND（HL），∴OM＝ON，在Rt△OMG和Rt△ONG中，∴Rt△OMG≌Rt△ONG（HL），∴GM＝GN，∵OM＝ON，∴OG⊥MN；（2）证明：∵OG⊥MN，CN∥OG，∴CN⊥MN，∴∠MNC＝90°，∵GM＝GN，∴∠GMN＝∠GNM，∵∠GMN+∠GCN＝90°，∠GNM+∠GNC＝90°，∴∠GCN＝∠GNC，∴GC＝GN，∵CM＝CB，AN＝AD，BC＝AD，∴CM＝AN，∴AG＝CG，∴AG＝GN＝CG＝GM，∴四边形AMNC是平行四边形，∵AN＝CM，∴四边形AMNC是矩形．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
专题13 圆的基本性质考纲要求:1．理解圆、弧、弦、圆心角、圆周角的概念；了解等圆、等弧的概念.2．了解弧、弦、圆心角的关系；理解圆周角与圆心角及其所对弧的关系. 3．能利用圆的有关概念、垂径定理、圆周角定理及其推论解决有关简单问题.基础知识回顾:知识点一：圆的有关概念1.与圆有关的概念和性质（1）圆：平面上到定点的距离等于定长的所有点组成的图形．如图所示的圆记做⊙O.（2）弦与直径：连接圆上任意两点的线段叫做弦，过圆心的弦叫做直径，直径是圆内最长的弦.（3）弧：圆上任意两点间的部分叫做弧，小于半圆的弧叫做劣弧，大于半圆的弧叫做优弧.（4）圆心角：顶点在圆心的角叫做圆心角.（5）圆周角：顶点在圆上，并且两边都与圆还有一个交点的角叫做圆周角. （6）弦心距：圆心到弦的距离.知识点二：垂径定理及其推论2.垂径定理及其推论定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．推论(1)平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧；(2)弦的垂直平分线经过圆心，并且平分弦所对的两条弧.延伸根据圆的对称性，如图所示，在以下五条结论中：① 弧AC=弧AD;②弧BC=弧BD ；③CE=DE; ④AB ⊥CD;⑤AB 是直径.只要满足其中两个，另外三个结论一定成立，即推二知三.知识点三 ：圆心角、弧、弦的关系3.圆心角、弧、弦的关系定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等． 推论 在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．知识点四 ：圆周角定理及其推论4.圆周角定理及其推论 （1）定理：一条弧所对的圆周角等于它所对的圆心角的一半. 如图a ，∠A=12∠O.图a 图b 图c( 2 )推论：① 在同圆或等圆中，同弧或等弧所对的圆周角相等.如图b ，∠A=∠C.② 直径所对的圆周角是直角.如图c ，∠C=90°.圆内接四边形的对角互补.如图a ，∠A+∠C=180°，∠ABC+∠ADC=180°.应用举例:招数一、垂径定理及其推论【例1】13的O 中，弦AB 与CD 交于点E ，75DEB ∠=︒，6AB =，1AE =，则CD 的长是( )A ．26B ．210C ．211D ．43【答案】C【解析】解：过点O 作OF CD ⊥于点F ，OG AB ⊥于G ，连接OB 、OD ，如图所示： 则DF CF =，132AG BG AB ===，2EG AG AE ∴=-=，在Rt BOG ∆中，221392OG OB BG =-=-=，EG OG ∴=，EOG ∴∆是等腰直角三角形，45OEG ∴∠=︒，222OE OG ==，75DEB ∠=︒，30OEF ∴∠=︒，122OF OE ∴==，在Rt ODF ∆中，2213211DF OD OF =-=-=，2211CD DF ∴==；故选：C ．招数二、圆周角定理及推论【例2】如图，AD 是O 的直径，AB CD =，若40AOB ∠=︒，则圆周角BPC ∠的度数是()A ．40︒B ．50︒C ．60︒D ．70︒【答案】D．【解析】解：AB CD=，40AOB∠=︒，40COD AOB∴∠=∠=︒，180AOB BOC COD∠+∠+∠=︒，140BOC∴∠=︒，1702BPC BOC∴∠=∠=︒，故选：D．招数三、圆内接四边形的相关计算【例3】如图，四边形ABCD内接于⊙O，AE⊥CB交CB的延长线于点E，若BA平分∠DBE，AD ＝5，CE，则AE＝（）A．3 B．3C．4D．2【答案】D【解析】连接AC，如图，根据圆内接四边形的性质和圆周角定理得到∠1＝∠CDA，∠2＝∠3，从而得到∠3＝∠CDA，所以AC＝AD＝5，然后利用勾股定理计算AE的长．解：连接AC，如图，∵BA平分∠DBE，∴∠1＝∠2，∵∠1＝∠CDA，∠2＝∠3，∴∠3＝∠CDA，∴AC＝AD＝5，∵AE⊥CB，∴∠AEC＝90°，∴AE2．故选：D．招数四、分类讨论在圆的基本性质计算中的应用【例4】半径为5的 O是锐角三角形ABC的外接圆，AB＝AC，连接OB，OC，延长CO交弦AB 于点D.若△OBD是直角三角形，则弦BC的长为______.【答案】5352或【解析】如图1，当∠BOD＝90°时，∠BOC＝90°，在Rt△BOC中，BO＝OC＝5，∴BC＝52;如图2，当∠ODB＝90°时，∵OB＝OC，设∠OBC＝∠OCB＝x，∴∠BOD＝2x，∠BOC＝180°－2x，∴∠ABO＝90°－2x，∠ABC＝∠ACB＝90°－x，∴∠A＝2x，∵∠BOC＝2∠A，即180－2x＝2×2x，∴x＝30°，∴∠BOC＝120°，∵OB＝OC＝5，∴BC＝53.综上所述，BC的长度为5352或图1 图2方法、规律归纳:1．圆心角、弧和弦之间的等量关系必须在同圆或等圆中才成立.2．在圆中求角度时，通常需要通过圆的性质进行转化.比如圆心角与圆周角间的转化；同弧或等弧的圆周角间的转化；连直径，得到直角三角形，通过两锐角互余进行转化等.3．垂径定理的计算常与勾股定理相结合，解题时往往需要添加辅助线，一般过圆心作弦的垂线，构造直角三角形.实战演练:1.《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著，与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题：“今有圆材埋在壁中，不知大小.以锯锯之，深一寸，锯道长一尺，问径几何？”小辉同学根据原文题意，画出圆材截面图如图所示，已知：锯口深为1寸，锯道AB=1尺（1尺=10寸），则该圆材的直径为寸.【答案】26.【解析】设⊙O的半径为r．在Rt△ADO中，AD=5，OD=r-1，OA=r，则有r2=52+(r-1)2，解得r=13，∴⊙O的直径为26寸，故答案为26．2.如图，正△ABC 的边长为2，点A、B在半径为的圆上，点C在圆内，将正△ABC绕点A 逆时针旋转，当点C 第一次落在圆上时，旋转角的正切值为_____．【答案】【解析】如图，分别连接 OA、OB、OD；∵OA ＝OB ＝ ，AB ＝2，∴△OAB 是等腰直角三角形，∴∠OAB ＝45°；同理可证：∠OAD ＝45°，∴∠DAB ＝90°；∵∠CAB ＝60°，∴∠DAC ＝90°﹣60°＝30°，∴旋转角的正切值是 ， 故答案为：．3. 如图，半径为3的⊙A 经过原点O 和点C （0，2），B 是y 轴左侧⊙A 优弧上的一点，则tan ∠OBC ＝（ ）A ．31B ．22 C ．322 D ．42【答案】D【解析】作直径CD ，在Rt △OCD 中，CD ＝6，OC ＝2，则OD ＝42，cos ∠CDO ＝OCOD ＝322， 由圆周角定理得，∠OBC ＝∠CDO ，第8题图则cos ∠OBC ＝322，故选：D ．4.如图，CD 为O 的直径，弦AB CD ⊥，垂足为E ，AB BF =，1CE =，6AB =，则弦AF 的长度为 ．【答案】485【解析】连接OA 、OB ，OB 交AF 于G ，如图，AB CD ⊥，132AE BE AB ∴===，设O 的半径为r ，则1OE r =-，OA r =，在Rt OAE ∆中，2223(1)r r +-=，解得5r =，AB BF =，OB AF ∴⊥，AG FG =，在Rt OAG ∆中，2225AG OG +=，①在Rt ABG ∆中，222(5)6AG OG +-=，②解由①②组成的方程组得到245AG =，4825AF AG ∴==． 故答案为485． 5.在半径为1的圆中，长度等于2的弦所对的圆周角的度数为（ ）A. 90︒B. 145︒C. 90︒或270︒D. 135︒或45︒【答案】D【解析】试题解析：45AOC ∴∠=，同理45BOC ∠=， 90AOB AOC BOC ∴∠=∠+∠=， ∵∠AOB 与∠ADB 都对AB ，1452ADB AOB ∴∠=∠=， ∵大角270AOB ∠=， 135AEB ∴∠=， 则弦AB 所对的圆周角为45或135.故选D.6. 如图，AC 是⊙O 的弦，AC =5，点B 是⊙O 上的一个动点，且∠ABC =45°，若点M 、N 分别是 AC 、BC 的中点，则 M N 的最大值是____________．【答案】52 2【解析】∵MN是△ABC的中位线，∴MN=12 AB．当AB为⊙O的直径时，AB有最大值，则MN有最大值．当AB为直径时，∠ACB=90°，∵∠ABC=45°，AC=5，∴AB=52，∴MN=522．7.如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°，点B为劣弧AN的中点．点P是直径MN上一动点，则PA+PB的最小值为（）A. 2B. 1C. 2D. 22【答案】A∵∠AMN=30°，∴∠AON=2∠AMN=2×30°=60°，∵点B为劣弧AN的中点，∴∠BON=12∠AON=12×60°=30°，由对称性，∠B′ON=∠BON=30°，∴∠AOB′=∠AON+∠B′ON=60°+30°=90°，∴△AOB′是等腰直角三角形，∴AB′=2OA=2×1=2，即PA+PB的最小值=2．故选A．8. 如图，在矩形中，，，以为直径作.将矩形绕点旋转，使所得矩形的边与相切，切点为，边与相交于点，则的长为__________．【答案】4解：连结EO并延长交CF于点H.∵矩形绕点旋转得到矩形，∴∠B′=∠B′CD′=90°，A′B′∥CD′，BC=B′C=4，∵A′B′切⊙O与点E，∴OE⊥A′B′，∴四边形EB′CH是矩形，∴EH=B′C=4，OH⊥CF，∵AB=5，∴OE=OC=AB=，∴OH=，在Rt △OCH 中，根据勾股定理得CH===2，∴CF=2CH=4.故答案为：4.9. 如图，AB 为O 的直径，点C 在O 上．（1）尺规作图：作BAC ∠的平分线，与O 交于点D ；连接OD ，交BC 于点E （不写作法，只保留作图痕迹，且用黑色墨水笔将作图痕迹加黑）；（2）探究OE 与AC 的位置及数量关系，并证明你的结论．【答案】（1）见解析；（2）见解析.【解析】（1）如图所示；（2）//OE AC ，12OE AC =．理由如下： AD 平分BAC ∠，12BAD BAC ∴∠=∠， 12BAD BOD ∠=∠，BOD BAC ∴∠=∠，//OE AC ∴， OA OB =，OE ∴为ABC ∆的中位线， //OE AC ∴，12OE AC =． 10. 如图，AB 是⊙O 的直径，AB ＝10，BC 、CD 、DA 是⊙O 的弦，且BC ＝CD ＝DA ，若点P 是直径AB 上的一动点，则PD+PC 的最小值为_____．【答案】10【解析】如图，作出点C关于AB的对称点C′，连接C′D，则C′D与AB的交点即为所求的点P，连接CP，C′D=PC+PD，∵AB是⊙O的直径，BC=CD=DA，∴∠B=××180°=60°，∵AD=BC，∴AB∥CD，∴∠BCD=120°，∴∠BCC′=×60°=30°，∴∠C′CD=120°-30°=90°，∴C′D为圆的直径，∵AB是⊙O的直径，AB=10，∴PD+PC的最小值为10，故答案为：10．。