附合导线按条件平差算例
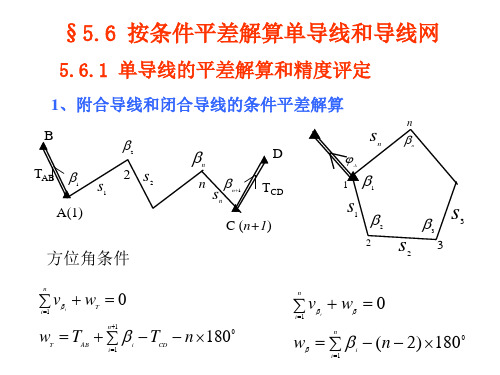
按条件平差解算单导线和导线网
n
n
1
wy = ∑ ∆yi,i+1
i =1
n
i =2
ρ
5.6.1 单导线的平差解算和精度评定
2、 无定向导线和单定向导线的平差解算 、
β
T1
2
β
s
2
n
2
s
1
n
1
Tn
sn
n+1
引入方位角条件未知数T1，Tn，采用附有未 知数的条件平差模型计算。其条件方程如下： 方位角条件：
∑ vβ + δ T − δ T + wT = 0
1
J
n
J+1
每个导线段可列出3个条件：
坐标方位角的条件式：∑ v β + δ TJ − δ TJ +1 + wT
i =1
i
nj
J , J +1
=0
其中： wT
J , J +1
= TJ + ∑ v β − TJ0+1 − n J × 180
0 i =1
i
nj
5.6.2 导线网的平差解算和精度评定
纵坐标条件式： ∑ cos Ti v s − ∑
i
ρ
1
ρ
n
wy = yA + ∑ ∆yi0,i+1 − yc
i =1
n
5.6.1 单导线的平差解算和精度评定
如果只在导线的一端引入方位角未知数 T1，则只 能列出如下两个坐标条件：
0 0 ∑ cosTi vs − ∑ ( yn+1 − yi )vβ − ( yn+1 − y1 )δ T + wx = 0 0 0 0 i =1
附合导线平差计算过程说明
附合导线平差计算过程说明1）道路观测左角∑β测左=308°2.'38"+70°35'41"+156°56'39"+185°39'2"+205°21'59"+174°36'43"+197°31'46"+157°36'36"+135°14'40"+167°38'50"=1759°14'34"ƒβ测=a始边- a终边=-15"。
ƒβ容=± 40√n =±126"。
ƒβ测＜ƒβ容，测角精度符合要求。
2）改正角：β=β测- ƒβ测/N。
3）坐标方位角的推算：根据起始边的坐标方位角及改正角，依据公式a下一边’= a始边+180°+转角（观测转左角）依次计算各边的坐标方位角。
4）坐标增量的计算及闭合差的调整坐标增量计算根据已经推算出的导线各边的坐标方位角和相应边的边长，按下面公式计算各边的坐标增量。
△ X AB=D AB*COS a AB，△ Y AB=D AB*SIN a AB，按附合导线要求，各边的坐标增量代数和的理论植，等于终起两点的已知坐标之差，所以，纵、横坐标增量闭合差按公式计算，Fx=∑△x测-（X终-X起）FY=∑△Y测-（Y终-Y起）导线全长闭合差f=√(ƒx2+ƒy2)=0.102m,k=f/∑D=1/38370＜1/2000.满足精度要求。
5）根据后一点的坐标及改正后的坐标增量，按公式推算前一点坐标。
X前=X后+△x改Y前=Y后+△Y改最后，推算出终止边的坐标，与原有设计值相等，以作检核。
附和导线、闭合导线的简易平差与支导线的计算
否 无法计算，
所
计算的类 型
跳出提示选 择的提醒框
示
是
点击计算
是否
否
保存
是
保存结果TXT
退出
•
程 序 设 计 流 程
图
基础理论
• 计算方位角闭合差fβ，判断Sβ<fβ容
• β=α’CD -αCD
• fβ容=60或40
n：角的个数
• 分配角闭合差（平均分配），计算改正后的角
度
• V=—β/n βi改=βi+V
政
关键技术和难点
• 度分秒与弧度间的互相转换
•
public static class hddfm
•
{
•
const double pi = 3.1415926;
•
//角度转化为弧度
•
public static double angle_r(double alfa)
•
{
度
•
double alfa1, alfa2;
弧 度
•
return (alfa1 / 180d * pi);
的
•
}
•
//弧度转化为角度
相
•
public static double redian_a(double alfa)
互
•
{
•
double alfa1, alfa2;
•
alfa = alfa * 180d / pi;
转 换
•
alfa1 = Math.Floor(alfa) + Math.Floor((alfa - Math.Floor(alfa)) * 60d) / 100d;
1-11单导线条件平差计算--附合导线坐标条件方程
平差值条件方程： ALˆ A0 0
改正数条件方程： AV W 0
STEP1
表达成角度和边
长平差值的形式
STEP2
表达成角度和边
长改正数的形式
附合导线坐标条件方程
1、纵坐标附合条件方程式
xˆN 1 xC 0
STEP1
xˆN 1 xB [xˆi ]1N
xˆi Sˆi cosTˆi
3
N
SN-1
SN
D
TCD
βN+1
C (N+1)
纵坐标符合条件方程式就是：xˆN 1 xC 0 横坐标符合条件方程式就是：yˆ N 1 yC 0
B点坐标的已知值 (xB , yB ) 或 (x1, y1)
C点坐标已知值
(xC , yC ) 或 (xN 1, yN 1)
C点坐标观测值
A
D
β2
β4
βN
2
4
β1 S1 S2 β3 S3
N
SN-1
SN βN+1
3
B(1)
附合导线示例图
C(N+1)
附合导线坐标条件方程
补充：具体计算时的单位选取
如果x、y 以米为单位，w、vS 以厘米为单位、vβ 以秒为单位。
[cos Ti
vSi
]1N
1
[( yN 1
yi )vi
]1N
STEP2
表达成角度和边 长改正数的形式
xˆN 1 xB [xˆi ]1N
xˆi Sˆi cosTˆi
非线性从这个式子着手！！
Tˆi TAB ˆ j
i
180
1-15条件平差精度评定--条件平差单位权中误差的计算
B
……
……
方位角T ……
条件平差精度评定
1.角度和边长的平差值（观测值平差值）的精度 2.未知点的坐标平差值（观测值平差值函数）的精度
已有的量
观测值的权阵
PLL
观测值的协因数阵
QLL
P 1 LL
待求的量
1.观测值平差值的协方差阵
DLˆLˆ
建立 联系
2.观测值平差值函数的协方差阵
测量平差的第二个任务
评定测量成果的精度
？ 具体来说评定什么量的精度
导线条件平差实例
图示为一四等附合导线，《规范》测角 中误差 2.5 ，测边所用测距仪的标称精 度公式 S 5mm 5 ppmDkm 。 已知数据和观测值见表1、表2。 试按条件平差法求：1.角度和边长的平差值；
0 0 0 0 0 1 0 0 0 0.833
0
0
0
0
0
0
1
0
0
0.612
0 0 0 0 0 0 0 1 0 0.049
0 0 0 0 0 0 0 0 1 3.246
3.2460
V T PV (W )T K 3.9 -1.6 1.71.0518 20.2761
3.4906
ˆ0
V T PV
r
20.276132 2.6 3
后验单位权中误差估值
单位权中误差
？ 0 2.5" 先验单位权中误差
理论
感谢聆听，批评指导
公式
思考
平差
算例
间接法 矩阵式
V T PV V T P(P1AT K ) V T AT K ( AV )T K (W )T K
附合导线平差计算(函数版)
22468
数据精度
由 两 点 坐 标 ， 求 得 方 位 角 ， 返 还 十 进 制 角 度
∑△y = 1464.520 fy=∑△y-（Yc-Yb）= 0.016 f=√(fx*fx+fy*fy) = 0.082 K=f/∑D≈1/22468＜1/15000 符合精度要求
3.43 #### 22′ 57.8″ ####### -121.569 148.092 3.43 43° 27′ 32.2″ ####### 115.012 3.43 61° 25′ 16.7″ ####### 116.022 3.43 #### 31′ 57.1″ ####### -99.987 3.43 64° 25′ 23.5″ ####### 3.43 #### 20′ 41.0″ ####### -65.986 3.43 29° 19′ 45.4″ ####### 210.005 3.43 #### 01′ 57.8″ ####### -68.994 3.43 44° 57′ 49.3″ ####### 148.645 3.43 83° 28′ 20.7″ 148.456 200.002 117.990 225.004 78.012 162.994 140.009 212.987 108.986
验 算
1801° 30′ 21″ fβ = Σ fβ 测-Σ fβ 理= -34″ fβ 允= ±10√n = ±32″ fβ >fβ 允 , 不符合精度要求
∑△x = 311.160 fx=∑△x-（Xc-Xb）=0.080 f=√(Βιβλιοθήκη x*fx+fy*fy) =
K=f/∑D≈1/22468＜1/15000
线 计 算 表
附合导线平差内业计算
附合导线平差内业计算一、主要公式（左角）：如图：有：αB1=αA B+βB±180°α12=αB1+β1±180°α23=α12+β2±180°α3C=α23+β3±180°αCD=α3C+βC±180°计算终边坐标方位角的一般公式为：α终边′=α始边+Σβ测±n×180°角度闭合差：?β测=α终边′-α终边，?β允=±10n（一级导线技术要求），式中n为导线观测角个数。
如果?β测>?β允，则说明测角误差超限，应停止计算，重新检测角度。
如果?β测>?β允，说明测角精度符合要求，此时需要进行角度闭合差的调整。
调整是应注意:当用左角计算α终边′时，改正数的符号与?β测符号相反；当用右角计算α终边′时，改正数的符号与?β测符号相同。
可将闭合差按相反符号平均分配给各观测角，而得出改正角：V改=-?β测/n式中n内角的个数，计算的改正数，取位至秒。
根据公式β＝β测+V改得出改正后的观测角，继而算出新的方位角。
为了检核，最后应重新推算结束边的坐标方位角，它应与已知数值相等。
否则，应重新推算。
坐标增量闭合差：ΔX AB=D AB×COS(αAB),ΔY AB=D AB×SIN(αAB)ΔX B1=D B1×COS(αB1),ΔY B1=D B1×SIN(αB1)ΔX12=D12×COS(α12),ΔY12=D12×SIN(α12)ΔX23=D23×COS(α23),ΔY23=D23×SIN(α23)ΔX3C=D3C×COS(α3C),ΔY3C=D3C×SIN(α3C)按附合导线的要求，各边坐标增量代数和的理论值ΣΔX i、ΣΔY i，应等于终、起两点的已知坐标值之差。
附和导线平差计算详细教程，留着慢慢学习！
附和导线平差计算详细教程，留着慢慢学习！本篇继续讲解附和导线的内业平差。
平差顾名思义就是把总误差进行平均分配，让每个点的误差都控制在允许的范围内。
平差有两种方式，一是手动平差，二是软件平差。
本文讲解手动平差，这个过程能让新手测量员们掌握平差的原理，和相关的基础知识。
本文还是以上篇的实例来讲解，开始前先来看看上篇文章中我们外业观测的记录。
第1步，制作平差计算表并填入已知数据在Excel中按适当格式制作一个《附和导线平差计算表》（表格我已经做好了，需要的可以给我发私信），然后按要求输入起始边和附和边的起、终点坐标并计算方位角和边长。
再参照观测记录表在”测点“栏中依次填入各个测点，在”观测左角值”栏中填入每个测站测得的平均角值，在“距离”栏中填入各导线边的平均边长。
填入后的效果如下图：注：已知边的方位角和边长的计算方式很多，比如用5800计算器的Pol函数，道路之星的测站、CASS查询等。
第2步，计算角度闭合差计算角度闭合差，是为了检验外业角度观测的精度是否满足相应等级导线的技术要求。
如果实测的角度闭合差<>相关计算公式：实测角度闭合差=实测附和边方位角-理论附和边方位角实测附和边方位角=起始边方位角-N*180+实测左角值之和容许角度闭合差各等级导线有相应规定（各等级导线的技术要求在上篇文章中）。
注：N为测量站数，方位角取值范围是0度（含）到360度（不含），大于360度的减去360度，小于0度的加上360度。
本案例经计算：角度闭合差=7.1秒，容许闭合差=22秒，观测精度合格。
第3步，计算左角改正数经过角度闭合差的计算，确定外业成果合格后，就要计算左角改正数。
左角改正数=角度闭合差的相反数/测站个数改正后左角值=观测左角值+左角改正数本案例角度闭合差=7.1秒，那么左角改正数=-7.1/5=-1.42秒。
分配说明：为尽量平均分配误差，我们可将改正数保留1位小数，所以案例中每个测站分配-1.4秒，这时还有0.1秒未得到分配。
1-10单导线条件平差计算--附合导线方位角条件方程-修改
坐标方位角条件就是： TˆN 1 TCD 0
TˆN 1 TCD 0
代入
TˆN 1
TAB
[ˆi
]N 1
1
(N
1) 180
？ 思考
TCD TN 1 TˆN1
TAB [ˆi ]1N 1 (N 1) 180 TCD 0 代入 ˆi i vi (i 1,2,, N 1)
[vi ]1N 1 wT 0
wT (TAB [i ]1N 1 (N 1) 180 TCD ) (TN 1 TCD )
A
D
β2
β4
βN
坐标方位角改正数条件方程: [vi ]1N 1 wT 0
β1 B(1)
2
4
S1 S2 β3 S3
3
N
SN-1
( xˆ N 1，yˆ N 1 )
条件方程类型:
1坐标方位角附合条件方程式 2纵坐标附合条件方程式 3横坐标附合条件方程式
A
D
β2
β4
βN
β1 B(1)
2
4
S1 S2 β3 S3
3
N
SN-1
SN βN+1
C(N+1)
附合导线示例图
理论
感谢聆听，批评指导
公式
思考
平差
算例
Xi’an University of Science & Technology
举一 反三
治学 严谨
Error Theory and Surveying Adjustment
逻辑
性强
主讲人：史经俭 张静 席晶
本讲内容
附合导线方位角条件方程
附合导线严密平差算法总结
附合导线严密平差算法总结图1如图的单一附合导线，有4个已知点A、B、C、D，2个未知点TP1、TP2。
设观测边数为n, 则未知点数为n-1, 观测角数为n+1。
以上图为例，n = 3。
观测边为：S1 = B->TP1,S2 = TP1->TP2, S3 = TP2->C思路：由于A、B坐标已知，则可以算出起始方位角，再根据B点坐标和每个观测角（夹角，左角）推算出TP1、TP2、C点的近似坐标值。
如果是用全站仪进行测量，则用盘左盘右重复观测求平均的方式，直接测出TP1、TP2、C点的近似坐标值以及CD的方位角。
再根据c点的已知坐标与近似坐标求坐标闭合差，由CD的已知方位角和近似方位角求角度闭合差，两个闭合差联立求得边长和角度的改正数，最后求得未知点的坐标平差值。
条件平差过程：1.建立条件方程，求得条件系数2.求法方程系数3.求权阵4.计算出联系数K5.解算出观测值改正数V6.由观测值和改正数计算平差值详细步骤如下：1、建立条件方程在单一附合导线中，只需要三个条件方程即：方位角附合条件、纵坐标附合条件和横坐标附合条件方程。
（省略了条件方程的推导过程，详细过程请查看参考资料：《测量平差.pps》）（1）方位角附合条件[Vβi]n+11+ Wβ= 0式中，Wβ= - （T0– T CD+ [βi]n+11 - （n+1）*180°）（角度闭合差）βi ——角度观测值（夹角，左角）Vβi ——各观测角的改正数。
如果是用全站仪观测，则Wβ= - （T CD– T CD）式中，T CD ——CD的方位角观测值，T CD ——CD的已知方位角（2）纵坐标X附合条件方程[Cos TI * VSi]1n - （1/ ρ”）* [(Yn+1- Yi) * Vβi]1n - W x = 0;式中，TI——各方位角观测值（近似值）VSi——边长改正数Yn+1—— C点即终止点的横坐标Y的观测值（近似值）Yi——待定点的横坐标Y的观测值Wx = - （Xn+1- XC）XC—— C点即终止点的纵坐标X的已知值ρ” = 2062.65（3）横坐标Y附合条件方程[Sin TI * VSi]1n + （1/ ρ”）* [(Xn+1- Xi) * Vβi]1n– W Y = 0;式中，TI——各方位角观测值（近似值）VSi——边长改正数Xn+1—— C点即终止点的纵坐标X的观测值（近似值）Xi——待定点的纵坐标X的观测值WX = - （Yn+1- YC）YC—— C点即终止点的横坐标Y的已知值ρ” = 2062.652、求条件方程的系数矩阵联立3个方程得改正数条件方程组：[Vβi]n+11+ Wβ= 0[Cos TI * VSi]1n - 1/ ρ”* [(Yn+1- Yi) * Vβi]1n - W x = 0;[Sin TI * VSi]1n + 1/ ρ”* [(Xn+1- Xi) * Vβi]1n– W Y = 0;其系数矩阵arrA为：（即改正数V的系数，此处以图1为例， n = 3）3、联系数法方程（简称法方程）AP-1A T K – W = 0A——系数矩阵arrAK ——乘系数P ——权阵W ——闭合差矩阵由上得法方程的系数阵N：N = AP-1A T（权的推导见参考资料：《全站仪观测导线测量平差方法的研究.pdf》）角度权：P βi = 1；（因为角度的标称精度是固定的，各观测角权值相等） 边长权：P Si = (μ0 *μ0 ) / （M D * M D ）（误差比例系数固定，边长的误差与距离有关，因此不一致）式中，μ0 ——先验测角中误差，以秒为单位 M D —— 距离观测中误差若 导线边长为S i （米），e1 为仪器的边长标称固定误差（mm ），e2为仪器的边长比例误差系数（无单位），则M D = ± （e1 + e2 * S i * 0.001）mm 需转化为厘米：M D = M D ** 0.1 （cm ）由于此处是要P 的逆矩阵P -1,因此要求P 的各元素的倒数（P 是对角矩阵，对角矩阵的逆矩阵就是原矩阵元素的倒数） Psi = 1/ Psi ；由上可得，P -1 矩阵如下：4、求改正数由于N 已经在前面的步骤中求出，求N 的逆矩阵。
单一附合导线平差计算
单一附合导线平差计算[PC1500]单一附合导线平差计算[PC1500]由本人在网络上收集整理2 W=1+G+5E-7:D$=STR$ (INT W-1):G$=STR$ (W-INT W)3 IF LEN D$<3LET D$=" "+D$:GOTO 34 IF LEN G$<8LET G$=G$+"0":GOTO 45 G$=D$+" "+MID$ (G$,3,2)+" "+MID$ (G$,5,2)+"."+MID$ (G$,7,2):RETURN6 Z=Z+B(I)-180:Z=Z-(SGN Z+SGN (Z-360))*180:RETURN7 X(I)=X(I-1)+S(I)*C:Y(I)=Y(I-1)+S(I)*S:RETURN8 "A"CLEAR :INPUT "M=";U,"MB=";M,"Ms:a(mm)=";A,"b(ppm)=";B,"SIDES=";N10 DIM B(N),S(N),Q(N),X(N),Y(N):S$="######.###":W$="####.##":WAIT 015 INPUT "Xa=";X(0),"Ya=";Y(0),"a(I)=";H,"Xb=";X,"Yb=";Y,"a(II)=";L,"TOTAL Mp=";F20 T=N+1:P=180/PI :K=5E-3:IF F=0THEN 4525 DIM P(F),F(F),G(F),H(F),I(F),J(F),K(F),C(F),D(F),E(F)30 FOR I=1TO F:IF F=N-1LET P(I)=I:GOTO 4035 PRINT I;":P";:INPUT P(I):CLS40 NEXT I45 FOR I=0TO N:IF IPRINT "S";I;"=";:INPUT S(I):CLS50 PRINT "B";I;"=";:INPUT B(I):CLS :NEXT I:END55 "B"PRINT "M=";U;" ";:INPUT U60 CLS :PRINT "MB=";M;" ";:INPUT M65 CLS :PRINT "a=";A;"mm";" ";:INPUT A70 CLS :PRINT "b=";B;"ppm";" ";:INPUT B75 CLS :PRINT "Xa=";X(0);" ";:INPUT X(0)80 CLS :PRINT "Ya=";Y(0);" ";:INPUT Y(0)85 CLS :PRINT "a(I)=";H;" ";:INPUT H90 CLS :PRINT "Xb=";X;" ";:INPUT X95 CLS :PRINT "Yb=";Y;" ";:INPUT Y100 CLS :PRINT "a(II)=";L;" ";:INPUT L105 CLS :FOR I=0TO N:IF IPRINT "S";I;"=";S(I);" ";:INPUT S(I)110 CLS :PRINT "B";I;"=";B(I);" ";:INPUT B(I)115 CLS :NEXT I:END120 "C"CSIZE 2:COLOR 2:LPRINT "M=";U;",MB=";M:LPRINT "Ms=";A;"mm+";B;"ppm"125 GOSUB 1:LPRINT "P B(Observed)":GOSUB 1:LF 2:H=DEG H:L=DEG L:Z=H130 FOR I=0TO N:G=B(I):GOSUB 2:IF I=0LPRINT "A";:GOTO 145135 IF I=NLPRINT "B";:GOTO 145140 LPRINT I;145 LPRINT TAB 4;G$:B(I)=DEG G:LF 2:GOSUB 6:NEXT I:LF -1:GOSUB 1:W=Z-L:W=W-180*SGN W*(SGN (ABS W-1)+1) 150 V=W/T:Z=H:E=0:G=0:L=0155 GOSUB 1:LPRINT TAB 7;"S(Observed)":GOSUB 1:LF 3160 FOR I=0TO N:IF I=0THEN 185165 Q(I)=((A+S(I)*B/1E3)/M)^2*12.96:LPRINT S(I):LF 2:C=COS Z:S=SIN Z170 D=D+Q(I)*C*C:E=E+Q(I)*S*S:G=G+Q(I)*C*S:GOSUB 7:L=L+S(I):IF F=0THEN 185175 IF O<FLET O=O+1180 IF I=P(O)LET F(O)=D:G(O)=E:J(O)=D:K(O)=G:C(O)=G:D(O)=E:E(O)=G185 B(I)=B(I)-V:GOSUB 6:Q=Q+X(I)/T:R=R+Y(I)/T:NEXT I:LPRINT :GOSUB 1:V=0190 X=X(N)-X:Y=Y(N)-Y:COLOR 2:LPRINT "WB=";USING W$;3600*W+K*SGN W195 LPRINT TAB 3;"WB(Ltd)=";2*SQR T*U+K:S=SQR (X*X+Y*Y):LPRINT TAB 3;USING S$;"L=";L200 LPRINT "Wx=";USING W$;X*100+K*SGN X:LPRINT "Wy=";Y*100+K*SGN Y:LPRINT "Ws=";S*100+K;"cm"205 USING :LPRINT TAB 3;"Ws/L=1/";INT (L/S/100+.5)*100:LPRINT :S=P*P210 FOR I=0TO N:X(I)=X(I)-Q:Y(I)=Y(I)-R:D=D+Y(I)^2/S:E=E+X(I)^2/S:G=G-X(I)*Y(I)/S215 NEXT I:Z=D*E-G*G:J=(G*Y-E*X)/Z:U=(G*X-D*Y)/Z220 M=SQR (W*W/T-J*X-U*Y)/SQR 3:LPRINT "Mo=";USING "###.##";M*3600+K:IF F=0THEN 275225 FOR A=1TO F:O=P(A):FOR I=0TO O-1:B=Y(O)-Y(I):C=X(O)-X(I):E(A)=E(A)-B*C/S230 F(A)=F(A)+B*B/S:G(A)=G(A)+C*C/S:H(A)=H(A)-B/P:I(A)=I(A)+C/P235 J(A)=J(A)-B*Y(I)/S:K(A)=K(A)+C*Y(I)/S:C(A)=C(A)+B*X(I)/S:D(A)=D(A)-C*X(I)/S240 NEXT I:NEXT A245 FOR I=1TO F:A=C(I)*D-J(I)*G:B=D(I)*D-K(I)*G250 L=F(I)-H(I)^2/T-J(I)^2/D-A*A/D/Z:V=G(I)-I(I)^2/T-K(I)^2/D-B*B/D/Z255 S=E(I)-H(I)*I(I)/T-J(I)*K(I)/D-A*B/D/Z260 C=ATN (2*S/(L-V))/2:C=C+45*(2-SGN C-SGN S):USING :LPRINT "P";P(I);":":CSIZE 1:LF -1:CSIZE 2:GRAPH :ROTATE 1 265 LPRINT "O":ROTATE 0:TEXT :LPRINT "le=";USING W$;C+K;"(DEG)"270 LPRINT "E=";USING "###.#";M*SQR (L+S*TAN C)*100+.05;",F=";M*SQR ABS (V-S*TAN C)*100+.05;"cm":NEXT I275 Z=H:GOSUB 1:LPRINT "B(Adjusted) / a":GOSUB 1:K=5E-4280 FOR I=0TO T:G=DMS Z:GOSUB 2:COLOR (I=0OR I=T)*3:LPRINT TAB 6;G$:LPRINT :IF I=0THEN 300290 IF I=TLF -1:GOTO 310295 S(I)=S(I)+(C*J+S*U)*Q(I)300 B(I)=B(I)+(J*Y(I)-U*X(I))/P:G=DMS B(I):GOSUB 2:IF IGOSUB 7305 COLOR 0:LPRINT G$:GOSUB 6:C=COS Z:S=SIN Z:IF I=0LET X(0)=X(0)+Q:Y(0)=Y(0)+R310 NEXT I:GOSUB 1:GOSUB 1:LPRINT TAB 7;"S(Adjusted)":GOSUB 1:LPRINT315 FOR I=1TO N:LF 2:LPRINT USING S$;S(I)+K:NEXT I:LF 3:GOSUB 1:GOSUB 1:LPRINT TAB 9;"X / Y":GOSUB 1320 USING "########.###":FOR I=0TO N:X=X(I):LPRINT :IF I=0OR I=NCOLOR 3:GOTO 330325 X=X+K*SGN X*(X<1E6)330 LPRINT X:LPRINT Y(I)+K*SGN Y(I):COLOR 0:NEXT I:LPRINT :GOSUB 1:USING :END10001 GRAPH :LINE -(216,0),0,0:TEXT :LPRINT :RETURNINT X:LPRINT Y(I)+K*SGN Y(I):COLOR 0:NEXT I:LPRINT :GOSUB 1:USING :END10001 GRAPH :L。
附和导线近似平差计算程序
附和导线近似平差计算程序P:A:B:I:J:K:L:Defm12 P=P+2:N=0:M=AW=60√P÷3600LbI0N=N+1{C}Z[2N-1]=C:M=M+CM>180=>M=M-180:≠=>M=M+180⊿N<P=>Goto0⊿F=M-B:F>360=>F=F-360⊿F▲AbsF<W=>F=-F÷P:≠=>Goto E⊿N=0:M=ALbI1N=N+1:M=M+Z[2N-1]+FM>180=>M=M-180▲≠=>M=M+180▲⊿Z[2N-1]=MN<P=>Goto1⊿N=0:M=0:G=0:H=0:P=P-1LbI2N=N+1{D}:Z[2N]=D:M=M+DX=DcosZ[2N-1]:Y=DsinZ[2N-1]G=G+X:H=H+YZ[2N-1]=X:Z[2N]=YN<P=>Goto2⊿G=G+I-K▲H=H+J-L▲T=√(G×G+H×H)▲Q=M÷T▲Q>2000=>G=-G÷M:H=-H÷M:≠=>Goto E⊿N=0:X=I:Y=JLbI3N=N+1▲D=√(Z[2N-1]×[2N-1]+Z[2N]×[2N])V=Z[2N-1]+DG▲U=Z[2N]+DH▲X=X+V▲Y=Y+U▲Z[2N-1]=X:Z[2N]=YN<P=>Goto3⊿LbI E说明:1程序中Defm12是按4个未知点设置的,计算时要进行修改。
如未知点数为n,修改数为2(n+2)。
1:P输入未知点数2:A输入起点方位角3:输入终点方位角4:I,J输入起点坐标5:K,L输入终点坐标6:C从导线起点依次观测角7:F角度闭合差8:M导线第一边依次方位角平差值9:D导线第一边依次输边长10:G,H为(⊿X,⊿Y)导线闭合差11:T为导线绝对误差12:Q为导线相对闭合差分母,分子为1 13:N导线未知点数14:V,U为导线第一边坐标增量平差值15:X,Y为导线未知点坐标平差值。
1-16条件平差精度评定--条件平差模型中的协因数阵
STEP1
STEP2
STEP3
STEP4
STEP5
STEP6
条件平差模型中的协因数阵
将其组成一个列向量，并以Z表示之
L E
0
Z
WK
A
1
Naa A
A0
1
L Naa A0
V
Lˆ
P
1
AT
N
QLK QWK QKK QVK QLˆK
QLV QWV QKV QVV QLˆV
QLLˆ QWLˆ
Q AQ
QKLˆ QVLˆ
QLˆLˆ
1
Naa AQ
QAT
N
1
aa
AQ
Q
QAT
N
1
aa
AQ
QAT N aa E QAT 0
QAT
N
1
aa
E
1
N aa
QAT
N
1
aa
0
QAT
N
1
aa
AQ
AQ
1
Naa AQ
QAT
N
1
aa
AQ
0
Q
QAT
N
1
aa
AQ
0
0
0
Q
QAT
N
1
aa
AQ
条件平差模型中的协因数阵
表1
条件平差有关向量的协因数结构一览表
附合导线平差计算过程说明
附合导线平差计算过程说明1）道路观测左角∑β测左=308°2.'38"+70°35'41"+156°56'39"+185°39'2"+205°21'59"+174°36'43"+197°31'46"+157°36'36"+135°14'40"+167°38'50"=1759°14'34"ƒβ测=a始边- a终边=-15"。
ƒβ容=± 40√n =±126"。
ƒβ测＜ƒβ容，测角精度符合要求。
2）改正角：β=β测- ƒβ测/N。
3）坐标方位角的推算：根据起始边的坐标方位角及改正角，依据公式a下一边’= a始边+180°+转角（观测转左角）依次计算各边的坐标方位角。
4）坐标增量的计算及闭合差的调整坐标增量计算根据已经推算出的导线各边的坐标方位角和相应边的边长，按下面公式计算各边的坐标增量。
△ X AB=D AB*COS a AB，△ Y AB=D AB*SIN a AB，按附合导线要求，各边的坐标增量代数和的理论植，等于终起两点的已知坐标之差，所以，纵、横坐标增量闭合差按公式计算，Fx=∑△x测-（X终-X起）FY=∑△Y测-（Y终-Y起）导线全长闭合差f=√(ƒx2+ƒy2)=0.102m,k=f/∑D=1/38370＜1/2000.满足精度要求。
5）根据后一点的坐标及改正后的坐标增量，按公式推算前一点坐标。
X前=X后+△x改Y前=Y后+△Y改最后，推算出终止边的坐标，与原有设计值相等，以作检核。
附合导线按条件平差算例
§9.4 附合导线按条件平差算例9.4.1附合导线的条件平差方程式如图9-6所示，符合在已知),(A A y x A ，),(C C y x C 之间的单一符合导线有n 条AB α与CD α是已知方位角。
设观测角为β、β、… …、β，测角中误差为 ，观测边长为s 、s 、… …、s ，故t 1为v 1=ii BA CD 011=+∑+=a i n i v ω （9-2）式中a ω—方位角条件的不符值，按ο180)1(ˆ11+-∑+-=+=n in i CD BA a βααω （9-3） 若导线的A 点与C 点重合，则形成一闭合导线，由此坐标方位角条件就成了多边形的图形闭合条件。
2、纵、横坐标条件 设以1ˆx∆、2ˆx ∆、…、n x ˆ∆表示图中各导线边的纵坐标增量之平差值；1ˆy∆、2y ∆、…、n y ˆ∆表示图中各导线边的横坐标增量之平差值；由图可写出以坐标增量平差值表示的纵、横坐标条件。
⎪⎪⎭⎪⎪⎬⎫∑+∆∑+=∆∑+=∑+∆∑+=∆∑+=∆∆yi ni n A i n A C xi ni n A i n A C v y y y y y v x x x x x 111111ˆˆ （9-4） σ令 ⎪⎪⎭⎪⎪⎬⎫--∆∑=--∆∑=)()(11A C i ny A C i nx y y y x x x ωω （9-5） 则 ⎪⎪⎭⎪⎪⎬⎫=+∑=+∑∆∆0011y yi nx xi nv v ωω （9-6） 以微分量代替改正数，则有)()()(211n xi nx d x d x d v ∆++∆+∆=∑∆Λ{}ρα1231211)()()(cos v y y y y y y v v n Csi i nxi n -'++-+--∑=∑∆Λ将上式代入式9-6得纵坐标条件式，且同理已可得横坐标的条件式即⎪⎪⎭⎪⎪⎬⎫=+-'∑+∑=+-'∑-∑====0)(1sin 0)(1cos 1111y i i Cni si i n i x i i Cni si i ni v x x v v y y v ωραωρα （9-7）上式就是单一符合导线的纵、横坐标条件方程x ω、y ω为条件式的不符值，按⎪⎪⎭⎪⎪⎬⎫-'=-∆∑+=-'=-∆∑+=C CC i n A y C CC i nA x y y y y y x x x x x 11ωω （9-8） 式中i x 、i y 是由观测值计算的各导线点的近似坐标。
附合导线平差范例
观测角度形式角度改正数改正后角度方位角度形式边长D°′″°″°°′″°m A D∑109650241096.84665.38相对中误差=F D ∶∑S =1∶2188.22说明：1、表中红色数据为观测值；蓝色数据为已知值；绿色数据为角度、方位角以度（不以度分秒）的表达形式，会自动计2、C19和D19处的数字不能为负或大于60，K列数字不能为负或大于360，否则需人工处理。
测量：记录：计算：审核：4C 27843122125230B 1292175156方位角α180.7322230.3706206.8761202.3833203.115631804354角度观测值（左角）点号31752630243063018180.731667222292.5016667156.505175.506667精度分析附合导线平差计算程序278.72212.87522278.7206212.8756175.507292.50222156.50563344242317.8683133.84154.7180.74148.93301.8361334.7117147.16ΔxΔyυxυyΔx′Δy′xy-357.369-387.255-0.13071-0.27455秒）的表达形式，会自动计算，可隐藏；紫色数据为平差结果。
-137.00277.59672日期：-125.021-0.02926-0.02891-58.5294-125.082-0.06145-0.060723802.8514006.77-70.00253903.6333805.1083833.6313943.138-103.137-30.77924028.533730.436坐标增量计算值(m)坐标增量改正数（m)改正后的坐标增量（m)坐标(m)-0.05522-0.06384-0.03331-0.02629-0.03039-85.3658程序-0.01586-85.3921-138.03-74.6727-103.082-69.9386-30.7459-137.999-74.6568-136.9733671.033619.243593.4333744.32277.62563-58.468。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§9.4 附合导线按条件平差算例
9.4.1附合导线的条件平差方程式
如图9-6所示，符合在已知),(A A y x A ，),(C C y x C 之间的单一符合导线有n 条AB α与CD α是已知方位角。
设观测角为
β、β、… …、β，测角中误差为 ，观测边长为s 、s 、… …、s ，
故t 1为v 1=i
i BA CD 01
1
=+∑+=a i n i v ω （9-2）
式中a ω—方位角条件的不符值，按
180)1(ˆ1
1+-∑+-=+=n i
n i CD BA a βααω （9-3） 若导线的A 点与C 点重合，则形成一闭合导线，由此坐标方位角条件就成了多边形的图形闭合条件。
2、纵、横坐标条件 设以1ˆx
∆、2ˆx ∆、…、n x ˆ∆表示图中各导线边的纵坐标增量之平差值；1ˆy
∆、2y ∆、…、n y ˆ∆表示图中各导线边的横坐标增量之平差值；由图可写出以坐标增量平差值表示的纵、横坐标条件。
⎪⎪⎭
⎪⎪⎬⎫∑+∆∑+=∆∑+=∑+∆∑+=∆∑+=∆∆yi n
i n A i n A C xi n
i n A i n A C v y y y y y v x x x x x 1111
11ˆˆ （9-4） βσ
令 ⎪⎪⎭
⎪⎪
⎬⎫--∆∑=--∆∑=)()(11
A C i n
y A C i n
x y y y x x x ωω （9-5） 则 ⎪⎪⎭
⎪
⎪
⎬⎫
=+∑=+∑∆∆0011y yi n
x xi n
v v ωω （9-6） 以微分量代替改正数，则有
)()()(211n xi n
x d x d x d v ∆++∆+∆=∑∆
{}ρ
α1
23121
1
)()()(cos v y y y y y y v v n C
si i n
xi n -'++-+--∑=∑∆
将上式代入式9-6得纵坐标条件式，且同理已可得横坐标的条件式即
⎪⎪⎭
⎪
⎪⎬⎫
=+-'∑+∑=+-'∑-
∑====0)(1sin 0)(1
cos 1111y i i C
n
i si i n i x i i C
n
i si i n
i v x x v v y y v ωραωρα （9-7）
上式就是单一符合导线的纵、横坐标条件方程x ω、y ω为条件式的不符值，按
⎪⎪⎭
⎪⎪⎬⎫
-'=-∆∑+=-'=-∆∑+=C C
C i n A y C C
C i n
A x y y y y y x x x x x 11
ωω （9-8） 式中i x 、i y 是由观测值计算的各导线点的近似坐标。
计算时一般i v 以秒为单位，si v 、x ω、y ω以cm 为单位；若x 、y 以m 为单位，则65.2062100206265==''ρ，从而使全式单位统一。
若单一导线的A 与C 点重合形成闭合导
线，则纵、横坐标条件成为多边形各边的坐标增量闭合条件，以增量平差值表示为
（9-9）
9.4.2符合导线的精度评定
⎪⎪⎭⎪⎪⎬⎫=∆∑=∆∑0ˆ0ˆ11
i n i n
y x {}ρ
ρn n C n C v y y v
y y y y y y )()()()(23423-'---'++-+--
1、单位权中误差：单一符合导线计算单位权中误差公式与边角网相同，按
（9-10）
2、平差值的权函数式：为了平定平差值函数的精度，必须要列出权函数式。
一般有下列三种函数式。
（1）边长平差值权函数式由导线边si i i v s s
+=ˆ 故其权函数式为 si Fsi v v = （9-11）
（2） 坐标方位角平差值权函数式
由图9-6得单一符合导线的任一边的坐标方位角的计算式为 180ˆ1n i n
BA i -∑+=βαα
n
i i F v v 1
∑=α （9-12）
（3） 坐标平差值的权函数式
由图9-6得j 点坐标平差值的权函数式为
⎪⎪
⎭
⎪
⎪
⎬⎫-∑+∑=-∑-∑=-=-=-=-=i i
j j i si i j i Fyi
i i
j j i si i j i Fxi v y x v v v y y v v ραρα11111
11
1sin cos （9-13）
9.4.3附合导线按条件平差算例
在图9-7所示附合导线中，B A ,为已知点，其坐标为 947.6556=A x m 735.4101=A y m 155.8748=B x m 647.6667=A y m
方位角4.130349'''= AB α，应用红外测距仪观测导线的转折角β和边长s 列入表9-5。
试按条件平差法，求各观测值及平差后3s 边的边长相对中误差。
[][][]r
v v P v v P r pvv s s s +±=±=βββσ0ˆ
表9-5 近似坐标计算
解：（1）确定观测值的权。
测角中误差0.3''
±
=
m
β
边长中误差按仪器给定公式为
26222)105()5.0()(i i c s s ppm s m m i ⨯⨯+±=+±=-（cm ） 式中i s 以cm 为单位。
由上式算得 96.01±=s m cm 82.02±=s m cm 79.03±=s m cm 92.04±=s m cm
以角度观测的权为单位权，即0.3''±==βμm
表9-6 条件方程及权函数式系数表
则边长的权为
76.9221
1==
s
m
s m m p β 38.132=s p
42.143=s p 63.104=s p 边长权倒数为 101.011=s p 074.012
=s p
070.013=s p 091.01
4
=s p （2）计算条件方程式不符值。
由表9-4-1得
0.54.1303494.080349''-='''-'''=-'=
AB AB a w αα
9.4155.8746204.8748+=-=-'=B B x x x w cm 9.2647.6667676.6667+=-=-'=B B y y y w cm
（3）计算条件方程式系数及权函数式系数列于表9-6中。
（4）组成法方程式并解算。
根据表9-6中系数组成法方程系数，然后填于表9-7中相应行内。
法方程式的解算在表9-7中进行。
表9-7 法方程式解算表
（5）计算改正数和平差值。
由法方程解算表解得的联系数和观测边加相应改正数，即得角度和边长平差值。
计算见表9-8。
（6）计算3s 边的精度。
1）单位权中误差，按 59.23
080
.26][''±=±=±
=r pvv μ 2） 计算3s 边的中误差。
cm p m s s 75.0064.095.21
3
3±=±=±=μ 3s 边边长相对中误
164000
112294275.033==s m s。