第七节 三角函数的化简与求值
三角函数式化简
三角函数式化简孙小龙所谓三角函数化简,就是灵活运用公式,对复杂的三角函数式进行变形,从而得到较为简单的三角函数式以便于进行问题讨论,所以三角函数式的化简是研究复杂三角函数式的基础;下面我们一起深入探究如何进行三角函数式化简;方法引导三角函数式化简通常是最让人头疼的一类题型,因为化简没有明确的方向,很难继续进行;其实化简只要遵守“三看”原则,即能顺利化简;一是看角,二是看名,三是看式子的结构和特征;（1） 看角的特点,充分利用角之间的关系,尽量向同角转化,利用已知角构建待求角；如倍角关系、半角关系、互余关系、互补关系等；（2） 看函数名的特点,向同名函数转化,弦切互化；（3） 看式子的结构特点,从整体出发,正用、逆用、变形应用这些公式;另外,根据式子的特点,还可以使用辅助角公式;了解了化简原则之后,下面我们开始化简了;例一 化简fx=2cosxsinx+3π－3sin 2x+sinxcosx分析：首先先看角,式子中的角度不统一,所以首要任务是统一角度,根据式子的结构特点和π3的特殊性,可以运用两角和的正弦公式将式子展开fx =2cos x sin x +3π-3sin2x +sin x cos x−−−−−→用三角公式展开2cos x sin x cos3π+cos x sin 3π-3sin2x +sin x cos x= 2sin x cos x +3cos2x -3sin 2x第一步化简完成后,再次观察式子的结构特点,每一个单项式都是二次的,所以再运用降幂公式把式子变为一次式2sin x cos x +3cos2x -3sin2x −−−−→降幂公式sin2x +3cos2x继续运用辅助角公式进行彻底化简sin2x +3cos2x −−−−→辅助角公式2sin2x +3π.例二 化简：42212cos 2cos 2.2tan()sin ()44x x x x ππ-+-+ 分析：我们还是先从角度入手,分子上角度统一,分母角度不统一,但仔细观察发现分母中两个角呈互余关系,再看函数名的特点,我们可以运用诱导公式进行化简;分子上仔细观察结构,提出12,可以得到完全平方式42212cos 2cos 2.2tan()sin ()44x x x x ππ-+-+诱导公式及完全平方式→ 12(4cos x−4cos x+1)242cot(π4+x)sin （π4+x ）2=（2cos x−12）24sin(π4+x)cos(π4+x) 统一角度后,分析式子的结构特点,运用降幂公式进行化简 （2cos x−12）24sin(π4+x)cos(π4+x)降幂公式→ 2cos 2x22sin(π2+2x)=2cos 2x 22cos 2x= 12cos 2x 我们可以通过两个例题发现化简题目中透露出来的隐藏信息,这就是三角函数式化简要求最终形式：正弦型函数通常情况 化简方法： 1、切割化弦； 2、降幂公式；3、用三角公式转化出现特殊角；4、 异角化同角；5、异名化同名；6、高次化低次；7、辅助角公式；8、分解因式;任何三角函数式化简只要掌握了化简的原则和要求,遇到化简题就能轻而易举的攻破了,但首先有个前提：熟练掌握常见三角函数变换公式,如同角三角函数变换公式、诱导公式、两角和与差的余弦正弦正切公式、倍角与半角公式、辅助角公式等;同时还要了解其他三角函数变换公式,如三角函数积化和差和和差化积公式、三倍角公式和万能置换公式等;小试牛刀1. 化简βαβαβα2cos 2cos 21cos cos sin sin 2222-+;2. 化简xxx x x x f 2sin 2cos sin cos sin )(2244-++=3. 已知t a n θ=2,求⎪⎭⎫ ⎝⎛+--θπθθ4sin 21sin 2cos 22的值4. 化简下列各式1⎪⎭⎫ ⎝⎛<<+-παπα2232cos 21212121;利用升次公式,去掉开方符号 242sin 42cos tan 5312sin 2cos 2tan 31--+--++x x xx x x ; 可使用换元化简,令t =t a n x 3se c 2280°－3c s c 2280°.化割为弦小试牛刀答案1. 原式βαβαβα2cos 2cos 21)2cos 1)(2cos 1(41)2cos 1)(2cos 1(41-+++--=)2cos 2cos 2cos 2cos 1(41)2cos 2cos 2cos 2cos 1(41βαβαβαβα+++++--=βα2cos 2cos 21- 212cos 2cos 21)2cos 2cos 1(21=-+=βαβα 2. xxx x x x f 2sin 2cos sin cos sin )(2244-++=)cos sin 1(2cos sin 122x x xx --=212sin 41+=x ; 3. 原式=⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-•=⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+-θπθπθπθππθπθθπθπθθ4sin 4cos 4sin 24sin 4cos 24sin 2sin 2sin 4sin 2sin cos .=2232121tan 1tan 14tan 1+-=+-=+-=⎪⎭⎫⎝⎛+θθθπ4. 1∵αααπαπcos |cos |2cos 2121,223==+∴<<, 又∵2sin ,2sin |2sin |cos 2121,243ααααπαπ=∴==-∴<<原式. 2令t =t a n x ,则原式=41811531121)1(231222222-+-+-+--+++-+t t t t tttt t t=x tt t t t t t t t t 2sec 212)1()1)(53()1)(51()1)(31()1()31(2222=-+=+++++-++•+ 3原式=csc 210°－3se c 210°=csc10°+3sec10°·csc10°－3sec10°=︒︒-︒•︒+︒=︒︒︒-︒•︒•︒︒+︒20sin )1030sin()1030sin(1610cos 10sin 10sin 310cos 10cos 10sin 10sin 310cos 2=32cos20°.。
(完整版)三角函数化简求值证明技巧
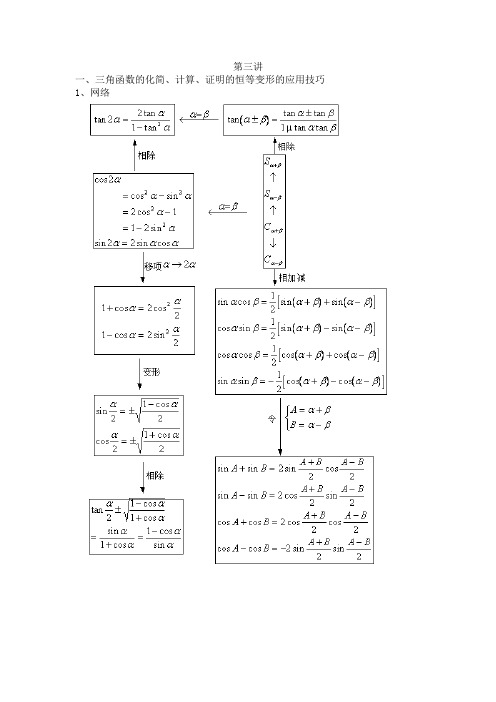
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结（1）变换函数名对于含同角的三角函数式，通常利用同角三角函数间的基本关系式及诱导公式，通过“切割化弦”，“切割互化”，“正余互化”等途径来减少或统一所需变换的式子中函数的种类，这就是变换函数名法．它实质上是“归一”思想，通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0，求a、b的关系。
练习：已知sin（α＋β）＝，cos（α－β）＝，求的值。
2）变换角的形式对于含不同角的三角函数式，通常利用各种角之间的数值关系，将它们互相表示，改变原角的形式，从而运用有关的公式进行变形，这种方法主要是角的拆变．它应用广泛，方式灵活，如α可变为（α＋β）－β；2α可变为（α＋β）＋（α－β）；2α－β可变为（α－β）＋α；α／2可看作α／4的倍角；（45°＋α）可看成（90°＋2α）的半角等等。
【例2】求sin（θ＋75°）＋cos（θ＋45°）－cos（θ＋15°）的值。
练习已知，求的值【例3】已知sinα＝Ａsin（α＋β）（其中cosβ≠A），试证明：tan（α＋β）＝提示：sin[（α＋β）－β]＝Ａsin （α＋β）（3）以式代值利用特殊角的三角函数值以及含有1的三角公式，将原式中的1或其他特殊值用式子代换，往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x＋cos2x, sec2x－tan2x, csc2x －cot2x，tanxcotx, secxcosx, tan45°等，根据解题的需要，适时地将“1”作某种变形，常能获得较理想的解题方法。
【例4】化简：（4）和积互化积与和差的互化往往可以使问题得到解决，升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。
三角函数的恒等变换与化简
三角函数的恒等变换与化简三角函数在数学中扮演着重要的角色，其中包括一系列的恒等变换和化简公式。
这些变换与化简公式不仅在解决三角函数问题时起着重要的作用，而且在数学推导和证明中也发挥着重要的作用。
本文将介绍一些常见的三角函数恒等变换和化简公式，旨在帮助读者更好地理解和应用这些概念。
1. 三角恒等变换（1）余弦定理在任意三角形ABC中，设边长分别为a、b、c，角A、B、C的对边分别为a、b、c，则余弦定理可以表示为：c² = a² + b² - 2abcosC。
这个定理在解决三角形问题中经常使用。
（2）正弦定理在任意三角形ABC中，设边长分别为a、b、c，角A、B、C的对边分别为a、b、c，则正弦定理可以表示为：a/sinA = b/sinB = c/sinC，其中a、b、c分别为三角形的边长，A、B、C为所对应的角。
（3）倍角公式正弦函数的倍角公式可以表示为：sin2θ = 2sinθcosθ，余弦函数的倍角公式可以表示为：cos2θ = cos²θ - sin²θ。
这些公式在求解具有倍角的三角函数问题时非常有用。
2. 三角函数化简公式（1）和差化积两角和公式可以表示为：sin(α +β) = sinαcosβ + cosαsinβ，cos(α + β) = cosαcosβ - sinαsinβ。
这个公式可以将两个角的三角函数和转化为单个角的三角函数和。
类似地，两角差公式可以表示为：sin(α - β) =sinαcosβ - cosαsinβ，cos(α - β) = cosαcosβ + sinαsinβ。
（2）平方公式正弦函数的平方公式可以表示为：sin²θ = (1 - cos2θ)/2，余弦函数的平方公式可以表示为：cos²θ = (1 + cos2θ)/2。
这些公式在化简复杂的三角函数表达式时非常有用。
（3）倒数公式正切函数的倒数公式可以表示为：cotθ = 1/tanθ，割函数的倒数公式可以表示为：secθ = 1/cosθ，余割函数的倒数公式可以表示为：cscθ =1/sinθ。
三角函数化简求值的技巧
三角函数化简与求值常用技巧
三角函数在高考中通常以中低档题型出现,难度不大,但由 于三角公式的特殊性,解题中往往也涉及一些小的变换技 巧,如果处理得当,往往可以事半功倍,快速而准确地得到 正确结论.通常情况下,三角变换应从“角度、函数、常数、 次数、结构”等几方面着手解决.
一、三角变换,角为先锋 三角函数作为一种特殊函数,其“角”的特殊性不容忽视,因此我们在三角函数恒等变换 中,应该首先注意角的形式,从统一角的角度出发,往往能够达到事半功倍的效果.
【例 1】已 知α、 β为 锐角,cos α＝
3 5
,tan (α−β)＝−
1 3
,则
tan β＝(
)
A、
1 3
B、 3
【变式演练】已知 sin
x－π
4
＝3,则
sin
2x 的值为(
)
5
A．－ 7 25
B. 7 25
C. 9 25
D.16 25
【解析】法一、sin 2x＝cos(2x－ π )＝1－2sin2(x－ π )＝1－2×(3)2＝ 7 ,选 B.
2
4
5 25
法二、依题意得 2(sin x－cos x)＝3,1(sin x－cos x)2＝ 9 ,1－sin 2x＝18,sin 2x＝ 7 ,选
C、
9 13
D、
13 9
【例
1】已 知α、 β为 锐角,cos α＝
3 5
,tan (α−β)＝−
1 3
,则
tan β＝(
)
A、
1 3
B、 3
C、
9 13
D、
13 9
【分析】依题意,可求得 tan α＝
三角函数的化简与求值
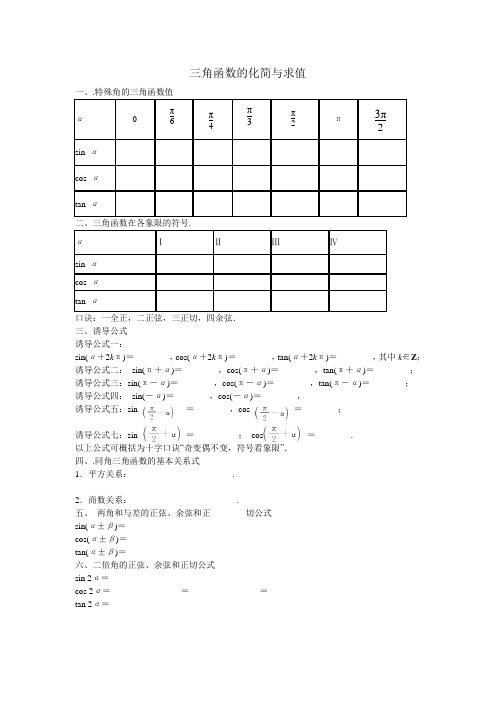
三角函数的化简与求值二、三角函数在各象限的符号. 口诀：一全正，二正弦，三正切，四余弦． 三、诱导公式 诱导公式一：sin(α＋2k π)＝________，cos(α＋2k π)＝________，tan(α＋2k π)＝________，其中k ∈Z ； 诱导公式二： sin(π＋α)＝________，cos(π＋α)＝________，tan(π＋α)＝________； 诱导公式三：sin(π－α)＝________，cos(π－α)＝________，tan(π－α)＝________； 诱导公式四： sin(－α)＝________，cos(－α)＝________，诱导公式五：sin ＝________，cos ＝________；诱导公式七：sin ＝__________； cos ＝________. 以上公式可概括为十字口诀“奇变偶不变，符号看象限”． 四、.同角三角函数的基本关系式1．平方关系：_______________________.2．商数关系：________________________.五、 两角和与差的正弦、余弦和正________切公式 sin(α±β)＝________________________ cos(α±β)＝________________________ tan(α±β)＝________________________ 六、二倍角的正弦、余弦和正切公式sin 2α＝________________cos 2α＝________________＝________________＝________________ tan 2α＝________________七、二倍角余弦公式的变式八、辅助角公式a sin x ＋b cos x ＝ sin(其中 角所在的象限由a, b 的符号确定， 角的值由tan ＝ 确定)．1． sin 330°等于( )2．求值sin 210°＝( )3．若sin α<0且tan α>0，则α是( )A ．第一象限角B ．第二象限角C ．第三象限角D ．第四象限角 4．使得函数y ＝lg(tan θcos θ)有意义的角在( ) A ．第一，四象限 B ．第一，三象限 C ．第一、二象限 D ．第二、四象限5．若 － <α<0，则点Q (cos α，sin α)位于( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限6．若z ＝sin θ－ ＋i 是纯虚数，则tan θ的值为( )7.sin 15°cos 75°＋cos 15°sin 105° 等于( )8.下列各式中，值为 的是( )A ．2sin 15°cos 15°B ．︒︒-15sin 15cos 22 C ．115sin 22-︒D ．︒︒+15cos 15sin 229.记cos(－80°)＝k ，那么tan 100°＝( )π21．降幂公式：cos 2α＝1＋cos 2α2，sin 2α＝1－cos 2α2；2．升幂公式：1＋cos 2α＝2cos 2α，1－cos 2α＝2sin 2α. a 2＋b 2 ()x ＋φ b a35 ⎝ ⎛⎭⎪⎫cos θ－45 A.34 B.43 C ．－34 D ．－43A.1－k 2k B ．－1－k 2kC.k 1－k 2 D ．－k 1－k2 A ．－32 B ．－12 C.12 D.32A.32 B ．－32 C.12 D ．－12A ．0 B.12C.32D ．1 3210．已知：tan(π＋α)＝－ ，则sin(α－7π)cos(α＋5π)的值是________． 11, =13.已知α为第二象限的角，sin α＝ ，则tan 2α＝ ______________.14.cos 43°cos 77°＋sin 43°cos 167°的值为________．15.已知 则f 的值为_____17.化简：(4) sin x ＋cos x; (5) x 2sin 21-＋2sin x cos x (6)x2sin＋2sin x cos x ＋3x 2cos ; (7)16．化简： (1)－sin (180°＋α)＋sin (－α)－tan (360°＋α)tan (α＋180°)＋cos (－α)＋cos (180°－α)；⎝ ⎛⎭⎪⎫－31π3 12计算：sin π4cos π3sin π2－cos πcos 3π2＋tan 2π6.cos π6tan π4sin 23π2－tan πcos 0＝________.f (α)＝sin (π－α)cos (2π－α)tan ⎝ ⎛⎭⎪⎫－α＋3π2cos (－π－α)(2)1－2sin 40°cos 40°.sin ⎝⎛⎭⎪⎫2x －π4－22sin 2x (1)1－2sin 2⎝⎛⎭⎫x ＋π8＋2sin ⎝⎛⎭⎫x ＋π8cos ⎝⎛⎭⎫x ＋π8； (2)2sin 2⎝⎛⎭⎫π4＋x －3cos 2x ；(3)cos 4x －4cos 2x ＋3.35()︒-440sin 13218.已知tan α＝2，求下列各式的值：20.已知sin α＝ ，α∈ ，tan β＝ . (1)求tan α的值； (2)求tan(α＋2β)的值．21.已知函数f (x )＝cos2x ＋sin x cos x (x ∈R )．(1)求f 的值；(2)求f (x )的单调递增区间．(1)2sin α－3cos α4sin α－9cos α；(2)2sin 2α－3cos 2α4sin 2α－9cos 2α； (3)4sin 2α－3sin αcos α－5cos 2α.tan θ＝2，求(1)cos θ＋sin θcos θ－sin θ；(2)1－sin θcos θ＋cos 2θ的值．55 ⎝⎛⎭⎪⎫0，π2 13⎝ ⎛⎭⎪⎫3π8。
三角函数式的化简与求值
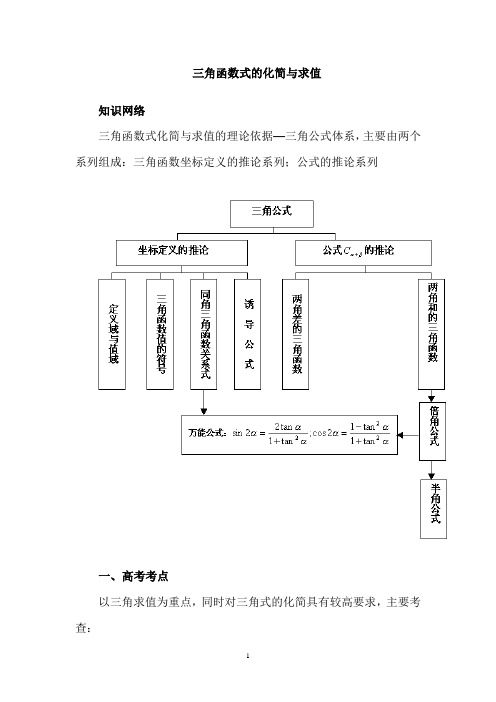
三角函数式的化简与求值知识网络三角函数式化简与求值的理论依据—三角公式体系，主要由两个系列组成：三角函数坐标定义的推论系列；公式的推论系列一、高考考点以三角求值为重点，同时对三角式的化简具有较高要求，主要考查：1、同角三角函数基本关系式与诱导公式的应用.运用诱导公式的“准确”；运用同角公式的“灵活”：正用、反用、变用。
2、两角和与差的三角函数与倍角公式的应用：正用、反用；有关公式的联合运用，主要应用于无附加条件的三角式的化简或求值（以选择题、填空题为主）；带有附加条件的三角式的求值问题（以解答题为主）；比较简单的三角恒等式的证明（多为解答题，不同某一小题）。
3、等价转化思想以及三角变换的基本技能重难点归纳1求值问题的基本类型①给角求值，②给值求值，③给式求值，④求函数式的最值或值域，⑤化简求值2技巧与方法①要寻求角与角关系的特殊性，化非特角为特殊角，熟练准确地应用公式②注意切割化弦、异角化同角、异名化同名、角的变换等常规技巧的运用③对于条件求值问题，要认真寻找条件和结论的关系，寻找解题的突破口，很难入手的问题，可利用分析法④求最值问题，常用配方法、换元法来解决二、知识要点（一）三角函数坐标定义的推论1、三角函数值的符号2、特殊角的三角函数值3、同角三角函数的基本关系式（同角公式）（1）课本中的公式：（2）同角公式“全家福”①平方关系：.②商数关系：.③倒数关系：4、诱导公式：（1）认知与记忆：对使三角函数有定义的任意角① k·360°＋（k∈Z），－，180°±，360°－（共性：偶数×90°±形式）的三角函数值，等于的同名函数值，前面放上一个把看作锐角时原函数值的符号；② 90°±，270°±（共性：奇数×90°±）的三角函数值，等于的相应余函数值，前面放上一个把看作锐角时原函数值的符号。
第讲三角函数的求值化简与证明
【互动探究】 1．已知函数 f(x)＝ 2cosisn2xx＋－2ππ4＋1. (1)求 f(x)的定义域； (2)若角 α 在第一象限且 cosα＝35，求 f(α)．
∴3<2sinx＋π6＋4≤6.即函数f(x)的值域为(3,6]．
易错、易混、易漏 11．三角函数中的二次函数问题，忽视了自变量范围的研究 例题：已知函数 f(x)＝2ssiinnxxc＋oscxo＋sx5，x∈0，2π.
(1)求 sinx＋cosx 的取值范围； (2)求函数3
C．0
D．1
－1 5．sin17°cos47°－sin73°cos43°＝_____2__.
考点1 三角函数式的化简
例1：(2011年北京)已知函数f(x)＝4cosxsinx＋π6－1. (1)求f(x)的最小正周期；
(2)求f(x)在区间－π6，π4上的最大值和最小值． 解析：(1)因为f(x)＝4cosxsinx＋π6－1
1．转化思想是本节三角变换的基本思想，包括角的变换、 函数名的变换、和积变换、次数变换等．三角公式中次数和角 的关系：次降角升；次升角降．常用的升次公式有：1＋sin2α ＝(sinα＋cosα)2；1－sin2α＝(sinα－cosα)2；1＋cos2α＝2cos2α； 1－cos2α＝2sin2α.
＝212cos50°－co2s35s0i°n50°sin70°
＝2sin30°cos50°－cocso5s03°0°sin50°sin70°
＝－2sicno2s05°0s°in70°＝－2sicno2s05°0c°os20°
三角函数式的化简与求值
４ 幂 的 变换
降 幂 是 三 角 变 换 时 常 用 方 法 ，对 次 数 较 高 的 三 角 函 数 式 ，
一
（ 求 ｆ ） Ｎ， 值及 取得 最小 值 时相 应 的 Ｘ的 值 ； ２ ） （Ｎ Ｊ ｘ ，
般 采 用 降 幂 处理 的方 法 ， ： ｎ Ｌ 如 ｓ Ｚ＝ ｉｏ
在 三 角 变形 中使 用 频 率 高 。 ２ 函数 名 称 变换
１ ｃ０｝１。 ＝ 一 。。 （ ｓ ｝ ｓ一 一４ ４ ｃ
解 法 二 ： ｘ ｓ Ｚ０ ＋ Ｏ ０ ＋ 设 ＝ ｉ ２ 。 Ｃ ８ 。 Ｖ ｓｎ ０ ｃ Ｓ ０ ． ｎ ８ ｉ２ ａｏ ８ 。
ｙ ｃｓ ０＋ｉ ０一 ／ ｃｓ０ｓ ８ 。则 ＝ ｏ２ 。ｓ ８ 。 、 ｏ２ 。ｉ ０ ， ２ ｎ ｎ ｘｙ １ １ 、 ｓ ６ 。 ， ＋ ＝ ＋ 一 ／ ｉ ０： ｎ
ｓｎ ２ ｉ２ ０。
＝
１＝。０６一ｏ ，（ｐｐ等 ｐ（孚） ５４一。０４＝ 仪 ）＝ ＋一 一 ， ￣５３＝。５孚 ＝＋一 （ ）Ｂ ２（ｐ １（＋）手 ，＋＝ 一 。 Ｑ ） 一＝ 仅 （一）１ 手 （ ） ＝＋＋ ３ ｝ 一 ） ２ ＂ ｝一
特 地 ＋ 与｝一 为 余 ， 们 间 以 相 化 别 ， Ｏ Ｌ ０互 角它 之 可 互 转 ， 【
１ ｃ０｝ｃｌｃ０ｓ２ｓｏｘ－２ 一 ０ 。 （ ２ 。。ｎ０ｎ。／ｓ０ 争 ｓ＋ ００ ｓ＿１ ｉ ） ３ｉ。 ４ ｓ 。４ ｉ 。４＋ ｎ
～
＝
（ ｓ０ｃｓ０－ｉ６ 。ｎ ０、 ｃ ６ 。ｏ２ 。ｓ ０ｓ ２ 。 ｏ ｎ ｉ
＝
在三角化简、 值 、 明中， 求 证 表达 式 往 往 出现 较 多 的相 异 角 ．
三角函数的化简与求值
1．三角恒等变换的两原则（1）化繁为简：变复角为单角，变不同角为同角，化非同名函数为同名函数，化高次为低次，化多项式为单项式，化无理式为有理式。
（2）消除异差：消除已知与未知、条件与结论、左端与右端以及各项的次数、角、函数名称、结构式等方面的差异。
2．三角函数式的化简 （1）化简要求①三角函数名称尽量少；②次数尽量低；③能求值的尽量求值； ④尽量使分母不含三角函数；⑤使被开方数不含三角函数． （2）化简思路对于和式，基本思路是降次、消项和逆用公式；对于三角分式，基本思路是分子与分母约分或逆用公式；对于二次根式，注意二倍角公式的逆用，另外，还可以用切割化弦、变量代换、角度归一等方法 (3)化简的方法弦切互化，异名化同名，异角化同角，降幂或升幂，和差化积，积化和差等。
3．三角恒等式的证明 (1)证明三角恒等式的方法观察等式两边的差异(角、函数、运算的差异)，从解决某一差异入手(同时消除其他差异)，确定从该等式的哪些证明(也可两边同时化简)，当从解决差异方面不易入手时，可采用转换命题法或用分析法等。
(2)证明三角条件等式的方法首先观察条件与结论的差异，从解决这一差异入手，确定从结论开始．通过变换，将已知表达式代入得出结论，或通过变换已知条件得出结论，如果这两种方法都证不出来，可采用分析法；如果已知条件含参数，可采用消去参数法；如果已知条件是连比的式子，可采用换元法等。
1. 三角函数的化简、计算、证明的恒等变形的基本思路是：一角二名三结构。
即首先观察角与角之间的关系，注意角的一些常用变式，角的变换是三角函数变换的核心！第二看函数名称之间的关系，通常“切化弦”；第三观察代数式的结构特点。
基本的技巧有:（1）巧变角（已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换. 如()()ααββαββ=+-=-+，2()()ααβαβ=++-，2()()αβαβα=+--，22αβαβ++=⋅，()()222αββααβ+=---等），如 （1）已知2tan()5αβ+=，1tan()44πβ-=，那么tan()4πα+的值是_____ （答：322）；（2）已知02πβαπ<<<<，且129cos()βα-=-，223sin()αβ-=，求cos()αβ+的值（答：490729）； （3）已知,αβ为锐角，sin ,cos x y αβ==，3cos()5αβ+=-，则y 与x 的函数关系为______（答：43(1)55y x x =<<）(2)三角函数名互化(切化弦)，如 （1）求值sin 50(13tan10)+（答：1）；（2）已知sin cos 21,tan()1cos 23αααβα=-=--，求tan(2)βα-的值（答：18）(3)公式变形使用（tan tan αβ±()()tan 1tan tan αβαβ=±。
三角函数的化简求值
三角函数的化简求值一.主要公式:1．诱导公式：=-)sin(απ =-)c o s (απ =+)s i n (απ=+)cos(απ =-)s i n (α =-)cos(α=-)2sin(απ =-)2c o s (απ =+)2sin(απ =+)2c o s (απ2．和、差角公式： =+)sin(βα =-)s i n (βα ； =+)cos(βα =-)c o s (βα ； =+)tan(βα =-)t a n (βα ； 3．二倍角公式：=α2sin =α2c o s = = =α2tan ； 4．降幂公式： =2sin 2α=2c o s2α=2t a n2α；5．半角公式sin 2α= c o s 2α= t a n 2α= ；6．升幂公式：=+αcos 1 ，=-αcos 1 ；=+αsin 1 ，=-αsin 1 。
7．万能公式：=αsin =αcos =αtan ； 8．三角形ABC 中的相关公式：=+)sin(B A =+)cos(B A =+)t a n (B A =+2sinBA =+2cosB A =+2tan B A ； 9．常用公式结论：=+ααcot tan =ααcos sin =-α2sin 1 =+α2sin 1 =+βαtan tan =-βαt a n t a n ；sin 3α= cos3α= 1tan 1tan αα+=-10．辅助角公式：=+ααcos sin = =+ααcos 3sin ==+x b x a cos sin = 。
二、例题分析:例1已知02πβαπ<<<<，且129cos()βα-=-，223sin()αβ-=，求cos()αβ+的值.例2.已知0,1413)cos(,71cos 且=β-α=α<β<α<2π,(Ⅰ)求α2tan的值.(（Ⅱ）求β. ( π3β=)例3．已知51cos sin ,02=+<<-x x x π. （I ）求sin x －cos x 的值；（Ⅱ）求xx x x x x cot tan 2cos 2cos 2sin 22sin 322++-的值.例 4.是否存在锐角,αβ，使得①223παβ+=；②22tantan αβ=同时成立？若存在，求出,αβ；若不存在，说明理由。
人教A版数学必修第一册期末复习：三角函数的化简与求值课件
变式训练
变式1 tan(-945°)的值为
tan(-945°)=-tan 945°
=-tan(225°+2×360°)
=-tan 225°
=-tan(180°+45°)
=-tan 45°=-1.
-1
.
变式2
已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(4)=3,
则f(202X)的值为
高一必修一
三角函数的化简与求值
考情分析
202X年
Ⅰ Ⅱ卷
三角函 卷
数的化
简与求
值
T6,T15
202X年
202X年
Ⅲ
Ⅰ
Ⅱ卷 Ⅲ卷 Ⅰ
Ⅱ
Ⅲ卷 新高考Ⅰ
卷
卷
卷
卷
卷
T7 T10
T9
T9
本部分内容以两角和与差的三角函数公式、倍角公式为
基础，考查三角函数的化简与求值.利用同角三角函数基本关
系式、辅助角公式，结合诱导公式、和差角公式及倍角公式
真题再现
例 (202X课标全国Ⅱ,10,5分)已知α∈
0,
2
, 2sin 2α=cos 2α+1,
则sin α=( B )
A.
1
5
B.
5
5
C.
3
3
D.
2 5
5
例 (202X课标全国Ⅱ,10,5分)已知α∈
0,
2
, 2sin 2α=cos 2α+1,
则sin α=( B )
A.
1
5
B.
5
5
C.
三角函数中的化简求值(经典版)
一、题型选讲
题型一灵活运用和与差的正弦、余弦和正切、二倍角等公式化简求值
通过两角和与差的正弦、余弦和正切以及二倍角公式或者公式的变形进行化简求值。
在应用同角三角函数的关系或两角和与差的三角函数公式求值时，需要注意解题的规范性，一要注意角的范围对三角函数值的符号的影响；二要注意“展示”三角函数的公式．否则，就会因为不规范而导致失分．
求tan()
αβ
-的值．
题型二探究角度之间的关系
在三角函数的化简求值中，往往出现已知角与所求角不同，此时要观察两个角度之间的关系，寻求角度之间的特殊性，通过二倍角、互补、互与余等公式进行转化。
应用三角公式解决问题的三个变换角度
(1)变角：目的是沟通题设条件与结论中所涉及的角，其手法通常是“配凑”.
(2)变名：通过变换函数名称达到减少函数种类的目的，其手法通常有“切化弦”、“升幂与降幂”等.
(3)变式：根据式子的结构特征进行变形，使其更贴近某个公式或某个期待的目标，其手法通常有：“常值代
换”、“逆用变用公式”、“通分约分”、“分解与组合”、“配方与平方”等.
．
题型三、运用构造法化简与求值
2、(2018南京、盐城一模）已知锐角α，β满足(tanα－1)(tanβ－1)＝2，则α＋β的值为________．。
三角函数化简的方法技巧
三角函数化简的方法技巧三角函数是数学中常见的函数，它们在许多领域中都有广泛的应用。
化简三角函数是数学中的重要技巧，它可以简化复杂的表达式，使计算更加简单和直观。
以下是一些常用的三角函数化简方法和技巧。
1. 基本公式使用三角函数的基本公式是化简的基础。
例如，正弦函数的基本公式是：$$\sin^2\theta + \cos^2\theta = 1$$这个公式可以用来化简包含正弦函数的表达式。
根据需要，还可以使用余弦函数、正切函数和余切函数的基本公式。
2. 和差化积公式和差化积公式是一种常见的化简方法。
对于两个角度$\alpha$ 和 $\beta$，我们有以下的和差化积公式：$$\sin(\alpha \pm \beta) = \sin\alpha \cos\beta \pm \cos\alpha\sin\beta$$$$\cos(\alpha \pm \beta) = \cos\alpha \cos\beta \mp \sin\alpha\sin\beta$$这些公式可以用来化简包含和差角的三角函数表达式，并将它们转化为乘积形式。
3. 二倍角公式二倍角公式是化简三角函数的另一种常用方法。
对于角度$\theta$，我们有以下的二倍角公式：$$\sin2\theta = 2\sin\theta\cos\theta$$$$\cos2\theta = \cos^2\theta - \sin^2\theta$$这些公式可以用来将包含二倍角的三角函数表达式转化为简单的乘积形式。
4. 三倍角公式类似于二倍角公式，三倍角公式也是化简三角函数的方法之一。
对于角度 $\theta$，我们有以下的三倍角公式：$$\sin3\theta = 3\sin\theta - 4\sin^3\theta$$$$\cos3\theta = 4\cos^3\theta - 3\cos\theta$$这些公式可以用来将包含三倍角的三角函数表达式转化为简单的表达形式。
三角恒等变换求值与化简
y
(1
m m)x
1
x
令 (1m )x1(m 0 ,x ≥ 1 )
x
则 (1m )x 1 2(1 x m 2)x 20
在 [ 1 , ) 上 为 增 函 数
≥ 1 m 1 2 m 0
又m0,y≤m m2
即 x1时 ,y取 得 最 大 值 m. 2m
三、针对性训练
(一)《状元360》P384 1. 3.
B． 6 10cm2
C． 3 55cm2
D． 20cm2
注:此类问题与解三角形结合时,应尽可能计算余
弦值或正切值.
变 式 1.已 知 、 都 是 锐 角 ， 且 sin 5,sin10,
5
10
求 .
答 案 : . 4
注:此类问题与解三角形结合时,应尽可能计算余弦值 或正切值.
变 式 2.已 知 函 数 f(x)tan(2x),f()2cos2,
42
其 中 0,4,求 角 .
(3)化运算：利用二倍角的三角函数公式实现函 数式的升幂或降幂的转化，或利用代数恒等式进行 运算的转化.
二、例题分析
考点一:知值求角
[方法点拨] 求角问题在高考中已降低要求，故若
有求角问题出现，往往应是特殊角，解决方法是
先求该角的某种三角函数值，再利用角的范围确
定角.
例 1.设、(0， π),且tan4,tan1,则
三、针对性训练
(二)补充练习 4
1 .已 知 t a n x 4 2 ,则 t t a a n n 2 x x 的 值 为 _ _ _ _ 9 _ _ _ _ _ .1
2 . 已 知 s i n 2 s i n 2 1 , 则 c o s c o s 的 最 大 值 是 _ _ 2 _ .
三角函数的化简、求值——诱导公式
三角函数的化简、求值——诱导公式
三角函数的化简和求值是解决三角函数问题中常见的任务，而诱导公式是一种常用的化简工具。
首先，让我们回顾一下三角函数的基本定义。
对于任意角θ，正弦函数sin(θ)定义为对边与斜边的比值，余弦函数cos(θ)定义为邻边与斜边的比值，而正切函数tan(θ)定义为对边与邻边的比值。
现在，让我们来讨论一下诱导公式。
诱导公式是指一组用于将一个角的三角函数表示为另一个角的三角函数的公式。
最常用的诱导公式包括：
1. 正弦函数的诱导公式，sin(α±β) = sinαcosβ ±
cosαsinβ。
2. 余弦函数的诱导公式，cos(α±β) = cosαcosβ ∓
sinαsinβ。
3. 正切函数的诱导公式，tan(α±β) = (tanα ± tanβ) / (1 ∓ tanαtanβ)。
这些诱导公式可以帮助我们化简复杂的三角函数表达式，或者求解包含多个角的三角函数表达式。
通过使用这些诱导公式，我们可以将一个角的三角函数表示为另一个角的三角函数，从而更容易地进行计算和分析。
当我们需要化简或求解涉及多个角的三角函数表达式时，诱导公式是非常有用的工具。
通过灵活运用这些公式，我们可以更加高效地解决各种三角函数相关的问题。
因此，熟练掌握诱导公式是学习和应用三角函数的重要一步。
高中数学三角函数化简技巧
高中数学三角函数化简技巧在高中数学中，三角函数是一个重要的概念，也是学生们经常会遇到的题型之一。
在解题过程中，化简三角函数是一项关键的技巧，能够简化计算过程，提高解题效率。
本文将介绍一些常见的三角函数化简技巧，并通过具体的例题进行说明，帮助读者更好地理解和掌握。
一、和差化积公式和差化积公式是化简三角函数的基础，也是其他化简技巧的基础。
和差化积公式包括正弦和余弦的和差化积公式以及正切的和差化积公式。
下面我们通过具体的例题来说明。
例题1：化简表达式sin(a+b)cos(a-b)。
解析：根据和差化积公式，我们有：sin(a+b)cos(a-b) = (sinacosb + cosasinb)(cosacosb + sinasinb)= sinacos^2b + sinbsin^2a + cosacos^2b + cosbsin^2a= sinacos^2b + cosasin^2b + cosacos^2b + cosbsin^2a= (sinacos^2b + cosacos^2b) + (cosasin^2b + cosbsin^2a)= cos^2b(sina + cosa) + sin^2a(cosb + cosb)= cos^2b + sin^2a因此，化简后的表达式为cos^2b + sin^2a，即1。
通过这个例题，我们可以看到，利用和差化积公式可以将原本复杂的表达式化简为简单的形式，从而更方便计算。
二、倍角公式倍角公式是化简三角函数的常用技巧之一，它能够将一个角的三角函数值表示为另一个角的三角函数值。
下面我们通过具体的例题来说明。
例题2：化简表达式sin2x。
解析：根据倍角公式，我们有：sin2x = 2sinxcosx因此，化简后的表达式为2sinxcosx。
通过这个例题，我们可以看到，利用倍角公式可以将一个角的三角函数值表示为另一个角的三角函数值，从而简化计算过程。
三、半角公式半角公式是化简三角函数的另一种常用技巧，它能够将一个角的三角函数值表示为另一个角的三角函数值。
第七节 三角函数的化简与求值(知识梳理)
第七节三角函数的化简与求值复习目标学法指导1.二倍角的正弦、余弦、正切公式.2.简单的三角恒等变换(1)利用三角恒等变换研究三角函数的性质. (2)能把一些简单实际问题转化为三角函数问题,通过三角变换解决.了解和、差、倍角公式的特点,并进行变形应用. 理解三角变换的基本特点和基本功能.了解三角变换中蕴含的数学思想和方法. 1.在理解倍角公式推理的过程中掌握公式特征.2.熟练掌握余弦的二倍角公式,能正用、逆用.3.准确把握三角变换的题型的特征,能从“角、名、式”三个方面分析特点、选择公式、正确转化求解.二倍角的正弦、余弦和正切公式1.二倍角的正弦公式sin 2α=2sin αcos α.2.二倍角的余弦公式cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α. 3.二倍角的正切公式tan 2α=22tan 1tan αα-.1.公式理解(1)二倍角公式就是两角和的正弦、余弦、正切公式中当α=β时的特殊情况.(2)倍角是相对的,例如2α是4α的倍角,3α是32α的倍角. 2.与倍角公式有关的变形公式(1)升幂公式:1+cos α=2cos 22α;1-cos α=2sin 22α; 1+sin α=(sin 2α+cos 2α)2;1-sin α=(sin 2α-cos 2α)2. (2)降幂公式:sin 2α=1cos22α-;cos 2α=1cos22α+; sin αcos α=sin 22α. (3)半角公式:sin 2α=±1cos 2α-;cos 2α=±1cos 2α+;tan 2α=±1cos 1cos αα-+=sin 1cos αα+=1cos sin αα-.1.已知α∈R,sin α+2cos α10则tan 2α等于( C )(A)43 (B)34 (C)-34 (D)-43解析:法一 (直接法)由已知得(sin α+2cos α)2=52, 所以2222sin 4cos 4sin cos sin cos αααααα+++=52.化简得3tan 2α-8tan α-3=0,tan α=3或tan α=-13,代入tan 2α=22tan 1tan αα-,得 tan 2α=-34.解析:法二 (猜想法)由给出的数据及选项的唯一性,记sin αα这时sin α+2cos α,此时tan α=3,代入二倍角公式得到答案C.故选C.2.函数y=sin 2x+2sin xcos x+3cos 2x 的最小正周期和最小值为( C )(A)π,0 (B)2π,0 (C)π(D)2π解析:y=sin 2x+2sin xcos x+3cos 2x =1+sin 2x+(1+cos 2x)π4),最小正周期为π,当sin(2x+π4)=-1时,y 取得最小值为故选C.3.(2018·嘉兴测试)cos π9·cos 2π9·cos(-23π9)= . 解析:cos π9·cos 2π9·cos(-23π9) =cos 20°·cos 40°·cos 100°=-cos 20°·cos 40°·cos 80°=-sin 20cos 20cos 40cos80sin 20︒︒︒︒︒=-1sin 40cos 40cos802sin 20︒︒︒︒⋅⋅=-1sin80cos804sin 20︒︒︒⋅=-1sin1608sin 20︒︒=-1sin 208sin 20︒︒=-18.答案:-184.化简sin 2(α-π6)+sin 2(α+π6)-sin 2α的结果是 . 解析:法一原式=π1cos 232α⎛⎫-- ⎪⎝⎭+π1cos 232α⎛⎫-+ ⎪⎝⎭-sin 2α=1-12[cos(2α-π3)+cos(2α+π3)]-sin 2α =1-cos 2α·cos π3-sin 2α =1-cos 22α-1cos22α- =12. 法二 令α=0,则原式=14+14=12. 答案:12考点一 三角函数式的化简与给角求值[例1] (1)已知a=sin 15°cos 15°,b=cos 2π6-sin 2π6,c=2tan 301tan 30︒︒-,则a,b,c 的大小关系是( ) (A)a<b<c (B)a>b>c (C)c>a>b (D)a<c<b 22cos8+1sin8-的化简结果为 .(3)1cos202sin 20︒︒+-sin 10°(1tan 5︒-tan 5°)= . 解析:(1)a=sin 15°cos 15°=12sin 30°=14,b=cos 2π6-sin 2π6=cos π3=12,c=2tan 301tan 30︒︒-=12tan 60°=3,由14<12<3,可知a<b<c.故选A.(2)原式=24cos 4+2()2sin4cos4-=2|cos 4|+2|sin 4-cos 4|,因为54π<4<32π, 所以cos 4<0,且sin 4<cos 4,所以原式=-2cos 4-2(sin 4-cos 4)=-2sin 4.(3)原式=22cos 1022sin10cos10︒︒︒⨯-sin 10°(cos5sin 5︒︒-sin 5cos5︒︒) =cos102sin10︒︒-sin 10°·22cos 5sin 5sin 5cos5︒︒︒︒-=cos102sin10︒︒-sin 10°·cos101sin102︒︒=cos102sin10︒︒-2cos 10°=cos102sin 202sin10︒︒︒-=()cos102sin 30102sin10︒︒︒︒--=13cos102cos10sin1022sin10︒︒︒︒⎛⎫-- ⎪ ⎪⎝⎭=3sin10︒=3.答案:(1)A (2)-2sin 4 (3)3(1)三角函数式的化简要遵循“三看”原则①一看“角”,这是最重要的一环,通过看角之间的差别与联系,把角进行合理的拆分,从而正确使用公式;②二看“函数名称”,看函数名称之间的差异,从而确定使用的公式,常见的有“切化弦”;③三看“结构特征”,分析结构特征,可以帮助我们找到变形的方向,如“遇到分式要通分”等.(2)“给角求值”:一般所给出的角都是非特殊角,从表面上来看是很难的,但仔细观察非特殊角与特殊角总有一定关系,解题时,要利用观察得到的关系,结合公式转化为特殊角并且消除非特殊角的三角函数而得解.1.若函数f(x)=5cos x+12sin x在x=θ时取得最小值,则cos θ等于( B )(A)513 (B)-513(C)1213(D)-1213解析:f(x)=5cos x+12sin x=13(513cos x+1213sin x)=13sin(x+α),其中sin α=513,cos α=1213,由题意知θ+α=2kπ-π2(k∈Z),得θ=2kπ-π2-α(k∈Z),所以cos θ=cos(2kπ-π2-α)=cos(π2+α)=-sin α=-513.故选B.2.化简:sin 2α·sin 2β+cos 2α·cos 2β-12cos 2α·cos 2β.解:法一 原式=sin 2α·sin 2β+cos 2α·cos 2β-12·(2cos 2α-1)·(2cos 2β-1)=sin 2α·sin 2β+cos 2α·cos 2β-12(4cos 2α·cos 2β-2cos 2α-2cos 2β+1)=sin 2α·sin 2β-cos 2α·cos 2β+cos 2α+cos 2β-12 =sin 2α·sin 2β+cos 2α·sin 2β+cos 2β-12 =sin 2β+cos 2β-12 =1-12 =12. 法二 原式=sin 2α·sin 2β+(1-sin 2α)·cos 2β-12cos 2α· cos 2β=cos 2β-sin 2α(cos 2β-sin 2β)- 12cos 2α·cos 2β =cos 2β-sin 2α·cos 2β-12cos 2α·cos 2β =cos 2β-cos 2β·(sin 2α+12cos 2α) =1cos22β+-cos 2β·[sin 2α+12(1-2sin 2α)] =1cos22β+-12cos 2β =12. 法三 原式=1cos22α-·1cos22β-+1cos22α+·1cos22β+-12cos 2α·cos 2β =14(1+cos 2α·cos 2β-cos 2α-cos 2β)+14(1+cos 2α· cos 2β+cos 2α+cos 2β)-12·cos 2α·cos 2β=12.法四 原式=(sin α·sin β-cos α·cos β)2+2sin α· sin β·cos α·cos β-12cos 2α·cos 2β=cos 2(α+β)+12sin 2α·sin 2β-12cos 2α·cos 2β=cos 2(α+β)-12cos(2α+2β) =cos 2(α+β)- 12[2cos 2(α+β)-1]=12. 考点二 三角函数的给值求值与给值求角问题[例2] 已知tan 2θ=3,则1cos sin 1cos sin θθθθ-+++= . 解析:因为tan 2θ=3, 所以原式=222sin sin 22cossin 2θθθθ++=222sin 2sin cos2222cos 2sin cos222θθθθθθ++=2tan tan221tan2θθθ++=tan 2θ =3. 答案:3已知三角函数值,求三角函数式值的一般思路(1)先化简所求式子;(2)观察已知条件与所求式子之间的联系(从三角函数名及角入手); (3)将已知条件代入所求式子,化简求值.1.(2019·台州高三模拟)在斜△ABC 中,sinBcos C,且tanB ·则角A 的值为 .解析:由已知所以所以又tan B ·所以tan(B+C)=tan tan 1tan tan B CB C+-=-1, 所以tan A=1, 又0<A<π,所以A=π4. 答案:π42.已知方程x 2+4ax+3a+1=0(a 为大于1的常数)的两根为tan α,tanβ,且α,β∈(-π2,π2),则tan 2αβ+的值是 . 解析:因为a>1,所以tan α+tan β=-4a<0,tan α·tan β=3a+1>0, 所以tan α,tan β是方程x 2+4ax+3a+1=0的两个负根,又α,β∈(-π2,π2), 所以α,β∈(-π2,0), 即2αβ+∈(-π2,0), 由tan (α+β)=tan tan 1tan tan αβαβ+-⋅=()4131aa --+= 43,可得tan 2αβ+=-2. 答案:-2考点三 三角恒等变换的应用[例3] (2018·金华十校模拟)如图,在平面直角坐标系xOy中,以x 轴正半轴为始边的锐角α与钝角β的终边与单位圆分别交于点A,B,x 轴正半轴与单位圆交于点M,已知S△OAM=5,点B的纵坐标是2.(1)求cos (α-β)的值;(2)求2α-β的值.解:(1)根据题意知,OA=OB=1.由S△OAM5和α为锐角,得sin α25,cos α5,又点B2,β为钝角,所以sin β2,cos β72所以cos(α-β)=cos αcos β+sin αsin β5×7225210解: (2)因为cos 2α=2cos2α-1=2×52-1=-35,sin 2α=2sin α·cos α=225545,且0<α<π2,所以2α∈(π2,π).因为β∈(π2,π),所以2α-β∈(-π2,π2).sin(2α-β)=sin 2α·cos β-cos 2α·sin β2,故2α-β=-π4.三角恒等变换的综合应用主要是将三角恒等变换与三角函数的性质相结合,通过变形,将复杂的函数式子化为y=Asin(ωx+ϕ)+b 的形式再研究性质,在研究性质时注意利用整体思想解决相关问题.已知函数f(x)=cos 2x+sin xcos x,x ∈R. (1)求f(π6)的值; (2)若sin α=35,且α∈(π2,π),求f(2α+π24). 解:(1)f(π6)=cos 2π6+sin π6cos π632+12333+.解: (2)因为f(x)=cos 2x+sin xcos x=1cos 22x ++12sin 2x =12+12(sin 2x+cos 2x) =122sin(2x+π4), 所以f(2α+π24)=122sin(α+π12+π4) =122sin(α+π3) =122(12sin α3cos α).又因为sin α=35,且α∈(π2,π), 所以cos α=-45, 所以f(2α+π24)=122(12×353×45)=102246+-.类型一三角函数式的化简与给角求值1.cos85sin25cos30cos25+o o oo等于( C )32(C)12(D)1解析:原式=3sin5252cos25o oo=3sin(3025)252cos25-o o oo=1cos252cos25oo=12.故选C.2.cos π5·cos 2π5的值是( B )(A)4 (B)14(C)2 (D)12解析:原式=ππ2πsin cos cos555πsin5=14πsin45πsin5=14.故选B.3.若θ是第二象限角,且cos2θ<0,1sinsin cos22θ--的值是.解析:θ是第二象限角,且cos2θ<0,所以2kπ+54π<2θ<2kπ+32π,k∈Z,1sinsin cos22θ--22cos2sin cos sin2222sin cos22θθθθθθ-+-=cos sin 22sincos22θθθθ--=-1. 答案:-14.化简sin 41cos 4x x +·cos 21cos 2x x +·cos 1cos xx += . 解析:原式=22sin 2cos22cos 2x x x ·cos 21cos 2x x +·cos 1cos x x+ =sin 21cos 2x x +·cos 1cos x x + =22sin cos 2cos x x x ·cos 1cos x x+ =sin 1cos x x+ =tan 2x . 答案:tan 2x类型二 三角函数求值5.若0<α<π2,-π2<β<0,cos(π4+α)=13,cos(π4-2β,则cos(α+2β)等于( C )(解析:cos(α+2β) =cos[(π4+α)-(π4-2β)] =cos(π4+α)cos(π4-2β)+sin(π4+α)sin(π4-2β), 因为0<α<π2, 所以π4<π4+α<3π4, 所以sin(π4+α又-π2<β<0,所以π4<π4-2β<π2, 所以sin(π4-2β.故cos(α+2β)=13故选C.6.已知sin x+cos x=1,则221sin 2cos sin xx x--= . 解析:由于221sin 2cos sin x x x --=2(sin cos )(sin cos )(cos sin )x x x x x x -+-=cos x-sin x,因为(sin x+cos x)2=1+2sin xcos x=1,故sin 0,cos 1x x =⎧⎨=⎩或cos 0,sin 1,x x =⎧⎨=⎩ 代入解得221sin 2cos sin x x x--=cos x-sin x=±1. 答案:±17.已知cos 2α-cos 2β=a,那么sin(α+β)·sin(α-β)等于 .解析:sin(α+β)·sin(α-β)=(sin αcos β+cos αsin β)·(sin αcos β-cos αsin β) =sin 2αcos 2β-cos 2αsin 2β =(1-cos 2α)cos 2β-cos 2α(1-cos 2β) =cos 2β-cos 2α =-a. 答案:-a8.已知α∈(0,π2),β∈(π2,π),cos 2β=-79,sin(α+β)= 79,则sin α的值为 .解析:cos 2β=1cos22β+=7192⎛⎫+- ⎪⎝⎭=19,又因为β∈(π2,π),所以cos β=-13.于是sin β由α∈(0,π2),β∈(π2,π),得 α+β∈(π2,3π2).cos(α+βsin α=sin(α+β-β)=sin(α+β)cos β-cos(α+β)sin β=79×(-13=13. 答案:13类型三 三角恒等变换的应用9.在△ABC 中,A,B,C 是△ABC 的内角,设函数f(A)=2sin 2B C +sin(π-2A )+sin 2(π+2A )-cos 22A ,则f(A)的最大值为 . 解析:f(A)=2cos 2A sin 2A +sin 22A -cos 22A =sin A-cos Aπ4),因为0<A<π,所以-π4<A-π4<3π4. 所以当A-π4=π2,即A=3π4时,f(A)答案10.定义一种运算a ⊗b=,,,.a ab b a b ≤⎧⎨⎩＞令f(x)=(cos 2x+sin x)⊗ 54.当x ∈[0,π2]时,函数f(x-π2)的最大值是 .解析:依题意得,当x ∈[0,π2]时,y=cos 2(x-π2)+sin(x-π2)=sin 2x-cos x=-cos 2x-cos x+1=-(cos x+12)2+54的值域是[-1,1],此时函数f(x-π2)的值域是[-1,1],所以f(x-π2)的最大值是1.答案:1。
三角函数的化简详解
【例4】 在△ABC 中,若sin 22A +sin 22B +sin 22C =cos 22B,求证:t a n312tan 2=∙C A .已知α+β=3π,且α、β满足关系式:3(t a n α·t a n β+a )+t a n α=0,则t a n β= ( ) A. 3(1+a ) B.3(1－a ) C.33(1+a ) D. 33(1－a )三角函数的化简1、三角函数式的化简：（1）常用方法：①直接应用公式进行降次、消项；②切割化弦，异名化同名，异角化同角；③ 三角公式的逆用等。
（2）化简要求：①能求出值的应求出值；②使三角函数种数尽量少；③使项数尽量少；④尽量使分母不含三角函数；⑤尽量使被开方数不含三角函数2、三角函数的求值类型有三类：（1）给角求值：一般所给出的角都是非特殊角，要观察所给角与特殊角间的关系，利用三角变换消去非特殊角，转化为求特殊角的三角函数值问题；（2）给值求值：给出某些角的三角函数式的值，求另外一些角的三角函数值，解题的关键在于“变角”，如2(),()()ααββααβαβ=+-=++-等，把所求角用含已知角的式子表示，求解时要注意角的范围的讨论；（3）给值求角：实质上转化为“给值求值”问题，由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。
3、三角等式的证明：（1）三角恒等式的证题思路是根据等式两端的特征，通过三角恒等变换，应用化繁为简、左右同一等方法，使等式两端的化“异”为“同”；（2）三角条件等式的证题思路是通过观察，发现已知条件和待证等式间的关系，采用代入法、消参法或分析法进行证明。
一、化简 【例1】求值：︒+︒︒⋅︒+︒+︒80cot 40csc 10sin 20tan 10cos 20sin 2.【变式】1、求值()︒+︒︒+︒+︒10cos 110tan 60tan 110cos 40cos 2【变式】2、求0020210sin 21)140cos 1140sin 3(⋅-。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第七节三角函数的化简与求值
[选题明细表]
知识点、方法题号
三角函数式的化简15
三角函数的求值1,2,3,5,9,10,11,13
三角变换的综合应用4,6,7,8,12,14
一、选择题
1.(2018·全国Ⅲ卷)若sin α=,则cos 2α等于( B )
(A)(B)(C)-(D)-
解析:因为sin α=,所以cos 2α=1-2sin2α=1-2×()2=.故选B.
2.设α为锐角,若cos(α+)=,则sin(2α+)的值为( A )
(A)(B)(C)(D)
解析:因为α为锐角,即0<α<,
所以<α+<+=.
因为cos(α+)=,
所以sin(α+)=.
所以sin(2α+)=2sin(α+)cos(α+)
=2××
=.
cos(2α+)=2cos2(α+)-1=.
所以sin(2α+)=sin(2α+-)
=sin(2α+)cos -cos(2α+)sin
=×-×
=.
故选A.
3.若α∈(,π),且3cos 2α=sin(-α),则sin 2α的值为( D )
(A)(B)-(C)(D)-
解析:cos 2α=sin(-2α)
=sin[2(-α)]
=2sin(-α)cos(-α),
代入原式,得6sin(-α)cos(-α)=sin(-α),
因为α∈(,π),所以cos(-α)=,
所以sin 2α=cos(-2α)=2cos2(-α)-1=-. 故选D.
4.函数y=的单调递增区间是( A )
(A)(2kπ-π,2kπ+)(k∈Z)
(B)(2kπ-,2kπ+)(k∈Z)
(C)(2kπ-,2kπ-)(k∈Z)
(D)(kπ-,kπ+)(k∈Z)
解析:y==
=
=
=tan(+),
当+∈(kπ-,kπ+),k∈Z时,函数为增函数, 此时x∈(2kπ-,2kπ+),k∈Z.
故选A.
5.函数f(x)=sin x-cos(x+)的值域为( B )
(A)[-2,2] (B)[-,]
(C)[-1,1] (D)[-,]
解析:f(x)=sin x-cos x+sin x
=(sin x-cos x)
=sin(x-).
因为x∈R,所以x-∈R,
所以f(x)∈[-,].故选B.
6.设α,β∈[0,π],且满足sin αcos β-cos αsin β=1,则sin (2α-β)+sin(α-2β)的取值范围为( A )
(A)[-1,1] (B)[-2,1]
(C)[-1,2] (D)[-2,2]
解析:由sin αcos β-cos αsin β=1,得sin(α-β)=1,
又α,β∈[0,π],所以α-β=,
所以
即≤α≤π,
所以sin(2α-β)+sin(α-2β)
=sin(2α-α+)+sin(α-2α+π)
=cos α+sin α
=sin(α+).
因为≤α≤π,
所以≤α+≤,
所以-1≤sin(α+)≤1,
即取值范围为[-1,1].故选A.
7.已知2sin θ=1+cos θ,则tan 等于( C )
(A)2 (B)
(C)或不存在(D)不存在
解析:4sin cos =2cos2,
所以cos =0或2sin =cos ,
所以tan =或不存在.
故选C.
8.函数y=(acos x+bsin x)cos x有最大值2,最小值-1,则实数 (ab)2的值为( C )
(A)6 (B)7 (C)8 (D)9
解析:y=(acos x+bsin x)cos x
=acos2x+bsin xcos x
=a+sin 2x
=sin(2x+φ)+,
所以
解得a=1,所以a2=1,b2=8,
所以(ab)2=8.故选C.
二、填空题
9.已知α∈(0, ),β-α∈(0, ),sin α=,cos (β-α)=,则sin (β-α)= ,sin β= .
解析:因为β-α∈(0, ),cos(β-α)=,
所以sin(β-α)==.
同理可得cos α=,
所以sin β=sin(β-α+α)=sin(β-α)cos α+cos(β-α)sin α= .
答案:
10.已知锐角α,β满足cos α=,tan β=3,则tan(α+
β)= ,α+β= .
解析:锐角α,β满足cos α=,
所以sin α==,所以tan α=2.
因为tan β=3,则tan(α+β)==-1,
锐角α,β满足0<α+β<π,
所以α+β=.
答案:-1
11.(2019·温岭高三模拟)已知0<α<,且sin α=,则tan(α+ π)= ,= .
解析:因为α为锐角,且sin α=,
所以cos α=,tan α=,
所以tan (α+)=tan (α+)
=
==7,
所以=
==.
答案:7
12.在△ABC中,A,B,C是其三个内角,设f(B)=4sin B·cos2(-)+ cos 2B.当f(B)-m<2恒成立时,实数m的取值范围是.
解析:原式=4sin B·+cos 2B
=2sin B(1+sin B)+(1-2sin2B)
=2sin B+1.
因为f(B)-m<2恒成立,
所以2sin B+1-m<2恒成立,
即m>2sin B-1恒成立.
因为0<B<π,
所以0<sin B≤1.
所以-1<2sin B-1≤1,故m>1.
答案:(1,+∞)
13.已知cos4α-sin4α=,且α∈(0,),则cos(2α+)= .
解析:因为cos4α-sin4α=(sin2α+cos2α)(cos2α-sin2α)=,
所以cos 2α=.
又α∈(0,),
所以2α∈(0,π),
所以sin 2α==.
所以cos(2α+)=cos 2α-sin 2α
=×-×
=.
答案:
三、解答题
14.已知函数f(x)=(2cos2x-1)·sin 2x+cos 4x.
(1)求f(x)的最小正周期及单调递减区间;
(2)若α∈(0,π),且f(-)=,求tan(α+)的值. 解:(1)f(x)=(2cos2x-1)sin 2x+cos 4x
=cos 2xsin 2x+cos 4x
=(sin 4x+cos 4x)
=sin (4x+),
所以f(x)的最小正周期T=.
令2kπ+≤4x+≤2kπ+,k∈Z,
得+≤x≤+,k∈Z.
所以f(x)的单调递减区间为[+,+],k∈Z.
(2)因为f(-)=,
所以sin(α-)=1.
因为α∈(0,π),-<α-<,
所以α-=,故α=.
因此tan(α+)===2-.
15.已知f(x)= (1+)sin2x-2sin(x+)·sin(x-).
(1)若tan α=2,求f(α)的值;
(2)若x∈[,],求f(x)的取值范围.
解:(1)f(x)=(sin2x+sin xcos x)+2sin(x+)·cos(x+) =+sin 2x+sin(2x+)
=+(sin 2x-cos 2x)+cos 2x
=(sin 2x+cos 2x)+.
由tan α=2,得sin 2α===.
cos 2α===-.
所以f(α)=(sin 2α+cos 2α)+=.
(2)由(1)得f(x)=(sin 2x+cos 2x)+ =sin(2x+)+.
由x∈[,],
得≤2x+≤.
所以-≤sin(2x+)≤1,
所以0≤f(x)≤,
所以f(x)的取值范围是[0,].。