三角函数化简求值证明技巧
三角函数的化简教学方法总结

三角函数的化简教学方法总结三角函数在高中数学中是一个重要的概念,它们在数理化以及工程学等领域有着广泛的应用。
化简三角函数是解决三角方程、三角恒等式和证明等问题的基础技巧。
本文将总结几种常见的三角函数化简教学方法,帮助学生更好地理解和运用三角函数。
一、借助特殊角的性质1. 利用正弦和余弦的周期性质:正弦函数和余弦函数的周期都是2π。
当我们需要化简一个三角函数时,可以将大角度化为小角度来简化计算。
2. 利用正弦和余弦的对称性质:正弦函数和余弦函数都具有关于y轴对称和关于原点对称的特点。
在化简时,可以利用这些性质来得到简化后的表达式。
3. 利用正弦和余弦的同一性质:正弦函数和余弦函数具有正负号的变化规律。
通过改变角度的正负号,可以得到等价的三角函数表达式。
二、利用三角函数的基本关系1. 正弦函数与余弦函数的关系:利用三角函数的基本定义,我们可以得到sin^2θ + cos^2θ = 1的恒等式。
在化简三角函数表达式时,可以利用这个关系来消去一个三角函数,从而简化计算。
2. 正切函数与余切函数的关系:通过定义和基本关系,可以得到tanθ = sinθ / cosθ和cotθ = cosθ / sinθ的恒等式。
在化简时,我们可以将正切和余切转化为正弦和余弦的形式。
三、使用三角函数的和差化积公式1. 正弦函数的和差化积公式:sin(A ± B) = sinA cosB ± cosA sinB。
当需要化简含有正弦函数的表达式时,可以利用这个公式将和差形式转化为积的形式。
2. 余弦函数的和差化积公式:cos(A ± B) = cosA cosB ∓ sinA sinB。
同样地,当需要简化一个含有余弦函数的表达式时,可以利用这个公式将和差形式转化为积的形式。
四、将三角函数化简为指数函数1. 欧拉公式:e^(ix) = cosx + isinx。
利用欧拉公式,可以将三角函数表示为指数函数,从而简化计算。
(完整版)三角函数化简求值证明技巧
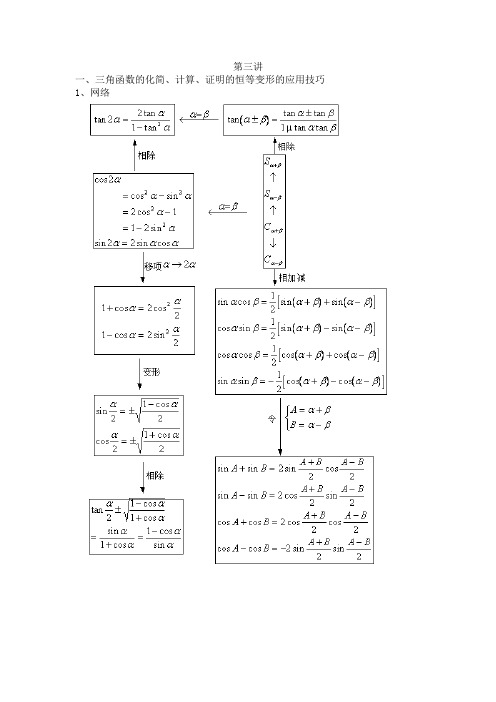
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结(1)变换函数名对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。
练习:已知sin(α+β)=,cos(α-β)=,求的值。
2)变换角的形式对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。
练习已知,求的值【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=提示:sin[(α+β)-β]=Asin (α+β)(3)以式代值利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
【例4】化简:(4)和积互化积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。
三角函数的化简与证明

三角函数的化简与证明三角函数是数学中的重要概念之一,它在解析几何、物理学、工程学等领域中有广泛应用。
在使用三角函数时,我们经常面临的一个问题就是如何将复杂的三角函数化简为简单形式,或者证明两个三角函数之间的等式。
本文将探讨三角函数的化简和证明方法。
一、三角函数的化简1. 三角恒等式三角恒等式是三角函数化简的基础。
它是一种等式关系,使得两个或多个三角函数能够互相转化。
下面是一些常见的三角恒等式:- 余弦函数的平方加正弦函数的平方等于1:$cos^2θ + sin^2θ = 1$- 2倍角公式:$cos(2θ) = cos^2θ - sin^2θ$- 倍角公式:$sin(2θ) = 2sinθcosθ$- 三角和差公式等通过运用这些恒等式,我们可以将复杂的三角函数化简为简单的形式,便于计算和理解。
2. 其他化简方法除了三角恒等式,还有一些其他的化简方法。
例如,使用欧拉公式,将三角函数转化为复指数函数进行化简。
这个方法可以将三角函数的复杂计算转化为简单的指数函数计算,能够提高计算效率。
在实际问题中,我们还可以利用对称性、周期性等性质进行化简。
这需要根据具体问题进行分析和推导,找到合适的化简方法。
二、三角函数的证明1. 等式的证明证明三角函数之间的等式是数学中的重要问题。
通过证明三角函数之间的等式,可以建立它们之间的联系,拓宽我们对三角函数的理解。
在证明三角函数等式时,我们可以运用三角恒等式、代数运算、数学归纳法等方法。
具体的证明过程需要根据问题的要求和条件进行推导。
2. 不等式的证明除了等式的证明,我们还经常需要证明三角函数之间的不等式。
三角函数的不等式证明在数学分析和优化等领域中有广泛应用。
在证明三角函数不等式时,我们可以使用极限、导数、积分和数学归纳法等方法。
通过分析三角函数的性质和变化趋势,找到合适的不等式证明方法。
需要注意的是,在证明过程中,要严谨而准确地推导,避免出现漏洞和错误,确保证明的有效性和可靠性。
三角函数化简求值的技巧

三角函数化简求值的技巧
一、三角函数的重要性质:
1、正弦函数sin x、余弦函数cos x、正切函数tanx和其逆函数的
关系:
sin x=1/cos x,cos x=1/sin x,tan x=1/cot x,cot x=1/tan x,cos x=1/csc x,csc x=1/cos x。
2、三角函数的基本性质:
sin2x+cos2x=1,sin2x=2sin(x/2)cos(x/2),cos2x=cos2(x/2)
-sin2(x/2),2sin xcos x=sin2x+cos2x=2sin2(x/2)=2cos2(x/2)。
3、三角函数的对称性:
sin(-x)=-sin x,cos(-x)=cos x,tan(-x)=-tan x,cot(-x)=-cot x,csc(-x)=-csc x。
二、用三角函数化简求值的常用方法:
1、用公式和定义:
用三角函数的基本公式来把表达式中的各个项拆分开明确每个项的意义,然后把各个项的值累加求值。
2、用对称性:
对变量进行绝对值化,然后利用三角函数的对称性变换变量或表达式,从而达到化简的目的。
3、用反函数求值:
把表达式中的三角函数换成其对应的反函数,然后利用反函数的性质进行化简,获得原函数的表达式。
四、利用三角函数化简求值的实例:
例1:求Sin(60°)
解:
1、用公式求值:
可以用公式sin 2x=2sin xcos x来求值。
1分钟学会-诱导公式化简求值问题【三角函数】

1分钟学会-诱导公式化简求值问题【三角函数】要解决诱导公式化简求值问题,我们需要熟练掌握三角函数的基本性质和诱导公式。
三角函数分为正弦函数、余弦函数、正切函数和余切函数。
诱导公式是指把角度推导至一定范围内的公式,如将三角函数的角度推导至0-90度范围内,以此进行计算简化。
在解决诱导公式化简求值问题的过程中,需要注意以下几个步骤:1. 确定所给的三角函数公式及其角度范围。
2. 将所给的角度表示成诱导公式中的角度形式。
3. 按照诱导公式进行化简,得到最简形式。
4. 根据所求解的范围,代入得到三角函数的精确值或近似值。
例如,我们要对三角函数$sin(105^{\circ})$进行化简求值。
由于$105^{\circ}$超出了0-90度的范围,因此需要使用诱导公式进行化简。
我们有以下步骤:1. 由于$sin(180^{\circ}-x)=sin(x)$,因此可以将$sin(105^{\circ})$表示为$sin(180^{\circ}-105^{\circ})=sin(75^{\circ})$。
2. 根据诱导公式$sin(A\pm B)=sinAcosB\pm cosAsinB$,将$sin(75^{\circ})$化简为$sin(45^{\circ}+30^{\circ})=sin45^{\circ}cos30^{\circ}+cos45^{\ circ}sin30^{\circ}$。
3. 代入$sin45^{\circ}=\frac{\sqrt{2}}{2}$,$cos30^{\circ}=\frac{\sqrt{3}}{2}$和$sin30^{\circ}=\frac{1}{2}$,得到$sin(105^{\circ})=\frac{\sqrt{6}+\sqrt{2}}{4}$。
最后,需要注意在求值时,应根据题目要求选择精确值或近似值,并保留正确的有效位数。
掌握诱导公式化简求值问题,对于解决三角函数相关计算问题具有重要意义。
三角函数式化简原则两角和与差的三角函数及三角恒等变换三角函数化简方法

一、三角函数式化简原则(1)一看"角".这是最重要的一点,通过角之间的关系,把角进行合理拆分与拼凑,从而正确使用公式.(2)二看"函数名称".看函数名称之间的差异,从而确定使用的公式.(3)三看"结构特征".分析结构特征,可以帮助我们找到变形得方向,常见的有"遇到分式要通分"等.二、三角函数化简方法提炼:(1)解决给值求值问题的一般思路:①先化简需求值得式子;②观察已知条件与所求值的式子之间的联系(从三角函数名及角入手);③将已知条件代入所求式子,化简求值.(2)解决给值求角问题的一般步骤:①求出角的某一个三角函数值;②确定角的范围;③根据角的范围确定所求的角.三、三角函数化简常用公式半角公式sin(A/2)=±√((1cosA)/2)cos(A/2)=±√((1+cosA)/2)tan(A/2)=±√((1cosA)/((1+cosA))三角函数和差化积公式sinA+sinB=2sin[(A+B)/2]cos[(AB)/2]sinAsinB=2cos[(A+B)/2]sin[(AB)/2]cosA+cosB=2cos[(A+B)/2]cos[(AB)/2]cosAcosB=2sin[(A+B)/2]sin[(AB)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1tanAtanB) tanAtanB=sin(AB)/cosAcosB=tan(AB)(1+tanAtanB) 三角函数积化和差公式sinAsinB=[cos(A+B)cos(AB)]/2cosAcosB=[cos(A+B)+cos(AB)]/2sinAcosB=[sin(A+B)+sin(AB)]/2cosAsinB=[sin(A+B)sin(AB)]/2三角函数降幂公式sin^2(α)=(1cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=vercos(2α)/2tan^2(α)=(1cos(2α))/(1+cos(2α))三角函数辅助角公式asinα+bcosα=(√a^2+b^2)sin(α+β),tanβ=b/a 3三角函数化简方法(1)切割化弦;(2)降幂公式;(3)用三角公式转化出特殊角;(4)异角化同角;(5)异名化同名;(6)高次转低次;(7)辅助角公式;(8)分解因式。
三角函数的化简详解

三角函数的化简1、三角函数式的化简:(1)常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③ 三角公式的逆用等。
(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数2、三角函数的求值类型有三类:(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如2(),()()ααββααβαβ=+-=++-等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。
3、三角等式的证明:(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端的化“异”为“同”;(2)三角条件等式的证题思路是通过观察,发现已知条件和待证等式间的关系,采用代入法、消参法或分析法进行证明。
一、化简 【例1】求值:︒+︒︒⋅︒+︒+︒80cot 40csc 10sin 20tan 10cos 20sin 2.【变式】1、求值()︒+︒︒+︒+︒10cos 110tan 60tan 110cos 40cos 2【变式】2、求0020210sin 21)140cos 1140sin 3(⋅-。
【例2】(三兄弟)已知23523sin cos παπαα<<=-,且,求αααtan 1sin 22sin 2-+的值【变式】(05天津)已知727sin(),cos 241025παα-==,求sin α及tan()3πα+.【例3】(最值辅助角)已知函数f (x )=2a sin 2x -23a sin x cos x +a +b -1,(a 、b 为常数,a <0),它的定义域为[0,2π],值域为[-3,1],试求a 、b 的值。
三角函数化简求值的技巧

三角函数化简与求值常用技巧
三角函数在高考中通常以中低档题型出现,难度不大,但由 于三角公式的特殊性,解题中往往也涉及一些小的变换技 巧,如果处理得当,往往可以事半功倍,快速而准确地得到 正确结论.通常情况下,三角变换应从“角度、函数、常数、 次数、结构”等几方面着手解决.
一、三角变换,角为先锋 三角函数作为一种特殊函数,其“角”的特殊性不容忽视,因此我们在三角函数恒等变换 中,应该首先注意角的形式,从统一角的角度出发,往往能够达到事半功倍的效果.
【例 1】已 知α、 β为 锐角,cos α=
3 5
,tan (α−β)=−
1 3
,则
tan β=(
)
A、
1 3
B、 3
【变式演练】已知 sin
x-π
4
=3,则
sin
2x 的值为(
)
5
A.- 7 25
B. 7 25
C. 9 25
D.16 25
【解析】法一、sin 2x=cos(2x- π )=1-2sin2(x- π )=1-2×(3)2= 7 ,选 B.
2
4
5 25
法二、依题意得 2(sin x-cos x)=3,1(sin x-cos x)2= 9 ,1-sin 2x=18,sin 2x= 7 ,选
C、
9 13
D、
13 9
【例
1】已 知α、 β为 锐角,cos α=
3 5
,tan (α−β)=−
1 3
,则
tan β=(
)
A、
1 3
B、 3
C、
9 13
D、
13 9
【分析】依题意,可求得 tan α=
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5. 图象变换
例7已知函数 该函数的图象可由 的图象经过怎样的平移和伸缩变换得到?
6. 求值
例8.已知函数f(x)= +sinxcosx。设α∈(0,π),f( )= ,求sinα的值。
7. 求系数
例9.若函数f(x)= 的最大值为2,试确定常数a的值。
8. 解三角不等式
【例1】已知θ同时满足 和 ,且a、b均不为0,求a、b的关系。
练习:已知sin(α+β)= ,cos(α-β)= ,求 的值。
2)变换角的形式
对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)- cos(θ+15°)的值。
练习已知 ,求 的值
【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=
提示:sin[(α+β)-β]=Asin(α+β)
(3)以式代值
利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。这其中以“1”的变换为最常见且最灵活。“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
(7)数形结合
有的三角变换问题蕴含着丰富的几何直观,此时若能以数思形,数形渗透,两者交融,则可开辟解题捷径。利用单位圆,构造三角形,利用直线、曲线的方程等方法都是数形结合的思想。
【例9】已知: , ,求 的值。
5. 非特殊角的化简、求值问题的解题方法探究
非特殊角的化简求值是给角求值中一类常见的三角求值类型,对于此类求值问题,由于涉及到的三角公式及其变形灵活多样,因而如何利用三角公式迅速准确的求值应是解决这类问题的重点,现在我们通过一个题目的解法探寻,体会非特殊角三角函数的求法。
ﻫ【例6】求证: =
(6)代数方法
三角问题有时稍作置换,用各种代数方法对三角函数式作因式分解、等量置换等的变形,从而将三角问题转换成代数问题来解,而且更加简捷。这其中有设元转化、利用不等式等方法。
【例7】锐角α、β满足条件 ,则下列结论中正确的是( )
A.α+β≠ B. α+β<
C. ห้องสมุดไป่ตู้+β> D. α+β=
【题目】求 的值。
练习
1若 ,则 的值为()
A. B.
C. D.
2函数 的值域是()
A. B. C. D.
3.已知等腰三角形顶角的余弦值等于 ,则这个三角形底角的正弦值为()
A. B. C. D.
4. 等于()
A.-1 B. 1C.2D.-2
2、辅助角公式及其应用
辅助角公式
对于形如y=asinx+bcosx的三角式,可变形如下:
三角函数化简求值证明技巧
———————————————————————————————— 作者:
———————————————————————————————— 日期:
第三讲
1、三角函数的化简、计算、证明的恒等变形的应用技巧
1、网络
2、三角函数变换的方法总结
(1)变换函数名
对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例4】化简:
(4)和积互化
积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。这往往用到倍、半角公式。
【例5】解三角方程:sin2x+sin22x=sin23x
(5)添补法
与代数恒等变换一样,在三角变换中有时应用添补法对原式作一定的添项裂项会使某些问题很便利地得以解决。将原式“配”上一个因子,同时除以这个式子也是添补法的一种特殊情形。
例10.已知函数f(x)=sin2x+sin2x,x ,求使f(x)为正值的x的集合。
y=asinx=bcosx 。
1 求周期
例1求函数 的最小正周期。
2. 求最值
例2.已知函数f(x)=cos4x-2sinxcosx-sin4x。若 ,求f(x)的最大值和最小值。
3求值域
例4.求函数
的值域。
4 图象对称问题
例6.如果函数y=sin2x+acos2x的图象关于直线x= 对称,那么a=( )
