同角三角函数的化简与证明
同角三角函数的基本关系式课件

行化简。
转换函数形式
通过同角三角函数的关系式,可 以实现三角函数的转换,如正弦 与余弦、正切与余切之间的转换。
证明恒等式
利用同角三角函数的基本关系式, 可以证明各种三角恒等式。
在解决实际问题中的应用
物理问题求解
在物理问题中,经常需要用到三角函数的知识,同角三角函数的 基本关系式是解决这类问题的重要工具。
03
代数证明法
通过代数运算和恒等变换, 利用已知的三角恒等式推 导出同角三角函数的基本 关系式。
几何证明法
利用单位圆的性质和三角 形的相似性质,通过几何 图形和角度关系证明同角 三角函数的基本关系式。
向量证明法
利用向量的数量积和向量 模的性质,通过向量的运 算证明同角三角函数的基 本关系式。
证明过程
证明结果
同角三角函数的基本关系式
sin^2θ + cos^2θ = 1,tanθ = sinθ/cosθ,cotθ = cosθ/sinθ等。
证明结果的应用
同角三角函数的基本关系式在解三角形、求三角函数的值、 判断三角函数的单调性等方面有广泛的应用。
பைடு நூலகம்
04
同角三角函数的基本关系式应用
在解三角形中的应用
代数证明过程
通过三角恒等式的变换,将同角 三角函数的基本关系式化简为已 知的三角恒等式或基本的代数恒
等式。
几何证明过程
利用单位圆的性质,将三角函数的 角度转化为单位圆上的弧长,再利 用三角形相似性质推导出同角三角 函数的基本关系式。
向量证明过程
利用向量的数量积和向量模的性质, 将同角三角函数的基本关系式转化 为向量的运算,通过向量的运算证 明。
同角三角函数的基本关系

课题:§3.1.2 同角三角函数的基本关系(2)
学习目标:
1、通过三角函数的定义导出同角三角函数的基本关系式;
2、能运用同角三角函数的基本关系式进行三角函数的求值、化简、证明.
学习重点:同角三角函数的基本关系式的推导与证明.
学习难点:能运用同角三角函数的基本关系式进行三角函数的求值、化简、证明.
【自主学习】预习教材第115~116页,完成下列问题.
1.同角三角函数的基本关系
(1)平方关系:sin2α+cos2α=1 变形公式:sin2α=;cos2α=;
(2)商数关系:tan α=sin α
cos α变形:sin α=;cos α=.
2. (sin α+cos α)2=;(sin α-cos α)2=.
3、若设sin α+cos α=t,则sin αcos α=;
若设sin α-cos α=t,则sin αcos α=.
【预习自测】首先完成课本第115页练习第1、2、3、4题,再完成下面的问题.
【合作探究】
探究1. 已知√1+sinα
1−sinα−√1−sinα
1+sinα
=−2tanα,试确定使等式成立的角α的集合。
探究2.已知sinα=−3
5
,且α是第四象限角,求tanα[cos(3π−α)−sin(5π+α)]的值。
探究4.证明:2(sinα−cosα)1+sinα+cosα=cosα
1+sinα−sinα1+cosα .
【基础检测】
1. 已知α是第二象限角,则√1−cos 2α+2√1−sin 2αcosα
=。
(完整版)三角函数化简求值证明技巧
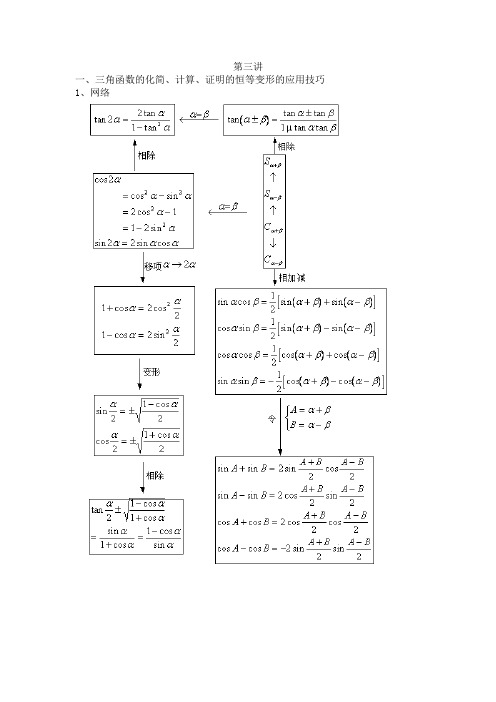
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结(1)变换函数名对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。
练习:已知sin(α+β)=,cos(α-β)=,求的值。
2)变换角的形式对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。
练习已知,求的值【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=提示:sin[(α+β)-β]=Asin (α+β)(3)以式代值利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
【例4】化简:(4)和积互化积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。
同角三角函数的基本关系

1.2.2 同角三角函数的基本关系 学习目标 1.能通过三角函数的定义推导出同角三角函数的基本关系式.2.理解同角三角函数的基本关系式.3.能运用同角三角函数的基本关系式进行三角函数式的化简、求值和证明.知识点 同角三角函数的基本关系式1.同角三角函数的基本关系式(1)平方关系:sin 2α+cos 2α=1.(2)商数关系:tan α=sin αcos α ⎝⎛⎭⎫α≠k π+π2,k ∈Z . 2.同角三角函数基本关系式的变形(1)sin 2α+cos 2α=1的变形公式sin 2α=1-cos 2α;cos 2α=1-sin 2α.(2)tan α=sin αcos α⎝⎛⎭⎫α≠k π+π2,k ∈Z 的变形公式 sin α=cos αtan α;cos α=sin αtan α.1.sin 2α+cos 2β=1.( × )提示 在同角三角函数的基本关系式中要注意是“同角”才成立,即sin 2α+cos 2α=1.2.sin 2θ2+cos 2θ2=1.( √ ) 提示 在sin 2α+cos 2α=1中,令α=θ2可得sin 2θ2+cos 2θ2=1. 3.对任意的角α,都有tan α=sin αcos α成立.( × ) 提示 当α=π2+k π,k ∈Z 时就不成立. 4.若cos α=0,则sin α=1.( × )题型一 利用同角三角函数的关系式求值命题角度1 已知角α的某一三角函数值及α所在象限,求角α的其余三角函数值例1 (1)若sin α=-513,且α为第四象限角,则tan α的值为( ) A.125 B .-125 C.512 D .-512考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 D解析 ∵sin α=-513,且α为第四象限角,∴cos α=1213, ∴tan α=sin αcos α=-512,故选D. (2)已知sin α+cos α=713,α∈(0,π),则tan α= . 考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 -125解析 ∵sin α+cos α=713, ∴(sin α+cos α)2=49169, 即2sin αcos α=-120169<0, 又α∈(0,π),则sin α>0,cos α<0,∴α∈⎝⎛⎭⎫π2,π,故sin α-cos α=(sin α+cos α)2-4sin αcos α=1713, 可得sin α=1213,cos α=-513,tan α=-125. 反思感悟 (1)同角三角函数的关系揭示了同角三角函数之间的基本关系,其常用的用途是“知一求二”,即在sin α,cos α,tan α三个值之间,知道其中一个可以求其余两个.解题时要注意角α的象限,从而判断三角函数值的正负.(2)已知三角函数值之间的关系式求其它三角函数值的问题,我们可利用平方关系或商数关系求解,其关键在于运用方程的思想及(sin α±cos α)2=1±2sin αcos α的等价转化,找到解决问题的突破口.跟踪训练1 已知tan α=43,且α是第三象限角,求sin α,cos α的值. 考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值解 由tan α=sin αcos α=43,得sin α=43cos α.① 又sin 2α+cos 2α=1,②由①②得169cos 2α+cos 2α=1,即cos 2α=925. 又α是第三象限角,∴cos α=-35,sin α=43cos α=-45. 命题角度2 已知角α的某一三角函数值,未给出α所在象限,求角α的其余三角函数值例2 已知cos α=-817,求sin α,tan α的值. 考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值解 ∵cos α=-817<0,且cos α≠-1, ∴α是第二或第三象限角.(1)当α是第二象限角时,则sin α=1-cos 2α=1-⎝⎛⎭⎫-8172=1517, tan α=sin αcos α=1517-817=-158. (2)当α是第三象限角时,则sin α=-1-cos 2α=-1517,tan α=158. 反思感悟 利用同角三角函数关系式求值时,若没有给出角α是第几象限角,则应分类讨论,先由已知三角函数的值推出α的终边可能在的象限,再分类求解.跟踪训练2 已知cos α=-45,求sin α和tan α. 考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值解 sin 2α=1-cos 2α=1-⎝⎛⎭⎫-452=925, 因为cos α=-45<0, 所以α是第二或第三象限角,当α是第二象限角时,sin α=35, tan α=sin αcos α=-34; 当α是第三象限角时,sin α=-35, tan α=sin αcos α=34. 题型二 齐次式求值问题例3 已知tan α=2,求下列代数式的值.(1)4sin α-2cos α5cos α+3sin α;(2)14sin 2α+13sin αcos α+12cos 2α. 考点 运用基本关系式化简和证明题点 运用基本关系式化简、求值解 (1)原式=4tan α-25+3tan α=611. (2)原式=14sin 2α+13sin αcos α+12cos 2αsin 2α+cos 2α=14tan 2α+13tan α+12tan 2α+1=14×4+13×2+125=1330. 反思感悟 (1)关于sin α,cos α的齐次式,可以通过分子、分母同除以cos α或cos 2α转化为关于tan α的式子后再求值.(2)假如代数式中不含分母,可以视分母为1,灵活地进行“1”的代换,由1=sin 2α+cos 2α代换后,再同除以cos 2α,构造出关于tan α的代数式.跟踪训练3 已知sin α+cos αsin α-cos α=2,计算下列各式的值. (1)3sin α-cos α2sin α+3cos α; (2)sin 2α-2sin αcos α+1.考点 运用基本关系式化简和证明题点 运用基本关系式化简、求三角函数值解 由sin α+cos αsin α-cos α=2,化简,得sin α=3cos α, 所以tan α=3.(1)原式=3×3cos α-cos α2×3cos α+3cos α=8cos α9cos α=89. (2)原式=sin 2α-2sin αcos αsin 2α+cos 2α+1 =tan 2α-2tan αtan 2α+1+1=32-2×332+1+1=1310. 三角函数式的化简与证明典例 (1)化简:sin 2αtan α+cos 2αtan α+2sin αcos α. 考点 运用基本关系式化简和证明题点 运用基本关系式化简解 原式=sin 2α·sin αcos α+cos 2α·cos αsin α+2sin αcos α =sin 4α+cos 4α+2sin 2αcos 2αsin αcos α=(sin 2α+cos 2α)2sin αcos α=1sin αcos α. (2)求证:tan αsin αtan α-sin α=tan α+sin αtan αsin α. 考点 运用基本关系式化简和证明题点 运用基本关系式证明证明 ∵右边=tan 2α-sin 2α(tan α-sin α)tan αsin α=tan 2α-tan 2αcos 2α(tan α-sin α)tan αsin α=tan 2α(1-cos 2α)(tan α-sin α)tan αsin α =tan 2αsin 2α(tan α-sin α)tan αsin α=tan αsin αtan α-sin α=左边, ∴原等式成立.[素养评析] (1)三角函数式的化简技巧①化切为弦,即把正切函数都化为正弦、余弦函数,从而减少函数名称,达到化繁为简的目的.②对于含有根号的,常把根号里面的部分化成完全平方式,然后去根号达到化简的目的. ③对于化简含高次的三角函数式,往往借助于因式分解,或构造sin 2α+cos 2α=1,以降低函数次数,达到化简的目的.(2)证明三角恒等式的过程,实质上是化异为同的过程,证明恒等式常用以下方法: ①证明一边等于另一边,一般是由繁到简.②证明左、右两边等于同一个式子(左、右归一).③比较法:即证左边-右边=0或左边右边=1(右边≠0). ④证明与已知等式等价的另一个式子成立,从而推出原式成立.(3)掌握逻辑推理的基本形式,学会有逻辑地思考问题;形成重论据、有条理、合乎逻辑的思维品质,提升逻辑推理的数学核心素养.1.若sin α=45,且α是第二象限角,则tan α的值为( ) A .-43 B.34 C .±34 D .±43考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 A解析 ∵α为第二象限角,sin α=45, ∴cos α=-35,tan α=-43. 2.已知sin α=55,则sin 4α-cos 4α的值为( ) A .-35 B .-15 C.15 D.35考点 运用基本关系式求三角函数值题点 运用基本关系式化简、求三角函数值答案 A解析 sin 4α-cos 4α=(sin 2α+cos 2α)(sin 2α-cos 2α)=sin 2α-(1-sin 2α)=2sin 2α-1=2×⎝⎛⎭⎫552-1=-35. 3.(2018·江西上高第二中学高二期末)若α为第三象限角,则cos α1-sin 2α+2sin α1-cos 2α的值为( )A .3B .-3C .1D .-1考点 运用基本关系式化简和证明题点 运用基本关系式化简答案 B解析 ∵α为第三象限角,∴cos α<0,sin α<0,∴原式=-cos αcos α-2sin αsin α=-3. 4.已知tan x =-12,则sin 2x +3sin x cos x -1的值为( ) A.13B .2C .-2或2D .-2考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 D5.已知:tan αtan α-1=-1,则sin α-3cos αsin α+cos α= . 答案 -53解析 由已知得:tan α=12, ∴sin α-3cos αsin α+cos α=tan α-3tan α+1=-53.1.利用同角三角函数的基本关系式,可以由一个角的一个三角函数值,求出这个角的其他三角函数值.2.利用同角三角函数的关系式可以进行三角函数式的化简,结果要求:(1)项数尽量少;(2)次数尽量低;(3)分母、根式中尽量不含三角函数;(4)能求值的尽可能求值.3.在三角函数的变换求值中,已知sin α+cos α,sin αcos α,sin α-cos α中的一个,可以利用方程思想,求出另外两个的值.4.在进行三角函数式的化简或求值时,细心观察题目的特征,灵活、恰当地选用公式,统一角、统一函数、降低次数是三角函数关系式变形的出发点.利用同角三角函数的基本关系主要是统一函数,要掌握“切化弦”和“弦化切”的方法.5.在化简或恒等式证明时,注意方法的灵活运用,常用技巧:(1)“1”的代换;(2)减少三角函数名的个数(化切为弦、化弦为切等);(3)多项式运算技巧的应用(如因式分解、整体思想等);(4)对条件或结论的重新整理、变形,以便于应用同角三角函数关系来求解.一、选择题1.已知α是第二象限角,tan α=-12,则cos α等于( ) A .-55 B .-15C .-255D .-45考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 C解析 ∵α是第二象限角,∴cos α<0.又sin 2α+cos 2α=1,tan α=sin αcos α=-12,∴cos α=-255.2.下列四个结论中可能成立的是( )A .sin α=12且cos α=12B .sin α=0且cos α=-1C .tan α=1且cos α=-1D .α是第二象限角时,tan α=-sin αcos α考点 同角三角函数基本关系题点 运用基本关系式求值答案 B3.已知cos ⎝⎛⎭⎫α+π4=13,0<α<π2,则sin ⎝⎛⎭⎫α+π4等于( )A .-223 B .-23 C.23 D.223考点 运用基本关系式求值题点 运用基本关系式求值答案 D解析 ∵0<α<π2,∴π4<α+π4<3π4,∴sin ⎝⎛⎭⎫α+π4= 1-⎝⎛⎭⎫132=223.4.已知α是锐角,且tan α是方程4x 2+x -3=0的根,则sin α等于() A.45 B.35 C.25 D.15考点 同角三角函数基本关系题点 运用基本关系式求值答案 B解析 由4x 2+x -3=0得x =-1或x =34.又∵α是锐角,∴tan α>0,sin α>0, ∴tan α=34.又∵tan α=sin αcos α=34,且sin 2α+cos 2α=1,∴sin 2α+⎝⎛⎭⎫43sin α2=1,解得sin α=35.5.已知θ是第三象限角,且sin 4θ+cos 4θ=59,则sin θcos θ的值为() A.23 B .-23 C.13 D .-13考点 运用基本关系式化简、求值题点 运用基本关系式化简、求值答案 A解析 由sin 4θ+cos 4θ=59,得(sin 2θ+cos 2θ)2-2sin 2θcos 2θ=59,∴sin 2θcos 2θ=29,∵θ是第三象限角,∴sin θ<0,cos θ<0, ∴sin θcos θ=23.6.已知sin θ+cos θsin θ-cos θ=2,则sin θcos θ的值是( ) A.34 B .±310 C.310 D .-310考点 运用基本关系式化简、求值题点 运用基本关系式化简、求值答案 C解析 由条件得sin θ+cos θ=2sin θ-2cos θ, 即3cos θ=sin θ,tan θ=3,∴sin θcos θ=sin θcos θsin 2θ+cos 2θ=tan θ1+tan 2θ=31+32=310. 7.若α为第二象限角,化简tan α·1sin 2α-1等于( ) A .1 B .2 C .-1 D.12考点 运用基本关系式化简题点 运用基本关系式化简答案 C解析 tan α·1sin 2α-1=tan α·1-sin 2αsin 2α=sin αcos α·|cos α||sin α|. 因为α为第二象限的角,所以cos α<0,sin α>0,原式=sin αcos α·-cos αsin α=-1. 二、填空题8.已知tan α=-12,则1+2sin αcos αsin 2α-cos 2α= . 考点 运用基本关系式化简、求值 题点 运用基本关系式化简、求值答案 -13解析 1+2sin αcos αsin 2α-cos 2α=(sin α+cos α)2sin 2α-cos 2α=sin α+cos αsin α-cos α=tan α+1tan α-1=-12+1-12-1=12-32=-13. 9.已知α为第二象限角,则cos α·1+tan 2α+sin α·1+1tan 2α= . 考点 运用基本关系式化简题点 运用基本关系式化简答案 0解析 原式=cos αsin 2α+cos 2αcos 2α+sin αsin 2α+cos 2αsin 2α=cos α·1|cos α|+sin α·1|sin α|. 因为α是第二象限角,所以sin α>0,cos α<0,所以cos α·1|cos α|+sin α·1|sin α|=-1+1=0,即原式=0.10.(2018·九江高一检测)若sin α+cos α=2,则tan α+1tan α的值为 . 考点 运用基本关系式化简、求值题点 运用基本关系式化简、求值答案 2 11.在△ABC 中,2sin A = 3cos A ,则角A = .考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 π3解析 由题意知cos A >0,即A 为锐角.将2sin A =3cos A 两边平方得2sin 2A =3cos A .∴2cos 2A +3cos A -2=0,解得cos A =12或cos A =-2(舍去), ∴A =π3. 三、解答题12.化简:1-2sin α2cos α2+1+2sin α2cos α2⎝⎛⎭⎫0<α<π2. 考点 运用基本关系式化简和证明题点 运用基本关系式化简解 原式=sin 2α2-2sin α2cos α2+cos 2α2+sin 2α2+2sin α2cos α2+cos 2α2 =⎝⎛⎭⎫cos α2-sin α22+⎝⎛⎭⎫cos α2+sin α22=⎪⎪⎪⎪cos α2-sin α2+⎪⎪⎪⎪cos α2+sin α2. ∵α∈⎝⎛⎭⎫0,π2,∴α2∈⎝⎛⎭⎫0,π4, ∴cos α2-sin α2>0,cos α2+sin α2>0, ∴原式=cos α2-sin α2+cos α2+sin α2=2cos α2. 13.已知tan 2α=2tan 2β+1,求证:sin 2β=2sin 2α-1.考点 运用基本关系式化简和证明题点 运用基本关系式化简证明 因为tan 2α=2tan 2β+1,所以tan 2α+1=2tan 2β+2,所以sin 2αcos 2α+1=2⎝⎛⎭⎫sin 2βcos 2β+1, 所以1cos 2α=2cos 2β,即cos 2β=2cos 2α, 所以1-sin 2β=2(1-sin 2α),即sin 2β=2sin 2α-1.14.若sin α+cos α=1,则sin n α+cos n α(n ∈N *)的值为 . 考点 运用基本关系式求三角函数值题点 运用基本关系式求三角函数值答案 1解析 ∵sin α+cos α=1,∴(sin α+cos α)2=1,又sin 2α+cos 2α=1,∴sin αcos α=0,∴sin α=0或cos α=0.当sin α=0时,cos α=1,此时有sin n α+cos n α=1;当cos α=0时,sin α=1,也有sin n α+cos n α=1,∴sin n α+cos n α=1.15.已知sin α,cos α为方程4x 2-4mx +2m -1=0的两个实根,α∈⎝⎛⎭⎫-π2,0,求m 及α的值.考点 运用基本关系式求三角函数值 题点 运用基本关系式求三角函数值 解 因为sin α,cos α为方程4x 2-4mx +2m -1=0的两个实根, 所以Δ=16(m 2-2m +1)≥0且sin α+cos α=m ,sin αcos α=2m -14. 代入(sin α+cos α)2=1+2sin αcos α,解得m =1±32. 又因为α∈⎝⎛⎭⎫-π2,0, 所以sin α·cos α=2m -14<0,m <12, 所以sin α+cos α=m =1-32, 所以sin α=-32,cos α=12. 又因为α∈⎝⎛⎭⎫-π2,0,所以α=-π3. 所以m =1-32,α=-π3.。
同角三角函数基本关系式、三角函数的诱导公式

一、知识概述1、同角三角函数的基本关系式同角三角函数基本关系可概括为平方关系,商数关系和倒数关系,如考虑sinα,cos α,tanα,cotα与secα,cscα六个函数,还可借助如下图表形象记忆:(1)对角线上两个函数的积为1(倒数关系)(2)任一顶点的函数等于与其相邻两个顶点的函数的积(商数关系)(3)阴影部分,顶角两个函数的平方和等于底角函数的平方(平方关系)由此图可得出公式的变形形式或其他同角函数关系式.平方关系:sin2α+cos2α=1,sec2α=1+tan2α,csc2α=1+cot2α.商数关系:倒数关系:tanα·cotα=1,sinα·cscα=1,cosα·secα=1.注:课本上只介绍了其中两个重要的关系式,事实上,掌握好其余的五个关系式能在有关解题中节省过程,带来方便.2、三角函数的诱导公式公式一:sin(α+k·)=sinαcos(α+k·)=cosαtan(α+k·)=tanα其中k∈Z.公式二:sin(+α)=-sinαcos(+α)=-cosαtan(+α)=tanα公式三:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanα公式四:sin(-α)=sinαcos(-α)=-cosαtan(-α)=-tanα总结:α+k·2(k∈Z),-α,±α的三角函数,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号。
公式五:sin(-α)=cosαcos(-α)=sinα公式六:sin(+α)=cosαcos(+α)=-sinα总结:±α的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号.二、重、难点知识归纳及讲解(一)利用诱导公式可以把任意角的三角函数转化为锐角三角函数,即:例1、求值:.分析:运用诱导公式,对于cot,可先求出sin,cos,然后由商数关系可求出cot.解:原式例2、设的值为()A.B.C.-1 D.1分析:利用诱导公式将条件等式和欲求式都化到α的同名三角函数上去,再利用同角三角函数基本关系式求解.解答:(二)同角三角函数关系式在求值、化简、证明中的应用.1、已知角α的某一三角函数值,可求出α的其余三角函数值.例3、已知tanα=2,求2sin2α-3sinαcosα-2cos2α的值.分析:由平方关系知1=sin2α+cos2α,可把式子的分母看成sin2α+cos2α,然后分子分母同除以cos2α,可得.解:2、利用同角三角函数关系式进行化简:化简结果的基本要求:(1)函数个数尽可能少;(2)次数尽可能低;(3)项数尽可能少;(4)尽可能地去掉根号;(5)尽可能地不含分母;(6)能求出值的要求出值来.例4、若sinαcosα<0,sinαtanα<0,化简:.分析:要想去掉根号,就应考虑将被开方数配成完全平方的形式.解:∵sinαcosα<0,sinαtanα<0.∴α是第二象限角.故是第一或第三象限角.原式若是第一象限角,此时1±sin>0,cos>0. 原式=若是第三象限角,此时1±sin>0,cos<0. 原式=.3、利用同角关系式进行三角恒等式的证明.证明三角恒等式的方法较多,既可由一边证向另一边,也可先证得另一个等式成立,从而得出要证的等式,还可用比较法证明等,关键是要依题而定。
同角三角函数化简求值

同角三角函数化简求值同角三角函数是指角度相同的三角函数,包括正弦、余弦、正切、余切、正割、余割等。
在化简和求值过程中,经常需要利用同角三角函数的性质进行变形和简化。
例如,常用的同角三角函数公式包括:1. 余角公式:sin(90°-x)=cos(x),cos(90°-x)=sin(x)2. 倍角公式:sin(2x)=2sin(x)cos(x),cos(2x)=cos^2(x)-sin^2(x)3. 和差角公式:sin(x±y)=sin(x)cos(y)±cos(x)sin(y),cos(x±y)=cos(x)cos(y)sin(x)sin(y)利用这些公式,可以化简和求解许多三角函数的式子和值。
例如,如果要求sin(120°),可以利用三角函数的周期性和正弦函数的奇偶性:sin(120°)=sin(120°-360°)=-sin(-240°)=-sin(240°) 再利用余角公式,得到:sin(240°)=cos(90°-240°)=-cos(150°)最后,利用正弦和余弦函数的周期性和奇偶性,得到:cos(150°)=cos(360°-150°)=cos(210°)因此,sin(120°)=-cos(150°)=-cos(360°-150°)=-cos(210°)这样,我们就成功地化简求解了sin(120°)的值。
除了以上的公式外,还有一些特殊角的三角函数值也需要掌握,例如30°、45°、60°等角度的正弦、余弦、正切值。
通过熟悉这些特殊角的值和同角三角函数的公式,我们可以更加轻松地进行三角函数的化简和求值。
三角函数中同角三角函数关系的推导过程

三角函数中同角三角函数关系的推导过程三角函数是数学中重要的概念之一,它描述了角度与其对应的三角比之间的关系。
在三角函数的研究中,同角三角函数关系是其中一个重要的推导过程。
本文将详细介绍同角三角函数关系的推导过程。
在开始推导之前,先明确一些基本概念。
在平面直角坐标系中,设有一个角度θ,该角度的终边与单位圆交于点P(x, y),其中x和y分别表示P点的横坐标和纵坐标。
根据三角函数定义,我们可以得到以下三个关系式:1. 正弦函数(Sine Function):sin(θ) = y2. 余弦函数(Cosine Function):cos(θ) = x3. 正切函数(Tangent Function):tan(θ) = y / x接下来,我们将推导出其他同角三角函数关系。
1. 同角余弦函数推导:我们已知余弦函数的定义为cos(θ) = x,可以将此式改写为:cos(θ) = 1 / sec(θ)其中sec(θ)为函数secant(θ),表示θ角的余割。
因此,同角余弦函数推导为:cos(θ) = 1 / sec(θ)2. 同角正切函数推导:我们已知正切函数的定义为tan(θ) = y / x,可以将此式改写为:tan(θ) = sin(θ) / cos(θ)其中sin(θ)和cos(θ)分别表示θ角的正弦和余弦。
因此,同角正切函数推导为:tan(θ) = sin(θ) / cos(θ)3. 同角余切函数推导:我们已知余切函数的定义为cot(θ) = 1 / tan(θ),可以将此式改写为:cot(θ) = cos(θ) / sin(θ)其中cos(θ)和sin(θ)分别表示θ角的余弦和正弦。
因此,同角余切函数推导为:cot(θ) = cos(θ) / sin(θ)4. 同角正割函数推导:我们已知正割函数的定义为sec(θ) = 1 / cos(θ),可以将此式改写为:sec(θ) = 1 / cos(θ)其中cos(θ)表示θ角的余弦。
高一数学同角三角函数的基本关系式知识精讲

高一数学同角三角函数的基本关系式【本讲主要内容】同角三角函数的基本关系式【知识掌握】 【知识点精析】1. 同角三角函数的基本关系式(1)平方关系:sin cos tan sec cot csc 222222111αααααα+=+=+=,, (2)商数关系:tan sin cos cot cos sin αααααα==, (3)倒数关系:tan cot cos sec sin csc αααααα⋅=⋅=⋅=111,,应用公式时需注意:①同角三角函数的基本关系式揭示了“同角不同名”的三角函数的运算规律,等式中涉及的角是同一个角,如sin cos 22331αα+=,tan()cot()-⋅-=1001001,而sin cos 221αβ+=就不一定成立。
②利用平方关系进行开方运算,要注意结果的符号,必要时,要进行分类讨论。
③这些关系式是对使它们有意义的那些角而言的。
如:tan sin cos ααα=是当αππ≠+∈k k z 2()时才有意义。
④在计算、化简、证明三角函数式时常用技巧有:i )“1”的代换。
根据需要,常将算式中的“1”用“sin cos 22αα+”;“sec tan 22αα-”;“sin csc αα⋅”;“tan cot αα⋅”代换。
ii )切化弦。
利用商数把正切、余切化为正弦、余弦函数。
iii )整体代换。
将算式适当变形使条件可以整体代入或将条件适当变形找出与算式之间的关系。
⑤公式应用非常广泛,因此除牢记公式原型外,还应注意公式的逆用,变形用。
如:cos sin 221αα=-,sin tan cos ααα=⋅,sin cos (sin cos )αααα⋅=+-212等等。
2. 同角三角函数基本关系式的应用(1)已知一个角的某个三角函数值,求它的其他三角函数值。
①尽可能地确定α所在的象限,以便确定三角函数值的符号。
②尽量避免使用平方关系(在一般情况下只能使用一次)。
