上海高一数学第一章集合与命题复习
上海市高三数学第一轮复习:集合与命题集合的概念

课题:集合的概念教学目标:集合、子集的概念,能利用集合中元素的性质解决问题,掌握集合问题的常规处理方法.教学重点:集合中元素的3个性质,集合的 3 种表示方法,集合语言、集合思想的运用.知识点归纳:1.集合①定义:某些指定的对象集在一起就成为一个集合,每个对象叫做集合的元素。
②表示:列举法:将集合中的元素一一列举出来,用大括号括起来,如 {a,b,c} 描述法:将集合中的元素的共同属性表示出来,形式为: P={x ∣P(x)}.如: { x yx 1}, { y yx 1}, { ( x, y) yx1}图示法:用文氏图表示题中不同的集合。
③分类:有限集、无限集、空集。
④性质确定性: a A或 a A 必居其一,互异性:不写 {1 ,1,2,3} 而是 {1 ,2,3} ,集合中元素互不相同,无序性: {1 ,2,3}={3 ,2,1}2.常用数集复数集 C 实数集 R 整数集 Z 自然数集 N 正整数集N(或 N+)有理数集 Q3.元素与集合的关系:a A或a A4.集合与集合的关系:①子集:若对任意x A 都有 x B [或对任意 x B 都有 x A] 则 A 是 B 的子集。
记作:A B②真子集:若 A B ,且存在x0B, 但 x0 A ,则A是B的真子集。
记作:A B③AB且BAAB④空集:不含任何元素的集合,用表示对任何集合 A 有A,若 A 则A5.子集的个数2n个,若 A { a1, a2 , a n } ,则A的子集个数、真子集的个数、非空真子集的个数分别为2n1个和 2n2 个。
主要方法:1.解决集合问题,首先要弄清楚集合中的元素是什么;2.弄清集合中元素的本质属性,能化简的要化简;3.抓住集合中元素的3 个性质,对互异性要注意检验;4.正确进行“集合语言”和普通“数学语言”的相互转化。
例题精选:例 1.( 1)用适当符号填空: 0{0 , 1} ;{ a, b}{ b, a} ;0;{3+17 }{ x|x>6+3 } (2)用列举法表示 { y|y=x2-1,|x|≤ 2, x Z}=.(3)M={ x|x2+2x- a=0,x∈R} ≠,则实数a的取值范围是(4)已知集合 A={ x|x2-px+15=0}, B={ x|x2-5x+ q=0} ,如果 A∩ B={3} ,那么 p+q=. (5)已知集合 A={ x|-1≤x≤2} , B={ x|x< a},如果 A∩ B=A,那么 a 的取值范围是 .(6)已知集合 A={ x|x≤2} ,B={ x|x> a},如果 A∪B=R,那么 a 的取值范围是 .(7)已知 P={0 ,1} ,M={x ∣x P} ,则 PM(8)设集合M { x x k 1, k Z}, N { x x k1, k Z},则M N2 4 4 2例 2、设集合 A 1,a,b , B a, a2 , ab ,且 A B ,求实数a, b的值。
上海地区高一数学知识点归纳
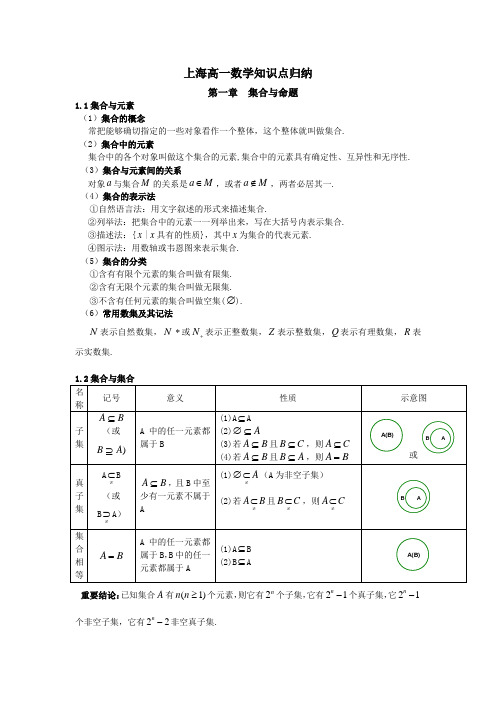
上海高一数学知识点归纳第一章 集合与命题1.1集合与元素 (1)集合的概念常把能够确切指定的一些对象看作一个整体,这个整体就叫做集合. (2)集合中的元素集合中的各个对象叫做这个集合的元素,集合中的元素具有确定性、互异性和无序性. (3)集合与元素间的关系 对象a 与集合M 的关系是a M ∈,或者a M ∉,两者必居其一. (4)集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合. ③描述法:{x |x 具有的性质},其中x 为集合的代表元素. ④图示法:用数轴或韦恩图来表示集合. (5)集合的分类①含有有限个元素的集合叫做有限集. ②含有无限个元素的集合叫做无限集. ③不含有任何元素的集合叫做空集(∅). (6)常用数集及其记法N 表示自然数集,N *或N +表示正整数集,Z 表示整数集,Q 表示有理数集,R 表示实数集.重要结论:已知集合A 有(1)n n ≥个元素,则它有2n 个子集,它有21n -个真子集,它21n-个非空子集,它有22n-非空真子集.1.3集合的基本运算 名称 记号意义性质示意图交集A B{|,x x A ∈且}x B ∈(1)A A A = (2)A∅=∅ (3)A B A ⊆ A B B ⊆ BA并集A B{|,x x A ∈或}x B ∈(1)A A A = (2)AA ∅= (3)AB A ⊇ AB B ⊇BA补集A C U{|,}x x U x A ∈∉且()()()B C A C B A C U U U ⋃=⋂ ()()()B C A C B A C U U U ⋂=⋃1.4命题的形式及等价关系(1)命题用语言、符号或式子表达的,可以判断真假的陈述句.“若p ,则q ”形式的命题中的p 称为命题的条件,q 称为命题的结论.(2)逆命题对于两个命题,如果一个命题的条件和结论分别是另一个命题的结论和条件,则这两个命题称为互逆命题.其中一个命题称为原命题,另一个称为原命题的逆命题。
第一章集合与逻辑全章复习高一数学新教材配套课件(沪教版2020)

2.集合与不等式的联系 已知全集U=R,集合A={x|1≤x≤3},B
={x|x=m+1,m∈A}. (1)求图中阴影部分表示的集合C; (2)若非空集合D={x|4-a<x<a},且D⊆(A∪B),
求实数a的取值范围.
解析:(1)因为A={x|1≤x≤3}, B={x|x=m+1,m∈A}, 所以B={x|2≤x≤4}, 由因而图 为A=可B={x得|{1x,|≤2xC≤≤=3x≤}A,4∩},则(∁则CUB=∁),UAB∩=(∁{UxB|)x=>4{或x|x1<≤2x}<,2}.
专题 四
思想方法归纳
典例剖析
1.数形结合思想 已C=知典{例集x|7合m-A=1<{xx|<-m+4<1x,<2m},∈BR=}.{x|x<-5或x>1}, (1)若A∩C=∅,求实数m的取值范围; (2)若(A∩B)⊆C,求实数m的取值范围.
思路探究:借助于数轴把集合表示出来,找出 满足条件的m的取值范围.
(2)因为集合 A={x|1≤x≤3},B={x|2≤x≤4}, 所以 A∪B={x|1≤x≤4}. 若非空集合 D={x|4-a<x<a},且 D⊆(A∪B),
4-a<a,
则有4-a≥1, a≤4,
解得 2<a≤3,
即实数 a 的取值范围为 2<a≤3.
专题 二
与集合有关的新定义问题
典例剖析
1.类比集合定义型 有整典例数3 组在成整一数个集“Z中类,”被,5记除为所[得k],余即数[为k]k=的{5所n +k|n∈Z},k=0,1,2,3,4.给出如下四个结论.
归纳提升:分类讨论就是当问题所给的对象不能进行统一研究时, 就需要对研究对象按某个标准分类,然后对每一类分别研究得出 每一类的结论,最后综合各类问题的结论得到整个问题的解 答.分类与整合就是化整为零,各个击破,再积零为整的数学思 想.
沪教版高一数学上—20—期末复习—教师版

期末复习一、集合与命题1.区分集合中元素的形式:{}|()x y f x ={}|()y y f x ={}(,)|()x y y f x =L 函数的定义域函数的值域函数图象上的点集L2.研究集合必须注意集合元素的特征,即集合元素的三性:确定性、互异性、无序性. 3.集合的性质:① 任何一个集合P 都是它本身的子集,记为P P ⊆. ② 空集是任何集合P 的子集,记为P ⊆∅. ③ 空集是任何非空集合P 的真子集,记为P ∅Ü.注意:若条件为B A ⊆,在讨论的时候不要遗忘了∅=A 的情况.集合的运算:④()()C B A C B A I I I I =、()()C B A C B A Y Y Y Y =; ()()()U UU A B A B =I U 痧?、()()()U UU A B A B =U I 痧?.⑤U UU A B A A B B A B B A A B =⇔=⇔⊆⇔⊆⇔=∅I U I 痧?.⑥对于含有n 个元素的有限集合M ,其子集、真子集、非空子集、非空真子集的个数 依次为:n2、12-n 、12-n 、22-n.4.命题是表达判断的语句.判断正确的叫做真命题;判断错误的叫做假命题. ① 命题的四种形式及其内在联系: 原命题:如果α,那么β;逆命题:如果β,那么α; 否命题:如果α,那么β; 逆否命题:如果β,那么α;② 等价命题:对于甲、乙两个命题,如果从命题甲可以推出命题乙,同时从命题乙也可以推出命题甲,既“甲⇔乙”,那么这样的两个命题叫做等价命题.③ 互为逆否命题一定是等价命题,但等价命题不一定是互为逆否命题. ④ 当某个命题直接考虑有困难时,可通过它的逆否命题来考虑. 5.常见结论的否定形式:原结论 是 都是 一定 p 或q p 且q 大于 小于否定形式 不是 不都是 不一定p 且q p 或q不大于 不小于原结论 至少一个 至多一个 至少n 个 至多n 个 对所有x 都成立 对任何x 不成立否定形式一个也没有至少两个至多1-n 个至少1+n 个存在某x 不成立存在某x 成立原命题逆命题否命题逆否命题互为 逆否互 逆互 逆互 否互 否知识梳理6在判断“充要条件”的过程中,应注意步骤性:首先必须区分谁是条件、谁是结论,然后由推导关系判断结果. 二、不等式 1.基本性质:(注意:不等式的运算强调加法运算与乘法运算) ① b a >且c b >⇒c a >;② 推论:ⅰ.a b a c b c >⇔±>±; ⅱ. b a >且d c >⇒d bc a +>+;③ 0000ac bcc a b ac bc c ac bc c >>⎧⎪>⇒===⎨⎪<<⎩;④ 推论:ⅰ.0,0a b c d ac bd >>>>⇒>; ⅱ.b a >且a 、b 同号11a b⇒<; ⅱ.b a >>0110a b ⇒>>; ⅲ.0,0,a b a b ααα>>>⇒>>; ⑤ 0>>b a ,0>m ⇒ ma mb a b ++<;⑥ ⎪⎩⎪⎨⎧<=>-000b a ⇔⎪⎩⎪⎨⎧<=>b b b a ;2.解不等式:(解集必须写成集合或区间的形式)① 一元二次或一元高次不等式以及分式不等式的解题步骤:ⅰ.分解因式⇒找到零点; ⅱ.画数轴⇒标根⇒画波浪线; ⅲ.根据不等号,确定解集; 注意点:ⅰ.分解因式所得到的每一个因式必须为x 的一次式; ⅱ.每个因式中x 的系数必须为正. ②绝对值不等式−−−→关键去绝对值:ⅰ.x a x a a >⇔><-或 )0(>a ; ⅱ.x a a x a <⇔-<<)0(>a ;ⅲ.22a b a b >⇔>; ⅳ.()()()()()(0)f x g x g x fx g x >>⇔<-或()()x g x f >;ⅴ.()()()()()f x g x g x f x g x <⇔-<<;③ 解含参数的不等式时,定义域是前提,函数增减性为基础,分类讨论是关键. 而分类讨论的关键在于“分界值”的确定以及注意解完之后要总结:综上所述L ④ 对于不等式恒成立问题,常用“函数思想....”、“分离变量思想......”以及“图象思想....”.3.基本不等式:①,a b ∈R ,则222a b ab +≥,当且仅当b a =时,等号成立.,a b +∈R ,则a b +≥b a =时,等号成立.综上,若,a b ∈R ,则ab b a b a 22)(222≥+≥+,当且仅当b a =时,等号成立. *②若,a b +∈R2112a b a b+≥≥+,当且仅当b a =时,等号成立.*③120,1,1120,1,x x x xx x x x x x⎧≥>==⎪⎪+⎨⎪≤-<==-⎪⎩当且仅当即时等号成立当且仅当即时等号成立,,.4.不等式的证明:① 比较法:作差 → 因式分解或配方 → 与“0”比较大小 →L ② 综合法:由因导果.③ 分析法:执果索因;基本步骤:要证L 即证L 即证L . ④ 反证法:正难则反.⑤ 最值法:()max x f a >,则)(x f a >恒成立; ()min x f a <,则)(x f a <恒成立. 三、函数1.函数的要素:定义域、值域、对应法则 ① 定义域:ⅰ.给出函数解析式,求函数的定义域(即求使函数解析式有意义的x 的范围) (1)0)()]([0≠⇒=x f x f y ;(2)()()0()P x y Q x Q x =⇒≠;(3)0)()(2≥⇒=x P x P y n . ⅱ.使实际问题有意义的自变量的范围. ⅲ.求复合函数的定义域:若()x f 的定义域为[]b a ,,则()[]x g f 的定义域由不等式()b x g a ≤≤解出; 若()[]x g f 的定义域为[]b a ,,则()x f 的定义域相当于[]b a x ,∈时()x g 的值域.② 值域:函数的值域(或最值)有哪几种常用解题方法?ⅰ.二次函数型或可化为二次函数型;ⅱ.单调性;ⅲ.基本不等式;ⅳ.换元法;ⅴ.数形结合;2.函数的基本性质: ① 奇偶性:ⅰ.定义判断奇偶性的步骤:(1)定义域D 是否关于原点对称;(2)对于任意D x ∈,判断)(x f -与)(x f 的关系: 若)()(x f x f =-,也即0)()(=--x f x f (),y f x x D ⇔=∈为偶函数; 若)()(x f x f -=-,也即0)()(=+-x f x f (),y f x x D ⇔=∈为奇函数.ⅱ.图象判断奇偶性:函数图象关于原点对称⇔奇函数; 函数图象关于y 轴对称⇔偶函数; ⅲ.判断函数的奇偶性时,注意到定义域关于原点对称了吗?ⅳ.如果奇函数)(x f y =在0=x 处有定义,则0)0(=f .ⅴ.一个函数既是奇函数又是偶函数,则该函数必为:()0,f x x D =∈(其中定义域D 关于原点对称) ⅵ.如果两个函数都是非零函数(定义域相交非空),则有:奇+奇⇒奇;奇+偶⇒非奇非偶;偶+偶⇒偶;奇×奇⇒偶;奇×偶⇒奇;偶×偶⇒偶. ② 单调性:设任意D x x ∈21,,且21x x <,则12()()f x f x =⇔无单调性12()()f x f x >⇔减函数1212()()0f x f x x x -⇔<-;12()()f x f x >⇔增函数1212()()0f x f x x x -⇔>-; 在比较)(1x f 与)(2x f 大小时,常用“作差法”,比较12()()f x f x -与0的大小. ⅰ.奇函数的图象在y 轴两侧的单调性一致;偶函数的图象在y 轴两侧的单调性相反. ⅱ.互为反函数的单调性一致.ⅲ.增函数+增函数⇒增函数;减函数+减函数⇒减函数. ⅳ.复合函数单调性由“同增异减”判定. ⅵ.注意函数“单调性”、“奇偶性”的逆用(即如何体现函数的“奇偶性”、“单调性”) 四、幂函数 ①定义:一般地,形如()ay xx R =∈的函数称为幂函数。
上海高一数学第一章集合与命题复习

word第一章集合与命题一.集合:1. 概念及符号的使用.:集合、元素,属于,自然数集,整数集,有理数集,实数集,有限集、无限集;空集,列举法、描述法、子集,包含(包含于),图示法,文氏图,真子集,真包含(真包含于),、交集,并集,全集,补集。
2. ∈⊆,的比较:元素与集合间关系用,∈∉;集合与集合间关系用⊆⊇,类; 3. 交集,并集,补集的比较4. 关于子集的等价关系:U A B A B A A B B AB U ⊆⇔=⇔=⇔=C 5. 集合的运算性质: ① A B =B A ,A B =B A② ()AB C =()A B C , ()A B C =()A B C ③ ()U C A B =U U C A C B , ()U U U C A B C A C B =④AA A =A A A =A ∅=∅A A ∅=6.有限集的元素个数有限集A 的元素的个数记为card( A),规定 card(φ) =0. 基本公式:(1)设有限集合A, card(A)=n,则(ⅰ)A 的子集个数为n2;(ⅱ)A 的真子集个数为12-n;(ⅲ)A 的非空子集个数为12-n;(ⅳ)A 的非空真子集个数为22-n.(2)设有限集合A 、B 、C ,card(B)=m, card(A)=n ,m<n,则(ⅰ) 若A C B ⊆⊆,则C 的个数为mn -2;word(ⅱ) 若A C B ⊂⊆,则C 的个数为12--m n ;⑶容斥原理:card(A ∪B)= card(A)+card(B)- card(A ∩B).二.四种命题形式及关系1. 概念:2.命题,真(假)命题 逆命题,否命题,逆否命题 等价命题2.一般地,四种命题的真假性有且仅有下面四种情况:3.常用词语的否定:三.充要条件1.若α⇒β,则称α是β的充分条件,也即β是α的必要条件; 若α⇔β,则称α是β的充要条件;原命题 若p 则q 否命题若p 则q逆命题 若q 则p逆否命题若q 则p互逆 为 ? ? 互 否 逆 ? 互 逆 为 互 否互 逆 否互 否在讨论p 是q 的什么条件时,就是指以下四种之一: ①若p ⇒q ,但q ≠> p ,则p 是q 的充分但不必要条件; ②若q ⇒p ,但p ≠> q ,则p 是q 的必要但不充分条件; ③若p ⇒q ,且q ⇒p ,则p 是q 的充要条件;④若p ≠> q ,且q ≠> p ,则p 是q 的既不充分也不必要条; ★要点:看清题目问的是:谁是谁的什么条件2.子集与推出关系 : 设A,B 是非空集合,A={}|x x α具有性质,B={}|y y β具有性质,则A ⊆B 与α⇒β等价。
沪教版(上海) 高一第一学期 新高考辅导与训练 第1章 集合和命题 1.5 命题的形式及等价关系(1

沪教版(上海) 高一第一学期新高考辅导与训练第1章集合和命题 1.5 命题的形式及等价关系(1)一、解答题(★) 1. 下列语句是否为命题?如果是,判断它的真假.(1)这道数学题有趣吗?(2)0不可能不是自然数;(3);(4);(5)91不是素数;(6)上海的空气质量越来越好.(★★) 2. 判断下列命题是真命题还是假命题,并说明理由.(1)任何一个集合必有两个子集;(2),,都是自然数,如果是的倍数,那么,中至少有一个是的倍数;(3)如果,BÜ C,那么.(★) 3. 在下列各题中,用符号“ ”把,连起来.(1)实数满足,或;(2),且;(3),;(4)是偶数,是偶数(其中,都是整数).(★★) 4. 已知与均为正有理数,且与均为无理数.证明:也是无理数.(★) 5. 判断下列命题的真假并说明理由.(1)某个整数不是偶数,则这个数不能被4整除;(2)若,且,则,且;(3)合数一定是偶数;(4)若,则;(5)两个三角形两边一对角对应相等,则这两个三角形全等;(6)若实系数一元二次方程满足,那么这个方程有两个不相等的实根;(7)若集合,,满足,则;(8)已知集合,,,如果,那么.(★) 6. 已知下列几个命题的推出关系为:,,,,.现有下列命题:① ;② 且;③ 且;④ 且.试判断哪些命题是正确的.(★) 7. 设是方程的根,求证:不是实数.二、单选题(★) 8. 下列语句中不是命题的是()A.B.是无限循环小数C.D.12是4的倍数(★) 9. 已知下列语句:①对角互补的四边形外接于一个圆;②今天会下雨吗;③你会讲日语吗;④ 是有理数,则,都是有理数;⑤ 或.其中不是命题的是()A.①②B.②③C.②④D.③⑤(★★★) 10. 下面命题中,真命题的个数是()① ,若,则;② ,若,则,都为0;③两个有理数的和是有理数;④ 或,则.A.1B.2C.3D.4(★) 11. 命题与命题,它们的推出关系是()A.B.C.D.以上都不正确(★★) 12. 下列命题是真命题的为()A.若,则B.若,则C.若,则D.若,则三、填空题(★★) 13. 用符号“ ”“ ”“ ”表示下列事件的推出关系:(1),,________ ;(2),,________ ;(3)设抛物线方程为,抛物线的图象与轴有两个交点,,________ ;(4),,________ .(★) 14. 下列命题中,真命题是________.①对角线互相平分的四边形是平行四边形;②对角线相等的四边形是矩形;③对角线互相平分且垂直的四边形是菱形;④对角线互相垂直且相等的四边形是正方形。
2019年沪教版高一第一学期第一章集合与命题单元练习题

2019年沪教版高一第一学期第一章集合与命题单元练习题学校:___________姓名:___________班级:___________考号:___________一、单选题1.若:||2,:p x q x a 剟,且p 是q 的充分不必要条件,则a 的取值范围是( ) A.{|2}a a … B.{|2}a a … C.{|2}a a -…D.{|2}a a -…2.已知集合(){}223A x y xy x Z y Z =+≤∈∈,,,,则A 中元素的个数为A .9B .8C .5D .43.设全集为R ,集合{}02A x x =<<,{}1B x x =≥,则()A B =R ðA.{}01x x <≤B.{}01x x <<C.{}12x x ≤<D.{}02x x <<4.设R x ∈,则“11||22x -<”是“31x <”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分也不必要条件5.已知集合{}1,3,5,7A =,{}2,3,4,5B =,则A B =A .{}3B .{}5C .{}3,5D .{}1,2,3,4,5,76.已知集合{|10}A x x =-≥,{0,1,2}B =,则A B =A .{0}B .{1}C .{1,2}D .{0,1,2}7.设集合{}1,2,4A =,{}240B x x x m =-+=.若{}1A B ⋂=,则B =( ) A .{}1,3-B .{}1,0C .{}1,3D .{}1,58. 设x ∈R ,则“38x >”是“2x >” 的 A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件二、填空题9.用列举法表示集合10|,1M m Z m Z m ⎧⎫=∈∈⎨⎬+⎩⎭=________. 10.已知集合{|34},{|211}A x x B x m x m =-≤≤=-<<+,且B A ⊆,则实数m 的取值范围是______.11.已知集合{}1,3,A m =-,{}3,5B =,若B A ⊆,则实数m 的值为__________. 12.已知集合**{|8}A a a N a N =∈-∈且,则A 的子集有__________个.三、解答题13.(天津市和平区2017-2018学年高二上学期期末考)已知命题P : 22114x y m m +=--表示双曲线,命题q : 22124x ym m+=-- 表示椭圆.(1)若命题P 与命题q 都为真命题,则P 是q 的什么条件?(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个)(2)若P q ∧ 为假命题,且P q ∨ 为真命题,求实数m 的取值范围. 14.若集合{}5|3A x x =-≤≤和{}232|B x m x m =-+≤≤. (1)当3m =-时,求集合AB ;(2)当B A ⊆时,求实数m 的取值集合.参考答案1.A 【解析】 【分析】先化简命题p ,再根据p 是q 的充分不必要条件得到a 的取值范围. 【详解】由题得:22p x -≤≤,:q x a £ 因为p 是q 的充分不必要条件,所以p 对应的集合是q 对应的集合的真子集, 所以2a ≥. 故选:A 【点睛】本题主要考查根据充分不必要条件求参数的范围,意在考查学生对这些知识的理解掌握水平. 2.A 【解析】分析:根据枚举法,确定圆及其内部整点个数. 详解:2223,3,,1,0,1x y x x x +≤∴≤∈∴=-Z ,当1x =-时,1,0,1y =-; 当0x =时,1,0,1y =-; 当1x =-时,1,0,1y =-; 所以共有9个,选A.点睛:本题考查集合与元素关系,点与圆位置关系,考查学生对概念理解与识别. 3.B 【解析】分析:由题意首先求得R C B ,然后进行交集运算即可求得最终结果. 详解:由题意可得:{}|1R C B x x =<,结合交集的定义可得:(){}01R A C B x ⋂=<<. 本题选择B 选项.点睛:本题主要考查交集的运算法则,补集的运算法则等知识,意在考查学生的转化能力和计算求解能力. 4.A 【解析】分析:首先求解绝对值不等式,然后求解三次不等式即可确定两者之间的关系. 详解:绝对值不等式1122x -<⇔111222x -<-<⇔01x <<,由31x <⇔1x <.据此可知1122x -<是31x <的充分而不必要条件. 本题选择A 选项.点睛:本题主要考查绝对值不等式的解法,充分不必要条件的判断等知识,意在考查学生的转化能力和计算求解能力. 5.C 【解析】分析:根据集合{}{}1,3,5,7,2,3,4,5A B ==可直接求解{3,5}AB =.详解:{}{}1,3,5,7,2,3,4,5A B ==,{}3,5A B ∴⋂=,故选C点睛:集合题也是每年高考的必考内容,一般以客观题形式出现,一般解决此类问题时要先将参与运算的集合化为最简形式,如果是“离散型”集合可采用Venn 图法解决,若是“连续型”集合则可借助不等式进行运算. 6.C 【解析】 【分析】由题意先解出集合A,进而得到结果。
上海高一上数学期末备考考点梳理

复习训练题组一、集合与不等式部分1、定义集合运算:{|(),,}A B z z xy x y x A y B ⊗==+∈∈.已知集合{1,2},{2,3}A B ==,则集合A B ⊗的所有元素之和为________.2、“1>x 且1>y ”是“2>+y x ,且1>⋅y x ”的 条件.3、不等式1425≤--x x的解集为4、不等式22x x x x-->的解集为_______ _ 5、不等式组23216210x x x x -⎧≤⎪-⎨⎪-->⎩的解集为6、已知不等式220ax x c ++>的解集为{|13}x x -<<,则a c ⋅= __.7、若关于x 的一元二次不等式()2140x k x +-+≤在实数范围内恒不成立,则实数k的取值范围是__________.8、若x ,a ,b R ∈,下列4个命题:①x x 232>+; ②322355b a b a b a +>+; ③()1222-+≥+b a b a ;④2≥+baa b 。
其中真命题的序号是 .9、已知2x >,则32x x +-的最小值为________ 10、已知01x <<,则(1)x x -的最大值是_______. 11、集合{,,}a b c 的子集有( )个A .4B .6C .7D .812、“不等式013≥-+x x 成立”是“不等式(3)(1)0x x +-≥成立”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件13、“062≠--x x ”是“3≠x ”的()A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件14、已知实数a b 、,且a b >,则下列结论中一定成立的是( )A .22a b > B .1ab < C .22a b > D .11a b< 15、设01a b <<<,且1a b +=,则下列四个数中最大的为( )A .bB .22a b +C .2abD .a二、函数部分一)函数基本概念1、下列各组函数是同一函数的是( ) ①32)(x x f -=与x x x g 2)(-=;②x x f =)(与()2)(x x g =③0)(x x f =与01)(xx g = ④12)(2--=x x x f 与12)(2--=t t t gA .①②B .①③C .③④D .①④2、函数1()2f x x x=-+的定义域是 . 3、若函数)(x f y =的定义域是[]2,2-,则)(x f 的定义域是_____________ 4、函数34)(2++=ax ax x f 的定义域为R ,求实数a 的取值范围____ .5、设函数()f x =121(0)2(0)x x x x ⎧+>⎪⎨≤⎪⎩,则[](2)f f -= ________.6、若函数()123log (6),(0),2,(0),x x x f x x ++≥⎧⎪=⎨⎪<⎩则()()2f f = . 7、已知()2-=x x x f ,()2-=x x g ,则()()=⋅x g x f.8、已知函数()()()()22,02xx f x x g x x x x+=>-=>+,若()()()F x f x g x =⋅,则()F x 的值域是 .9、函数12+--=x x y 的值域是__________10、国家规定个人稿费纳税办法是:不超过800元的不纳税;超过800元而不超过4000元的按超过800元部分14%的纳税;超过4000元的按全部稿酬的11%纳税。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 集合与命题
一.集合:
1. 概念及符号的使用.:集合、元素,属于,自然数集,整数集,有理数集,实数集,
有限集、无限集;空集,列举法、描述法、子集,包含(包含于),图示法,文氏图,真子集,真包含(真包含于),、交集,并集,全集,补集。
2. ∈⊆,的比较 :元素与集合间关系用,∈∉;集合与集合间关系用⊆⊇,类;
4. 关于子集的等价关系:U A B A B A A B B A
B U ⊆⇔=⇔=⇔=
C 5. 集合的运算性质:
① A B =B A ,A B =B A
② ()A
B C =()A B C , ()A B C =()A B C ③ ()U C A
B =U U
C A C B , ()U U U C A B C A C B =
④ A A A = A A A = A ∅=∅ A A ∅=
6.有限集的元素个数 有限集A 的元素的个数记为card( A),规定 card(φ) =0. 基本公式:
(1)设有限集合A, card(A)=n,则
(ⅰ)A 的子集个数为n
2;
(ⅱ)A 的真子集个数为12-n
;
(ⅲ)A 的非空子集个数为12-n ;(ⅳ)A 的非空真子集个数为22-n
.
(2)设有限集合A 、B 、C ,card(B)=m, card(A)=n , m<n,则
(ⅰ) 若A C B ⊆⊆,则C 的个数为m
n -2;
(ⅱ) 若A C B ⊂⊆,则C 的个数为12--m
n ;
⑶ 容斥原理:card(A ∪B)= card(A)+card(B)- card(A ∩B).
二.四种命题形式及关系
1. 概念: 2. 命题,真(假)命题 逆命题,否命题,逆否命题
等价命题 原命题
若p 则q 否命题
若p 则q
逆命题
若q 则p
逆否命题
若q 则p
互逆 为
? 互
否 逆 互 逆 为 互 否
互 逆 否
互 否
2.一般地,四种命题的真假性有且仅有下面四种情况:
原命题 逆命题 否命题 逆否命题 真 真 真 真 真 假 假 真 假 真 真 假 假
假
假
假
3.常用词语的否定:
正面词语 否定 正面词语 否定 等于 不等于
任意的 某个 小于 不小于(大于或等于) 所有的 某些 大于 不大于(小于或等于) 至多有一个 至少有两个 是 不是
至少有一个 一个也没有 都是
不都是(至少有一个不是)
三.充要条件
1.若α⇒β,则称α是β的充分条件,也即β是α的必要条件; 若α⇔β,则称α是β的充要条件;
在讨论p 是q 的什么条件时,就是指以下四种之一:
①若p ⇒q ,但q ≠> p ,则p 是q 的充分但不必要条件; ②若q ⇒p ,但p ≠> q ,则p 是q 的必要但不充分条件; ③若p ⇒q ,且q ⇒p ,则p 是q 的充要条件;
④若p ≠> q ,且q ≠> p ,则p 是q 的既不充分也不必要条; ★要点:看清题目问的是:谁是谁的什么条件
2.子集与推出关系 : 设A,B 是非空集合,
A={}|x x α具有性质, B={}
|y y β具有性质,则A ⊆B 与α⇒β等价。
四.例题
例1 .下列关系式:(1){}a a ⊂;(2)
{}a φ⊂;(3) {}{},a a b ∈;(4) {}{}a a ⊆;(5){},a b φ∈;
(6) {},,a a b c ∈,(7){}0φ∈,⑻ 0∈∅;中正确的是_________________ 例 2 .关于数集: ⑴ Z Z Z +
-=,⑵R C Q Q R =, ⑶N Z *+=, ⑷Z Q ++⊆,
⑸{}()0R C Q
Q +
-=, ⑹ N
Z
Q R ;其中正确的是_________________
例3.对集合.A B ,定义{}
x x A x B A B -=∈∉且,若{}1,3,5,7,9M =,{}3,4,5,6N =, 则集合M N -子集的个数是____.
例4.设集合{}|12A x x =-≤<,
{}a x x B <=|,
① 若φ≠B A ,则a 的取值范围是____ ② 若A B φ=,则a 的取值范围是____
③ 若A
B A =,则a 的取值范围是____
例5.一同学解某不等式组得到≤≥⎧⎪⎨⎪⎩x-1或x>4
x 3或x<-2x>-5
,则该不等式的解集是____
例6.⑴ 写出命题“若 xy= 0 则 x = 0或 y = 0”的逆命题、否命题、逆否命题 ⑵ 对实数2
2
a b a b 0+=.,若,则a=b=0,写出该命题的逆否命题. 例7.若a 2能被2整除,a 是整数,求证:a 也能被2整除 例8.⑴.2a =a是0≥a的( )条件.
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要 ⑵.已知p 是r 的充分不必要条件,q 是r 的充分条件,s 是r 的必要条件,q 是s 的必
要条件,下列命题 ①s 是q 的充要条件. ②p 是q 的充分而不必要条件. ③r 是q 的必要而不充分条件. ④p s 是的必要而不充分条件.⑤r 是s 的必要而不充分条件.中正确的是( ).
例9.设5αβαβ≤≤≤∈:1x<, :2m+1x m+4,m R,是的必要条件,求m 的取值范围. 例10.小故事:
三个古希腊哲学家,由于争论和天气炎热感到疲倦了,于是在花园里的一棵大树下躺下来休息一会,结果都睡着了.这时一个爱开玩笑的人用炭涂黑了他们的前额.三个人醒来以后,彼此看了看,都笑了起来.但这并没引起他们之中任何一个人的担心,因为每个人都以为是其他两人在互相取笑.这时其中有一个突然不笑了,因为他发觉自己的前额也给涂黑了.那么他是怎样觉察到的呢? 练习.
1.已知{}
22|≥∈=x R x M ,π=a ,则下列四个式子 ①M a ∈; ② {}
a M ;③ M a ⊂; ④ {}a π=M ,其中正确的是
(A)①② (B)①④ (C) ②③ (D)①②④ ( )
2.如果集合{
}8,7,6,5,4,3,2,1=U ,{}8,5,2=A ,{}7,5,3,1=B ,那么(A U
)B 等于
(A){}5 (B) {}8,7,6,5,4,3,1 (C) {}8,2 (D) {}7,3,1 ( )
3.如果集合⎭⎬⎫⎩⎨⎧∈+=
=Z k k x x M ,412|,⎭
⎬⎫
⎩⎨⎧∈+==Z k k y y N ,214|,那么 ( ) (A)φ=N M (B)N M = (C)M
N (D) M
N
4.下列命题中假命题...
是 ( ) (A)“正三角形边长与高的比是2︰3”的逆否命题 (B)“若x,y 不全为0,则02
2
≠+y x ”的否命题 (C)“p 或q 是假命题”是“非p 为真命题”的充分条件
(D)若C A B A =,则C B =
5命题: 若{}
(x,y)x y 10, 0x 2B =-+=≤≤<1 则 -1<x<1;的逆否命题是( )
(A)若≥2
x1,则≥≤x1或x-1 (B) 若 -1<x<1 则 2x <1 (C)若x<-1或x>1,则2x >1 (D)若≥≤x1或x-1,则≥2x1
6.若集合{}22|≤≤-∈=x Z x A ,{}
2000|2
+==x y y B ,则用列举法表示集合
=B
7.若集合{
}x A ,3,1=,{}2
,1x B =,且{}x B A ,3,1= ,则=x
8.两个三角形面积相等且两边对应相等,是两个三角形全等的 条件 9.若0)2)(1(=+-y x ,则1=x 或2-=y 的否命题是
10.使方程x -ax+2a+1=02
的两根都大于1的充要条件是
2
1
∆≥≥≥⎧⎪⎨⎪⎩0
x+x12xx12,是否正确?
如不正确,写出你的答案.
11.已知集合{
}
2
(x,y)x mx y 20,x A R =+-+=∈,{}
(x,y)x y 10, 0x 2B =-+=≤≤
若A
B =∅,求实数m的取值范围.
12.一次联欢晚会中,某班选出最聪明的三位同学做智力游戏,游戏是这样的:拿出五顶帽
子(三顶蓝的,两顶红的),三位同学看过后,用布条蒙上他们的眼睛,给他们每人戴上一顶帽子(两顶蓝的,一顶红的),剩下的两顶帽子藏起来,然后解开蒙住眼睛的布条,每个人都能看到别人戴的帽子,但是看不到自己的,然后让他们判断自己戴的帽子的颜色.刚开始,三人都不说话,过了一会,一个同学说出了自己所戴帽子的颜色.很快另两个同学也说出了自己所戴帽子的颜色,他们是怎么判断的呢?。
