why is psl(27) - notes why is psl(27) gl(3 2)
PSL、PSQ电子式执行机构
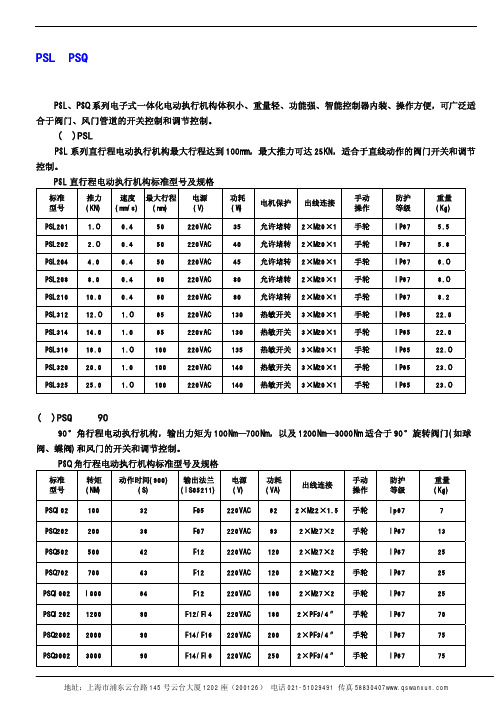
PSL、PSQ 电子式执行机构
一、产品选型
PSL、PSQ 系列电子式一体化电动执行机构体积小、重量轻、功能强、智能控制器内装、操作方便,可广泛适
合于阀门、风门管道的开关控制和调节控制。
(一)PSL 直行程电动执行机构
PSL 系列直行程电动执行机构最大行程达到 100mm,最大推力可达 25KN,适合于直线动作的阀门开关和调节
PSAP4
独立位置变送器
PSMF2NS PSMF2AC
支架
PSMY
说
明
在适当位置输出无源触点信号(220VAC,5A)
在适当转矩要求输出无源触点信号(220VAC,5A)(仅用于PSQ角行程执行器)
输出一组0~lOOOΩ电阻信号(调节动作时接人伺服放大器作为实际阀位值)
执行器调节动作时选用,输入/输出4~20mA
1、PSL 执行程执行机构
PSL 直行程执行机构主要是由相互隔离的电器控制部分和齿轮传动部分组成, 电机作为连接两隔离部分的中间部件。电机按控制要求输出转矩通过多级正齿轮 传递到梯形丝杆上,丝杆通过杆螺纹变换转矩为推力。因此杆螺纹必须自锁并且 将直线行程通过与阀门的适配器传递到阀杆。执行机构出轴带有—个防止转动的 止转销,出轴的径向锁定装置也可以做动位置指示器。锁定装置连有一个连杆, 连杆随输出轴同步运行,通过与连杆连接的开关板将输出轴位移转换成电信号提 供给智能控制器作为比较信号和阀位反馈输出,同时执行机构的行程也可由开关 板上的两个主限位开关来限制,并由两机械限位保护。
7
8.2
PSL312 12.O
1.O
65
220VAC
130 热敏开关 3×M20×1 手轮
IP65
22.0
《商务英语阅读I》-课程教学大纲

《商务英语阅读I》课程教学大纲一、课程基本信息课程代码:16133102课程名称:商务英语阅读I英文名称:Reading of Business English Literature I课程类别:专业方向课学时:32学分:2适用对象: 商务英语专业、英语专业(国际商务管理)、非英语专业考核方式:分散考试(笔试)先修课程:综合英语/大学英语二、课程简介本课程是外国语学院商务英语以及英语(国际商务与管理方向)本科学生的专业方向必修课,同时也作为向全校非英语专业学生开设的选修课。
本课程旨在帮助学生了解管理、财务、国际商务、营销等基本理论和常用术语,并同时提高学生的英语综合水平,特别是阅读商务材料的能力。
由于教学对象大多为今后的涉外人才,在本课程中融入社会主义思想政治教育尤其重要。
思政内容将特别体现在中外经济制度和商务实践的比较研读部分,教学过程中将着重介绍中国特色社会主义的经济制度和商务实践与西方完全市场经济和自由竞争条件下商务实践的重大区别。
通过案例探讨来说明共同富裕、协调发展优先于个别企业的利益导向原则,以彰显在党中央宏观调控下的社会主义特色市场经济对中国特殊国情的专适性和优越性。
This course is offered to Business English majors (with an International Business and Management orientation) as a compulsory course. It is also designed as an elective course for all students from specializations other than English. The course is intended to introduce the fundamental knowledge and nomenclature in management, finance, international business, marketing, etc.三、课程性质与教学目的通过对指定教材和教师所选材料的阅读、分析、探讨和讲介,在课程结束时,学生应熟练掌握常用的商务英语词汇和表达法,具备较强的商务英语阅读理解能力。
PSL-646U线路保护测控装置(多合一)技术说明书_V3.00_印刷

目录
版本声明 1. 概述 ............................................................................................................................................................ 1
国电南自 DL/T 1075-2007
PSL-646U 线路保护测控装置(多合一)
技术说明书
国电南京自动化股份有限公司 GUODIAN NANJING AUTOMATION CO.,LTD
PSL-646U 线路保护测控装置
技术说明书 (多合一)
V 3.00 国电南京自动化股份有限公司
2015 年 3 月
版本声明
z 本说明书适用于 PSL-646U 线路保护测控装置(多合一)。保护的设计标准引用了国网公司 Q/GDW 766 -2014《10kV~110(66)kV 线路保护及辅助装置标准化设计规范》。
z 本说明书适用于 PSL-646U 线路保护测控装置(多合一)V3.00 及以上版本的保护软件。
1.1. 保护功能配置 ...................................................................................................................................... 1 1.2. 测控功能配置 ..............................................
110kV变电站由内桥接线改为线变组接线的保护整定方案分析_邱志强

为主变的后备保护,考虑 适 当 分 别 伸 入 朝 星 站 #1、#2 主 变,并
与 朝 星 站 #1、#2 主 变 的 小 差 及 后 备 保 护 配 合 。
1)距离 Ⅰ 段、零 序 Ⅰ 段:定 值 按 保 护 线 路 全 长 并 伸 入 主 变
70%整定,Zd=XL+Zb×0.7,时间整定为 0s,以保证瞬 时 切 除 线路及主变高压侧故障。
[参 考 文 献] [1] 叶 顺 .浅 谈 铁 路 电 力 远 动 技 术[J].铁 道 建 筑 技 术 ,2011(5) [2] 郭 丽 .浅 谈 铁 路 电 力 远 动 控 制 技 术 [J].黑 龙 江 科 技 信 息 ,2012
(15)
收 稿 日 期 :2014-06-20 作 者 简 介 :王 亚 光 (1984—),男 ,河 北 沧 州 人 ,助 理 工 程 师 ,研
2)距 离 Ⅱ 段:定 值 按 保 主 变 变 低 有 足 够 灵 敏 度,伸 出 主 变
120%整定 ,Zd=XL+Zb×1.2,时间整定为 0.6s。 3)零序Ⅱ段:定值按不大 于 300 A 电 流 整 定,时 间 整 定 为
0.6s。
4)距 离 Ⅲ 段:定 值 按 躲 最 大 负 荷 电 流 整 定,若 计 算 值 小 于
究 方 向 :电 气 工 程 及 其 自 动 化ቤተ መጻሕፍቲ ባይዱ。
(上 接 第31页) (5)榭平岭站 110kV 线 路 间 隔:因 朝 星 站 #1、#2 变 变 高 侧中性点改为直 接 接 地,为 防 止 零 序 Ⅰ 段 保 护 范 围 超 越 ,造 成 保护误动,退出榭平岭站所有110kV 线路零序Ⅰ段保护。
0 引 言 在变电站一次设 备 改 造 的 施 工 过 程 中 ,由 于 工 期 较 长,经
PSL-603U调试手册(智能站)国网版本V1.0

PSL-603U 智能站调试手册
版本说明
装置软件版本 PSL-603UA-DA-G-RPLDYK V3.00 2014-04-23 04BF PSL-603UA-FA-G-RPLDYK V3.00 2014-04-23 04BF PSL-603UA-G-RPLDY V3.00 2014-04-23 1BE0 注 1:-G 表示国网常规装置,常规采样、常规跳闸 注 2:-DA-G:国网智能化装置,SV 采样,GOOSE 跳闸。 注:3:-DG-G:国网智能化装置,常规采样,GOOSE 跳闸。 注 4:-FA-G:国网智能化前接线装置,SV 采样,GOOSE 跳闸。 注:5:R:零序反时限过流保护。P:三相不一致保护。L:过流过负荷功能。D:电铁、钢厂等冲击性负荷。Y:过电压及远方跳 闸保护。K:3/2 断路器接线(仅适用于智能站。不选时,为双母线接线;选择时,为 3/2 断路器接线)。 注 6:V3.XX:基础软件版本。201X-XX-XX:基础软件生成日期。04BF、1BE0:程序校验码。 备注 PSL-603U:适用(220kV 及以上系统)双母接线及 3/2 接线的智能站保护装置。 RPLDYK:六种选配功能码,可任意组合使用。P、K 两种 选配功能,不得同时选用。 PSL-603U:适用(220kV 及以上系统)双母接线及 3/2 接线的传统站保护装置。 RPLDY:五种选配功能码,可任意组合使用。
工具软件名称 SGVIEW UpdateTool VSCL61850 PS61850 CONNER SACWaveAnalysis
版本 V3.60 V1.28 V4.10 V4.10 V2.60 使用低版本工具!!
备注 表中为新六统一保护配套工具最低匹配版本,工程应用中严禁
最新-奥林匹克格言中英语版 精品

奥林匹克格言中英语版1. lypi is pp iilly i 1920 p gs奥林匹克格言在1920年安特卫普奥运会上正式出现。
2. lypi s b ispiig lypis si is iui 1920 gs自1920年奥运会奥林匹克格言被使用以来,它就一直激励着现代奥运健儿。
3. lypi suppss pgss u piy bsis l pysil ipv ' s ul quliis奥林匹克格言认为应以提高人类精神和身体自然品质为基础来使人类的能力进步。
4. lypi spu ls b lypi spii p bs i bliis奥林匹克格言和信条激励着运动员实践奥林匹克精神,并且在比赛中表现出他们最好的一面。
5. lypi spu ls b lypi spii p bs i biliis奥林匹克格言和信条激励着运动员实践奥林匹克精神,并且在比赛中表现出他们最好的一面。
6. suk by suiss is ps , b pi ubi i lypi , piig u " ls " xss "奥林匹克格言,亦称奥林匹克座右铭或口号,系奥林匹克运动宗旨之一。
奥林匹克格言是: "更快更高更强" 。
7. ss lypi is big is is ssily piiy , bu givig ' s bs sivig psl xll is il gl奥林匹克格言的意义在于,夺取第一并不是要优先考虑的事,但全力以赴并为取得个人最好成绩而奋力拼搏却是值得追求的目标。
8. ig lypi , lypi xpsss ssg i i sss ll blg lypi v , iviig xl i i lypi spii。
PSL603U系列线路保护技术说明书_1.30(传统版本)
国电南自 GB/T 15145-2008
说明书
国电南京自动化股份有限公司
GUODIAN NANJING AUTOMATION CO.,LTD
ห้องสมุดไป่ตู้
PSL 603U 系列 线路保护装置 说明书
编写 审核 批准
V:1.30
国电南京自动化股份有限公司 2010 年 3 月
安全声明
为保证安全、正确、高效地使用装置,请务必阅读以下重要信息: 1.装置的安装调试应由专业人员进行; 2.装置上电使用前请仔细阅读说明书。应遵照国家和电力行业相关规程,并参照说明书对装置进行操 作、调整和测试。如有随机材料,相关部分以资料为准; 3.装置上电前,应明确连线与正确示图相一致; 4.装置应该可靠接地; 5.装置施加的额定操作电压应该与铭牌上标记的一致; 6.严禁无防护措施触摸电子器件,严禁带电插拔模件; 7.接触装置端子,要防止电触击; 8.如要拆装装置,必须保证断开所有地外部端子连接,或者切除所有输入激励量。否则,触及装置内 部的带电部分,将可能造成人身伤害; 9.对装置进行测试时,应使用可靠的测试仪; 10.装置的运行参数和保护定值同样重要,应准确设定才能保证装置功能的正常运行; 11.改变当前保护定值组将不可避免地要改变装置的运行状况,在改变前应谨慎,并按规程作校验; 12.装置操作密码为:99。
2 技术性能及指标 ................................................................................................................................................. 1 2.1 额定电气参数 ............................................................................................................................................ 1 2.2 主要技术性能及指标 ................................................................................................................................ 1 2.3 绝缘和耐湿热性能 .................................................................................................................................... 2 2.4 电磁兼容性能 ............................................................................................................................................ 3 2.5 机械性能 .................................................................................................................................................... 3 2.6 环境大气条件 ............................................................................................................................................ 3
发现问题的原因英语作文
发现问题的原因英语作文Title: Identifying the Causes of Problems。
In the process of problem-solving, identifying the root cause is crucial for effective resolution. Understanding the underlying factors contributing to a problem not only helps in addressing the immediate issue but also prevents its recurrence. This essay aims to explore various methods and approaches to uncover the reasons behind problems.Firstly, one of the primary techniques in discovering the cause of a problem is root cause analysis (RCA). RCA is a systematic process that involves investigating and analyzing the deeper layers of an issue to determine the underlying cause or causes. It often employs techniques such as the "5 Whys," where one repeatedly asks "why" until the fundamental cause is identified. Through this method, teams can delve beyond surface-level symptoms to uncover the true origins of the problem.Another valuable approach is to utilize data analysis and metrics. Data can provide valuable insights into patterns, trends, and anomalies that may indicate thesource of a problem. By collecting and analyzing relevant data, such as performance metrics, customer feedback, or process logs, organizations can pinpoint areas of concern and identify potential causes. Moreover, data-driven approaches enable organizations to make informed decisions and prioritize areas for improvement based on empirical evidence.Furthermore, conducting thorough investigations and audits can help uncover hidden causes of problems. This may involve reviewing documentation, interviewing stakeholders, or conducting site visits to observe processes firsthand.By engaging with relevant parties and gathering information from multiple sources, investigators can gain a comprehensive understanding of the problem's context and identify contributing factors that may have been overlooked.Additionally, adopting a proactive approach to problem identification can prevent issues from escalating.Implementing preventive measures, such as regular inspections, quality control procedures, or risk assessments, can help identify potential problems before they occur. By anticipating and addressing risks in advance, organizations can mitigate the likelihood of problemsarising and minimize their impact on operations.Moreover, fostering a culture of open communication and continuous improvement is essential for identifying problems early on. Encouraging employees to report issues, share feedback, and participate in problem-solvinginitiatives creates a collaborative environment where problems are addressed swiftly and effectively. Additionally, providing training and resources to enhance employees' problem-solving skills empowers them to identify and resolve issues at their source.In conclusion, identifying the causes of problems requires a multifaceted approach that combines analytical techniques, data analysis, investigative methods, and proactive measures. By employing these strategies, organizations can uncover the root causes of problems,implement targeted solutions, and prevent recurrence. Ultimately, fostering a culture of problem-solving and continuous improvement is essential for building resilience and achieving long-term success.。
PSL601(602)系列保护装置运行说明
PSL601/602系列保护装置运行说明一、装置功能概述1、保护功能整体描述:PSL601 /602(A、C、D)数字式超高压线路保护装置以纵联距离和纵联零序作为全线速动主保护,以距离保护和零序方向电流保护作为后备保护。
保护有分相出口,可用作220kV及以上电压等级的输电线路的主保护和后备保护。
保护功能由数字式中央处理器CPU模件完成,其中CPU1模件完成纵联保护功能,CPU2模件完成距离保护和零序电流保护功能。
对于单断路器接线的线路,保护装置中还增加了实现重合闸功能的CPU3模件,可根据需要实现单相重合闸、三相重合闸、综合重合闸或者退出。
2、保护装置CPU分工描述:CPU1模件完成纵联保护功能,CPU2模件完成距离保护和零序电流保护功能。
CPU3模件实现重合闸功能。
3、其它功能描述:PSL 601 /602(A、C、D)数字式超高压线路保护装置还具有完善的自动重合闸功能,可以实现单重检线路三相有压重合闸方式,专用于大电厂侧,以防止线路发生永久故障,电厂侧重合于故障对电厂机组造成冲击。
强大的故障录波功能,可以保存1000次事件,12至48次故障录波报告(含内部元件动作过程),故障时有重要开关量多次变化时会自动多次启动录波并且记录重要开关量(如发信、收信、跳闸、合闸、TWJ等)的变化。
录波数据可以保存为COMTRADE格式。
4、保护主要参数:二、装置背板结构图简介图4.1.2.2是装置的背面面板布置图。
插件注释:组成装置的模件有:交流模件(AC)、AD模件(AD)、保护模件(CPU1、CPU2、CPU3),COM模件(COM)、电源模件(POWER)、跳闸出口模件(TRIP1、TRIP2)、信号模件(SIGNAL)、重合闸出口模件(TRIP3)、人机对话模件(MMI)。
三、装置面板说明操作密码:99 内部定值设置密码:3138图4.1.2.1是装置的正面面板布置图。
国电南京自动化股份有限公司图4.1.2.1 面板布置图液晶显示器(LCD):用以显示正常运行状态、跳闸报告、自检信息以及菜单。
psl硕士网申流程
psl硕士网申流程PSL (Paris Seine Graduate School) offers a wide range of master's programs for international students. PSL is known for its strong academic reputation and diverse student body. PSL的硕士网申流程包括几个步骤,面向国际学生开放。
PSL以其良好的学术声誉和多元化的学生群体而闻名。
The application process for PSL master's programs typically begins with researching the available programs and their respective requirements. You will need to carefully review the program descriptions, admission criteria, and application deadlines. PSL硕士项目的申请流程通常始于研究可用程序及其各自的要求。
您需要仔细阅读项目描述、录取标准和申请截止日期。
Once you have identified the programs that align with your academic and professional goals, the next step is preparing your application materials. This typically includes gathering official transcripts, preparing your CV or resume, writing a Statement of Purpose, and securing letters of recommendation. 一旦确定了与您的学术和职业目标一致的项目,下一步是准备申请材料。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NOTESEdited by Ed ScheinermanWhy is PSL(2,7)∼=GL(3,2)?Ezra Brown and Nicholas Loehr1.INTRODUCTION.The groups of invertible matrices overfinitefields are among thefirst groups we meet in a beginning course in modern algebra.Eventually,we find out about simple groups and that the unique simple group of order168has two representations as a group of matrices.And this is where we learn that the group of 2×2unimodular matrices over a seven-elementfield,with I and−I identified,is isomorphic to the group of invertible3×3matrices over a2-elementfield.In short,it is a fact that PSL(2,7)∼=GL(3,2).Many of us are surprised by this fact:why should a group of2×2matrices with mod-7integer entries be isomorphic to a group of3×3binary matrices?There are a number of proofs of this remarkable theorem.Dickson[1,p.303]gives a proof based on his general theorem giving uniform sets of generators and relations for the family of groups SL(2,q),where q is any prime power.One checks that the relations appearing in Dickson’s presentation of PSL(2,7)are satisfied by certain gen-erators of GL(3,2),implying that these groups have the same presentations and are therefore isomorphic.Dummit and Foote[2,p.207–212]show that every simple group of order168is necessarily isomorphic to the automorphism group Aut(F)of the Fano plane F.They then show that Aut(F)∼=GL(3,2)and that PSL(2,7)is a simple group of order168;the isomorphism theorem follows.Rotman gives the result as an exer-cise[5,Exercise9.26,p.281].A hint is to begin with a simple group G of order168 and use the seven conjugates of a Sylow2-subgroup P of G to construct a seven-point projective plane;the proof is similar to Dummit and Foote’s proof.Jeurissen[4] proves the result by showing that both PSL(2,7)and GL(3,2)are subgroups of index 2of the automorphism group of a Coxeter graph.Elkies[3]gives a clever proof that uses the automorphism group G of the3-(8,4,1)Steiner system—also known as the Steiner S(3,4,8)design.He shows that PSL(2,7)is contained in G,which in turn maps homomorphically onto GL(3,2).The result follows from the simplicity of the two groups and the fact that they are both of order168.We remark that there do exist non-isomorphic simple groups of the same order.For example,Schottenfels showed that PSL(3,4)and A8are non-isomorphic simple groups of order20,160[5,Theorem 8.24,p.233].The aim of this paper is to give a proof that PSL(2,7)∼=GL(3,2)that is elementary in the sense that it uses neither simplicity,nor projective geometry,nor block designs. We will not prove the fact that any two simple groups of order168are isomorphic, nor will we use this fact in our proof.What makes our proof work is that:(a)we can identify GL(3,2)with the set of invertible F2-linear transformations on thefinitefield with eight elements;(b)7=23−1;(c)the nonzero squares mod7are precisely the powers of2mod7;(d)squaring mod2is additive(the Freshman’s Dream);and(e) the mapping k→−1/k mod7translates to a bit-switch mod2—which is linear. We begin by giving functional descriptions for both groups,determining their sizes, doi:10.4169/193009709X460859and exhibiting sets of generators for them.After this we define a mapping between the groups and prove that the mapping is a bijective group homomorphism.Let’s begin with GL(3,2).2.THE GROUP GL(3,2).Let F2={0,1}be thefield with two elements.The group GL(3,2)consists of all invertible3×3matrices with entries in F2.To construct our isomorphism,we need three basic facts about this group.1.Functional Description of the Group.Let F8=F2[X]/ X3+X+1 ,andlet x=X+ X3+X+1 ∈F8.On one hand,F8is an eight-elementfield whose multiplicative group is generated by x.On the other hand,F8is a three-dimensional vector space over F2with ordered basis B=(x0,x1,x2).Let GL(F8)be the set of all invertible F2-linear transformations of this vector space.This means that GL(F8)consists of all bijections L:F8→F8such that L(u+v)=L(u)+L(v)for all u,v∈F8.We note that L(cu)=cL(u)holds automatically,since the only available scalars c are0and1.Let[L]B denote the matrix of L relative to the ordered basis B.Then the map L→[L]B defines an isomorphism between GL(F8)and GL(3,2).From now on,we identify these two groups by means of this isomorphism.2.The Size of GL(3,2).The following counting argument proves that|GL(3,2)|=168.Let us build an invertible3×3matrix of0s and1s one row at a time.The first row can be any nonzero bit string of length3;there are seven such bit strings.The second row can be any nonzero bit string different from thefirst row;there are six such bit strings.When choosing the third row,we must pick a bit string that is not a linear combination of thefirst two rows.There are four such linear combinations(zero,thefirst row,the second row,or the sum of thefirst two rows),so there are8−4=4choices for the third row.By the product rule,|GL(3,2)|=7·6·4=168.3.Generators for GL(3,2).It will be useful to have a small set of generators forGL(3,2).Starting with any matrix A∈GL(3,2),we can use elementary row operations(Gaussian elimination)to reduce A to the identity matrix.Each ele-mentary operation can be accomplished by multiplying on the left by one of the following nine elementary matrices:E12=⎛⎝110010001⎞⎠,E13=⎛⎝101010001⎞⎠,E23=⎛⎝100011001⎞⎠,E21=⎛⎝100110001⎞⎠,E31=⎛⎝100010101⎞⎠,E32=⎛⎝100010011⎞⎠,S12=⎛⎝010100001⎞⎠,S23=⎛⎝100001010⎞⎠,S13=⎛⎝001010100⎞⎠.For example,multiplying A on the left by E12adds the the second row of A to thefirst row,whereas multiplying A on the left by S13interchanges thefirst and third rows of A.Thus,the row-reduction of A to the identity matrix via elemen-tary row operations translates to a matrix equation of the form E1···E k A=I,where each E i is an elementary matrix.Solving for A and noting that each ele-mentary matrix equals its own inverse,we see that GL (3,2)is generated by the nine elementary matrices listed above.In fact,many of these matrices are redun-dant,and the set {E 23,S 12,S 23}already generates the whole group.This remark follows from the formulasS 13=S 12S 23S 12,E 13=S 12E 23S 12,E 32=S 23E 23S 23,E 21=S 13E 23S 13,E 12=S 13E 32S 13,E 31=S 12E 32S 12.Now consider the three matrices A 1=⎛⎝100001010⎞⎠,A 2=⎛⎝001101010⎞⎠,A 3=⎛⎝100001011⎞⎠.We have E 23=A 1A 3,S 12=A 22A 1A 32A 3,S 23=A 1,and so GL (3,2)= A 1,A 2,A 3 .And now,on to a description of PSL (2,7).3.THE GROUP PSL(2,7).Let F 7={0,1,2,3,4,5,6}be the field with seven ele-ments.The group SL (2,7)consists of all 2×2matrices with entries in F 7and deter-minant 1.The group PSL (2,7)is the quotient group SL (2,7)/{I ,−I }.To construct our isomorphism,we need three basic facts about this group.1.Functional Description of the Group.LetF 7=F 7∪{∞}={0,1,2,3,4,5,6,∞}.As in complex analysis,we define a linear fractional transformation on F 7to be a function f :F 7→F 7of the formf (k )=ak +bck +d (k ∈F 7),(1)where a ,b ,c ,d ∈F 7are constants such that ad −bc =0.(The same defini-tion works for any field F .)In the formula for f (k ),division by ck +d means multiplication by the inverse of ck +d in the field F 7;any nonzero element divided by 0is ∞;and anything (other than ∞)divided by ∞is 0.We have f (∞)=a /c when c =0,and f (∞)=∞when c =0.The transformation f is called special if a ,b ,c ,d can be chosen so that ad −bc =1.There is a natural map φfrom SL (2,7)to the set SLF (7)of special linear fractional transforma-tions on F 7,which sends the matrix a b c dto the function f given in (1).A routine calculation shows that φ(A )◦φ(B )=φ(AB )(which says composing linear fractional transformations is done by matrix multiplication),so that φis a group homomorphism.Furthermore,one sees that φ(A )=φ(B )iff B =A or B =−A .It follows that ker (φ)={I ,−I },so that φinduces a group isomor-phism from PSL (2,7)onto SLF (7).Henceforth,we identify these two groups by means of this isomorphism.2.The Size of PSL (2,7).The following counting argument proves that |SL (2,7)|=336.Let us build a matrix a b c dwith entries in F 7such that ad −bc =1.There are two cases:c=0or c=0.In the case where c=0,choose a to be anynonzero element(6possibilities);then choose d=a−1to force the determinantto be1(one possibility);then choose b to be anything(7possibilities).Thisgives42upper-triangular matrices in SL(2,7).In the case where c=0,choosec(6possibilities);then choose a and d arbitrarily(7possibilities each);then we must choose b=c−1(ad−1)to get the right determinant.This gives6·7·7= 294more matrices,for a total of336.Taking the quotient by the two-elementsubgroup{I,−I}cuts the number of group elements in half,so|PSL(2,7)|=336/2=168.3.Generators for PSL(2,7).We can use the functional description of PSL(2,7)tofind a convenient set of generators for this group.We define three special linearfractional transformations r,t,δby setting•r(k)=−1/k(the“reflection map”);•t(k)=k+1(the“translation map”);and•δ(k)=2k(the“doubling map”).We will prove that SLF(7)= r,t,δ .Consider a special linear fractional trans-formation f(k)=(ak+b)/(ck+d).If c=0,we must have ad=1and d= a−1,so f(k)=a2k+ab.The nonzero squares mod7are1,2,4,so f=t ab◦δj for a suitable j∈{0,1,2}.For example,given f(k)=(3k+6)/5,we have f(k)=2k+4=t(t(t(t(δ(k))))).Next,consider f(k)=(ak+b)/(ck+d) where c=0.Division givesf(k)=(ac−1)+bc−adc(ck+d)=(ac−1)+−1c2k+cd.Writing c2=2j,it is now evident that f=t ac−1◦r◦t cd◦δj.Hence,SLF(7)is generated by r,t,andδ.4.THE ISOMORPHISM PSL(2,7)∼=GL(3,2).We now have all the ingredients needed to define the promised group isomorphism between PSL(2,7)and GL(3,2). Using the functional descriptions of these groups,it will suffice to define an isomor-phism T:SLF(7)→GL(F8).We proceed in four stages.1.Definition of T.For each function f∈SLF(7),we need to define an associatedfunction T(f)=T f∈GL(F8).How can we use the function f,whose domain is F7,to build a function T f,whose domain is F8?To relate these two domains, we define x∞=0and then observe that F8={x k:k∈F7}.This observation suggests the map x k→x f(k)as a possibility for T f.However,this map is not always linear,since zero maps to zero only if f(∞)=∞.To account for this difficulty,we instead defineT f(x k)=x f(k)+x f(∞)(k∈F7).(2) With this definition,T f(0)=0always holds,though it is not yet evident that T f must belong to GL(F8).Let us illustrate the formula by computing T(r),T(t),and T(δ).This com-putation will reveal that each of these three functions does indeed lie in GL(F8).The function r(k)=−1/k is given in two-line form as follows:r=0123456∞∞6325410.Since x 3+x +1=0in F 8,we havex 3=x +1,x 4=x 2+x ,x 5=x 2+x +1,x 6=x 2+1.Let us represent an element b 2x 2+b 1x 1+b 0x 0in F 8by the bit string b 2b 1b 0.In this notation,x 0=001,x 1=010,x 2=100,x 3=011,x 4=110,x 5=111,x 6=101,x ∞=000.Putting all this information into (2),we conclude thatT (r )= 001010100011110111101000001100010101110111011000.Note that T r just interchanges the first two bits.Thus,T r is the invertible linear map on F 8that interchanges the basis vectors x 1and x 2,and so the matrix of T r relative to the ordered basis B =(x 0,x 1,x 2)is[T (r )]B =⎛⎝100001010⎞⎠=A 1.It is even easier to compute T (t )and T (δ).We have T t (0)=0and,for k =∞,T t (x k )=x t (k )+x t (∞)=x k +1=x (x k ).Thus,T t is simply left-multiplication by x in the field F 8.This map is linear by the distributive law in F 8,and it is invertible since the inverse map is left-multiplication by x −1=x 6.The matrix of T t is[T (t )]B =⎛⎝001101010⎞⎠=A 2.Finally,T δ(0)=0and,for k =∞,T δ(x k )=x 2k =(x k )2.So T δis the squaring map in F 8.This map is linear (and even a ring homomorphism)since (u +v)2=u 2+2u v +v 2=u 2+v 2for u ,v ∈F 8.The map is one-to-one (hence onto)since the kernel is zero.The matrix of T δis[T (δ)]B =⎛⎝100001011⎞⎠=A 3.2.The key lemma.Suppose f ,g ∈SLF (7)are two functions such that T (f )and T (g )lie in GL (F 8).Then T (f ◦g )=T (f )◦T (g ),and hence T (f ◦g )also lies in GL (F 8).Proof:For any k ∈F 7,we computeT f ◦T g (x k )=T f (T g (x k ))=T f (x g (k )+x g (∞))=T f(x g(k))+T f(x g(∞))(since T f is linear)=(x f(g(k))+x f(∞))+(x f(g(∞))+x f(∞))=x f(g(k))+x f(g(∞))(since u+u=0for all u∈F8)=T f◦g(x k).3.Proof that T is a homomorphism mapping into GL(F8).We have seen that eachelement of SLF(7)can be written as a product of the generators r,t,andδ(using only positive powers,in fact).Since T(r),T(t),and T(δ)are known to lie in GL(F8),repeated application of the lemma shows that T(h)lies in GL(F8) for all h∈SLF(7).Having drawn this conclusion,the lemma now shows that T is a group homomorphism.4.Proof that T is a bijection.So far,we know that T is a group homomorphismmapping SLF(7)into GL(F8).T is actually onto,since the image of T contains T(r),T(t),T(δ) ,which is the whole group GL(F8).Since SLF(7)and GL(F8) both have168elements,T must also be one-to-one.Our proof that PSL(2,7)∼=GL(3,2)is now complete.We leave it as a challenge for the reader tofind an explicit description of the inverse bijection T−1:GL(F8)→SLF(7).REFERENCES1.L.E.Dickson,Linear Groups,B.G.Teubner,Leipzig,1901.2. D.S.Dummit and R.M.Foote,Abstract Algebra,3rd ed.,John Wiley,Hoboken,NJ,2004.3.N.Elkies,Handout for Math155(1998),available at /~elkies/M155.98/h4.ps.4.R.H.Jeurissen,A proof by graphs that PSL(2,7)∼=GL(3,2),Discrete Math.70(1988)315–317.doi:10.1016/0012-365X(88)90008-85.J.J.Rotman,An Introduction to the Theory of Groups,4th ed.,Springer-Verlag,New York,1995.Department of Mathematics,Virginia Tech,Blacksburg,VA24061-0123brown@nloehr@Angles as ProbabilitiesDavid V.Feldman and Daniel A.KlainAlmost everyone knows that the inner angles of a triangle sum to180◦.But if you ask the typical mathematician how to sum the solid inner angles over the vertices of a tetrahedron,you are likely to receive a blank stare or a mystified shrug.In some cases you may be directed to the Gram-Euler relations for higher-dimensional polytopes[4, 5,7,8],a19th-century result unjustly consigned to relative obscurity.But the answer is really much simpler than that,and here it is:The sum of the solid inner vertex angles of a tetrahedron T,divided by2π, gives the probability that the orthogonal projection of T onto a random2-plane is a triangle.doi:10.4169/193009709X460868。
