哈工大小波实验报告
小波实验1
哈尔滨工业大学小波理论及应用上机报告院（系）电气工程及自动化学院学科仪器仪表工程姓名陈鹏宇学号15S101121上机实验内容Butterworth滤波器实验一：滤波器一、实验内容Butterworth 滤波器冲击响应函数为：,0()0,0t Ae t h t t α-⎧≥=⎨<⎩若若 ⑴ 求()ˆhω； ⑵ 判断是否因果；是低通、高通、带通还是带阻？⑶ 对于信号3()(sin 22sin 40.4sin 2sin 40)t f t e t t t t -=++，0t π≤≤，画出()f t 图形；⑷ 画出滤波后图形()f h t *，比较滤波前后图形，你会发现什么，这里取10A α==⑸ 取()(sin5sin3sin sin 40),t f t e t t t t -=+++采用不同的变量值A α=()10A α==初始设定，画出原信号图形与滤波后图形，比较滤波效果 二、实验过程（1） 由连续傅里叶变换公式可求得()ˆhω： ()()0ˆi t t i t A h h t e dt Ae e dt i ωαωωαω+∞+∞----∞===+⎰⎰ (1) （2） 由冲击响应函数 h(t)可知，t<0时h(t)=0;可以得出滤波器为因果滤波器；由()ˆhω可知该信号的幅频特性为： ()H ω= (2) 当α1A ==时，其幅频特性曲线如图1所示，因此为低通滤波器。
图1 滤波器幅频特性（3）()f t，(b)为幅频特性f t的图形如图二所示，(a)为()图2 时域和频域图形（4）画出*()f h t的结果如图2所示，A= α = 10：图3 f*h(t)卷积结果其中图3（a）、（b）分别为原始信号f(t)的时域和频域，（c）、（d）为h t(A =α = 10)卷积后的信号的时域和频域图。
可以看出信号中高频分量被抑制，信号的信噪比明显改善了。
（5）实验中A和的取值，通过实验得到的结果分别如下：1)A= α = 102)A= α = 20，滤波时域和频域图形3)A= α= 100，滤波时域和频域图形4)A= α= 5，滤波时域和频域图形5)A= α= 1，滤波时域和频域图形图8 A= α= 1，滤波时域和频域图形通过对比各种参数滤波器的滤波效果，可以发现A值的大小会影响信号的幅值，A值越大滤波器对信号的放大作用越大，但噪声也被放大，而则影响滤波器的截止频率，越小h(t)的截止频率越小，对高频信号的滤除效果越好。
小波实验报告一维Haar小波2次分解
一、题目：一维Haar 小波2次分解二、目的：编程实现信号的分解与重构三、算法及其实现：离散小波变换离散小波变换是对信号的时－频局部化分析，其定义为：/2200()(,)()(),()()j j Wf j k a f t a t k dt f t L R φ+∞---∞=-∈⎰ 本实验实现对信号的分解与重构：（１）信号分解：用小波工具箱中的dwt 函数来实现离散小波变换，函数dwt 将信号分解为两部分，分别称为逼近系数和细节系数（也称为低频系数和高频系数）,实验中分别记为cA1,cD1，它们的长度均为原始信号的一半，但dwt 只能实现原始信号的单级分解。
在本实验中使用小波函数db1来实现单尺度小波分解，即：[cA1,cD1]＝dwt(s,’db1’)，其中s 是原信号;再通过[cA2,cD2]＝dwt(cA1,’db1’)进行第二次分解，长度又为cA2的一半。
（２）信号重构：用小波工具箱中的upcoef 来实现，upcoef 是进行一维小波分解系数的直接重构,即：A1 = upcoef('a',cA1,'db1'); D1 = upcoef('a',cD1,'db1')。
四、实现工具：Matlab五、程序代码：%装载leleccum 信号load leleccum;s = leleccum(1:3920);%用小波函数db1对信号进行单尺度小波分解[cA1,cD1]=dwt(s,'db1');subplot(3,2,1);plot(s);title('leleccum 原始信号');%单尺度低频系数cA1向上一步的重构信号A1 = upcoef('a',cA1,'db1');%单尺度高频系数cD1向上一步的重构信号D1 = upcoef('a',cD1,'db1');subplot(3,2,3);plot(A1);title('单尺度低频系数cA1向上一步的重构信号');subplot(3,2,5);plot(D1);title('单尺度高频系数cD1向上一步的重构信号');[cA1,cD1]=dwt(cA1,’db1');subplot(3,2,2);plot(s);title('leleccum 第一次分解后的cA1信号');%第二次分解单尺度低频系数cA2向上一步的重构信号A2= upcoef('a',cA2,'db1',2);%第二次分解单尺度高频系数cD2向上一步的重构信号D2 = upcoef('a',cD2,'db1',2);subplot(3,2,4);plot(A2);title('第二次分解单尺度低频系数cA2向上一步的重构信号');subplot(3,2,6);plot(D2);title('的二次分解单尺度高频系数cD2向上一步的重构信号');六、运行结果：七、结果分析：。
小波实验报告
小波分析实验报告
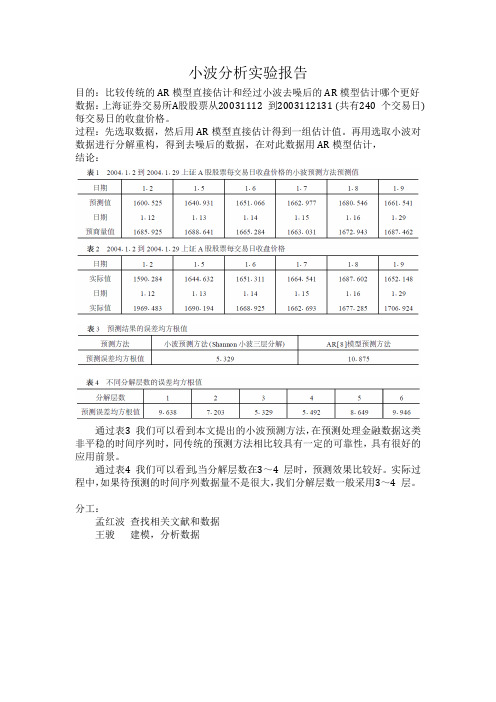
目的：比较传统的AR模型直接估计和经过小波去噪后的AR模型估计哪个更好数据：上海证券交易所A股股票从20031112 到2003112131 (共有240 个交易日) 每交易日的收盘价格。
过程：先选取数据，然后用AR模型直接估计得到一组估计值。
再用选取小波对数据进行分解重构，得到去噪后的数据，在对此数据用AR模型估计，
结论：
通过表3 我们可以看到本文提出的小波预测方法，在预测处理金融数据这类非平稳的时间序列时，同传统的预测方法相比较具有一定的可靠性，具有很好的应用前景。
通过表4 我们可以看到,当分解层数在3～4 层时，预测效果比较好。
实际过程中，如果待预测的时间序列数据量不是很大，我们分解层数一般采用3～4 层。
分工：
孟红波查找相关文献和数据
王骏建模，分析数据。
小波分析实验报告
实验四一、实验目的理解小波阈值去噪法原理。
对所得的去噪效果进行分析。
二、实验要求在载入原始图片后，对图片进行含噪和消噪处理，再对所得的图片效果进行分析。
三、主要内容载入原始图片，对原始图片添加一个随机噪声，得出含噪图片。
用sym6小波对图像进行1层分解，设置一个全局阈值，对图像分解系数，将低频系数进行重构，得出消噪后的图像。
再与原图像，含噪图像一起进行分析比较。
运行代码如下clear all;load woman;subplot(2,2,1);image(X);colormap(map);xlabel('(a)原始图像');axis square;init=2055615866;randn('seed',init);x=X+48*randn(size(X));subplot(2,2,2);image(x);colormap(map);xlabel('(b)含噪图像');axis square;%用sym6小波对图像进行1层分解t1=wpdec2(x,1,'sym6');%设置一个全局阈值thr=10.358;%对图像分解系数t2=wpthcoef(t1,0,'s',thr);%对低频系数进行重构x1=wprcoef(t1,1);subplot(2,2,3);image(x1);运行结果四、思考体会小波去噪的根本任务是在小波域将信号的小波变换与噪声的小波变换有效的分离。
噪声的能量分布于整个小波域内，小波分解后，信号的小波系数幅值要大于噪声的系数幅值，也可以认为，幅值比较大的小波系数一般以信号为主，而比较小的系数在很大程度上是噪声。
于是，采用阈值的方法可把信号系数保留，而把大部分噪声系数减少至零。
将含噪信号在各尺度上进行小波分解，保留大尺度（低分辨率）下的全部系数，对于小尺度（高分辨率）下的小波系数，设定一个阈值，幅值不超过阈值的小波系数设置为零，幅值高于该阈值的小波系数或者完整保留，或者做相应的收缩处理，最后将处理后的小波系数利用逆小波变换进行重构，恢复出有效信号。
哈尔滨工业大学小波理论与应用上机报告
Harbin Institute of Technology上机报告课程名称：小波理论与应用院系：电信学院班级： 13硕小波1班学生：位飞13S105006 诚意21邹赛13S005016 诚意12高德奇13S005023诚意12姜希12S005106 诚意11 指导教师：李福利时间： 2014-06-09哈尔滨工业大学位 飞13S105006 电信学院 电子与通信工程 电子2班 小波1班 完成上机报告（一） 邹 赛13S005016电信学院 信息与通信工程 电子2班 小波1班 完成上机报告（二）（三） 高德奇13S005023电信学院 信息与通信工程 电子1班 小波1班 完成上机报告（四） 姜 希12S005106电信学院 信息与通信工程 电子2班 小波1班 整理上机报告（一）一．实验目的和任务已知Butterworth 滤波器，其冲击响应函数为,0()0,0t Ae t h t t α-⎧≥=⎨<⎩若若，求：1、 求()ˆhω 2、 判断是否因果；是低通、高通、带通还是带阻？3、 对于信号3()(sin 22sin 40.4sin 2sin 40),t f t e t t t t -=++0t π≤≤，画出()f t 图形4、 画出滤波后图形()f h t *，比较滤波前后图形，你会发现什么，这里取10A α==5、 取()(sin5sin3sin sin 40),t f t e t t t t -=+++采用不同的变量值A α=()10A α==初始设定，画出原信号图形与滤波后图形，比较滤波效果二．实验原理1、低通滤波器从0～f2 频率之间，幅频特性平直，它可以使信号中低于f2的频率成分几乎不受衰减地通过，而高于f2的频率成分受到极大地衰减。
2、高通滤波器与低通滤波相反，从频率f1～∞，其幅频特性平直。
它使信号中高于f1的频率成分几乎不受衰减地通过，而低于f1的频率成分将受到极大地衰减。
小波变换图像拼接实验报告
图像拼接实验报告一、实验目的选用适当的拼接算法实现两幅图像的拼接。
二、实验原理图像拼接技术就是将数张有重叠部分的图像（可能是不同时间、不同视角或者不同传感器获得的）拼成一幅大型的无缝高分辨率图像的技术。
图像配准和图像融合是图像拼接的两个关键技术。
图像配准是图像融合的基础,而且图像配准算法的计算量一般非常大,因此图像拼接技术的发展很大程度上取决于图像配准技术的创新。
早期的图像配准技术主要采用点匹配法,这类方法速度慢、精度低,而且常常需要人工选取初始匹配点,无法适应大数据量图像的融合。
图像拼接的方法很多,不同的算法步骤会有一定差异,但大致的过程是相同的。
一般来说,图像拼接主要包括以下五步:（1）图像预处理：包括数字图像处理的基本操作(如去噪、边缘提取、直方图处理等)、建立图像的匹配模板以及对图像进行某种变换(如傅里叶变换、小波变换等)等操作。
（2）图像配准：就是采用一定的匹配策略,找出待拼接图像中的模板或特征点在参考图像中对应的位置,进而确定两幅图像之间的变换关系。
（3）建立变换模型：根据模板或者图像特征之间的对应关系,计算出数学模型中的各参数值,从而建立两幅图像的数学变换模型。
（4）统一坐标变换：根据建立的数学转换模型,将待拼接图像转换到参考图像的坐标系中,完成统一坐标变换。
（5）融合重构：将带拼接图像的重合区域进行融合得到拼接重构的平滑无缝全景图像。
图像拼接技术主要包括两个关键环节即图像配准和图像融合对于图像融合部分，由于其耗时不太大，且现有的几种主要方法效果差别也不多，所以总体来说算法上比较成熟。
而图像配准部分是整个图像拼接技术的核心部分，它直接关系到图像拼接算法的成功率和运行速度，因此配准算法的研究是多年来研究的重点。
目前的图像配准算法基本上可以分为两类:基于频域的方法(相位相关方法)和基于时域的方法。
相位相关法对拼接的图像进行快速傅立叶变换，将两幅待配准图像变换到频域，然后通过它们的互功率谱直接计算出两幅图像间的平移矢量，从而实现图像的配准。
哈工大电磁场与电磁波实验报告
哈⼯⼤电磁场与电磁波实验报告电磁场与电磁波实验报告班级：学号：姓名：同组⼈：实验⼀电磁波的反射实验1.实验⽬的：任何波动现象（⽆论是机械波、光波、⽆线电波），在波前进的过程中如遇到障碍物，波就要发⽣反射。
本实验就是要研究微波在⾦属平板上发⽣反射时所遵守的波的反射定律。
2.实验原理：电磁波从某⼀⼊射⾓i射到两种不同介质的分界⾯上时，其反射波总是按照反射⾓等于⼊射⾓的规律反射回来。
如图（1-2）所⽰，微波由发射喇叭发出，以⼊射⾓i设到⾦属板MM',在反射⽅向的位置上，置⼀接收喇叭B，只有当B处在反射⾓i'约等于⼊射⾓i时，接收到的微波功率最⼤，这就证明了反射定律的正确性。
3.实验仪器：本实验仪器包括三厘⽶固态信号发⽣器，微波分度计，反射⾦属铝制平板，微安表头。
4.实验步骤：1）将发射喇叭的衰减器沿顺时针⽅向旋转，使它处于最⼤衰减位置；2）打开信号源的开关，⼯作状态置于“等幅”旋转衰减器看微安表是否有显⽰，若有显⽰，则有微波发射；3）将⾦属反射板置于分度计的⽔平台上，开始它的平⾯是与两喇叭的平⾯平⾏。
4）旋转分度计上的⼩平台，使⾦属反射板的法线⽅向与发射喇叭成任意⾓度i，然后将接收喇叭转到反射⾓等于⼊射⾓的位置，缓慢的调节衰减器，使微µ）。
安表显⽰有⾜够⼤的⽰数（50A5）熟悉⼊射⾓与反射⾓的读取⽅法，然后分别以⼊射⾓等于30、40、50、60、70度，测得相应的反射⾓的⼤⼩。
6）在反射板的另⼀侧，测出相应的反射⾓。
5.数据的记录预处理记下相应的反射⾓，并取平均值，平均值为最后的结果。
5.实验结论：?的平均值与⼊射⾓0?⼤致相等，⼊射⾓等于反射⾓，验证了波的反射定律的成⽴。
6.问题讨论：1.为什么要在反射板的左右两侧进⾏测量然后⽤其相应的反射⾓来求平均值？答：主要是为了消除离轴误差，圆盘上有360°的刻度，且外部包围圆盘的基座上相隔180°的两处有两个游标。
【优质】小波实验报告-推荐word版 (7页)
本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==小波实验报告篇一：小波分析实验报告小波分析实验报告姓名班级:学号:成绩: 教师签名篇二：小波课程实验报告小波变换与信号时频分析实验报告院班级：姓名：学号：指导老师：哈尔滨工业大学二维图像信号的小波分解与重构1.1 实验目的结合小波多分辨率分解与重构原理，掌握利用MATLAB实现二维图像信号小波分解与重构的具体实现方法，重点理解二维图像信号分解与重构过程中小波基选择、图像信号边缘延拓方式对于分解和重构质量的影响，进而加深对于小波正交特性、完善重建特性的理解。
1.2 实验内容主要利用MATLAB提供的小波工具箱Wavelet Toolbox实现小波分解与重构，具体包括：(1)小波基的选择(要求三种以上小波基)(2)延拓方式的选择(3)分解过程中的抽样与非抽样(4)重构结果的分析，要求分析不同小波基、不同延拓方式、抽样/非抽样对于小波重构的影响(5)分析小波对于图像信号表示的方向特性1.3 实验步骤1. 小波变换Matlab实现编程实现图片的分解与重构，程序如下：dwtmode('zpd');X=imread('BARB.BMP');X=im2double(X);nbcol = 255;[cA1,cH1,cV1,cD1] = dwt2(X,'haar');cod_X=wcodemat(X,nbcol);cod_cA1=wcodemat(cA1,nbcol);cod_cH1=wcodemat(cH1,nbcol);cod_cV1=wcodemat(cV1,nbcol);cod_cD1=wcodemat(cD1,nbcol);dec2d = [cod_cA1,cod_cH1;cod_cV1,cod_cD1];X1=idwt2(cA1,cH1,cV1,cD1,'haar');cod_X1=wcodemat(X1,nbcol);subplot(221);imshow(X,[],'InitialMagnification','fit');title('orig image');subplot(222);imshow(dec2d,[],'InitialMagnification','fit');title('dec image');subplot(223);imshow(cod_cA1,[],'InitialMagnification','fit');title('appro image');subplot(224);imshow(cod_X1,[],'InitialMagnification','fit');title('syn image');在Zero-padding延拓方式下，分别取Haar、db3、sym小波基得到的图像分解与重构的结果如下：1) Haar小波基orig imagedec imageappro imagesyn image2) Db3小波基orig imagedec imageappro imagesyn image3) Sym3小波基orig imagedec imageappro imagesyn image在采用db4小波实现图像的分析和重构，分别采用四种不同的延拓方式，得到的的结果如下：1) extension mode为Zero-padding模式，分解与重构的结果为orig imagedec imageappro imagesyn image。
小波分析的实验报告三
1
>> D1=upcoef('d',cD1,'sym2',1); >> subplot(4,1,1);plot(s);title('原始信号') >> subplot(4,1,2);plot(A1);title('低频') >> subplot(4,1,3);plot(D1);title('高频') >> s0=idwt(cA1,cD1,'sym2'); >> subplot(4,1,4);plot(s0);title('重构信号')
2) 多尺度小波分解重构程序： >> s0=idwt(cA1,cD1,'db3'); >> [C,L]=wavedec(s,3,'db3'); >> cA5=appcoef(C,L,'db3',3); >> A3=wrcoef('a',C,L,'db3',3);
4
Hale Waihona Puke >> D1=wrcoef('d',C,L,'db3',1); >> D2=wrcoef('d',C,L,'db3',2); >> D3=wrcoef('d',C,L,'db3',3); >> figure(2); >> subplot(4,1,1);plot(A3);title('第三层低频') >> subplot(4,1,2);plot(D3);title('第三层高频') >> subplot(4,1,3);plot(D2);title('第二层高频') >> subplot(4,1,4);plot(D1);title('第一层高频') >> figure(3); >> s1=waverec(C,L,'db3'); >> subplot(3,1,1);plot(s);title('原始信号') >> subplot(3,1,2);plot(s1);title('重构信号') >> subplot(3,1,3);plot(s-s1);title('误差信号') 运行结果如下：
小波分析实验报告
( x) e
x2 2
e i0 x
0 5
程序代码： >> syms x i w0; >> f=exp(-x^2/2)*exp(i*w0*x); >> F=fourier(f,x); F= (2^(1/2)*pi^(1/2))/exp((x + i*w0*sqrt(-1))^2/2) >> f=ifourier(F) f= exp((i^2*w0^2)/2 - (t - i*w0)^2/2) 2．Marr 小波
小波分析实验报告
姓名: 班级: 学号: 成绩: 教师签名:
实验一名称： 小波函数的 Fourier 变换和 Fourier 逆变换 实验目的
用 Matlab 实现函数的 Fourier 变换和 Fourier 逆变换
实验内容 一、用 Matlab 实现下列函数的 Fourier 变换和 Fourier 逆变换 1．Morlet 小波
1.4 g1 g2 g3
1.2
1
0.8
0.6
0.4
0.2
0 -5
-4
-3
-2
-1
0
1
2
3
4
5
5．定义信号 f (t ) sin(2t ) sin(4t ) sin(10t ) ，并画出图形
N=1024; >> t=1:N; >> s1=sin(2*pi*t); >> s2=sin(4*pi*t); >> s3=sin(10*pi*t); >> s=s1+s2+s3; >> plot(t,s); >> xlabel('时间 t/s'); >> ylabel('幅值 A');
哈工大小波分析上机实验报告
小波分析上机实验报告院系：电气工程及自动化学院学科：仪器科学与技术实验一小波分析在信号压缩中的应用一、试验目的（1）进一步加深对小波分析进行信号压缩的理解；（2）学习Matlab中有关信号压缩的相关函数的用法。
二、相关知识复习用一个给定的小波基对信号进行压缩后它意味着信号在小波阈的表示相对缺少了一些信息。
之所以能对信号进行压缩是因为对于规则的信号可以用很少的低频系数在一个合适的小波层上和一部分高频系数来近似表示。
利用小波变换对信号进行压缩分为以下几个步骤来完成：（1）进行信号的小波分解；（2）将高频系数进行阈值量化处理。
对从1 到N 的每一层高频系数都可以选择不同的阈值并且用硬阈值进行系数的量化；（3）对量化后的系数进行小波重构。
三、实验要求（1）对于某一给定的信号（信号的文件名为leleccum.mat），利用小波分析对信号进行压缩处理。
（2）给出一个图像，即一个二维信号（文件名为wbarb.mat），利用二维小波分析对图像进行压缩。
四、实验结果及程序（1）load leleccum%将信号装入Matlab工作环境%设置变量名s和ls，在原始信号中，只取2600-3100个点s = leleccum(2600:3100); ls = length(s);%用db3对信号进行3级小波分解[c,l] = wavedec(s, 3, 'db3');%选用全局阈值进行信号压缩thr = 35;[xd,cxd,lxd,perf0,perfl2] = wdencmp('gbl',c,l,'db3',3,thr,'h',1);subplot(2,1,1);plot(s);title('原是信号s');subplot(2,1,2);plot(xd);title('压缩后的信号xd');图1 实验1压缩结果图2 不同阈值下实验1压缩结果（2）clear %清除Matlab工作环境中现有的变量load wbarb;%显示图像subplot(221); image(X); colormap(map);title('原始图像');axis square;disp('压缩前图像X的大小')whos('X')%==================================================== %对图像用bior3.7小波进行2层小波分解[c,s] = wavedec2(X,2,'bior3.7');%提取小波分解结构中第1层的低频系数和高频系数ca1 = appcoef2(c,s,'bior3.7',1);ch1 = detcoef2('h',c,s,1); %小波分解结构中第1层的水平方向高频系数cv1 = detcoef2('v',c,s,1); %小波分解结构中第1层的垂直方向高频系数cd1 = detcoef2('d',c,s,1); %小波分解结构中第1层的斜线方向高频系数%分别对小波分解结构中第1层的各频率成份进行重构a1 = wrcoef2('a',c,s,'bior3.7',1);h1 = wrcoef2('h',c,s,'bior3.7',1);v1 = wrcoef2('v',c,s,'bior3.7',1);d1 = wrcoef2('d',c,s,'bior3.7',1);c1 = [a1,h1;v1,d1];%显示分解后各频率成分的信息subplot(222);image(c1);axis squaretitle('分解后低频和高频信息');%==================================================== %下面进行图像的压缩处理%保留小波分解结构中第1层的低频信息，进行图像压缩%第1层的低频信息为ca1，显示第1层的低频信息%首先对第1层信息进行量化编码ca1 = wcodemat(ca1,440,'mat',0);%改变图像的亮度ca1 = 0.5*ca1;subplot(223);image(ca1);colormap(map);axis square;title('第一次压缩图像');disp('第一次压缩图像的大小为:')whos('ca1')%==================================================== %保留小波分解第二层低频信息，进行图像的压缩，此时压缩比更大%第2层的低频信息即为ca2，显示第2层的低频信息ca2 = appcoef2(c,s,'bior3.7',2);%首先对第2层低频信息进行量化编码ca2 = wcodemat(ca2,440,'mat',0);%改变图像的亮度ca2 = 0.25*ca2;subplot(224);image(ca2);colormap(map);axis square;title('第2次压缩图像');disp('第2次压缩图像的大小为');whos('ca2')图3 实验2压缩结果五、实验分析及结论（1）根据实验1压缩结果分析得到，压缩后的信号保持了原有信号的轮廓信息，即低频信息，而大部分细节信息（高频信息）得到了消除。
小波实验报告
小波实验报告小波实验报告引言小波分析是一种数学工具，可以将信号分解成不同频率的成分。
它在信号处理、图像处理、数据分析等领域有着广泛的应用。
本实验旨在通过对小波变换的实际应用，探索其在信号处理中的效果和优势。
一、实验背景小波分析是一种基于频域的信号分析方法，与传统的傅里叶变换相比，小波分析可以更好地捕捉信号的瞬时特性和局部特征。
它通过将信号与一组基函数进行卷积运算，得到信号在不同尺度和位置上的频谱信息。
二、实验目的1. 了解小波变换的基本原理和概念；2. 掌握小波变换的实现方法和工具；3. 分析小波变换在不同信号处理任务中的应用效果。
三、实验步骤1. 选择适当的小波基函数和尺度参数；2. 将待处理信号进行小波变换；3. 分析小波变换后的频谱信息；4. 根据实际需求，选择合适的尺度和位置，重构信号。
四、实验结果与分析本实验选择了一段音频信号进行小波变换。
首先，选择了Daubechies小波作为基函数，并调整尺度参数。
经过小波变换后，得到了信号在不同频率上的能量分布图。
通过分析能量分布图，可以清晰地观察到信号的频率成分和时域特征。
进一步分析小波变换的结果，可以发现小波变换具有良好的局部化特性。
不同于傅里叶变换将整个信号分解成各个频率的正弦波，小波变换可以将信号分解成不同频率的局部波包。
这种局部化特性使得小波变换在信号分析和处理中更加灵活和精确。
五、实验应用1. 信号去噪小波变换可以将信号分解成不同频率的成分，通过滤除高频噪声成分，实现信号的去噪。
在音频处理和图像处理中，小波去噪已经成为一种常用的方法。
2. 图像压缩小波变换可以将图像分解成不同频率的局部波包，通过保留重要的低频成分，可以实现对图像的压缩。
小波压缩在数字图像处理和视频编码中有着重要的应用。
3. 时频分析小波变换可以提供信号在不同时间和频率上的分布信息，通过时频分析，可以更好地理解信号的时域和频域特性。
在语音识别、心电图分析等领域，时频分析是一种常用的方法。
小波实验报告
小波实验报告
《小波实验报告》
小波分析是一种用于信号处理和数据分析的强大工具。
在本次实验中，我们将探索小波分析的基本原理，并通过实验验证其在信号处理中的有效性。
首先，我们介绍了小波分析的基本概念和原理。
小波分析是一种基于窗口函数的信号分析方法，它可以将信号分解成不同频率和时间尺度的成分。
与傅里叶变换不同，小波分析可以同时提供频域和时域的信息，因此在处理非平稳信号和非线性系统时具有独特优势。
接下来，我们进行了一系列实验，验证了小波分析在信号处理中的应用。
我们首先使用小波分析对一段包含多个频率成分的信号进行了分解，并成功地提取出了各个频率成分的时域和频域信息。
接着，我们对一个非平稳信号进行了小波变换，并观察到了小波分析在处理非平稳信号时的优越性。
最后，我们还利用小波分析进行了信号去噪和压缩，结果表明小波分析在这些应用中具有良好的效果。
通过本次实验，我们深刻理解了小波分析的原理和应用，并验证了其在信号处理中的有效性。
小波分析不仅可以帮助我们更好地理解信号的时频特性，还可以在实际工程中发挥重要作用。
我们相信，在未来的研究和应用中，小波分析将会得到更广泛的应用和发展。
哈工大电波传播实验报告
一、实验目的1. 了解电磁波的基本特性和传播规律。
2. 掌握电波传播实验的基本原理和方法。
3. 通过实验验证电磁波在均匀介质和非均匀介质中的传播特性。
4. 熟悉电波传播测量仪器的使用。
二、实验原理电磁波是一种电场和磁场相互垂直、同时与传播方向垂直的波动。
在均匀介质中，电磁波的传播速度为常数，且与传播方向无关。
而在非均匀介质中，电磁波的传播速度会因介质的不均匀性而发生变化。
本实验主要研究电磁波在均匀介质和非均匀介质中的传播特性，包括：1. 电磁波在均匀介质中的传播速度。
2. 电磁波在非均匀介质中的折射和反射现象。
3. 电磁波的衰减和相速度。
三、实验仪器与设备1. 电磁波传播实验装置：包括发射天线、接收天线、信号发生器、功率计、衰减器、电波传播测量仪等。
2. 测量仪器：示波器、频率计、电平计等。
四、实验步骤1. 准备实验装置：将发射天线、接收天线、信号发生器、功率计、衰减器等连接好，确保电路连接正确。
2. 设置实验参数：根据实验要求，设置信号发生器的频率、幅度等参数，调整衰减器的衰减值。
3. 测量电磁波在均匀介质中的传播速度：- 将发射天线和接收天线放置在同一水平面上，保持一定距离。
- 打开信号发生器，调整频率和幅度，使发射天线产生电磁波。
- 观察接收天线接收到的信号强度，记录数据。
- 重复实验，改变距离，记录数据。
- 根据实验数据，计算电磁波在均匀介质中的传播速度。
4. 测量电磁波在非均匀介质中的折射和反射现象：- 将发射天线和接收天线放置在两个不同介质的交界面上。
- 打开信号发生器，调整频率和幅度，使发射天线产生电磁波。
- 观察接收天线接收到的信号强度和相位，记录数据。
- 重复实验，改变介质，记录数据。
- 根据实验数据，分析电磁波在非均匀介质中的折射和反射现象。
5. 测量电磁波的衰减和相速度：- 将发射天线和接收天线放置在同一水平面上，保持一定距离。
- 打开信号发生器，调整频率和幅度，使发射天线产生电磁波。
小波实验报告信号去噪
一、题目：信号去噪二、目的：编程实现信号的去噪三、算法及其实现：小波去噪设信号在某一尺度2L上的离散逼近()f n 被被加性噪声()W n 污染，观测数据：()()()X n f n W n =+。
将()X n 在正交规范基{}{},.,[(),()]J m j m m L j J m B n n φψ∈<≤∈=上分解，小波去噪是对分解系数取阈值后进行重构，即对f 的估计可写成：,,,,1(,)(,)J T j m j m T J m J m j L m mF X X ρψψρφφ=+=<>+<>∑∑∑其中，T ρ表示对分解系数取硬阈值或软阈值。
小波去噪相当于一个自适应平滑过程，它只在信号的正则部分平滑掉噪声，而在其锐变部分保留了信号的细节，也可以说，小波去噪是一个幅值域滤波的过程。
本实验中先给信号加入噪声，然后用ddencmp 函数获得消噪阈值，并确定对系数取阈值的方式（硬阈值或软阈值方式）以及是否对图像进行压缩，再用wdencmp 函数去噪。
四、实现工具：Matlab五、程序代码：load noisdopp;indx = 1:1000;x = noisdopp(indx);% 产生含噪信号init=2055615866;randn('seed',init);nx = x + 32*randn(size(x));% 获取消噪的阈值[thr,sorh,keepapp] = ddencmp('den','wv',nx);% 对信号进行消噪xd = wdencmp('gbl',nx,'db4',2,thr,sorh,keepapp);subplot(2,2,1);plot(x);title('原始信号');subplot(2,2,2);plot(nx);title('含噪信号');subplot(2,2,3)plot(xd);title('消噪后的信号');六、运行结果：七、结果分析：。
哈工大测试技术基础实验报告
实验一波形的合成与分解一、实验目的1、了解信号分析手段之一的傅里叶变换的基本思想和物理意义。
2、观察和分析由多个频率、幅值和相位成一定关系的正弦波叠加的合成波形。
3、观察和分析频率、幅值相同，相位角不同的正弦波叠加的合成波形。
4、通过本实验熟悉信号合成、分解的操作方法，了解信号频谱的含义。
二、实验结果图1.1方波图1.2锯齿波图1.3三角波图1.4正弦整流波实验二典型信号的频谱分析一、实验目的1、在理论学习的基础上，通过本实验熟悉典型信号的频谱特征，并能够从信号频谱中读取所需的信息。
2、了解信号频谱的基本原理和方法，掌握用频谱分析提取测量信号特征的方法。
二、实验原理信号频谱分析是采用傅里叶变换将时域信号x(t)变换为频域信号X(f)，从而帮助人们从另一个角度来了解信号的特征。
工程上习惯将计算结果用图形方式表示，以频率f为横坐标，X(f)的实部a(f)和虚部b(f)为纵坐标画图，称为时频—虚频谱图；以频率f为横坐标，X(f)的幅值A(f)和相位φ(f)为纵坐标画图，则称为幅值—相位谱；以f为横坐标，A(f)2为纵坐标画图，则称为功率谱。
频谱是构成信号的各频率分量的集合，它完整地表示了信号的频率结构，即信号由哪些谐波组成，各谐波分量的幅值大小及初始相位，揭示了信号的频率信息。
三、实验结果实验结果如下图所示：图2.1 白噪声信号幅值频谱特性图2.2 正弦波信号幅值频谱特性图2.3 方波信号幅值频谱特性图2.4 三角波信号幅值频谱特性图2.5 正弦波信号+白噪声信号幅值频谱特性四、思考题1、与波形分析相比，频谱分析的主要优点是什么？答：信号频谱()X f代表了信号在不同频率分量成分的大小，能够提供比时域信号波形更直观，丰富的信息。
2、为何白噪声信号对信号的波形干扰很大，但对信号的频谱影响很小？答：白噪声是指在较宽的频率范围内，各等带宽的频带所含的噪声能量相等的噪声。
在时域上，白噪声是完全随机的信号，叠加到波形上会把信号的波形完全搅乱，所以对信号的波形干扰很大。
小波变换应用实验报告——去噪,融合,水印
一. 基础原理 1.小波简介小波一词由Morlet 和Grossman 在1980年代早期提出，其思想来源于伸缩平移方法。
小波分析(wavelet analysis), 或小波转换(wavelet transform)是指用有限长或快速衰减的、称为母小波(mother wavelet)的振荡波形来表示信号。
该波形被缩放和平移以匹配输入的信号。
小波变换是将时间信号展开为小波函数族的线性叠加，小波变换的核函数是小波函数，它在时间和频率域内都是局部化的。
所以，小波变化可对信号同时在时－频域内进行联合分析。
小波变换分成两个大类：离散小波变换 (DWT) 和连续小波转换 (CWT)。
两者的主要区别在于，连续变换在所有可能的缩放和平移上操作，而离散变换采用所有缩放和平移值的特定子集。
小波分析的一个重要领域就是是图像处理。
小波分解可以把小波分层次按照小波基展开，并可以根据图像的性质及给定的图像处理标准确定具体要展开到哪一级，还可以把细节分量和近似分量展开，所以小波分析常用于信号的压缩、去噪等方面，是图像处理的一个极其重要的工具。
本报告中将具体实例说明小波分解在图像中的应用。
2. 小波变换应用包括去噪，图像的压缩，图像的融合以及水印技术。
2.1去噪原理：在实际工程应用中，通常所分析的信号具有非线性，非平稳,并且奇异点较多的特点。
含噪的一维信号模型可表示为：式1其中，f(t)为真实信号，s(t)为含噪信号，e(t)为噪声， σ为噪声标准偏差。
有用信号通常表现为低频信号或是相对比较平稳。
而噪声信号通常表现为高频信号。
利用小波对含噪的原始信号分解后，含噪部分主要集中在高频小波系数中，并且，包含有用信号的小波系数幅值较大，但数目少；而噪声对应的小波系数幅值小，数目较多。
基于上述特点，可以应用门限阈值法对小波系数进行处理。
（即对较小的小波系数置为０，较大的保留或削弱），然后对信号重构即可达到消噪的目的。
在去噪方面，小波分析由于能同时在时－频域中对信号进行分析，具有多分辨分析的功能，所以在不同的分解层上有效的区分信号的突变部分和噪声，从而实现信号的消噪。
小波理论与应用课程的实践教学设计
［摘要］在哈尔滨工业大学工科研究生小波理论与应用的教学过程中，加入上机实践教学内容后，学生的反响比较强烈，普遍反映以往抽象的概念和理论更加易于接受，而且提高了动手实践能力。
［关键词］小波；滤波器；Mallat 分解与重构算法；实践教学［中图分类号］G642［文献标志码］A［文章编号］2096-0602（2020）40-0202-02小波理论与应用课程的实践教学设计李福利（哈尔滨工业大学数学学院，黑龙江哈尔滨150001）近几年来，哈尔滨工业大学工科研究生学位课中，小波理论与应用的选修人数稳定在300人左右。
这是一门理论性和应用性都比较强的交叉学科。
在以往的研究生小波理论的教学过程中，教师往往偏重于理论教学，忽视了实践教学，导致学生学过小波理论后，不知道如何用小波解决具体的实际问题。
学生课堂上似乎听懂了，实际动手操作起来，就很茫然，不知所以然了。
为此，我们在教学过程中，向哈尔滨工业大学研究生院主管研究生教学培养和哈尔滨工业大学数学学院主抓研究生公共教学的领导申请了12学时的上机实践，申明了实践教学的迫切性和重要性，得到了有关部门领导和研究生院的大力支持。
由于课时限制，经过5年多的教学实践摸索，我们把上机实践内容分成两大块，一块是基础篇内容上机实践部分，另一块是提高篇内容上机实践部分。
我们在基础篇内容实践部分，为了使实践教学不流于形式，特别加强设计了八个实践教学任务，使学生上机实践的时候感觉到任务充实。
基础部分要求学生完成实验报告，报告内容包括实验目的、实验原理、实验结论、实验结果分析、MATLAB 源程序、上机收获体会等内容。
从而加深了学生对基本概念、基本理论的理解，提高了学生的动手能力、实践能力，并有效防止了高分低能现象的产生。
具体的八个实践任务如下。
一、Butterworth 滤波器的原理与实践设计这一实践任务的目的是为了加深学生对滤波器概念的理解，体会到滤波器对信号的滤波作用，和不同参数的Butterworth 滤波器对信号的滤波效果的影响是不同的。
哈工大小波实验报告
小波理论实验报告院（系）专业学生学号日期2015年12月实验报告一一、 实验目的1. 运用傅立叶变换知识对常用的基本函数做基本变换。
2. 加深对因果滤波器的理解，并会判断因果滤波器的类型。
3. 运用卷积公式对基本信号做滤波处理并分析，以加深理解。
4. 熟悉Matlab 中相关函数的用法。
二、 实验原理1.运用傅立叶正、反变换的基本公式：()ˆ()() ()(),11ˆ()(),22i x i t i ti t i t f f x e dx f t e dt f t e f t fe df t e ωωωωωωωωππ∞∞---∞-∞∞--∞=====⎰⎰⎰及其性质，对所要处理信号做相应的傅里叶变换和逆变换。
2.运用卷积的定义式：1212()()()()+∞-∞*=-⎰f t f t f f t d τττ对所求信号做滤波处理。
三、 实验步骤与内容1.实验题目：Butterworth 滤波器，其冲击响应函数为,0()0,0若若α-⎧≥=⎨<⎩t Ae t h t t 1. 求$()hω 2. 判断是否因果；是低通、高通、带通还是带阻？ 3. 对于信号3()(sin 22sin 40.4sin 2sin 40)，-=++t f t et t t t 0π≤≤t ,画出图形()f t4. 画出滤波后图形()*f h t ，比较滤波前后图形，你会发现什么，这里取10α==A5. 取()(sin5sin3sin sin 40)，-=+++tf t e t t t t 采用不同的变量值α=A (初始设定A=α=10) 画出原信号图形与滤波后图形，比较滤波效果。
2.实验步骤及分析过程：1.求$()hω 由傅里叶变换的定义式可得：()0ˆαϖαϖωαω+∞+∞-----∞=⋅=⋅=+⎰⎰t i t t i t Ah Ae e dt Ae e dt i （1） 故该滤波器的幅频特性为：()ω==H ，转折频率τα=；假定1,2A α==，绘制该滤波器的幅频特性曲线如下：图1.1滤波器的幅频特性曲线2. 判断是否因果；是低通、高通、带通还是带阻？（1）观察滤波器响应函数可知，只有在输入信号到达后，该滤波器才会有输出响应，此外实际应用的滤波器均是因果滤波器，所以，题中滤波器是因果滤波器。
小波实验报告用小波函数db1,db2,db3对小波1次分解
一、题目：用小波函数db1,db2,db3对小波１次分解二、目的：编程实现信号的分解与重构并对比db1,db2,db3几种小波变换三、算法及其实现：离散小波变换离散小波变换是对信号的时－频局部化分析，其定义为：/2200()(,)()(),()()j j Wf j k a f t a t k dt f t L R φ+∞---∞=-∈⎰ 本实验实现对信号的分解与重构：（１）信号分解：用小波工具箱中的dwt 函数来实现离散小波变换，函数dwt 将信号分解为两部分，分别称为逼近系数和细节系数（也称为低频系数和高频系数）,实验中分别记为cA1,cD1，它们的长度均为原始信号的一半，但dwt 只能实现原始信号的单级分解。
在本实验中使用小波函数db1来实现单尺度小波分解，即：[cA1,cD1]＝dwt(s,’db1’)，其中s 是原信号;（２）信号重构：用小波工具箱中的upcoef 来实现，upcoef 是进行一维小波分解系数的直接重构,即：A1 = upcoef('a',cA1,'db1'); D1 = upcoef('a',cD1,'db1')。
四、实现工具：Matlab五、程序代码：%装载leleccum 信号load leleccum;s = leleccum(1:3920);%用小波函数db1对信号进行单尺度小波分解[cA1,cD1]=dwt(s,'db1');subplot(3,3,1);plot(s);title('leleccum 原始信号');%单尺度低频系数cA1向上一步的重构信号A1 = upcoef('a',cA1,'db1');%单尺度高频系数cD1向上一步的重构信号D1 = upcoef('a',cD1,'db1');subplot(3,3,4);plot(A1);title('单尺度低频系数cA1向上一步的重构信号');subplot(3,3,7);plot(D1);title('单尺度高频系数cD1向上一步的重构信号');%%用小波函数db2对信号进行单尺度小波分解[cA2,cD2]=dwt(s,'db2');subplot(3,3,2);plot(s);title('leleccum 原始信号');%单尺度低频系数cA1向上一步的重构信号A2 = upcoef('a',cA1,'db2');%单尺度高频系数cD1向上一步的重构信号D2 = upcoef('a',cD1,'db2');subplot(3,3,5);plot(A2);title('单尺度低频系数cA2向上一步的重构信号'); subplot(3,3,8);plot(D2);title('单尺度高频系数cD2向上一步的重构信号');%%用小波函数db3对信号进行单尺度小波分解[cA3,cD3]=dwt(s,'db3');subplot(3,3,3);plot(s);title('leleccum原始信号');%单尺度低频系数cA1向上一步的重构信号A3 = upcoef('a',cA1,'db3');%单尺度高频系数cD1向上一步的重构信号D3 = upcoef('a',cD1,'db3');subplot(3,3,6);plot(A3);title('单尺度低频系数cA3向上一步的重构信号'); subplot(3,3,9);plot(D3);title('单尺度高频系数cD3向上一步的重构信号');六、运行结果：七、结果分析：。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
小波理论实验报告院（系）专业学生学号日期2015年12月实验报告一一、 实验目的1. 运用傅立叶变换知识对常用的基本函数做基本变换。
2. 加深对因果滤波器的理解，并会判断因果滤波器的类型。
3. 运用卷积公式对基本信号做滤波处理并分析，以加深理解。
4. 熟悉Matlab 中相关函数的用法。
二、 实验原理1.运用傅立叶正、反变换的基本公式：()ˆ()() ()(),11ˆ()(),22i x i t i ti t i t f f x e dx f t e dt f t e f t fe df t e ωωωωωωωωππ∞∞---∞-∞∞--∞=====⎰⎰⎰及其性质，对所要处理信号做相应的傅里叶变换和逆变换。
2.运用卷积的定义式：1212()()()()+∞-∞*=-⎰f t f t f f t d τττ对所求信号做滤波处理。
三、 实验步骤与内容1.实验题目：Butterworth 滤波器，其冲击响应函数为,0()0,0若若α-⎧≥=⎨<⎩t Ae t h t t 1. 求()h ω2. 判断是否因果；是低通、高通、带通还是带阻？3. 对于信号3()(sin 22sin 40.4sin 2sin 40)，-=++t f t et t t t 0π≤≤t 画出图形()f t4. 画出滤波后图形()*f h t ，比较滤波前后图形，你会发现什么，这里取10α==A5. 取()(sin5sin3sin sin 40)，-=+++tf t e t t t t 采用不同的变量值α=A (初始设定A=α=10) 画出原信号图形与滤波后图形，比较滤波效果。
2.实验步骤及分析过程：1.求()h ω由傅里叶变换的定义式可得：()0ˆαϖαϖωαω+∞+∞-----∞=⋅=⋅=+⎰⎰t i t t i t Ah Ae e dt Ae e dt i （1） 故该滤波器的幅频特性为：()ω==H ，转折频率τα=；假定1,2A α==，绘制该滤波器的幅频特性曲线如下：图1.1滤波器的幅频特性曲线2. 判断是否因果；是低通、高通、带通还是带阻？（1）观察滤波器响应函数可知，只有在输入信号到达后，该滤波器才会有输出响应，此外实际应用的滤波器均是因果滤波器，所以，题中滤波器是因果滤波器。
（2）由图1可知，该滤波器为低通滤波器。
3. 对于信号3()(sin 22sin 40.4sin 2sin 40)t f t et t t t -=++0t π≤≤，画出图形()f t编写matlab 程序：t=linspace(0,pi,80000);f=exp(-t/3).*(sin(2*t)+2*sin(4*t)+0.4*sin(2*t).*sin(40*t)); plot(t,f); xlabel('时间/t');ylabel('信号值/f(t)'); grid on绘制信号的图形如下：图1.2 f(t)波形图4. 画出滤波后图形()f h t *，比较滤波前后图形，你会发现什么，这里取10A α==。
对f(t)进行卷积运算，编写MATLAB 程序，如下： A=10;a=10;t=linspace(0,pi,80000);f=exp(-t/3).*(sin(2*t)+2*sin(4*t)+0.4*sin(2*t).*sin(40*t)); h=A*exp(-a*t); F=conv(f,h); plot(F); xlabel('时间/t');ylabel('滤波后信号值/f(t)'); grid on运行程序，得到的图形如下：图1.3 滤波后的f(t)比较图1.2和图1.3中，可以看出：经滤波处理后，信号f （t ）的幅值变大，高频成分得到了有效的抑制，信号的曲线特征变得平滑，而且持续分布相位并未失真，信号的基本信息得到无损传递。
5. 取()(sin5sin3sin sin 40)tf t e t t t t -=+++采用不同的变量值A α=(初始设定A=α=10) 画出原信号图形与滤波后图形，比较滤波效果。
对A 和a 分别取A=a=2，5，10，15，25，并将几个图形放在一起比较，MATLAB 程序如下：A=25;a=25; %A==a,a=2,5,10,15,25% t=linspace(0,pi,80000);f=exp(-t/3).*(sin(2*t)+2*sin(4*t)+0.4*sin(2*t).*sin(40*t)); h=A*exp(-a*t); F=conv(f,h); hold on ; plot(F); xlabel('ʱ¼ä/t');ylabel('Â˲¨ÐźÅÖµ/f(t)'); grid on可以得到如下图形：图1.4 取不同A和a值后的f(t)比较以上图形中的曲线：可以看出随着A、a值逐渐增大，波形幅值增大，滤波后信号毛刺（高频波动信号）也随着增多，即对高频信号的抑制效果变差，同时也可以看出滤波器输出信号中的低频成分也呈增大趋势。
由此可知，滤波器在A、a值较小时对高频的抑制效果最好，但这种情况下低频信号也受到一定的削弱，滤波效果并不一定是最好，因此，需要根据实际使用需求设定参数。
实验报告二一、 实验目的1． 学习Haar 小波的定义及性质，掌握Haar 小波分解与重构的原理。
2． 通过例子学习小波分析在一维信号奇异性检测中的应用； 3． 学习并掌握信号处理的相关步骤。
4． 熟悉Matlab 中相关函数的用法二、实验原理一般来说，噪声信号多包含在具有较高频率细节中，在对信号进行了小波分解之后，再利用门限阈值等形式对所分解的小波系数进行权重处理，然后对小信号再进行重构即可达到信号去噪的目的。
具体步骤为：a.一维信号的小波分解，选择一个小波并确定分解的层次，然后进行分解计算。
b.小波分解高频系数的阈值量化，对各个分解尺度下的高频系数选择一个阈值进行软阈值量化处理。
C ．一维小波重构，根据小波分解的最底层低频系数和各层高频系数进行一维小波的重构。
利用小波分析检测信号突变点的一般方法是：对信号进行多尺度分析，在信号出现突变时，其小波变换后的系数具有模极大值，因而可以通过对模极大值点的检测来确定故障发生的时间点。
通常情况下，信号的奇异性分两种情况，一种是信号在某一个时刻内其幅值发生突变，引起信号的非连续，幅值的突变处是第一种类型的间断点。
另一种是信号外观上很光滑，幅值没有突变，但是，信号的一阶微分有突变发生，且一阶微分是不连续的，成为第二种类型的间断点。
三、实验步骤与内容实验题目：1. 设信号()()()()()24sin 32cos 50.2sin cos 55-=++x f ex x x x 将区间[0 1]实行256等分并得到信号在这些节点上的离散值 （1）利用Haar 小波对离散后的信号进行分解；（2）画出1,8,7,...,1-=j V j 中的分量并与原信号j f 进行比较；（3）进行压缩比为80%的压缩，画出压缩后的图像与原图像比较； （4）选择合适的参数去噪，画出去噪后的图像与原图像比较； 2.定义区间[0 1]上存在间断点的信号：21,8/91()0,08/9⎧-≤≤=⎨≤<⎩x x g x x 去信号g 在区间[0 1]上128等分节点的值，按照Haar 小波分解与重构算法实现一次分解，描述第6层小波系数的值。
确定最大的小波系数以及对应该系数的值。
判断间断点的大致位置，输出你的理由。
实验步骤及分析过程： 1.第一题（1）利用Haar 小波对离散后的信号进行分解； 先画出原信号的波形，程序如下：x=linspace(0 1 256);f=exp(-x.^2/4).*(sin(3*x)+2*cos(5*x)+0.2*sin(x).*cos(55*x)).*(x>=0&x<=1); plot(x f)； 得到图形如下：图2.1 原信号波形下面运用Haar 小波对已知函数进行分解，程序如下所示： x=linspace(0,1,256); j7=linspace(0,1,128);f=exp(-x.^2/4).*(sin(3*x)+2*cos(5*x)+0.2*sin(x).*cos(55*x)).*(x>=0&x<=1); [a,b]=dwt(f,'haar'); subplot(2,1,1); plot(j7,a); xlabel('尺度空间'); grid on subplot(2,1,2); plot(j7,b); xlabel('小波空间'); grid on得到的波形如下：图2.2 haar 小波对函数进行分解（2）画出1,8,7,...,1-=j V j 中的分量并与原信号j f 进行比较； MATLAB 程序如下：x=linspace(0,1,256);f=exp(-x.^2/4).*(sin(3*x)+2*cos(5*x)+0.2*sin(x).*cos(55*x)).*(x>=0&x<=1);[C,L]=wavedec(f,8,'Haar');v0=wrcoef('a',C,L,'Haar',8);subplot(2,4,1);plot(x,v0);title('V0');grid onv1=wrcoef('a',C,L,'Haar',7);subplot(2,4,2);plot(x,v1);title('V1');grid onv2=wrcoef('a',C,L,'Haar',6);subplot(2,4,3);plot(x,v2);title('V2');grid onv3=wrcoef('a',C,L,'Haar',5);subplot(2,4,4);plot(x,v3);title('V3');grid onv4=wrcoef('a',C,L,'Haar',4);subplot(2,4,5);plot(x,v4);title('V4');grid onv5=wrcoef('a',C,L,'Haar',3);subplot(2,4,6);plot(x,v5);title('V5');grid onv6=wrcoef('a',C,L,'Haar',2);subplot(2,4,7);plot(x,v6);title('V6');grid onv7=wrcoef('a',C,L,'Haar',1);subplot(2,4,8);plot(x,v7);title('V7');grid on画出的波形如下：图2.3 v中的各个分量将图2.3跟图2.1作比较可知，随着j的增大，得到的图形越接近原函数波形。