实验 杨氏模量的测定(梁弯曲法)
实验杨氏模量的测定（梁弯曲法）
实验 杨氏模量的测定(梁弯曲法)【实验目的】用梁的弯曲法测定金属的杨氏模量。
【仪器用具】攸英装置，光杠杆，望远镜及直尺，螺旋测微计，游标卡尺，米尺，千分表。
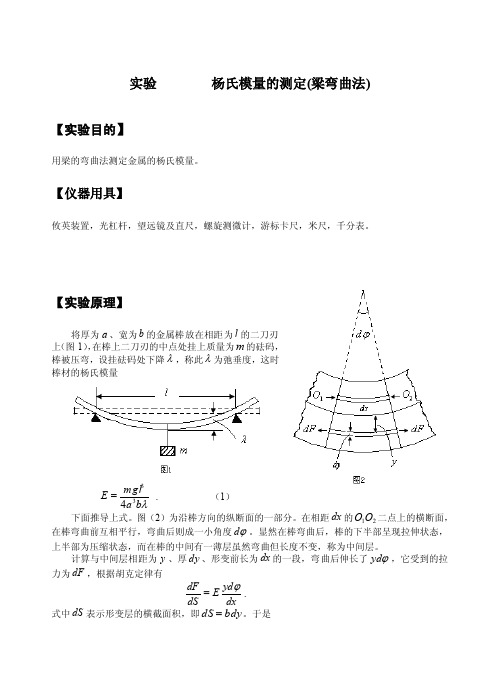
【实验原理】将厚为a 、宽为b 的金属棒放在相距为l 的二刀刃上（图1），在棒上二刀刃的中点处挂上质量为m 的砝码，棒被压弯，设挂砝码处下降λ，称此λ为弛垂度，这时棒材的杨氏模量λb a mgl E 334= . （1） 下面推导上式。
图（2）为沿棒方向的纵断面的一部分。
在相距dx 的21O O 二点上的横断面，在棒弯曲前互相平行，弯曲后则成一小角度ϕd 。
显然在棒弯曲后，棒的下半部呈现拉伸状态，上半部为压缩状态，而在棒的中间有一薄层虽然弯曲但长度不变，称为中间层。
计算与中间层相距为y 、厚dy 、形变前长为dx 的一段，弯曲后伸长了ϕyd ，它受到的拉力为dF ，根据胡克定律有dxyd E dS dF ϕ=. 式中dS 表示形变层的横截面积，即bdy dS =。
于是y d y dxd EbdF ϕ=. 此力对中间层的转矩为dM ，即 dy y dx d EbdM 2ϕ=. 而整个横断面的转矩M 应是dxd b Ea dy y dx d Eb M a ϕϕ32021212==⎰ . （2） 如果将棒的中点C 固定,在中点两侧各为2l 处分别施以向上的力mg 21(图3)，则棒的弯曲情况当和图1所示的完全相同。
棒上距中点C 为x 、长为dx 的一段，由于弯曲产生的下降λd 等于ϕλd x l d )2(-= （3） 当棒平衡时，由外力mg 21对该处产生的力距)2(21x l mg -应当等于由式（2）求出的转距M ，即 dxd b Ea x l mg ϕ3121)2(21=-. 由此式求出ϕd 代入式(3)中并积分,可求出弛垂度bEa mgl dx x l b Ea mg 33210234)2(6=-=⎰λ, (4) 即 λb a m g l E 334=. (1)【仪器介绍】攸英装置如图4所示，在二支架上设置互相平的钢制刀刃，其上放置待测棒和辅助棒。
弯曲模量 杨氏模量 值
弯曲模量杨氏模量值在材料力学中，弯曲模量和杨氏模量是描述材料在受力时变形特性的两个重要参数。
它们分别反映了材料在弯曲和拉伸过程中的刚度，是工程设计和材料选择中不可或缺的参考指标。
一、弯曲模量概述弯曲模量，又称挠曲模量，是指材料在受力弯曲时，应力与应变之间的比例系数。
它反映了材料抵抗弯曲变形的能力，是评价材料弯曲刚度的重要指标。
在工程应用中，弯曲模量常用于计算梁、板等结构的弯曲变形和应力分布。
弯曲模量的测量通常采用三点弯曲试验或四点弯曲试验。
在这些试验中，试样被放置在两个支点之间，并在试样中央施加集中载荷。
通过测量试样在载荷作用下的挠度（变形量），结合试样的几何尺寸和载荷大小，可以计算出材料的弯曲模量。
二、杨氏模量概述杨氏模量，又称拉伸模量或弹性模量，是指材料在受拉伸力时，应力与应变之间的比例系数。
它反映了材料抵抗拉伸变形的能力，是评价材料拉伸刚度的重要指标。
在工程应用中，杨氏模量广泛用于计算杆、轴等结构的拉伸变形和应力分布。
杨氏模量的测量通常采用拉伸试验。
在拉伸试验中，试样被夹持在试验机的夹具之间，并施加逐渐增大的拉伸力。
通过测量试样在拉伸过程中的伸长量（变形量），结合试样的原始尺寸和拉伸力大小，可以计算出材料的杨氏模量。
三、弯曲模量与杨氏模量的区别与联系虽然弯曲模量和杨氏模量都是描述材料变形特性的参数，但它们在物理意义、测量方法以及工程应用等方面存在显著差异。
1. 物理意义不同：弯曲模量描述的是材料在弯曲过程中的刚度，而杨氏模量描述的是材料在拉伸过程中的刚度。
这意味着两者分别反映了材料在不同受力状态下的变形行为。
2. 测量方法不同：弯曲模量通常通过三点弯曲试验或四点弯曲试验来测量，而杨氏模量则通过拉伸试验来测量。
这两种试验方法在试样的准备、加载方式以及变形量的测量等方面都有所不同。
3. 工程应用不同：由于弯曲模量和杨氏模量分别反映了材料在弯曲和拉伸过程中的变形特性，因此它们在工程应用中的侧重点也有所不同。
杨氏模量
杨氏模量的测量实验目的与要求1. 掌握伸长法和弯曲法测杨氏模量的原理和实验方法；2. 掌握卷尺、千分尺、游标卡尺和读数显微镜等长度测量仪器的使用方法；3. 掌握不确定度的计算。
4. 掌握数据处理方法及实验误差分析。
实验原理根据虎克定律，固体材料的伸缩形变正比于拉压外力的大小，其比例系数即为材料的杨氏模量。
测出材料在不同拉压外力作用下的伸缩形变，即可求出其杨氏模量。
杨氏模量杨氏模量是弹性模量的一种，若长为l ，截面积为S 的均匀金属丝或棒，在其长度方向上受到的作用力F 而伸长l ∆，那么根据虎克定路：在弹性限度内，协强F/S 与协变l l /∆成正比，即：ll E S F ∆⋅= 其中的比例系数E 即为该金属材料的杨氏模量，那么，lS FlE ∆=因为F ，S ，以及l 都是比较容易测量的量。
由于金属的杨氏模量一般都比较大，所以引起的长度变化比较微小，很难用普通的测量长度的仪器测准。
在验中测量钢丝的杨氏模量，其截面为圆形，其直径为时，相应的截面积2DS π=，作用力F=mg 金属丝的产生的微小伸长量为l ∆，无法用一般的长度测量仪器测量，因此实验中用光杠杆法进行测量，测量公式：h Bbl ∆=∆2 于是可得实验中的杨氏模量测量公式：hb D Blmg E ∆=28πh ∆为望远镜中观察到的刻度的变化。
不确定度公式由计算公式hb D BlmgE ∆=28π，两边取微分，然后将微分换成不确定度，求平方和的平方根，得到杨氏模量的不确定公式d222222)()2()()()()()1121111(h u D ub u B u l u m u E u h d h dD D db b dB B dl l dm m E dE h D b B l m E ∆+++++=⇒∆∆+++++⋅=∆实验装置各测量仪器的不确定度限值： 千分尺 a = 0.004mm 卷尺 a = 1mm读数显微镜 a = 0.02mmFD-HY-MT 型霍尔位置传感器杨氏模量实验仪——复旦天欣仪器厂 千分尺（0–25mm ）——上海量具刀具厂 游标卡尺 （0–150mm ）—上海量具刀具厂 不锈钢直尺 （0–300mm ）—上海量具刀具厂 黄铜片和人造骨（PEEK ）–复旦天欣仪器厂 照明灯实验内容一、伸长法测量杨氏模量1. 仪器的调节。
实验报告模板杨氏模量的测量
i m/×10-3 kg Zi/×10-3 m Ui/×10-3 v
0 0.00
1 10
2 20
3 30.
4 40
5 50
6 60
7 70
2.铁板的实验记录 铁板的弯曲记录
i 0 1 2 3 4 5
平均值
M/×10-3kg Z/×10-3m Z2/×10-6 U/×10-3v ZU/×10-6 U2/×10-6 0.00 20.00 40.00 60.00 80.00 100.00 Z= Z2= U= ZU= -U2=
警示：严禁抄袭，雷同卷均判零分。
4/5
【实验题目】杨氏模量的测量实验
班级
姓名
学号
【实验数据处理】
【思考题】
【实验小结】
警示：严禁抄袭，雷同卷均判零分。
5/5
2. 3.
【预习要点】 1. 阅读教材《杨氏模量测量实验》中微弯法的相关内容。 2. 阅读教材《数据处理》中最小二乘法的内容理解并掌握其计算方法。 3. 阅读教材《自修性实验》中钢尺、游标卡尺、螺旋测微仪的使用方法。 【实验目的】 1. 熟知霍尔位置传感器的特性，并会用已测量的数据给传感器定标。 2. 学会使用读数显微镜。 3. 掌握用霍尔位置传感器法（微弯法）测位移测量材料的杨氏模量。 【实验原理】 1. 霍尔传感器电势差与位置的对应关系。
课程网站地址: /dxwl.html
大 学 物 理 实 验 报 告
班 月 姓名 学号 座位号
【实验题目】杨氏模量测量实验 教师姓名
上课日期 2013 年
日 教室 7 教 B 段 604 房间
（以上信息请根据网络选课页面填写完整。 ）
任课教师签字：
最终成绩：
杨氏模量的测定
①利用底脚螺丝将仪器调至水平，使小圆柱 不能触碰钳形平台 ，旋转钳形平台 上的螺丝，使其轻松旋入刻槽中。
②调节读数显微镜目镜，使眼睛观察到清晰十字准线后，将物镜对准小圆柱中部，调节显微镜距离小圆柱距离，直到看清小圆柱上刻线的像，并调节消除误差。
（2）金属丝伸长的测量
①先放上一个砝码直接用肉眼观察示数，再放上全部砝码观察示数，调节显微镜高度，使实验过程中读数全部处于显微镜图象中，保留一个砝码，将显微镜目镜对准CCD系统信号输入端。
本实验我们分别采用拉伸法与弯曲法测量样品的杨氏模量，并采用逐差法与线性拟合两种方法。
二、实验原理
1、拉伸法测量杨氏模量
当一根横截面积为 的金属丝沿其径向受 的力时，我们定义其应力为
，若金属丝原长为 ，因为受力发的形变为 ，我们定义其应变为
，则根据杨氏模量的定义 ，在实验中我们用砝码的重力充当 ，并测出金属丝的直径 ，则杨氏模量可以表示为
= ，所以应变 。
根据虎克定律有： ,又因为 ，所以
，对中性面的扭矩为
；
积分后得到
对梁上个点，又有 ，当梁的弯曲较小时， ，得
，梁平衡时，在x处的转矩应与梁右端支撑力 对x处的力矩平衡，有 ，从而得到 ，根据边界条件 ，解得微分方程 ，代入 ，得到：
③
三、实验器材与实验步骤
实验器材
实验步骤：
1、伸长法测量杨氏模量
2、弯曲法测量杨氏模量
①用直尺测出横梁上两个刀口间距离。
②用千分尺在尺上从右至左基本等距离地选取五个点测量金属梁的厚度。
③用游标卡尺在尺上从右至左基本等距离地选取五处测量金属梁的宽度。
④将金属梁对称置于两刀口上，将铜件放到两刀口的中间位置。
⑤调节读数显微镜目镜使看到清楚的十字准线，再调节物镜，使小圆柱上的刻线清晰成像并没有视差。
杨氏模量的测量
杨氏模量的测量大学物理实验论文摘要：物体受外力作用时要发生形变，只要外力不超过一定限度，则作用力和相应形变之间将遵循胡克定律。
根据胡克定律，在物体的弹性限度内，应力与应变成正比，比值被称为材料的杨氏模量，它是表征材料性质的一个物理量。
杨氏模量测试方法一般有静态法和动态法，静态法包括拉伸法、扭转法和弯曲法，动态法包括弯曲共振法、横向共振法、扭转共振法。
关键词：杨氏模量拉伸法弯曲共振法Measurement of Young's modulusAbstract: The object to be deformed by external force, as long as the external force does not exceed a certain limit, then force of action and corresponding deformation will follow the Hooke's law . According to Hooke's law, the object within the elastic limit stress and strain is proportional to the ratio of the Young's modulus of the material is known, it is a physical characterization of material properties. Young's modulus testing methods are generally static and dynamic method, static method including stretching, twisting and bending method, dynamic method includes bending resonance method, the transverse resonance method, torsional resonance method.Keywords: Young's modulus, stretching method, bending resonance method引言：杨氏模量的大小标志了材料的刚性，杨氏模量越大，越不容易发生形变。
弯梁法测量杨氏模量
3.5弯梁法测量杨氏模量实验目的1．学习用弯曲法测量金属的杨氏模量。
2．了解和使用霍尔位置传感器。
3．学习微位移的测量方法。
仪器用具霍尔位置传感器杨氏模量装置（包括读数显微镜、95A 型集成霍尔传感器等），霍尔位置传感器输出信号测量仪（数字电压表）。
实验原理在弹性限度内，物体在长度方向单位横截面积所受的力/F S 称为应力，物体在长度方向产生的相对形变/L L ∆称为应变，由胡克定律可知，这二者是成正比的，即F LES L ∆= （3.5-1） 其比例系数E 称做杨氏弹性模量，即//F SE L L=∆ （3.5-2） 杨氏模量是描述固体材料在线度方向受力后，抵抗形变的能力的重要物理量。
它与材料的物质结构、化学结构及其加工制作方法等自身性质有关，与材料的几何形状和所受外力的大小无关，是工程设计中机械构件选材的重要参数和依据。
测量杨氏模量的常用方法有拉伸法、弯曲法和振动法等。
本实验采用弯曲法测量金属的杨氏模量，运用霍尔位置传感器法测量微位移。
一．用弯曲法测量金属的杨氏模量。
将厚为a 、宽为b 的金属板放在相距为d 的二刀口上（图3.5-1），在金属板上二刀口的中点处挂上质量为m 的砝码，板被压弯，设挂砝码处下降Z ∆，这时板材的杨氏模量334d mgE a b Z =∆ （3.5-3） 下面推导式(3.5-3)。
图3.5-2为沿金属板方向的纵断面的一部分。
在相距dx 的O 1O 2二点上的横断面，在金属板弯曲前互相平行，弯曲后则成一小角d ϕ。
显然，在金属板弯曲后，其下半部呈现拉伸状态，上半部为压缩状态，而在金属板的中间的一薄层虽弯曲但长度不变，称为中间层。
计算与中间层相距为y 、厚dy 、形变前长为dx 的一段，弯曲后伸长了yd ϕ，它受到的拉力为dF ，根据胡克定律有dF yd EdS dxϕ= 式中，dS 表示形变层的横截面积，即dS bdy =，于是d dF Eb ydy dx ϕ=此力对中间层的转矩为dM ，即2d dM Eby dy dxϕ= 而整个横断面的转矩M 应是22301212a d d M Eb y dy Ea b dx dxϕϕ==⎰ （3.5-4）层图3.5-1 图3.5-2如果将金属板的中点C 固定，在中点两侧各为2d 处分别施以向上的力12mg （图3.5-3），则金属板的弯曲情况应当和图3.5-1所示的完全相同。
大学物理实验教案(霍耳位置传感器法测杨氏弹性模量)
即
C为比例系数。
因而
在电流不变情况下，
(2)
式中
图1
图2
即传感器输出信号电压只与Y方向位移有关。
当铜刀口下面挂上砝码m时，横梁中心下降了Z，使得铜杠杆顶端霍尔传感器上升一距离Y1，根据杠杆原理Z与Y1关系为
3、学习用逐差法处理实验数据；
实验内容
提要
1、正确安装实验装置；
2、调试好读数显微镜；
3、记录在不同负载下铜尺的下垂量；
4、测量铜尺厚度和宽度；
5、计算杨氏模量和百分偏差。
测量与数据处理要求
1、正确测量并记录铜尺厚度和宽度；
2、下垂量各组数据的均匀度；
3、杨氏模量计算结果的有效数字和数量级、单位；
4、正确表示测量结果的百分偏差。
二、报告的评分标准（满分100）
铜尺厚度a，宽度b的测量数据：各10分；共20分。
表格数据（有效数字、分布）25分；
Z和V的平均值、比例系数各10分，其中：有效数字、单位各5分；共30分。
杨氏模量15分，其中：有效数字、单位、数量级各5分。
百分偏差10分
（1）
式中L为二刀口之间的距离，a、b分别为金属薄板的厚度和宽度。
根据(1)式，测出等号右边各量，就可以求得杨氏模量E。式中a、b、L、m这四个量用一般方法容易测得。Z是一个微小变化量，本实验用读数显微镜和霍尔位置传感器来测量。
2.霍尔位置传感器测微小位移原理
本实验使用的95A型霍尔集成传感器，其输出信号电压V为
思考题
1、为什么要用逐差法处理数据？有何优点？
大学物理实验讲义实验10 杨氏模量的测定
实验1 拉伸法测量杨氏模量杨氏弹性模量(以下简称杨氏模量)是表征固体材料性质的重要的力学参量，它反映材料弹性形变的难易程度，在机械设计及材料性能研究中有着广泛的应用。
其测量方法有静态拉伸法、悬臂梁法、简支梁法、共振法、脉冲波传输法，后两种方法测量精度较高；本实验采用静态拉伸法测量金属丝的杨氏模量，因涉及多个长度量的测量，需要研究不同测量对象如何选择不同的测量仪器。
【实验目的】1. 学习用静态拉伸法测量金属丝的杨氏模量。
2. 掌握钢卷尺、螺旋测微计和读数显微镜的使用。
3. 学习用逐差法和作图法处理数据。
4.掌握不确定度的评定方法。
【仪器用具】杨氏模量测量仪（包括砝码、待测金属丝）、螺旋测微计、钢卷尺、读数显微镜【实验原理】1. 杨氏模量的定义本实验讨论最简单的形变——拉伸形变，即棒状物体(或金属丝)仅受轴向外力作用后的伸长或缩短。
按照胡克定律：在弹性限度内，弹性体的应力S F 与应变LL δ成正比。
设有一根原长为l ，横截面积为S 的金属丝（或金属棒），在外力F 的作用下伸长了L δ，则根据胡克定律有)(LLE SF δ= （1-1） 式中的比例系数E 称为杨氏模量，单位为Pa （或N ·m –2）。
实验证明，杨氏模量E 与外力F 、金属丝的长度L 、横截面积S 的大小无关，它只与制成金属丝的材料有关。
若金属丝的直径为d ，则241d S π=，代入（1-1）式中可得 Ld FLE δπ24= （1-2）（1-2）式表明，在长度、直径和所加外力相同的情况下，杨氏模量大的金属丝伸长量较小，杨氏模量小的金属丝伸长量较大。
因此，杨氏模量反映了材料抵抗外力引起的拉伸（或压缩）形变的能力。
实验中，测量出L d L F δ、、、值就可以计算出金属丝的杨氏模量E 。
2. 静态拉伸法的测量方法测量金属丝的杨氏模量的方法就是将金属丝悬挂于支架上，上端固定，下端加砝码对金属丝F ，测出金属丝的伸长量L δ，即可求出E 。
《大学物理实验》06杨氏模量测定
实验六 杨氏模量测定1、拉伸法测量金属丝杨氏弹性模量一、实验目的1．掌握用光杠杆测量微小长度的原理和方法，测量金属丝的杨氏模量。
2．训练正确调整测量系统的能力。
3．学习一种处理实验数据的方法——逐差法。
二、实验原理1. 杨氏模量固体在外力作用下都会发生形变，同外力与形变相关的两个物理量应力与应变之间的关系一般较为复杂。
由胡克定律可知，在弹性限度内，钢丝的应力与应变成正比，比例系数 Y 称为杨氏模量；杨氏模量描述材料抵抗弹性形变能力的大小，与材料的结构、化学成分及制造方法有关。
杨氏模量是工程技术中常用的力学参数。
设有一根长为L ，横截面积为S 的钢丝，在轴向力F 的作用下，形变是轴向伸缩，且为△L,在弹性限度内，胁强F S 和胁变L L Δ成正比，既F Y S LL Δ= （1） 式中比例系数Y 称为该固体的杨氏模量。
在国际单位中，它的单位是牛顿/，记为。
是用一般长度量具不易测准的微小量，本实验用光杠杆法对其进行测量。
2米2−Nm L Δ设实验中所用钢丝直径为d ，则241d S π=，将此公式代入上式整理以后得24FLY d Lπ=Δ （2） 上式表明，对于长度L ，直径d 和所加外力F 相同的情况下，杨氏模量Y 大的金属丝的伸长量L Δ小。
因而，杨氏模量表达了金属材料抵抗外力产生拉伸(或压缩)形变的能力。
2.光杠杆原理如图1，光杠杆是一个支架，前两脚与镜面平行，后脚会随金属丝的伸长而上升或下降。
由三角函数理论可知，在θ很小时有tg θ≈θ、tg2θ≈2θ，于是根据图示几何关系可得图1将(3)式代入(2)式有： 28FLDY d l xπ=Δ将F ＝mg 代入上式，得出用伸长法测金属的杨氏模量Y 的公式为三、实验仪器杨氏模量仪（带光杠杆、望远镜和标尺），1kg 砝码若干，米尺，游标卡尺，千分尺，试样为1m 左右的钢丝。
图2所示为杨氏模量装置，待测钢丝由上夹具固定在立柱的顶端，下端用圆柱活动夹具头夹紧，圆柱形夹具穿过固定平台的圆孔，能随金属丝的伸缩而上下移动，其下端挂有砝码挂钩。
杨氏模量(梁弯曲)
霍耳位置传感器法测杨氏模量一、实验内容：1.了解霍耳效应及霍耳位置传感器的原理2.学会使用霍耳位置传感器法测杨氏模量二、实验仪器：杨氏模量测试仪、千分尺、游标卡尺三、实验原理：1．霍耳元件置于磁感应强度为B 的磁场中，在垂直于磁场方向通以电流I ，则与这二者平面垂直的方向上产生霍耳电势差：B I K U H ⋅⋅= （1）上式中K 为元件的霍耳灵敏度。
如果保持霍耳元件的电流I 不变，而使其在一均匀梯度的磁场中移动时，则输出的霍耳电势差变化量为： Z dZdB I K UH∆⋅⋅⋅=∆ （2）上式中Z ∆为位移量，此式说明若dZdB 为常数时，U ∆与Z ∆成正比。
2．一段固体棒，在其两端沿轴发现施加大小相等、方向相反的外力F ，其长度L 发生改变L ∆，杨氏模量测试仪以S 表示横截面面积，称F/S 为胁强，相对长变L ∆/L 为胁变。
在弹性限度内，由胡克定律有：LL E S F ∆⋅=E 称为杨氏模量，其数值与材料性质有关。
在横梁受力弯曲的情况下，杨氏模量E 得测量表达式为： Zb a MgdE ∆⋅⋅⋅=334 （3）其中：d 为两刀口之间的距离；M 为所加砝码的质量；a 为梁的厚度；b 为梁的宽度；Z ∆为梁中心由于外力作用而下降的距离；g 为重力加速度。
四、实验步骤：1．调节三维调节架的上下前后位置的调节螺丝，使传感器探测元件处于磁铁中间位置。
2．用水准器观察是否在平衡位置，若偏离可用底座螺丝调节到水平位置。
3．调节霍耳位置传感器的毫伏表。
磁铁盒可上下调节调节螺丝使磁铁上下移动，当毫伏表读数值很小时，停止调节并固定螺丝，最后调节零电位器使毫伏表读数为零。
4．调节读数显微镜，使眼睛观察十字线及分划板刻度线和数字清晰。
然后移动读数显微镜前后位置，使能清晰看到铜刀上的基线。
转动读数显微镜的鼓轮使刀口架上的基线与读数显微镜内十字刻度线重合，记下初始读数值。
5．逐次增加砝码，每次增加10.00g ，相应从读数显微镜读出梁中心的位置i Z （mm ）及毫伏表的读数i U （mv ）。
应用静态横梁弯曲法测量杨氏模量
数据记录和处理
01
02
03
数据记录
在实验报告中详细记录每 次施加砝码的重量、对应 的位移和弯曲程度。
数据处理
根据测量数据，计算杨氏 模量值，并进行误差分析。
结果分析
根据实验结果，分析杨氏 模量的影响因素，并得出 结论。
03 实验结果分析
数据分析和处理
数据收集
对实验过程中获取的原始数 据进行整理，确保数据准确 无误。
实验结束后，应清理实验区域，确保没有杂物和危 险品残留。
遵守操作规程
操作人员应严格遵守实验操作规程，不要随意改变 实验步骤或操作方式，以免发生意外事故。
05 实验改进和拓展
实验误差分析和改进方法
误差来源
静态横梁弯曲法测量杨氏模量时，可能存在 多种误差来源，如测量工具精度、环境温度 变化、人为操作误差等。
精确测量
在测量过程中，应尽量减小误差， 如测量横梁长度、高度等参数时 要精确，以获得更准确的结果。
注意观察实验现象
在实验过程中，应注意观察横梁 弯曲程度、砝码悬挂位置等细节， 以便及时发现异常情况。
安全防范措施
佩戴防护眼镜
实验过程中，操作人员应佩戴防护眼镜，以防实验 过程中产生的飞溅物伤害眼睛。
保持实验区域整洁
在实验中，通常将试样放在支架上，一端固定，另一端施加 集中力使其发生弯曲。通过测量横梁的弯曲曲率，结合集中 力的值，可以计算出材料的杨氏模量。
杨氏模量的定义和意义
杨氏模量是描述材料在弹性范围内抵抗变形能力的物理量，其值越大表示材料越 不易变形。
杨氏模量是材料的重要力学性能参数，广泛应用于材料科学、工程领域和日常生 活等方面。了解材料的杨氏模量对于评估其机械性能、优化产品设计、提高产品 质量等方面具有重要意义。
(整理)实验报告：杨氏模量的测量.
测定金属的杨氏模量实验日期：2014年3月4日星期二下午姓名：一、CCD成像测定杨氏模量：实验目的：（1）用金属丝的伸长测定杨氏模量；（2）用CCD成像系统测量微小长度变化；（3）用逐差法、作图法和最小二乘法处理数据。
实验仪器：测定杨氏模量专用支架，显微镜，CCD CAMERA 型号WAT-308A DC+12V（CCD摄像机，监视器），米尺（带有卡口），螺旋测微器（分度0.01mm，量程0-25mm），电子天平（精度0.01g）实验原理：（1）由胡克定律我们知道在弹性限度内：，其中是应力，E为杨氏模量，为应变。
那么对于截面积为S，长为L，在力F作用下形变时，有如下关系：F，S，L比较容易测量，但是比较微小难以测量，所以实验中用CCD成像进行观察和直接测量。
则由此可以测定杨氏模量E。
（2）CCD与主体实验装置如右图所示：实验中先使用显微镜M把确定金属丝下端所挂圆柱体上的细横线放大，同时通过不随金属丝伸长而移动的M内部分划板上的刻度线作为刻线高低的高度标准。
然后利用CCD成像进行观察。
实验内容与数据处理：1、认识和调节仪器：（1）预热CCD显示屏，调节支架S竖直，调节钳形平台的两边螺丝的松紧，使得钳形平台既可以很好的限制金属丝的转动又不用造成过多的摩擦干扰。
（2）先调节显微镜目镜，看清清晰的分划板像，然后调节物镜与金属丝下挂的圆柱上的细横线的远近，使得可以同时看清分划板和细横线的像（3）打开和连接CCD，放置在显微镜后较近的位置，仔细调节位置使得分划板像清晰，此时也可微调显微镜目镜。
然后调节显微镜的前后位置旋钮，使得细横线也变清晰。
（此时要注意微调显微镜前后的旋钮时要对应移动CCD的前后，保持分划板的清晰）反复调节可以得到分划板和细横线都比较清晰的像。
2、观测金属丝受外力拉伸后的变化：在砝码盘上一次加砝码，质量约为200.0g(需要具体重新测定精确值)。
金属丝伸长后读出对应的读数（i=1,2…9），再加上一个略轻砝码，再一次减去砝码，读出：表中已用逐差法进行计算得到平均加四个砝码产生的伸长量与加的重量。
《弯曲法测量杨氏模量》实验报告(无数据版)-王艳东
实验（实训）报告辽宁科技大学 学院（系） 年 月 日 课程名称： 实验题目：班级：姓名：学号：机台号：同组人：任课教师：实验目的1、掌握基本长度和微小位移量测量的方法，学习游标卡尺、千分尺等常用长度测量仪器的使用；2、熟悉霍尔位置传感器的特性；3、弯曲法测量铁的杨氏模量；4、学会用逐差法、作图法处理数据。
<实验原理>杨氏模量的定义：反映材料应变(即单位长度变化量L L ∆)与物体内部应力(即单位面积所受到的力的大小F S )之间关系的物理量，反映材料的抗拉或抗压能力。
即：F LYS L∆= 测量杨氏模量的方法一般有拉伸法、梁弯曲法、振动法、内耗法等，还出现了利用光纤位移传感器、莫尔条纹、电涡流传感器和波动传递技术（微波或超声波）等实验技术和方法测量杨氏模量。
1、杨氏模量的测量杨氏模量测定仪主体装置如图3所示,在横梁弯曲的情况下，杨氏模量Y 可以用下式表示：Z b a Mgd Y ∆⋅⋅⋅=334； 其中：d 为两刀口之间的距离，M 为所加砝码的质量，a 为梁的厚度，b 为梁的宽度，Z ∆为梁中心由于外力作用而下降的距离，g 为重力加速度。
上面公式的具体推导见附录。
图1 实验装置图其中：1.铜刀口上的基线 2.读数显微镜 3.刀口 4.横梁 5.铜杠杆（顶端装有A 95型集成霍尔传感器） 6.磁铁盒 7.磁铁（N 极相对放置） 8.调节架 9砝码图2 实验原理图2、微小位移△z 的测量方法： （1）读数显微镜方法：（2）霍尔位置传感器方法：定义：一块半导体薄片处于垂直于它的磁场B 中，当通以电流I 时，则在垂直于B 、I 方向上产生霍耳电势差，这种现象称为霍耳效应。
图4 霍耳效应霍尔元件置于磁感应强度为B 的磁场中，在垂直于磁场方向通以电流I ，则与这二者相垂直的方向上将产生霍尔电势差H U ：0H U K I B =⋅⋅ （1）（1）式中0K 为元件的霍尔灵敏度。
如果保持霍尔元件的电流I 不变，而使其在一个均匀梯度的磁场中移动时，则输出的霍尔电势差变化量为：0H dBU K I Z dZ∆=⋅⋅⋅∆ （2） （2）式中Z ∆为位移量，此式说明若dBI dZ⋅为常数时，H U ∆与Z ∆成正比，即： H U K Z ∆=⋅∆为实现均匀梯度的磁场，可以如图5所示，两块相同的磁铁（磁铁截面积及表面磁感应强度相同）相对放置，即N 极与N 极相对，两磁铁之间留一等间距间隙，霍尔元件平行于磁铁放在该间隙的中轴上。
3.5弯梁法测量杨氏模量
3.5弯梁法测量杨氏模量实验目的1．学习用弯曲法测量金属的杨氏模量。
2．了解和使用霍尔位置传感器。
3．学习微位移的测量方法。
仪器用具霍尔位置传感器杨氏模量装置（包括读数显微镜、95A 型集成霍尔传感器等），霍尔位置传感器输出信号测量仪（数字电压表）。
实验原理在弹性限度内，物体在长度方向单位横截面积所受的力/F S 称为应力，物体在长度方向产生的相对形变/L L ∆称为应变，由胡克定律可知，这二者是成正比的，即F L E S L∆= （3.5-1） 其比例系数E 称做杨氏弹性模量，即//F S E L L=∆ （3.5-2） 杨氏模量是描述固体材料在线度方向受力后，抵抗形变的能力的重要物理量。
它与材料的物质结构、化学结构及其加工制作方法等自身性质有关，与材料的几何形状和所受外力的大小无关，是工程设计中机械构件选材的重要参数和依据。
测量杨氏模量的常用方法有拉伸法、弯曲法和振动法等。
本实验采用弯曲法测量金属的杨氏模量，运用霍尔位置传感器法测量微位移。
一．用弯曲法测量金属的杨氏模量。
将厚为a 、宽为b 的金属板放在相距为d 的二刀口上（图3.5-1），在金属板上二刀口的中点处挂上质量为m 的砝码，板被压弯，设挂砝码处下降Z ∆，这时板材的杨氏模量334d mg E a b Z=∆ （3.5-3） 下面推导式(3.5-3)。
图3.5-2为沿金属板方向的纵断面的一部分。
在相距dx 的O 1O 2二点上的横断面，在金属板弯曲前互相平行，弯曲后则成一小角d ϕ。
显然，在金属板弯曲后，其下半部呈现拉伸状态，上半部为压缩状态，而在金属板的中间的一薄层虽弯曲但长度不变，称为中间层。
计算与中间层相距为y 、厚dy 、形变前长为dx 的一段，弯曲后伸长了yd ϕ，它受到的拉力为dF ，根据胡克定律有dF yd E dS dxϕ= 式中，dS 表示形变层的横截面积，即dS bdy =，于是d dF Eb ydy dxϕ= 此力对中间层的转矩为dM ，即2d dM Eby dy dxϕ= 而整个横断面的转矩M 应是 22301212a d d M Eb y dy Ea b dx dxϕϕ==⎰ （3.5-4）层图3.5-1 图3.5-2如果将金属板的中点C 固定，在中点两侧各为2d 处分别施以向上的力12mg （图3.5-3），则金属板的弯曲情况应当和图3.5-1所示的完全相同。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验 杨氏模量的测定(梁弯曲法)
【实验目的】
用梁的弯曲法测定金属的杨氏模量。
【仪器用具】
攸英装置，光杠杆，望远镜及直尺，螺旋测微计，游标卡尺，米尺，千分表。
【实验原理】
将厚为a 、宽为b 的金属棒放在相距为l 的二刀刃
上（图1），在棒上二刀刃的中点处挂上质量为m 的砝码，
棒被压弯，设挂砝码处下降λ，称此λ为弛垂度，这时
棒材的杨氏模量 λb a mgl E 334= . （1） 下面推导上式。
图（2）为沿棒方向的纵断面的一部分。
在相距dx 的21O O 二点上的横断面，在棒弯曲前互相平行，弯曲后则成一小角度ϕd 。
显然在棒弯曲后，棒的下半部呈现拉伸状态，上半部为压缩状态，而在棒的中间有一薄层虽然弯曲但长度不变，称为中间层。
计算与中间层相距为y 、厚dy 、形变前长为dx 的一段，弯曲后伸长了ϕyd ，它受到的拉力为dF ，根据胡克定律有
dx
yd E dS dF ϕ=. 式中dS 表示形变层的横截面积，即bdy dS =。
于是
ydy dx d Eb dF ϕ=. 此力对中间层的转矩为dM ，即 dy y dx d Eb dM 2ϕ=. 而整个横断面的转矩M 应是
dx
d b Ea dy y dx d Eb M a ϕϕ320
21212==⎰ . （2） 如果将棒的中点C 固定,在中点两侧各为2l 处分别施以向上的力mg 21(图3)，则棒的弯曲情况当和图1所示的完全相同。
棒上距中点C 为x 、长为dx 的一段，由于弯曲产生的下降λd 等于
ϕλd x l d )2
(-= （3） 当棒平衡时，由外力mg 21对该处产生的力距)2
(21x l mg -应当等于由式（2）求出的转距M ，即 dx
d b Ea x l mg ϕ3121)2(21=-. 由此式求出ϕd 代入式(3)中并积分,可求出弛垂度
b
Ea mgl dx x l b Ea mg 3321
0234)2(6=-=⎰λ, (4) 即 λ
b a mgl E 33
4=. (1)
【仪器介绍】
攸英装置如图4所示，在二支架上设置互相平的钢制刀刃，其上放置待测棒和辅助棒。
在待测棒上二刀刃间的中点处，挂上有刀刃的挂钩和砝码托盘，往托盘上加砝码时待测棒将被压弯，通过在待测棒和辅助棒上放置的千分表测量出棒弯曲的情况，从而求出棒材的杨氏模量。
【实验内容与要求】
1． 按图4安置好仪器，用千分表直接测出。
2． 用螺旋测微计在棒的各处测厚度a ，要测10次取平均值。
3． 用游标卡尺在棒的各处测宽度b （测4次）。
4． 用米尺测二刀刃间的距离l ，测4次。
5． 将测得的量代入（1）求出棒材的杨氏模量。
单位用2
-⋅m N 。
6． 求测量结果的误差。
【注意事项】
【思考问题】
1． 调节仪器的程序分几步，每一步要达到什么要求？
2． 测量时哪些量要特别仔细测？为什么？
3． 什么是弛垂度？怎样测量它？
4． 如果被测物是半径为R 的圆棒，式（1）将是什么样子的？
5． 如果用读数显微镜或螺旋测微计去测弛垂度，应当怎样进行测量？。