实验杨氏模量的测定(梁弯曲法)
《弯曲法测杨氏模量》物理实验报告(有数据)
弯曲法测定杨氏模量一、实验目的1.学习用弯曲法测量金属的杨氏模量。
2.学习用读数显微镜法测量微小位移。
3.掌握用最小二乘法及逐差法处理数据。
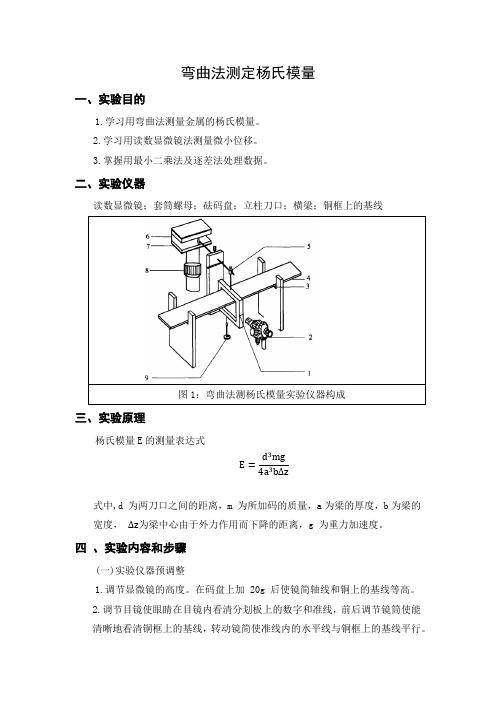
二、实验仪器读数显微镜;套筒螺母;砝码盘;立柱刀口;横梁;铜框上的基线图1:弯曲法测杨氏模量实验仪器构成三、实验原理杨氏模量E的测量表达式E=d3mg 4a3b∆z式中,d 为两刀口之间的距离,m 为所加码的质量,a为梁的厚度,b为梁的宽度,∆z为梁中心由于外力作用而下降的距离,g 为重力加速度。
四、实验内容和步骤(一)实验仪器预调整1.调节显微镜的高度。
在码盘上加 20g 后使镜简轴线和铜上的基线等高。
2.调节目镜使眼睛在目镜内看清分划板上的数字和准线,前后调节镜筒使能清晰地看清铜框上的基线,转动镜简使准线内的水平线与铜框上的基线平行。
(二)记录弯曲数据1.当砝码盘上为初始负载的情况下,转动读数鼓轮使目镜视场中的水平准线和铜框上的基线重合,记录显微镜上的初始读数。
2.在初始负载20g的基础上向砝码盘上逐次加10g的砝码,记录数据。
(三)测量黄铜的杨氏模量1.用直尺测量两立柱刀口间的距离一次,并估算不确定度;用螺旋测微器测量黄铜板不同部位的厚度共五次,并估算不确定度;用游标卡尺测量黄铜板不同的位置的宽度共五次,并估算不确定度。
2.重复(二)中的步骤,向砝码盘中逐次加10g的砝码,测出相应的8个值,用同样的方法测量并记录黄铜板的弯曲记录。
3.用逐差法处理数据,计算在40g重力下的黄铜板中心下降的距离,并计算黄铜的杨氏模量E及其误差。
五、数据处理d=230mm,a=0.8mm,b=23.34mm=130GPaE=d3mg4a3b∆z六、实验结论和分析可以根据实验结果,分析样品的结构特性。
杨氏模量是描述材料刚度和弹性特性的重要参数,对于材料的设计和性能评估具有重要意义。
需要注意的是,弯曲法测定杨氏模量是一种近似方法,实验结果可能受到多种因素的影响。
因此,在进行实验结论和分析时,应充分考虑实验条件、样品准备和测量误差等因素,以得出准确和可靠的结论。
实验6霍尔传感器的测杨氏模量

实验6 霍尔传感器测杨氏模量杨氏模量是描述固体材料抵抗形变能力的重要物理量,在工程上作为选择材料的依据之一,是工程技术中常用的参数。
利用霍尔位置传感器测量微小位移,可以改进传统粱弯曲法实验中的测量方法,使古老的实验又增添新的技术内容。
而霍尔元件及集成霍尔传感器具有尺寸小、外围电路简单、频响宽、使用寿命长,特别是抗干扰能力强等特点,近年来被广泛应用于物理量的测量、自动控制及信息处理等领域。
【实验目的】1.了解霍尔位置传感器的结构原理、特性及使用方法。
2.学习掌握粱弯曲法测量金属板的杨氏弹性模量。
3.学会确定灵敏度的方法,并确定仪器的灵敏度。
4.掌握逐差法处理数据。
【实验仪器】霍尔位置传感器、霍尔位置传感器输出信号测量仪、游标卡尺、螺旋测微器。
【实验原理】霍尔传感器置于磁感应强度为B 的磁场中,在垂直于磁场的方向通入电流I ,则会产生霍尔效应,即在与这二者相互垂直的方向上将产生霍尔电势:IB K U H H = (5.2.1)其中H K 为霍尔传感器的灵敏度,单位为T mA mV ⋅。
如果保持通入霍尔元件的电流I 不变,而使其在一均匀梯度的磁场中移动,则输出的霍尔电势的变化量为:z dzdBIK U H H ∆=∆ (5.2.2) 其中:z ∆为位移量;dzdB为磁感应强度B 沿位移方向的梯度,为常数。
为了实现上述均匀梯度磁场,选用两块相同的磁铁。
磁铁平行相对而放,即N 极相对放置。
两磁铁之间的空隙内放入霍尔元件,并使此元件平行于磁铁,且与两磁铁的间距相等,即霍尔元件放置两磁铁空隙的中心,如图6.1所示。
若间隙中心截面的中心点A 的磁感应强度为零,霍尔元件处于该处时输出的霍尔电势应为零。
当霍尔元件偏离中心沿Z 轴发生位移,由于磁感应强度不再为零,霍尔元件也就有相应电势输出,其大小可由数字电压表读出。
一般地,将霍尔电势为零时元件所处的位置作为位移参考点。
霍尔电势与位移量之间存在一一对应的关系,当位移量较小时(小于2mm ),对应关系具有良好的线性,如图6.2所示。
实验八(b)杨氏弹性模量的测量(用弯曲法)

实验八(b ) 杨氏弹性模量的测量(用弯曲法) 实验目的1.学会使用梁的弯曲法测定杨氏弹性模量。
2.熟悉用读数显微镜测量微小长度变化的方法。
实验仪器梁的弯曲实验仪,螺旋测微器,游标卡尺,米尺,读数显微镜(或测高仪),砝码。
实验原理设有效长度为l 厚度为h 宽为a 的均匀矩形梁,置在一对平行的刀口上,在矩形梁的中点竖直向下作用一个力F 如图2-8b -1所示,在弹性限度内,梁中点下垂量λ(挠度),在λ<<1时,梁的杨氏模量为 334ah Fl E λ= (2-8b -1)本实验通过测F 、l 、a 、h 、λ而测量E ,由于λ很小,用读数显微镜测出不同F 下的λ的变化值来求E 。
实验内容1.使用梁的弯曲法测定金属梁的杨氏模量(1)将待测材料安放在仪器刀口上,套上金属框架并使其刀刃恰好在仪器刀口中间,框架的下面挂上砝码盘;(2)调读数显微镜的上下位置,使望远镜的轴线对正金属框架上的小窗,调节显微镜的目镜看清十字线,前后移动显微镜,直到从望远镜中看到清楚的梁的边缘,再调整显微镜中十字线与梁的某一边重合,并消除视差;(3)从显微镜中读出初始位置r 0 ;(4)在砝码托盘上加一个砝码记下位置。
这样顺次增加200g 砝码,记下相应的位置(注意在改变砝码时,不要让砝码盘歪斜);(5)顺次将砝码取下,记下相应的位置;(6)用游标卡尺测a ,用千分尺测h ,用米尺测l 。
数据处理1.使用逐差法求挠度λ记录l 、a 、h 的测量数值及误差。
2.计算E 值(1)将l 、a 、h 、λ代入公式(2-8b -1)可以求出E ,并表示成E E E ∆±=的形式。
(2)用作图的方法求出E 的数值。
使用坐标纸,以λ为横坐标,以F 为纵坐标,作F ~λ图,应为一直线,其斜率为334l Eah k = (2-8b -2) 从图上求出k ,则 334aEhkl E = (2-8b -3)思考题1.采用光杠杆和望远镜等组成的测量系统测量λ,应如何安装仪器,简要写出实验步骤。
实验杨氏模量的测定(梁弯曲法)
实验 杨氏模量的测定(梁弯曲法)【实验目的】用梁的弯曲法测定金属的杨氏模量。
【仪器用具】攸英装置,光杠杆,望远镜及直尺,螺旋测微计,游标卡尺,米尺,千分表。
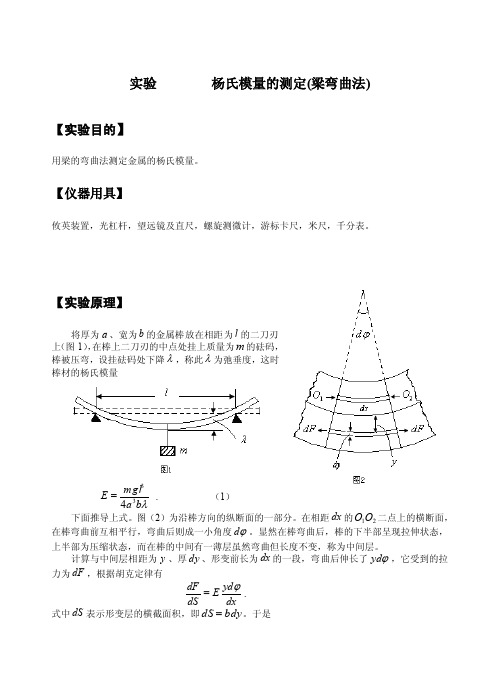
【实验原理】将厚为a 、宽为b 的金属棒放在相距为l 的二刀刃上(图1),在棒上二刀刃的中点处挂上质量为m 的砝码,棒被压弯,设挂砝码处下降λ,称此λ为弛垂度,这时棒材的杨氏模量λb a mgl E 334= . (1) 下面推导上式。
图(2)为沿棒方向的纵断面的一部分。
在相距dx 的21O O 二点上的横断面,在棒弯曲前互相平行,弯曲后则成一小角度ϕd 。
显然在棒弯曲后,棒的下半部呈现拉伸状态,上半部为压缩状态,而在棒的中间有一薄层虽然弯曲但长度不变,称为中间层。
计算与中间层相距为y 、厚dy 、形变前长为dx 的一段,弯曲后伸长了ϕyd ,它受到的拉力为dF ,根据胡克定律有dxyd E dS dF ϕ=. 式中dS 表示形变层的横截面积,即bdy dS =。
于是y d y dxd EbdF ϕ=. 此力对中间层的转矩为dM ,即 dy y dx d EbdM 2ϕ=. 而整个横断面的转矩M 应是dxd b Ea dy y dx d Eb M a ϕϕ32021212==⎰ . (2) 如果将棒的中点C 固定,在中点两侧各为2l 处分别施以向上的力mg 21(图3),则棒的弯曲情况当和图1所示的完全相同。
棒上距中点C 为x 、长为dx 的一段,由于弯曲产生的下降λd 等于ϕλd x l d )2(-= (3) 当棒平衡时,由外力mg 21对该处产生的力距)2(21x l mg -应当等于由式(2)求出的转距M ,即 dxd b Ea x l mg ϕ3121)2(21=-. 由此式求出ϕd 代入式(3)中并积分,可求出弛垂度bEa mgl dx x l b Ea mg 33210234)2(6=-=⎰λ, (4) 即 λb a m g l E 334=. (1)【仪器介绍】攸英装置如图4所示,在二支架上设置互相平的钢制刀刃,其上放置待测棒和辅助棒。
弯曲法测量杨氏模量实验心得

弯曲法测量杨氏模量实验心得刚开始,老师给我们讲了一个道理:当两根平行的长方体放在一起时,会发生什么?同学们都不知所措。
但我有一点头绪,应该把他们叠加在一起就可以测量出杨氏模量来吧!大家都兴奋地讨论着怎样去做。
我想:其中肯定会存在一些小问题和困难。
只要我努力克服它,相信成功一定属于自己的!老师叫我拿几条木板去弯曲测量它的硬度。
我从小组里借来几块木板,然后带到了操场上,经过一番仔细地打磨之后,变得光滑无比。
我轻而易举地就将它们完美结合在了一起,紧接着我按照老师教的方法进行了第二步、第三步……第七步。
最后,一个重要的一步——画图。
我终于绘制好了整个装置图。
随后,老师给我们演示了一遍,并且亲身试验了一下,果真很灵敏。
虽然现在已经五月份了,太阳高高挂在天空上,但老师还是坚持每日为我们演示,真让人敬佩啊!老师说我们明白了它的原理后就可以用它测量我们需要的物品的硬度了。
于是,我迫不及待地跑回了教室,再一次演练了整个实验过程,又发现了许多新的问题。
例如:有些人的手会不听使唤,或者木棍太粗导致很费劲儿;木棍与手掌摩擦产生的热气影响了我们的精确性等等……但总的来说,没有遇见特别严峻的考验,也没有失败。
时间飞逝,转眼间,两周过去了,两次实验就快圆满结束了。
我既兴奋又担心,因为怕测量出错误。
随着最后一声“叮”的清脆铃声,我感觉像坐过山车似的刺激极了。
不仅没有损坏物品,而且测量准确率达到100%,我和其他小组成员顿时欢呼雀跃,激动万分。
通过这次实验,我们懂得了物理学习任何事情都要脚踏实地,不能浮躁。
这次实验我们是用木棒做的。
木材质软,受压后容易断裂。
因此要采取恰当的方式对它施加外力,才能顺利完成整个实验。
一旦不注意就会引发危险。
因此,实验的时候一定要集中注意力。
《大学物理实验》-06杨氏模量测定

实验六 杨氏模量测定1、拉伸法测量金属丝杨氏弹性模量一、实验目的1.掌握用光杠杆测量微小长度的原理和方法,测量金属丝的杨氏模量。
2.训练正确调整测量系统的能力。
3.学习一种处理实验数据的方法——逐差法。
二、实验原理1. 杨氏模量固体在外力作用下都会发生形变,同外力与形变相关的两个物理量应力与应变之间的关系一般较为复杂。
由胡克定律可知,在弹性限度内,钢丝的应力与应变成正比,比例系数 Y 称为杨氏模量;杨氏模量描述材料抵抗弹性形变能力的大小,与材料的结构、化学成分及制造方法有关。
杨氏模量是工程技术中常用的力学参数。
设有一根长为L ,横截面积为S 的钢丝,在轴向力F 的作用下,形变是轴向伸缩,且为△L,在弹性限度内,胁强F S 和胁变L L Δ成正比,既F Y S LL Δ= (1) 式中比例系数Y 称为该固体的杨氏模量。
在国际单位中,它的单位是牛顿/,记为。
是用一般长度量具不易测准的微小量,本实验用光杠杆法对其进行测量。
2米2−Nm L Δ设实验中所用钢丝直径为d ,则241d S π=,将此公式代入上式整理以后得24FLY d Lπ=Δ (2) 上式表明,对于长度L ,直径d 和所加外力F 相同的情况下,杨氏模量Y 大的金属丝的伸长量L Δ小。
因而,杨氏模量表达了金属材料抵抗外力产生拉伸(或压缩)形变的能力。
2.光杠杆原理如图1,光杠杆是一个支架,前两脚与镜面平行,后脚会随金属丝的伸长而上升或下降。
由三角函数理论可知,在θ很小时有tg θ≈θ、tg2θ≈2θ,于是根据图示几何关系可得图1将(3)式代入(2)式有: 28FLDY d l xπ=Δ将F =mg 代入上式,得出用伸长法测金属的杨氏模量Y 的公式为三、实验仪器杨氏模量仪(带光杠杆、望远镜和标尺),1kg 砝码若干,米尺,游标卡尺,千分尺,试样为1m 左右的钢丝。
图2所示为杨氏模量装置,待测钢丝由上夹具固定在立柱的顶端,下端用圆柱活动夹具头夹紧,圆柱形夹具穿过固定平台的圆孔,能随金属丝的伸缩而上下移动,其下端挂有砝码挂钩。
弯曲法测量横梁的杨氏模量

弯曲法测量横梁的杨氏模量【实验目的】(1)熟悉霍尔位置传感器的特性;(2)弯曲法测量黄铜的杨氏模量;(3)测黄铜杨氏模量的同时,对霍尔位置传感器定标;(4)用霍尔位置传感器测量可锻铸铁的杨氏模量。
【实验原理】(1)霍尔位置传感器霍尔元件置于磁感应强度为的磁场中,在垂直于磁场方向通以电流,则与这二者相垂直的方向上将产生霍尔电势差:(1)(1)式中为元件的霍尔灵敏度。
如果保持霍尔元件的电流不变,而使其在一个均匀梯度的磁场中移动时,则输出的霍尔电势差变化量为:(2)(2)式中为位移量,此式说明若为常数时,与成正比。
为实现均匀梯度的磁场,可以如图1所示,两块相同的磁铁(磁铁截面积及表面磁感应强度相同)相对放置,即极与极相对,两磁铁之间留一等间距间隙,霍尔元件平行于磁铁放在该间隙的中轴上。
间隙大小要根据测量范围和测量灵敏度要求而定,间隙越小,磁场梯度就越大,灵敏度就越高。
磁铁截面要远大于霍尔元件,以尽可能的减小边缘效应影响,提高测量精确度。
若磁铁间隙内中心截面处的磁感应强度为零,霍尔元件处于该处时,输出的霍尔电势差应该为零。
当霍尔元件偏离中心沿轴发生位移时,由于磁感应强度不再为零,霍尔元件也就产生相应的电势差输出,其大小可以用数字电压表测量。
由此可以将霍尔电势差为零时元件所处的位置作为位移参考零点。
霍尔电势差与位移量之间存在一一对应关系,当位移量较小(),这一对应关系具有良好的线性。
(2)杨氏模量杨氏模量测定仪主体装置如图2所示,在横梁弯曲的情况下,杨氏模量可以用下式表示:(3)其中:为两刀口之间的距离,为所加砝码的质量,为梁的厚度,为梁的宽度,为梁中心由于外力作用而下降的距离,为重力加速度。
上面公式的具体推导见附录。
【实验仪器】(1)霍尔位置传感器测杨氏模量装置一台(底座固定箱、读数显微镜、95型集成霍尔位置传感器、磁铁两块等);(2)霍尔位置传感器输出信号测量仪一台(包括直流数字电压表)。
其中:1.铜刀口上的基线 2.读数显微镜 3.刀口 4.横梁 5.铜杠杆(顶端装有型集成霍尔传感器) 6.磁铁盒 7.磁铁(极相对放置) 8.调节架 9砝码【实验过程】1.基本内容:测量黄铜样品的杨氏模量和霍尔位置传感器的定标。
杨氏模量

杨氏模量的测量实验目的与要求1. 掌握伸长法和弯曲法测杨氏模量的原理和实验方法;2. 掌握卷尺、千分尺、游标卡尺和读数显微镜等长度测量仪器的使用方法;3. 掌握不确定度的计算。
4. 掌握数据处理方法及实验误差分析。
实验原理根据虎克定律,固体材料的伸缩形变正比于拉压外力的大小,其比例系数即为材料的杨氏模量。
测出材料在不同拉压外力作用下的伸缩形变,即可求出其杨氏模量。
杨氏模量杨氏模量是弹性模量的一种,若长为l ,截面积为S 的均匀金属丝或棒,在其长度方向上受到的作用力F 而伸长l ∆,那么根据虎克定路:在弹性限度内,协强F/S 与协变l l /∆成正比,即:ll E S F ∆⋅= 其中的比例系数E 即为该金属材料的杨氏模量,那么,lS FlE ∆=因为F ,S ,以及l 都是比较容易测量的量。
由于金属的杨氏模量一般都比较大,所以引起的长度变化比较微小,很难用普通的测量长度的仪器测准。
在验中测量钢丝的杨氏模量,其截面为圆形,其直径为时,相应的截面积2DS π=,作用力F=mg 金属丝的产生的微小伸长量为l ∆,无法用一般的长度测量仪器测量,因此实验中用光杠杆法进行测量,测量公式:h Bbl ∆=∆2 于是可得实验中的杨氏模量测量公式:hb D Blmg E ∆=28πh ∆为望远镜中观察到的刻度的变化。
不确定度公式由计算公式hb D BlmgE ∆=28π,两边取微分,然后将微分换成不确定度,求平方和的平方根,得到杨氏模量的不确定公式d222222)()2()()()()()1121111(h u D ub u B u l u m u E u h d h dD D db b dB B dl l dm m E dE h D b B l m E ∆+++++=⇒∆∆+++++⋅=∆实验装置各测量仪器的不确定度限值: 千分尺 a = 0.004mm 卷尺 a = 1mm读数显微镜 a = 0.02mmFD-HY-MT 型霍尔位置传感器杨氏模量实验仪——复旦天欣仪器厂 千分尺(0–25mm )——上海量具刀具厂 游标卡尺 (0–150mm )—上海量具刀具厂 不锈钢直尺 (0–300mm )—上海量具刀具厂 黄铜片和人造骨(PEEK )–复旦天欣仪器厂 照明灯实验内容一、伸长法测量杨氏模量1. 仪器的调节。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【实验目的】 用梁的弯曲法测定金属的杨氏模量。
【仪器用具】
攸英装置,光杠杆,望远镜及直尺,螺旋测微计,游标卡尺,米尺,千分表。
【实验原理】
将厚为a 、宽为b 的金属棒放在相距为 丨的二刀刃 上
(图1),在棒上二刀刃的中点处挂上质量为 m 的砝码, 棒被压
弯,设挂砝码处下降 ■,称此-为弛垂度,这时 棒材的杨氏模
量
下面推导上式。
图(2)为沿棒方向的纵断面的一部分。
在
相距 dx 的0Q 2二点上的横断面,
在棒弯曲前互相平行,弯曲后则成一小角度 d :。
显然在棒弯曲后,棒的下半部呈现拉伸状态, 上半部
为压缩状态,而在棒的中间有一薄层虽然弯曲但长度不变,称为中间层。
计算与中间层相距为 y 、厚dy 、形变前长为dx 的一段,弯曲后伸长了
yd 「,它受到的拉
力为dF ,根据胡克定律有 dF —匚 yd®
dS dx .
式中dS 表示形变层的横截面积,即 dS 二bdy 。
于是
实验
杨氏模量的测定(梁弯曲法)
E 審. (1)
d®
dF =Eb ydy.
dx
此力对中间层的转矩为dM ,即
d® 2
dM -Eb y dy .
dx
而整个横断面的转矩M应是
d—a 2 1 3d®
M =2Eb 2 y2dy Ea'b . (2)
dx 012 dx
1 1
如果将棒的中点C固定,在中点两侧各为处分别施以向上的力mg (图3),则棒的弯曲情
2 2
况当和图1所示的完全相同。
棒上距中点C为x、长为dx的一段,由于弯曲产生的下降d等于
(3)
1 1 l
当棒平衡时,由外力mg对该处产生的力距mg( x)应当等于由式(2)求出的转距M ,
2 2 2
即
1 J 、 1 3少:
mg( x) Ea b -
2 2 12 dx
由此式求出d代入式(3)中并积分,可求出弛垂度
mgl 3
4a 'b ■
【仪器介绍】
攸英装置如图4所示,在二支架上设置互相平的钢制刀刃,其上放置待测棒和辅助棒。
在待 测棒上二刀刃间的中点处,挂上有刀刃的挂钩和砝码托盘,往托盘上加砝码时待测棒将被压弯, 通过在待测棒和辅助棒上放置的千分表测量出棒弯曲的情况,从而求出棒材的杨氏模量。
【实验内容与要求】
1. 按图4安置好仪器,用千分表直接测出。
2. 用螺旋测微计在棒的各处测厚度 a ,要测10次取平均值。
3. 用游标卡尺在棒的各处测宽度 b (测4次)。
4. 用米尺测二刀刃间的距离 I ,测4次。
5.
将测得的量代入(1)求出棒材的杨氏模量。
单位用
N 。
6. 求测量结果的误差。
6mg Ea 3b 1 l o 2”dx mgl 3 4Ea 3b
【注意事项】
【思考问题】
1.调节仪器的程序分几步,每一步要达到什么要求?
2.测量时哪些量要特别仔细测?为什么?
3.什么是弛垂度?怎样测量它?
4.如果被测物是半径为R 的圆棒,式(1)将是什么样子的?5.如果用读数显微镜或螺旋测微计去测弛垂度,应当怎样进行测量?。
