升第八讲容斥原理之重叠问题
(小学奥数)容斥原理之重叠问题(二)
1. 瞭解容斥原理二量重疊和三量重疊的內容；2. 掌握容斥原理的在組合計數等各個方面的應用．一、兩量重疊問題 在一些計數問題中，經常遇到有關集合元素個數的計算．求兩個集合並集的元素的個數，不能簡單地把兩個集合的元素個數相加，而要從兩個集合個數之和中減去重複計算的元素個數，即減去交集的元素個數，用式子可表示成：A B A B A B =+-(其中符號“”讀作“並”，相當於中文“和”或者“或”的意思；符號“”讀作“交”，相當於中文“且”的意思．)則稱這一公式為包含與排除原理，簡稱容斥原理．圖示如下:A 表示小圓部分，B 表示大圓部分，C 表示大圓與小圓的公共部分，記為：A B ，即陰影面積．圖示如下:A 表示小圓部分，B 表示大圓部分，C 表示大圓與小圓的公共部分，記為：A B ，即陰影面積．包含與排除原理告訴我們，要計算兩個集合A B 、的並集AB 的元素的個數，可分以下兩步進行：第一步：分別計算集合A B 、的元素個數，然後加起來，即先求A B +(意思是把A B 、的一切元素都“包含”進來，加在一起)；第二步：從上面的和中減去交集的元素個數，即減去C AB =(意思是“排除”了重複計算的元素個數)．二、三量重疊問題A 類、B 類與C 類元素個數的總和A =類元素的個數B +類元素個數C +類元素個數-既是A 類又是B 類的元素個數-既是B 類又是C 類的元素個數-既是A 類又是C 類的元素個數+同時是A 類、B 類、C 類的元素個數．用符號表示為：A B C A B C A B B C A C A B C =++---+．圖示如下：教學目標知識要點7-7-2.容斥原理之重疊問題（二）1．先包含——A B +重疊部分A B 計算了2次，多加了1次；2．再排除——A B A B +-把多加了1次的重疊部分A B 減去．在解答有關包含排除問題時，我們常常利用圓圈圖(韋恩圖)來幫助分析思考．模組一、三量重疊問題【例 1】 一棟居民樓裏的住戶每戶都訂了2份不同的報紙。
初中数学专题-重叠问题(精华版)
初中数学专题-重叠问题(精华版)
重叠问题是初中数学中的一个经典问题，很多同学在研究中会
遇到这个问题，现在我们来深入探讨一下。
什么是重叠问题？简单来说，就是用图形去模拟交集的情况。
例如，我们经常听说的“集体婚礼中，每个男士都握着另外四个女
士的手，每个女士也握着另外四个男士的手，问这次婚礼有多少人？”，这就是一个重叠问题。
在解决重叠问题时，我们需要注意以下几点：
1. 画图：重叠问题通常需要用图形来表示，画图是必不可少的。
2. 分类讨论：根据具体的题目条件，我们可以把问题分成不同
情况进行讨论，从而得到最终的答案。
3. 列方程：对于一些比较复杂的重叠问题，我们可以通过列方
程的方式来解决。
4. 推广应用：重叠问题是初中数学中的一个经典问题，但它在
实际生活中也有很多应用，例如科学研究、经济分析、交通规划等
领域都有重叠问题的存在。
通过学习重叠问题，我们不仅可以提高自己的数学能力，还可
以锻炼我们的思维能力和创新能力。
希望同学们能够重视这个问题，认真学习，在学习的过程中不断提高自己的解决问题的能力。
重叠问题详解
重叠问题详解【探究必备】日常生活或数学问题中，在把一些数据按照某个标准分类时，常常出现其中的一部分数据同时属于两种或两种以上不同的类别，这样在计算总数时就会出现重复计算的情况，这类问题就叫做重叠问题，解答重叠问题常用方法是：先不考虑重叠的情况，把有重复包含的几个计数部分加起来，再从它们的和中排除重复部分元素的个数，使得计算的结果既无遗漏又不重复。
这个原理叫做包含与排除原理，也叫容斥原理。
容斥原理包含以下两条基本计算公式：①容斥原理一，如果被计数的对象，被分为A、B两大类，则：被计数对象的总个数=A类元素个数+B类元素个数—同时属于A类和B类的元素个数。
②容斥原理二，如果被计数的对象，被分为A、B、C三大类，则：被计数对象的总个数=A类元素+B类元素个数+C类元素个数—同时属于A类和B类的元素个数—同时属于A类和C类的元素个数—同时属于B类和C类的元素个数+同时属于A、B、C三类的元素个数。
运用容斥原理解答重叠问题应用题的关键是，画出示意图，认真分析已知条件，找出哪些是重复的，重复了几次？题目要求的又是哪一部分？借助示意图进行思考，找到正确的解答方法。
【王牌题目】1、三（1）班有48人，其中订《少年报》的有32人，订《数学报》的有38人，有25人两份报都订，那么：（1）只订《少年报》而没有订《数学报》的有多少人？（2）只订《数学报》而没有订《少年报》的有多少人？（3）有多少人两种报都没订？【解析】：先画出订报情况示意图，如下图：用长方形的面积表示全班人数；字母A所在的椭圆表示订《少年报》的人数32人；字母B所在的椭圆表示订《数学报》的人数38人；字母C所在区域即两个椭圆的重叠部分表示同时订了两份报的人数25人；字母D所在的空白部分表示两种报都没有的订的人数。
（1）用订《少年报》的总人数A，减去重叠部分C,剩下来的就是只订《少年报》而没有订《数学报》的人数：32-25=7（人）；（2）同理,(B-C)就是只订《数学报》而没有订《少年报》的人数：38-25=13（人）；（3）先求出订报的总人数，即图中所有阴影部分表示的人数，再用班级总人数减去订报总人数，即是两种报都没订的人数D。
重叠问题(容斥问题)
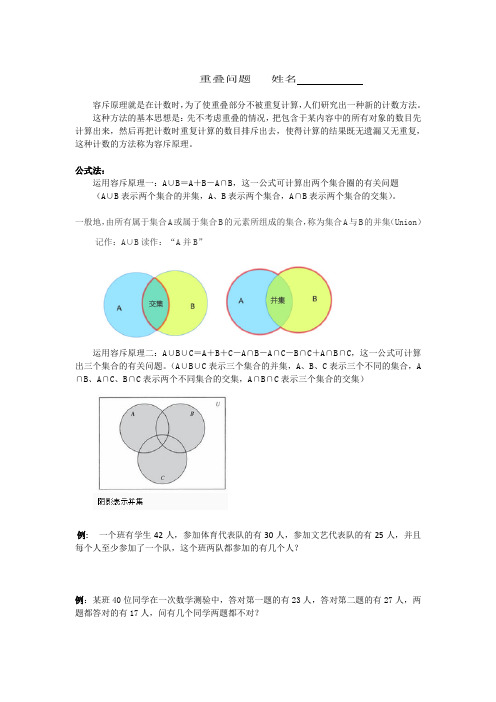
重叠问题姓名容斥原理就是在计数时，为了使重叠部分不被重复计算，人们研究出一种新的计数方法。
这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。
公式法：运用容斥原理一：A∪B＝A＋B－A∩B，这一公式可计算出两个集合圈的有关问题（A∪B表示两个集合的并集，A、B表示两个集合，A∩B表示两个集合的交集）。
一般地，由所有属于集合A或属于集合B的元素所组成的集合，称为集合A与B的并集（Union）记作：A∪B读作：“A并B”运用容斥原理二：A∪B∪C＝A＋B＋C－A∩B－A∩C－B∩C＋A∩B∩C，这一公式可计算出三个集合的有关问题。
（A∪B∪C表示三个集合的并集，A、B、C表示三个不同的集合，A ∩B、A∩C、B∩C表示两个不同集合的交集，A∩B∩C表示三个集合的交集）例:一个班有学生42人，参加体育代表队的有30人，参加文艺代表队的有25人，并且每个人至少参加了一个队，这个班两队都参加的有几个人？例：某班40位同学在一次数学测验中，答对第一题的有23人，答对第二题的有27人，两题都答对的有17人，问有几个同学两题都不对？练习: 有100位旅客，其中10人既不懂英语，又不懂俄语，有75人懂英语，有83人懂俄语。
那么这100位旅客中既懂英语又懂俄语的有多少人？例：某校有三个兴趣小组，体育、书法和美术。
已知参加这三个兴趣小组的学生人数分别是25人、24人和30人。
同时参加体育、书法兴趣小组的有5人，同时参加体育、美术兴趣小组的有2人，同时参加书法、美术兴趣小组的有4人，有1人同时参加了这三个兴趣小组，问：共有多少人参加兴趣小组？练习：某校对五年级100名同学进行学习兴趣调查，结果有58人喜欢语文，有38人喜欢数学，有52人喜欢外语。
而且喜欢语文和数学(但不喜欢外语)的有6人，喜欢数学和外语(但不喜欢语文)的有4人，三科都喜欢的有12人，而且每人至少喜欢一科。
7-7-2 容斥原理之重叠问题(二).学生版
1.了解容斥原理二量重叠和三量重叠的内容； 2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-(其中符号“”读作“并”，相当于中文“和”或者“或”的意思；符号“”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：AB ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B 的元素的个数，可分以下两步进行：第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =(意思是“排除”了重复计算的元素个数)．二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+．图示如下：在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．教学目标知识要点7-7-2.容斥原理之重叠问题（二）1．先包含——A B +重叠部分A B 计算了2次，多加了1次； 2．再排除——A B A B +-把多加了1次的重叠部分A B 减去．图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆表示C 的元素的个数．1．先包含：A B C ++重叠部分A B 、B C 、C A 重叠了2次，多加了1次． 2．再排除：A B C A B B C A C ++---重叠部分A B C 重叠了3次，但是在进行A B C ++- A B B C A C --计算时都被减掉了． 3．再包含：A B C A B B C A C A B C ++---+．例题精讲模块一、三量重叠问题【例1】一栋居民楼里的住户每户都订了2份不同的报纸。
第八讲容斥原理案例
|A|=17 |B|=30 |C|=13 |A∩B∩C|=5 |A∪B∪C|=|A|+|B|+|C| -|A∩B|-|A∩C|-|B∩C| +|A∩B∩C|=35 所以 |A∩B|+|A∩C|+|B∩C|=30 所求数目= |A|-|A∩B|-|A∩C| +|A∩B∩C| +|B|-|B∩C| |-|A∩B +|A∩B∩C| +|C|-|A∩C|-|B∩C| +|A∩B∩C| =60-2×30+3×5=15
70、36。问阴影部分（黄色）的面积是多少？ A．15 B．16 C．14 D．18
11.三位专家为10幅作品投票，每位专家分别都投 出了5票，并且每幅作品都有专家投票。如果 三位专家都投票的作品列为A等，两位专家投 票的列为B等，仅有一位专家投票的作品列为 C等，则下列说法正确的是（ D ）。 A. A等和B等共6幅 B. B等和C等共7幅
120-(50+45+40-15-10-8+4)=14(人)
6.分母是1001的最简分数一共有多少个？ 解：这一题实际上就是找分子中不能整除 1001 的数。由于 1001=7×11×13 ，所以就 是找不能被7，11，13整除的数。
如图
7的倍数143个 11的倍数91个
13
11 7
13的倍数77个
子一共被剪成了多少段？
59+39-19=79
9.在游艺会上，有100名同学抽到了标签分别为1至100的奖 券。按奖券标签号发放奖品的规则如下： （1）标签号为2的倍数，奖2支铅笔； （2）标签号为3的倍数，奖3支铅笔； （3）标签号既是2的倍数，又是3的倍数可重复领奖； （4）其他标签号均奖1支铅笔。那么游艺会为该项活动准备 的奖品铅笔共有多少支？ 解：(50-16)×2+(33-16)×3+16×5+33×1=242
三年级上册数学重叠问题
三年级上册数学重叠问题一、引言在小学数学学习中，三年级上册数学是一个承上启下的阶段，对于学生后续数学学习具有重要意义。
其中，重叠问题是一个相对较难但非常重要的知识点。
本文将通过具体案例，深入探讨三年级上册数学重叠问题的概念、解题方法和应用场景，帮助学生们更好地理解和掌握这一知识点。
二、重叠问题的概念重叠问题是指两个或多个集合元素同时属于两个或多个集合的情况。
在三年级上册数学中，常见的重叠问题包括容斥原理、两堆物体等问题。
这类问题需要学生们能够准确识别元素的重叠情况，并运用适当的数学原理进行求解。
三、解题方法1. 列举法：对于简单的重叠问题，可以通过列举法直接求解。
例如，有两个盒子，其中一个盒子中有3个红球和2个白球，另一个盒子中有2个红球和3个黑球。
求至少有一个红球但颜色未知的球的总数。
通过列举，我们可以得到共有5个球。
2. 容斥原理：容斥原理是一种常用的解题方法，适用于两个集合之间存在重叠的情况。
通过将重叠元素的个数加到两个集合的并集元素个数上，再减去重复计算的部分，可以求出最终结果。
例如，有5个男生和3个女生参加了数学竞赛，问至少有一个男生参加竞赛的学生人数。
根据容斥原理，至少有一个男生参加竞赛的学生人数为5+3-1=7人。
3. 画图法：对于较复杂的问题，可以通过画图来帮助理解。
通过将重叠部分用阴影标出，可以直观地看到元素的分布情况，从而快速找到答案。
四、应用场景重叠问题在日常生活和工作中也经常出现，如运动会报名、志愿者招募等。
学生们可以通过解决重叠问题培养逻辑思维和判断能力，为未来的学习和工作打下基础。
例如，在志愿者招募中，如果有两个志愿者团队同时申请了一些职位，就需要用到重叠问题的知识来计算最终的招募结果。
又如，在超市购物时，需要计算会员卡同时属于两种会员类型的人数，从而决定是否给予优惠。
五、总结三年级上册数学重叠问题是一个相对较难但非常重要的知识点，需要学生们认真理解和掌握。
通过列举法、容斥原理等解题方法，我们可以解决各种类型的重叠问题。
重叠问题(容斥原理,包含与排除)
包含与排除例题1，(1)五年级一班参加体育兴趣小组的有30人，参加文艺兴趣小组的有25人，两项活动都参加的有13人，全班每人至少参加一项活动。
问这个班有多少人？(2)三年级一班参加合唱队的有40人，参加舞蹈队的有20人，既参加合唱队又参加舞蹈队的有14人。
这两队都没有参加的有10人。
请算一算，这个班共有多少人？1，学校文艺组每人至少会演奏一种乐器，已知会拉手风琴的有24人，会弹电子琴的有17人，其中两种乐器都会演奏的有8人。
这个文艺组一共有多少人？2,某班在一次测验中有26人语文获优，有30人数学获优，其中语文、数学双优的有12人，另外还有8人语文、数学均未获优。
这个班共有多少人？3，第一小组的同学们都在做两道数学思考题，做对第一题的有15人，做对第二题的有10人，两题都做对的有7人，两题都做错的有2人。
第一小组共有多少人？例题2，(1)五年级一班有42人，参加体育兴趣小组的有30人，参加文艺兴趣小组的有25人，全班每人至少参加一项活动。
问这个班两项活动都参加的有多少人？(2)一个旅行社有36人，其中会英语的有24人，会法语的有18人，两样都不会的有4人。
两样都会的有多少人？(3)3,某班有36个同学在一项测试中，答对第一题的有25人，答对第二题的有23人，两题都答对的有15人。
问多少个同学两题都答得不对？1，五年级有122名学生参加语文、数学考试，每人至少有一门功课取得优秀成绩。
其中语文成绩优秀的有65人，数学优秀的有87人。
语文、数学都优秀的有多少人？2，一个俱乐部有103人，其中会下中国象棋的有69人，会下国际象棋的有52人，这两种棋都不会下的有12人。
问这两种棋都会下的有多少人？3，学校开展课外活动，共有250人参加。
其中参加象棋组和乒乓球组的同学不同时活动，参加象棋组的有83人，参加乒乓球组的有86人，这两个小组都参加的有25人。
问这250名同学中，象棋组、乒乓球组都不参加的有多少人？例题3，(1)四年级一班有54人，订阅《小学生优秀作文》和《数学大世界》两种读物的有13人，订《小学生优秀作文》的有45人，每人至少订一种读物，订《数学大世界》的有多少人？(2)全班46名同学，仅会打乒乓球的有28人，会打乒乓球又会打羽毛球的有10人，不会打乒乓球又不会打羽毛球的有6人。
重叠问题课件ppt
诊断重叠问题的工具和方法
鱼骨图
用于展示问题产生的原因和影 响，帮助团队全面了解问题的
各个方面。
5W分析法
通过对问题进行“为什么、是 什么、在哪里、何时、谁”的 分析，深入挖掘问题的根源。
流程图
用于梳理业务流程，发现流程 中的瓶颈和问题。
数据分析
利用统计学和数据挖掘技术， 对大量数据进行深入分析，发
现数据背后的规律和趋势。
重叠问题的根源分析
组织结构问题
组织结构不合理，导致 部门间沟通不畅、职责
不明确。
流程问题
业务流程存在缺陷或不 合理之处，导致工作效
率低下、资源浪费。
文化问题
企业文化不健康，缺乏 团队协作精神、创新精
神。
人员素质问题
员工素质不高，缺乏必 要的技能和知识，导致
工作质量低下。
2023
流程再造
对不合理流程进行重新设计，提高 流程效率和效益。
信息化管理
利用信息技术手段，实现流程自动 化和智能化。
资源整合
资源共享
实现资源在不同部门间的共享， 提高资源利用效率。
集中采购
通过集中采购降低成本，提高采 购效益。
内部市场
建立内部市场机制，促进资源优 化配置和有效利用。
激励机制设计
目标管理
2023
重叠问题课件
REPORTING
2023
目录
• 引言 • 重叠问题的识别与诊断 • 解决重叠问题的策略 • 重叠问题的案例分析 • 总结与展望
2023
PART 01
引言
REPORTING
什么是重叠问题
重叠问题是指两个或多个物体 或形状在空间上部分或全部重 叠在一起的问题。
重叠问题知识要点
重叠问题是指在概率统计中，多个事件之间存在共同发生的可能性。
解决重叠问题的关键是正确计算相互影响的事件发生的概率。
主要知识点包括：
1. 重叠事件的概率计算：重叠事件A和B同时发生的概率P(A∩B)可以通过公式P(A∩B)=P(A)P(B|A)计算，其中P(B|A)表示在事件A发生的条件下事件B发生的概率。
2. 独立事件：如果两个事件A和B相互独立，那么事件A发生对事件B发生的概率没有影响，即P(B|A)=P(B)。
独立事件的重叠概率P(A∩B)=P(A)P(B)。
3. 互斥事件：如果两个事件A和B互斥，那么它们不可能同时发生，即P(A∩B)=0。
4. 一般重叠问题的求解方法：对于一般重叠问题，可以采用先分类后分步的方法，将问题拆分为多个互斥事件的和，然后分别计算每个互斥事件的概率，最后将这些概率相加得到结果。
5. 重叠问题的实际应用：重叠问题在实际生活中有很多应用，如保险、排队理论、可靠性工程等领域。
掌握重叠问题的解决方法对于解决实际问题具有重要意义。
小学思维数学讲义：几何中的重叠问题-带详解
几何中的重叠问题1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-(其中符号“”读作“并”，相当于中文“和”或者“或”的意思；符号“”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B 的元素的个数，可分以下两步进行： 第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =(意思是“排除”了重复计算的元素个数)． 二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+．图示如下：在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．教学目标 知识要点 1．先包含——A B + 重叠部分A B 计算了2次，多加了1次； 2．再排除——A B A B +- 把多加了1次的重叠部分A B 减去．图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆表示C 的元素的个数．1．先包含：A B C ++ 重叠部分A B 、B C 、C A 重叠了2次，多加了1次． 2．再排除：A B C A B B C A C ++--- 重叠部分A B C 重叠了3次，但是在进行A B C ++- A B B C A C --计算时都被减掉了． 3．再包含：A B C A B B C A C A B C ++---+．【例 1】 把长38厘米和53厘米的两根铁条焊接成一根铁条．已知焊接部分长4厘米，焊接后这根铁条有多长？【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 因为焊接部分为两根铁条的重合部分，所以，由包含排除法知，焊接后这根铁条长3853487+-=(厘米)．【答案】87厘米【巩固】 把长23厘米和37厘米的两根铁条焊接成一根铁条．已知焊接部分长3厘米，焊接后这根铁条有多长？【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 焊接部分为两根铁条的重合部分，由包含排除法知，焊接后这根铁条长：2337357+-=(厘米)．【答案】57厘米【例 2】 两张长4厘米，宽2厘米的长方形纸摆放成如图所示形状．把它放在桌面上，覆盖面积有多少平方厘米？【考点】几何中的重叠问题 【难度】1星 【题型】解答图32厘米4厘米【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为2厘米的正方形，如果利用两个42⨯的长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，被覆盖面积=长方形面积之和-重叠部分．于是，被覆盖面积4222212=⨯⨯-⨯=(平方厘米)．【答案】12厘米【巩固】 如图3，一张长8厘米，宽6厘米，另一个正方形边长为6厘米，它们中间重叠的部分是一个边长为4厘米的正方形，求这个组合图形的面积．【考点】几何中的重叠问题 【难度】1星 【题型】解答图3 【解析】 两个图形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用长方形和正方形面积之和来计算被覆盖桌面的面积，那么重叠部分在长方形和正方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积+正方形面积-重叠部分．于是，组合图形的面积：86664468⨯+⨯-⨯=(平方厘米)．【答案】68平方厘米【巩固】 一个长方形长12厘米，宽8厘米，另一个长方形长10厘米，宽6厘米，它们中间重叠的部分是一个边长4厘米的正方形，求这个组合图形的面积．【考点】几何中的重叠问题 【难度】1星 【题型】解答例题精讲12【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用两个长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积之和-重叠部分．于是，组合图形的面积12810644140=⨯+⨯-⨯=(平方厘米)．【答案】140平方厘米【例 3】 三个面积均为50平方厘米的圆纸片放在桌面上(如图)，三个纸片共同重叠的面积是10平方厘米．三个纸片盖住桌面的总面积是100厘米．问：图中阴影部分面积之和是多少？【考点】几何中的重叠问题 【难度】2星 【题型】解答CBA10 【解析】 将图中的三个圆标上A 、B 、C ．根据包含排除法，三个纸片盖住桌面的总面积=(A 圆面积B +圆面积C +圆面积-）（A 与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积+）三个纸片共同重叠的面积，得：100505050A =++-（）（与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积10+），得到A 、B 、C 三个圆两两重合面积之和为：16010060-=平方厘米，而这个面积对应于圆上的那三个纸片共同重叠的面积的三倍与阴影部分面积的和，即：60103=⨯+阴影部分面积，则阴影部分面积为：603030-=(平方厘米)．【答案】30平方厘米【巩固】 如图，已知甲、乙、丙3个圆的面积均为30，甲与乙、乙与丙、甲与丙重合部分的面积分别为6，8，5，而3个圆覆盖的总面积为73．求阴影部分的面积．【考点】几何中的重叠问题 【难度】2星 【题型】解答【解析】 设甲圆组成集合A ，乙圆组成集合B ，丙圆组成集合C ． A B C ===30，A B =6，B C =8，A C =5，A B C =73，而A B C =A B C +--A B B C A C A B C --+.有73=30×3-6-8-5+AB C ，即A B C =2，即甲、乙、丙三者的公共面积(⑧部分面积)为2．那么只是甲与乙(④)，乙与丙(⑥)，甲与丙(⑤)的公共的面积依次为6-2=4，8-2=6，5-2=3，所以有阴影部分(①、②、③部分之和)的面积为73-4-6-3-2=58．【答案】58【例 4】 如图，三角形纸板、正方形纸板、圆形纸板的面积相等，都等于60平方厘米．阴影部分的面积总和是40平方厘米，3张板盖住的总面积是100平方厘米，3张纸板重叠部分的面积是多少平方厘米？【考点】几何中的重叠问题 【难度】3星【题型】解答【解析】 阴部分的面积60310040220=⨯--÷=（）(平方厘米)．【答案】20平方厘米【巩固】如图所示，A、B、C分别是面积为12、28、16的三张不同形状的纸片，它们重叠在一起，露在外面的总面积为38．若A与B、B与C的公共部分的面积分别为8、7，A、B、C这三张纸片的公共部分为3．求A与C公共部分的面积是多少？【考点】几何中的重叠问题【难度】3星【题型】解答【解析】设A与C公共部分的面积为x，由包含与排除原理可得：⑴先“包含”：把图形A、B、C的面积相加：12281656++=，那么每两个图形的公共部分的面积都重复计算了1次，因此要排除掉．⑵再“排除”：5687x---，这样一来，三个图形的公共部分被全部减掉，因此还要再补回．⑶再“包含”：56873---+，这就是三张纸片覆盖的面积．x根据上面的分析得：5687338x=．x---+=，解得：6【答案】6。
小学思维数学讲义：容斥原理之重叠问题(一)-带答案解析
容斥原理之重叠问题（一）1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-(其中符号“”读作“并”，相当于中文“和”或者“或”的意思；符号“”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B 的元素的个数，可分以下两步进行： 第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =(意思是“排除”了重复计算的元素个数)．二、三量重叠问题 A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+．图示如下：在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．教学目标 例题精讲知识要点 1．先包含——A B +重叠部分A B 计算了2次，多加了1次；2．再排除——A B A B +-把多加了1次的重叠部分A B 减去． 图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆表示C 的元素的个数．1．先包含：A B C ++ 重叠部分A B 、B C 、C A 重叠了2次，多加了1次． 2．再排除：A B C A B B C A C ++--- 重叠部分A B C 重叠了3次，但是在进行A B C ++- A B B C A C --计算时都被减掉了． 3．再包含：A B C A B B C A C A B C ++---+．两量重叠问题【例 1】小明喜欢：踢足球、上网、游泳、音乐、语文、数学；小英喜欢：数学、英语、音乐、陶艺、跳绳。
小学-重叠问题-中学-容斥原理
重叠问题一、专题简析解答重叠问题要用到数学中的一个重要原理——包含与排除原理，即当两个计数部分有重复包含时，为了不重复计数，应从它们的和中排除重复部分。
解答重叠问题的应用题，必须从条件入手进行认真的分析，有时还要画出图示，借助图形进行思考，找出哪些是重复的，重复了几次？明确求的是哪一部分，从而找出解答方法。
二、精讲精练【例题1】六一儿童节，学校门口挂了一行彩旗。
小张从前数起，红旗是第8面；从后数起，红旗是第10面。
这行彩旗共多少面？练习1：1.学校组织看文艺演出，冬冬的座位从左数起是第12个，从右数起是第21个。
这一行座位有个。
2.同学们排队去参观展览，无论从前数还是从后起起，李华都排在第8个。
这一排共有个同学。
【例题2】同学们排队做操，每行人数同样多。
小明的位置从左数起是第4个，从右数起是第3个，从前数起是第5个，从后数起是第6个。
做操的同学共有多少个？练习2：1.同学们排队跳舞，每行、每列人数同样多。
小红的位置无论从前数从后数，从左数还是从右数起都是第4个。
跳舞的共有人。
2.三（4）班排成每行人数相同的队伍入场参加校运动会，梅梅的位置从前数是第6个，从后数是第5个；从左数、从右数都是第3个。
三（4）班共有学生人。
【例题3】把两块一样长的木板像下图这样钉在一起成了一块木板。
如果这块钉在一起的木板长120厘米，中间重叠部分是16厘米，这两块木板各长多少厘米？练习3：1.把两段一样长的纸条粘合在一起，形成一段更长的纸条。
这段更长的纸条长30厘米，中间重叠部分是6厘米，原来两段纸条各长多少厘米？2.把两块一样长的木板钉在一起，钉成一块长35厘米的木板。
中间重合部分长11厘米，这两块木板各长多少厘米？3.两根木棍放在一起，从头到尾共长66厘米，其中一根木棍长48厘米，中间重叠部分长12厘米。
另一根木棍长多少厘米？【例题4】一次数学测试，全班36人中，做对第一道聪明题的有21人，做对第二道聪明题的有18人，每人至少做对一道。
容斥原理之重叠问题
第八讲：容斥原理之重叠问题导入文氏图 -------------------------------文氏图，也叫维恩图”是由英国著名数学家Venn发明的.维恩（公元1834 年8月4日「公元1923 年4月4日）十九世纪英国著名的数学家和哲学家，生于英国赫尔.他1883 年获得理学博士学位，同年被选为英国皇家学会会员.维恩最主要的成就是系统解释并发展了几何表示的方法，也就是发明了文氏图.他作出一系列简单闭曲线（圆或更复杂的图形），将平面分为许多间隔.利用这种图表，维恩阐明了演绎推理的基本原理.为了进一步明确起见，他还引入了一些数学难题作为实例.虽然在维恩之前，莱布尼茨（Leibniz ）已系统地运用过这类逻辑图，但今天这种逻辑图仍称作维恩图”另外, 维恩在概率论和逻辑学方面也有很大贡献，他的著作一一《机会逻辑》和《符号逻辑》，在19 世纪末20 世纪初曾享有很高的声誉.当澳洲板球队在1909 年到访剑桥大学时，维恩的机器依然运作正常，并使他们其中一位成员打空四次.除了数学以外，维恩还有一项较为特别的技能制作机器.他曾制作过一部板球发球机,什么是容斥原理？这一讲我们主要学习和“包含”与“排除”有关的问题，这样的问题在生活中就有不少，比如吃瓜子.我们说吃掉了一斤瓜子，指的是带壳的瓜子，并非真的吃到肚子里一斤，因为这一斤中还“包含”着瓜子壳.如果要计算到底吃了多少，最简单的方法就是称一称瓜子壳，用原来的一斤“排除”掉瓜子壳的重量.瓜子的例子相对简单，一斤瓜子里一部分是瓜子仁，另一部分就是瓜子壳，两者各不相关.但本讲要学习的包含与排除问题要复杂一些，各部分之间会有重叠.比如一个办公室中每个人都至少爱喝茶或咖啡中的一种，已知有7个人爱喝茶，10个人爱喝咖啡，那能不能就说办公室里有17 个人呢？显然不能，因为可能有一些人既爱喝茶也爱喝咖啡，如果直接将喝茶的人数和喝咖啡的人数相加，会把既爱喝茶又爱喝咖啡的人计算2次，计算人数的时候要把这一部分减去才行.比如，如果有3个人既爱喝茶又爱喝咖啡，那总的人数就应该是7 + 10 - 3 = 14 人.这就是我们今天要来研究的问题一一有重叠的计数问题，即包含与排除问题•研究这种问题通常需要画出示意图，这样的示意图又叫做文氏图，下面我们就用文氏图推导两个对象的容斥原理公式.两个量之间的重叠例1、某班有34名同学参加了学校的运动会，其中有17名参加了跳绳，有20名参加了拔河，问：及参加了跳绳又参加了拔河的又多少人？如右图所示，如果要计算三个部分的总数，直接计算A+B就会算多了，而多算的正好是共同部分，只要把多算的减掉就可以了•上述分析总结成公式就是：木R总数="+占一』、刀巫輕这个公式就是两个对象的容斥原理.17+20-34=37-34=3 （人）答：即参加跳绳又参加拔河的同学有3人练一练1、五年级有122 名学生参加语文、数学考试，每人至少有一门功课的成绩是优秀，其中语文成绩优秀的有65人，数学优秀的有87人•语文、数学都优秀的有多少人？2、在一次数学测试中有两道题全班同学都至少答对一题，答对第一题的有33人，答对第二题的又38人，两题都答对的又15人，问全班又多少人？3、学校文艺组每人至少会演奏一种乐器。
容斥原理之重叠问题(一)
7-7-1.容斥原理之重叠问题（一）教学目标1.了解容斥原理二量重叠和三量重叠的内容；2.掌握容斥原理的在组合计数等各个方面的应用．知识要点一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+- (其中符号“ ”读作“并”，相当于中文“和”或者“或”的意思；符号“ ”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B 的元素的个数，可分以下两步进行：第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B = (意思是“排除”了重复计算的元素个数)．二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+ ．图示如下：在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．1．先包含——A B+重叠部分A B 计算了2次，多加了1次；2．再排除——A B A B+- 把多加了1次的重叠部分A B 减去．图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆表示C 的元素的个数．1．先包含：A B C++重叠部分A B 、B C 、C A 重叠了2次，多加了1次．2．再排除：A B C A B B C A C++--- 重叠部分A B C 重叠了3次，但是在进行A B C ++-A B B C A C -- 计算时都被减掉了．3．再包含：A B C A B B C A C A B C ++---+ ．例题精讲两量重叠问题【例1】小明喜欢：踢足球、上网、游泳、音乐、语文、数学；小英喜欢：数学、英语、音乐、陶艺、跳绳。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第八讲：容斥原理之重叠问题
导入
文氏图■■■■■■■■■■■■■■■
文氏图，也叫维恩图”是由英国著名数学家Venn发明的.
维恩（公元1834 年8月4日「公元1923 年4月4日）十九世纪英国著名的数学家和哲学家，生于英国赫尔.他1883 年获得理学博士学位，同年被选为英国皇家学会会员.
维恩最主要的成就是系统解释并发展了几何表示的方法，也就是发明了文氏图.■他作出一系列
・
简单闭曲线（圆或更复杂的图形），将平面分为许多间隔.利用这种图表，维恩阐明了演绎推理的基本原
理.为了进一步明确起见，他还引入了一些数学难题作为实例.虽然在维恩之前，
莱布尼茨（Leibniz ）已系统地运用过这类逻辑图，但今天这种逻辑图仍称作维恩图”另外, 维
恩在概率论和逻辑学方面也有很大贡献，他的著作一一《机会逻辑》和《符号逻辑》，在19 世纪末20
世纪初曾享有很高的声誉.
除了数学以外，维恩还有一项较为特别的技能一一制作机器.他曾制作过一部板球发球机，
当澳洲板球队在1909 年到访剑桥大学时，维恩的机器依然运作正常，并使他们其中一位成员打空四次.
什么是容斥原理?
这一讲我们主要学习和“包含”与“排除”有关的问题，这样的问题在生活中就有不少，比如吃瓜子.我们说吃掉了一斤瓜子，指的是带壳的瓜子，并非真的吃到肚子里一斤，因为这一斤中还“包含”着瓜子壳.如果要计算到底吃了多少，最简单的方法就是称一称瓜子壳，用原来的一斤“排除”掉瓜子壳的重量.瓜子的例子相对简单，一斤瓜子里一部分是瓜子仁，另一部分就是瓜子壳，两者各不相关.但本讲要学习的包含与排除问题要复杂一些，各部分之间会有重叠.
比如一个办公室中每个人都至少爱喝茶或咖啡中的一种，已知有7个人爱喝茶，10个人爱喝咖啡，那能不能就说办公室里有17 个人呢？显然不能，因为可能有一些人既爱喝茶也爱
喝咖啡，如果直接将喝茶的人数和喝咖啡的人数相加，会把既爱喝茶又爱喝咖啡的人计算2
次，计算人数的时候要把这一部分减去才行.
比如，如果有3个人既爱喝茶又爱喝咖啡，那总的人数就应该是7 + 10 - 3 = 14 人.
这就是我们今天要来研究的问题一一有重叠的计数问题，即包含与排除问题•研究这种问题通常需要画出示意图，这样的示意图又叫做文氏图，下面我们就用文氏图推导两个对象的容斥原理公式.
两个量之间的重叠
例1、某班有34名同学参加了学校的运动会，其中有17名参加了跳绳，有20名参加了拔河，问：及参加了跳绳又参加了拔河的又多少人？
如右图所示，如果要计算三个部分的总数，直接计算A+B 就会算多了，
而多算的正好是共同部分，只要把多算的减掉就可以了•上述分析总结成公式
就是：
R总数=沖+丹一』、号重拄
这个公式就是两个对象的容斥原理.
练一练
1、五年级有122 名学生参加语文、数学考试，每人至少有一门功课的成绩是优秀，其中语
文成绩优秀的有65人，数学优秀的有87人•语文、数学都优秀的有多少人？
2、在一次数学测试中有两道题全班同学都至少答对一题，答对第一题的有33人，答对第二
题的又38人，两题都答对的又15人，问全班又多少人？
3、学校文艺组每人至少会演奏一种乐器。
已知会拉手风琴的有24人，会弹电子琴的有17
人，其中两种乐器都会的有8人，这个文艺组一共有多少人？
挑战思维
1、为了参加一次竞赛，某班46人中，每人至少参加一项。
其中有20人参加语文兴趣小组，，
参加语文同时又参加数学兴趣小组的有2人，两项都没有报的有10人，那么参加数学兴趣小组的有多少人？
换个思路想一想至少报
一项的有多少人?
三个量之间的重叠
1、某单位元旦期间组织旅游，每人至少说出一个想去的地方。
其中想去海南的有42人，想
去桂林的有44人，想去港澳的有36人，既想去海南又想去桂林的有12人，既想去桂林又想去港澳的有8人，既想去海南又想去港澳的有10人，三个地方都想去的有4人。
问这个单位一共有多少人？
(42=44+36 )-12-8-10+4
=122- ( 12+8+10 )+4
=122-30+4
=96 (人)
答：这个单位一共有96人。
方法总结:
（1）三个量的重叠问题中，如果是全部参与，则总人数等于参加三项的人数和减去同时参加两项的人数和，再加上同时参加的三项人数。
（2 ）三个量的重叠问题中，如果是部分参与，则总人数等于至少参加一项的人数和三项都没有参加的人数和，
如果都参加了，总数等于三个量的和减去两两重叠的部分，在加上三个量重叠的部分
公式:s=a + b + c-ab-bc-ac+abc
部分参与
练一练
1、学校对150名大学生做关于《业余生活》的调查，统计到喜欢看电影的有63人，喜欢玩球的有66人，喜欢读书的有54人，既喜欢看电影又喜欢玩球的有18人，既喜欢玩球又喜欢读书的有12人，既喜欢看电影又喜欢读书的有15人•问：三种都喜欢的有多少人？
2、在校园艺术活动中，五（2 ）班的同学参加了美术和声乐比赛。
参加美术比赛的有25人, 参加声乐比赛的有20人，两项都参加的有12人，两项都没有参加的有10人。
五（2 ）班一共有多少人？
挑战竞赛
3、学校举行运动会。
四年级共有 60名同学，其中参加百米赛跑的有 21人，参加投掷的有 26人，即参加百米有参加跳远的有12人，即参加跳远有参加投掷的有 9人，即参加百米有 参加投掷的有14人，三项都参加的有5人，三项都没有参加的有12人，问参加跳远的有 多少人？
重叠问题中的极值问题
1、40人参加某次晚会，其中28人在晚会上唱了歌，25人在晚会上跳舞，那么即唱歌有
跳舞的人最多有多少人，最少有多少人?
方法总结:
f
I 、 两个量的极值中，两项都参加的人最多，就是较少的一项；两项都参加的人数最少，就是求 重叠部分。
< __________________________________________
J 最多：25人 最少:(28+25)-40=13 人 答：最多25人最少13人
换个思路想一想
要使人数最多则重叠最多， 怎么画图才
可以重叠最多呢？要使人数最少， 可以
图形不重叠吗？
练一练
1、某校100名学生中，爱好音乐的有56好美术的最多有多少人？最少有多少人？
人，爱好美术的有75人，那么即爱好音乐有爱
换个思路想一想
最多56人还是75人，最少是0人吗? 为什么？
2、某班30名同学。
在一项测试中，答对一题的有19人，答对2题的14人，那么两题都答对的最多有多少人？最少有多少人?
挑战思维
3、希望小学音乐兴趣小组有37人，其中20人会手风琴，16人会钢琴，24人会电子琴, 即会手风琴又会钢琴的8人，即会电子琴又会钢琴的10人，即会手风琴又会电子琴的8人，那么三种都不会的至少多少人？换个思路想一想
根据：：s=a + b + c-ab-bc-ac+abc+d 若要 d
方法总结:
两个量的极值中，两项都参加的人最多，就是较少的一项；两项都参加的人数最少，就是求、重叠部分。
三个量的极值中，如果要不参加的最多，就要参加的尽量少。
最大，则abc必须怎么样？
<_____________________________________________ __ _________________________________________ 丿家庭作业
1、一个班有48人，班主任在班会上问：谁做完语文作业？请举手！”有37人举手。
又问：谁做完数学作
业?请举手！”有42人举手。
最后问：谁语文、数学作业没有做完？”没有人举手。
求这个班语文、数学作业
都完成的人数是 _____ 人。
2、某个班的全体学生进行了短跑、游泳、篮球三个项目的测试，有4名学生在这三个项目上都没有达到优
3、某班共有30名男生，其中20人参加足球队，12人参加蓝球队，10人参加排球队。
已知没一个人同时参加3个队，且每人至少参加一个队，有6人既参加足球队又参加蓝球队，有2人既参加蓝球队又参加排球队，那么既参加足球队又参加排球队的有多少人？
4、班有46人其中会弹琴的有30人，会拉小提琴的有28人，则这个班级会弹琴又会拉小提琴的至少有
多少人?
5、某班同学中，有26人爱打篮球，17人爱打排球，19人爱踢足球，有9人既爱打篮球又爱踢足球, 有4人既爱打排球又
爱踢足球，有7人既爱打篮球又爱打排球，没有一个人三种球都爱玩，也没有一个人
三种球都不爱玩，问：这个班共有多少学生?
6、某班有45名同学，其中22名同学参加科技兴趣小组，27名同学参加数学兴趣小组，同时参加两个
小组的人数是两个小组均未参加的人数的2倍，那么至少参加一个兴趣小组的同学有多少名？
7、我校六年级三班学生每人至少参加了一种竞赛，其中有32人参加数学竞赛，27人参加英语竞赛，22
人参加语文竞赛•其中参加英语和数学两科的有12人，参加英语和语文两科的有14人，参加数学和语文两科的有10人•问：这个班至少有多少人？至多有多少人？。