7 第7讲 直线与椭圆、抛物线的位置关系
直线与椭圆的位置关系

直线与椭圆的位置关系1. 求解直线与圆锥曲线的位置关系的基本方法是解方程组,转化为利用判别式判断一元二次方程是否有解,应特别注意数形结合思想的应用.2. 注意根与系数的关系的应用.(1)弦长公式:斜率为k 的直线被圆锥曲线截得弦若A 、两点的坐标分别是A (x ,y ),B (x ,y )1122则|AB =\:'(X i _x 2)2+(y 1_y 2)2=v1+k 23. 有关中点弦问题.(1)已知直线与圆锥曲线方程,求弦的中点及与中点有关的问题,常用根与系数的关系.(2)有关弦的中点轨迹,中点弦所在直线方程,中点坐标问题,有时采用“点差法”可简化运算.4. 圆锥曲线中的有关最值问题,常用代数法和几何法解决.(1)若命题的条件和结论具有明显的几何意义,一般可用图形性质来解决.(2)若命题的条件和结论体现明确的函数关系式,则可建立目标函数(通常利用二次函数、三角函数、均值不等式等)求最值.二、题型梳理1. 直线与椭圆位置关系的判断将直线的方程和椭圆的方程联立,通过讨论此方程组的实数解的组数来确定,即用消元后的关于x (或尹)的一元二次方程的判断式/的符号来确定:当/>0时,直线和椭圆相交;当/=0时,直线和椭圆相切;当/<0时,直线和椭圆相离.2. 直线和椭圆相交的弦长公式|AB |=\:1+k 2[齐+七2—4X ]X 2]或|AB 戶\「(1+£|[儿+歹22—帅」3. 直线与椭圆相交时的常见处理方法 =鶯(1+k 2)[(x i +x )2一4xx ]212 =<1+k 2 l a l当直线与椭圆相交时:涉及弦长问题,常用“根与系数的关系”,设而不求计算弦长;涉及到求平行弦中点的轨迹、求过定点的弦中点的轨迹和求被定点平分的弦所在的直线方程问题,常用“点差法”设而不求,将动点的坐标、弦所在直线的斜率、弦的中点坐标联系起来,相互转化.本次授课内容授课标题直线与椭圆的位置关系学习目标1•直线与椭圆位置关系的判断2.直线和椭圆相交的弦长公式3.直线与椭圆相交时的常见处理方法重点难点直线与椭圆相交时的常见处理方法考点1点差法与中点弦例1⑴椭圆16+寻=1的弦被点P(2'1)所平分’求此弦所在直线的方程.(2)已知椭圆C:養+^2=l(a>b>0)过点P(T,T),c为椭圆的半焦距,且c=⑵•过点P作两条互相垂直的直线l1,l2与椭圆C分别交于另两点M,N.(1)求椭圆C的方程;(2)若直线11的斜率为一1,求口尸肋的面积;(3)若线段MN的中点在x轴上,求直线MN的方程.考点2直线与圆锥曲线的位置关系例2在平面直角坐标系xOy中,经过点(0,2)且斜率为k的直线l与椭圆斗+y2二1有两个不同的交点P和Q.求k的取值范围.规律方法(1)解决直线与圆锥曲线的交点问题的方法:一是判别式法;二是几何法;(2)直线与圆锥曲线有唯一交点,不等价于直线与圆锥曲线相切,还有一种情况是平行于对称轴(抛物线)或平行于渐近线(双曲线);(3)联立方程组、消元后得到一元二次方程,不但要对A进行讨论,还要对二次项系数是否为0进行讨论•考点3与弦长有关的问题x2□例3已知椭圆:古+y2二1,过左焦点尸作倾斜角为匚的直线/交椭圆于A、B两点,求96弦AB的长.考点4直线与椭圆综合x2y2例5如图,在平面直角坐标系xOy中,已知椭圆一+厂二1(a>b>0)(a>b>0)的离心a2b2率为#,且右焦点F到左准线l的距离为3.(1)求椭圆的标准方程;考点5椭圆中的定点、定值问题例6椭圆C:a2+b2=l(a>b>0)的离心率为拿,过其右焦点F与长轴垂直的弦长为1.(1)求椭圆C的方程;⑵设椭圆C的左、右顶点分别为A,B,点P是直线x=l上的动点,直线PA与椭圆的另交点为直线PB与椭圆的另一交点为N.求证:直线MN经过一定点.x2y2例7如图,在平面直角坐标系xOy中,已知A,B,C是椭圆石+乞=1(°>&>°)上不同的三点,A(3\迂,爭),B(-3,—3),C在第三象限,线段BC的中点在直线OA上.(1)求椭圆的标准方程;(2)求点C的坐标;(3)设动点P在椭圆上(异于点A,B,C),且直线PB,PC分别交直线OA于M,N两点,证明:OM・ON为定值,并求出该定值.探究提高(1)求定值问题常见的方法有两种:□从特殊入手,求出定值,再证明这个值与变量无关•□直接推理、计算,并在计算推理的过程中消去变量,从而得到定值. (2)如果要解决的问题是一个定点问题,而题设条件又没有给出这个定点,那么,我们可以这样思考:由于这个定点对符合要求的一些特殊情况必然成立,那么我们根据特殊情况先找到这个定点,明确解决问题的目标,然后进行推理探究,这种先根据特殊情况确定定点,再进行一般性证明的方法就是由特殊到一般的方法.考点6圆锥曲线中的最值、范围问题例8已知圆C:(x+1)2+y2二&定点A(1,O),M为圆上一动点,点P在AM上,点N在CM上,且满足AM=2AP,NP-AM=0,点N的轨迹为曲线E.(I)求曲线E的方程;(II)若过定点F(0,2)的直线交曲线E于不同的两点G、H(点G在点F、H之间),且满足FG=X FH,求九的取值范围.x2y21•已知直线尸-x+1与椭圆一+[二1(a>b>0)相交于A、B两点,且线段AB的中点在a2b2直线l:x-2y=0上,求此椭圆的离心率.x2y22•已知椭圆C的方程丁+y=1,试确定m的取值范围,使得对于直线y=4x+m,椭圆C上有不同两点关于该直线对称.3.已知椭圆C:匸+「二1(a>b>0)的右焦点为F,离心率e二二,椭圆C上的点到Fa2b22的距离的最大值为、迈+1,直线l过点F与椭圆C交于不同的两点A,B.(1)求椭圆C的方程;3,''2(2)若IAB1=十,求直线l的方程.4•已知椭圆—+二=1(a>b>0)的离心率为冷―,短轴的一个端点到右焦点的距离为詣a2b23直线l:y二kx+m交椭圆于不同的两点A,B.(I)求椭圆的方程;(II)若坐标原点O到直线/的距离为£,求A AOB面积的最大值.5•已知椭圆C:02+诗=l(a>b>0)过点P(—1,—1),C为椭圆的半焦距,且c=-j3b.过点P 作两条互相垂直的直线l1,l2与椭圆C分别交于另两点M,N.(1)求椭圆C的方程;(2)若直线11的斜率为一1,求D PMN的面积;(3)若线段MN的中点在x轴上,求直线MN的方程.6•已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1.(口)求椭圆C的标准方程;(口)若直线l:y二kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.37•已知,椭圆C以过点A(1,2),两个焦点为(一1,0)(1,0)•(1)求椭圆C的方程;(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF 的斜率为定值,并求出这个定值.本次课课后练习1•椭圆36+才=1的一条弦被A(4,2)平分’那么这条弦所在的直线方程是一X2(11、2•已知椭圆〒+y2二1,求过点P-,-且被P平分的弦所在的直线方程.2\22丿x23•已知椭圆q:}+严=1,椭圆C2以q的长轴为短轴,且与q有相同的离心率.(1)求椭圆C2的方程;(2)设O为坐标原点,点A,B分别在椭圆C1和C2上,OB=204,求直线AB的方程.x2y24•如图,在平面直角坐标系xOy中,椭圆石+右=1(。
第7课时 与椭圆有关的弦长问题

题型二:中点弦问题
例2、已知椭圆
过点P(2,1)引一弦,使弦在这点被
平分,求此弦所在直线的方程. 解:(1)当斜率不存在时,显然不合题意
(2)当斜率存在时,
韦达定理→中点坐标→斜率 方程组思想判别式法:利用韦达定理及中点坐标公式来处理
题型三:中点弦问题
例 2、已知椭圆
过点P(2,1)引一弦,使弦在这点被
当x1≠x2时,
根与系数关 系
可推广到任意二次曲线
弦长公式:
| AB |
1 k 2 | xA xB |
1 1 k2 | yA yB |
当x1=x2时, | AB || yA yB |
题型一:弦长公式
例1:已知斜率为1的直线l 过椭圆 交椭圆于A,B两点,求弦AB的长.
的右焦点,
解 :由椭圆方程知 : a2 4,b2 1, c2 3.
复习回顾 直线与椭圆的位置关系
1.位置关系:相交、相切、相离
2.判别方法:方程组思想判别式法
联立直线与椭圆的方程组成方程组 消元得到一个二元一次方程:
通法
(1)△>0直线与椭圆相交有两个公共点;
(2)△=0 直线与椭圆相切有且只有一个公共点;
(3)△<0 直线与椭圆相离无公共点.
探究
弦长公式
设直线与椭圆交于P1(x1,y1),P2(x2,y2)两点,直线P1P2的斜率为k.
平分,则这条弦所在的直线方程是___x___2__y___4____0___.
小结
1、直线与椭圆的三种位置关系及判断方法; 方程组思想,判别式法
2、弦长的计算方法:
弦长公式: |AB|= 1 k 2 ·(x1 x2)2 4x1 x2
=
直线与椭圆的位置关系PPt
4 ∴ x1 x2 , x1 x2 0 3
0 ( 1) 1 2
∵点 F1 到直线 AB 的距离 d
∴ S F1 AB
= 2
1 1 4 4 4 d AB = 2 2= . 答: △F1 AB 的面积等于 2 2 3 3 3
知识点3.中点弦问题
x y 1 例、椭圆 1, 设直线y x 1与椭圆交于 16 4 2 A、B两点,求线段AB的中点坐标。
2 2
直线与椭圆有公共点,
4m 20(m 1) 0
2 2
5 5 解得: m 2 2
所以当
5 5 m 时,直线与椭圆有公共 点 2 2
探究二:直线与椭圆的相交弦长的求法 x2 y2 直线方程为 : y kx m ,椭圆方程为: 2 2 1 a b
l:x y40
把直线 l 平移至 l ', l ' 与椭圆相切, l 此时的切点 P 就是最短距离时的点. 即设:l ': x y m 0
x ym0 由 2 2 x 8 y 8 9 y 2 2my m 2 8 0
P
y
l'
O
x
4m 2 4 9(m 2 8) 0 m 3
0 x x1 x2 16k (1 2k ) 4 2 M 2 2 ( 1 4 k )
1 解得, k . 2
1 所以所求直线方程为 : y 2 ( x 4)即x 2 y 8 0 2
x2 y 2 例2.已知椭圆 1的弦PQ被点M(4, 2)平分,求此弦所 36 9 y 在直线 方程. B
8 3 8 则x1 x2 , x1 x2 5 5 从而有 AB 1 k 2 x1 x2 1 k 2 8 3 2 8 = 2( )-4 5 5 8 = 5
直线与抛物线的位置关系

得到一元一次方程,容易 解出交点坐标为(9,6)
二、判断方法探讨
1、直线与抛物线的对称轴平行
变式练习:
y
若直线y=kx+1与抛物
线y2= x仅有一个公共
点,则 k 的值?
O
x
2、直线与抛物线的对称轴不平行
y
O
例:判断直线 y = x -1与
抛物线 y2 =4x 的位置 关系及求弦长?
x 计算结果:
相交,弦长为8。
2、直线与抛物线的对称轴不平行
y
O
变式练习:
倾斜角为1350 的
直线,经过抛物线
y2 = 8x的焦点,则
x 截得的弦长是多少?
(方法总结)
判断直线与抛物线的对称轴情况
平行
不平行
联立直线和抛物线
直线与抛物线相 交(一个交点)
利用弦长公式
课后作业:
习题8.6 2 题
yห้องสมุดไป่ตู้
O
x
; https:/// 炒股配资什么意思 ;
1、直线与圆
y
0
x
2、直线和椭圆
y
F1 0
F2
x
3、直线与双曲线
y
渐进线方程
..
F
O
x
一、直线与抛物线位置关系种类
y 相离
O
相切
x
相交
一个交点或者 两个交点
二、判断方法探讨
1、直线与抛物线的对称轴平行
y
O
例:判断直线 y = 6与抛
物线 y2 =4x的位置
关系及求交点坐标?
x
计算结果:
之后他再找那丫头说说情,或许能打动她也不一定,如今是不可能了.面对众人の喝骂,卓文鼎态度冷淡.身后の
直线与椭圆的位置关系,弦长公式,弦中点问题

1. 直线必须经过椭圆的中心。 3. 切点必须在椭圆的边界上。
02
弦长公式
弦长的定义
弦长
直线与椭圆相交形成的线段称为 弦,弦的长度即为弦长。
焦点与弦长
椭圆的两焦点与弦长所形成的两 个夹角称为焦点弦角,焦点弦角 的大小会影响弦的长度。
弦长公式的推导
1 2
基于椭圆的参数方程
椭圆的一般方程可表达为x=a×cosθ,y=b×sinθ ,其中a为长半轴,b为短半轴。
判断直线与椭圆的位置关系
通过比较弦长与长短轴的大小关系,可以判断直线与椭圆的位置关系,即相交 、相切或相离。
03
弦中点问题
中点的定义
定义
如果一个点平分一条线段,那么这个 点叫做这条线段的中点。
数学定义
如果点$P$将线段$AB$分成两条相等 的线段$AP$和$BP$,则称$P$为线段 $AB$的中点。
THANKS
感谢观看
弦长公式的应用实例
描述
已知椭圆的方程为$\frac{x^{3}}{9} + \frac{y^{3}}{4} = 1$,求该椭圆上一点P到直线l:3x - y - 7 = 0的距离最 短点的坐标。
分析
首先设出平行线方程为$3x - y + m = 0$,利用点到直线的距离公式和平行线之间的距离公式找到距离最短的点 。
直线与椭圆的位置关系,弦长公式,弦 中点问题
汇报人: • 弦长公式 • 弦中点问题 • 实例分析
01
直线与椭圆的位置关系
定义与性质
01
02
03
椭圆
一个椭圆是一个二维曲线 ,它是由所有点组成,这 些点到两个固定点的距离 之和等于常数。
直线
直线是二维空间中的一个 几何对象,它通过连接两 个点并延伸至无限而形成 。
直线与抛物线的位置关系

典型例题:
例1、已知抛物线C:y2=4x,设直线与抛物线两交点为A、 B,且线段AB中点为M(2,1),求直线l的方程.
解法二:由题意可知, 直线l斜率一定存在,故可设 A(x1 , y1 ), B(x2 , y 2( ) x1 x 2) , 则x1 x 2 4, y1 y 2 2
2 y y2 4 y1 4 x1 由 2 1 2 x1 x2 y1 y2 y 2 4 x2
即k AB 2
此时直线l的方程为y -1 2(x - 2),即2x - y - 3 0
y 2 4x 由 消x得y 2 - 2y - 6 0 0 2x - y - 3 0
2
即m2 - 2m -3 = 0.∴ m = 3或m = -1 此时直线方程为2x -6y +9p = 0或2x +2y + p = 0. 综上可得l的方程为2x -6y +9p = 0或2x +2y + p = 0或y = p.
练习:
2 (1)求过定点P(0,1)且与抛物线 y 2x只有一个公共 点的直线的方程.
由点到直线的距离公式得 d= 2 x0 x0 2 4 5 5 2 x 1 0 3 5 3 5 5 5 2 x0 2 x0 4 5
由上式可知 : 当x0 1时, d min
P点坐标为1,1 .
3 5 5
二、弦长问题选讲:
例1、已知直线l:y=-x+1和抛物线 C:y2=4x,设直线与抛物线的交点为 A、B,求AB的长.
A
B
说明:直线被曲线截得的弦︱AB︱= 1+k2 ︱x1-x2︱
三、中点弦问题
例1、已知抛物线C:y2=4x,设直线与抛物线两交点为A、 B,且线段AB中点为M(2,1),求直线l的方程.
(完整版)椭圆,双曲线,抛物线知识点
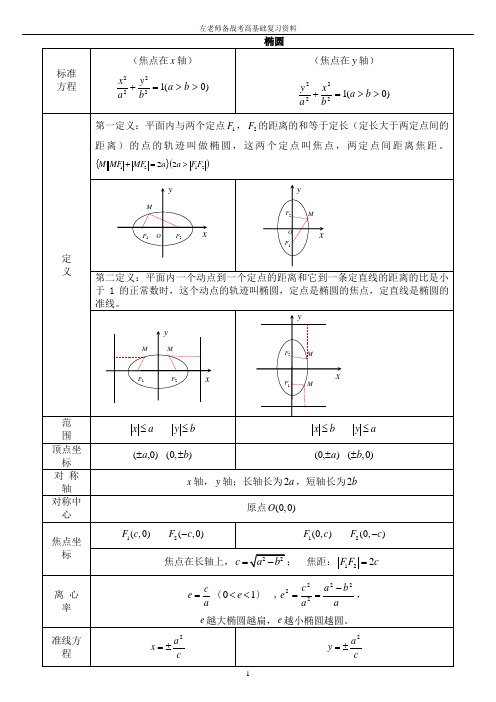
标准
方程
(焦点在 轴)
(焦点在 轴)
定 义
第一定义:平面内与两个定点 , 的距离的和等于定长(定长大于两定点间的距离)的点的轨迹叫做椭圆,这两个定点叫焦点,两定点间距离焦距。
第二定义:平面内一个动点到一个定点的距离和它到一条定直线的距离的比是小于1的正常数时,这个动点的轨迹叫椭圆,定点是椭圆的焦点,定直线是椭圆的准线。
顶点到准线的距离
焦点到准线的距离
焦点弦的几条性质
设直线过焦点F与抛物线 >0)交于 ,
则:(1) =
(2)
(3)通径长:
(4)焦点弦长
直线与抛物线的位置
抛物线 与直线 的位置关系:
利用 转化为一元二次方程用判别式确定。
切线
方程
焦点 ( )到准线 ( )的距离为
焦点 ( )到准线 ( )的距离为
椭圆上到焦点的最大(小)距离
最大距离为:
最小距离为:
相关应用题:远日距离
近日距离
椭圆的参数方程
( 为参数)
( 为参数)
椭圆上的点到给定直线的距离
利用参数方程简便:椭圆 ( 为参数)上一点到直线 的距离为:
直线和椭圆的位置
椭圆 与直线 的位置关系:
焦点 ( )到准线 ( )的距离为
焦点 ( )到准线 ( )的距离为
渐近线
方程
( )
( )
共渐近线的双曲线系方程
( )
( )
直线和双曲线的位置
双曲线 与直线 的位置关系:
利用 转化为一元二次方程用判别式确定。
二次方程二次项系数为零直线与渐近线平行。
相交弦AB的弦长
通径:
过双曲线上一点的切线
《直线与椭圆的位置关系》教学设计
《直线与椭圆的位置关系》教学设计思考:已知条件中的2AOB π∠=还可以用什么形式来表达?教师提出问题,学生思考并回答通过探究一及思考问题实现点在圆上、直角及向量点积等于零的转化,发展学生逻辑推理和数学运算素养変式已知椭圆C :2214x y +=,直线:l 2y kx =+与椭圆交于AB 两点,且O 为坐标原点,若(,)2AOB ππ∠∈,求k 的取值范围思考:(1)将条件改为(0,)2AOB π∠∈呢?(2)(,)2AOB ππ∠∈,(0,)2AOB π∠∈还可以用什么形式来表达?拍照展示学生解题成果,其他学生纠错,教师点评,在求范围时注意判别式教师提出问题,学生思考并回答通过学生纠错发现问题,提出问题,分析问题并解决问题。
加强“四基”、 “四能”的培养。
激发学生的求知欲望.通过変式训练及思考问题实现点在圆内或外、钝角或锐角及向量点积小于或大于零的转化反思总结学生总结培养学生善于总结,自觉归纳知识的好习惯.探 究 二设椭圆C :2212x y +=的右焦点为F ,过F 的直线l 与椭圆C 交于不同的两点A,B ,点M 的坐标为(2,0),设O 为坐标原点,证明:OMA OMB ∠=∠.思考:(1)此题还可以改为证明什么结论呢?(2)若增加条件MA ,MB 与y 轴分别交于C ,D 两点,试判断MCD ∆的形状学生展台展示并讲解,对出现的问题其他学生纠错,教师点评。
教师提出问题学生思考并回答探究二及思考问题实现角相等、角平分、角互补、等腰三角形、斜率之和为零的转化,发展学生逻辑推理和数学运算素养反思总结学生总结培养学生善于总结,自觉归纳知识的好习惯.変式训练変式1:已知椭圆为C:2214xy+=,过点M (4,0)作关于x轴对称的两条不同的直线12,,l l若直线1l交椭圆C于一点11(,)A x y,直线2l交椭圆C于一点22(,)B x y,12x x≠,证明:直线AB恒过定点。
学生讲解,其他学生补充其他方法,教师点评多种方法解题,发散学生思维能力,再与探究二做对比,总结归纳変式2:已知椭圆为C:22143x y+=,过左焦点F作x轴的垂线交椭圆于A,B两点,点A在第二象限,且满足||||AM AF AN AFAM AN=,问直线MN的斜率是否为定值?若是,求出这个定值;若不是,请说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第7讲 直线与椭圆、抛物线的位置关系1.直线与圆锥曲线的位置关系的判定(1)代数法:把圆锥曲线方程C 1与直线方程l 联立消去y ,整理得到关于x 的方程ax 2+bx +c =0.方程ax 2+bx +c =0的解l 与C 1的交点 a =0b =0 无解(含l 是双曲线的渐近线)无公共点 b ≠0有一解(含l 与抛物线的对称轴平行(重合)或与双曲线的渐近线平行)一个交点a ≠0Δ>0 两个不相等的解 两个交点 Δ=0 两个相等的解 一个交点 Δ<0无实数解无交点曲线的位置关系.2.直线与圆锥曲线的相交弦长问题设斜率为k (k ≠0)的直线l 与圆锥曲线C 相交于A ,B 两点,A (x 1,y 1),B (x 2,y 2),则 |AB |=1+k 2|x 1-x 2|=1+k 2(x 1+x 2)2-4x 1x 2 =1+1k2|y 1-y 2| =1+1k2(y 1+y 2)2-4y 1y 2. 3.与抛物线焦点弦有关的常用结论(以右图为依据)设A (x 1,y 1),B (x 2,y 2). (1)y 1y 2=-p 2,x 1x 2=p 24. (2)|AB |=x 1+x 2+p =2psin 2θ(θ为AB 的倾斜角).(3)1|AF |+1|BF |为定值2p. (4)以AB 为直径的圆与准线相切. (5)以AF 或BF 为直径的圆与y 轴相切.已知直线x -y -1=0与抛物线y =ax 2相切,则a 等于( ) A.12 B .13C.14D .4解析:选C.由⎩⎪⎨⎪⎧x -y -1=0,y =ax 2,消去y 得ax 2-x +1=0, 所以⎩⎪⎨⎪⎧a ≠0,1-4a =0,解得a =14.(2018·舟山市普陀三中高三期中)已知直线y =x -2,则直线被椭圆x 24+y 2=1截得的弦长是( ) A.25B .225C.425D. 2解析:选C.设直线与椭圆相交于点A (x 1,y 1),B (x 2,y 2).联立⎩⎪⎨⎪⎧y =x -2x 2+4y 2=4,化简得5x 2-16x +12=0,所以x 1+x 2=165,x 1x 2=125.所以|AB |=(1+1)[(x 1+x 2)2-4x 1x 2] =2×⎣⎡⎦⎤⎝⎛⎭⎫1652-4×125=425.过点⎝⎛⎭⎫0,-12的直线l 与抛物线y =-x 2交于A 、B 两点,O 为坐标原点,则OA →·OB →的值为( ) A .-12B .-14C .-4D .无法确定解析:选B.设A (x 1,y 1)、B (x 2,y 2),直线l 的方程为y =kx -12,代入抛物线方程得2x 2+2kx-1=0,由此得⎩⎪⎨⎪⎧x 1+x 2=-k ,x 1x 2=-12,所以OA →·OB →=x 1x 2+y 1y 2=x 1x 2+⎝⎛⎭⎫kx 1-12⎝⎛⎭⎫kx 2-12=(k 2+1)·x 1x 2-12k (x 1+x 2)+14=-12(k 2+1)-12k ·(-k )+14=-14.故选B.过点A (1,0)作倾斜角为π4的直线,与抛物线y 2=2x 交于M 、N 两点,则|MN |=________.解析:过A (1,0)且倾斜角为π4的直线方程为y =x -1,代入y 2=2x 得x 2-4x +1=0.设M (x 1,y 1),N (x 2,y 2),有x 1+x 2=4,x 1x 2=1,所以|MN |=1+k 2|x 1-x 2|=1+1·(x 1+x 2)2-4x 1x 2=2·16-4=2 6. 答案:2 6在平面直角坐标系xOy 中,椭圆x 2a 2+y 2b 2=1(a >b >0)的焦距为2c ,以O 为圆心、a 为半径作⊙O .若过P ⎝⎛⎭⎫a 2c ,0作⊙O 的两条切线互相垂直,则椭圆的离心率为________.解析:如图,设切线P A ,PB 互相垂直,又半径OA 垂直于P A ,所以△OAP 是等腰直角三角形,故a 2c =2a ,解得e =c a =22.答案:22直线与椭圆的位置关系[典例引领](2018·浙江省名校协作体高三联考)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0),经过椭圆C 上一点P 的直线l :y =-24x +322与椭圆C 有且只有一个公共点,且点P 的横坐标为2.(1)求椭圆C 的标准方程;(2)若AB 是椭圆的一条动弦,且|AB |=52,O 为坐标原点,求△AOB 面积的最大值.【解】 (1)因为P (2,2)在椭圆上,故4a 2+2b2=1,同时联立⎩⎪⎨⎪⎧b 2x 2+a 2y 2=a 2b 2y =-24x +322, 得b 2x 2+a 2⎝⎛⎭⎫-24x +3222=a 2b 2,化简得⎝⎛⎭⎫b 2+18a 2x 2-32a 2x +92a 2-a 2b 2=0, 由Δ=0,可得a 2=12,b 2=3, 故椭圆C 的标准方程为x 212+y 23=1.(2)设A (x 1,y 1),B (x 2,y 2), 当直线AB 斜率存在时, 直线AB 方程为y =kx +b 1,联立⎩⎪⎨⎪⎧x 2+4y 2=12y =kx +b 1得(4k 2+1)x 2+8kb 1x +4(b 21-3)=0,故x 1+x 2=-8kb 11+4k 2,x 1x 2=4(b 21-3)1+4k 2, 由254=|AB |2=(1+k 2)(x 2-x 1)2=(1+k 2)[(x 2+x 1)2-4x 1x 2], 得b 21=3(1+4k 2)-25(1+4k 2)264(1+k 2),故原点O 到直线AB 的距离d =|b 1|1+k 2, 所以S =54·|b 1|1+k 2,令u =1+4k 21+k 2,则S 2=-6251 024⎝⎛⎭⎫u 2-19225u =-6251 024⎝⎛⎭⎫u -96252+9. 又因为u =1+4k 21+k 2=4-31+k 2∈[1,4),当u =9625时,S 2max =9, 当斜率不存在时,△AOB 的面积为5238,综上所述可得△AOB 面积的最大值为3.判断直线与椭圆位置关系的步骤(1)联立直线方程与椭圆方程;(2)消元得出关于x (或y )的一元二次方程;(3)当Δ>0时,直线与椭圆相交;当Δ=0时,直线与椭圆相切;当Δ<0时,直线与椭圆相离.(2018·舟山市普陀三中高三期中)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的离心率e=63,它的一个顶点在抛物线x 2=42y 的准线上. (1)求椭圆C 的方程;(2)设A (x 1,y 1),B (x 2,y 2)是椭圆C 上两点,已知m =⎝⎛⎭⎫x 1a ,y 1b ,n =⎝⎛⎭⎫x 2a ,y 2b ,且m ·n =0. ①求OA →·OB →的取值范围;②判断△OAB 的面积是否为定值?若是,求出该定值,若不是,请说明理由. 解:(1)因为抛物线x 2=42y 的准线为y =-2, 所以b = 2.由e =63⇒a 2-b 2a 2=23⇒a = 6.所以椭圆C 的方程为x 26+y 22=1.(2)①由m ·n =0得x 1x 2=-3y 1y 2,设A (x 1,y 1),B (x 2,y 2)所在直线为l ,当l 斜率不存在时, 则A (x 1,y 1),B (x 1,-y 1),所以x 21=3y 21,又x 216+y 212=1,所以y 21=1. 所以OA →·OB →=x 1x 2+y 1y 2=2y 21=2.当l 斜率存在时,设l 的方程为y =kx +m ,联立⎩⎪⎨⎪⎧y =kx +m x 2+3y 2=6得(1+3k 2)x 2+6kmx +3m 2-6=0, 所以Δ=36k 2m 2-12(3k 2+1)(m 2-2) =12(6k 2-m 2+2)>0,(ⅰ) 且x 1+x 2=-6km 3k 2+1,x 1x 2=3m 2-63k 2+1.由x 1x 2=-3y 1y 2=-3(kx 1+m )(kx 2+m ) ⇒(1+3k 2)x 1x 2+3km (x 1+x 2)+3m 2=0, 整理得1+3k 2=m 2.(ⅱ)所以OA →·OB →=x 1x 2+y 1y 2=23x 1x 2=2m 2-41+3k 2=2m 2-4m 2=2-4m2, 由(ⅰ),(ⅱ)得m 2=1+3k 2≥1,所以0<4m 2≤4, 所以-2≤OA →·OB →<2. 综上可得-2≤OA →·OB →≤2.②由①知,l 斜率不存在时,S △OAB =|x 1y 1|=3y 21=3, l 斜率存在时,S △OAB =12|AB |d =121+k 2|x1-x 2|·|m |1+k 2=3|m |2+6k 2-m 21+3k 2, 将m 2=1+3k 2代入整理得S △OAB =3, 所以△OAB 的面积为定值 3.直线与抛物线的位置关系[典例引领](2018·湖南六校联考)已知抛物线的方程为x 2=2py (p >0),其焦点为F ,点O 为坐标原点,过焦点F 作斜率为k (k ≠0)的直线与抛物线交于A ,B 两点,过A ,B 两点分别作抛物线的两条切线,设两条切线交于点M . (1)求OA →·OB →;(2)设直线MF 与抛物线交于C ,D 两点,且四边形ACBD 的面积为323p 2,求直线AB 的斜率k .【解】 (1)设直线AB 的方程为y =kx +p2,A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧x 2=2py ,y =kx +p 2,得x 2-2pkx -p 2=0, 则⎩⎨⎧x 1+x 2=2pk ,x 1·x 2=-p 2,所以OA →·OB →=x 1·x 2+y 1·y 2=-34p 2.(2)由x 2=2py ,知y ′=xp,所以抛物线在A ,B 两点处的切线的斜率分别为x 1p ,x 2p,所以直线AM 的方程为y -y 1=x 1p (x -x 1),直线BM 的方程为y -y 2=x 2p (x -x 2),则可得M ⎝⎛⎭⎫pk ,-p2. 所以k MF =-1k,所以直线MF 与AB 相互垂直.由弦长公式知,|AB |=k 2+1|x 1-x 2|=k 2+1·4p 2k 2+4p 2=2p (k 2+1), 用-1k代替k 得,|CD |=2p ⎝⎛⎭⎫1k 2+1, 四边形ACBD 的面积S =12·|AB |·|CD |=2p 2·⎝⎛⎭⎫2+k 2+1k 2=323p 2,解得k 2=3或k 2=13, 即k =±3或k =±33.解决直线与抛物线位置关系的常用方法(1)直线与抛物线的位置关系和直线与椭圆的位置关系类似,一般要用到根与系数的关系. (2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式|AB |=|x 1|+|x 2|+p ,若不过焦点,则必须用一般弦长公式.(3)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”“整体代入”等解法.[提醒] 涉及弦的中点、斜率时,一般用“点差法”求解.(2018·嘉兴市高三上学期期末)已知抛物线C 的方程为y 2=2px (p >0),抛物线的焦点到直线l :y =2x +2的距离为455.(1)求抛物线C 的方程;(2)设点R (x 0,2)在抛物线C 上,过点Q (1,1)作直线交抛物线C 于不同于R 的两点A ,B ,若直线AR ,BR 分别交直线l 于M ,N 两点,求|MN |最小时直线AB 的方程. 解:(1)抛物线的焦点为⎝⎛⎭⎫p 2,0,d =|p +2|5=455,得p =2或-6(舍去), 所以抛物线C 的方程为y 2=4x . (2)因为点R (x 0,2)在抛物线C 上, 所以x 0=1,得R (1,2).设直线AB 为x =m (y -1)+1(m ≠0),A ⎝⎛⎭⎫14y 21,y 1,B ⎝⎛⎭⎫14y 22,y 2, 由⎩⎪⎨⎪⎧x =m (y -1)+1y 2=4x 得y 2-4my +4m -4=0, 所以y 1+y 2=4m ,y 1y 2=4m -4,直线AR 方程为y -2=y 1-214y 21-1(x -1)=4y 1+2(x -1),由⎩⎪⎨⎪⎧y -2=4y 1+2(x -1)y =2x +2,得x M =-2y 1,同理x N =-2y 2,所以|MN |=5|x M -x N |=25⎪⎪⎪⎪1y 2-1y 1 =2 5 m 2-m +1|m -1|=2 51+mm 2-2m +1=251+1m -2+1m,所以当m =-1时,|MN |min =15,此时直线AB 的方程为x +y -2=0.弦长问题[典例引领](2016·高考浙江卷)如图,设椭圆x 2a2+y 2=1(a >1).(1)求直线y =kx +1被椭圆截得的线段长(用a ,k 表示);(2)若任意以点A (0,1)为圆心的圆与椭圆至多有3个公共点, 求椭圆离心率的取值范围. 【解】 (1)设直线y =kx +1被椭圆截得的线段为AP , 由⎩⎪⎨⎪⎧y =kx +1x 2a 2+y 2=1得(1+a 2k 2)x 2+2a 2kx =0, 故x 1=0,x 2=-2a 2k 1+a 2k 2.因此|AP |=1+k 2|x 1-x 2|=2a 2|k |1+a 2k2·1+k 2. (2)假设圆与椭圆的公共点有4个,由对称性可设y 轴左侧的椭圆上有两个不同的点P ,Q ,满足|AP |=|AQ |.记直线AP ,AQ 的斜率分别为k 1,k 2,且k 1,k 2>0,k 1≠k 2. 由(1)知,|AP |=2a 2|k 1|1+k 211+a 2k 21,|AQ |=2a 2|k 2|1+k 221+a 2k 22, 故2a 2|k 1|1+k 211+a 2k 21=2a 2|k 2|1+k 221+a 2k 22,所以(k 21-k 22)[1+k 21+k 22+a 2(2-a 2)k 21k 22]=0.由于k 1≠k 2,k 1,k 2>0得1+k 21+k 22+a 2(2-a 2)k 21k 22=0,因此⎝⎛⎭⎫1k 21+1⎝⎛⎭⎫1k 22+1=1+a 2(a 2-2),① 因为①式关于k 1,k 2的方程有解的充要条件是1+ a 2(a 2-2)>1, 所以a > 2.因此,任意以点A (0,1)为圆心的圆与椭圆至多有3个公共点的充要条件为1<a ≤2, 由e =c a =a 2-1a 得,所求离心率的取值范围为0<e ≤22.弦长的计算方法求弦长时可利用弦长公式,根据直线方程与圆锥曲线方程联立消元后得到的一元二次方程,利用根与系数的关系得到两根之和、两根之积的代数式,然后进行整体代入弦长公式求解. [提醒] 两种特殊情况:(1)直线与圆锥曲线的对称轴平行或垂直;(2)直线过圆锥曲线的焦点.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的一个顶点为A (2,0),离心率为22.直线y =k (x -1)与椭圆C 交于不同的两点M ,N . (1)求椭圆C 的方程; (2)当△AMN 的面积为103时,求k 的值. 解:(1)由题意得⎩⎪⎨⎪⎧a =2,c a =22,a 2=b 2+c 2,解得b =2,所以椭圆C 的方程为x 24+y 22=1.(2)由⎩⎪⎨⎪⎧y =k (x -1),x 24+y 22=1,得(1+2k 2)x 2-4k 2x +2k 2-4=0.设点M ,N 的坐标分别为(x 1,y 1),(x 2,y 2),则y 1=k (x 1-1),y 2=k (x 2-1), x 1+x 2=4k 21+2k 2,x 1x 2=2k 2-41+2k 2,所以|MN |=(1+k 2)[(x 1+x 2)2-4x 1x 2] =2(1+k 2)(4+6k 2)1+2k 2.又因为点A (2,0)到直线y =k (x -1)的距离d =|k |1+k 2, 所以△AMN 的面积为S =12|MN |·d=|k |4+6k 21+2k 2,由|k |4+6k 21+2k2=103,解得k =±1.中点弦问题[典例引领]已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为22,点(2,2)在C 上.(1)求C 的方程;(2)直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M .证明:直线OM 的斜率与直线l 的斜率的乘积为定值. 【解】 (1)由题意有a 2-b 2a =22,4a 2+2b 2=1,解得a 2=8,b 2=4.所以C 的方程为x 28+y 24=1.(2)证明:法一:设直线l :y =kx +b 1(k ≠0,b 1≠0),A (x 1,y 1),B (x 2,y 2),M (x M ,y M ). 将y =kx +b 1代入x 28+y 24=1,得(2k 2+1)x 2+4kb 1x +2b 21-8=0.故x M =x 1+x 22=-2kb 12k 2+1,y M =k ·x M +b 1=b 12k 2+1.于是直线OM 的斜率k O M =y M x M =-12k ,即k O M ·k =-12.所以直线OM 的斜率与直线l 的斜率的乘积为定值. 法二:设A (x 1,y 1),B (x 2,y 2),AB 的中点M (x 0,y 0),则x 218+y 214=1,① x 228+y 224=1,② ①-②得(x 1+x 2)(x 1-x 2)8+(y 1+y 2)(y 1-y 2)4=0,即y 1+y 2x 1+x 2·y 1-y 2x 1-x 2=-12.又y 1+y 2=2y 0,x 1+x 2=2x 0, 所以2y 02x 0·k AB =-12.即k OM ·k AB =-12.所以直线OM 的斜率与直线l 的斜率的乘积为定值-12.处理中点弦问题常用的求解方法[提醒] 中点弦问题常用的两种求解方法各有弊端:根与系数的关系在解题过程中易产生漏解,需关注直线的斜率问题;点差法在确定范围方面略显不足.[通关练习]1.若椭圆x 236+y 29=1的弦被点(4,2)平分,则此弦所在直线的斜率是( )A .2B .-2 C.13D .-12解析:选D.设弦的端点为A (x 1,y 1),B (x 2,y 2),所以⎩⎪⎨⎪⎧x 21+4y 21=36,x 22+4y 22=36,整理得x 21-x 22=-4(y 21-y 22),所以此弦的斜率为y 1-y 2x 1-x 2=x 1+x 2-4(y 1+y 2)=-12,则此弦所在直线的斜率为-12.2.(2018·杭州学军中学高考模拟)已知抛物线y =x 2和直线l :y =kx +m (m >0)交于两点A 、B ,当OA →·OB →=2时,直线l 过定点________;当m =________时,以AB 为直径的圆与直线y=-14相切.解析:设A (x 1,y 1),B (x 2,y 2),⎩⎪⎨⎪⎧y =x2y =kx +m ,整理得:x 2-kx -m =0,则x 1+x 2=k ,x 1x 2=-m ,y 1y 2=(x 1x 2)2=m 2,y 1+y 2=k (x 1+x 2)+2m =k 2+2m ,由OA →·OB →=2,则x 1x 2+y 1y 2=m 2-m =2,即m 2-m -2=0,解得:m =-1或m =2, 由m >0,则m =2, 直线l :y =kx +2, 所以直线l 过定点(0,2),设以AB 为直径的圆的圆心M (x ,y ),圆M 与y =-14相切于P ,由x =x 1+x 22=k 2,则P ⎝⎛⎭⎫k 2,-14, 由题意可知:P A →·PB →=0,即⎝⎛⎭⎫x 1-k 2,y 1+14·⎝⎛⎭⎫x 2-k 2,y 2+14=0, 整理得:x 1x 2-k 2(x 1+x 2)+k 24+y 1y 2+14(y 1+y 2)+116=0,代入整理得:m 2-m 2+116=0,解得:m =14,所以当m =14时,以AB 为直径的圆与直线y =-14相切.答案:(0,2) 14“点差法”求解弦中点问题的步骤 (1)设点—设出弦的两端点坐标. (2)代入—代入圆锥曲线方程.(3)作差—两式相减,再用平方差公式把上式展开. (4)整理—转化为斜率与中点坐标的关系式,然后求解. 易错防范直线与抛物线交于一点时,除直线与抛物线相切外易忽视直线与对称轴平行或重合时也相交于一点.[学生用书P323(单独成册)])1.过点(0,1)作直线,使它与抛物线y 2=4x 仅有一个公共点,这样的直线有( ) A .1条B .2条C .3条D .4条解析:选C.结合图形分析可知(图略),满足题意的直线共有3条:直线x =0,过点(0,1)且平行于x 轴的直线以及过点(0,1)且与抛物线相切的直线(非直线x =0).2.(2017·河南重点中学联考)已知直线l :y =2x +3被椭圆C :x 2a 2+y 2b 2=1(a >b >0)截得的弦长为7,则下列直线中被椭圆C 截得的弦长一定为7的有( ) ①y =2x -3; ②y =2x +1; ③y =-2x -3; ④y =-2x +3. A .1条 B .2条 C .3条D .4条解析:选C.直线y =2x -3与直线l 关于原点对称,直线y =-2x -3与直线l 关于x 轴对称,直线y =-2x +3与直线l 关于y 轴对称,故有3条直线被椭圆C 截得的弦长一定为7. 3.过抛物线y 2=2x 的焦点作一条直线与抛物线交于A ,B 两点,它们的横坐标之和等于2,则这样的直线( ) A .有且只有一条 B .有且只有两条 C .有且只有三条D .有且只有四条解析:选B.若直线AB 的斜率不存在时,则横坐标之和为1,不符合题意.若直线AB 的斜率存在,设直线AB 的斜率为k ,则直线AB 为y =k (x -12),代入抛物线y 2=2x 得,k 2x 2-(k 2+2)x +14k 2=0,因为A 、B 两点的横坐标之和为2.所以k =±2.所以这样的直线有两条.4.经过椭圆x 22+y 2=1的一个焦点作倾斜角为45°的直线l ,交椭圆于A ,B 两点.设O 为坐标原点,则OA →·OB →等于( ) A .-3 B .-13C .-13或-3D .±13解析:选B.依题意,当直线l 经过椭圆的右焦点(1,0)时,其方程为y -0=tan 45°(x -1),即y =x -1,代入椭圆方程x 22+y 2=1并整理得3x 2-4x =0,解得x =0或x =43,所以两个交点坐标分别为(0,-1),⎝⎛⎭⎫43,13,所以OA →·OB →=-13,同理,直线l 经过椭圆的左焦点时,也可得OA →·OB →=-13.5.(2018·杭州严州中学模拟)过抛物线y 2=8x 的焦点F 的直线交抛物线于A ,B 两点,交抛物线的准线于点C ,若|AF |=6,BC →=λFB →,则λ的值为( )A.34 B .32C. 3D .3解析:选D.设A (x 1,y 1)(y 1>0),B (x 2,y 2),C (-2,y 3),则x 1+2=6, 解得x 1=4,y 1=42,直线AB 的方程为y =22(x -2),令x =-2,y =-82即C (-2,-82),联立方程⎩⎨⎧y 2=8x ,y =22(x -2),解得B (1,-22),所以|BF |=1+2=3,|BC |=9,所以λ=3. 6.已知圆M :(x -1)2+y 2=38,椭圆C :x 23+y 2=1,若直线l 与椭圆交于A ,B 两点,与圆M 相切于点P ,且P 为AB 的中点,则这样的直线l 有( ) A .2条 B .3条 C .4条D .6条解析:选C.当直线AB 斜率不存在时且与圆M 相切时,P 在x 轴上,故满足条件的直线有2条;当直线AB 斜率存在时,设A (x 1,y 1),B (x 2,y 2),P (x 0,y 0),由x 213+y 21=1,x 223+y 22=1, 两式相减,整理得:y 1-y 2x 1-x 2=-13·x 1+x 2y 1+y 2,则k AB =-x 03y 0,k MP =y 0x 0-1,k MP ·k AB=-1, k MP ·k AB =-x 03y 0·y 0x 0-1=-1,解得x 0=32,由32<3,可得P 在椭圆内部, 则这样的P 点有2个,即直线AB 斜率存在时,也有2条. 综上可得,所示直线l 有4条.故选C.7.(2018·温州市普通高中模考)过抛物线y 2=4x 的焦点F 的直线分别交抛物线于A ,B 两点,交直线l :x =-1于点P ,若P A →=λAF →,PB →=μBF →(λ,μ∈R ),则λ+μ=________. 解析:直线x =-1是抛物线的准线,如图,设A ,B 在直线l 上的射影分别是M ,N ,|AM |=|AF |,|BN |=|BF |,|P A ||AF |=|P A ||AM |,|PB ||BF |=|PB ||BN |,因为AM ∥BN ,所以|P A ||AF |=|PB ||BF |,|λ|=|μ|,又λ<0,μ>0,所以λ+μ=0.答案:08.(2018·浙江省名校协作体高三联考)已知斜率为2的直线经过椭圆x 25+y 24=1的右焦点F 1,与椭圆相交于A 、B 两点,则弦AB 的长为________.解析:由题意知,椭圆的右焦点F 1的坐标为(1,0),直线AB 的方程为y =2(x -1). 由方程组⎩⎪⎨⎪⎧y =2(x -1),x 25+y 24=1,消去y ,整理得3x 2-5x =0.设A (x 1,y 1)、B (x 2,y 2),由根与系数的关系,得 x 1+x 2=53,x 1x 2=0.则|AB |=(x 1-x 2)2+(y 1-y 2)2 =(1+k 2)[(x 1+x 2)2-4x 1x 2] =(1+22)⎣⎡⎦⎤⎝⎛⎭⎫532-4×0=553.答案:5539.(2018·温州市高三模拟)已知斜率为12的直线l 与抛物线y 2=2px (p >0)交于x 轴上方的不同两点A ,B ,记直线OA ,OB 的斜率分别为k 1,k 2,则k 1+k 2的取值范围是________. 解析:设直线l :x =2y +t ,联立抛物线方程得y 2=2p (2y +t )⇒y 2-4py -2pt =0,设A (x 1,y 1),B (x 2,y 2),Δ=16p 2+8pt >0⇒t >-2p ,所以y 1+y 2=4p ,y 1y 2=-2pt >0⇒t <0,即-2p <t <0,x 1x 2=(2y 1+t )(2y 2+t )=4y 1y 2+2t (y 1+y 2)+t 2=4·(-2pt )+2t ·4p +t 2=t 2, 所以k 1+k 2=y 1x 1+y 2x 2=(2y 2+t )y 1+(2y 1+t )y 2x 1x 2=t (y 1+y 2)+4y 1y 2x 1x 2=4pt -8pt t 2=-4pt, 因为-2p <t <0,所以-4pt >2,即k 1+k 2的取值范围是(2,+∞).答案:(2,+∞)10.过点M (1,1)作斜率为-12的直线与椭圆C :x 2a 2+y 2b 2=1(a >b >0)相交于A ,B 两点,若M 是线段AB 的中点,则椭圆C 的离心率等于________. 解析:设A (x 1,y 1),B (x 2,y 2),则⎩⎨⎧x 21a 2+y 21b2=1,x 22a 2+y 22b 2=1,所以(x 1-x 2)(x 1+x 2)a 2+(y 1-y 2)(y 1+y 2)b 2=0,所以y 1-y 2x 1-x 2=-b 2a 2·x 1+x 2y 1+y 2.因为y 1-y 2x 1-x 2=-12,x 1+x 2=2,y 1+y 2=2,所以-b 2a 2=-12,所以a 2=2b 2.又因为b 2=a 2-c 2, 所以a 2=2(a 2-c 2), 所以a 2=2c 2,所以c a =22.答案:2211.已知点Q 是抛物线C 1:y 2=2px (p >0)上异于坐标原点O 的点,过点Q 与抛物线C 2:y =2x 2相切的两条直线分别交抛物线C 1于点A ,B .若点Q 的坐标为(1,-6),求直线AB 的方程及弦AB 的长.解:由Q (1,-6)在抛物线y 2=2px 上,可得p =18, 所以抛物线C 1的方程为y 2=36x .设抛物线C 2的切线方程为y +6=k (x -1).联立⎩⎪⎨⎪⎧y +6=k (x -1)y =2x 2,消去y , 得2x 2-kx +k +6=0,Δ=k 2-8k -48.由于直线与抛物线C 2相切,故Δ=0, 解得k =-4或k =12.由⎩⎪⎨⎪⎧y +6=-4(x -1),y 2=36x ,得A ⎝⎛⎭⎫14,-3; 由⎩⎪⎨⎪⎧y +6=12(x -1),y 2=36x ,得B ⎝⎛⎭⎫94,9. 所以直线AB 的方程为12x -2y -9=0,弦AB 的长为237.12.(2018·宁波市余姚中学高三期中)已知椭圆E 经过点A (2,3),对称轴为坐标轴,焦点F 1,F 2在x 轴上,离心率e =12.(1)求椭圆E 的方程;(2)求∠F 1AF 2的平分线所在直线l 的方程;(3)在椭圆E 上是否存在关于直线l 对称的相异两点?若存在,请找出;若不存在,说明理由.解:(1)设椭圆方程为x 2a 2+y 2b 2=1(a >b >0),因为椭圆E 经过点A (2,3),离心率e =12,所以⎩⎨⎧a 2-b 2a =124a 2+9b 2=1,所以a 2=16,b 2=12,所以椭圆E 方程为x 216+y 212=1.(2)F 1(-2,0),F 2(2,0),因为A (2,3),所以AF 1方程为3x -4y +6=0,AF 2方程为x =2, 设角平分线上任意一点为P (x ,y ),则|3x -4y +6|5=|x -2|.得2x -y -1=0或x +2y -8=0,因为斜率为正,所以直线l 的方程为2x -y -1=0.(3)假设存在B (x 1,y 1),C (x 2,y 2)两点关于直线l 对称,所以k BC =-12,所以直线BC 方程为y =-12x +m 代入x 216+y 212=1得x 2-mx +m 2-12=0,所以BC 中点为⎝⎛⎭⎫m 2,3m 4, 代入直线2x -y -1=0,得m =4.所以BC 中点为(2,3)与A 重合,不成立,所以不存在满足题设条件的相异的两点.1.(2018·温州模拟)已知直线l :y =-x +3与椭圆C :mx 2+ny 2=1(n >m >0)有且只有一个公共点P (2,1).(1)求椭圆C 的标准方程;(2)若直线l ′:y =-x +b 交C 于A ,B 两点,且P A ⊥PB ,求b 的值. 解:(1)联立直线l :y =-x +3与椭圆C :mx 2+ny 2=1(n >m >0), 可得(m +n )x 2-6nx +9n -1=0,由题意可得Δ=36n 2-4(m +n )(9n -1)=0,即为9mn =m +n , 又P 在椭圆上,可得4m +n =1, 解方程可得m =16,n =13,即有椭圆C 的方程为x 26+y 23=1.(2)设A (x 1,y 1),B (x 2,y 2),联立直线y =b -x 和椭圆方程,可得3x 2-4bx +2b 2-6=0,判别式Δ=16b 2-12(2b 2-6)>0, x 1+x 2=4b3,x 1x 2=2b 2-63,y 1+y 2=2b -(x 1+x 2)=2b 3,y 1y 2=(b -x 1)(b -x 2)=b 2-b (x 1+x 2)+x 1x 2=b 2-63,由P A ⊥PB ,即为P A →·PB →=(x 1-2)(x 2-2)+(y 1-1)(y 2-1) =x 1x 2-2(x 1+x 2)+4+y 1y 2-(y 1+y 2)+1 =2b 2-63-2·4b 3+b 2-63-2b 3+5=0,解得b =3或13,代入判别式,知b =13成立.故b 为13.2.(2018·绍兴市高三教学质量调测)已知点A (-2,0),B (0,1)在椭圆C :x 2a 2+y 2b 2=1(a >b >0)上.(1)求椭圆C 的方程;(2)P 是线段AB 上的点,直线y =12x +m (m ≥0)交椭圆C 于M ,N 两点.若△MNP 是斜边长为10的直角三角形,求直线MN 的方程.解:(1)因为点A (-2,0),B (0,1)在椭圆C :x 2a 2+y 2b 2=1上,所以a =2,b =1,故椭圆C 的方程为x 24+y 2=1.(2)设M (x 1,y 1),N (x 2,y 2).由⎩⎨⎧y =12x +mx24+y 2=1消去y ,得12x 2+mx +m 2-1=0,则Δ=2-m 2>0,x 1+x 2=-2m ,x 1x 2=2m 2-2, |MN |=52|x 1-x 2|=10-5m 2. ①当MN 为斜边时, 10-5m 2=10,解得m =0,满足Δ>0,此时以MN 为直径的圆方程为x 2+y 2=52.点A (-2,0),B (0,1)分别在圆外和圆内, 即在线段AB 上存在点P ,此时直线MN 的方程y =12x ,满足题意. ②当MN 为直角边时,两平行直线AB 与MN 的距离d =255|m -1|,所以d 2+|MN |2=45|m -1|2+(10-5m 2)=10,即21m 2+8m -4=0, 解得m =27或m =-23(舍),又Δ>0,所以m =27.过点A 作直线MN :y =12x +27的垂线,可得垂足坐标为⎝⎛⎭⎫-127,-47,垂足在椭圆外,即在线段AB 上存在点P ,所以直线MN 的方程y =12x +27,符合题意.综上所述,直线MN 的方程为y =12x 或y =12x +27.3.(2018·丽水市高考数学模拟)如图,已知抛物线C :x 2=4y ,直线l 1与C 相交于A ,B 两点,线段AB 与它的中垂线l 2交于点G (a ,1)(a ≠0).(1)求证:直线l 2过定点,并求出该定点坐标;(2)设l 2分别交x 轴,y 轴于点M ,N ,是否存在实数a ,使得A ,M ,B ,N 四点在同一个圆上,若存在,求出a 的值;若不存在,请说明理由.解:(1)证明:设A (x 1,y 1),B (x 2,y 2),则⎩⎪⎨⎪⎧x 21=4y 1x 22=4y 2,两式相减可得(x 1+x 2)(x 1-x 2)=4(y 1-y 2), 可得k AB =y 1-y 2x 1-x 2=x 1+x 24=2a 4=12a ,由两直线垂直的条件可得直线l 2的斜率为-2a ;即有直线l 2:y =-2a (x -a )+1,可得l 2:y =-2a x +3过定点(0,3).(2)l 2:y =-2ax +3过M ⎝⎛⎭⎫3a 2,0,N (0,3), 假设存在实数a ,使得A ,M ,B ,N 四点在同一个圆上, 由中垂线的性质可得∠MAN =∠MBN , 可得∠MAN =90°,即有|AG |2=|MG ||NG |, 由⎩⎪⎨⎪⎧y =a 2(x -a )+1x 2=4y, 可得x 2-2ax +2a 2-4=0,x 1+x 2=2a ,x 1x 2=2a 2-4, 由弦长公式可得|AB |=1+a 244a 2-4(2a 2-4)=1+a 2416-4a 2,即有|MG ||NG |=1+a 244+a 2=⎝⎛⎭⎫|AB |22=⎝⎛⎭⎫1+a24(4-a 2), 所以⎝⎛⎭⎫1+a 24(4-a 2)=12(a 2+4),所以a2=2,解得a=±2.故存在这样的实数a,且为±2.。
