n维欧氏空间中的点集——【多元函数微分学】
n维欧氏空间定义

n维欧氏空间定义在n维欧氏空间中,我们可以进行各种有趣的探索和想象。
这是一个抽象的数学概念,但我们可以用生动的语言描绘它,让读者仿佛身临其境。
想象一下,我们置身于一个n维空间中,无论是二维、三维还是更高维度,我们能够感受到其中的奇妙之处。
空间中充满了各种形状和结构,它们交织在一起,形成了独特的景象。
在这个n维空间中,我们可以观察到不同维度的几何体。
比如,在二维空间中,我们能看到各种各样的平面图形,如圆、三角形和矩形等。
而在三维空间中,我们能够看到更加立体的形状,如球体、立方体和锥体等。
当然,在更高维度的空间中,我们可能无法直观地想象几何体的形状,但我们可以用数学语言进行描述。
在n维欧氏空间中,距离的概念也有所改变。
在二维空间中,我们可以用直线距离来描述两点之间的距离。
而在三维空间中,我们可以通过勾股定理来计算点之间的距离。
但在更高维度的空间中,我们需要使用更复杂的数学工具来计算距离。
除了几何形状和距离,n维欧氏空间还有许多其他有趣的性质。
比如,我们可以探讨向量在空间中的运动和变换。
我们可以考虑向量的长度、方向和角度,以及向量之间的运算规则。
这些概念在物理学、工程学和计算机科学等领域中都有广泛的应用。
在n维欧氏空间中,我们还可以探讨点的分布和集合的性质。
我们可以研究点的密度、连通性和紧致性等特征。
这些概念在拓扑学和概率论等领域中有着重要的应用。
n维欧氏空间是一个富有想象力和探索性的领域。
通过生动的语言和形象的描述,我们可以将这个抽象的数学概念呈现给读者,让他们感受到其中的奇妙之处。
无论是几何形状、向量运算还是点的分布,n维欧氏空间都是一个充满挑战和乐趣的领域。
让我们一起踏上这个数学之旅,探索未知的世界吧!。
多元函数微分学知识点梳理

多元函数微分学知识点梳理
第九章多元函数微分学
内容复
一、基本概念
1.多元函数的基本概念包括n维空间、n元函数、二重极限、连续等。
其中,偏导数和全微分也是重要的概念。
2.重要定理:
1)二元函数中,可导、连续、可微三者的关系为偏导数
连续→可微。
同时,偏导数存在和函数连续是可微的必要条件。
2)二元函数的极值必须满足必要条件和充分条件。
二、基本计算
一)偏导数的计算
1.偏导数值的计算有三种方法:先代后求法、先求后代法
和定义法。
2.偏导函数的计算包括简单的多元初等函数和复杂的多元
初等函数。
对于复杂的函数,可以使用链式法则,或者隐函数求导法。
3.高阶导数的计算需要注意记号表示和求导顺序。
二)全微分的计算
1.叠加原理可以用于计算全微分,即dz=∂z/∂x dx+∂z/∂y dy。
2.一阶全微分形式不变性对于自变量和中间变量均成立。
三、偏导数的应用
在优化方面,多元函数的极值和最值是常见的应用。
1.无条件极值可以用必要条件和充分条件来求解。
2.条件极值可以使用Lagrange乘数法来求解。
3.最值可以通过比较区域内部驻点处函数值和区域边界上最值的大小来确定。
维欧氏空间中的点集

在 n 维向量空间 Rn 中,按照以下定义内积:
设 x ( x1, x2 , , xn ) Rn , y ( y1, y2,
n
x, y xi yi i 1
构成一个 n 维 Euclid 空间.
, yn ) Rn
对于 x ( x1, x2 , , xn ) Rn , y ( y1, y2, , yn ) Rn
(5) 界点要么是聚点,要么是孤立点。
15
聚点
关于聚点,下面三条是等价的:
(1) a是A的聚点;
(2) a的任意邻域内,至少含有一个属于A而 异于a点;
(3) 存在A中互异的点所成的点列 xn,
lim
n
xn
a
See P.4定义1.2
16
内部、边界、外部、导集、闭包 定义:(1) A的全体内点所成的集合,称为A的内部, 记作 A ,或 int A
Rn 中的向量的长度(或范数)定义为: x ( x, x) x12 x22 xn2
定义距离
( x, y) x - y ( x1 - y1)2 ( x2 - y2 )2 ( xn - yn )2
4
2. Rn中点列的极限
定义1.3(邻域):设a Rn ,d 0,称点集
U(a,d )= x Rn | ( x,a) d 为点a的d邻域,简记为
U (a);
显然,在R1, R2, R3 中, U(a,d分别是以a为中心以d为
半径的开区间、开圆和开球.
o
U (a,d )=:x Rn | 0 ( x,a) d ---点a的去心d邻域。
d
d
M0
d
d
M0
ad
a
ad x
5
点列的极限
n维欧氏空间定义

n维欧氏空间定义
在n维欧氏空间中,我们可以想象一个抽象的世界,其中存在着超越我们常见的三维空间的更多维度。
这个空间可以用来描述复杂的现象和问题,如高维数据分析、量子力学等。
在这个虚拟的世界里,我们可以拥有超越普通人类感知能力的洞察力。
在n维欧氏空间中,物体的位置可以用n个坐标来表示。
例如,在三维空间中,一个点可以由(x, y, z)来表示,其中x、y、z分别代表了该点在三个轴上的位置。
而在n维空间中,一个点的位置则需要n个坐标来描述。
这让我们可以想象,如果我们生活在一个n维空间中,我们的感知将会是怎样的呢?
在这个虚拟的世界里,我们可以自由地在不同维度之间穿梭,探索未知的领域。
我们可以想象,如果我们能够进入四维空间,我们将能够看到物体在时间上的变化,甚至可以预测未来的发展趋势。
而在更高维的空间中,我们将能够看到更加复杂的现象,如量子纠缠、黑洞等。
然而,尽管在n维欧氏空间中我们可以拥有更多的洞察力和理解力,但我们也会面临更多的困惑和挑战。
在这个虚拟的世界里,我们可能会遭遇到无法想象的现象和问题,挑战我们的思维和理解能力。
我们需要不断学习和探索,以适应这个新的世界。
在n维欧氏空间中,我们也可以与其他生命体进行交流和互动。
他
们可能来自不同的维度,拥有不同的感知和思维方式。
通过与他们的交流,我们可以更好地理解自己和这个世界,拓宽我们的视野和思维。
在n维欧氏空间中,我们可以拥有更广阔的世界观和更深入的洞察力。
这个虚拟的世界给予我们思考和探索的机会,使我们能够更好地理解自己和宇宙的奥秘。
让我们一起踏入这个神秘的世界,探索其中的奥妙吧!。
高等数学多元函数微分学 - 简明版

盾 。记
| a b | r, r .
2
由于重极限存在并且 lim f ( x, y) a,,存在 , ( x , y )( x0 , y0 )
当 | x x0 | | y y0 | 时,| f ( x, y) a | 。记
由于
lim
y y0
f
( x,
y)
(x,
y0 )
(1)
因此有
0 0 ( p U ( p0, ) D f ( p) U ( f ( p0 ), ))
即
0, 0, p D,
( p p0 | f ( p) f ( p0 ) | )
也就是
lim
p p0
f ( p)
f ( lim p p0
p)
f ( p0 )
则称函数在 p0 点处是连续的。
3.多元函数
(1)多元函数的定义-本质上就是n维空间某个子集 到实数集的映射。
符号与概念:自变量、因变量、定义域、值域(这个 集合的表示);自然定义域约定。
【例6-1】一定量的理想气体的压强p,体积V和绝对温 度T之间具有关系 p RT , 其中R为常数.
V
【例6-2】长方体体积V是它的长x,宽y,高z的三元函
对照一元函数函数连续的定义,可以看出,这里的 多元函数连续定义,并没有本质区别。所不同的是, 这里的点不是一个数,而是一个“多维点”,它是 由n个数描述的。因此在具体分析多元函数连续性的 时候,所要分析的情形也可能复杂一些。
比如说,下面用函数增量的形式表述多元(这里以
二元函数为例)函数的连续性,就会产生一些新的概 念。记
(2)连续函数的某些性质
(i)对四则运算的封闭性-初等函数的连续性。
14 欧氏空间中的点集

x0 R n , r > 0 , 则 x0 的 r -邻域 U ( x0 , r ) 是 R n 中的开集. 因此 U ( x0 , r ) 又称为以 x0
(1) 空集 和全空间 R n 是开集.
(2) 任意个开集的并集是开集.
(3) 有限个开集的交集是开集.
证明
(1). 显然. (2). 设 { A , Î I } 是 R n 中的一族开集Î I 使得 x Î A . 因为 A 是开集, 存在 x 的一个邻域 U ( x, ) 使得 U ( x, ) Ì A .
为中心, 以 r 为半径的开球. 例 1 设 f ( x ) 是 定 义 在 R n 上 的 连 续 函 数 . 则 对 任 意 实 数 a, 记 E = {x Î R n : f ( x) > a}. 设 x0 Î E , 则 f ( x0 ) > a. 由于 f ( x) 在 x0 连
{x Î R n : f ( x) > a} 和 {x Î R n : f ( x) < a} 都是开集.
( x1 ,, xn ) + ( y1 ,, yn ) = ( x1 + y1 ,, xn + yn ),
λ( x1 ,, xn ) = ( λx1 ,, λxn ). x = ( x1 , , xn ) 称为是 R n 中的点或向量 , 称 xi (i = 1, , n) 为 x 的第 i 个坐标 . 对
多元微积分教学大纲
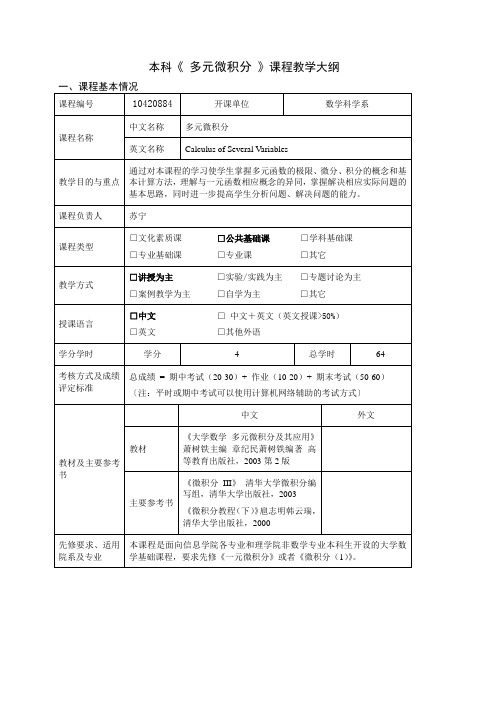
二、偏导数的计算
三、导数的应用
四、重积分计算
五、第二类曲线曲面积分
六、Green公式,Gauss公式,Stokes公式
七、常微分方程
〔注:平时或期中考试可以使用计算机网络辅助的考试方式〕
教材及主要参考书
中文
外文
教材
《大学数学多元微积分及其应用》萧树铁主编章纪民萧树铁编著高等教育出版社,2003第2版
主要参考书
《微积分III》清华大学微积分编写组,清华大学出版社,2003
《微积分教程(下)》扈志明韩云瑞,清华大学出版社,2000
先修要求、适用院系及专业
本科《多元微积分》课程教学大纲
一、课程基本情况
课程编号
10420884
开课单位
数学科学系
课程名称
中文名称
多元微积分
英文名称
Calculus of Several Variables
教学目的与重点
通过对本课程的学习使学生掌握多元函数的极限、微分、积分的概念和基本计算方法,理解与一元函数相应概念的异同,掌握解决相应实际问题的基本思路,同时进一步提高学生分析问题、解决问题的能力。
课程负责人
苏宁
课程类型
□文化素质课□公共基础课□学科基础课
□专业基础课□专业课□其它
教学方式
□讲授为主□实验/实践为主□专题讨论为主
□案例教学为主□自学为主□其它
授课语言
□中文□中文+英文(英文授课>50%)
□英文□其他外语
学分学时
学分
4
总学时
64
考核方式及成绩评定标准
总成绩=期中考试(20-30)+作业(10-20)+期末考试(50-60)
第2章 欧式空间中的点集

N ( x0 , r ) 是 R n 中的开集,因此,我们也称 N ( x0 , r ) 为以 x0 为中心,以 r 为半径的开球。
定理 2.5(开集的基本性质)开集具有如下性质: (1) (2) (3) 空集 及全空间 R n 是开集; 任意多个开集的并是开集; 有限个开集的交是开集。
证明 (1) 显然。 (2) 设 A
2.2
开集、闭集与完备集
开集与闭集是本章的重点,特别是开集与闭集的构造,必须熟炼地掌握,实际上,在下 一章我们将看到开集、闭集与测度理论密切相关,是构成测度理论的一个重要环节。 定义 2.3 设 E R n ,若 E 中每个点都是 E 的内点,则称 E 为开集。 由开集的定义易知 E 是开集当且仅当 E E 0 ,任何非空有限集都不是开集,每个开区 间 ( a, b), ( a, ), ( , b) 都是 R1 上的开集(在 R 2 中就不是) 。若 x0 R , r 0 ,则邻域
A , I 是 R n 中的一族开集, 任取 x 则存在 I I
- 41 -
使 x A ,因 A 是开集,存在 x 的邻域 N ( x, ) 使得 N ( x, ) A ,于是更有
N ( x, ) A , I A 的内点,这表明 A 是开集。 因此 x 是 I I
■ 利用距离可考虑有界集 设 M R n ,若有正数 K 0 ,使对任意 x ( x1 , x2 , xn ) M ,都有
xi K (i 1, 2, , n) ,
则称 M 为有界集。
- 38 -
显然 M 有界的充要条件是:存在正数 K ' 0 ,使对一切 x M 都有 d( x, o) K ' 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
y
闭区域
y
o
x
y
o 1 2x
o
x
o 1 2x
2007年8月 南京航空航天大学 理学院 数学系
9
整个平面 是最大的开域 , 也是最大的闭域
;点集 (x, y) x 1是开集,
但非区域 .
y
1o 1 x
• 有界集: 对于平面点集E, 如果存在某一正数r, 使得
E U(O,r), 其中O为坐标原点.
2007年8月 南京航空航天大学 理学院 数学系
3
三、 平面点集R2的基本知识
平面点集:
xoy平面上满足某一条件的一切点的集合
1. 邻域 点集
例如,在平面上,
U ( P0 ,δ ) (x, y)
在空间中,
U ( P0 , ) (x, y, z )
2007年8月 南京航空航天大学 理学院 数学系
则称 D 是连通的 ; • 连通的开集称为开区域 ,简称区域 ; • 开区域连同它的边界一起称为闭区域.
D
。 。
2007年8月 南京航空航天大学 理学院 数学系
8
例如,在平面上
(x, y) x y 0
开区域
(x, y) 1 x2 y2 4
(x, y) x y 0
(x, y) 1 x2 y2 4
O.
2007年8月 南京航空航天大学 理学院 数学系
2
R n 中的点 x (x1, x2 ,, xn ) 与点 y ( y1, y2 ,, yn )
的距离记作
规定为
R n 中的点 x (x1, x2 ,, xn )与零元 O 的距离为 x x12 x22 xn2
二、Rn中点列的极限
N维欧氏空间点集的初步知 识
n维欧氏空间 n维欧氏空间中的各类点集
2007年8月
南京航空航天大学 理学院 数学系
1
一、 n 维欧氏空间
n 元有序数组
记作 R n ,即 Rn R R R
的全体称为 n 维欧氏空间,
n 维空间中的每一个元素
称为空间中的
一个点,
称为该点的第 k 个坐标 .
当所有坐标
称该元素为 R n中的零元,记作
显然, E 的内点必属于 E , E 的外点必不属于 E , E 的
边界点可能属于 E, 也可能不属于 E .
2007年8月 南京航空航天大学 理学院 数学系
6
(2) 聚点
若对任意给定的 , 点P 的去心
E
邻域
内总有E 中的点 , 则
称 P 是 E 的聚点. 聚点可以属于 E , 也可以不属于 E (因为聚点可以为
2007年8月 南京航空航天大学 理学院 数学系
10
E 的边界点 )
所有聚点所成的点集成为 E 的导集 .
2007年8月 南京航空航天大学 理学院 数学系
7
(3) 开区域及闭区域
• 若点集 E 的点都是内点,则称 E 为开集;
• E 的边界点的全体称为 E 的边界, 记作E ;
• 若点集 E E , 则称 E 为闭集;
• 若集 D 中任意两点都可用一完全属于 D 的折线相连 ,
5
2. 区域
(1) 内点、外点、边界点
E
设有点集 E 及一点 P :
• 若存在点 P 的某邻域 U(P) E ,
则称 P 为 E 的内点;
• 若存在点 P 的某邻域 U(P)∩ E = ,
则称 P 为 E 的外点 ;
• 若对点 P 的任一邻域 U(P) 既含 E中的内点也含 E
的外点 , 则称 P 为 E 的边界点 .
PP0 δ 称为点 P0 的邻域.
(圆邻域)
(球邻域)
4
说明:若不需要强调邻域半径 0 δ
在讨论实际问题中也常使用方邻域, 因为方邻域与圆
邻域可以互相包含.
。P0
平面上的方邻域为
U(P0,δ ) (x, y)
2007年8月 南京航空航天大学 理学院 数学系
