南邮信号与系统B习题答案05(课堂PPT)

合集下载

南邮信号与系统课后答案精选精品PPT课件

如图所示，试求该系统的零状态响应。
xk
hk
4
3 2
4
2 1
-2 -1 0 1 2 3 k
-2
-1 0 1 2 3 4 k
-1
解： xk 4, 2,3,2 hk 4,,1,2,1
4 2 3 2 4 1 2 1
4 2 3 2 8 4 6 4 4 2 3 2 16 8 12 8 16 12 22 5 2 7 2
k
1
uk
4 3
1k 1
8 3
0.5k 1 u k
2 3
1k 2
4 3
0.5k 2
k 1
k 1
2 3
1k
2
4 3
0.5k 2
4 3
1k
1
8 3
0.5k 1
uk
2 3
1k
1 3
0.5k
4 3
1k
4 3
0.5k
uk
21k 0.5k uk
2-25 计算下列卷积
2 2 e3tut
hh00
1 0 2 1
c1c1 0.02.55cc22
0 1
c1
c2
2
3 4
3
h0
k
2 3
1k
4 3
0.5k
uk
1
hk h0 k 2 2h0 k 1
2 3
1k 2
4 3
0.5k 2
uk
1
2
2 3
1k 1
4 3
0.5k 1 u k
2 3
1k 2
4 3
0.5k 2
第二章信号与系统的时域分析
作业
1

南邮信号与系统B习题答案04

(3)
解：
s
s
2
a
2 2

a shatu (t ) 2 2 s a
由频域微分性：
d a 2as 2 tshatu(t ) 2 2 2 2 ds s a (s a )
s t shatu(t ) 由线性： 2 2 2 (s a ) 2a
4-7 用部分分式展开法求下列函数的拉氏反变换。
1 2 3 原式 e t 2e 2t 3e 3t u t s 1 s 2 s 3

2s 4 (4) s s2 4
A Bs C 解：原式是真分式，可表示为：原式 2 s s 4 2s 4 用遮挡法得： A 2 1 s 4 s 0
s 2 8s 10 (1) 2 s 5s 4
解：原式不是真分式，用长除法将其分解为：
3s 6 原式 1 2 s 5s 4 3s 6 则f 0 lim s 2 3 t s 5s 4
平面，故f 存在：
由于原式的极点为 1、 4，均位于s平面的左半
s 1 1 2s 1 4 2 2s 5 Y s 2 2 s 4s 4 s 1 s 4s 4 s 22
设Y s
s 2
2
2s 5
2

s 22
A
B s 2
用遮挡法求系数 A： A s 2 Y s s 2 2s 5 s 2 6
4-3 已知f t F s ，求下列信号的拉氏变换。
(2) e
解：
at
t f a
t f aF as a

南京邮电学院《信号与系统》第一次习题课

此时F1() 与F2(t-)无重叠， F1(t) ＊F2(t) =0;
b.当-1≤t-0.5（头部进入）并且t-3.5<-1（尾部
没有进入）时，即 -0.5≤t<2.5，如图④
图④ F2(t-)
F1()
此时
-3.5+t -1 0 -0.5+t
t 0.5
y(t) 1
F10 ( )F 2[(t 1) (t 1)]
-1 0 1 tt
F2(t) 3
01 4 t
F2 (t)
(t 1)[ (t 1) (t 4)]
F3(t) 2 24
0
t
-2
F3(t) 2t[(t) (t 1)] 2(t 2)[(t 1) (t 3)] 2(t 4)[(t 3) (t 4)]
四、已知函数的波形如图所示：
f1(t) 1
0 123
f2(t)
(1)
(1)
1
t
t
-0.5 (1)
1.5
求： (a) f 1(t) f 2(t)
f3(t)
(1)
(1)
-1 0 1
t
(b) f 1(t) f 3(t) f 3(t)
(c) {[ f 1(t) f 3(t)][(t 1) (t 3)]} f 3(t)
c.当t-3.5≥-1（尾部进入）并且t-0.5<3（头部没有出来）时，即 2.5≤t<3.5，如图⑤
图⑤
F2(t-) F1()
-1 –3.5+t-0.5+t 3
此时
t 0.5
y(t) t3.5 F10 ( )F20 (t )d
d.当t-3.5<3（尾部没有出来），t-0.5≥3（头部已出来）时，即 3.5≤t<6.5，如图⑥

南京邮电大学电路分析基础课后习题解答第5--11章 (课堂PPT)

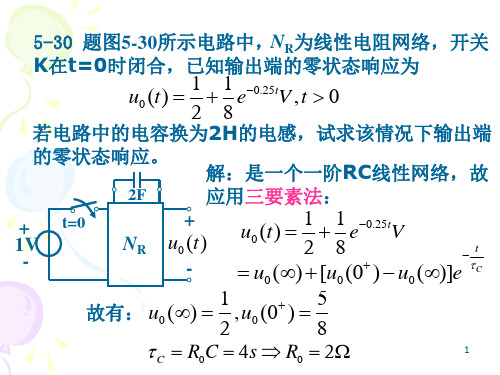
uC (T ) 10(1 et )V
(2)T t 2T时：
uC (T ) uC (T ) 10(1 et )V
uC () US
14
uC (t)
U S
[10(1
e1
)
U
s
]e
t T RC
V
uC (2T ) US [10(1 e1) Us ]e1 0
US 10e1 3.68V
13
5-38 题图5-38中所示脉冲宽度T=RC，施加于RC串联
电路，电路为零状态。试求使uS (t) 在t=2T时仍能回到
零状态所需负脉冲的幅度U
。
S
uS /V
10
U S
T 2T
t/s
+
us
-
+
-uC
解：(1) 0 t T 时：
uC () us 10V
t
uC (t) 10(1 e RC )V
3)求时间常数：
R0C
[(100 //100) 50] C1C2 C1 C2
104 S
5
4) 写出响应表达式： uC1(t) 5(1 e104t )V ,t 0 i1(t) 0.2 0.05e104t A,t 0
6
5-34 电路如图5-34所示，已知 is (t) 10 15 (t) A ，试
50
+
+
40V
-
100
10-V
i1(0 )
用迭加法求 i1(0 )：
i1
(0
)
100
40 100
//
50
50 100
50
10
100
50 100 //100 100 100

南京邮电通信原理课件

(a)
(b) 1 0 0 1
an
+E 0
bn (0)
1
1
0 (e)
1
1
1
0
(f)
4
6.1 数字基带信号及其频谱特性

单极性(NRZ)波形：该波形的特点是电脉冲之间无间隔，极性单一，易于用TTL、CMOS电路产生；缺点是有直流分量，要求传输线路具有直流传输能力，因而不适应有交流耦合的远距离传输，只适用于计算机内部或极近距离的传输。双极性(NRZ)波形：当“1”和“0”等概率出现时无直流分量，有利于在信道中传输，并且在接收端恢复信号的判决电平为零值，因而不受信道特性变化的影响，抗干扰能力也较强。单极性归零(RZ)波形：信号电压在一个码元终止时刻前总要回到零电平。通常，归零波形使用半占空码，即占空比为 50%。从单极性RZ波形可以直接提取定时信息。与归零波形相对应，上面的单极性波形和双极性波形属于非归零(NRZ)波形，其占空比等于100％。双极性归零(RZ)波形：兼有双极性和归零波形的特点。使得接收端很容易识别出每个码元的起止时刻，便于同步。
G1 ( f ) g1 (t )e j 2 ft dt

15
6.1 数字基带信号及其频谱特性
于是
U T ( f ) U T ( f )U T ( f ) 2

m N n N

N
N
N
am an e j 2 f ( n m )TS [G0 ( f ) G1 ( f )][G0 ( f ) G1 ( f )]
N
E[ U T ( f ) ] (2 N 1)Ts
2
即可求得u (t)的功率谱密度 2 (2 N 1) P(1 P) G0 ( f ) G1 ( f ) Pu ( f ) lim N (2 N 1)Ts

南邮信号与系统答案第5章

信号与系统 · 习题解答
第11页
5-8 试用单位阶跃序列表示图示离散信号。 (b) f (k)
2
3
2
1 −2 −1 0 1 2 3
4 5
6
−1
k
解：f 2 (k ) = ε (k + 2) + ε (k ) + ε (k − 2) − 4ε (k − 4) + ε (k − 6)
信号与系统 · 习题解答
10 5
k<0 k =0 k ≥1
∴ f1 (k − 1) + f 2 (k + 1) 0 k <0 ⎧ ⎪ =⎨ 1 k =0 ⎪2 k + k − 1 k ≥ 1 ⎩
2
1
−1 0 1 2
L
3 k
信号与系统 · 习题解答
第5页
*（4） f1 (k − 1) ⋅ f 2 (k + 1) 解：
f1 (k − 1) ⋅ f 2 (k + 1) ⎧ 0 ⎪ =⎨ 0 ⎪2 k (k − 1) ⎩ ⎧ 0 =⎨ k ⎩2 (k − 1) k <0 k =0 k ≥1 k <1 k ≥1
⎧C1 = 0 解得 C1 = 0 ， ⎪ 2 ⎨ 2 2 C2 = ⎪2[C1 cos 3 π + C2 sin 3 π ] = 2 3 ⎩
2 2 sin kπ 所以 yzi (k ) = 2 ⋅ 3 3
k
k ≥0
信号与系统 · 习题解答
第19页
5-15 试求下列差分方程的单位函数响应（1） y (k + 2) + 3 y (k + 1) + 2 y (k ) = x(k + 1) + x(k )

南京邮电学院《信号与系统》第二次习题课PPT课件

数F3()。
18
解:(1)对于f1(t)，求其导数f1’(t)
f1(t) 1
f1(t) ()S( a 2)•ej 2ejT
0
1 Tt
f1’(t)
Sa()•ej2 ejT
1
T
f1(t)F1()
2
j
0 1 (1) t
19
由图可看出
f2(t)f1( tT)
f1(t)
F 2 () F 1 ()• e j T
35
(五(1 ))求[下( 列信5 号) 的傅( 氏反5 变)换• ]co s
5
解：由公式 ( t 5 ) ( t 5 ) 1 0 S a 5
由对称性 1 0 S a 5 t 2 ( 5 ) ( 5 )
由公式 co s 5 5 tS a5 t ( ( 5 )5 ) ( ( 55 ) ) (t 5)(t 5) 2cos5 36
周期矩形脉冲：幅高A，周期 T，脉宽
Fn
A
T
Sa(n0)
2
…
-2T
f(t)
A
-T
-/2 /2
T
…
2T
4
（二）非周期信号
1. 傅里叶变换正反变换的定义式；
2. 频谱密度F()的物理意义；
3. 周期信号fT (t) 的复系数 Fn 与非周期信号 f (t ) 的频谱密度F()的关系；
F ()
cost[(t1)(t1)] 则
2 fa(t)
1
fa ( t) fa 0 ( t 2 ) fa 0 ( t) fa 0 ( t 2 )
(t 1 ) (t 1 ) 1 •2 S( a •2 ) 2 S( a )
fa0(t) S( a 2) 2 S( a 2)

南邮计算机控制系统设计与实现PPT课件

➢ 如果某参数是—系列有序数据的集合，如采样信号序列，
则不只有数据类型问题，还有一个数据存放格式问题，
即数据结构问题。
.
24
3、资源分配
➢ 系统资源包括ROM、RAM、定时器/计数器、个断源、 I/O地址等。
➢ ROM资源用来存放程序和表格，I/O地址、定时器/计数器、中断源在任务分析时已分配
➢ 因此，资源分配的主要工作是RAM资源的分配，RAM 资源规划好后，应列出一张RAM资源的详细分配清单，作为编程依据
51系列单片机作为控制器铂电阻温度计作为温度检测元件控制固态继电器的导通和断开时间的长短来控制电热元件的通电时间实现导热油温度控制通过控制过零触发型固态继电器的通断比来控制输入到加热炉的功率从而达到控制温度的目的固态继电器有两个输入控制端另外两端为输出控制端中间利用光电耦合器实现电气隔离输入端只要很小的输入电流便能控制它的导通没有输入电流则截止与有触点的继电器相比固态继电器控制电路简单开关速度快使用寿命长没有噪音等一系列优点462单片机的选择选择at89s52单片机作为控制系统的核心at89s52内部有8k的程序储存器256字节的数据储存器因而无需再扩展储存器使系统大大简化主要完成温度的采集控制显示和报警等功能3数据储存器扩展设定的温度曲线需要长期保存扩展一片串行eepromat24c256来保存设定的温度曲线474传感器的选择目前在温度测量领域内除了广泛使用热电偶以外电阻温度计也得到了广泛的应用尤其工业生产中120500范围内的温度测量常常使用电阻温度计本例中采用铂电阻来测量温度电阻的初值100欧温度每升高一度铂电阻的阻值约增加039欧48图86铂电阻及其信号放大电路图测量部分是一个不平衡电桥铂电阻与固定电阻组成不平衡电桥的四个桥臂为了保证测温的精度采用两次稳压在温度为0时铂电阻的阻值电桥平衡对角线ab两点没有电压差当温度变化时铂电阻的阻值变化其变化值与温度成正比电桥不平衡使对角线ab两点有电压差此电压差送到运算放大器的输入端经过放大后送到ad转换芯片505ad转换器的选择与接口设计eavp31x119x218resetrd17wr16int012int113t014t115p10p0039p0138p0237p0336p0435p0534p0633p0732p2021p2122p2223p2324p2425p2526p2627p2728psen29alep30txd11rxd10u189s52ncu2at24c256ncvcc14di13clk12sart11do10agndu3tlc0834vccvccoutvccr3r4vccr5r6l1l2vccr7vccy1c230pfc130pfvcccs1cs2clkzdiozkeyintu4b74f04u4a7404u8ssrr2r1vccvccu7j1220v516显示器键盘接口设计温度的设定与测量结果通过键盘和数码管显示电路完成

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1
X z 1 2z 1 y1 2 y 2
1 z 1 2z 2
1 z 1 2z 2
将X z z ，y1 1，y 2 1 代入，得：
z 1
4
Y
z
z
z3
1z 1z
2
z
1 z2 2z 2
1z 2
Yzs
z
Yzi
z
Yzs z
z
z
z2
1z 1z
2
z
A 1
B z 1
C z
2
1 1 1 1 4 1 遮挡法
求出f 。
(1)
F
z
z2 z 1
z 1z 3
解：Fz的极点为 z1 1，z2 3
由于z2 3位于单位圆外，因此不能用终值定理
5-7 计算下列卷积。
(1) akuk k 2
解： akuk z , k 2 z 2
za 由时域卷积定理得：
akuk k 2 z z 2
za
z
AB 2 1
z z2 3 z 1 z 1 z 1 z 1 z 1
48
2
4
2
4
hk
2 1 k
1 k
uk
2 4
3 由H z Y (z)
z2
可得系统差分方程：
X (z) z2 3 z 1
48
yk 2 3 yk 1 1 yk xk 2
4
8
或 yk 3 yk 1 1 yk 2 xk
求F z 的反变换：
z a z 1
F z 1 1 A B 遮挡法
z z a z 1 z a z 1 1 1 1 1 1 1 1 a 1 z a 1 a z 1 1 a z 1 z a
f k 1 uk akuk 1 ak uk
1 a
1 a
akuk uk 1 1 ak uk 1 ak uk 1
1 a
1 a
5-8 用Z变换解下列差分方程。
(2) yk 2 3yk 1 2yk 3k uk ，y0 y1 0
解：由于y0 y1 0为零状态，对差分方程作Z变换得：
z 2Y z 3zY z 2Y z z ，即Y z 1 z
z3
z2 3z 2 z 3
Y z
1
1 ABC
第五章离散时间信号与系统的变换域分析
作业
1
南京邮电大学
通信与信息工程学院
信息工程系
5-1 用定义求下列序列的Z变换。
(5)
1
k
uk
uk
3
2
解：
Fz
k 0
1 2
k
u
k
u
k
3z k
2 1 k
k0 2
z k
2
1
k
1
0
1
1
1
2
1
1
1
2
k0 2z 2z 2z 2z
Y (z)
2 单位函数响应hk ；
X (z)
z 1
z 1
3 4
1 8
3 写出系统差分方程； 4 求系统单位阶跃响
应gk 。
解： 1 对加法器列方程得：
Y z X z 3 z 1Y z 1 z 2Y z
4
8
Hz
Y z X z
1
1 3 z 1 1 z 2
z2
z2 3z1
48
48
2 H z
4
8
4 系统阶跃响应为：
Gz HzX z z2 z
z3
z2 3 z 1 z 1 48
z 1 z 1 z 1
2 4
8
1
Gz
z2
3 2 3
z z 1 z 1 z 1 z 1 z 1 z 1
2 4
2
4
gk
8
2 1 k
1 1 k
uk
3 2 3 4
f 1 lim zFz f 0 1
z
f 2 lim z 2 Fz f 0 f 0z 1
z
lim
z
z
2
z
z2
2z z z2
z 2 1 z 0.5
1 z 0.5
lim
z
z
2
z
2.5z 2 z 0.5
z 2 1 z 0.5
2.5
5-6 序列Z变换如下，能否应用终值定理，如果能，
2z 2z
(8) 2 1 3
解：F z f k zk f 0z0 f 1z1 1 3z1 k 0
5-3 用Z变换的性质求下列序列的Z变换。
k
(4) n2 n0
解： k 2uk zz 1 z 13
k
n2
z
zz 1 z2 z 1
序列求和
k 0
z 1 z 13 z 14
(5) k 12uk 1
5-14 已知离散系统函数 H z的零极点分布如题图 5 2所示，
且
lim
k
hk
1 ，系统的初始状态 3
yzi
0
2，yzi
1
1，求
j Imz
求：1 求H z；
解： k 2uk zz 1 z 13
k
12 uk
1
1 z
zz 1 z 13
z 1
z 13
因果序列右移
5-5 序列Z变换如下，试求 f 0，f 1，f 2。
(1) Fz
z2 2z
z2 1 z 0.5
解：由初值定理得：
也可以通过长除得：
f 0 lim Fz 0 z
F (z) z 1 2.5z 2
yk yk 1 2 yk 2 xk ，已知y1 1，
y 2 1 ，输入xk uk ，求该系统的零输入响应
4
yzi k ，零状态响应yzs k 及全响应yk 。
解：对差分方程进行Z变换，得：
Y z z 1Y z y1 2 z 2Y z z 1 y1 y 2 X z
Yz
2 z 1 6 z 1 3 z 2
y zs
k
1 2
1 6
1k
4 3
2k
uk
Yzi z
z
1 z 2 2
z 1z 2
D z 1
z
E 2
1 2
1 z 1
z
1
2
遮挡法
yzi k
1 1k
2
2k ,
k 0
yk
y zs
k
yzi k
1 2
2 3
1k
1 2k
3
,
k 0
5-11 某离散系统得模拟图如下图所示。求：1 求H z YXzz；
z z2 3z 2 z 3 z 1 z 2 z 3
1 1 1 1 1 1 遮挡法
4 z 1 5 z 2 20 z 3
yk
1 4
1k
1 5Leabharlann 2k1 3k20
uk
或 0.251k 0.2 2k 0.053k uk
5-9 某线性时不变离散系统，其差分方程为
a k－2uk－2 z z 2
za
因果序列右移性质
a kuk k 2 a k－2uk－2
另解：根据含信号的卷积运算性质直接可得
a kuk k 2 a k－2uk－2
(2) akuk uk 1
解： akuk z , uk 1 z 1 z 1
za
z 1 z 1
由时域卷积定理得：akuk uk 1 z 1 Fz