相量法的运算公式
合集下载
正弦量与相量法的基本概念

U1
解:
•
U 1 = 220
0 ,
•
U 2 = 220
120
+ •
•
U 1 + U2 = 220
0
220 120
-120o
•
U2
•
•
U1+ U2
= 220 (cos0 + j sin 0 ) + 220[cos(120 ) + j sin(120 )] = 110 j190.5 = 1102 + (190.5)2 arctan 190.5 = 220 60
复常数
A(t)包含了三要素:I, , 复常数包含了I , 。
•
称 I = I 为正弦量 i(t) 对应的有效值相量。
13
•
i(t) = 2I cos(t + ) I = I
正弦量的有效值相量表示:
以正弦量的有效值作为相量的模 正弦量的初相位作为相量的幅角
•
u(t) = 2U cos(t + ) U = U
注意:只适用正弦量
Im = 2I
i(t) = Im cos(t + ) = 2I cos(t + )
同理: u(t ) = Um cos(t + ) = 2U cos(t + )
★ 正弦量的有效值与最大值之间有固定的 2 关系,即
Im = 2I U m = 2U
10
二、 相 量 法 的 基 本 概 念
110
u1(t ) + u2 (t ) = 2 220cos(t 60 )
19
•
•
U 1 U2 = 220
0
220 120
解:
•
U 1 = 220
0 ,
•
U 2 = 220
120
+ •
•
U 1 + U2 = 220
0
220 120
-120o
•
U2
•
•
U1+ U2
= 220 (cos0 + j sin 0 ) + 220[cos(120 ) + j sin(120 )] = 110 j190.5 = 1102 + (190.5)2 arctan 190.5 = 220 60
复常数
A(t)包含了三要素:I, , 复常数包含了I , 。
•
称 I = I 为正弦量 i(t) 对应的有效值相量。
13
•
i(t) = 2I cos(t + ) I = I
正弦量的有效值相量表示:
以正弦量的有效值作为相量的模 正弦量的初相位作为相量的幅角
•
u(t) = 2U cos(t + ) U = U
注意:只适用正弦量
Im = 2I
i(t) = Im cos(t + ) = 2I cos(t + )
同理: u(t ) = Um cos(t + ) = 2U cos(t + )
★ 正弦量的有效值与最大值之间有固定的 2 关系,即
Im = 2I U m = 2U
10
二、 相 量 法 的 基 本 概 念
110
u1(t ) + u2 (t ) = 2 220cos(t 60 )
19
•
•
U 1 U2 = 220
0
220 120
电路第五版 8、相量法

=180.2 + j126.2 + 2.238 + j6.329
=182.5 + j132.5 = 225.5∠36
o
旋转因子: 旋转因子: e j = 1∠ 任何一个复数乘以一个旋转因子, 任何一个复数乘以一个旋转因子,就旋转一个角 j 例8-1 F=F1e j F F1 +1
π
2
特殊: 特殊:
同理,可得正弦电压有效值与最大值的关系: 同理,可得正弦电压有效值与最大值的关系:
1 U = Um 2
或
Um = 2U
若交流电压有效值为 U=220V ,
注意
U=380V 其最大值为 Um≈311V Um≈537V
工程上说的正弦电压、 电流一般指有效值, ① 工程上说的正弦电压 、 电流一般指有效值 , 如 设备铭牌额定值、电网的电压等级等。但绝缘水平、 设备铭牌额定值、电网的电压等级等。但绝缘水平、 耐压值指的是最大值。因此,在考虑电器设备的耐 耐压值指的是最大值。因此, 压水平时应按最大值考虑。 压水平时应按最大值考虑。
i2
i1 i2
i1+i2 →i3
ω
I1 o
ω
I2
i3
ω
I3
ωt
Ψ1
Ψ2
Ψ3
同频的正弦量相加仍得到同频的正弦量, 结论 同频的正弦量相加仍得到同频的正弦量, 所以,只需确定初相位和有效值。因此采用 所以,只需确定初相位和有效值。 正弦量 复数 变换的思想
§8. 2 正弦量的相量表示
一、正弦量的相量表示: 正弦量的相量表示:
F1 F2
F1 F2 = ( a1 a 2 ) + j ( b1 b2 )
(3)乘法运算: )乘法运算:
第8章 相量法_电气09级

*注意区分电压、电流的瞬时值、 注意区分电压、电流的瞬时值、 注意区分电压 最大值、有效值的符号。 最大值、有效值的符号。 宁波工程学院
i , Im , I
上页 下页
8-23
返回
第8章 相量法 章
正弦电流、 正弦电流、电压的有效值 ———— 同理,正弦电压有效值: 同理,正弦电压有效值: 1 T 2 I = √ —∫ 0 i dt 1 T U= Um 2 i = Imcos( ωt + ϕ ) 或 Um = 2U —————————— Im
+j b
F
F=a+jb
F
θ
称为复数 的模 +1
0
a
——— F = √ a2 + b2
a = Fcos θ b = Fsin θ
宁波工程学院
θ = arg F = arctan ( b/a )
称为复数 的辐角
8-5
上页
下页
返回
第8章 相量法 章
3 指数形式和极坐标形式
指数形式 欧拉公式
F = F(cosθ + jsinθ ) = Fe jθ e jθ = cosθ + jsinθ F = F/θ
正弦交流电变化的快慢; 正弦交流电变化的快慢; ϕu、ϕi 为正弦交流电的初相位。 为正弦交流电的初相位。
相位角
u = Umcos ( ωt + ϕu ) or u = Umsin( ωt + ϕu ) 瞬时值: 瞬时值:
宁波工程学院 简称相角或相( u = U m cos(ω t + ϕ u ) 简称相角或相 phase) 单位:弧度或度 单位: i = I m cos(ω t + ϕ i )
i , Im , I
上页 下页
8-23
返回
第8章 相量法 章
正弦电流、 正弦电流、电压的有效值 ———— 同理,正弦电压有效值: 同理,正弦电压有效值: 1 T 2 I = √ —∫ 0 i dt 1 T U= Um 2 i = Imcos( ωt + ϕ ) 或 Um = 2U —————————— Im
+j b
F
F=a+jb
F
θ
称为复数 的模 +1
0
a
——— F = √ a2 + b2
a = Fcos θ b = Fsin θ
宁波工程学院
θ = arg F = arctan ( b/a )
称为复数 的辐角
8-5
上页
下页
返回
第8章 相量法 章
3 指数形式和极坐标形式
指数形式 欧拉公式
F = F(cosθ + jsinθ ) = Fe jθ e jθ = cosθ + jsinθ F = F/θ
正弦交流电变化的快慢; 正弦交流电变化的快慢; ϕu、ϕi 为正弦交流电的初相位。 为正弦交流电的初相位。
相位角
u = Umcos ( ωt + ϕu ) or u = Umsin( ωt + ϕu ) 瞬时值: 瞬时值:
宁波工程学院 简称相角或相( u = U m cos(ω t + ϕ u ) 简称相角或相 phase) 单位:弧度或度 单位: i = I m cos(ω t + ϕ i )
正弦量的相量法表示法资料

①三角函数表示法: u +
u U m sin( t )
②正弦波形图示法: ③ 相量表示法。
(见右图)
0
_
t
正弦量的相量表示法 相量法
一个正弦量可以用旋转的有向线段表示。 有向线段的长度表示正弦量的幅值; 有向线段(初始位置)与横轴的夹角表示正弦量的初相位; 有向线段旋转的角速度表示正弦量的角频率。 正弦量的瞬时值由旋转的有向线段在纵轴上的投影表示。
正弦量的相量表示法
例 题 把下列电量的相量转换为瞬时值函数式。
(设f=50Hz)
(1) U 100e j 30V
(2) I (60 80 j ) A
(3) U m 20045V
解
(1)u 2U sin(2ft ) 100 2 sin(100t 30)V
6 j
极坐标式为:A r 5
B
5 6
6
+j
0
+1
复数及其运算 复数的运算
1.复数加减法运算
A1 a1 jb1 , A2 a2 jb2 则有
A1 A2 a1 a2 (b1 b2 ) j A1 A2 a1 a2 (b1 b2 ) j
例题
把下列正弦量用相量形式表示出来。 t 30)V (1)u 100sin 314tV (2)u 20 2 sin(628
(3)i 5 sin(100 t 60) A
解
(1)U m 1000V (2)U 20 30V (3) I 5 60 A
解
指数式,极坐标式。
1 3 r a 2 b2 ( )2 ( )2 1 2 2
u U m sin( t )
②正弦波形图示法: ③ 相量表示法。
(见右图)
0
_
t
正弦量的相量表示法 相量法
一个正弦量可以用旋转的有向线段表示。 有向线段的长度表示正弦量的幅值; 有向线段(初始位置)与横轴的夹角表示正弦量的初相位; 有向线段旋转的角速度表示正弦量的角频率。 正弦量的瞬时值由旋转的有向线段在纵轴上的投影表示。
正弦量的相量表示法
例 题 把下列电量的相量转换为瞬时值函数式。
(设f=50Hz)
(1) U 100e j 30V
(2) I (60 80 j ) A
(3) U m 20045V
解
(1)u 2U sin(2ft ) 100 2 sin(100t 30)V
6 j
极坐标式为:A r 5
B
5 6
6
+j
0
+1
复数及其运算 复数的运算
1.复数加减法运算
A1 a1 jb1 , A2 a2 jb2 则有
A1 A2 a1 a2 (b1 b2 ) j A1 A2 a1 a2 (b1 b2 ) j
例题
把下列正弦量用相量形式表示出来。 t 30)V (1)u 100sin 314tV (2)u 20 2 sin(628
(3)i 5 sin(100 t 60) A
解
(1)U m 1000V (2)U 20 30V (3) I 5 60 A
解
指数式,极坐标式。
1 3 r a 2 b2 ( )2 ( )2 1 2 2
正弦交流电路的相量表示法
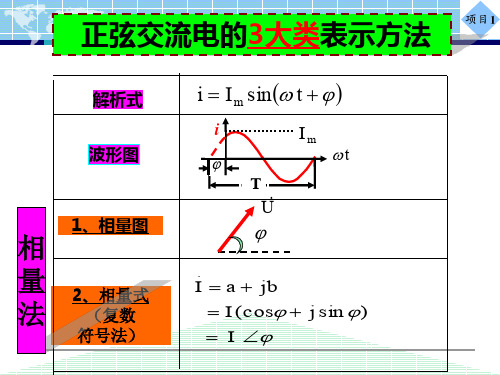
220
23
3
220 [cos( ) j sin( )] (110 j 190 .5)V
3
3
I
100 / 6
/3
220
U
u 正弦量
对应
相量图 U
t
例4
已知: u1(t) 100sin(314t 48)V ,
u2 (t) 50sin(314t 45)V
相量图: 把相量表示在复平面的图形
可不画坐标轴
2、相量式的书写方式:
模用最大值表示 ,则用符号:Um 、Im、E. m 模用有效值表示,则用符号: U 、I、E.
3注.3 意正弦:量在的实相量际表应示用法 中,模更多采用有效值表示
U I
注 意:
1) 相量只是表示正弦量,而不等于正弦量。
为了与一般的复数相区别,我们把表示正弦量的
复数称为相量,并在大写字母上打“.”表示。
设正弦量 u Umsin(ωt ψ)
相量表示:
U Uejψ Uψ 相量的模=正弦量的有效值
相量辐角=正弦量的初相角
或
Um Umejψ Umψ
相量的模=正弦量的最大值 相量辐角=正弦量的初相角
U• 220 45?
4 2 sin (ω t 30 ) ?
2
有效值
j45
瞬时值
4.已知:
U m 220 ? e45
U 100 15V
2.已知:I 1060A
i 10 sin ( ω t 60)?A
最大值
U 100V ?负号 ? U 100 ej15 V
+j
b
A
相量法 (Phasor method)

Chapter 8 相量法 (Phasor method)
相量 — 用于表示正弦量的复数。 相量法 — 复数分析法
概述 正弦量 正弦量的相量表示和相量的主要性质 电路定律的相量形式
1、正弦量 Am
f (t) = Amcos(t + )
振幅(有效值)、角频率、
0
和初相角三个要素。
T
2、复数几种表示形式
i 2I cos(t i )
U Ue ju U u I Ie ji I i
相量 vs
正弦量
相量的模表示正弦量的有效值 相量的幅角表示正弦量的初相位
符号说明
瞬时值 --- 小写 有效值 --- 大写 最大值 --- 大写+下标 复数(相量) --- 大写+ “.”
u、i U、I Um
U
R 1/jC I
代入元件的VAR,得:
RI
1
jC
I
jLI U s
U
+
s
+ U R
+
U C
jL
+
U
L
I
Us
200
200
R j(L 1C)
1
j(3
1 2
1 3 2
)
1 j
200 2450
2 45 A
3
i 2 cos(3t 45 ) A
UR RI 2 45V
UC
1 jC
I
j1 2
电压、电流关系
瞬时值
有效值
设
u 2U cost
R则
U IR
i 2I cost
相量图
相量式
I U
u、 i 同相
相量 — 用于表示正弦量的复数。 相量法 — 复数分析法
概述 正弦量 正弦量的相量表示和相量的主要性质 电路定律的相量形式
1、正弦量 Am
f (t) = Amcos(t + )
振幅(有效值)、角频率、
0
和初相角三个要素。
T
2、复数几种表示形式
i 2I cos(t i )
U Ue ju U u I Ie ji I i
相量 vs
正弦量
相量的模表示正弦量的有效值 相量的幅角表示正弦量的初相位
符号说明
瞬时值 --- 小写 有效值 --- 大写 最大值 --- 大写+下标 复数(相量) --- 大写+ “.”
u、i U、I Um
U
R 1/jC I
代入元件的VAR,得:
RI
1
jC
I
jLI U s
U
+
s
+ U R
+
U C
jL
+
U
L
I
Us
200
200
R j(L 1C)
1
j(3
1 2
1 3 2
)
1 j
200 2450
2 45 A
3
i 2 cos(3t 45 ) A
UR RI 2 45V
UC
1 jC
I
j1 2
电压、电流关系
瞬时值
有效值
设
u 2U cost
R则
U IR
i 2I cost
相量图
相量式
I U
u、 i 同相
电路分析相量法

量的相量乘以 jω ,即表示di/dt 的相量为
j I I( i 90o )
该相量的模为ωI ,辐角则超前原相量π/2 。
对 i 的高阶导数 dni/dtn ,其相量为 ( j )。n I
3)正弦量的积分
设 i 2I cos( t i ),则
idt Re[ 2Ie j t ] dt Re[ (
F1F2 | F1 | 1 | F2 | 2 | F1 || F2 | (1 2 )
可见复数的乘法运算使用指数形式或极坐标形式较为简便。
3)除法运算
a)代数形式
F1 F2
a1 a2
jb1 jb2
(a1 (a2
jb1 )(a2 jb2 )(a2
jb2 ) jb2 )
(a1a2
b1b2 ) j(a2b1 a22 b22
设 F1 a1 jb1 , F2 a2 jb2 ,则
F1 F2 (a1 jb1 ) (a2 jb2 ) (a1 a2 ) j(b1 b2 )
平行四边形法则:
+j F1 +F2 F1
F2 o
+1
+j F1
F2 o
F1-F2 +1
2)乘法运算 a)代数形式
F1F2 (a1 jb1 )(a2 jb2 ) (a1a2 b1b2 ) j(a1b2 a2b1 )
di d Re[ 2Ie j t ] Re[ d ( 2Ie j t )] Re[ 2( j I)e j t ]
dt dt
dt
Re[ 2 Ie ] j( ti 90o ) 2 I cos( t i 90o )
上式表明:
复指数函数实部的导数等于复指数函数导数的实部;
3.2相量表示法
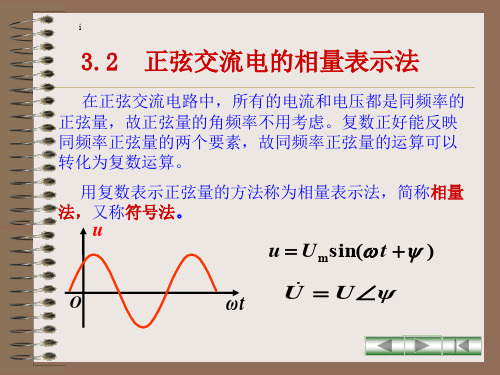
设相量 A rejψ A 将相顺量时针A 乘旋以转e9-0j9,0 得,到C
例已知正弦电量的瞬时值表达式分别为
,
e 180 2 sin(t 60) V i 10 2 sin(t 30) A
要求(1)写出各正弦量对应的最大值相量和有效值相量。
(2)画出各正弦量对应相量的相量图。
方法2:用图解法求总电流i
① 根据电流i1、i2的瞬时值表达式,写出对应的相量表
达式。
I1
630
A
I 2 8 60 A
② 画出 I1 I 2 ,用矢
量求和法作出电流的相量
图,如图(b)所示。由
相量图确定正弦电流的有
效值和初相位
I 10 A 23.1
③ 写出电流对应的相量表达式
最大值
3.已知:
I 4 e
j30
A
复数
4 2 sin (ω t 30 )A?
瞬时值
4.已知:
U 100 15V
U 100V ? ? U 100 ej15 V
负号
3.2.3相量的计算
(1)复数的加减运算 设两个复数分别为A1 = a1 + jb1,A2 = a2 + jb2,
② 用复数符号法求和,得到电流i对应的相量表达式
I I1 I2
(5.196 j3) (4 j6.928)
I 10 23.1A
9.296 j3.928 10 23.1A
③写出电流i的瞬时值表达式。
i 10 2 sin(t 23.1)A
解:(1)写出各正弦量对应的最大值相量和有效值相量。
例已知正弦电量的瞬时值表达式分别为
,
e 180 2 sin(t 60) V i 10 2 sin(t 30) A
要求(1)写出各正弦量对应的最大值相量和有效值相量。
(2)画出各正弦量对应相量的相量图。
方法2:用图解法求总电流i
① 根据电流i1、i2的瞬时值表达式,写出对应的相量表
达式。
I1
630
A
I 2 8 60 A
② 画出 I1 I 2 ,用矢
量求和法作出电流的相量
图,如图(b)所示。由
相量图确定正弦电流的有
效值和初相位
I 10 A 23.1
③ 写出电流对应的相量表达式
最大值
3.已知:
I 4 e
j30
A
复数
4 2 sin (ω t 30 )A?
瞬时值
4.已知:
U 100 15V
U 100V ? ? U 100 ej15 V
负号
3.2.3相量的计算
(1)复数的加减运算 设两个复数分别为A1 = a1 + jb1,A2 = a2 + jb2,
② 用复数符号法求和,得到电流i对应的相量表达式
I I1 I2
(5.196 j3) (4 j6.928)
I 10 23.1A
9.296 j3.928 10 23.1A
③写出电流i的瞬时值表达式。
i 10 2 sin(t 23.1)A
解:(1)写出各正弦量对应的最大值相量和有效值相量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相量法的运算公式
相量的运算公式包括:
1.相量的加减法:
a+b = (a_x + b_x) + (a_y + b_y) j
a-b = (a_x - b_x) + (a_y - b_y) j
其中,a_x和a_y分别为向量a在x轴和y轴上的分量,b_x和b_y分别为向量b在x轴和y轴上的分量,j为虚数单位。
2.相量的乘法:
a*b = (a_magnitude * b_magnitude) * exp(j * (a_angle +
b_angle))
其中,a_magnitude和b_magnitude分别为向量a和b的模长,a_angle和b_angle分别为向量a和b与实部轴之间的夹角,exp为指数函数,j为虚数单位。
相量法拓展:
1.相量法不仅适用于平面向量,在空间向量中同样适用,只是需要增加z轴分量。
2.相量法不仅适用于电学领域中的交流电路分析,还适用于机械学、热力学的分析,以及计算机图形学中的向量运算等领域。
3.利用相量法,可以求解平面图形的面积、角度、垂直平分线、内心、外心等问题。
