盘形凸轮的四种设计方法
第4.3节(盘形凸轮廓线的设计)
第三节 盘形凸轮廓线的设计当根据工作要求和结构条件选定了凸轮机构的类型、从动件的运动规律和凸轮的基圆半径（其确定将在下节中介绍）等结构参数后，就可以设计凸轮的轮廓曲线。
凸轮廓线的设计方法有图解法和解析法，其设计原理基本相同。
本节先简要介绍图解法，后重点介绍解析法设计凸轮廓线。
一、凸轮廓线设计的基本原理图4-13 反转法设计凸轮廓线基本原理图4-13所示为一尖顶对心盘形凸轮机构，设凸轮以等角速度ω逆时针转动，推动从动件2在导路中上、下往复移动。
当从动件处于最低位置时，凸轮轮廓曲线与从动件在A 点接触，当凸轮转过1ϕ角时，凸轮的向径A A 0将转到A A '0位置，而凸轮轮廓将转到图中虚线所示的位置。
从动件尖端从最低位置A 上升至B '，上升的位移为B A S '=1，这是从动件的运动位移。
若设凸轮不动，从动件及其运动的导路一起绕A 0点以等角速度-ω转过1ϕ角，从动件将随导路一起以角速度-ω转动，同时又在导路中作相对导路的移动，如图中的虚线位置，此时从动件向上移动的位移为B A 1。
而且，11S B A B A ='=，即在上述两种情况下，从动件移动的距离不变。
由于从动件尖端在运动过程中始终与凸轮轮廓曲线保持接触，所以从动件尖端的运动轨迹即为凸轮轮廓。
设计凸轮廓线时，可由从动件运动位移先定出一系列的B 点，将其连接成光滑曲线，即为凸轮廓线。
由于这种方法是假设凸轮固定不动而使从动件连同导路一起反转，故称为反转法。
对其它类型的凸轮机构，也可利用反转法进行分析和凸轮廓线设计。
二、图解法设计凸轮廓线1. 移动从动件盘形凸轮廓线的设计（1）尖端从动件 图4-14a 所示为一偏置移动尖端从动件盘形凸轮机构。
设已知凸轮的基圆半径为b r ，从动件导路偏于凸轮轴心A 0的左侧，偏距为e ，凸轮以等角速度ω顺时针方向转动。
从动件的位移曲线如图4-14b 所示，试设计凸轮的轮廓曲线。
图4-14 尖端从动件盘形凸轮廓线设计依据反转法原理，具体设计步骤如下。
机械设计对心直动滚子从动件盘形凸轮的设计
机械设计对心直动滚子从动件盘形凸轮的设
计
心直动滚子从动件盘形凸轮的设计：
心直动滚子从动件是一种常见的机械传动件，在机械设计中有广
泛的应用。
其中，盘形凸轮是心直动滚子从动件的重要组成部分之一。
盘形凸轮的制作需要遵循以下步骤：
1. 计算凸轮尺寸：首先，需要根据设计要求和需求计算凸轮的
外径、凸起高度和凸起角度等参数。
2. 绘制凸轮图形：根据凸轮尺寸和形状，利用CAD等软件绘制
凸轮的二维图形，包括凸轮的内外形状和凸起部分的形状。
3. 加工凸轮模具：根据凸轮的二维图形制作凸轮模具，可以采
用数控加工等先进工艺，确保凸轮的制作精度和质量。
4. 利用凸轮模具生产凸轮：将凸轮模具放在凸轮加工机床上，
根据需要生产出对应的盘形凸轮。
在盘形凸轮的制作中，需要考虑凸轮与滚子的配合精度和接触面积，以确保传动的可靠性和稳定性。
同时还需要考虑加工工艺和材料
选择，保证凸轮的强度和寿命。
盘形凸轮项目设计方案
盘形凸轮项目设计方案第一章绪论1.1研究背景凸轮机构由于结构简单、易于实现复杂的运动规律,因此广泛应用于众多机械中。
但是由于凸轮与从动件之间的高副接触方式会增加机构的功率损耗,因此对其在高效率传动系统中的使用形成了较大限制。
如何实现直动从动件凸轮机构的纯滚动接触是解决相对滑动接触方式,并迅速提高凸轮机构工作效率的最有效途径。
低副机构一般只能近似地实现给定运动规律,而且设计较为复杂。
当从动件的位移、速度和加速度必须严格地按照预定规律变化,尤其当原动件作连续运动而从动件必须作间歇运动时,则以采用凸轮机构最为简便。
凸轮机构由凸轮、从动件或从动件系统和机架组成,凸轮通过直接接触将预定的运动传给从动件。
凸轮机构具有结构简单,可以准确实现要求的运动规律等优点。
只要适当地设计凸轮的轮廓曲线,就可以使推杆得到各种预期的运动规律。
在各种机械,特别是自动机械和自动控制装置中,广泛地应用着各种形式的凸轮机构。
凸轮机构之所以能在各种自动机械中获得广泛的应用,是因为它兼有传动、导引及控制机构的各种功能。
当凸轮机构用于传动机构时,可以产生复杂的运动规律,包括变速围较大的非等速运动,以及暂时停留或各种步进运动；凸轮机构也适宜于用作导引机构,使工作部件产生复杂的轨迹或平面运动；当凸轮机构用作控制机构时,可以控制执行机构的自动工作循环。
因此凸轮机构的设计和制造方法对现代制造业具有重要的意义。
本文基于"两构件的相对运动可以用与这两构件相固连的一对瞬心线的纯滚动来实现"这一瞬心线性质,推导出能够满足预定的从动件运动规律要求的纯滚动接触直动从动件盘形凸轮机构轮廓曲线的计算公式,并分析了该种凸轮机构的临界压力角、许用压力角、机构效率、基圆半径等各项参数的特征和机构特征。
根据分析结果,完成了一套能够实现预定从动件运动规律的纯滚动接触凸轮机构的完整轮廓曲线设计的方案,设计得到的凸轮机构不但能够在回程、近休止和推程的机构运动阶段保持纯滚动接触,还能实现远休止运动阶段,并且针对运动规律相同但行程大小不同的凸轮机构提出缩放轮廓的设计方式,大大简化了该种凸轮机构的制造工艺。
机械设计对心直动滚子从动件盘形凸轮的设计
机械设计对心直动滚子从动件盘形凸轮的设计摘要：本文主要介绍了机械设计中心直动滚子从动件盘形凸轮的设计，包括设计原理、设计方法、设计流程和设计实例等内容。
通过本文的学习，读者可以了解到机械设计中心直动滚子从动件盘形凸轮的设计技术，从而为机械设计工作提供参考和借鉴。
关键词：机械设计；中心直动滚子从动件；盘形凸轮；设计一、引言在机械设计中，中心直动滚子从动件盘形凸轮是一种常见的传动机构，其主要作用是将旋转运动转换为直线运动。
因此，对于机械设计师来说，掌握中心直动滚子从动件盘形凸轮的设计技术是非常重要的。
本文将介绍机械设计中心直动滚子从动件盘形凸轮的设计原理、设计方法、设计流程和设计实例等内容，希望能为机械设计工作者提供参考和借鉴。
二、设计原理中心直动滚子从动件盘形凸轮的设计原理是利用凸轮的轮廓形状，使滚子在其上滚动，从而实现直线运动。
具体来说，凸轮的轮廓形状可以是圆弧、椭圆、抛物线等，而滚子的数量和大小则根据实际需要进行设计。
在运动过程中，凸轮的轮廓形状决定了滚子的运动轨迹，而滚子的直线运动则通过滑块和导轨等部件实现。
因此，在设计中心直动滚子从动件盘形凸轮时，需要考虑凸轮的轮廓形状、滚子的数量和大小以及滑块和导轨等部件的设计。
三、设计方法中心直动滚子从动件盘形凸轮的设计方法主要包括以下几个步骤：1. 确定传动比和运动要求：首先需要确定传动比和运动要求，包括传动比、滚子数量和大小、滑块和导轨的设计等。
2. 计算凸轮的轮廓形状：根据运动要求和传动比，计算出凸轮的轮廓形状。
具体来说，可以利用数学模型或计算机模拟等方法进行计算。
3. 设计滑块和导轨：根据凸轮的轮廓形状和滚子的运动轨迹，设计滑块和导轨等部件。
其中，滑块的设计需要考虑其密封性、耐磨性和承载能力等因素。
4. 完善设计：在完成初步设计后，需要进行完善设计，包括进行力学分析、动态模拟和优化设计等。
同时，还需要考虑制造工艺、材料选择和装配等问题。
四、设计流程中心直动滚子从动件盘形凸轮的设计流程主要包括以下几个步骤：1. 确定传动比和运动要求：首先需要确定传动比和运动要求，包括传动比、滚子数量和大小、滑块和导轨的设计等。
设计盘形凸轮的轮廓时常用的方法
设计盘形凸轮的轮廓时常用的方法设计盘形凸轮的轮廓时常用的方法可以说是机械工程设计中非常重要的一环。
盘形凸轮是一种机械传动装置，通过其轮廓形状的设计，可以实现不同的轴向位移或转矩传递。
在实际工程设计中，常用的方法有很多种，包括基本轮廓设计、轮廓修正、尺寸计算等。
在本文中，我将简要介绍一些设计盘形凸轮的轮廓时常用的方法，并共享一些个人观点和理解。
一、基本轮廓设计1. 根据运动要求：设计盘形凸轮的首要任务是要根据运动规律和要求确定轮廓形状。
不同的运动要求可能会对轮廓形状有不同的要求，比如有些情况需要正弧，有些情况需要余弦曲线。
在设计之初需要首先明确轮廓的基本形状。
2. 考虑受力情况：在确定基本轮廓形状之后，需要考虑受力情况，根据承受的载荷确定凸轮的弧形和高度的比例关系，以保证凸轮在工作时能够承受所需的载荷并保持安全。
二、轮廓修正1. 加工余量考虑：设计盘形凸轮的轮廓时，需要考虑到加工余量，尤其是在实际加工中难免会有一些误差，因此需要对轮廓进行适当的修正，以保证在加工后能够满足实际的使用要求。
2. 润滑和磨损：凸轮在工作时需要不断地与其他机械零部件接触，因此轮廓设计时需要考虑到润滑和磨损的情况，尽量减小接触面积，以降低摩擦，延长零部件的使用寿命。
三、尺寸计算1. 轴向位移和转矩传递计算：设计盘形凸轮的轮廓时需要考虑到其在工作时的轴向位移和转矩传递情况，通过相关的尺寸计算，可以确定每个点的坐标和曲线的方程，从而实现所需的运动规律。
2. 运动学分析：在进行尺寸计算时，还需要进行运动学分析，确定凸轮与从动件之间的相对运动情况，保证从动件能够按照设计要求作出相应的运动。
总结和回顾设计盘形凸轮的轮廓时常用的方法包括基本轮廓设计、轮廓修正和尺寸计算。
在实际设计中，需要根据具体的运动要求和受力情况进行综合考虑，保证设计的轮廓能够满足实际的使用要求。
还需要考虑加工余量、润滑和磨损情况，以及进行相关的尺寸计算和运动学分析。
盘形凸轮的四种设计方法
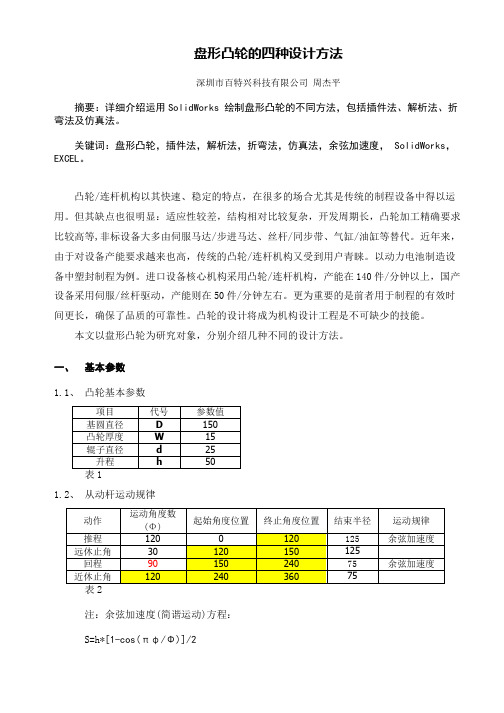
盘形凸轮的四种设计方法深圳市百特兴科技有限公司 周杰平摘要：详细介绍运用SolidWorks 绘制盘形凸轮的不同方法，包括插件法、解析法、折弯法及仿真法。
关键词：盘形凸轮，插件法，解析法，折弯法，仿真法，余弦加速度， SolidWorks，EXCEL。
凸轮/连杆机构以其快速、稳定的特点，在很多的场合尤其是传统的制程设备中得以运用。
但其缺点也很明显：适应性较差，结构相对比较复杂，开发周期长，凸轮加工精确要求比较高等,非标设备大多由伺服马达/步进马达、丝杆/同步带、气缸/油缸等替代。
近年来，由于对设备产能要求越来也高，传统的凸轮/连杆机构又受到用户青睐。
以动力电池制造设备中塑封制程为例。
进口设备核心机构采用凸轮/连杆机构，产能在140件/分钟以上，国产设备采用伺服/丝杆驱动，产能则在50件/分钟左右。
更为重要的是前者用于制程的有效时间更长，确保了品质的可靠性。
凸轮的设计将成为机构设计工程是不可缺少的技能。
本文以盘形凸轮为研究对象，分别介绍几种不同的设计方法。
一、基本参数1.1、凸轮基本参数项目 代号 参数值基圆直径 D 150凸轮厚度 W 15辊子直径 d 25升程 h 50表11.2、从动杆运动规律动作 运动角度数(Φ)起始角度位置 终止角度位置 结束半径 运动规律推程 120 0 120 125 余弦加速度 远休止角 30 120 150 125 回程 90 150 240 75 余弦加速度 近休止角 120 240 360 75 表2注：余弦加速度(简谐运动)方程：S=h*[1-cos(πφ/Φ)]/2图1二、SolidWorks 插件法2.1、如图2，打开SolidWorks，新建零件，关闭草图。
菜单栏Toolbox -> 凸轮如菜单栏无Toolbox，先加入插件。
图2 图32.2、设置。
如图3凸轮类型为圆形，推杆类型为平移，如果是偏心的，可作相应的选择；开始半径为基圆半径，开始角度根据<表2>填写；旋转方向为顺时针2.3、运动如图4图4运动部分，根据<表2>，进行设置，运动的类型为谐波；2.4、 生成 如图5图5生成部分：坯件的外径要满足：>(D+d)/2；近毂和远榖分别为凸轮两侧的圆柱状台阶，要大于孔的直径，厚度自行定义，但需要大于圆角半径和倒角大小；本例子缺省。
摆动滚子从动件盘形凸轮机构设计的解析法
摆动滚⼦从动件盘形凸轮机构设计的解析法摆动滚⼦从动件盘形凸轮机构设计的解析法①0前⾔摆动滚⼦从动件盘形凸轮机构的设计主要包括基本尺⼨的确定[ 1 ]和凸轮轮廓的设计. 基本尺⼨主要是根据压⼒⾓确定的, 凸轮轮廓是根据基本尺⼨和从动件的运动规律设计的. 过去这两部分的设计常常采⽤图解法, 虽然图解法简单、直观, 但精度低, 随着计算机技术的发展和数控机床的普及, 凸轮机构设计的解析法[ 2 ]正逐步取代传统的图解法.图1摆动从动件盘形凸轮机构的压⼒⾓1机构压⼒⾓的计算如图1 所⽰, 为摆动从动件盘形凸轮机构的压⼒⾓⽰意图. 摆杆长度O 2A = l, 机架长O 1O 2 = a.过瞬⼼P 作摆杆O 2A 的垂直线, 交O 2A延长线于B 点. 则有:tan A= BAPB=O 2P cos (W0 + W) - lO 2P sin (W0 + W)P 点为机构的瞬⼼, 则有:X1O 1P = X2O 2PX2X1=O 1PO 2P=d Wd U=O 1PO 1P + a∴O 1P =d Wd U a1 -d Wd UO 2P = O 1P + a = a1 -d Wd U∴tan A=a cos (W0 + W) - l (1 -d Wd U)a sin (W0 + W)上式是按X1 和X2 同向推出的, 否则tan A=a cos(W0 + W) - l (1 +d Wd U)a sin (W0 + W)⼯程设计中, 必须对凸轮机构的最⼤压⼒⾓加以限制, 凸轮机构的最⼤压⼒⾓应⼩于许⽤压⼒⾓. 2机构基本尺⼨的确定图2确定基本尺⼨⽰意图2. 1基本尺⼨确定的⽅法图2 中O 2 为摆杆的回转中⼼,A 为滚⼦摆杆的滚⼦中⼼. A 0 到A 6 为按给定运动规律W= f (U) 作出的摆杆各个位置, 位置个数可任选. 在摆杆的每位置上截取长为ld Wd U,其中l 为摆杆长, W为摆杆摆⾓, U为凸轮转⾓.截取⽅法为: 若摆杆与凸轮转向相同, 由A 点向着回转中⼼O 2 取; 若摆杆与凸轮转向相反, 由A 点背着回转中⼼O 2 取.图2 中凸轮与摆杆的相对转动关系为: 凸轮逆时针转,摆杆推程逆时针转, 回程顺时针转. 若推程许⽤压⼒⾓为[A], 回程许⽤压⼒⾓为[A′], 线段A 1a1,A 2a2, ?为对应推程截取的; 线段A 1a′1,A 2a′2, ?为对应回程截取的. 过端点a1, A2, ?和a′1 , a′2, ?作与相应的摆杆成(90°- [A]) 或(90°- [A]) 的直线, 简称a 斜线和a′斜线. 这些线的包络线é , ê , ? 所包围的阴影区域为满⾜许⽤压⼒⾓的前提下, 凸轮回转中⼼的可选区域. O ′1A 0 为最⼩基圆半径,O ′1O 2 为对应的中⼼距.以O 2 为原点,O 2A 0 为x 轴, 使A 1,A 2, ?各点y 坐标为正值的⽅向为y 轴, 建⽴直⾓坐标系. 若已知包络线é , ê , ? 的⽅程, 则可知凸轮回转中⼼O 1 的许⽤区域.2. 2包络线⽅程的求法及基本尺⼨的确定在图2 中, 任意a 斜线的斜率为k = tan A= cot (- [A] - W) , 各a 点的坐标为:x = l (1 -d Wd U cos W) , y = l (1 -d Wd U) sin W, 由点斜式可写出任意a 斜线的⽅程. 同理, 对任意a′斜线, 斜率为k′= cot ( [A] - W) , 各a′点的坐标为: x ′= l (1 +d Wd U) cos W, y ′= l (1 +d Wd U) sin W, 同样可写出任意a′斜线的⽅程.由以上包络线⽅程相交, 可求出凸轮回转中⼼O 1 的许⽤区域, 此过程较繁, 可上机求解. 在O 1 的取值范围内任取⼀点(x , y ) 作为凸轮的回转中⼼, 则凸轮的基圆半径可确定:图3反转法设计凸轮的轮廓r0 = ( l - x ) 2 + y 2.3凸轮轮廓的设计图3 中, 直⾓坐标系的原点位于凸轮的回转中⼼O 1 点. 机架长为a, 摆杆长为l. 摆动滚⼦从动件的初始位置在⾏程起始位置1 时的O 20A 0. 反转U⾓后, 到达位置2 的O 2A. 凸轮与从动件的接触点A 0 到达A 点,A ′A为对应的弧位移s, 对应从动件的摆⾓W.从动件O 2A的运动可以看作O 20A 0 绕O 1 点反转U⾓, 到达O 2A ′位置,O 2A ′再摆动W⾓到达O 2A 位置. 从动件O 2A 的运动还可以看作O 20A 0 绕O 20 点反转(U+ W) ⾓, 到达O 20A ″点,O 20A ″再平移到O 2A 位置. 设A 0 点的坐标为(x A 0,第1 期毕艳丼等: 摆动滚⼦从动件盘形凸轮机构设计的解析法37y A 0) ,A 点的坐标为(x , y ) ,O 2A 的复合运动可⽤下述的坐标旋转和平移变换来实现. x y=cos(U+ W) sin (U+ W)- sin (U+ W) cos (U+ W)x A 0 - x O20y A 0 - y O20+x O2y O2(1)式中: x O 2 = a sin U, y O 2 = a co s U, x O20 = 0, y O20 = a, x A 0 = - l sin W0, y A 0 = a - l co s WW0 为摆杆的初始位置⾓, 其值为W0 = arccosa2 + l2 - r202al将其代⼊⽅程(1) 并整理, 可得理论廓线⽅程:x = a sin U- l sin (U+ W+ W0) ; y = a cos U- l cos (U+ W+ W0)则其实际廓线⽅程[ 2 ] 为:x A= x ±r rd yd Ud xd U2+d yd U2, y A= y or rd xd Ud xd U2+d yd U2其中r r 为滚⼦半径; 滚⼦圆的包络线有两条, 上⾯⼀组符号⽤于求解外凸轮的包络线⽅程, 下⾯⼀组符号⽤于求解内凸轮的包络线⽅程.4结束语本⽂利⽤解析法设计摆动滚⼦从动件盘形凸轮机构, 适⽤于⽤计算机辅助运算设计凸轮机构, 其精度⾼, 使⽤⽅便, 特别适合⾼精度凸轮机构的设计.参考⽂献:[ 1 ]尚锐等. 摆动从动件盘形凸轮机构基本尺⼨确定的解析法[J ]. 辽宁⼯学院学报, 1999, (6) : 29- 32. [ 2 ]邹慧君等. 机械原理[M ]. 北京: ⾼等教育出版社, 1999, 117- 132.。
图解法设计盘形凸轮轮廓曲线
推程彳
回程[a]=80°
:摆动从动件=45°
七、基圆半径的确定
max三
诺模图
讲授新课
四、摆动从动件盘形凸轮轮廓曲线的绘制（例图3—17P52）
讲授法
五、滚子半径的选择
aminrT――工作轮廓曲率半径
min――理论轮廓曲率半径
rt基圆半径rtVmin
丁ItW0、8min
推存rtv
O.4ro
a3：
J5mm
课堂练习
课堂例题讲解
六、压力角的选择和检验
roV2
smaxW移动从动
疔30°
图解法设计盘形凸轮轮廓曲线
教学难点
设计凸轮机构应注意的问题
课前准备
教具模型
备注
山东理工职业学院教案纸
教学过程
教学内容
教学方法
导入
一、对心移动尖顶从动件盘形凸轮轮廓曲线的绘制（例图3—13P49）
二、对心移动滚子从动件盘形凸轮轮廓曲线的绘制（例图3—14P50）
三、对心移动平底从动件盘形凸轮轮廓曲线的绘制（例图3—15P50）
山东理工职业学院教案首页
2015-2016学年第 二 学期
课程名称
机械设计基础
任课教师
授课班级
授课时间
第周
第周
第周第周第周 Nhomakorabea第周星期
星期
星期
星期
星期
星期
第节
第节
第节
第节
第节
第节
月日
月日
月日
月日
月日
月日
授课课题
图解法设计盘形凸轮轮廓曲线
教学目的
图解法设计盘形凸轮轮廓曲线 设计凸轮机构应注意的问题
教学重点
8盘型凸轮轮廓曲线设计
“反转法”原理
凸轮转动、从动件 在导路中移动
对整个系统施 加-运动
凸轮保持不动 推杆：复合运动=
反转运动(-) + 预期运动(s)
机
械
基
-
础
A
AA
AA
AAAA
r0
r
0
对心尖顶移动从动件盘形凸轮轮廓的设计
已设知计：：r凸0，轮推廓杆线运动规律，凸轮逆s 时针方向转动
简单直观，可直接得出凸轮的轮廓，但作图有一定误差，设计精度不高。
机
工程上应用较多。
械
基
础
解析法
精度较高，但设计计算量大，
多用于精密或高速凸轮机构的设计中
凸轮轮廓的设计方法 图解法
依据“反转法” 对整个系统施加-w运动
机 械 基 础上面的图，在图片中 是动画，帮录下来凸轮轮廓的设计方法
1、偏置尖顶移动从动件盘形凸轮轮廓的设计
凸轮轮廓的设计方法
2、滚子移动从动件盘形凸轮轮廓的设计
已知：r0，推杆运动规
机 械
律，滚子半径r1, 凸 轮逆时针方 向转
基
动
础
设计：凸轮廓线
h
s
0
120 600
900
900
理论轮廓 实际轮廓
凸轮轮廓的设计方法
总结
1、偏置尖顶移动从动件盘形凸轮轮廓曲线设计
机
械
2、滚子移动从动件盘形凸轮轮廓的设计
h
机
解：
械
基
1. 定比例尺l
φ
0
120 1800
2700 3600
础
2. 初始位置及推杆位移曲线
3. 确定推杆反转运动占据的各 角度位置
第18讲盘形凸轮
压力角越小， 传力越好。
自锁 ：如果凸轮机构运动到某 一位置的压力角大到使有效分力 不足以克服摩擦阻力，不论推力 多大，都不能使从动件运动。这 种现象称为凸轮机构的自锁。机 构开始出现自锁时的压力角称为 临界压力角 。
2.凸轮机构的压力角
K
c min 0
实际轮廓相交而造成 从动件运动失真 对于内凹的凸轮廓线 ： 实际轮廓为光滑曲线
c 0
K
0 . 8 min
c min 1 ~ 5 mm
2.凸轮机构的压力角
压力角：不计摩擦时，凸轮对从 动件的作用力（法向力）与从动 件上受力点速度方向所夹的锐角。 该力可分解为两个分力 ：
对心滚子移动从动件盘形凸轮轮廓曲线的设计
实 际 轮 廓 曲 线
理 论 轮 廓 曲 线
偏置尖顶移动从动件盘形凸轮轮廓曲线的设计
已知：如图所示
e
凸轮机构设计中应 注意的几个问题
设计凸轮机构，不仅要保证从动件能实现预定的运动规律， 还须使设计的机构传力性能良好，结构紧凑，满足强度和 安装等要求，为此，设计时应注意处理好下述问题。
移动从动件盘形凸轮 轮廓曲线的图解设计
设计方法：
1.图解法 2.解析法
设计一般精度凸轮时常被采用图解法。而设计高精度 凸轮，则必须用解析法，但计算复杂。本节主要讨论 图解法。
基本原理：
反转法原理
移动从动件盘形凸轮 轮廓曲线的图解设计
反转法原理
：
反转法原理
：
设想给凸轮机构加上一个绕凸轮轴心并与凸轮角速度等值 反向的角速度。根据相对运动原理，机构中各构件间的相对 运动并不改变，但凸轮已视为静止，而从动件则被看成随同 导路以角速度绕点转动，同时沿导路按预定运动规律作往复 移动。从动件尖顶的运动轨迹即为凸轮的轮廓。这就是图解 法绘制凸轮轮廓曲线的原理，称为“反转法”。
概述从动件常用运动规律图解法设计盘形凸轮
第四章 凸轮机构
1
第四章 凸轮机构
§4-1 概述 §4-2 从动件常用运动规律 §4-3 图解法设计盘形凸轮轮廓 §4-5 凸轮机构设计中的几个问题 §4-6 凸轮常用材料和结构
第四章 凸轮机构
15
要求：滚子密集。
⑶注意： ①理论廓线按给定运动规律绘制 理论rb＞实际rb ②实际廓线不等于向径减去滚子半径 ③从动件的转动方向
第四章 凸轮机构
16
3.移动平底从动件盘形凸轮
⑴设计思路：
①平板与导路的交点是尖顶从动件的尖端。
②任何时刻平板都与廓线相切、与向径垂直， 而导路与向径重合。
当理论廓线外凸时： 取 rr ≤ 0.8ρmin
会不如够果。此应时加rr太大小rb，，对重安新装绘不制利理，轮并廓且线滚，子既轴可强增度大 ρmin。为防止凸轮磨损过快，工作轮廓线上的ρmin/ ＞1-5mm。 在实际设计凸轮机构时，通常取rT=(0.1-0.5)rb
2）、平底长度的确定：
L=2lmax+5-7mm。
第四章 凸轮机构
2
第一节 概述
一、组成、应用及特点：
1.组成：
高副 凸轮:具有曲线轮廓或凹槽的构件 从动件：移动，摆动
2.应用：
从动件的位移、速度、加速度严格按预定规 律变化的场合
第四章 凸轮机构
3
3.特点：
⑴主要用于转换运动形式
高副
凸轮
从动件往复
(转动、移动）
移动 摆动
（连续或间歇）
⑵可实现从动件任意预定的运动规律，且机构简单、紧凑
总结偏置直动尖顶从动件盘形凸轮设计详细步骤及注意事项
总结偏置直动尖顶从动件盘形凸轮设计详细步骤及注
意事项
偏置直动尖顶从动件盘形凸轮的设计步骤和注意事项如下：
设计步骤：
1. 确定从动件的工作要求和运动特点，包括运动速度、加速度、停留时间等。
2. 根据工作要求确定凸轮的基本形状和大小。
3. 根据所选凸轮的直径和工作要求，计算螺纹推进机构的传动比和螺纹高度。
4. 根据计算结果，设计螺纹推进机构的螺纹结构和传动装置。
5. 根据所选凸轮的直径和工作要求，计算凸轮的齿数和模数。
6. 根据计算结果，确定凸轮的齿轮参数，包括齿轮材料、齿轮齿条等。
7. 根据设计要求，绘制凸轮的图纸，并制造凸轮。
注意事项：
1. 在设计过程中需要考虑从动件的承载能力和耐磨性，选择适当的材料。
2. 凸轮的运动速度和加速度需要根据从动件的工作要求进行合理分配，防止超过从动件的承受能力范围。
3. 凸轮的结构设计应满足从动件的运动规律和力学要求，保证运动的平稳性和精度。
4. 在凸轮制造过程中要确保凸轮的尺寸精度和表面质量，以提高传动效率和使用寿命。
5. 设计时要考虑从动件的装配和调整方便性，确保凸轮的正确安装和调整。
6. 在使用过程中要定期检查凸轮和从动件的磨损情况，及时进行维护和更换。
综上所述，设计偏置直动尖顶从动件盘形凸轮需要确定工作要求，计算凸轮参数，设计螺纹推进机构和齿轮传动装置，并注意材料选取、运动规律、力学要求、尺寸精度和磨损维护等问题。
图解法设计盘形凸轮轮廓
压力角↑， 有效分力↓， 有害分力↑，
Ff↑， 当压力角α 大到一定程度时，
Ｆf Ｆr FN
t v
n
机构卡死。
平面机构的组成
3、许用压力角
Ｆf nα
直动从动件: 推程[α] ≤ 30°~ 40° 摆动从动件: 推程[α] ≤ 40°~ 50°
回程：[α] ≤ 70°~ 80°
Ｆ
Ｆr
t
v
Ｆt
凸轮机构运动中，压力角是变化。
③将基圆分成与位移相对应的若干 等分。
④量取各个位移段，沿径向确定位置点。
⑤将位置点连接为光滑的曲线。
δ
900
图解法设计盘形凸轮轮廓
三、压力角及许用值
1、压力角α：接触点作
用力与从动件速度方向所夹
Fr Ff
的锐角。
nα Ｆ
Fr F cos 有效分力
Ｆt
Ft F sin 有害分力 t
2、自锁
CONTENTS
目
2 图解法设计盘形凸轮轮廓
录
图解法设计盘形凸轮轮廓
1.尖顶对心直动盘形凸轮
s
已知：基圆半径rb=50mm，推杆运 动规律，凸轮逆时针方向转动。
h=50mm
设计：凸轮廓线 解：作图步骤：
0
120 600
900
①定比例尺 1=1:1000，作推杆的位
移线图 ，将其坐标分成若干等分。
②按比例尺 1定基圆及初始位置 。
凸轮机构
图解法设计盘形凸轮轮廓
1 盘形凸轮轮廓设计的基本原理
CONTENTS
目
2 图解法设计盘形凸轮轮廓
录
盘形凸轮轮廓设计的基本原理
1、“反转法”原理
-
图解法设计凸轮轮廓曲线法设计凸轮轮廓曲线
设计方法：图解法 解析法 1. 凸轮廓线设计基本原理 设计凸轮廓线时，假 设凸轮静止，使推杆相对 于凸轮作反向转动，推杆 又在导轨内作预期运动， 推杆尖顶的复合运动的轨 迹即是凸轮轮廓曲线，这 种方法又叫反转法 种方法又叫 反转法。 。
2. 图解法设计凸轮轮廓曲线
1）偏置直动尖顶推杆盘形凸轮机构
5）摆动尖顶推杆盘形凸轮机构 已知：基圆半径r ，凸轮逆时针 0 转动w，推杆的运动规律 j=j(d)，LOA、LAB
A B
确定基圆 A点所在圆、AB初始位置 确定基圆、 将A点所在圆瓜分
O
自基圆向外量取等分点角位移 确定推程、远休、回程、近休廓线
3）对心直动滚子推杆盘形凸轮机构
以滚子中心为尖顶，按尖顶推杆设计凸轮廓线 按尖顶推杆设计凸轮廓线， 得到理论廓线。 以理论廓线上的各点为圆心，滚子半径为半径 滚子半径为径， 画一系列滚子圆，这些滚子圆的包络线即为 这些滚子圆的包络线即为实 际廓线。 注意：基圆半径是理论廓线上的最小向径。
4）对心直动平底推杆盘形凸轮机构 以平底中心A为尖顶，按尖顶推杆 设计凸轮廓线，得到理论廓线。 以理论廓线上的各点为平底中心， 画一系列平底，这些平底的包络线 即为实际廓线。
已知：基圆半径r ，凸轮逆时针转动w，推 0 杆的运动规律s=s(d),偏距为e，推杆在 凸轮回转中心右侧。
作偏距圆、基圆、推杆的初始位置 将偏距圆瓜分 将推程运动角等分，作偏距圆的切线 从基圆向外量推杆的位移，得推程廓线
2）对心直动尖顶推杆盘形凸轮机构
对心直动尖顶推杆盘形凸轮机构推杆在反转过 程中始终通过凸轮的回转中心。
移动从动件盘形凸轮轮廓曲线的图解设计
在结构空间允许条件 下，可适当将基圆半径 取大些，以利于改善机 构的传力性能，减少磨 损和减少凸轮廓线的制 造误差。
4.凸轮机构的材料
凸轮机构工作时，往往承受动载荷的作用，同时 凸轮表面承受强烈磨损。因此，要求凸轮和滚子的工 作表面硬度高，具有良好的耐磨性，心部有良好的韧 性。当低速、轻载时，可以选用铸铁作为凸轮的材料。 中速、中载时可以选用优质碳素结构钢、合金钢作为 凸轮的材料,并经表面淬火或滲碳淬火，使硬度达到。 高速、重载凸轮可以用优质合金钢材料，并经表面淬 火或滲氮处理。
1、原料采购与监控
通过推广“公司+基地+农户”的产业化发展模式，将 产品的产、供、销链紧紧联系在一起，公司按照市场 的需要，与农民签订《种植/养殖收购合同》，由公 司给农民提供市场信息、资金、技术和良种等服务， 采用欧盟良好农业规范（GLOBALG.A.P）管理模式， 种植甜玉米、白萝卜、紫苏叶、苹果、马铃薯、胡萝 卜、地瓜、滑子蘑等，由于生产需求的不断扩大近几 年公司还建立了专门的蘑菇养殖基地。对于部分外购 的原料还有定性判定的农残检测仪进行监控。对于原 料的监控主要按照日本肯定列表制的条例要求进行控 制。同时日方每年对基地的水质、蘑菇培养基料、原 料在日本进行检测。
1.滚子半径的选择 2.凸轮机构的压力角 3.凸轮基圆半径的确定 凸轮机构的材料
1.滚子半径的选择
cmin min K
对于外凸的凸轮廓线 ：
minK cmin0
实际轮廓为光滑曲线
minK cmin0
实际廓线出现尖点
minK cmin0
实际轮廓相交而造成 从动件运动失真
对于内凹的凸轮廓线 ：
3.分别自基圆圆周向外量 取从动件位移线图中相 应的位移量 ；
设计平底直动从动件盘形凸轮机构
设计平底直动从动件盘形凸轮机构需要考虑以下几个方面：
1. 确定凸轮的基本参数：包括凸轮的基圆半径、升程、运动规律等。
这些参数需要根据实际工作要求和从动件的运动特性来确定。
2. 选择合适的从动件类型：平底直动从动件是一种常见的从动件类型，适用于低速、轻载的场合。
根据实际工作要求，可以选择不同类型的从动件，如滚子从动件、尖顶从动件等。
3. 设计凸轮轮廓曲线：根据凸轮的基本参数和从动件的运动特性，设计凸轮的轮廓曲线。
轮廓曲线的形状决定了从动件的运动轨迹和速度特性。
4. 考虑凸轮机构的传动方式：凸轮机构可以通过齿轮、链条等方式与驱动装置相连。
需要根据实际情况选择合适的传动方式，并设计相应的传动装置。
5. 考虑凸轮机构的支撑结构：凸轮机构需要一个稳定的支撑结构来保证其正常工作。
支撑结构的设计需要考虑凸轮机构的安装位置、受力情况等因素。
6. 进行凸轮机构的强度校核：根据实际工作条件和载荷要求，对凸轮机构进行强度校核，确保其在工作过程中不会发生破坏或失效。
7. 制作凸轮机构的原型并进行试验验证：根据设计结果制作凸轮机构的原型，并进行试验验证，以检验其性能是否满足设计要求。
如有需要，可以对设计进行优化和改进。
§4-4盘形凸轮的结构设计.
a r
rr a 0
rr a 0
一般推荐： rr
ρmin Δ
Δ 3 ~ 5mm
rr a 0
max 即：
凸轮机构的许用压力角
[ ]
[α] αc
根据实践经验，推荐的许用压力角取值为:
推程： 直动从动件取 [ ] 30 ～ 40 ；
摆动从动件取 [ ] 35 ～ 45 ；
回程：
直动和摆动从动件荐取 [ ] 70 ～ 80 。
二、按许用压力角 [ ]确定凸轮机构的基本尺寸
考虑摩擦时驱动力的表达式
F12 Q 2b cos (α 1 ) ( 1 ) sin (α 1 ) tan 2 l
理想情况（无摩擦）时驱动力的表达式
F120 Q cos α
凸轮机构的瞬时效率
2b cos( α 1 ) (1 ) sin ( α 1 ) tan 2 F120 l η F12 cos α
§4-4 盘形凸轮的结构设计
一、压力角 及其许用值 x： F12 sin( 1 ) ( R1 R2 ) cos2 0
y：
F12 cos( 1 ) Q ( R1 R2 ) sin 2 0
M :
R2 cos 2 (l b) R1 cos 2b 0
η 0 时，机构自锁
解方程
2b cos (α 1 ) ( 1 ) sin (α 1 ) tan 2 l η 0 cos α
得临界压力角
c：
凸轮设计方法
平面凸轮机构基本尺寸的确定
凸轮基圆半径的确定 一、基圆半径对压力角的影响
ds/d e PD OP e tan s0 s BD r02 e 2 s
增大基圆半径，可使凸轮机构的压力角减小； 增大基圆半径会使凸轮机构的整体尺寸增大 在压力角不超过许用值的原则下，应尽可能采用 较小的基圆半径。
凸轮机构的压力角 一、压力角
压力角：从动件与凸轮在接触点 处的受力方向与其在该点绝对速
度方向之间所夹的锐角
ds/d e PD OP e tan s0 s BD r02 e 2 s
平面凸轮机构基本尺寸的确定
说明：凸轮逆时针方向转动，当从动件导路中心偏在凸轮 轴心右侧时，推程取减号，回程取加号；偏在左侧时，推 程取加号，回程取减号。 若凸轮顺针方向转动，则加减号的取法与上述相反。
基圆半径 r0 的确定应使 从动件运动不失真，即
应保证凸轮廓线全部外 凸，或各点处的曲率半 径 0
平面凸轮机构基本尺寸的确定
滚子半径的选择
一、滚子半径对实际廓线的影响
１、凸轮理论廓线外凸的情况
平面凸轮机构基本尺寸的确定
r
可画出正常的实际廓线
r
实际廓线干涉，导致 运动失真。
r
实际廓线变尖
特点：
• • • 结构简单、紧凑 容易实现各种运动规律 高副接触，易磨损
常用于传力不大的场合。
凸轮机构的类型
按凸轮的形状分：盘形、圆柱形 按从动件的形式分：尖顶、平底、滚子 按保持接触的方式分：力锁合、几何锁合 （观看“电脑陈列柜”中凸轮内容）
压力角α：从动件运动方向与正压力（不考虑f）方 向之间的夹角； 凸轮转角δ： 一般设从动件在最低位置时凸轮转角为零（起始位 置）； 反转法：凸轮不动，从动件反转； 偏心时：从动件导路线与凸轮转心距离始终不变， 相切于偏心圆。 偏心凸轮转角δ：偏心圆两切点间圆心角。 推程：当凸轮以角速度ω逆时针转动，向径渐增的 轮廓B0B1与尖底接触时，从动件以一定运动规律被 凸轮推向远方，这一行程称推程。
凸轮解析法设计和M文件
ds 2 s s0 d d 2s ds ds s s0 d e 2 d e d 2 s s0
2 1.5
2.当凸轮理论廓线外凸时，凸轮实际轮廓曲率半 径 rT ，此时可能出现3种情况： ⑴当 rT 时，实际轮廓为一条平滑曲线； ⑵当 rT 时，实际轮廓上产生尖点； ⑶当 rT 时，实际轮廓已相交，产生运动失真。
理论轮廓最小曲率半径 CE可用作图方法确定： 如图5-27所示。 轮廓曲率半径计算公式
5.4.2 凸轮基圆半径的确定
设计凸轮机构时，基圆半径选的越小，所 设计的机构越紧凑。但基圆半径的减小， 会使压力角增大。压力角的正切
DP OP OD tan BD BD ds / d e ds / d e 2 2 s s0 s rb e
5.4.3 滚子半径的确定
等加速-等减速运动
2h s 2 2 ds 4h 2 d d 2 s 4 h 2 2 d
2h 2 s h 2 ds 4h d 2 d 2s 4h 2 d d 2s d 2 h 1 cos 2 h sin 2 2h cos 2 2
凸轮机构中，经常采用滚子从动件。选择滚子半 径时要考虑的因素较多。从滚子本身的结构设计 和强度方面考虑，滚子半径大些较好，这样有利 于提高滚子的接触强度，便于滚子的结构设计与 安装。但是滚子半径的增大也要受到一定的限制， 因为滚子半径的大小 将给凸轮实际轮廓带来较大 的影响。滚子半径与凸轮理论廓线的最小曲率半 径，及对应的凸轮实际廓线上的曲率半径，有如 图5-24所示的关系： 1.当凸轮理论廓线内凹时，如图5-26（a）所示凸 轮实际轮廓曲率半径，此时不论滚子半径大小如 何，均可作出内凹的凸轮实际轮廓。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
盘形凸轮的四种设计方法深圳市百特兴科技有限公司 周杰平摘要：详细介绍运用SolidWorks 绘制盘形凸轮的不同方法，包括插件法、解析法、折弯法及仿真法。
关键词：盘形凸轮，插件法，解析法，折弯法，仿真法，余弦加速度， SolidWorks，EXCEL。
凸轮/连杆机构以其快速、稳定的特点，在很多的场合尤其是传统的制程设备中得以运用。
但其缺点也很明显：适应性较差，结构相对比较复杂，开发周期长，凸轮加工精确要求比较高等,非标设备大多由伺服马达/步进马达、丝杆/同步带、气缸/油缸等替代。
近年来，由于对设备产能要求越来也高，传统的凸轮/连杆机构又受到用户青睐。
以动力电池制造设备中塑封制程为例。
进口设备核心机构采用凸轮/连杆机构，产能在140件/分钟以上，国产设备采用伺服/丝杆驱动，产能则在50件/分钟左右。
更为重要的是前者用于制程的有效时间更长，确保了品质的可靠性。
凸轮的设计将成为机构设计工程是不可缺少的技能。
本文以盘形凸轮为研究对象，分别介绍几种不同的设计方法。
一、基本参数1.1、凸轮基本参数项目 代号 参数值基圆直径 D 150凸轮厚度 W 15辊子直径 d 25升程 h 50表11.2、从动杆运动规律动作 运动角度数(Φ)起始角度位置 终止角度位置 结束半径 运动规律推程 120 0 120 125 余弦加速度 远休止角 30 120 150 125 回程 90 150 240 75 余弦加速度 近休止角 120 240 360 75 表2注：余弦加速度(简谐运动)方程：S=h*[1-cos(πφ/Φ)]/2图1二、SolidWorks 插件法2.1、如图2，打开SolidWorks，新建零件，关闭草图。
菜单栏Toolbox -> 凸轮如菜单栏无Toolbox，先加入插件。
图2 图32.2、设置。
如图3凸轮类型为圆形，推杆类型为平移，如果是偏心的，可作相应的选择；开始半径为基圆半径，开始角度根据<表2>填写；旋转方向为顺时针2.3、运动如图4图4运动部分，根据<表2>，进行设置，运动的类型为谐波；2.4、 生成 如图5图5生成部分：坯件的外径要满足：>(D+d)/2；近毂和远榖分别为凸轮两侧的圆柱状台阶，要大于孔的直径，厚度自行定义，但需要大于圆角半径和倒角大小；本例子缺省。
结果如图6图6至此，采用SolidWorks 自带插件的方法设计完成了满足表1、表2要求的凸轮。
将文件保存为凸轮（插件）1。
三、解析法3.1、数学模型建立。
3.1.1、辊子中心运动轨迹图7X1=S * COS(θ)Y1=S * SIN(θ)S=D/2+h* (1- COS(θ))/2（升程） ；Z1=D/2 +h-h * (1- COS(θ))/2（回程）；θ=πφ/Φ ---角度转换其中：D - 凸轮基圆直径；S – 向径；h - 为升程；φ - 为凸轮转动的角度（弧度值）3.2、EXCEL自动计算3.2.1、打开EXCEL，依次将相关参数及公式输入到表中。
3.2.2、采用下拉复制，相关参数即可自动计算并显示在表中。
如图8。
图8（部分截图）3.2.3、 按图9整理，加入Z值。
（便于SolidWorks导入）X1 Y1 Z175 0 074.99714 1.30908 074.98855 2.618658 074.97418 3.92923 074.95392 5.241289 074.92767 6.555321 074.89525 7.871808 074.85647 9.191219 074.8111 10.51401 074.75887 11.84064 0图9（部分截图）3.2.4、复制图9中参数黏贴到TXT文件中，保存为jx1.txt。
3.3、在SolidWorks中绘制凸轮3.3.1、打开SolidWorks零件绘制环境，关闭草图3.3.2、插入曲线，如图10图10 图11 3.3.3、按图11点击浏览，找到参数文件jx1.txt存放位置。
注意:文件类型要切换到 *.txt文件类型.插入后的结果如图12。
图12 图123.3.4、利用等距实体命令绘制凸轮轮廓草图，如图13。
偏移距离为辊子半径.3.3.5、草图拉伸 15，如图18。
绘制中心孔，如图19.图18 图19四、折弯法4. 1、数学模型建立图20 （图中凸轮曲线可为任意，便于分析即可）展开前的凸轮轮廓线曲线X1=S * COS(θ)Y1=S * SIN(θ)S=D/2+h* (1- COS(θ))/2（升程） ；S =D/2 +h–h * (1- COS(θ))/2（回程）；θ=πφ/Φ –角度转换其中：D - 凸轮基圆直径；S – 向径；h - 为升程；φ - 为凸轮转动的角度（弧度值）展开后，展开长度与向径之间的关系以直径D’=100为展开圆S’=S- D’/2= S-50 --D’为展开圆直径S=D/2+h*(1-COS(θ))/2 （细节需作补偿？）4. 2、EXCEL自动计算4.2.1、打开EXCEL，依次将相关参数及公式输入到表中。
4.2.2、采用下拉复制，相关参数即可自动计算并显示在表中。
图21为计算表部分截图。
图21按图9整理，加入Z值。
（便于SolidWorks导入）4.2.4、复制图9中参数黏贴到TXT文件中，保存为jx1.txt。
4.3、在SolidWorks中绘制凸轮4.3.1、打开SolidWorks零件绘制环境，关闭草图4.3.2、插入曲线(参考3.3.2)图224.3. 3、绘制凸轮展开后草图、利用等距实体命令绘制凸轮轮廓线及其它边界线。
如图图234.3.4、拉伸，厚度15，插入坐标原点如图24，注意坐标轴方向（弯曲时绕X轴），如图26图24 图254.3.5、插入弯曲特征。
选取实体-点选折弯--折弯角度为360度--选取坐标系（上一步建立）如图26，勾选确定，得到特征，如图274.3.5、完善设计如图28。
保存文件名为凸轮(弯曲)图28五、仿真法5.1、凸轮设计的模型准备使用SOLIDWORKS完成如图29所示装配体的建模，并添加恰当的配合。
(建模过程省略)图29 图30 5.2、从动件运动数据点的准备建立从动件位移与时间的关系。
设定凸轮转动一周的时间为3秒。
则时间与转动角度的关系：t=φ*3/（2π） ； --φ为凸轮转动角度S= -h* (1- COS(θ))/2（升程） ；S = -h+h * (1- COS(θ))/2（回程）；θ=πφ/Φ –角度转换其中： S --从动件位移；h --为升程；φ-- 为凸轮转动的角度（相对角度）注：1)、从动件位移以基圆为起始点；2)、离开凸轮中心为负，反之为正。
（与后续仿真设计设置有关）5.3、EXCEL 自动计算5.3.1、打开EXCEL，依次将相关参数及公式输入到表中。
5.3.2、采用下拉复制，相关参数即可自动计算并显示在表中。
图31为计算表部分截图。
图315.3.2、选取表格t、S ,插入图表如图32，可得到图33，从动件位移与时间的关系。
图32图335.3.2、选取表格t、S，复制黏贴（选择性黏贴-值）到新开启的EXCEL表中，另存为CSV 格式，文件名fz1。
5.4、运动分析边界条件设定5.4.1、启动SOLIDWORKS Motion插件如图34开启新的运动算例，并将分析模式切换到Motion分析。
在视项和相机视图中右键并单击禁用观阅键码播放。
（在此之前视图摆放到合适的位置，从动件的顶点设置为与圆盘表面接触装配关系，在仿真运动之前解除装配关系）图345.4.2、我们已知从动件的运动需要符合数据点的规律。
为了能满足此要求，我们需要设置一个线性马达来驱动从动件。
如图35马达的位置选择从动件的顶面，方向向下，运动的模式切换到数据点模式以打开函数编制程序对话框。
在此对话框中设置值为位移，自变量为时间，插值类型选择Akima样条曲线。
如图36，点击输入数据，找到文件名fz1并打开。
在函数编制对话框中确定，在马达编辑中确定。
图35 图365.4.3、前面我们设定凸轮转动一周的时间是3秒，为了保持同步。
拖动时间栏的关键帧到3秒，将仿真的周期设置为3秒，如图37。
图375.4.4、给凸轮添加旋转马达，使凸轮在从动件的一个运动周期中旋转一圈。
如图38，旋转马达的位置选择传动轴的边线。
运动类型设置为等速，每分钟20圈（注：3秒一圈），确定。
5.3.4、添加重力，如图39，方向沿Y轴负方向。
图38 图395.4.5、添加接触，如图40，选择凸轮和从动杆。
图40 图415.4.6、设置运动算例属性为了使获取的凸轮的轮廓精度更高，每秒帧数设置为100，并选择精确接触，如图41。
5.4.7、如图42，单击计算，运行运动仿真。
此时可以看到预期的运动，凸轮转动一圈，从动件同时完成一个周期的运动。
图425.4.8、获取凸轮轮廓为了获取凸轮的轮廓，我们只需找到从动件上与凸轮接触的一点相对于凸轮的跟踪路径。
此跟踪路径即为凸轮的轮廓。
如图42和43，44所示，单击结果和图解，选择位移/速度/加速度——>跟踪路径。
在要测量的实体中选择从动件的顶点及凸轮的圆柱面。
确定之后即获得一个跟踪路径，此路径即为凸轮的轮廓。
图42图43 图445.4.9、将跟踪路径转化为曲线输入到凸轮中。
5.4.10、将其转化为曲线并输入到凸轮中，如图45。
5.4.11、在结果图解1上右键——>从跟踪路径生成曲线——>在参考零件中从路径生成曲线。
图455.4.12、打开凸轮，在设计树中将有一个曲线，在前视基准面上绘制草图，并用转换实体引用命令，将此曲线引用，接着对草图进行拉伸。
如图46图46 图475.4.13、将零件图另存为文件名为凸轮FZ1。
六、仿真验证分析以仿真法绘制凸轮为例轮廓是否正确。
6.1、打开文件FZ1，在当前的仿真中，从动件是依靠线性马达驱动的。
在实际凸轮机构中应当是依靠凸轮的轮廓保证从动件的运动。
因此在验证的时候我们需要将加在从动件上的线性马达去掉，并在从动件和凸轮之间添加接触。
6.2、将时间调整到0秒的位置，压缩线性马达，如图48。
在从动件和凸轮之间添加接触。
如图49。
图48图496.3、查看从动件在Y方向上的线性位移如图50，点击图解，选择位移/速度/加速度——>线性位移——>Y分量。
选择从动件的一个面，确定。
其在Y方向的线性位移如图51.图50 图51对比图33与图50，可以看出，从动件是符合所设定的运动规律的。
七、几种设计方法的比较7.1、插件法是运用SolidWorks自带的插件，优点是按照操作提示逐步操作，填写完对话框的参数生成即可。
缺点是其绘制过程太过“自动化”，无法深入理解凸轮的真正的绘制过程，精度没法设定。