9.2-1利用直角坐标计算二重积分
第9章 二重积分的计算方法 9.2
y
2
y
x y
D
2
(4, 2) x y2
O 1
x
(1, 1)
图9．14
第9章 重积分及其应用
§ 9.2 二重积分的计算方法
方法二 把区域 D 看成是X—型区域，则积分区域 D 分成
D1 和 D2 两部分，如图9.15．
其中 D1 与 D2 可表示为
y
D1 :0 x 1, x y x; D2 :1 x 4, x 2 y x .
y
y 2 ( x)
y 1 ( x )
o a
x — 型区域
bx
第9章 重积分及其应用
§ 9.2 二重积分的计算方法
Y—型区域：D ( x, y ) c y d , 1 ( y ) x 2 ( y )
其中 1 ( y) 与 2 ( y) 在区间 [c, d ] 上连续．
先介绍所谓的X—型区域和Y—型区域的概念． X—型区域：D ( x, y ) a x b, 1 ( x ) y 2 ( x ) 其中 1 ( x) 与
D
2 ( x) 在区间 [ a, b] 上连续
．
这种区域的特点是： 穿过区域且平行于y 轴的直线与区域的边界 至多有两个交点.
1 x [ ( xy 2 ) ] dx 1 2 x2
4
1 4 2 x x( x 2) 2 dx 2 1 1 4 2 (5x x 3 4x) dx 2 1
1 5 3 1 4 45 2 4 ( x x 2x ) 2 3 4 1 8
y
y x
§ 9.2 二重积分的计算方法
直角坐标系下二重积分的计算
直角坐标系下二重积分的计算二重积分是数学中的一种重要的积分形式，常用于计算平面区域上的物理量的总量。
在直角坐标系下，二重积分的计算可以通过将被积函数表示为被积函数关于自变量的函数进行积分的累次积分方式来进行。
设在平面上有一个闭合区域D，我们要计算函数f(x,y)在该区域上的积分，即要计算二重积分∬Df(x,y)dxdy。
二重积分的计算可以通过转化为极坐标下的积分来简化。
设在直角坐标系下，点(x,y)的极坐标为(r,θ)，则x=r*cosθ，y=r*sinθ。
对于被积函数f(x,y)，若能将其表示为关于极坐标的函数f(r,θ)时，就可以方便地进行极坐标下的积分计算。
此时二重积分可以写为∬Df(r,θ)rdrdθ。
要在直角坐标系下计算二重积分，有两种常用的方法：直接法和间接法。
一、直接法：假设被积函数为f(x,y)，而积分区域D的边界方程为g(x,y)=0（边界方程可以是函数表达式或者隐函数表达式），那么二重积分可以按照以下步骤进行计算：1.求出区域D的边界方程g(x,y)=0，并确定积分区域D的内部。
2.将被积函数f(x,y)表示为关于x和y的函数。
3.对于区域D内部的任意一点(x,y)，可以用参数方程表示为x=x(t)，y=y(t)（通常情况下选取参数t为角度θ，即x=r*cosθ，y=r*sinθ）。
4.计算被积函数在参数方程的变换下的雅可比行列式，即计算J =dx/dt * dy/dt。
根据换元公式，二重积分可以转化为参数方程下的积分，如下所示：∬Df(x,y)dxdy = ∫∫f(x(t),y(t))*Jdtdt。
5.计算在变换后的区域D'上的二重积分：∬D'f(x(t),y(t))Jdtdt。
二、间接法：假设被积函数为f(x,y)，而积分区域D的边界方程为g(x,y)=0（边界方程可以是函数表达式或者隐函数表达式），那么二重积分可以按照以下步骤进行计算：1.求出区域D的边界方程g(x,y)=0，并确定积分区域D的内部。
§9.2.1二重积分的计算
： ， ： ，
。
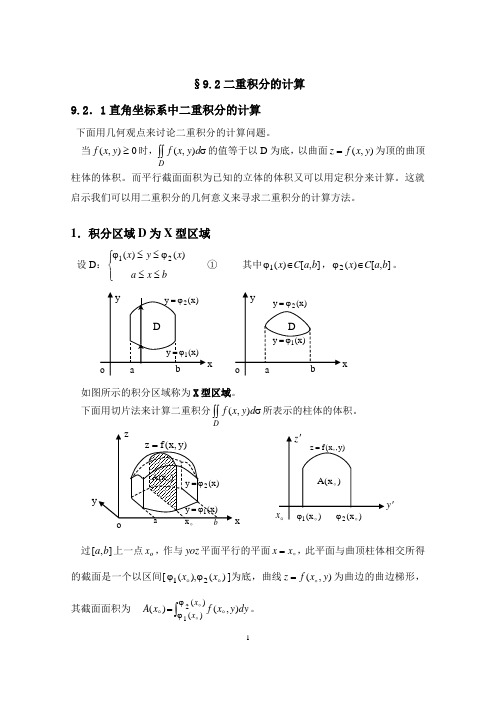
（2）
解：先积 后积 ，则 ，
： ， ： ，
先积 后积 ，D： ，
∴ 。
例5．设 是 平面上以 ， 和 为顶点的三角形区域， 是 在第一象限的部分，若 ，试问下列等式是否成立？
（1） ；（2） ；
（3） 。
解：将区域 分为四个子区域： 、 、 、 。
显然 与 关于 轴对称， 与 关于 轴对称，
将 分为两个二重积分，记
， 。
∵ 关于 和关于 都是奇函数，
∴ ， ，∴ 。
∵ 是关于 的奇函数，关于 的偶函数，
∴ ， ，
∴ ，
从而 ，故等式（1）、（3）不成立；等式（2）成立。
5．利用积分区域的对称性和被积函数的奇偶性简化重积分的计算：
设 在有界闭区域 上的可积， ，
（1）若 关于 对称，则
（2）若 关于 对称，则
第一卦限内的图形。
所求立体在第一卦限的部分可看作是以圆柱面 为顶，以 面上四分之一的圆域 为底的曲顶柱体，其体积为
，
故所求体积为 。
讨论二重积分时，ቤተ መጻሕፍቲ ባይዱ三种类型的题目：置限、换序和计算。
例1．计算 ，其中 是由直线 ， 及 所围成的闭区域。
解法1： 是X型的， ： ，
解法2： 是 型的。
注：①化二重积分为二次积分时，积分限的确定顺序
与积分顺序相反。
②在计算内积分时，外积分变量是常数。
例2．计算 ，其中 由 和 所围成。
解： 既是X型区域，又是Y型区域。
⑤
上式右端的积分称为先对 、后对 的二次积分公式。
用公式⑤时，必须是Y型区域。Y型区域的特点是：穿过 内部且平行于 轴的直线与 的边界相交不多于两点。
吴9-2(1)直角坐标系下二重积分的计算法
2021/4/22
18
§9.2 二重积分的计算法
19/29
一、直角坐标系下计算 二、交换二次积分次序 三、利用对称性奇偶性
【练习1】应用二重积分求由曲线 y x2, y x 2
所围区域 D的面积
【解】据二重积分的性质4（几何意义） dxdy
D
交点
y x2
(1,1)，(2,4)
y x2
1 x 2
DX
:
x
2
y
x
2
2
x2
dx dy
2
(x 2
x2 )dx
9
1
x2
1
2
2021/4/22
19
§9.2 二重积分的计算法
20/29
一、直角坐标系下计算 二、交换二次积分次序 三、利用对称性奇偶性
【练习2】计算
D
sin y
y
dxdy
其中 D 是由直线 y=x 及抛物线
= x 所围成
一、直角坐标系下计算 二、交换二次积分次序 三、利用对称性奇偶性
［法2］
DY
:
1 1
y1 x y
原式
1
y
ydy
1 x2 y2dx
－1
D
1
1
y
1
y y=x
o
1x
－1
注意到先对x 的积分较繁，故应用法1较方便
注意两种积分次序的计算效果！
2021/4/22
16
§9.2 二重积分的计算法
17/29
§9.2 二重积分的计算法
11/29
一、直角坐标系下计算 二、交换二次积分次序 三、利用对称性奇偶性
【解Ⅱ】 看作Y－型域
9.2二重积分的计算(直角)
D: y ≤ x ≤ 2
2 y=x y 1
o
1 x 2x
2 2 I =∫1 d y ∫ x yd x= ∫1 y 2
[
1 2
2 x y ] dy y
2
= ∫ [ 2y −
2 1
1 2
y ]dy
3
9 = 8
例2. 计算
∫∫
D
x ydσ , 其中 是抛物线 y = x 及直线 其中D
2
所围成的闭区域. y = x − 2 所围成的闭区域 为计算简便,看成 型区域, 看成Y型区域 解: 为计算简便 看成 型区域 则
0
2
x2 2 0
2 2
2
dx∫
8− x2
0
f ( x, y)dy
y
x2 + y 2 = 8
D2
积分域由两部分组成: 解: 积分域由两部分组成
0≤ x ≤ 2 2≤ x ≤ 2 2 D : , D2 : 1 2 1 2 0≤ y ≤ 2 x 0 ≤ y ≤ 8 − x
视为Y–型区域 将D = D1 + D2 视为 型区域 , 则 0≤ y ≤ 2 D : 2 y ≤ x ≤ 8 − y2 2 I = ∫∫ f ( x, y)d xd y= ∫ dy∫
先对x 后对y的累次积分
D c ≤ y ≤ d ψ 1( y) ≤ x ≤ψ2( y)
按 , 在计算中括号中定积分 时 , 积分变量为 x , 而将 y 暂时固定 .
一、利用直角坐标计算二重积分
由曲顶柱体体积的计算可知, 由曲顶柱体体积的计算可知 若D为 X – 型区域 为 a≤ x≤b D: ϕ1( x) ≤ y ≤ ϕ2( x) 则
0902二重积分的计算法-1
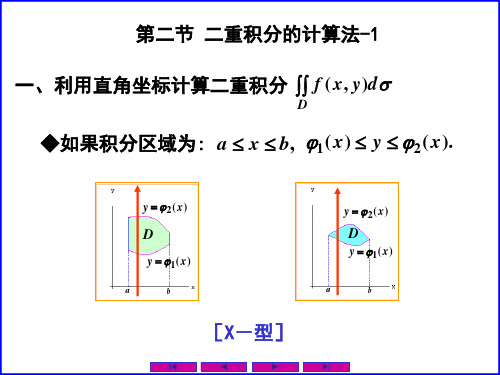
b ϕ2( x) f ( x , y )dy ; = dx a ϕ1 ( x )
∫
∫∫ f ( x , y )dσ ∫
D
d ϕ2 ( y) f ( x , y )dx . = dy c ϕ1 ( y )
∫
［混合型］ 混合型］ （在积分过程中要正确选择积分次序） 在积分过程中要正确选择积分次序） 积分次序
y
A(x)
a
x
y = ϕ2 ( x)
b
x
D
y = ϕ1( x)
b ϕ ( x) ∴ ∫∫ f ( x , y )dσ =∫a dx ∫ϕ 2( x ) f ( x , y )dy . ……二次积分公式 ? 1 二次积分公式
D
◆如果积分区域为：c ≤ y ≤ d , ϕ1 ( y ) ≤ x ≤ ϕ 2 ( y ). 如果积分区域为：
π
练习1 练习 改变下列积分的积分次 序
∫
1 2 x− x2 2 2− x dx f ( x , y )dy + dx f ( x , y )dy . 0 0 1 0
∫
∫
∫
解 积分区域如图： 积分区域如图：
y = 2− x
原式 = ∫0 dy ∫
1
2− y
2
y = 2x − x2
1− 1− y
f ( x , y )dx.
1
o
1
x
2.设f ( x , y )在D上连续 , 其中 D是由直线 y = x , y = a及x = b (b > a )所围成的闭区域 , 证明 :
(1)∫
b x dx a a
∫ f ( x , y )dy = ∫
b b dy y a
直角坐标系下二重积分的计算
直角坐标系下二重积分的计算二重积分是一个非常重要的数学概念，在多种实际的问题中都得到了广泛应用。
通过对直角坐标系下二重积分的计算，可以深入地理解这个概念的含义。
在本篇文章中，我们将对直角坐标系下二重积分的计算进行详细的讲解。
一、二重积分的定义在直角坐标系下，二重积分可以定义为：如果在平面上有一个区域D，在D中每一点(x,y)都有一个实数f(x,y)，那么二重积分可以表示为：∬Df（x,y）dxdy其中，dxdy是对x和y的区域积分。
从数学上来讲，二重积分可以看做是对一个多元函数在一个二维区域上的积分。
在物理学、工程学和经济学等领域中，二重积分可以用来计算物体的质量、电荷或利润等量。
二、二重积分的计算接下来，我们将具体介绍如何计算直角坐标系下的二重积分。
1、以矩形为例当区域D为矩形时，可以使用以下公式进行求解：∬Df（x,y）dxdy=∫ab[∫cd f（x,y）dy]dx其中，a、b、c和d是矩形的四个顶点。
从右到左积分是对x的积分，从下到上积分是对y的积分。
这个公式建立在f（x,y）在矩形D内是连续函数的条件下。
如果f（x,y）不连续，那么需要将图形分割成多个子区域，再对每个子区域使用上述公式求解。
如果积分上下限为定值，则直接将定值带入公式中进行计算。
2、以圆形为例当区域D为圆形时，可以使用以下公式进行求解：∬Df（x,y）dxdy=∫0R[∫0 2πf（rcosθ，rsinθ）rdθ]dr其中，R是圆的半径，r是极径。
θ是极角，取值从0到2π。
这个公式建立在f（x,y）在圆形D内是连续函数的条件下。
如果不连续，需要将圆形分割成多个区域，再对每个区域使用上述公式求解。
3、以三角形为例当区域D为三角形时，可以使用以下公式进行求解：∬Df（x,y）dxdy=∫a b[∫c(x)(d(x)−c(x))/b a f(x,y)dy]dx 其中，a和b是三角形底边的两个端点。
c（x）是左侧斜线的端点函数，d（x）是右侧斜线的端点函数。
高等数学 9-2-1二重积分的计算法(1)
第二节二重积分的计算法（1）
内容提要利用直角坐Fra bibliotek系计算二重积分
重点分析
利用直角坐标计算二重积分
难点分析
二重积分化为二次积分时积分次序的选择及积分限的选择
习题布置
1（单）、2（单）、4、6（单）、8、10
备注
教学内容
一、利用直角坐标系计算二重积分
如果积分区域为：
［X－型］
其中函数 、 在区间 上连续.
应用计算“平行截面面积为已知的立体求体积”的方法,
得
如果积分区域为：
［Y－型］
X型区域的特点：穿过区域且平行于y轴的直线与区域边界相交不多于两个交点.
Y型区域的特点：穿过区域且平行于x轴的直线与区域边界相交不多于两个交点.
若区域如图，则必须分割.
在分割后的三个区域上分别使用积分公式
例1改变积分 的次序.
解积分区域如图
原式 .
例2改变积分 的次序.
解积分区域如图
原式 .
例3改变积分 的次序.
解
原式=
例4求 ，其中 是由抛物线 和 所围平面闭区域.
解两曲线的交点
例5求 ，其中D是以 为顶点的三角形.
解 无法用初等函数表示
积分时必须考虑次序
例6计算积分 .
解 不能用初等函数表示
先改变积分次序.
原式
例7求由下列曲面所围成的立体体积， ， ， ， ， .
解曲面围成的立体如图.
所围立体在 面上的投影是
所求体积
二、小结
二重积分在直角坐标下的计算公式
［X－型］
［Y－型］
（在积分中要正确选择积分次序）
思考题
设 在 上连续，并设 ，
高等数学 重积分 (9.2.1)--二重积分的计算
导出
V
b A(x)dx
a
b a
2 ( x) 1 ( x)
f (x, y)dy dx
D
f (x, y)dxdy
ab
2 (x) 1 ( x)
f
(x,
y)dy dx
写成
f (x, y)dxdy bdx 2 (x) f (x, y)dy
x2 y 2 Rx 所割下部分的体积 V
z
y
r=Rcos
D
O
x
xR
y
例 求双纽线 (x2 y2 )2 2a2 (x2 y2 ) 所围 区域的面积
乐
例 求二次积分
2
2 dy
1y2 arctan ydx
0
y
x
例 求积分 I ex2 dx 0
乐
9.2.3 二重积分的变量代换
设变换
x x(u, v)
y
y(u, v)
有连续偏导数，且
满足
J
(x, y) (u, v)
xu xv
yu yv
0
而 f (x, y) C(D) ，那么
f (x, y)dxdy f (x(u, v), y(u, v)) J dudv
D
D
乐
uv 平面小矩形AﾢBﾢCﾢDﾢﾢ ﾢﾢ xy 平面曲边四边形 ABCD
D
a 1 ( x)
乐
若积分区域
D {(x, y)1( y) x 2 ( y), c y d}
y 型正 则区域
则有
f (x, y)dxdy d dy 2 ( y) f (x, y)dx
9[1].2_二重积分的计算法
![9[1].2_二重积分的计算法](https://img.taocdn.com/s3/m/9562ce3d0912a2161479290c.png)
n
n
1 (C) ∫ dx ∫ dy . 0 0 (1 + x )(1 + y )
n
1 (D) ∫ dx ∫ dy . 2 0 0 (1 + x )(1 + y )
1 1
∫∫ f ( x, y)dσ = lim ∑ f (ξi ,ηi )∆σi λ→0 i =1 D
10
9.2 二重积分的计算法
lim∑ f (ξi )∆xi = ∫ f ( x)dx
为底, 是区间 [ϕ 1 ( x0 ), ϕ 2 ( x0 )]为底 曲线 z = f (x0, y)为曲边的 为曲边的 曲边梯形. 曲边梯形
ϕ2( x0 )1 0z来自z = f ( x, y)
z = f (x0, y)
y = ϕ2( x)
D
A( x0 ) = ∫ϕ ( x ) f ( x0 , y )dy
y
1
原式 = ∫ dy ∫
0
1
y 2 − xy d x
3 y 2 0
y= x
D
2 y( y − x) = −∫ 0 3
2 2 1 2 = ∫ y dy = . 9 3 0
dy
O
1
x
积分域既是 X型又是 型 型又是Y型 型又是
14
9.2 二重积分的计算法
计算二次积分
2 计算二次积分∫ dx ∫ sin y dy 例 0 x 1 1
13
9.2 二重积分的计算法
研究生考题(三 研究生考题 三, 四) 7分 分
其中D是由直线 计算二重积分 ∫∫ y 2 − xy dxdy , 其中 是由直线 所围成的平面区域. y = x , y = 1, x = 0 所围成的平面区域 解 原式 =
高数习题答案二
2π
1
2π
2
1 2 1 4 1 1 4 1 2 2 = 2π ( r − r )|0 +2π ( r − r )|1 = 5π. 2 4 4 2 y r = cosθ 3.利用极坐标计算下列二重积分 (1) ∫∫ xdxdy, D: x2 + y2 ≤ x D 0 1 x 解: 画出D的图形:
y
7.交换下列积分次序,并计算: (1)
∫ dy∫ e dx
y 0 y
1
1
1 y=x
0
D
解: 由已给积分次序知
y ≤ x ≤1 D: 0 ≤ y ≤1 ,
x =1 x 1
画出D的图形:
机动 目录 上页 下页 返回 结束
x eydy = ey |0dx = ∫ dx ∫0 ∫ 0 0
1
x
1
y 1 y=x
x
1 x
机动 目录 上页 下页 返回 结束
u v
2.将二重积分
∫∫ f ( x, y) dxdy 化为二次积分:
D
(1) D 是由 y = 2, y = 2x 及 x = 0 所围成的区域; 解: 画D的图形: 1 2 ∫∫ f ( x, y)dxdy = ∫ dx∫ f ( x, y)dy
D
y
2D
0
D
x =1 1 x
(2) 解: 由已给积分次序知
0 ≤ x ≤1 D: 2 x ≤ y ≤1 ,
画出D的图形:
机动
目录
上页
下页
返回
结束
8. 计算下列二重积分
(1) I = ∫∫ yexy dxdy,其中D 是由直线 y = 2, x =1,
x = 2及曲线
直角坐标系下二重积分的计算
直角坐标系下二重积分的计算在直角坐标系下，二重积分是对一个平面区域上的函数进行积分。
它的计算可以通过几何方法或者代数方法来进行，下面我们将介绍二重积分的计算方法以及一些相关的概念和定理。
一、二重积分的概念1.二重积分的定义设函数f(x, y)在平面区域D上有界，D在xOy平面上的投影为Ω，若Ω上有限个点构成的网格P={ (x1,y1), (x2,y2), ..., (xn,yn) }，其中每个小区域ΔS1,ΔS2,...,ΔSn（ΔSk的形状和大小可以不一样）,则每个ΔS_k上取点(xi_k)Σf(xi_k, yi_k)ΔS_k,称为这些和的极限Σf(xi_k, yi_k)ΔS_k,当格数无穷，网格直径趋于0时，如果此极限存在，则称此极限为平面区域D上函数f(x, y)的二重积分，记为∬D f(x, y)dxdy。
2.二重积分的几何意义从几何意义上理解，二重积分可以表示在平面区域D上函数f(x, y)的值在x轴与y轴所确定的平面区域上的总体积。
通过对平面区域上的小区域求和得到总体积。
3.二重积分的代数意义从代数意义上理解，二重积分可以将一个平面区域上的函数表示为两个单变量函数的积分，即先对y进行积分，再对x进行积分。
这种方法可以简化对复杂函数的积分运算。
二、计算二重积分的方法1.直角坐标系下的二重积分计算在直角坐标系下，二重积分的计算可以通过对x或y进行积分，然后再对另一个变量进行积分来进行。
具体而言，对于函数f(x, y)，可以先对y进行积分，再对x进行积分，或者先对x进行积分，再对y 进行积分。
这种计算方法又称为换序积分。
2.计算中间量的选择在进行二重积分计算时，为了简化计算，可以选择合适的中间量来进行变量替换。
例如，可以选择极坐标中的r和θ来替代x和y，从而简化计算过程。
3.区域的划分在计算二重积分时，需要将平面区域D划分为若干小区域，然后对每个小区域进行积分。
可以选择直线或者曲线来进行划分，也可以选择矩形或者圆形等形状的小区域来进行划分。
二重积分在直角坐标系下的计算
x.
y
3 x 3 y
x 2y
1D
x
O2
2y
3
3 y
0 f ( x, y)dx 1 dy0 f ( x, y)dx
2
3 x
0 dx1 x f ( x, y)dy.
2
例
改变积分
2a
dx
0
2ax
2axx2 f ( x, y)dy (a 0)
的次序.
解
D : 2ax x2 y 2ax
0 x 2a
原式
1 1 y
dy f ( x, y)dx .
00
例 改变积分
y 1 x
y2 x y 2x x2
1
dx
2 x x2
f ( x, y)dy
2
dx
2x f ( x, y)dy的次序.
0
0
1
0
D1 : 0 y 2x x2 , D2 : 0 y 2 x, 0 x 1,
0 x 1, y 2x x2 , ( x 1)2 y2 1
x2e y2dxdy
1
dy
y x2e y2 dx
00
D
e1 y2 y3dy e1 y2 y2dy2 1 (1 2).
0
3
0
6
6e
例 求I 1dx 1ey 2dy .
0
x
解 ： 由 于 函 数e y2的 原 函 数 不 是 初 等 函 数， 所 以 这 个
二次积分无法直接积出. 注意到二重积分可以有两种
的直线与区域边界的交点不多于两个.
2） Y型区域
积分区域表示为：
c y d, 1( y) x 2( y).
的区域，称为Y型
二重积分的计算法直角坐标
二重积分的计算法直角坐标二重积分是微积分中的重要概念，用来计算平面区域上的其中一种性质，比如面积、质心等。
在直角坐标系中，二重积分的计算需要将被积函数表示成两个变量的函数，并确定积分区域的边界。
下面将介绍二重积分的计算方法及其应用。
一、二重积分的定义二重积分是对一个平面区域上的函数进行积分，其定义如下：设函数$f(x,y)$在有界闭区域$D$上有定义，且$D$为$x$轴上$[a,b]$的一个闭区间，$y$轴上$[c,d]$的一个闭区间，将$D$划分为有限个小区域，每个小区域用$(\Delta x_i,\Delta y_j)$表示，其中$i=1,2,...,m$，$j=1,2,...,n$，则二重积分$\iint_D f(x,y)dxdy$定义为：$$\iint_D f(x,y)dxdy=\lim_{\lambda\rightarrow0}\sum_{i=1}^{m}\sum_{j=1}^{n}f(x_{ij}^*,y{j}^*)\Delta A_{ij}$$其中$x_{ij}^*,y_{ij}^*$为$(x,y)$在第$i$行第$j$列小区域内的任意一点，$\Delta A_{ij}=\Delta x_i\Delta y_j$为第$i$行第$j$列小区域的面积，$\lambda$为小区域的最大直径，$\lambda=\max\{\Deltax_1,\Delta x_2,...,\Delta x_m,\Delta y_1,\Delta y_2,...,\Delta y_n\}$。
二、二重积分的计算在直角坐标系中，二重积分的计算分为三种情况：换序积分、累次积分和极坐标积分。
下面将依次介绍这三种情况的计算方法。
1.换序积分当被积函数是可分离变量的函数时，可以进行换序积分。
换序积分可以简化计算过程。
设函数$f(x,y)=g(x)h(y)$，则有：$$\iint_D f(x,y)dxdy=\int_a^bg(x)dx\int_c^dh(y)dy$$也可以先对$y$积分再对$x$积分，即：$$\iint_D f(x,y)dxdy=\int_c^dh(y)dy\int_a^bg(x)dx$$2.累次积分对于一般的被积函数，可以通过累次积分的方法进行计算。
x9-2(1)二重积分的计算
d y
y 2 ( x)
x 1 ( y)
x 2 ( y)
dy
2 ( y)
D
y 1 ( x )
1( y)
c
o
a
x
为计算方便,可选择积分序, 必要时还可以交换积分序.
b
x
机动
目录
上页
下页
返回
结束
例1. 计算 I xyd 其中D 是直线 y＝1, x＝2, 及
y＝x 所围的闭区域. 1 y x 解法1. 将D看作X–型区域, 则 D : 1 x 2 x 2 2 1 x y y I d x x y dy x y 2 dx 1 1 1 2 1 2
D
1 3 1 9 x x dx 1 2 2 8
a
b
f ( x , y )d a [ ( x )
b
2 ( x )
1
f ( x , y )dy]dx
2 ( x )
1
D
记
a dx ( x )
b
f ( x , y )dy
称先对 y , 再对 x 的二次积分。
机动 目录 上页 下页 返回 结束
如果积分区域为：
d
c y d , 1 ( y ) x 2 ( y ).
D
1 y2 3
2 2
2 2
机动
目录
上页
下页
返回
结束
三角形.
解 e
y2
dy 无法用初等函数表示
1 y
2
x 2e y dxdy 0 dy 0 x 2e y dx
2
积分时必须考虑次序
精品文档-高等数学(上册)(张涛-第9章
第9章 多元函数积分学
f (x, y)d 等于这些曲顶柱体体积的代数和.这就是二重
D
积分的几何意义. 9.1.2 二重积分的性质
二重积分与定积分有着类似的性质，列举如下： 设函数f(x，y)、g(x，y)在闭区域D上的二重积分存在， 则 性质9-1 被积函数的常数因子可以提到二重积分号的外
b
b 2(x)
V A(x)d x f (x, y)d yd x
这个体积也就是所a 求的二重积a分的积1(x分) 值，从 而有等式
b 2(x)
f (x, y)d f (x, y)d yd x
D
a 1( x)
第9章 多元函数积分学
上式右端的积分就称为先对y、后对x的二次积分.也就是说, 先把x看成常数，把二元函数z=f(x，y)只作为y的一元函数， 对y计算从φ1(x)到φ2(x)的定积分；然后再把计算结果对x计 算从a到b的定积分. 因此，把这个先对y、后对x的二次积分 也常记为
图9-5
第9章 多元函数积分学
注意 Y—型区域的特点为：穿过D内部且平行于x轴的直 线与D的边界相交不多于两点.
按照X—型区域的计算方法，可得公式
d 2(y)
f (x, y)d f (x, y)d xd y
c 1( y)
D
d
2 ( y)
d y f (x, y)d x
b
2 ( x)
f (x, y)d d x f (x, y)d y
a
1( x)
这就是化二重D积分为先对y、后对x的二次积分的公式.
在上述讨论中，我们假定f(x，y)≥0，可以证明，公式
的成立并不受此限制.
直角坐标系下二重积分的计算
直角坐标系下二重积分的计算二重积分是多元函数在二维平面上的积分运算，它可以用来求取平面区域内某个函数的平均值、质心、面积等。
在直角坐标系下进行二重积分的计算，需要掌握对被积函数的区域进行分割、积分区域的确定、积分的限制条件和积分计算的方法等基本步骤。
本文将从这些方面展开讨论，并通过数个例题来具体说明二重积分的计算过程。
一、二重积分的基本概念1.二重积分的定义二重积分是对二元函数在某个有界闭区域上进行积分运算，其定义如下：设函数f(x,y)在闭区域D上有界，且D的边界为简单闭曲线，记为∂D，D的面积为A(D)。
如果对于任意的(x,y)∈D，都有f(x,y)≥0，那么称f(x,y)在D上可积，记为∬D f(x,y) dxdy，其中dxdy表示对x和y的积分。
2.二重积分的几何意义二重积分在几何上表示为对某个闭区域D上的函数f(x,y)进行投影，并对其投影面积进行积分。
它可以用来求取区域D的面积、平均值、质心等几何量。
3.二重积分的存在性对于某个区域上的函数f(x,y)，其在区域D上的二重积分只有在f(x,y)有界、D为有界闭区域且f(x,y)在D上几乎处处连续时才存在。
二、二重积分的计算步骤1.区域的分割对于给定的被积函数在闭区域D上的二重积分运算，首先需要对D 进行分割，使得D可以用简单区域的边界和分割线将其分成若干小区域。
2.积分区域的确定确定积分区域后，需要找出在此积分区域上的极限条件，即确定积分的上下限。
3.积分的限制条件在确定积分区域和积分的上下限后，需要根据积分区域的特点建立积分的限制条件。
4.积分计算利用二重积分的性质和积分的定理来进行具体的积分计算。
以上是进行二重积分计算的基本步骤，下面通过数个例题来具体说明二重积分的计算过程。
例1：计算函数f(x,y)=x^2+y^2在区域D={(x,y)|0≤x≤1,0≤y≤1}上的二重积分。
解：根据给定的区域D，我们可以很容易地确定积分的上下限，并进行积分区域的分割。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
为顶的曲顶柱体的体积．
z
应用计算“平行截 面面积为已知的立 体求体积”的方法, y
z f (x, y)
A(x0 )
y 2(x)
a x0 b x
y 1(x)
得 f ( x, y)d （b 2( x) f ( x, y)dy）dx.
D
a 1 ( x )
f ( x, y)d 的值等于以 D 为底，以曲面 z f ( x, y)
e xdx 不能用初等函数表示
先改变积分次序.
1
xy
I dx e xdy
1 2
x2
1 x(e e x )dx 1 2
3e 1 e. 82
y x y x2
例 6
改变积分
1
dx
1x f ( x, y)dy的次序.
0
0
解 积分区域如图
y 1 x
原式
只能用 Y-型.
I
1
dy
y e y2 dx
0
0
1 ye y2dy 1 (1 e1 ).
0
2
例4 计算 sin x dxdy, 其中D 是直线 Dx 所围成的闭区域.
解: 由被积函数可知,先对 x 积分不行, y
因此取D 为X – 型域 :
yx
D
:
0 0
1
1 y
dy f ( x, y)dx.
0
0
例 7 改变积分
1
2 x x2
2
2 x
0 dx0
f ( x, y)dy dx f ( x, y)dy的次序.
［X－型］
y 2(x)
D
y 1( x)
a
b
y 2(x)
D
y 1( x)
a
b
其中函数1( x) 、2( x)在区间 [a,b]上连续.
得
f ( x, y)d
b
dx
2( x) f ( x, y)dy.
D
a
1 ( x )
利用直角坐标计算二重积分
二、二重积分化为二次积分（Y-区域）
f ( x, y)d
b
dx
2( x) f ( x, y)dy.
D
a
1 ( x )
Y型区域的特点：穿过区域且平行于x 轴的直 线与区域边界相交不多于两个交点.
f ( x, y)d
d
dy
2 ( y) f ( x, y)dx.
D
c
1 ( y )
若区域如图，则必须分割. 在分割后的三个区域上分别使用积分公式
a x0 b x y 1(x)
f ( x, y)d 的值等于以 D 为底，以曲面 z f ( x, y)
D
为顶的曲顶柱体的体积．
z f (x, y)
z
y
y 2(x)
A(x0 )
a x0 b x y 1(x)
f ( x, y)d 的值等于以 D 为底，以曲面 z f ( x, y)
y4 8
y2 4
]12
9 8
例 2 求 ( x2 y)dxdy，其中D是由抛物
D
线 y x2和 x y2所围平面闭区域.
解 两曲线的交点
x y2
y x2
x
(0,0) y2
, (1,1),
( x2 y)dxdy
1
dx
x ( x2 y)dy
D
y 1( x)
a
b
其中函数1( x) 、2( x)在区间 [a,b]上连续.
f ( x, y)d 的值等于以 D 为底，以曲面 z f ( x, y)
D
为顶的曲顶柱体的体积．
z
应用计算“平行截 面面积为已知的立 体求体积”的方法, y
z f (x, y)
A(x0 )
y 2(x)
0
x2
D
1
[
x
2
(
x x2 ) 1 ( x x4 )]dx 33 .
0
2
140
y x2
利用直角坐标计算二重积分
四、积分次序的选择举例
例 3 求I e y2d ，其中 D 是由直线 y x, y 1及
D
y 轴所围成的闭区域.
解
e y2dy 不能用初等函数计算
Y=2 2
I
2
dx
1
2
xydy
x
2
[x
1
y2 2
]2x
dx
2
(2x
1
x3 2
)dx
[x2
x4 8
]12
9 8
解法二 [Y-型]
I
2
y
dy xydx
1
1
2
[
X=Y
1
1X 2
2
(
1
y3 2
y )dy 2
[
D
为顶的曲顶柱体的体积．
z
应用计算“平行截 面面积为已知的立 体求体积”的方法, y
z f (x, y)
A(x0 )
y 2(x)
a x0 b x
y 1(x)
得
f ( x, y)d
b
dx
2( x) f ( x, y)dy.
D
a
1 ( x )
总结：如果积分区域为：a x b, 1( x) y 2( x).
利用直角坐标计算二重积分
第九章 多元函数积分学 第2节(1)直角坐标计算二重积分
主讲 韩 华
利用直角坐标计算二重积分
一、二重积分化为二次积分（X-区域）
如果积分区域为：a x b, 1( x) y 2( x).
［X－型］
y 2(x)
D
y 1( x)
a
b
y 2(x)
如果积分区域为：c y d , 1( y) x 2( y). ［Y－型］
d
x 1( y) D x 2( y)
c
d
x 1( y)
c
D
x 2( y)
f ( x, y)d
d
dy
2 ( y) f ( x, y)dx.
D
c
1 ( y )
X型区域的特点： 穿过区域且平行于y 轴的 直线与区域边界相交不多于两个交点.
y x
x
D x o x
D
sin x
x
dxd
y
0
sin x
x
dx
x
0 d
y
0 sin x dx
2
利用直角坐标计算二重积分
五、改变积分次序举例
例5
1
计算积分 I 2 dy
yy
1
e xdx dy
yy
e xdx.
1
1
4
2
1 2
y
y
解
f (x, y)d f (x, y)d f (x, y)d f (x, y)d .
D
D1
D2
D3
D3 D1
D2
利用直角坐标计算二重积分
三、计算举例
例 1 求I xyd ,其中 D 是 x 1、
D
y x及 y 2所围成的闭区域.
解法一 [X-型]