高中数学《交集、并集》课件3苏教版必修
合集下载
新教材苏教版必修第一册 第1章 1.3 交集、并集 课件(53张)

知
养
线y=3x+b求出参数b的值.
课
合
(3)由A∩B={9}可得9∈A,依次讨论a2,2a-1等于9的可能性来 时
作
分
探 究
求解.
层 作
释
业
疑
难
返 首 页
21
(1){x|3<x<4} (2)2 [(1)因为B={x|-1≤x≤3},
素
知
养
(a,+∞)= {x|x>a} ,(-∞,b)= {x|x<b} ,
合
_(_-__∞_,__+__∞__)___=R.
课 时
作
分
探 究
_[a_,__b_]__, (a,b) 分别叫作闭区间、开区间;
层 作
释 疑
_[_a_,__b_)__, (a,b] 叫作半开半闭区间;
业
难
__a_,__b__叫作相应区间的端点.
层 作
释
疑 区间内的端点,用 空心点 表示不包括在区间内的端点.
业
难
返 首 页
14
课
情
堂
景
小
导
学
1.思考辨析(正确的打“√”,错误的打“×”)
结 提
探
新 知
素
(1)A∩B中的元素一定比A,B任何一个集合的元素都少.( ) 养
(2)A∩B=A∩C,则B=C.
合
作
(3)两个集合A,B没有公共元素,记作A∩B=∅.
b},则b=
.
课
合
时
作 探
(3)已知集合A={-4,2a-1,a2},B={a-5,1-a,9},若A∩B
分 层
究
作
释 ={9},求a的值.
苏教版高中数学必修一 1.3 交集、并集PPT
= {x | x≠0} .
5.已知A ={x|x是锐角三角形},B={x|x是钝角三角形},则A∩B = ,A∪B = {x|x是斜三角形} .
6.已知A ={x|x是矩形},B={x|x是菱形},则A∩B= {x|x是正方形},
{ A∪B= x|x是矩形或菱形}
.
7.若A={x|x为等腰三角形},B={x|x为直角三角形},则A∩B=
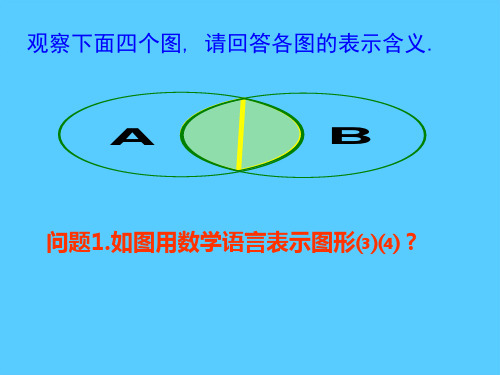
一般地,由所有属于A或属于B的元素 所组成的集合,叫做A与B的并集,记作A∪B, 读作“A并B”.
图形语言:
符号语言:A∪B={x|x∈A,或x∈B}
问题2.下列关系式能成立吗? A∩B=B∩A,A∪B=B∪A, A∩B⊆A⊆A∪B,A∩B⊆B⊆A∪B
A
B
问题3.A∩B=A可能成立吗? A∪B=B可能成立吗?
{ } x|x为等腰直角三角形} ,A∪B= {x|x为等腰或直角三角形 .
小结
对象 两个集合A、B
要素分析 关系 A与B是任意两个集合
定义 交集
并集
A∩B
A∪B
={x|xA,且xB}.={x|xA,或xB}
直观理解 A B
A
BA B
作业
P 13习题 5,6,7
71.当你快乐时,你要想,这快乐不是永恒的。当你痛苦时,你要想,这痛苦也不是永恒的。 42.小时侯,幸福是很简单的事;长大了,简单是很幸福的事! 35.美丽属于自信者,从容属于有备者,奇迹属于执着者,成功属于顽强者。 34.以智慧时时修正偏差,以慈悲处处给人方便。 97.在你渐渐迷失在你的人生道路上的时候,记得这句话:千万不要因为走的太久,而忘记了我们为什么出发。 16.成功与不成功之间有时距离很短,只是后者再向前了几步。 43.成功人记住经验,忘记痛苦所以勇往直前;失败人记住痛苦忘记经验所以裹足不前。 34.以智慧时时修正偏差,以慈悲处处给人方便。 2.心存希望,幸福就会降临你;心存梦想,机遇就会笼罩你。 11.如果你是野花,没人欣赏,你也要芬芳;如果你是小草,即使践踏,你也要成长。 56.人最可悲的是自己不能战胜自己。 54.没有风浪,便没有勇敢的弄潮儿;没有荆棘,也没有不屈的开拓者。 14.选择自己所爱的,爱自己所选取的。 90.你不要一直不满人家,你应该一直检讨自己才对。不满人家,是苦了你自己。 26.不经历风雨,怎么见彩虹。 94.要想人前显贵,必须人后受罪! 40.泉水,奋斗之路越曲折,心灵越纯洁。 4.幸福就像香水,洒给别人也一定会感染自己。 24.每个牛逼的人,都有一段苦逼的坚持。 68.不要言过其实夸大其词会使人怀疑你的判断力。精明的人表现出的是严谨,有时还会故意缩小其词。 8.逆风的方向,更适合飞翔。 70.如果把才华比作剑,那么勤奋就是磨刀石。 34.这个世界不是因为你能做什么,而是你该做什么。 45.活在这世上,就会被人攻击。要谈恋爱,就会被感情伤。
5.已知A ={x|x是锐角三角形},B={x|x是钝角三角形},则A∩B = ,A∪B = {x|x是斜三角形} .
6.已知A ={x|x是矩形},B={x|x是菱形},则A∩B= {x|x是正方形},
{ A∪B= x|x是矩形或菱形}
.
7.若A={x|x为等腰三角形},B={x|x为直角三角形},则A∩B=
一般地,由所有属于A或属于B的元素 所组成的集合,叫做A与B的并集,记作A∪B, 读作“A并B”.
图形语言:
符号语言:A∪B={x|x∈A,或x∈B}
问题2.下列关系式能成立吗? A∩B=B∩A,A∪B=B∪A, A∩B⊆A⊆A∪B,A∩B⊆B⊆A∪B
A
B
问题3.A∩B=A可能成立吗? A∪B=B可能成立吗?
{ } x|x为等腰直角三角形} ,A∪B= {x|x为等腰或直角三角形 .
小结
对象 两个集合A、B
要素分析 关系 A与B是任意两个集合
定义 交集
并集
A∩B
A∪B
={x|xA,且xB}.={x|xA,或xB}
直观理解 A B
A
BA B
作业
P 13习题 5,6,7
71.当你快乐时,你要想,这快乐不是永恒的。当你痛苦时,你要想,这痛苦也不是永恒的。 42.小时侯,幸福是很简单的事;长大了,简单是很幸福的事! 35.美丽属于自信者,从容属于有备者,奇迹属于执着者,成功属于顽强者。 34.以智慧时时修正偏差,以慈悲处处给人方便。 97.在你渐渐迷失在你的人生道路上的时候,记得这句话:千万不要因为走的太久,而忘记了我们为什么出发。 16.成功与不成功之间有时距离很短,只是后者再向前了几步。 43.成功人记住经验,忘记痛苦所以勇往直前;失败人记住痛苦忘记经验所以裹足不前。 34.以智慧时时修正偏差,以慈悲处处给人方便。 2.心存希望,幸福就会降临你;心存梦想,机遇就会笼罩你。 11.如果你是野花,没人欣赏,你也要芬芳;如果你是小草,即使践踏,你也要成长。 56.人最可悲的是自己不能战胜自己。 54.没有风浪,便没有勇敢的弄潮儿;没有荆棘,也没有不屈的开拓者。 14.选择自己所爱的,爱自己所选取的。 90.你不要一直不满人家,你应该一直检讨自己才对。不满人家,是苦了你自己。 26.不经历风雨,怎么见彩虹。 94.要想人前显贵,必须人后受罪! 40.泉水,奋斗之路越曲折,心灵越纯洁。 4.幸福就像香水,洒给别人也一定会感染自己。 24.每个牛逼的人,都有一段苦逼的坚持。 68.不要言过其实夸大其词会使人怀疑你的判断力。精明的人表现出的是严谨,有时还会故意缩小其词。 8.逆风的方向,更适合飞翔。 70.如果把才华比作剑,那么勤奋就是磨刀石。 34.这个世界不是因为你能做什么,而是你该做什么。 45.活在这世上,就会被人攻击。要谈恋爱,就会被感情伤。
1.3交集、并集课件(苏教版)

高中数学
必修第一册
配套江苏版教材
四、德·摩根定律
集合运算中的两个重要等式,即德·摩根定律.
(1)綂U(A∩B)=(綂UA)∪(綂UB)
(简记为“交的补”=“补的并”),如图;
(2) 綂U(A∪B)=(綂UA)∩(綂UB)
(简记为“并的补”=“补的交”),如图.
高中数学
必修第一册
配套江苏版教材
【示例】设集合U={1,2,3,4,5},A={1,2,3},B={2,3,4},则(綂UA)∪(綂UB)=( B )
核心素养:数学抽象、直观想象、数学运算
高中数学
必修第一册
配套江苏版教材
新知学习
一、交集
1.交集的概念
(1)文字语言:一般地,由所有属于集合A且属于集合B的元素构成的集合,称为集合A与B
的交集,记作A∩B(读作“A交B”).
(2)符号语言:A∩B={x|x∈A,且x∈B}.
(3)图形语言:可用Venn图表示.
【概念理解】(1)两个集合的交集仍是一个集合.
(2)交集概念中的“且”即“同时”的意思,两个集合交集中的元素必须同时是两个集合中的元素.
(3)理解交集定义中“所有”两字的含义:
① A∩B中的任一元素都是A与B的公共元素;② A与B的所有公共元素都属于A∩B;
③ 当集合A与B没有公共元素时,A∩B=
.
第1章
1.3
交集、并集
高中数学
必修第一册
配套江苏版教材
学习目标
1.理解两个集合的交集与并集的含义,明确数学中的“且”“或”的含义.
2.会求两个集合的交集与并集,并能利用交集与并集的性质解决相关问题.
3.能使用Venn图或数轴表示集合之间的运算,体会数形结合思想对理解抽象概念的作用.
高中数学苏教版必修一《1.3交集、并集》课件

3.有关区间的规定:
设a,b R,且a<b,规定
[a,b]={x | a≤x≤b},
(a,b)={x | a<x<b},
a
b
[a,b)={x | a≤x<b},
(a,b]={x | a<x≤b},
(a,+)={x | x>a },
(-,b)={x | x<b},
a
(-,+)=R.
b
数学应用 例3. 设A=(0, +),B=(-,1],求A∩B和A∪B.
1.如果A={-1,0,1},B={0,1,2,3},则A∩B = {0,1} ,A∪B= {-1,0,1,2,3} .
2.已知A∪B={-1,0,1,2,3},A∩B={-1,1},如 果A={-1,0,1} ,则B= {-1,1,2,3} .
例1.已知A={( x,y)| x+y =2},B={( x,y)| x-y =4},求集合A∩B.
-5ห้องสมุดไป่ตู้
-1
4
8
则有:A∩B=[4,8), A∪B=(-,-5)∪(-1,+).
要素分析
对象 关系 定义
两个集合A、B
A与B是任意两个集合
交集
并集
A∩B
A∪B
={x|xA,且xB=}.{x|xA,或xB}.
直观理解 A B
A
BA
B
若B A,则A∩B=B,A∪B=A
课本P13习题2,3,5,7.
1.3
1.3
交集、并集
苏教版 高中数学
用列举法表示下列集合: A={ x|x3-x2-2x=0}; B={ x|(x+2)(x+1)(x-2)=0}.
思考:集合A与B之间有包含关系么? 那你能用图示来反应集合A与B之间的关系吗?
交集并集课件-高一上学期数学苏教版

注意
两个集合的交集还是一 个集合,所以要用集合 的表示方式.
03
(2)因为C和D没有公共元素,所以C∩D=∅. (3)在数轴上表示出区间E和F,如图所示,
-3 -2 -1 O 1 2 3 x 如图可知E∩F=(1,2).
提示
弄懂空集概念, 此题即可立即写出答案
03 经典例题
解 设U={x|x为高一(1)班的同学},A={x|x为参加排球赛的同学}, B={x|x为参加田径赛的同学}.则A∩B={x|x为排球赛和田径赛都参加 的同学}.
01 名师提醒
x, y| x>0x, y| y>0 x, y| x>0,y>0,
02 一般地,由所有属于集合A或者属于集合B的元素构成的集合,
称为A与B的并集,即
A B {x | x A,或x B}.
记作:A∪B
读作:“A 并 B”
两个集合的并集可用如图所示的阴影部分形象地表示.
02
例如,
01 从定义可以看出,A∩B表示由集合A,B按照指定的法则构
造出一个新集合,因此“交”可以看成集合之间的一种运算, 通常称为交集运算. 交集运算具有以下性质,对于任意两个集合A,B,都有: (1) A B B A; (2) A A A;
(3) A A ;
(4)如果A B, 则A B A, 反之也成立.
§1. 3 交集、并集
学习目标
1.理解并集、交集的概念. 2.会用符号、维恩图和数轴表示并集、交集. 3.会求简单集合的并集和交集.
01
考察下面的问题,集合C 与集合A、B 之间有什么关系吗?
(1)A={-1,1,2,3}, B={-2,-1,1},C={-1,1}; (2)A ={x|x≤3},B= {x|x>0},C= {x|0<x≤3}; (3)A ={x|x为矩形},B= {x|x为菱形},C= {x|x是正方形};
2016-2017学年苏教版必修一 交集、并集 课件(36张)

读法
Venn 图
答案
思考
(1)当两个集合没有公共元素时,这两个集合就没有交集吗?
(2)对于A∩B=∅,存在哪几种可能的情况? 答 (1)当两个集合没有公共元素时,这两个集合的交集为空集.
(2)存在三种情况:
①集合A,B均为空集;
②集合A,B中有一个是空集;
③集合A,B均为非空集,但无相同元素.
答案
自主学习
知识点一 名称表示
交集与并集的概念 交集 并集
由所有属于集合A 且属于集合B 由所有属于集合A 或 属于集合B 自然语言 的元素构成的集合 的元素构成的集合 符号语言
{x|x∈A,且x∈B} A∩B=_________________ A交B
x|x∈A,或x∈B} A∪B= { ________________ A并B
[a,b)
(a,b] [a,+∞) (a,+∞)
答案
{x|x≤a}
(-∞,a] (-∞,a) (-∞,+∞)
{x|x<Leabharlann }R答案返回
题型探究
重点突破
题型一 并集的简单运算
例1 (1)设集合M={4,5,6,8},集合N={3,5,7,8}, {3,4,5,6,7,8} 那么M∪N=____________. 解析 由定义知M∪N={3,4,5,6,7,8}.
则由交集的定义可得A∩B={x|0≤x≤2}.
反思与感悟 解析答案
跟踪训练 2
5 已知集合 A={x|-1<x≤3},B={x|x≤0,或 x≥2},
求 A∩B,A∪B.
解 5 ∵A={x|-1<x≤3},B={x|x≤0,或 x≥2},
把集合A与B表示在数轴上,如图.
5 5 ∴A∩B={x|-1<x≤3}∩{x|x≤0, 或 x≥2}={x|-1<x≤0, 或2≤x≤3}; 5 A∪B={x|-1<x≤3}∪{x|x≤0 或 x≥2}=R.
苏教版高中数学必修一课件《1.3交集与并集》2.pptx
(a,+∞)={x|x>a}, (-∞,b)={x|x<b}, (-∞,+∞)=R.
其中[a,b]叫做闭区间;(a,b)叫做开区间;[a,b), (a,b]叫做半开半闭区间;a,b叫做相应区间的端 点.
三、例题讲解
例1学校小卖部进了两次货,第一次进的货的品种是集合
A 圆珠笔, 钢笔,橡皮,笔记本,方便面,汽水
(A)A∪D=D(B)C∪B=B
(C)C∪B=C(D)B∪D=B
2.若A={1,3,x},B={,x12},且A∪B={1,3,x},则 这样不同的x有()C个.
(A)1(B)2(C)3(D)4
3.设集合M={1,-3,0),N={}t,2 若t M1∪N=M,
则t=.
1或0
四、练习:
4.设A x x 2, B x x 3,
(1)没有公共元素AB
A∩B=Φ
(2)有公共元素AB
A∩B≠Φ
(3)包含AB
A∩B=B
二、几个区间的概念 设a、b∈R,且a<b,规定: [a,b]={x|a≤x≤b},(闭区间) (a,b)={x|a<x<b},(开区间) [a,b)={x|a≤x<b},(左闭右开区间) (a,b]={x|a<x≤b}.(左开右闭区间)
求实数a,b的值。
解:由{(2,3)}A∩B,得(2,3)∈A且(2,3)∈B
2a b 9 3a b 4
解得a=-5,b=19.
三、例题讲解
例5已知x∈R,集合A={-3,x2,x+1}, B={x-3,2x-1,x2+1},若A∩B={-3},求A∪B. 解:由A∩B={-3},得-3∈B,
三、例题讲解
例2 设f (x) 0的解集是A 1,2,g(x) 0 的解集是B 2,3,分别写出下列方程的解集.
其中[a,b]叫做闭区间;(a,b)叫做开区间;[a,b), (a,b]叫做半开半闭区间;a,b叫做相应区间的端 点.
三、例题讲解
例1学校小卖部进了两次货,第一次进的货的品种是集合
A 圆珠笔, 钢笔,橡皮,笔记本,方便面,汽水
(A)A∪D=D(B)C∪B=B
(C)C∪B=C(D)B∪D=B
2.若A={1,3,x},B={,x12},且A∪B={1,3,x},则 这样不同的x有()C个.
(A)1(B)2(C)3(D)4
3.设集合M={1,-3,0),N={}t,2 若t M1∪N=M,
则t=.
1或0
四、练习:
4.设A x x 2, B x x 3,
(1)没有公共元素AB
A∩B=Φ
(2)有公共元素AB
A∩B≠Φ
(3)包含AB
A∩B=B
二、几个区间的概念 设a、b∈R,且a<b,规定: [a,b]={x|a≤x≤b},(闭区间) (a,b)={x|a<x<b},(开区间) [a,b)={x|a≤x<b},(左闭右开区间) (a,b]={x|a<x≤b}.(左开右闭区间)
求实数a,b的值。
解:由{(2,3)}A∩B,得(2,3)∈A且(2,3)∈B
2a b 9 3a b 4
解得a=-5,b=19.
三、例题讲解
例5已知x∈R,集合A={-3,x2,x+1}, B={x-3,2x-1,x2+1},若A∩B={-3},求A∪B. 解:由A∩B={-3},得-3∈B,
三、例题讲解
例2 设f (x) 0的解集是A 1,2,g(x) 0 的解集是B 2,3,分别写出下列方程的解集.
1.3交集、并集课件(苏教版)
1.3 交集、并集
一、交集
1.交集的定义 2.交集的性质 3.各图中的A∩B
二、并集
1.并集的定义 2.并集的性质 3.各图中的A∪B
1
一、交集
• 1 交集的定义
一般地,由所有属于集合A且属于 集合B的元素所组成的集合,叫做A与B 的交集,记作A∩B,即A∩B={x∣x∈A, 且x∈B } .
A
A∩B B
={x∣-2<x<3}
-2
3
8
例2 设A= {x∣x是等腰三角形}, B= {x∣x是直角三角形},求A∩B.
解: A∩B={x∣x是等腰三 角形}∩{x∣x是直角三角形}
={x∣x是等腰直角三角形}
9
例3 设A= {4,5,6,8},B= {3,5, 7,8},求A∪B.
解: A∪B={4,5,6,8} ∪ {3,5,7,8}
={x∣x是斜三角形}
11
例5 设A= {x∣-1< x<2}, B= {x∣1<x< 3},求A∪B.
解: A∪B={x∣-1< x<2} ∪ {x∣1< x< 3}
={x∣-1< x<3}
练习
1.设A={3,5,6,8},B={4,5,7,8} (1)求A∩B,A∪B . (2)用适当的符号填空: A∩B___A,B___A∩B, A∪B ___A,A∪B ___A, A∩B____A∪B .
A
B
5
• 2 并集的性质 (1)(A∪B) A, (A∪B) B (2)A∪A=A (3)A∩Ф =Ф (4)A∪B=B∪A
6
• 3 试讨论下列各图中的并集
B
A
A
B
A(B)
A A∪B B
A
B
一、交集
1.交集的定义 2.交集的性质 3.各图中的A∩B
二、并集
1.并集的定义 2.并集的性质 3.各图中的A∪B
1
一、交集
• 1 交集的定义
一般地,由所有属于集合A且属于 集合B的元素所组成的集合,叫做A与B 的交集,记作A∩B,即A∩B={x∣x∈A, 且x∈B } .
A
A∩B B
={x∣-2<x<3}
-2
3
8
例2 设A= {x∣x是等腰三角形}, B= {x∣x是直角三角形},求A∩B.
解: A∩B={x∣x是等腰三 角形}∩{x∣x是直角三角形}
={x∣x是等腰直角三角形}
9
例3 设A= {4,5,6,8},B= {3,5, 7,8},求A∪B.
解: A∪B={4,5,6,8} ∪ {3,5,7,8}
={x∣x是斜三角形}
11
例5 设A= {x∣-1< x<2}, B= {x∣1<x< 3},求A∪B.
解: A∪B={x∣-1< x<2} ∪ {x∣1< x< 3}
={x∣-1< x<3}
练习
1.设A={3,5,6,8},B={4,5,7,8} (1)求A∩B,A∪B . (2)用适当的符号填空: A∩B___A,B___A∩B, A∪B ___A,A∪B ___A, A∩B____A∪B .
A
B
5
• 2 并集的性质 (1)(A∪B) A, (A∪B) B (2)A∪A=A (3)A∩Ф =Ф (4)A∪B=B∪A
6
• 3 试讨论下列各图中的并集
B
A
A
B
A(B)
A A∪B B
A
B
新教材高中数学第1章集合3交集并集课件苏教版必修第一册
∴A={2,5,13,17,23},B={2,11,17,19,29}. 易错警示 集合的交、并、补集的混合运算要注意两点:①各个集合的正确化简;②集合的 运算顺序.求解方法有分步求解法和数形结合法.
2 | 利用集合的运算性质求参数的值或取值范围
由集合的运算性质求参数的值或取值范围的思路 1.将集合中的运算关系转化为两个集合之间的关系.若集合中的元素能一一列举,则 可用观察法得到不同集合之间的关系;若是与不等式有关的集合,则可利用数轴得到 不同集合之间的关系. 2.将集合之间的关系转化为方程(组)或不等式(组)是否有解,或解集满足某些条件的 形式. 3.利用解方程(组)或解不等式(组)来确定参数的值或取值范围时,需注意以下两点: (1)由集合间的运算得到的新集合一定要满足集合中元素的互异性.在求解含参数的 问题时,要注意这一隐含条件. (2)对于涉及A∪B=A或A∩B=B的问题,可利用集合的运算性质,转化为相关集合之间 的关系求解,注意空集的特殊性.
解题模板 在探求解决新定义问题的方法时,可以寻找相近知识点,研究它们的不同点和相同点, 通过类比的方法解题.
解析 易知M={y|y=x2,x∈R}={y|y≥0}={x|x≥0}. ∵N={x|-3≤x≤3}, ∴M∩N=N∩M={x|0≤x≤3}, ∴M-N=∁M(M∩N)={x|x>3},N-M=∁N(N∩M)={x|-3≤x<0}. 又∵M△N=(M-N)∪(N-M), ∴M△N={x|-3≤x<0或x>3}.
符号语言 A∪B=⑥ {x|x∈A,或x∈B}
图形语言
运算性质 A∪B=B∪A,A∪A=A,A∪⌀=A=⌀∪A,A⊆(A∪B),B⊆(A∪B),A⊆B⇔A∪B=B
2.两个常用结论 (1)∁U(AB).
2 | 利用集合的运算性质求参数的值或取值范围
由集合的运算性质求参数的值或取值范围的思路 1.将集合中的运算关系转化为两个集合之间的关系.若集合中的元素能一一列举,则 可用观察法得到不同集合之间的关系;若是与不等式有关的集合,则可利用数轴得到 不同集合之间的关系. 2.将集合之间的关系转化为方程(组)或不等式(组)是否有解,或解集满足某些条件的 形式. 3.利用解方程(组)或解不等式(组)来确定参数的值或取值范围时,需注意以下两点: (1)由集合间的运算得到的新集合一定要满足集合中元素的互异性.在求解含参数的 问题时,要注意这一隐含条件. (2)对于涉及A∪B=A或A∩B=B的问题,可利用集合的运算性质,转化为相关集合之间 的关系求解,注意空集的特殊性.
解题模板 在探求解决新定义问题的方法时,可以寻找相近知识点,研究它们的不同点和相同点, 通过类比的方法解题.
解析 易知M={y|y=x2,x∈R}={y|y≥0}={x|x≥0}. ∵N={x|-3≤x≤3}, ∴M∩N=N∩M={x|0≤x≤3}, ∴M-N=∁M(M∩N)={x|x>3},N-M=∁N(N∩M)={x|-3≤x<0}. 又∵M△N=(M-N)∪(N-M), ∴M△N={x|-3≤x<0或x>3}.
符号语言 A∪B=⑥ {x|x∈A,或x∈B}
图形语言
运算性质 A∪B=B∪A,A∪A=A,A∪⌀=A=⌀∪A,A⊆(A∪B),B⊆(A∪B),A⊆B⇔A∪B=B
2.两个常用结论 (1)∁U(AB).
交集、并集ppt 苏教版
首页
上一页
下一页
末页
数学
(苏教版 ·必修1)
3.集合的交、并运算 (1)对于元素个数有限的集合,可直接根据集合的“交”、“并”定义求解, 但要注意集合元素的互异性. 第 一 章 集 合 (2)对于元素个数无限的集合,进行交、并运算时,可借助数轴,利用数轴分 析法求解,但要注意端点值取到与否.
首页
上一页
首页 上一页 下一页 末页
数学
(苏教版 ·必修1)
1.(1)若本例(1)中,问题改为求A∪B. (2)本例(2)中,问题改为求M∩N. 【解析】 (1)由例1中的数轴表示知A∪B=R. 【答案】 R 第 一 章 集 合 (2)由例1中的数轴表示知M∩N
【答案】
首页
上一页
下一页
末页
数学
(苏教版 ·必修1)
交集、并集运算性质的运用问题
设A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0}. (1)若A∩B=B,求a的值; (2)若A∪B=B,求a的值. 【解题方向】 集合A、B均为有限集,可用列举法表示集合,根据两集 第 一 章 集 合 合的关系求解问题.
【解题方法】
首页
上一页
下一页
已知集合的交集、并集求参数
设集合A={x|-1<x<a},B={x|1<x<3}且A∩B 【解题方向】 集合B非空,集合A不确定,且A∩B 【解题方法】 分A 【解题易错】 忽略A 第 一 章 集 合 【解题过程】 由A∩B (1)若A (2)若A≠ ,如图 则有 ∴-1<a≤1 a≤-1 A≠ 两种情况讨论,结合数轴分析法求解. A∩B 1<a≤1,从而漏解. a的取值范围.
次? 因为集合中元素的互异性 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
2
1 0
得a=1
例5、设A= {x | x 2 4 x 0} ,B= {x | 2 2(a 1) x 2 1 0} x a ⑴若A∩B=B,求a的值
⑵、由A∪B=B知
⑵若A∪B=B,求a的值
A B ,又A={-4,0},且B中至
∴A=B, ∴ 0∈B且-4∈B
例1、设A={(x,y)|y=-4x+6},B={(x,y)|y=5x-3},求
A∩B
解: A∩B={(x,y)| y=-4x+6} ∩ {(x,y)|y=5x-3}
= {(x,y)|
{ y=5x-3
y=-4x+6
} ={(1,2)}
注意: (1) (x,y)可以看成是两直线交点的坐标,也可以看作一 个二元一次方程组的解。 (2) {(1,2)} ≠{1,2}
C (C
(CU A) (CU B) , B, A , C U U A) (CU B) U
例4、已知A={2,-1, x x 1 },B={2y,-4,x+4}, C={-1,7},且A∩B=C,求x,y的值及A∪B。
解:由A∩B=C知 7∈A,7 ∈B,-1 ∈B
2
在A中, x x 1 =7有x=-2或3
{ {
a
1 0
2
(4) 8(a 1) a 1 0
2
2
0 B且 4 B 有 ⅲ、当B= {-4}时, 得a=7(舍去) ⅳ、当B={-4,0)时,0∈B且-4∈B由
由以上四点知a≦-1或a=1
(4) 8(a 1) a 1 0
2 2
a
1 0
{ a=7 或a=1
解:由A= { x | ⅰ、当B
⑵若A∪B=B,求a的值
x
2
4 x 0} 得A={-4,0}
1) ∵ A∩B=B ∴
B A 则 B 或{0}或{-4}或{-4,0}
4 时,
(a 1)
2
4a 4 0 , 即a<-1 2
2
ⅱ、当B= {0}时,0∈B且4 B 有 得a=-1
=______
= ∩A (3) A ∩B_____B
(8) (A∪B)______ A,(A∪B)_________B (7)若A ∩B=A,则A________B ;反之是否仍然成立?
(8)若A ∪B=A,则B________A ;反之是否仍然成立?
2、奇数集与偶数集
1) 形如2n(n∈Z)的整数叫做偶数;形如 2n+1(n∈Z)的整数叫做奇数。 2) 全体奇数的集合叫做奇数集;全体偶数的 集合叫做偶数集。
得a=1
多有两个元素 2
由{a 2
1 0
a
8a 7 0
注意:⑴ 分类讨论思想的应用
⑵
B 不要忘了
课堂练习:
书P13 练习1—4
课堂小结
弄清交集、并集的性 质。 注意灵活、准确的运 用性质问题。 充分利用数轴法(数 形结合)、文氏图(直 观形象) 要有分类讨论的意识
(CU A) B =_____________ Z
2.已知U=R,A={x|-4≦x<2},B={x|-1<x≦3},
C
作业
教科书P14 习题1.3 7,8 指导与学习
预习:含绝对值的不等式的解法
若x=-2,则B中x+4=2,即2 ∈B,又2 ∈A
2
∴2 ∈2,-1,7}, B={2y,-4,7} 1 此时由-1 ∈B知2y=-1 ∴y= 2 故A={2,-1,7}, B={-1,-4,7} A∪B={-4,-1,2,7}
例5、设A= {x | x 2 4 x 0} ,B= {x | 2 2(a 1) x 2 1 0} x a ⑴若A∩B=B,求a的值
例2、已知A为奇数集,B为偶数集,Z为整数集,求
A∩B,A ∩Z,B ∩Z,A∪B,A ∪Z,B ∪Z
解: A∩B={奇数} ∩{偶数}=
; A ∩Z=A
B ∩Z=B; A∪B=Z; A ∪Z=Z;B ∪Z=Z 例3、设U={1,2,3,4,5,6,7,8},A={3,4,5} B={4,7,8},求
3.设A= {x | x ax a 19 0} ,B= {x | x 5 x 6 0} C= {x | x 2 x 8 0} ,且 A B , A C a=-2 求a的值. 2 4.设U=R,A={x | x 3 x 10 0} ,B={x|a+1≦x≦2a-1}, 且 B UA ,求实数a 的取值范围. a≦ 3
2
{x|0<x<2} A B (CU P) =__________________
2 2
5 P={x|x≦0或x≧ 2 },则A∩B=_____________ {x|-1<x<2}
2
随 堂 练 习
1. 设集合A={x∈Z|x≦-3},B= {x∈Z|x≦2}, {-2,-1,0,1,2} U=Z,则 (CU A) B =_________________
复习:
两个集合的交集、并集的含义 怎样求两个集合的交集与并集 1. 两个集合交、并的有关性质
(1) A∩A=____ A (2) A ∩ A A = (4) A ∪A=____(5)A ∪ =______ (6)A ∪B_____B ∪A B (7)(A∩B)_____A , (A∩B)______
