线段垂直平分线综合练习题
线段的垂直平分线经典习题及答(精.选)

线段的垂直平分线一、选择题(共8小题)1、如图,在△ABC 中,分别以点A 和点B 为圆心,大于的21AB 的长为半径画孤,两弧相交于点M ,N ,作直线MN , 交BC 于点D ,连接AD .若△ADC 的周长为10,AB=7,则△ABC 的周长为( ) A 、7 B 、 14 C 、17 D 、20第1题 第2题 第3题2、如图,在Rt △ACB 中,∠C=90°,BE 平分∠ABC ,ED 垂直平分AB 于D .若AC=9,则AE 的值是( )A 、6B 、4C 、6D 、43、如图,直线CD 是线段AB 的垂直平分线,P 为直线CD 上的一点,已知线段PA=5,则线段PB 的长度为( )A 、6B 、5C 、4D 、34、如图,等腰△ABC 中,AB=AC ,∠A=20°.线段AB 的垂直平分线交AB 于D ,交AC 于E ,连接BE ,则∠CBE 等于( )A 、80°B 、70°C 、60°D 、50°第4题 第 5题 第6题 5、如图,直线CP 是AB 的中垂线且交AB 于P ,其中AP=2CP .甲、乙两人想在AB 上取两点D 、E ,使得AD=DC=CE=EB ,其作法如下:(甲)作∠ACP 、∠BCP 之角平分线,分别交AB 于D 、E ,则D 、E 即为所求;(乙)作AC 、BC 之中垂线,分别交AB 于D 、E ,则D 、E 即为所求.对于甲、乙两人的作法,下列判断何者正确( )A 、两人都正确B 、两人都错误C 、甲正确,乙错误D 、甲错误,乙正确6、如图,在Rt △ABC 中,∠C=90°,∠B=30°.AB 的垂直平分线DE 交AB 于点D ,交BC 于点E ,则下列结论不正确的是( )A 、AE=BEB 、AC=BEC 、CE=DED 、∠CAE=∠B7、如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )A 、△ABC 的三条中线的交点B 、△ABC 三边的中垂线的交点 C 、△ABC 三条角平分线的交点D 、△ABC 三条高所在直线的交点第7题 第8题8、如图,AC=AD ,BC=BD ,则有( ) A 、AB 垂直平分CD B 、CD 垂直平分AB C 、AB 与CD 互相垂直平分 D 、CD 平分∠ACB二、填空题(共12小题)9、如图,在△ABC中,∠B=30°,ED垂直平分BC,ED=3.则CE长为_________.第9题第10题第11题10、如图,△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE=_________度.11如图,等腰三角形ABC中,已知AB=AC,∠A=30°,AB的垂直平分线交AC于D,则∠CBD的度数为_________°.12、如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC 的周长之差为12,则线段DE的长为_________.第12题第13题第14题第15题13、如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB=_________度.14、如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠ADC=_________度.15、如图,∠ABC=50°,AD垂直且平分BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是_________度.16、如图,有一腰长为5cm,底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有_________个不同的四边形.第16题第17题第18题17已知如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,则△ADE的周长等于_________.18、如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC,AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=1/2∠DAC;④△ABC是正三角形.请写出正确结论的序号_________(把你认为正确结论的序号都填上)19、如图,△ABC的周长为19cm,AC的垂直平分线DE交BC于D,E为垂足,AE=3cm,则△ABD的周长为_________cm.20、在△ABC中,∠A=50°,AB=AC,AB的垂直平分线DE交AC于D,则∠DBC的度数是_________°.三、解答题(共6小题)21、如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.(1)求∠ECD的度数;(2)若CE=5,求BC长.22、如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.1、如图,在△ABC中,分别以点A和点B为圆心,大于的AB的长为半径画孤,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为()A、7B、14C、17D、20考点:线段垂直平分线的性质。
北师大版数学八年级下线段的垂直平分线 同步练习含答案

线段的垂直平分线第1课时线段垂直平分线的性质定理及其逆定理1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=3 cm,则线段PB的长为()A.6 cm B.5 cmC.4 cm D.3 cm第1题图第2题图2.如图,AB是CD的垂直平分线.若AC=2.3 cm,BD=1.6 cm,则四边形ACBD的周长是()A.3.9 cm B.7.8 cmC.4 cm D.4.6 cm3.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.若BC=6,AC =5,则△ACE的周长为()A.8 B.11C.16 D.17第3题图第4题图4.如图,在△ABC中,AC的垂直平分线交AB于点D,DC平分∠ACB.若∠A=50°,则∠B的度数为.5.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.6.如图,AC=AD,BC=BD,则有()A.AB垂直平分CDB.CD垂直平分ABC.AB与CD互相垂直平分D.CD平分∠ACB第6题图第7题图7.如图,已知△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB.下列描述正确的是()A.P是AC的垂直平分线与AB的交点B.P是BC的垂直平分线与AB的交点C.P是∠ACB的平分线与AB的交点D.P是以点B为圆心,AC长为半径的弧与边AB的交点8.如图,在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC交AC于点D.求证:点D在AB的垂直平分线上.9.在△ABC中,AB=AC,边AB的垂直平分线与边AC所在的直线相交所得的锐角为50°,则∠C的度数为.10.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB;②若PA=PB,EA=EB,则直线PE是线段AB的垂直平分线;③若EA=EB,则直线EP是线段AB的垂直平分线;④若PA=PB,则点P在线段AB的垂直平分线上.其中正确的有()A.1个B.2个C.3个D.4个11.如图,在△ABC中,DE是AC的垂直平分线,AC=6 cm,且△ABD的周长为13 cm,则△ABC的周长为()A.13 cm B.19 cmC.10 cm D.16 cm第11题图第12题图12.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=.13.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为.第13题图第14题图14.如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=39°,则∠AOC=.15.如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,DE交AC于点F.求证:点E在AF的垂直平分线上.16.如图1,在△ABC中,AB=AC,点D是△ABC外的一点(点D与点A分别在直线BC的两侧),且DB=DC,过点D作DE∥AC,交射线AB于点E,连接AD交BC于点F.(1)求证:AD垂直平分BC;(2)请从A,B两题中任选一题作答,我选择________题.A:如图1,当点E在线段AB上且不与点B重合时,求证:DE=AE;B:如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE之间的等量关系,并证明你的结论.第2课时三角形三边的垂直平分线1.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定()A.是边AB的中点B.在边AB的中线上C.在边AB的高上D.在边AB的垂直平分线上2.在三角形的内部,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形()A.三条中线的交点B.三条角平分线的交点C.三条边的垂直平分线的交点D.三条高的交点3.如果三角形中两条边的垂直平分线的交点在第三条边上,那么这个三角形一定是()A.锐角三角形B.钝角三角形C.等边三角形D.直角三角形4.如图,已知直线MN为△ABC的边BC的垂直平分线.若AB,AC两边的垂直平分线相交于点O,当顶点A的位置移动时,点O始终在()A.直线MN上B.直线MN的左侧C.直线MN的右侧D.直线MN的左侧或右侧5.下列作图语句正确的是()A.过点P作线段AB的垂直平分线B.在线段AB的延长线上取一点C,使AB=ACC.过直线a和直线b外一点P作直线MN,使MN∥a∥bD .过点P 作直线AB 的垂线6.如图,点E ,F ,G ,Q ,H 在一条直线上,且EF =GH ,我们知道按如图所作的直线l 为线段FG 的垂直平分线.下列说法正确的是( )A .l 是线段EH 的垂直平分线B .l 是线段EQ 的垂直平分线C .l 是线段FH 的垂直平分线D .EH 是l 的垂直平分线第6题图 第7题图7.如图,在Rt △ABC 中,∠B =90°,分别以点A ,C 为圆心,大于12AC 的长为半径画弧,两弧相交于点M ,N ,连接MN ,分别与AC ,BC 交于点D ,E ,连接AE ,则:(1)∠ADE = ;(2)AE EC ;(填“=”“>”或“<”)(3)当AB =3,AC =5时,△ABE 的周长等于 .8.为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P ,使P 到该镇A 村、B 村、C 村所属的村委会所在地的距离都相等(A ,B ,C 不在同一直线上,地理位置如图),请你用尺规作图的方法确定点P 的位置.要求:写出已知、求作,不写作法,保留作图痕迹.A 村 ·B 村 ·C 村·9.在平面内,到三点A,B,C距离相等的点()A.只有一个B.有两个C.有三个或三个以上D.有一个或没有10.如图,在△ABC中,∠BAC=90°,AB>AC.按下列步骤作图:①分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N;②作直线MN,与边AB相交于点D,连接CD.下列说法不一定正确的是()A.∠BDN=∠CDN B.∠ADC=2∠BC.∠ACD=∠DCB D.2∠B+∠ACD=90°11.等腰三角形的底角为40°,两腰的垂直平分线交于点P,则()A.点P在三角形内B.点P在三角形外C.点P在三角形底边上D.点P的位置与三角形的边长有关12.如图,由于水资源缺乏,B,C两地不得不从黄河上的扬水站A引水,这就需要A,B,C之间铺设地下输水管道,有人设计了三种铺设方案:如图①②③,图中实线表示管道铺设线路,在图②中,AD垂直BC于点D;在图③中,OA=OB=OC.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短,已知△ABC恰好是一个边长为a的等边三角形,那么通过计算,你认为最好的铺设方案是方案.13.如图所示,已知线段a,b,求作等腰三角形,使高为a,腰长为b(a<b,尺规作图,保留作图痕迹).14.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.(1)若∠ACB=120°,求∠MCN的度数;(2)若△CMN的周长为15 cm,求AB的长;(3)若∠MFN=70°,求∠MCN的度数.【变式】如图,在△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.(1)求∠PAQ的度数;(2)若△APQ周长为12,BC长为8,求PQ的长.参考答案:第1课时线段垂直平分线的性质定理及其逆定理1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=3 cm,则线段PB的长为(D)A.6 cm B.5 cmC.4 cm D.3 cm第1题图第2题图2.如图,AB是CD的垂直平分线.若AC=2.3 cm,BD=1.6 cm,则四边形ACBD的周长是(B)A.3.9 cm B.7.8 cmC.4 cm D.4.6 cm3.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.若BC=6,AC =5,则△ACE的周长为(B)A.8 B.11C.16 D.17第3题图第4题图4.如图,在△ABC中,AC的垂直平分线交AB于点D,DC平分∠ACB.若∠A=50°,则∠B的度数为30°.5.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.证明:∵DE是AB的垂直平分线,∴EA=EB.∴∠EAB=∠B.∵∠C=90°,∴∠CAB+∠B=90°.又∵∠AED+∠EAB=90°,∴∠CAB=∠AED.6.如图,AC=AD,BC=BD,则有(A)A.AB垂直平分CDB.CD垂直平分ABC.AB与CD互相垂直平分D.CD平分∠ACB第6题图第7题图7.如图,已知△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB.下列描述正确的是(B)A.P是AC的垂直平分线与AB的交点B .P 是BC 的垂直平分线与AB 的交点 C .P 是∠ACB 的平分线与AB 的交点D .P 是以点B 为圆心,AC 长为半径的弧与边AB 的交点8.如图,在△ABC 中,∠C =90°,∠A =30°,BD 平分∠ABC 交AC 于点D.求证:点D 在AB 的垂直平分线上.证明:∵∠C =90°,∠A =30°, ∴∠ABC =90°-30°=60°. ∵BD 平分∠ABC , ∴∠ABD =12∠ABC =30°.∴∠A =∠ABD. ∴DA =DB.∴点D 在AB 的垂直平分线上.9.在△ABC 中,AB =AC ,边AB 的垂直平分线与边AC 所在的直线相交所得的锐角为50°,则∠C 的度数为20°或70°.10.下列说法:①若直线PE 是线段AB 的垂直平分线,则EA =EB ;②若PA =PB ,EA =EB ,则直线PE 是线段AB 的垂直平分线;③若EA =EB ,则直线EP 是线段AB 的垂直平分线;④若PA =PB ,则点P 在线段AB 的垂直平分线上.其中正确的有(C)A .1个B .2个C .3个D .4个11.如图,在△ABC 中,DE 是AC 的垂直平分线,AC =6 cm ,且△ABD 的周长为13 cm ,则△ABC 的周长为(B)A .13 cmB .19 cmC .10 cmD .16 cm第11题图 第12题图12.如图,在Rt △ABC 中,∠BAC =90°,AD ⊥BC 于点D ,将AB 边沿AD 折叠,发现B 点的对应点E 正好在AC 的垂直平分线上,则∠C =30°.13.如图,在Rt △ABC 中,∠ACB =90°,BC =3,AC =4,AB 的垂直平分线DE 交BC 的延长线于点E ,则CE 的长为76.第13题图 第14题图14.(2020·南京)如图,线段AB ,BC 的垂直平分线l 1,l 2相交于点O.若∠1=39°,则∠AOC =78°.15.如图,在△ABC 中,∠ACB =90°,D 是BC 延长线上一点,E 是BD 的垂直平分线与AB 的交点,DE 交AC 于点F.求证:点E 在AF 的垂直平分线上.证明:∵E 是BD 的垂直平分线上的一点, ∴EB =ED. ∴∠B =∠D. ∵∠ACB =90°,∴∠A=90°-∠B,∠CFD=90°-∠D.∴∠CFD=∠A.又∵∠AFE=∠CFD,∴∠AFE=∠A.∴EF=EA.∴点E在AF的垂直平分线上.16.如图1,在△ABC中,AB=AC,点D是△ABC外的一点(点D与点A分别在直线BC的两侧),且DB=DC,过点D作DE∥AC,交射线AB于点E,连接AD交BC于点F.(1)求证:AD垂直平分BC;(2)请从A,B两题中任选一题作答,我选择________题.A:如图1,当点E在线段AB上且不与点B重合时,求证:DE=AE;B:如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE之间的等量关系,并证明你的结论.解:(1)证明:∵AB=AC,∴点A在线段BC的垂直平分线上.∵DB=DC,∴点D在线段BC的垂直平分线上.∴AD垂直平分BC.(2)选择A,证明:由(1),得AD⊥BC,又∵AB=AC,∴∠BAF=∠CAF.∵DE∥AC,∴∠CAF=∠ADE.∴∠BAF=∠ADE.∴DE=AE.选择B,线段DE,AC,BE之间的等量关系为DE=BE+AC.证明:由(1),得AF⊥BC,又∵AB=AC,∴∠BAF=∠CAF.∵DE∥AC,∴∠EDA=∠CAF.∴∠BAF=∠EDA.∴AE=DE.∵AE=EB+AB,AB=AC,∴DE=BE+AC.第2课时三角形三边的垂直平分线1.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定(D)A.是边AB的中点B.在边AB的中线上C.在边AB的高上D.在边AB的垂直平分线上2.在三角形的内部,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形(C)A.三条中线的交点B.三条角平分线的交点C.三条边的垂直平分线的交点D.三条高的交点3.如果三角形中两条边的垂直平分线的交点在第三条边上,那么这个三角形一定是(D) A.锐角三角形B.钝角三角形C.等边三角形D.直角三角形4.如图,已知直线MN为△ABC的边BC的垂直平分线.若AB,AC两边的垂直平分线相交于点O,当顶点A的位置移动时,点O始终在(A)A.直线MN上B.直线MN的左侧C.直线MN的右侧D.直线MN的左侧或右侧5.下列作图语句正确的是(D)A.过点P作线段AB的垂直平分线B.在线段AB的延长线上取一点C,使AB=ACC.过直线a和直线b外一点P作直线MN,使MN∥a∥bD.过点P作直线AB的垂线6.如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是(A)A.l是线段EH的垂直平分线B.l是线段EQ的垂直平分线C.l是线段FH的垂直平分线D.EH是l的垂直平分线第6题图 第7题图7.如图,在Rt △ABC 中,∠B =90°,分别以点A ,C 为圆心,大于12AC 的长为半径画弧,两弧相交于点M ,N ,连接MN ,分别与AC ,BC 交于点D ,E ,连接AE ,则:(1)∠ADE =90°;(2)AE =EC ;(填“=”“>”或“<”) (3)当AB =3,AC =5时,△ABE 的周长等于7.8.为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P ,使P 到该镇A 村、B 村、C 村所属的村委会所在地的距离都相等(A ,B ,C 不在同一直线上,地理位置如图),请你用尺规作图的方法确定点P 的位置.要求:写出已知、求作,不写作法,保留作图痕迹.解:已知:A ,B ,C 三点不在同一直线上. 求作:作一点P ,使PA =PB =PC. 如图所示,点P 即为所求的点.9.在平面内,到三点A ,B ,C 距离相等的点(D) A .只有一个B .有两个C .有三个或三个以上D .有一个或没有10.如图,在△ABC 中,∠BAC =90°,AB >AC.按下列步骤作图:①分别以点B 和点C 为圆心,大于BC 一半的长为半径作圆弧,两弧相交于点M 和点N;②作直线MN,与边AB相交于点D,连接CD.下列说法不一定正确的是(C)A.∠BDN=∠CDN B.∠ADC=2∠BC.∠ACD=∠DCB D.2∠B+∠ACD=90°11.等腰三角形的底角为40°,两腰的垂直平分线交于点P,则(B)A.点P在三角形内B.点P在三角形外C.点P在三角形底边上D.点P的位置与三角形的边长有关12.如图,由于水资源缺乏,B,C两地不得不从黄河上的扬水站A引水,这就需要A,B,C之间铺设地下输水管道,有人设计了三种铺设方案:如图①②③,图中实线表示管道铺设线路,在图②中,AD垂直BC于点D;在图③中,OA=OB=OC.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短,已知△ABC恰好是一个边长为a的等边三角形,那么通过计算,你认为最好的铺设方案是方案③.13.如图所示,已知线段a,b,求作等腰三角形,使高为a,腰长为b(a<b,尺规作图,保留作图痕迹).解:作法:(1)作线段AD=a;(2)过点D作直线MN⊥AD于点D;(3)以点A为圆心,b为半径画弧,交MN于B,C两点,连接AB,AC,△ABC即为所求,如图所示.14.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.(1)若∠ACB=120°,求∠MCN的度数;(2)若△CMN的周长为15 cm,求AB的长;(3)若∠MFN=70°,求∠MCN的度数.解:(1)∵DM,EN分别垂直平分AC和BC,∴AM=CM,CN=BN.∴∠A=∠ACM,∠B=∠BCN.∴∠MCN=180°-(∠CMN+∠CNM)=180°-(2∠A+2∠B)=180°-2(180°-∠ACB)=60°.(2)∵AM=CM,BN=CN,∴△CMN的周长为CM+MN+CN=AM+MN+BN=AB.∵△CMN的周长为15 cm,∴AB=15 cm.(3)∵∠MFN=70°,∴∠MNF+∠NMF=180°-70°=110°.∵∠AMD=∠NMF,∠BNE=∠MNF,∴∠AMD+∠BNE=∠NMF+∠MNF=110°.∴∠A+∠B=90°-∠AMD+90°-∠BNE=70°.又∵∠A=∠ACM,∠B=∠BCN,∴∠MCN=180°-2(∠A+∠B)=40°.【变式】如图,在△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.(1)求∠PAQ的度数;(2)若△APQ周长为12,BC长为8,求PQ的长.解:(1)设∠PAQ=x,∠CAP=y,∠BAQ=z,∵MP和NQ分别垂直平分AB和AC,∴AP=PB,AQ=CQ.∴∠B=∠BAP=x+z,∠C=∠CAQ=x+y.∵∠BAC=80°,∴∠B+∠C=100°,即x+y+z=80°,x+z+x+y=100°.∴x=20°.∴∠PAQ=20°.(2)∵△APQ周长为12,∴AQ+PQ+AP=12.∵AQ=CQ,AP=PB,∴CQ+PQ+PB=12,即BC+2PQ=12.∵BC=8,∴PQ=2.21。
八年级数学重点题型强化训练05 线段垂直平分线专题(解析版)

八年级数学重点题型强化训练5——线段垂直平分线专题第1题第2题【分析】本题考查的是线段垂直平分线的性质:熟记:线段垂直平分线上的点到这条线段两个端点的距离第3题可证BEF CED ≌△△,可得EF =BC 的中点,第5题第6题第7题第8题 第9题【答案】B 【分析】利用全等三角形的判定以及垂直平分线的性质得出OBC Ð,以及40,OBC OCB Ð=Ð=°,再利用翻折变换的性质得出,CEF FEO =Ð进而求出即可.50,BAC BAC Ð=°ÐQ 12OAB CAO \Ð=Ð=25OAB ABO Ð=Ð=∵在等腰ABC V 中,DG Q 是BC 的垂直平分线,BD CD \=,AD Q 是BAC Ð的平分线,DE DF \=,在Rt BDE △和Rt CDF △中,C .60°D 【分析】先根据线段垂直平分线的性质得到BE CE =,则AC EC =,再根据等腰三角形的性质和三角形内,接着利用三角形外角性质计算出EBC Ð=Ð的度数.故选:C .题型2:线段垂直平分线的判定11.如图,AD AC =,BD BC =,则下列判断一定正确的是( )A .AB 垂直平分CDB .CD 垂直平分ABC .CD 平分ACB ÐD .以上都不正确第11题第12题【答案】A【分析】根据线段垂直平分线的判定求解即可.【详解】解:∵AD AC =,BD BC =,∴点A 、B 在线段CD 的垂直平分线上,即AB 垂直平分CD ,故选:A .12.如图,ABC AB AC BC >>V ,,边AB 上存在一点P ,使得PA PC AB +=.下列描述正确的是( )A .P 是AC 的垂直平分线与AB 的交点B .P 是ACB Ð的平分线与AB 的交点C .P 是BC 的垂直平分线与AB 的交点D .P 是AB 的中点【答案】C【分析】根据线段垂直平分线的判定解答即可.【详解】解:PA PC AB PA BP AB +=+=Q ,,PC BP \=,∴P 是BC 的垂直平分线与AB 的交点.故选:C .13.如图,将长方形纸片沿AC 折叠后点B 落在点E 处,则下列关于线段BE 与AC 的关系描述正确的是( )A .AC BE =B .AC 和BE 相互垂直平分C .AC BE ^且AC BE=D .AC BE ^且AC 平分BE【答案】D 【分析】只要证明AC 是线段BE 的垂直平分线即可解决问题.【详解】解:ACE QV 是由ACB △翻折得到,AE AB \=,CB CE =,AC EB \^,AC 平分EB ,故选:D .14.如图,已知:AB AC =,MB MC =.求证:直线AM 是线段BC 的垂直平分线.下面是小彬的证明过程,则正确的选项是( )证明:∵AB AC=∴点A 在线段BC 的垂直平分线上①∵MB MC=∴点M 在线段BC 的垂直平分线上②∴直线AM 是线段BC 的垂直平分线③A .①处的依据是:线段垂直平分线上的点与这条线段两个端点的距离相等B .②处的依据是:与线段两个端点距离相等的点在这条线段的垂直平分线上C .③处的依据是:与线段两个端点距离相等的点在这条线段的垂直平分线上D .以上说法都不对【答案】B【分析】根据垂直平分线的判定方法逐项判断即可.【详解】解:①处的依据是:与线段两个端点距离相等的点在这条线段的垂直平分线上,故A 选项错误,不合题意;②处的依据是:与线段两个端点距离相等的点在这条线段的垂直平分线上,故B 选项正确,符合题意;③处的依据是:两点确定一条直线;故C 选项错误,不合题意;综上可知,选项D 错误,不合题意;故选B .15.下列说法错误的是( )A .若点P 是线段AB 的垂直平分线上的点,则PA PB=B .若PA PB =,QA QB =,则直线PQ 是线段AB 的垂直平分线C .若PA PB =,则点P 在线段AB 的垂直平分线上D .若PA PB =,则过点P 的直线是线段AB 的垂直平分线【答案】D【分析】根据线段垂直平分线的判定方法,即可一一判定.【详解】解:A.若点P 是线段AB 的垂直平分线上的点,则PA PB =,故该说法正确,不符合题意;B.若PA PB =,QA QB =,则直线PQ 是线段AB 的垂直平分线,故该说法正确,不符合题意;C.若PA PB =,则点P 在线段AB 的垂直平分线上,故该说法正确,不符合题意;D.若PA PB =,则过点P 的直线不一定是线段AB 的垂直平分线,故该说法错误,符合题意;故选:D .16.如图,AD 是ABC V 的角平分线,交BC 于D ,DE DF 、分别是ABD △和ACD V 的高,分别交AB AC 、于E 、F ,连接EF 交AD 于G .下列结论:①AD 垂直平分EF ;②EF 垂直平分AD ;③AED AFD V V ≌;④当BAC Ð为60°时,AEF △是等边三角形,其中正确的结论的个数为( )A .4个B .3个C .2个D .1个第16题第17题【答案】B 【分析】根据角平分线性质求出DE DF =,证AED AFD V V ≌,推出AE AF =,再逐个判断即可.【详解】解:∵AD 是ABC V 的角平分线,DE DF 、分别是ABD △和ACD V 的高,∴DE DF =,90AED AFD Ð=Ð=°,在Rt AED △和Rt AFD △中,AD AD DE DF =ìí=î,∴()Rt Rt HL AED AFD ≌△△,故③正确;∴AE AF =,∴AD 垂直平分EF ,①正确;②错误;∵60BAC Ð=°,且AE AF =,∴AEF △是等边三角形,④正确.综上,①③④正确,共3个.故选:B .17.如图,在△ABC 中,AD 是△ABC 的角平分线,点E 、F 分别是AD 、AB 上的动点,若∠BAC =50°,当BE +EF 的值最小时,∠AEB 的度数为( )A .105°B .115°C .120°D .130°【答案】B【分析】过点B 作BB ′⊥AD 于点G ,交AC 于点B ′,过点B ′作B ′F ′⊥AB 于点F ′,与AD 交于点E ′,连接BE ′,证明AD 垂直平分BB ′,推出BE =BE ′,由三角形三边关系可知,BE EF B E EF B F B F ¢¢¢¢+=+³³,即BE +EF 的值最小为B F ¢¢,通过证明△ABE ′≌△AB ′E ′,推出∠AE ′B =AE ′B ′,因此利用三角形外角的性质求出AE ′B ′即可.【详解】解:过点B 作BB ′⊥AD 于点G ,交AC 于点B ′,过点B ′作B ′F ′⊥AB 于点F ′,与AD 交于点E ′,连接BE ′,如图:此时BE +EF 最小.∵AD 是△ABC 的角平分线,∠BAC =50°,∴∠BAD =∠B ′AD =25°,∵BB ′⊥AD ,∴∠AGB =∠AGB ′=90°,在△ABG 和△AB ′G 中,BAG B AG AG AGAGB AGB Ð=Ðìï=íïТ=Ðî¢,∴△ABG ≌△AB ′G (ASA ),∴BG =B ′G , AB =AB ′,∴AD 垂直平分BB ′,∴BE =BE ′,在△ABE ′和△AB ′E ′中,BE BE AE AE AB AB ¢¢¢¢ìï=íï=î=,∴△ABE ′≌△AB ′E ′(SSS ),∴∠AE ′B =AE ′B ′,∵AE ′B ′=∠BAD + AF ′E ′=25°+90°=115°,∴∠AE ′B =115°.即当BE +EF 的值最小时,∠AEB 的度数为115°.故选B .18.如图,点P 是AOB Ð内的一点,PC OA ^于点C ,PD OB ^于点D ,连接OP ,CD .若PC PD =,则下列结论不一定成立的是( )A .AOP BOPÐ=ÐB .OPC OPD Ð=ÐC .PO 垂直平分CD D .PD CD=【答案】D【分析】根据角平线的判定定理可判断A ,证明Rt COP Rt DOP V V ≌,可判断B ,根据Rt COP Rt DOP V V ≌,可得OC =OD ,进而可判断C ,根据等边三角形的定义,可判断D .【详解】解:∵点P 是AOB Ð内的一点,PC OA ^于点C ,PD OB ^于点D ,PC PD =,∴OP 是∠AOB 的平分线,即AOP BOP Ð=Ð,故A 成立,不符合题意;∵OP =OP ,AOP BOP Ð=Ð,第19第20题=,利用ASA Ð,再根据E是CD的中点可求出ECECF=,结合已知可得BE的垂直平分线,根据线段垂直AE EF=+,进而即可求解.即可证得AB BC AD故答案为:70.题型3:与线段垂直平分线相关的尺规作图21.如图,在ABC V 直线MN ,交BC A .9【答案】B 【分析】由题意可得MN ADC C AC BC =+V ,求解即可.【详解】解:由题意可得,A.3B 【答案】B【分析】利用基本作图得到V的周长为20再利用ABC【详解】解:由作法得DE \==,,DA DB AE BEA .①③B .①④C .②④D .③④【答案】B 【分析】依次对各个图形的作图痕迹进行分析即可.【详解】 由图①知AD AC =,AB AD >,AB AC \>,故图①能说明AB AC >;由图②知射线BD 是ABC Ð的平分线,不能说明AB AC >;由图③知CD AB ^,不能说明AB AC >;由图④知DE 是BC 的垂直平分线,DB DC \=.ADC QV 中AD DC AC +>,AD DB AC \+>,即AB AC >.故图④能说明AB AC >.故选:B24.如图所示,在Rt ABC △中,90C Ð=°,以B 为圆心,以任意长度为半径作弧,与BA ,BC 分别交于A.20°B.36【答案】C【分析】由作图可知:BO为=,再根据等腰三角形的性质得AD BD和定理即可求出AÐ的度数.【详解】解:由作图可知:平分EAC Ð;③AC CD =;④ABC S V C .①③DA .只有甲的答案正确B .甲和乙的答案合在一起才正确C .甲和丙的答案合在一起才正确D .甲乙丙的答案合在一起才正确【答案】D 【分析】分四种情况讨论:当APB Ð为锐角时,当APB Ð为钝角时,当APB Ð为直角时,当135APB Ð=°时,分别画出图形,求出x 与y 的关系,即可得出答案.【详解】解:当APB Ð为锐角时,如图所示:∵AD BP ^,∴90ADP Ð=°,∴90PAD APD Ð+Ð=°,即90x y +=;当APB Ð为钝角时,如图所示:∵AD BP ^,∴90ADP Ð=°,∵APB Ð为ADP △的外角,∴APB ADP DAP Ð=Ð+Ð,∴90x y =+,即90x y -=;当APB Ð为直角时,如图所示:此时直线n 与PA 重合,∴此时直线n 与PA 所夹的角为0°,即90x y +=或90x y -=;当135APB Ð=°时,如图所示:18013545DPA Ð=°-°=°,∵AD BP ^,∴90ADP Ð=°,∴904545DAP Ð=°-°=°,∴45135180DAP APB Ð+Ð=°+°=即180x y +=;1AB 的长为半径作弧,两弧相交于AM ;的长为半径作弧,与BC 边相交于点N ,连接C.9AC,根据中垂线的定义和性质找到相等的边,进而由AC,A .15B .16C .18D .20【答案】A 【分析】根据题意得到MN 是线段AB 的垂直平分线,进而得到点D 是AB 的中点,根据三角形的面积公式计算,得到答案.【详解】解:由尺规作图可知,MN 是线段AB 的垂直平分线,\点D 是AB 的中点,ACD BCD S S \=△△,ADE CDE CDB S S S \+=V V V ,Q CDB △的面积为12,ADE V 的面积为9,1293CDE CDB ADE S S S \=-=-=V V V ,\四边形EDBC 的面积为:12315CDE CDB EDBC S S S =+=+=V V 四边形,故选:A .30.如图,在ABC V 中,根据尺规作图痕迹,下列说法不一定正确的是( ).A .AF BF=B .90AFD FBC Ð+Ð=°C .DF AB^D .BAF CAFÐ=Ð【答案】D 【分析】由图中尺规作图痕迹可知,BE 为ABC Ð的平分线,DF 为线段AB 的垂直平分线,结合角平分线的定义和垂直平分线的性质逐项分析即可.【详解】解:由图中尺规作图痕迹可知, BE 为ABC Ð的平分线,DF 为线段AB 的垂直平分线.上求作点D ,使;,若点D 在边上,在上求作点E ,使.)作BC 的垂直平分线与BC 的交点即为所求;)如图:由题意得,只要作12BDE ABC S S △△=即可,由第(1)问得,12ABP ABC S S △△=,只要作BC ABD ACD S S =V V AB BC BDE ADEC S S △四边形=作BC 的垂直平分线与BC 交于D 点,BD CD \=,ABD QV 与ACD V 高相同,ABD ACD S S \=V V .如图1:点D 即为所求;(2)如图:由题意得,只要作12BDE ABC S S △△=即可,作BC 的垂直平分线交BC 于P 点,由第(1)问得,12ABP ABC S S △△=,故只要作BDE ABP S S △△=即可,连接D 、P ,要使得BDE ABP S S △△=,只要作根据“夹在平行线之间的垂线段相等”,即,高相等,如图2:点E 即为所求.32.如图,在中,点E 在上且.(1)请用尺规作图的方法在边上确定点D ,使得;(保留作图痕迹,不写作法)(2)在(1)的条件下,若的周长为,求的长.【分析】(1)线段AB 的垂直平分线与BC 边的交点即为所求;(2)根据线段垂直平分线的性质,通过等量代换求解.【详解】(1)解:如图所示,线段AB 的垂直平分线与BC 边交于点D ,点D 即为所求;(2)解:Q ADE V 的周长为12cm ,\12AD AE DE ++=,Q BD AD =,AE CE =,\12BC BD CE DE AD AE DE =++=++=,即BC 的长为12cm .题型4:与线段垂直平分线相关的计算与证明33.如图,在ABC V 中,AB 、AC 边的垂直平分线相交于点O ,分别交BC 边于点M 、N ,连接AM ,AN .(1)若AMN V 的周长为6,求BC 的长;(2)若30B Ð=°,25C Ð=°,求MAN Ð的度数;(3)若MON a Ð=,请用a 表示MAN Ð的度数(直接写出即可).ABC V BC AE CE =BC BD AD =ADE V 12cm BC【答案】(1)6(2)70°(3)1802MAN aÐ=°-【分析】(1)由垂直平分线的性质可得,AM BM AN CN ==,再由BC AM MN AN =++可得结论;(2)由垂直平分线的性质可得30,30,B BAM C CAN Ð=Ð=°Ð=Ð=°,再根据三角形内角和定理可得结论;(3)根据三角形内角和定理可得()1802MAN B C Ð=°-Ð+Ð,再由四边形内角和定理可得180B C MAN O Ð+Ð=°-Ð-Ð,代入求解即可【详解】(1),OM ON Q 分别是AB 、AC 边的垂直平分线,,,AM BM AN CN \==6AM MN AN ++=Q 6BM MN CN \++=,即6BC =(2),,AM BM AN CN ==Q 30,25,BAM B CAN C \Ð=Ð=°Ð=Ð=°180,B BAC C Ð+Ð+Ð=°Q 且BAC BAM MAN CANÐ=Ð+Ð+Ð180,B BAM MAN CANC \Ð+Ð+Ð+Ð+Ð=°即180,B B MANC C Ð+Ð+Ð+Ð+Ð=°18022180605070MAN B C \Ð=°-Ð-Ð=°-°-°=°(3)如图,180,B BAC C Ð+Ð+Ð=°Q 且BAC BAM MAN CAN Ð=Ð+Ð+Ð180,B BAM MAN CANC \Ð+Ð+Ð+Ð+Ð=°即180,B B MANC C Ð+Ð+Ð+Ð+Ð=°()1802MAN B C \Ð=°-Ð+Ð,,OM ON Q 分别是AB 、AC 边的垂直平分线,90AEO AFO \Ð=Ð=360AEO EAF AFO FOE \Ð+Ð+Ð+Ð=°180EAF O \Ð+Ð=°180,BAF MAN CAN O \Ð+Ð+Ð+Ð=°180,B C MAN O \Ð+Ð+Ð+Ð=°180B C MAN O\Ð+Ð=°-Ð-Ð()()180********MAN B C MAN O \Ð=°-Ð+Ð=°-°-Ð-Ð\解得,1802MAN aÐ=°-34.如图,在Rt ABC △中,45,90,ACB BAC AB AC Ð=°Ð=°=,点D 是AB 的中点,AF CD ^于H 交BC 于F ,BE AC ∥交AF 的延长线于E .求证:BC 垂直且平分DE .【答案】见解析【分析】根据全等三角形的判定证明(ASA)ABE CAD ≌V V ,在再证明(SAS)DBP EBP ≌V V 即可解决问题;【详解】证明:由题意可知,9090DAH ADH ACH ADH ÐÐÐÐ+=°+=°,,∴DAH ACH ÐÐ=,∵90BAC Ð=°,BE AC ∥,∴90CAD ABE ÐÐ==°.又∵AB CA =,∴在ABE V 与CAD V 中,DAH ACH AB AC CAD ABE Ð=Ðìï=íïÐ=Ðî,∴(ASA)ABE CAD ≌V V .∴AD BE =,又∵AD BD =,∴BD BE =,在Rt ABC V 中,45,90,ACB BAC AB AC ÐÐ=°=°=,故45ABC Ð=°.∵90ABE Ð=°,∴904545EBF Ð=°-°=°,∴(SAS)DBP EBP ≌V V ,∴DP EP =,∴BC 垂直且平分DE .35.如图,ABC V 中,AD 平分BAG Ð,DG 垂直平分BC ,DE AB ^于E ,DF AC ^于F .(1)求证:BE CF =;(2)如果9AB =,5AC =,求BE 的长.【答案】(1)见解析;(2)2BE =.【分析】(1)由DG 垂直平分BC 可得DB DC =,由AD 平分BAG Ð, DE AB ^,DF AC ^,可得DE DF =,90DEB DFC Ð=Ð=°,从而证得()Rt Rt HL DBE DCF V V ≌,得证BE CF =;(2)易证()Rt Rt HL ADE ADF ≌△△,得到AE AF =,又BE CF =,因此2AB AE BE AF BE AC CF AC BE =+=+=+=+,代入即可解答.【详解】(1)连接DB ,DC ,∵DG 垂直平分BC ,∴DB DC =,∵AD 平分BAG Ð,DE AB ^,DF AC ^,∴DE DF =,90DEB DFC Ð=Ð=°,∴在Rt DBE V 和Rt DCF V 中DB DC DE DF=ìí=î∴()Rt Rt HL DBE DCF V V ≌,∴BE CF =.(2)∵DE AB ^,DF AC ^,∴在Rt ADE △和Rt ADF V 中AD AD DE DF=ìí=î∴()Rt Rt HL ADE ADF ≌△△,∴AE AF=∵BE CF=∴2AB AE BE AF BE AC CF AC BE =+=+=+=+,∵9AB =,5AC =,∴952BE =+,∴2BE =.36.如图,AB AC >,BAC Ð的平分线与BC 边的垂直平分线GD 相交于点D ,过点D 作DE AB ^于点E ,DF AC ^于点F ,求证:BE CF =.【答案】见解析【分析】连接DC ,根据GD 是BC 边的垂直平分线,得到DC DB =,根据AD 是BAC Ð的平分线,且DE AB ^,DF AC ^,得到DE DF =,根据DE DF DB DC =ìí=î,得到()HL DEB DFC V V ≌即可得证.【详解】如图,连接DC ,∵GD 是BC 边的垂直平分线,∴DC DB =,∵AD 是BAC Ð的平分线,且DE AB ^,DF AC ^,∴DE DF =,∵DE DF DB DC =ìí=î,∴()HL DEB DFC V V ≌∴BE CF =.37.如图,在ABC V 中,BAC Ð的平分线与BC 的中垂线DE 交于点E ,过点E 作AC 边的垂线,垂足N ,过点E 作AB 延长线的垂线,垂足为M .(1)求证:BM CN =;(2)若2AB =,8AC =,求BM 的长.【分析】(1)连接BE ,CE ,由题意易得BE CE =,EM EN =,进而可证Rt Rt BME CNE ≌V V ,然后问题得解;(2)由(1)得:EM EN =,进而可证Rt Rt AME ANE ≌V V ,则有AB BM AC CN +=-,然后根据线段的和差关系可求解.【详解】(1)证明:连接BE ,CE ,DE Q 是BC 的垂直平分线,BE CE \=,AE Q 是BAC Ð的平分线,EM AB ^,EN AC ^,EM EN \=,在Rt BME △和Rt CNE △中,BE CE EM EN=ìí=î()Rt Rt BME CNE HL \V V ≌,BM CN \=;(2)由(1)得:EM EN =,在Rt AME △和Rt ANE △中,AE AE EM EN=ìí=îRt Rt AME ANE \≌V V ,请根据所给教材内容,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程.定理应用:V中,AB、AC的垂直平分线分别交BC于点D、E,垂足分别为M,N,已知)如图②,在ABC的周长为20,则BC的长为__________.∵AB AC AD BC ^=,,的周长为7,可得∴19712AB BE +=-=,∴6AB BE ==;(2)∵30ABC Ð=°,45C Ð=°,∴1803045105BAC Ð=°-°-°=°,在BAD V 和BED V 中,BA BE BD BD DA DE =ìï=íï=î,∴()SSS BAD BED V V ≌,∴105BED BAC Ð=Ð=°,∴1054560CDE BED C Ð=Ð-Ð=°-°=°.40.如图,在ABC V 中,点E 在AB 上,点D 在BC 上,BD BE =,BAD BCE Ð=Ð,AD 与CE 相交于F .(1)求证:AF CF =;(2)连接,试判断与的位置关系,并说明理由.【分析】(1)根据全等三角形的判定与性质,可得BA BC =,BDA BEC Ð=Ð,根据补角的性质,可得FDC FEA Ð=Ð,根据全等三角形的判定与性质,可得答案.(2)由AB CB =,AF CF =可得点B ,F 在AC 的垂直平分线,即可得出结论【详解】(1)在BAD V 和BCE V 中,∵B B BAD BCE BD BE Ð=ÐìïÐ=Ðíï=î,∴BAD V ≌BCE V ,∴AB CB =,BF BF AC与点A 重合,则 , .,四边形的直角沿直线l 折叠后(如图2),点B 落在四边形的边与AB 相交于点F ,猜想OF 、EF 、AB 三者数量关系,并证明.若折叠后点D 恰为AB 的中点(如图3),求的度数;45°,8数量关系为:AB OF EF =+;证明见解析q ==a OABC OCB ÐOABC q∴E O D FO D Ð=Ð.由折叠可得FOD EOC EOD q Ð=Ð=Ð=,∴390COA q Ð==°,∴30q =°.。
线段的垂直平分线的性质和判定精选优秀练习

13.1.2 线段的垂直平分线的性质第1课时线段的垂直平分线的性质和判定一、选择题(共8小题)1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,CD边垂直平分线的交点,连接EC;则∠AEC等于()F,:第1题图第2题图第5题图第6题图第7题图第8题图B二、填空题(共10小题)9.到线段AB两个端点距离相等的点的轨迹是_________ .10.如图,有A、B、C三个居民小区是位置成三角形,现决定在三个小区之间修建一个休闲广场,使广场到三个小区的距离相等,则广场应建在_________ .11.在阿拉伯数字中,有且仅有一条对称轴的数字是____________.12、如图,△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE= _________ 度.13、如图,△ABC的周长为19cm,AC的垂直平分线DE交BC于D,E为垂足,AE=3cm,则△ABD的周长为_________ cm.14.如图,已知在△ABC中,AB=AC=10,DE垂直平分AB,垂足为E,DE交AC于D,若△BDC的周长为16,则BC= _________ .15.如图,在△ABC中,∠B=30°,直线CD垂直平分AB,则∠ACD的度数为_________ .16.已知如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,则△ADE的周长等于_________ .17.如图,AB=AC,AC的垂直平分线DE交AB于D,交AC于E,BC=6,△CDB的周长为15,则AC= _________ .18.如图,△ABC中,AB=AC,∠A=40°,AC的垂直平分线分别交AB,AC于D,E两点,连接CD.则∠BCD=_________ 度.第10题图第12题图第13题图第14题图第15题图第16题图第17题图第18题图三、解答题(共5小题)19.如图,四边形ABCD中,AC垂直平分BD于点O.(1)图中有多少对全等三角形?请把它们都写出来;(2)任选(1)中的一对全等三角形加以证明.20.如图,在△AB C中,AB=AC,D是AB的中点,且DE⊥AB,△BCE的周长为8cm,且AC﹣BC=2cm,求AB、BC的长.21.如图,已知:在ABC中,AB、BC边上的垂直平分线相交于点P.求证:点P在AC的垂直平分线上.22.如图,△ABC中,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F.求证:AD垂直平分EF.23.如图,已知∠C=∠D=90°,AC与BD交于O,AC=BD.(1)求证:BC=AD;(2)求证:点O在线段AB的垂直平分线上.13.1.2 线段的垂直平分线的性质一、选择题(共8小题)1.B 2.A 3.A 4.A 5.C 6.C 7.A 8.A二.填空题(共10小题)9. 线段AB的中垂线;10. 三边垂直平分线的交点处;11. 3;12. 50;3. 13 ;14. 615. 60°;16. 8 ;17. 9 ;18.35°三.解答题(共5小题)19.(1)解:图中有三对全等三角形:△AOB≌△AOD,△COB≌△COD,△ABC≌△ADC;(2)证明△ABC≌△AD C.证明:∵AC垂直平分BD,∴AB=AD,CB=CD(中垂线的性质),又∵AC=AC,∴△ABC≌△ADC.20. 解:∵△ABC中,AB=AC,D是AB的中点,且DE⊥AB,∴AE=BE,∵△BCE的周长为8cm,即BE+CE+BC=8cm,∴AC+BC=8cm…①,∵AC﹣BC=2cm…②,①+②得,2AC=10cm,即AC=5cm,故AB=5cm;①﹣②得,2BC=6cm,BC=3cm.故AB=5cm、BC=3cm.21.证明:∵P在AB、BC的垂直平分线上∴AP=BP,BP=CP∴AP=CP,∴P点在AC的垂直平分线上.22.证:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,∴DE=DF,∠AED=∠AFD=90°,在Rt△AED和Rt△AFD中∴Rt△AED≌Rt△AFD(HL),∴AE=AF,∵AD是∠BAC的平分线,∴AD垂直平分EF(三线合一)23. 证明:(1)∵∠C=∠D=90°,∴在Rt△ACB和Rt△BDA中,,∴Rt△ACB≌Rt△BDA,∴AD=BC;(2)∵Rt△ACB≌Rt△BDA,∴∠CAB=∠DBA,∴OA=OB,∴点O在线段AB的垂直平分线上.。
《垂直平分线》练习题(含答案)
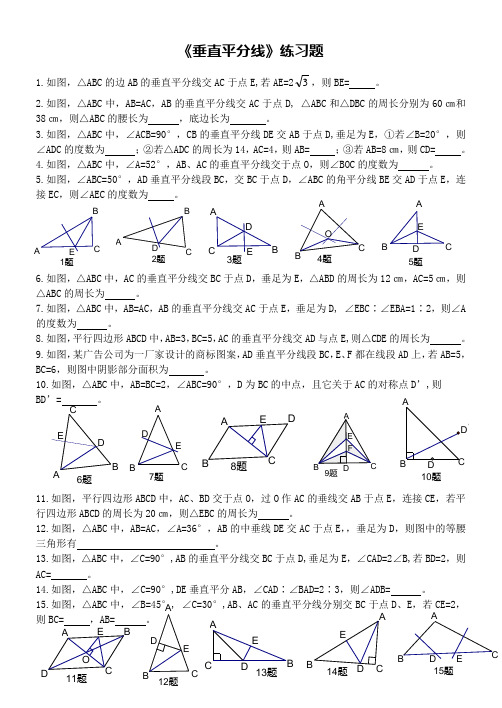
1题A B E C 2题D A B C 3题D AB EC 4题A B C O 5题D A BE C 11题D A B E C O 12题D A B E C 13题D A B E C 14题D A B E C 15题D A B E C6题D A BE C 8题D A B E C 7题D A B E C 10题'9题《垂直平分线》练习题1.如图,△ABC 的边AB 的垂直平分线交AC 于点E,若AE=23,则BE= 。
2.如图,△ABC 中,AB=AC ,AB 的垂直平分线交AC 于点D, △ABC 和△DBC 的周长分别为60㎝和38㎝,则△ABC 的腰长为 ,底边长为 。
3.如图,△ABC 中,∠ACB=90°,CB 的垂直平分线DE 交AB 于点D,垂足为E ,①若∠B=20°,则∠ADC 的度数为 ;②若△ADC 的周长为14,AC=4,则AB= ;③若AB=8㎝,则CD= 。
4.如图,△ABC 中,∠A=52°,AB 、AC 的垂直平分线交于点O ,则∠BOC 的度数为 。
5.如图,∠ABC=50°,AD 垂直平分线段BC ,交BC 于点D ,∠ABC 的角平分线BE 交AD 于点E ,连接EC ,则∠AEC 的度数为 。
6.如图,△ABC 中,AC 的垂直平分线交BC 于点D ,垂足为E ,△ABD 的周长为12㎝,AC=5㎝,则△ABC 的周长为 。
7.如图,△ABC 中,AB=AC ,AB 的垂直平分线交AC 于点E ,垂足为D, ∠EBC ∶∠EBA=1∶2,则∠A 的度数为 。
8.如图,平行四边形ABCD 中,AB=3,BC=5,AC 的垂直平分线交AD 与点E,则△CDE 的周长为 。
9.如图,某广告公司为一厂家设计的商标图案,AD 垂直平分线段BC ,E 、F 都在线段AD 上,若AB=5,BC=6,则图中阴影部分面积为 。
10.如图,△ABC 中,AB=BC=2,∠ABC=90°,D 为BC 的中点,且它关于AC 的对称点D ’,则 BD ’= 。
垂直平分线专项练习30题(有答案)ok

垂直平分线专项练习30题(有答案)1.如图,在△ABC中,∠BAC=2∠B,DE⊥AB于点D,交BC于点E,AC=AD=BD,请你猜想∠C的度数并证明.2.如图,在△ABC中,∠BAC的平分线与BC的垂直平分线PQ相交于点P,过点P分别作PN⊥AB于N,PM⊥AC 于点M,求证:BN=CM.3.如图,在△ABC中,D是BC的垂直平分线DH上一点,DF⊥AB于F,DE⊥AC交AC的延长线于E,且BF=CE.(1)求证:AD平分∠BAC;(2)若∠BAC=80°,求∠DCB的度数.4.如图,在△ABC中,AB=AC,∠A=52°,AB的垂直平分线MN交AC于点D.求∠DBC的度数.5.如图,在Rt△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,点D是AB的中点,AF⊥CD于H交BC于F,BE∥AC 交AF的延长线于E.求证:BC垂直且平分DE.6.已知△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于F.求证:∠BAF=∠ACF.7.如图,△ABC中,边AB、BC的垂直平分线交于点P.(1)求证:PA=PB=PC;(2)点P是否也在边AC的垂直平分线上?由此你还能得出什么结论?8.如图,在Rt△ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,求BD的长.9.如图,在△ABC中,AD平分∠BAC,AD的垂直平分线EF交BC的延长线于点F,连接AF,求证:∠CAF=∠B.10.如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB、BC延长线于F、E.求证:(1)∠EAD=∠EDA;(2)DF∥AC;(3)∠EAC=∠B.11.如图所示,AD是△ABC中∠BAC的平分线,AD的垂直平分线EF交BC的延长线于F,试说明∠BAF=∠ACF 的理由.12.如图所示,在△ABC中,AB=AC=16cm,D为AB的中点,DE⊥AB交AC于E,△BCE的周长为26cm,求BC的长.13.如图,在△ABC中,EN,DM分别是AB,AC边的垂直平分线,BC=8cm.求△AED的周长.14.如图,在△ABC中,0E,OF分别是AB,AC的中垂线,∠ABO=20°,∠ABC=45°,求∠BAC和∠ACB的度数.15.如图所示,△ABC中,∠BAC的平分线与BC的垂直平分线相交于点E,EF⊥AB,EG⊥AC,垂足分别为F、G,则BF=CG吗?说明理由.16.在△ABC中,BC边的垂直平分线DE交BC于D,交AB于E,BE=5,△BCE的周长为18 即BE+CE+BC=18,求BC的长?17.如图1,△ABC中,AB=AC,∠BAC=130°,边AB、AC的垂直平分线交BC于点P、Q.(1)求∠PAQ的度数;(2)如图2,△ABC中,AB>AC,且90°<∠BAC<180°,边AB、AC的垂直平分线交BC于点P、Q.①若∠BAC=130°,则∠PAQ=_________°,若∠BAC=α,则∠PAQ用含有α的代数式表示为_________;②当∠BAC=_________°时,能使得PA⊥AQ;③若BC=10cm,则△PAQ的周长为_________cm.18.如图,△ABC中,AB=AC=14cm,D是AB的中点,DE⊥AB于D交AC于E,△EBC的周长是24cm,求BC 的长度.19.已知:如图,在△ABC中,AB=AC=32,AB的垂直平分线DE分别交AB、AC于点E、D.(1)若△DBC的周长为56,求BC的长;(2)若BC=21,求△DBC的周长.20.在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE 的周长为6cm.(1)求BC的长;(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长.21.如图,在△ABC中,E、F分别是AB、AC上的点,AD平分∠BAC,DE⊥AB,DF⊥AC,求证:AD垂直平分EF.22.如图,AD是△ABC的角平分线,AD的垂直平分线交BC的延长线于点F.求证:∠FAC=∠B.23.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于P、Q.(1)若BC=10,求△APQ周长是多少?(2)若∠BAC=110°,求∠PAQ的度数是多少?24.已知,如图,AD是BC的垂直平分线,DE⊥AB于点E,DF⊥AC于点F,求证:(1)∠ABD=∠ACD;(2)DE=DF.25.如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,连接EF.求证:AD垂直平分EF.26.如图,△ABC中,E是BC边上的中点,DE⊥BC于E,DM⊥AB于M,DN⊥AC于N,BM=CN 试证明:点D在∠BAC的平分线上.27.如图,△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.求△AEG的周长.28.如图,在△ABC中,M为BC的中点,DM⊥BC,DM与∠BAC的角平分线交于点D,DE⊥AB,DF⊥AC,E、F为垂足,求证:BE=CF.29.已知,如图,DE为△ABC的边AB的垂直平分线,CD为△ABC的外角平分线,与DE交于D,DM⊥BC于M,DN⊥AC于N,求证:AN=BM.30.如图所示,在△ABC中,AB=8,AC=4,∠BAC的平分线与BC的垂直平分线交于点D,过点D作DE⊥AB 于点E,DF⊥AC(或AC的延长线)于点D.(1)求证:BE=CF;(2)求AE的长.参考答案:1.解:∠C=90°.证明:如图,连接AE,在Rt△AED和Rt△BED中,,∴△AED≌△BED(HL),∴∠DAE=∠B,又∵∠BAC=2∠B,∴∠DAE=∠CAE,在△AED和△BED中,,∴△ACE≌△ADE,∴∠C=∠ADE=90°.2.证明:连接PB,PC,∵AP是∠BAC的平分线,PN⊥AB,PM⊥AC,∴PM=PN,∠PMC=∠PNB=90°,∵P在BC的垂直平分线上,∴PC=PB,在Rt△PMC和Rt△PNB中,∴Rt△PMC≌Rt△PNB(HL),∴BN=CM.3.(1)证明:如图,连接BD,∵DH垂直平分BC,∴BD=CD,在Rt△BDF和Rt△CDE中,,∵DF⊥AB于F,DE⊥AC,∴AD平分∠BAC;(2)解:∵Rt△BDF≌Rt△CDE,∴∠CDE=∠BDF,∴∠BDC=∠EDF,∵∠BAC=80°,∴∠EDF=360°﹣90°×2﹣80°=100°,∴∠BDC=100°,∵BD=CD,∴∠DCB=(180°﹣100°)=50°4.解:∵AB=AC,∠A=52°,∴∠ABC=∠ACB==64°,∵AB的垂直平分线MN,∴AD=BD,∠A=∠ABD=52°,∴∠DBC=∠ABC﹣∠ABD=64°﹣52°=12°5.证明:在△ADC中,∠DAH+∠ADH=90°,∠ACH+∠ADH=90°,∴∠DAH=∠DCA,∵∠BAC=90°,BE∥AC,∴∠CAD=∠ABE=90°.又∵AB=CA,∴在△ABE与△CAD中,∴△ABE≌△CAD(ASA),∴AD=BE,又∵AD=BD,∴BD=BE,在Rt△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,故∠ABC=45°.∵BE∥AC,∴∠EBD=90°,∠EBF=90°﹣45°=45°,∴△DBP≌△EBP(SAS),∴DP=EP,即可得出BC垂直且平分DE6.证明:∵AD是∠BAC的平分线,∴∠1=∠2,∵FE是AD的垂直平分线,∴FA=FD(线段垂直平分线上的点到线段两端的距离相等),∴∠FAD=∠FDA(等边对等角),∵∠BAF=∠FAD+∠1,∠ACF=∠FDA+∠2,∴∠BAF=∠ACF7.证明:(1)∵边AB、BC的垂直平分线交于点P,∴PA=PB,PB=PC.∴PA=PB=PC.还可得出结论:①三角形三边的垂直平分线相交于一点.②这个点与三顶点距离相等8.解:因为CE垂直平分AD,所以AC=CD=5cm.所以∠ACE=∠ECD.因为CD平分∠ECB,所以∠ECD=∠DCB.因为∠ACB=90°,所以∠ACE=∠ECD=∠DCB=30°.所以∠A=90°﹣∠ACE=60°.所以∠B=90°﹣∠A=30°.所以∠DCB=∠B.所以BD=CD=5cm9.证明:∵EF垂直平分AD,∴AF=DF,∠ADF=∠DAF,∵∠ADF=∠B+∠BAD,∠DAF=∠CAF+∠CAD,又∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠CAF=∠B10.解:(1)∵EF是AD的垂直平分线,∴AE=DE,∴∠EAD=∠EDA;(2)∵EF是AD的垂直平分线,∴AF=DF,∴∠FAD=∠FDA,∵AD是∠BAC平分线,∴∠FAD=∠CAD,∴∠FDA=∠CAD,∴DF∥AC;(3)∵∠EAC=∠EAD﹣∠CAD,∠B=∠EDA﹣∠BAD,且∠BAD=∠CAD,∠EAD=∠EDA,∴∠EAC=∠B11.解:∵EF垂直平分AD,∴AF=DF,∴∠FAD=∠FDA.又∵AD平分∠BAC,∴∠BAD=∠CAD,∵∠BAF=∠BAD+∠FAD,∠ACF=∠DAC+∠FDA,∴∠BAF=∠ACF12.解:∵点D中AB的中点,DE⊥AB,∴DE是AB的中垂线,∴AE=BE,∴△BCE的周长=BE+EC+BC=AE+EC+BC=AC+BC=26,∴BC=26﹣AC=26﹣16=10cm13.解:∵EN,DM分别是AB,AC边的垂直平分线,∴BE=AE,CD=AD,14.解:连接AO并延长,交BC于点D,∵0E,OF分别是AB,AC的中垂线,∴OB=OA,OC=OA,∴OC=OB,∠ABO=∠BAO=20°,∠CBO=∠BCO,∠CAO=∠ACO,∵∠ABC=45°,∴∠CBO=∠BCO=25°,∴∠BOC=180°﹣∠CBO﹣∠BCO=130°,∵∠BOD=∠ABO+∠BAO,∴∠BOD=40°,∠COD=90°.∵∠COD=∠CAO+∠ACO,∴∠CAO=45°,∴∠BAC=∠BAO+∠CAO=65°,∠ACB=∠BCO+∠ACO=70°15.解:BF=CG;理由如下:因为点E在BC的垂直平分线上,所以BE=CE.因为点E在∠BAC的角平分线上,且EF⊥AB,EG⊥AC,所以EF=EG,在Rt△EFB和Rt△EGC中,因为BE=CE,EF=EG,所以Rt△EFB≌Rt△EGC(HL).所以BF=CG16.解:∵BC边的垂直平分线DE,∴BE=CE=5,∵BE+CE+BC=18,∴BC=18﹣5﹣5=8,答:BC的长是817.解:(1)∵边AB、AC的垂直平分线交BC于点P、Q,∴AP=BP,AQ=CQ,∴∠BAP=∠B,∠CAQ=∠C,∵∠BAC=130°,∴∠B+∠C=180°﹣∠BAC=50°,∴∠BAP+∠CAQ=50°,∴∠PAQ=∠BAC﹣(∠BAP+∠CAQ)=130°﹣50°=80°;(2)①∵边AB、AC的垂直平分线交BC于点P、Q,∴AP=BP,AQ=CQ,∴∠BAP=∠B,∠CAQ=∠C,∵∠BAC=130°,∴∠B+∠C=180°﹣∠BAC=50°,∴∠BAP+∠CAQ=50°,∴∠PAQ=∠BAC﹣(∠BAP+∠CAQ)=130°﹣50°=80°;∵边AB、AC的垂直平分线交BC于点P、Q,∴AP=BP,AQ=CQ,∴∠BAP=∠B,∠CAQ=∠C,∵∠BAC=α,∴∠B+∠C=180°﹣∠BAC=180°﹣α,∴∠BAP+∠CAQ=180°﹣α,∴∠PAQ=∠BAC﹣(∠BAP+∠CAQ)=α﹣(180°﹣α)=2α﹣180°;②当∠PAQ=90°,即2α﹣180°=90°时,PA⊥AQ,解得:α=135°,∴当∠BAC=135°时,能使得PA⊥AQ;③∵边AB、AC的垂直平分线交BC于点P、Q,∴AP=BP,AQ=CQ,∵BC=10cm,即BP+PQ+CQ=AP+PQ+AQ=10cm,∴△PAQ的周长为10cm.故答案为:①80,2α﹣180°;②135;③1018.解:在△ABE中,∵D是AB的中点,DE⊥AB于D交AC于E,∴AE=BE;在△ABC中,∵AB=AC=14cm,AC=AE+EC,又∵CE+BE+BC=24cm,∴BC=10cm19.解:(1)∵DE是线段AB的垂直平分线,∴AD=BD,∴AD+CD=BD+CD=AC,∵△DBC的周长为56,AC=32,∴BC=56﹣32=24;(2)∵AD=BD,AC=32,∴AD+CD=BD+CD=AC=32,∵BC=21,∴△DBC的周长=BD+CD+BC=32+21=53.故答案为:24;5320.解:(1)∵DF、EG分别是线段AB、AC的垂直平分线,∴AD=BD,AE=CE,∴AD+DE+AE=BD+DE+CE=BC,∵△ADE的周长为6cm,即AD+DE+AE=6cm,∴BC=6cm;(2)∵AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,∴OA=OC=OB,∵△OBC的周长为16cm,即OC+OB+BC=16,∴OC+OB=16﹣6=10,∴OC=5,∴OA=OC=OB=5.21.证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,∠EAD=∠FAD,∠AED=∠AFD=90°,∴∠EDA=180°﹣∠AED﹣∠EAD,∠FDA=180°﹣∠AFD﹣∠FAD,∴∠EDA=∠FDA,∵DE=DF(已证),∴DG垂直平分EF(三线合一),即AD垂直平分EF.22.证明:∵EF是AD的垂直平分线,∴AF=DF,∴∠FAD=∠FDA,∵∠FAD=∠FAC+∠CAD,∠FDA=∠B+∠BAD,∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠FAC=∠B23.解:(1)∵MP、NQ分别是AB、AC的垂直平分线,∴AP=BP,AQ=CQ,∴△APQ周长=AP+PQ+AQ=BP+PQ+QC=BC,∵BC=10,∴△APQ周长=10;(2)∵∠BAC=110°,∴∠B+∠C=180°﹣110°=70°,∵AP=BP,AQ=CQ(已证),∴∠BAP=∠B,∠CAQ=∠C,∴∠PAQ=∠BAC﹣∠BAP﹣∠CAQ=∠BAC﹣∠B﹣∠C=110°﹣70°=40°24.证明:(1)∵AD是BC的垂直平分线,∴AB=AC,BD=CD,∴∠ABC=∠ACB,∠DBC=∠DCB,∴∠ABD=∠ACD;(2)∵AB=AC,AD是BC的垂直平分线,∴∠BAD=∠CAD,∵DE⊥AB,DF⊥AC,∴DE=DF25.证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,在△ADE和△ADF中,,∴△ADE≌△ADF(HL),∴AE=AF,又∵AD平分∠BAC,∴AD垂直平分EF26.证明:如图,连接BD、CD,∵DE⊥BC,E是BC边上的中点,∴BD=CD,在△BDM和△CDN中,,∴△BDM≌△CDN(HL),∴DM=DN,又∵DM⊥AB,DN⊥AC,∴点D在∠BAC的平分线上.27.解:∵DE为AB的中垂线,∴AE=BE,∵FG是AC的中垂线,∴AG=GC,△AEG的周长等于AE+EG+GA,分别将AE和AG用BE和GC代替得:△AEG的周长等于BE+EG+GC=BC,所以△AEG的周长为BC的长度即7.故答案为:728.解:连接DB.∵点D在BC的垂直平分线上,∴DB=DC;∵D在∠BAC的平分线上,DE⊥AB,DF⊥AC,∴DE=DF;∵∠DFC=∠DEB=90°,在Rt△DCF和Rt△DBE中,,∴Rt△DCF≌Rt△DBE(HL),∴CF=BE(全等三角形的对应边相等).29.证明:∵DE为△ABC的边AB的垂直平分线,∴AD=BD,∵CD为△ABC的外角平分线,与DE交于D,DM⊥BC于M,DN⊥AC于N,∴DN=DM,在Rt△ADN和Rt△BDM中,,∴Rt△ADN≌Rt△BDM(HL),∴AN=BM.30.(1)证明:连结BD,CD.∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴∠AED=∠BED=∠AFD=90°,DE=DF.∵DE垂直平分BC,∴DB=DC.在Rt△DEB和Rt△DFC中,∴Rt△DEB≌Rt△DFC(HL),∴BE=CF;(2)解:在Rt△ADE和Rt△ADF中,,∴Rt△ADE≌Rt△ADF(HL).∴AE=AF.∵AB=AE+BE,∴AB=AF+EB,∴AB=AC+CF+EB.∵AB=8,AC=4,∴8=4+CF+EB,∴CF+EB=4,∴2EB=4,∴EB=2.∴AE=8﹣2=6.答:AE的长为6.。
七年级数学下册5.3.2线段垂直平分线练习

《线段垂直平分线》一、选择——基础知识运用1.到三角形三个顶点的距离都相等的点是这个三角形的()A.三条高的交点B.三条角平分线的交点C.三条中线的交点D.三条边的垂直平分线的交点2.如图,△ABC中,∠BAC=100°,DF,EG分别是AB,AC的垂直平分线,则∠DAE等于()A.50° B.45°C.30° D.20°3.如图,在△ABC中,DE是边AB的垂直平分线,BC=8cm,AC=5cm,则△ADC的周长为()A.14cm B.13cm C.11cm D.9cm4.已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是70cm和48cm,则△ABC的腰和底边长分别为()A.24cm和22cm B.26cm和18cm C.22cm和26cm D.23cm和24cm5.如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:甲:分别作∠ACP、∠BCP的平分线,分别交AB于D、E,则D、E即为所求;乙:分别作AC、BC的垂直平分线,分别交AB于D、E,则D、E两点即为所求.下列说法正确的是()A.甲、乙都正确 B.甲、乙都错误C.甲正确,乙错误 D.甲错误,乙正确二、解答——知识提高运用6.利用尺规作三角形的三条边的垂直平分线,观察这三条垂直平分线的位置关系,你发现了什么?再换一个三角形试一试。
7.如图,在△ABC中,∠C=40°,∠B=68°,AB、AC的垂直平分线分别交BC于D、E.求∠EAD 的度数。
8.在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N。
(1)求△AEN的周长;(2)求证:BE=EN=NC。
9.敌军基地在三条公路围成的三角区域内,我军一队战士在一条公路中点垂直射击,另一队战士在另一条公路中点垂直射击,均击中敌军基地,问第三队战士在公路何处垂直射击可击中目标?10.如图,已知在△ABC中,∠C=90°,AB的垂直平分线MN交BC于点D。
线段垂直平分线专题试题精选

线段垂直平分线专题试题精选一.解答题(共30小题)1.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.(1)求证:△ABD是等腰三角形;(2)若∠A=40°,求∠DBC的度数;(3)若AE=6,△CBD的周长为20,求△ABC的周长.2.如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于AC长为半径画弧,两弧相交于点M、N,连结MN,与AC、BC分别交于点D、E,连结AE,则:(1)∠ADE=°;(2)AE EC;(填“=”“>”或“<”)(3)当AB=3,AC=5时,△ABE的周长=.3.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:(1)FC=AD;(2)AB=BC+AD.4.如图,在四边形ABCD中,AD∥BC,对角线AC的中点为O,过点O作AC的垂线分别与AD、BC相交于点E、F,连接AF.求证:AE=AF.5.如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.(1)求证:OE是CD的垂直平分线.(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.6.如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于H.(1)求证:①△BCG≌△DCE;②BH⊥DE.(2)试问当点G运动到什么位置时,BH垂直平分DE?请说明理由.7.如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数.8.数学来源于生活又服务于生活,利用数学中的几何知识可以帮助我们解决许多实际问题.李明准备与朋友合伙经营一个超市,经调查发现他家附近有两个大的居民区A、B,同时又有相交的两条公路,李明想把超市建在到两居民区的距离、到两公路距离分别相等的位置上,绘制了如下的居民区和公路的位置图.聪明的你一定能用所学的数学知识帮助李明在图上确定超市的位置!请用尺规作图确定超市P的位置.(作图不写作法,但要求保留作图痕迹.)9.如图,在△ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于D,E.若∠CAE=∠B+30°,求∠AEB的度数.10.如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2,过点D作DE∥AB,交∠BCD的平分线于点E,连接BE.(1)求证:BC=CD;(2)将△BCE绕点C,顺时针旋转90°得到△DCG,连接EG.求证:CD垂直平分EG;(3)延长BE交CD于点P.求证:P是CD的中点.11.如图,已知DE是AC的垂直平分线,AB=10cm,BC=11cm,求△ABD的周长.12.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.(1)求∠ECD的度数;(2)若CE=5,求BC长.13.某公园有海盗船、摩天轮、碰碰车三个娱乐项目,现要在公园内建一个售票中心,使得三个娱乐项目所处位置到售票中心的距离相等,请在图中确定售票中心的位置.14.联想三角形外心的概念,我们可引入如下概念.定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.举例:如图1,若PA=PB,则点P为△ABC的准外心.应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD=AB,求∠APB的度数.探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA 的长.15.在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交BC于M,交AB于E,AC 的垂直平分线交BC于N,交AC于F,求证:BM=MN=NC.16.已知:如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线MN分别交BC,AB于点M,N,求证:CM=2BM.18.如图,在梯形ABCD中,AD∥BC,E为CD中点,连接AE并延长AE交BC的延长线于点F(1)求证:CF=AD;(2)若AD=2,AB=8,当BC为多少时,点B在线段AF的垂直平分线上,为什么?19.如图所示,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC边上的中点,CE⊥AD于点E,BF∥AC交CE的延长线于点F,求证:AB垂直平分DF.20.在△ABC中,AB边的垂直平分线交直线BC于点D,垂足为点F,AC边的垂直平分线交直线BC于点E,垂足为点G.(1)当∠BAC=100°(如图)时,∠DAE=°;(2)当∠BAC为一任意角时,猜想∠DAE与∠BAC的关系,并证明你的猜想.21.如图所示,在△ABC中,DE是边AB的垂直平分线,交AB于E,交AC于D,连接BD.(1)若∠ABC=∠C,∠A=50°,求∠DBC的度数.(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.22.如图,在△ABC中,AD为∠BAC的平分线,FE垂直平分AD,交AD于E,交BC 的延长线于F,那么∠B与∠CAF相等吗?为什么?23.如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB、BC延长线于F、E.求证:(1)∠EAD=∠EDA;(2)DF∥AC;(3)∠EAC=∠B.24.如图,在△ABC中,DE,FG分别是AB,AC的垂直平分线,连接AE,AF,已知∠BAC=80°,请运用所学知识,确定∠EAF的度数.25.如图,已知:在△ABC中,∠BAC=90°,延长BA到点D,使AD=AB,点G、E、F分别为边AB、BC、AC的中点.求证:DF=BE.26.如图,DE是△ABC边AB的垂直平分线,分别交AB、BC于D、E.AE平分∠BAC.设∠B=x(单位:度),∠C=y(单位:度).(1)求y随x变化的函数关系式,并写出自变量x的取值范围;(2)请讨论当△ABC为等腰三角形时,∠B为多少度?27.在△ABC中,AD是高,在线段DC上取一点E,使BD=DE,已知AB+BD=DC,求证:E点在线段AC的垂直平分线上.28.已知:在梯形ABCD中,AD∥BC,CA平分∠DCE,AB⊥AC,E为BC的中点.求证:DE、AC互相垂直平分.29.如图,在△ABC中,BC=AC,∠ACB=90°,D是AC上一点,AE⊥BD交BD的延长线于点E,且AE=BD,求证:BD是∠ABC的角平分线.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二课型 精讲点拨
学习目标:
1、 能利用轴对称图形的特点,补全简单
的轴对称图形,能掌握两个图形关于某条直线成轴对称和轴对称图形的区别与联系.
2、 能掌握线段垂直平分线的概念与性
质.
3、 能利用过一点作已知直线的垂线解决
问题,如“解决最短路径问题”.
第三学段 精讲点拨
题型一:轴对称图形的概念
例1、下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )
A .
B .
C .
D .
同步练习: 下面四个多边形:等边三角形,正方形,梯形,正六边形.其中是轴对称图形的个数有( )
A .1个
B .2个
C .3个
D .4个 题型二:作轴对称图形的对称轴 例2、如图所示的图形分别有几条对称轴?分别画出它们的对称轴
.
同步练习: 1、如图,AB 左边是计算器上的数字“5”,若以直线AB 为对称轴,那么
它的轴对称图形是数字
.
2、求作△ABC 关于对称轴l 的轴对称图形△A B C '''
.
题型三:线段垂直平分线的性质 例3、如图,在△ABC 中,AB =AC =14 cm,AB 的垂直平分线MN 交AC 于点D ,△DBC 的周长为24cm ,则BC =
.
分析:
同步练习:如图,AC 垂直平分BD ,垂足为E ,连接AB ,BC ,CD ,AD ,下列结论不一定成立的是( )
A .AB=AD
B .A
C 平分∠BCD
C .AE=CE
D .△BEC ≌△DEC
题型四:应用线段垂直平分线性质解决最短路径问题
例4、如图,直线m 表示一条公路,,A B 表示两所大学,要在公路旁修建一个车站P 使到两所大学的距离相等,请在图上找出这点P
.
分析:
同步练习:课本50页“挑战自我”. 三、合作学习 展示反馈(依据学情)
第四学段 训练二(检测)
一、 题型练习(共5题,1-4题每题5分,5题10分,共30分)
1、下列说法中错误的是( ) A .过“到线段两端点距离相等的点”的直线是线段的垂直平分线
B .线段垂直平分线的点到线段两端点的距离相等
C .线段有且只有一条垂直平分线
D .线段的垂直平分线是一条直线 2、如图,已知在△ABC 中,AD 垂直平分BC ,AC=EC ,点B 、D 、C 、
E 在同一直线上,则AB DB +与DE 之间的关系是() A .AB DB DE +> B .AB DB DE +< C .AB DB DE += D .以上都不对
第2题 第3题
3、如图,CD 是线段AB 的垂直平分线,若AC=1.6cm ,BD=2.3cm ,则四边形ABCD 的周长是______cm .
4、下列图形:①角;②线段;③等边三角形;④有一个角为30°的直角三角形中
是轴对称图形的有(填序号)______.
5、如图,在△ABC 中,BC=10,AB 、 AC 的垂直平分线分别交BC 于点D 、E, 求△ADE 的周长.
三、展示反馈(依据学情)
第二课型课后巩固练习
1.下列奥运会会徽的图案中是轴对称图形的是()
A.B.C. D.
2.下列结论错误的是()
A.等边三角形是轴对称图形
B.轴对称图形的对应边相等,对应角相等
C.成轴对称的两条线段必在对称轴同侧
D.成轴对称的两个图形的对应点的连线被对称轴垂直平分
3.如图,△ABC中,BC=10,DH为AB的中垂线,EF垂直平分AC,则△ADE的周长是()A.6 B.8 C.10 D.12
第3题第4题
4.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为()
A.30°B.40°C.50°D.60°
5.在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有______个.
第5题第6题
6.两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有______.(填序号).
①AC⊥BD;②AC、BD互相平分;③AC平分∠BCD;④∠ABC=∠ADC=90°;⑤筝形ABCD的面积为.
7.如图,某住宅小区拟在休闲场地的三条道路上修建三个凉亭A、B、C且凉亭用长廊两两连通.如果凉亭A、B的位置己经选定,那么凉亭C建在什么位置,才能使工程造价最低?请用尺规作出图形(不写作法,但保留作图痕迹),并简要说明理由.
8.如图,△ABC中,∠BAC=110°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)如果BC=10cm,求△DAF的周长.
9.如图,已知:△ABC中,BD、CE分别是AC、AB边上的高,G、F分别是BC、DE 的中点.
(1)试探索FG与DE的关系.
(2)ED=7,BC=12,求△EGD的周长.。
