超高渐变长度计算
超高加宽公式

△Y=D(各段距离)×SIN(X)(距离对应的角度)增量改正计算:Fx=∑△x测Fy=∑△y测Vxi=[﹣Fx/∑D(距离总和)]×D(各段距离)Vyi=[﹣Fy/∑D(距离总和)]×D(各段距离)既得各段增量值线性超高公式:I=(Z-C)*(N-M)÷S+MN为超高段终点横坡,无则不输,M为超高起点横坡,Z待求桩号,C超高渐变段起点桩号,无则不输.S为超高渐变段长度。
三次抛物线超高公式:I=(3K²-2K³)*(N-M)+M K=(Z-C)÷SN为超高段终点横坡,无则不输,M为超高起点横坡,Z待求桩号,C超高渐变段起点桩号,无则不输.S为超高渐变段长度。
线性加宽公式:BX=(Z-C)*(B-A)÷S+AB为加宽段终点宽度,无则不输,A为加宽段起点宽度,Z待求桩号,C渐变段起点桩号,无则C=Z。
S为加宽渐变段长度,无则不输。
三次抛物线加宽公式:BX=(3K²-2K³)*(B-A)+A K=(Z-C)÷SB为加宽段终点宽度,无则不输,A为加宽段起点宽度,Z待求桩号,C加宽渐变段起点桩号,无则C=Z。
外矢距计算公式: L=T2/2R切线长计算公式:T=1/2*R*(I前-I后)凹曲线任一点计算公式:H =E+Abs(Q-C)*I + L凸曲线任一点计算公式:H =E-Abs(Q-C)*I - L说明:H=所求点高程,E=竖曲线交点高程,Q=起点桩号,C=所求点桩号I=线路纵坡坡率,计算前坡时用I前,计算后坡时用I后,S为加宽渐变段长度,无则不输。
基本导线测量的内业计算一、基本计算导线内业计算包括角度闭合差的计算和调整、方位角的推算、坐标增量闭合差的计算和调整及未知点的坐标计算。
1、角度闭合差的计算和调整!)角度闭合差计算:a)附合导线:CD的方位角推算值与其已知值若不等,其差值即称为角度闭合差。
超高设置与计算说明

超高设置与超高加宽计算说明一、超高设置1、《JTG D20-2006公路路线设计规范》取消了《JTJ 011-94公路路线设计规范》中的“圆曲线半径与超高值”表,各圆曲线半径所设置的超高值应根据设计速度、圆曲线半径、公路条件、自然条件等经计算确定。
路线程序根据《JTG D20-2006公路路线设计规范》送审稿提供的“圆曲线半径与超高值”表编制了圆曲线半径、设计速度等计算超高值的表格模板。
用户可以结合项目情况修改表格模板,该表格模板存储在路线程序安装目录下的“superelevation”文件夹中。
表5 最大超高值10%2、在超高自动计算前,用户可以先进行超高设置,程序中的命令:[数据处理]→[超高分段] →[超高值设置],设置窗体如图1图1 超高值设置3、路线程序根据最大超高值自动选用相应的表,若用户需要修改表格模板可点击“浏览”按钮弹出表格模板,然后修改表格模板。
点击“确定”按钮后,程序就会把用户设置的超高值存入数据库,超高自计算就会以用户设置的超高值进行计算。
若用户不进行超高设置,程序会按程序内默认的超高值进行计算。
4、表格模板格式不能修改,只能修改模板中的数据。
二、超高计算命令:[数据处理]→[超高分段] →[自动计算]图2 超高自动计算1、超高自动计算窗体说明(如图2)1、1 当选中窗体中的“全缓和曲线范围内超高”,程序不考虑渐变率计算的超高缓和长度,默认超高在缓和曲线上完成;反之考虑渐变率计算的超高缓和长度。
1、2 当选中窗体中的“S型曲线YH(HY)全超高”,程序认为S型曲线YH(HY)刚好达到全超高,然后向GQ点推;反之由GQ点向YH(HY)推。
1.3 当选中窗体中的“S型曲线公切点横坡0%”,则公切点超高为0%,若未选中,则公切点为正常路拱。
2、超高自动计算时,线元划分成如下单元进行计算:2、1直线——圆曲线和圆曲线——直线(1)中间没有缓和曲线,超高缓和长度直线和圆曲线上各一半。
超高过渡段长度计算

超高过渡段长度计算
超高过渡段长度是指在高速公路上,为了使车辆从平稳路段过渡到下坡路段或上坡路段时,设置的特殊路段长度。
其长度可通过以下公式计算得出:
超高过渡段长度 = (车辆行驶速度/重力加速度)×(车辆高度差/道路曲率半径)
其中,车辆行驶速度是指车辆在进入超高段前的平稳路段上的速度;重力加速度为9.81m/s²;车辆高度差是指车辆在通过超高段时,车辆底部与路面之间的高度差;道路曲率半径为超高段所在路段的曲率半径。
需要注意的是,在实际计算中,应该将超高段的长度向上取整,确保车辆能够平稳通过超高段,保证行车安全。
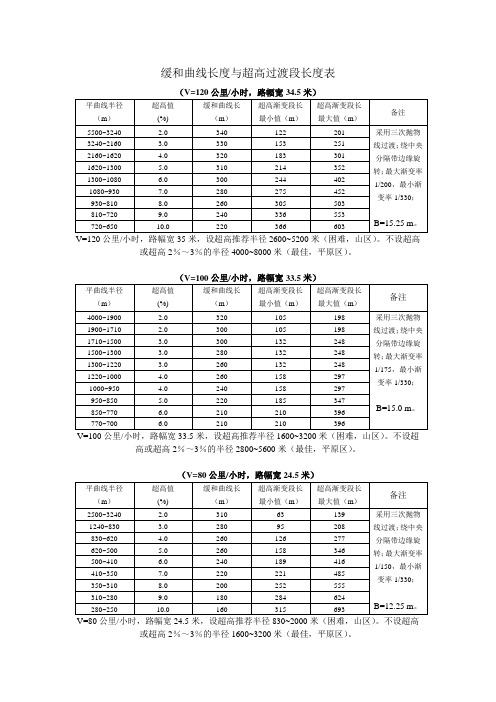
缓和曲线长度与超高过渡段长度表
132
248
1500~1300
3.0
280
132
248
1300~1220
3.0
260
132
248
1220~1000
4.0
260
158
297
1000~950
4.0
240
158
297
950~850
5.0
220
185
347
850~770
6.0
210
210
396
770~700
6.0
210
210
396
V=100公里/小时,路幅宽33.5米,设超高推荐半径1600~3200米(困难,山区)。不设超高或超高2%~3%的半径2800~5600米(最佳,平原区)。
693
V=80公里/小时,路幅宽24.5米,设超高推荐半径830~2000米(困难,山区)。不设超高或超高2%~3%的半径1600~3200米(最佳,平原区)。
超高渐变段长最小值(m)
超高渐变段长最大值(m)
备注
4000~1900
2.0
320
105
198
采用三次抛物线过渡;绕中央分隔带边缘旋转;最大渐变率1/175,最小渐变率1/330;
B=15.0 m。
1220 m以上不能在全长范围内超高过渡
1900~1710
2.0
300
105
198
1710~1500
3.0
(V=80公里/小时,路幅宽24.5米)
平曲线半径
(m)
超高值
(%)
缓和曲线长
(m)
超高渐变段长最小值(m)
超高渐变段长最大值(m)
高速公路曲线上超高值计算PPT课件

从直线上的双向横坡逐渐过渡到圆曲线上的超高横坡的过渡段,称为超高缓和段。
b b 超高值计算方法——双坡断面(x≤L 1)
jx j 旋转阶段:当外侧路面变成与内侧相同的单向内倾横坡后,路面保持内侧边缘不动,整个路面绕内边缘向上旋转,直到缓和段终点,
b jx
x Lc
bj
Image
超高值计算方法——旋转断面(X>L 1)
超高值计算方法——双坡断面(x≤L 1)
超高值计算方法——圆曲线段的全超高断面
x h ai ( a b ) i 超高值计算方法——旋转断面(X>L 1)
w
2
x
i i 从直线上的双向横坡逐渐过渡到圆曲线x 上的超高横坡的b 过渡段,称为超高缓和段。
曲线上的超高值计算——例题
某公路的计算行车速度V=40km/h,路基宽为, 现有一弯道曲线半径R=200米,超高横坡度 ib=6%,行车道路拱横坡为i1=2%,路肩横坡为 i2=3%,采用绕路面内边轴旋转的方法设置超高, 超高渐变率p=1/100,圆曲线的加宽值米,计算 超高缓和起点和距超高缓和起点15米处、全超 高断面和距超高缓和起点30米处路基内侧、路 中线、路基外侧的超高值。
坡阶段长度L1,根据超高渐变的要求,路拱 坡度变化也是按离开缓和段起点的距离呈正
比变化的
L1
i1 ib
Lc
超高形成过程——旋转阶段
旋转阶段:当外侧路面变成与内侧相同的单
向内倾横坡后,路面保持内侧边缘不动,整 个路面绕内边缘向上旋转,直到缓和段终点, 路面达到超高横坡度ib,即达到圆曲线的全 超高阶段。
曲线上的超高值计算——计算步骤
首先计算超高缓和段的长度 计算L1的长度 判断所求位置位于双坡阶段还是位于旋转
S型曲线间的超高过渡
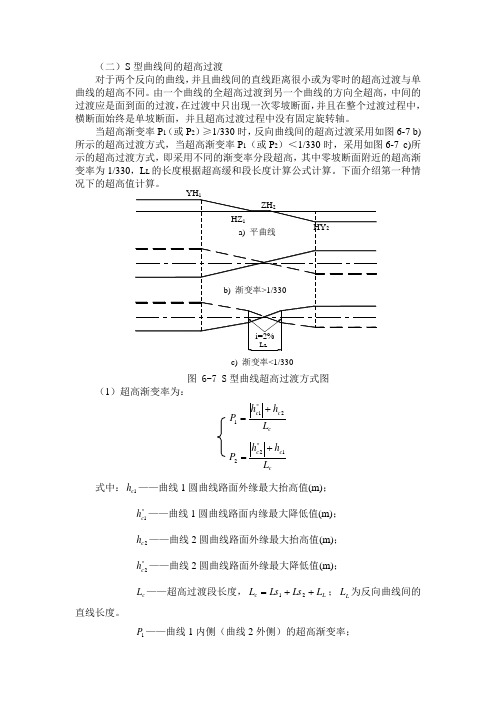
(二)S 型曲线间的超高过渡 对于两个反向的曲线,并且曲线间的直线距离很小或为零时的超高过渡与单曲线的超高不同。
由一个曲线的全超高过渡到另一个曲线的方向全超高,中间的过渡应是面到面的过渡,在过渡中只出现一次零坡断面,并且在整个过渡过程中,横断面始终是单坡断面,并且超高过渡过程中没有固定旋转轴。
当超高渐变率P 1(或P 2)≥1/330时,反向曲线间的超高过渡采用如图6-7 b)所示的超高过渡方式,当超高渐变率P 1(或P 2)<1/330时,采用如图6-7 c)所示的超高过渡方式,即采用不同的渐变率分段超高,其中零坡断面附近的超高渐变率为1/330,L L 的长度根据超高缓和段长度计算公式计算。
下面介绍第一种情况下的超高值计算。
图 6-7 S 型曲线超高过渡方式图(1)超高渐变率为:c c c L h h P 2''11+=cc c L h h P 1''22+=式中:1c h ——曲线1圆曲线路面外缘最大抬高值(m);''1c h ——曲线1圆曲线路面内缘最大降低值(m); 2c h ——曲线2圆曲线路面外缘最大抬高值(m); ''2c h ——曲线2圆曲线路面外缘最大降低值(m);c L ——超高过渡段长度,Lc L Ls Ls L ++=21;L L 为反向曲线间的直线长度。
1P ——曲线1内侧(曲线2外侧)的超高渐变率;c) 渐变率<1/3302P ——曲线2内侧(曲线1外侧)的超高渐变率。
(2)零坡断面位置计算21''110P P h h x c c +-=式中:0x ——零坡断面距曲线1的 YH 点的距离(m); 其余同前。
(3)任意点超高值计算S 型曲线间超高过渡超高值计算公式 表6-17。
高速公路竖曲线及超高渐变段高程计算研究
在高速公路纵断面设计中 , 需要计算 出中心点以 及两边线点设计高程 , 在现场施工 中, 也需要计算许 多点 的纵断面设计高程。用手工逐一计算 , 工作量极
大 , 用 Ecl 大 的编 辑 、 算 功能 , 利 xe强 计 将变 坡 点里 程 、
参数 , 参数输入完成即可计算 。
变坡点高程、 凸竖曲线和凹竖曲线半径输入设计好 的 公式中, 计算各个设计 中心 点设计 高程 、 两边 线超高 高程等则能节省时间和资金 , 提高工作效率 。 。
M1 5
纵 坡竖 直 角 t ( ) M1 =A A 2。, 5 T N(¥ ¥ /0 ) M 9 10
1 0 P ( 8/ I )
t an
13 竖 曲线主点桩号与设计高程计算 .
竖 曲线 主点 桩号 与 设计 高 程计 算 见 表 3 。
表 3 竖 曲线主点桩 号与设计 高程计算表
(¥G¥ 2一 {C¥2 )¥10 } ) 0
△ 1一 r 2 1
( 直圆点高程 )
z 圆直点桩号 ) (
M1 9
M2O
H 圆直点 高程 ) (
J :t ~1 『 a i 1 n I
,= tn , a ~iJ
:
M1 7= ¥C ¥2— 3M ¥1 C S(¥M ¥1 :P 5 0 O 4l I :
Байду номын сангаас
¥F¥2 T N( B A A S(¥M ¥1 P () ( 2) I /2 反 之 T= ¥E¥2 T AN( B A S(¥M ¥1 P 2) I
(/8 ) ) 10
M2 0= 3D 82+ 3M ¥1 :SN(¥M ¥1 P 5 5 0I I : 5 I
1 0 ) 8) , ( / 2¥1 0 ) )( 8 ) M1 0=I F(¥E ¥2=” ”,¥F ¥2 ¥T AN( S AB
公路超高缓和段长度的计算公式
公路超高缓和段长度的计算公式为:Lc=B’×i/p超高横坡在超高缓和段内按三次抛物线计算:i=i1+(i2 -i1)*(3-2*(1/ Ls))*(1/ Ls)^2 (三)超高缓和段长度的确定为了行车的舒适、路容的美观和排水的通畅,必须设置一定长度的超高缓和段,超高的过渡是在超高缓和段全长范围内进行的。
双车道公路超高缓和段长度按下式计算:(1.4.19)式中:——超高缓和段长(m);——旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m);——超高坡度与路拱坡度的代数差(%);——超高渐变率,即旋转轴与行车道(设路缘带时为路缘带)外侧边缘之间的相对坡度,其值见表1.4.11。
前面讲到缓和曲线,已经考虑到超高缓和段所需的最短长度。
所以一股情况下,超高缓和段与缓和曲线长度相等。
但有时因照顾到线形的协调性,在平曲线中配置了较长的缓和曲线,则超高的过渡可仅在缓和曲线某一区段内进行。
因为过小的渐变率对路面排水不利。
从利于排除路面降水考虑,横坡度由2%(或1.5%)过渡到0%路段的超高渐变率不得小于1/330。
(四)超高值的计算平曲线上设置超高以后,道路中线和内、外侧边线与原中线上的设计标高之高差h,应予以计算并列于“路基设计表”中,以便于施工。
这些超高值的计算公式见教材表1.4.12和表1.4.13,计算图式见教材图1.4.17和图1.4.18。
三、路基土石方调配土石方调配的目的是为确定填方用土的来源、挖方弃土的去向,以及计价土石方的数量和运量等。
通过调配合理地解决路段土石方平衡与利用问题,使从路堑挖出的土石方,在经济合理的调运条件下移挖作填,达到填方有所“取”,挖方有所“用”,避免不必要的路外借土和弃土,以减少占用耕地和降低公路造价。
(一)土石方调配原则.1.在半填半挖断面中,应首先考虑在本路段内移挖作填进行横向平衡,然后再作纵向调配,以减少总的运输量。
2.土石方调配应尽量考虑桥涵位置对施工的影响,一般大沟不作跨越调运,同时尚应注意施工的可能与方便,尽可能避免和减少上坡运土。
超高讲解与程序
1.超高方式3种①绕路面内边缘旋转(常用)②绕路面中心线旋转(多用于旧路改建,以便控制中线标高)③绕路面外边缘旋转(路基很高或从路容考虑时才可能采用)2.超高缓和段长度Lc=B*▵i÷P(B为旋转轴到外侧路边缘距离,▵i为超高度与旋转轴外侧路拱度之代数差,P为超高渐变率,一般来说Lc采用缓和曲线长度L1)3.超高值的计算⑴第一种方式(内副路面坡度保持不变,外副路面绕路中心线旋转,旋转至和内副路面同坡度时,全副路面绕内边缘旋转到超高度。
)①正常断面h中=a*i2+b/2*i1 h内=h外=0②提肩断面(距缓和段起点1-2m内完成提肩。
即路肩坡度和路面坡度一致)h中=a*i2+b/2*i1 h内=h外=a(i2-i1)③双坡断面h内=a*i2-(a+e x)*i1 (e x=x/Lc*e) (e为加宽值,x为缓和段内任意计算点到缓和起点的距离。
)h中=a*i2+b/2*i1h外=h1*x/L1+a(i2-i1) ( L1=i1/ib*Lc h1=(b+2a)*i1 )④旋转断面(X≥L1)h内=a*i2-(a+e x)*i x (i x=x/Lc*i b;i b为超高)h中=a*i2+b/2*i xh外=a*i2+(a+b)*i x⑤全超高断面h内=a*i2-(a+e x)*i bh中=a*i2+b/2*i bh外=a*i2+(a+b)*i b⑵第二种方式(内副路面坡度保持不变,外副路面绕路中心线旋转,旋转至和内副路面同坡度时,全副路面绕路中心线旋转到超高度。
)①正常断面h中=a*i2+b/2*i1 h内=h外=0②提肩断面(距缓和段起点1-2m内完成提肩。
即路肩坡度和路面坡度一致)h中=a*i2+b/2*i1 h内=h外=a(i2-i1)③双坡断面h内=a*i2-(a+e x)*i1 (e x=x/Lc*e)h中=a*i2+b/2*i1h外=h1*x/L1+a(i2-i1) ( L1=2*i1/(i b+i1)*Lc h1=(b+2a)*i1 ) ④旋转断面(X≥L1)h内=a*i2+b/2*i1-(a+e x+b/2)i x ( i x=x/Lc*i b-(Lc-x)/Lc*i1 ) h中=a*i2+b/2*i1h外=a*i2+b/2*i1+(a+b/2)i x⑤全超高断面h内=a*i2+b/2*i1-(a+e+b/2)*i bh中=a*i2+b/2*i1h外=a*i2+b/2*i1+(a+b/2)*i bFx-5800平曲线超高、加宽计算程序(已测试)CG --- JKLbI 0:CIs:“ZH”?C:“HZ”?E:“LBK”?A:“I1”?B:“IC”?P:“Z-1,Y+1”?Z:“LS1”? G:“LS2”? N:“JK”?X←LbI 1 :CIs:DO:“CD,<0=>Return”?S: “SJBG=”?Y:If S<0 Or S>E:Then Goto 0:If End ←G=0=>Goto5 ←N=0=>Goto5 ←S<C=>Goto5 ←S>E=>Goto5 ←S>C+G=>Goto2 ←0.04G÷(P+B)+C→H:(S-C)÷G→L:L(P+B)-B→I: LX+A→J←If S<H:Then -BJ→D:AI→F:EIse -IJ→D:AI→F:If End ←Goto4←LbI 2 :S>E-N=>Goto3 ←X+A→J:-P(A+X)→D:AP→F:Goto4 ←LbI 3 :E-0.04N÷(P+B)→K:(E-S)÷N→L:LX+A→J:L(P+B)-B→I←If S<K:Then -IJ→D:AI→F:EIse -BJ→D:AI→F:If End ←Goto4←LbI 4:If Z<0:Then J→H:A→K:D→L:F→M:Goto6:If End ←If Z≥0:Then A→H:J→K:F→L:D→M:Goto6:If End ←LbI 5 :A→H:A→K:-BA→L:-BA→M:Goto6←LbI 6:CIs←“ZK=”:Locate 4,1,H◢“YK=”:Locate 4,2,k◢“Z-H=”:Locate 5,3,L◢“Y-H=”:Locate 5,4,M◢“HL=”:Y+L◢“HP=”:Y◢“HR=”:Y+M÷K*L◢“IZ(%)=”:L÷H*100◢“IY(%)=”:M÷K*100◢Goto1←说明:该程序适用于绕中轴旋转的一、二级公路,三、四级公路设计I 类加宽可用,II 类加宽需将LbI 3 =(4L^3-3L^4)X+A→J改为LX+A→J 即可。
超高过渡
公路超高过渡一、低等级公路超高计算【示例1】山岭重丘区某新建二级公路,设计速度为40km/h,其中一平曲线半径R=150m,缓和曲线Ls=70m,路面宽度为B=7.0m,路肩宽度为0.75m,路拱坡度为iG=2%,路肩坡度iJ=3%,该曲线的主点桩号分别为:ZH=K1+028.665 、HY=K1+098.665 、QZ=K1+131.659 、YH=K1+164.653 、HZ=K1+234.653。
试计算各主点桩以及下列桩号:K1+040、K1+070、K1+180、K1+210处横断面上内外侧和路中线三点的超高值(设计高为路基边缘)。
(1)确定超高缓和段长度根据公路等级、设计速度和平曲线半径查表得圆曲线的超高值iy=5%,新建公路一般采用绕边线旋转,超高渐变率p=1/100,所以超高缓和段长度:Lc=B'△i/p=7×5%/(1/100)=35.0(m)而缓和曲线Ls=70m,先取Lc=Ls=70m,然后检查横坡从路拱坡度(-2%)过渡到超高横坡(2%)时的超高渐变率:p=3.5×[2%-(-2%)]/X0=3.5×[2%-(-2%)]/28=1/200>1/330或p=7×5%/70=1/200>1/330所以取Lc=Ls=70m。
(2)计算临界断面x0X0=iG/ih×Lc=2%/5%×70=28.0m(3)计算各桩号处的超高值超高起点为ZH(HZ)点,分别计算出x值,然后分别代入超高值计算公式(见《道路勘测设计》书)中计算,加宽过渡采用比例过渡,加宽值b=1.0m。
土路肩在超高起点前1m变成与路面相同的横坡,且在整个超高过过渡段保持与相邻行车道相同的横坡。
计算结果见下表。
超高值计算结果表桩号x 加宽值bx 外侧超高值中线超高值内侧超高值K1+028.665(ZH)0.000<x0=28 0.000 0.008 0.093 0.008+040 11.335< x0=28 0.162 0.073 0.093 0.004+070 41.335 >x0=28 0.591 0.245 0.126 -0.017+098.665(HY) 1.000 0.410 0.198 -0.065+131.659(QZ) 1.000 0.410 0.198 -0.0651+164.653(YH) 1.000 0.410 0.198 -0.065+180 54.653> x0=28 0.781 0.322 0.159 -0.037+210 24.653< x0=28 0.352 0.149 0.093 0.000+234.653(HZ)0.000< x0=28 0.000 0.008 0.093 0.008(已知第一段坡度i1,第二段坡度i2,过度段长度l,待求点离第二横坡距离xa=x/l待求点i=(i2-i1)(1-3a2+2a3)+i1)二.超高缓和段长度计算超高缓和段的长度按下式计算:Lc=B'×△i/P式中:Lc——超高缓和段长度(m);B' ——旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m);△i——旋转轴外侧的超高与路拱坡度的代数差;P ——超高渐变率,其值根据计算行车速度和超高过渡方式从下表中查取。
