2-3节点分析法
合集下载
节点分析法
补： uB uD 8
UB 8
1
11
10
UA
4
UB
(1
4
5 )U Dຫໍສະໝຸດ 111四、无伴的理想电压源处理
方法3：含有两条无伴电压源支路的，将一条 电压源支路的一端接地；设另一条理想电压源 支路的电流，将此电流暂当作电流源电流列写 方程，并利用理想电压源与相应节点电位关系 补充方程。
12
例9 ：求图示电路中电流i。
电阻不计自电导与互电导）
解： 选择参考节
A
UA
点， 列写方程：
I1
I2
I3
(1 10
1 4
1 2 )uA
1.6
70 2
1.6 70
uA
(
1
2 1 1)
10 4 2
若电路只有一个独立节点，其节点
43.06V
I1 =-4.306A I2 = 10.76A
电压方程为： u
I3 = -13.47A
Rs Us
(1)
图(1)伏安关系:
u = Us - iRs
图(2)伏安关系:
Is
u = (Is - i) Rs'
= Is Rs ' - i Rs '
Rs'
(2)
等效变换关系： Us = Is Rs′ Rs= Rs′
4
三、节点分析法： 依据：KCL
支路VCR UA
UB
UC
步骤：
1、选择参考节点，
标出其余节点电压
I sk Gk ( 弥尔曼定理)
9
四、无伴的理想电压源处理
方法1： 含有一条无伴电压源支路的，可选合 适的参考节点使理想电压源成为一个已知节点 电压，列写其余节点电压方程。
电路分析基础 5节点分析
注意事项：
1、参考点的选择：a、最多支路的连接点；
b、将电压源的一端作为参考点。
2、若电压源有串联电阻时，则先做戴维南到诺顿 等效变换。若电压源无串联电阻且两端都不是参考点 时，需给电压源支路设电流，并增加方程。
3、有受控源时，一般要有补充方程：控制量用 节点电压表示。
4、电流源支路上串有电阻，冗余元件
§2-3 节点分析法 (可用于非平面电路分析）
一、节点方程的建立
节点电压（位）： 必须选定参考点。
1、节点电压的独立性:n-1个节点电压线性无关 2、节点电压的完备性：支路电压可用节点电压 表示出来
建立节点方程
(G1 G2 )U a G2Ub G1U c I s1 G2U a (G2 G3 G4 )Ub G3U c 0 G1U a G3Ub (G1 G3 )U c I s2
一
般 G11U1 G12U2 ... G1n1Un1 Is11
形 式
n 个
G21U1 G22U2 ... G2n1Un1 Is22 ...
节 Gn11U1 Gn12U2 ... Gn1n1Un1 Isn1n1
点
或矩阵形式：
G11
G21
.....
G(n1)1
G12 G22 .... G( n 1) 2
要点与难点 理想电压源支路的处理；受控电源的处理
例5、求ua
+us1 R1
ua
+us2 R2
-us3
R3
R4
例6 求：U，I= ?
解：(1)选定参考点， 标出节点电压
(2)列节点方程
U a 12(V )
解得
UUcb
6(V ) 4(V )
U e 5(V )
电路分析之节点法
§2-2节点（电压）分析法1.为什么要引入节点（电压）分析法目的：2.什么是节点（电压）分析法3.参考节点4.节点（电压）分析法具体步骤5.特殊情况使用支路分析法时，独立方程数目与支路数相等，当电路的支路数很多而节点较少时，使用支路分析法仍要解很多方程，是否有办法可使方程数减少呢？一、引入2、目的：1、原因：减少电路方程的数目。
3、如何实现？二、节点分析法1.指导思想：用未知的节点电压代替未知的支路电压来建立电路方程。
2.节点电压：独立节点对非独立（参考）节点的电压。
对于有n个节点的电路，只有（n－1）个独立的节点。
3.节点分析法：用KCL建立节点电流方程，然后用节点电压去表示支路电流，最后求解节电电压的方法。
注意：这里“节点”的含义（1）从节点出发（KCL），（2）用节电电压作变量①选参考节点；标出各支路电流参考方向和节点电压。
②对独立节点列节电电流方程[（n－1）个]。
③通过KVL和元件特性用节点电压表示支路电流。
④将以节点电压表示的支路电流代入步骤（2）中的节点方程，整理后可得以节点电压为变量的规范化的电路方程。
三、具体步骤和注意事项：1.解题步骤R4i4例说明：⎧u u 111111其它量类似。
当支路含有电流源时，该支路等效电流源就是电流源本身；当支路含有的是有伴电压源时，该支路等效电流源大小为电压源与该支路电导的乘积，方向与电压源为非关联。
有伴电压源支路等效电流源与该支路电流不同（等效电流源只是该支路电流的一部分）。
等效电流源：注意：G kk —是连接到节点k 的各支路电导的总和，称为节点k 的自电导，总为“＋”。
G kj —是联接节点k 和节点j 的各支路电导之和的“－”值，称为节点i 和节点j 的互电导。
I Sk —是流入节点k 的各等效电流源电流的代数和（流入为“＋”，流出为“—”）。
I Sk ＝i S1＋…＋i Sj +…其中:对于任何具有n个独立节点的电路，有n个方程且每个节点方程可由下述方程描述:自导×本节点电压＋∑互导×相邻节点电压＝∑(±电压源×该支路电导)＋∑±电流源 具体为，对第k个独立节点，节点方程为:节点k ：G k1u 1+…+G kk u k +…+G kn u n =I S k2、注意事项1)各支路中的电导应该是该支路中的总电导。
2-3节点分析法
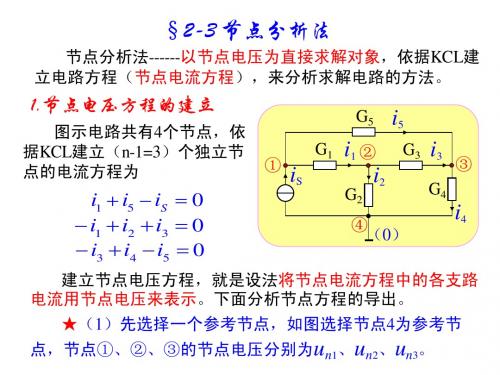
再令
iS11 iS iS 22 0 iS 33 0
G5 ① G1
i5
G3
iS
i1 ② i2
G2
i3
G4
③
④ （0）
i4
注意到: iS11、iS22、iS33分别是电源输入给节点①、节点②、节点 ③的电流的代数和（流入节点取 “ + ”，从节点流出取 “－”） 节点电压方 程可改写成
G11 un1 G12 un 2 G13 un3 iS11 G21 un1 G22 un 2 G23 un3 iS 22 G31 un1 G32 un 2 G33 un3 iS 33
[例题]列出图示电路的节点方程 解：（1）设参考节点如图所示 （2）列节点方程
自电导 互电导
①
6A
②
1 1 1 1 G11 ; G22 6 3 2 2 G12 0 ; G21 0
2Ω 2A (0)
6Ω
3Ω
电源输入给节点的电流的代数和
列节点方程
iS11 2 6 8 iS 22 6
i4
G1 G5 G11
G11为节点①的自电导，是所有 与节点①相连支路的电导之和 G22为节点②的自电导，是所有 与节点②相连支路的电导之和 G33为节点③的自电导，是所有 与节点③相连支路的电导之和
G1 G2 G3 G22
G3 G4 G5 G33
G5 ① G1
i5
3I
un1 12
列节点方程
1 1 1 u 3I un1 n2 4 4 2
③
节点方程中含有 I ，因为 I 是受控电流源的控制量，它也是
一个未知量，所以必须补充一个方程，需将 I 用节点电压表示。
第5讲 电阻电路的分析-节点法、电源转移
IS2
n2 US3 G7 G6 n4 US8 G3 I8 n3
3
4
n1
I1
G5 G4 n5
US1
− G6U n1 − (G3 + G7 )U n 2 + (G3 + G4 )U n 3 + (G5 + G6 + G7 )U n 4 = −G3U S 3
n2 (G3 + G7 )U n 2 − G3U n 3 − G7U n 4 = I S 2 + G3U S 3
1 A 5
I 4 = (U n 4 − U n 2 + U S 4 )G4 =
1
4.含受控源的节点电压法 4.含受控源的节点电压法
R1 US1
§2-4 节点电压法( 节点电压法(节点分析法) 节点分析法)
µU12
§2-4 节点电压法( 节点电压法(节点分析法) 节点分析法)
4.含受控源的节点电压法 4.含受控源的节点电压法（ 含受控源的节点电压法（续）
解题步骤： 解题步骤： 特点： 特点：
§2-4 节点电压法(节点分析法)
1）选参考节点； 选参考节点；标出各支路电流参考方向和节点电压。 标出各支路电流参考方向和节点电压。 2）对独立节点列节点电流方程[ 对独立节点列节点电流方程[（n－1）个]。 3）通过KVL 通过KVL和元件特性用节点电压表示支路电流 KVL和元件特性用节点电压表示支路电流。 和元件特性用节点电压表示支路电流。 4）将以节点电压表示的支路电流代入步骤2 将以节点电压表示的支路电流代入步骤2）中的节点方程， 中的节点方程， 整理后可得以节点电压为变量的规范化的 整理后可得以节点电压为变量的规范化的电路方程 规范化的电路方程。 电路方程。 1）电路方程数少——只需独立节点数（ 只需独立节点数（n—1）个。 2）可根据电路图直接列写方程， 可根据电路图直接列写方程，且方程规范， 且方程规范，求解化 为数学上解代数方程组。 为数学上解代数方程组。 3）独立节点数少于独立回路数的电路。 独立节点数少于独立回路数的电路。 4）适用于平面或非平面电路。 适用于平面或非平面电路。 5）用于计算机求解电路， 用于计算机求解电路，如：PSPICE电路分析软件 PSPICE电路分析软件。 电路分析软件。
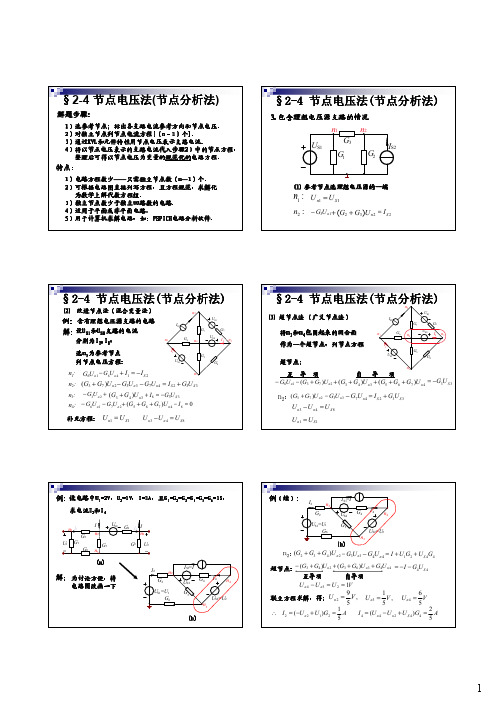
n2 US3 G7 G6 n4 US8 G3 I8 n3
3
4
n1
I1
G5 G4 n5
US1
− G6U n1 − (G3 + G7 )U n 2 + (G3 + G4 )U n 3 + (G5 + G6 + G7 )U n 4 = −G3U S 3
n2 (G3 + G7 )U n 2 − G3U n 3 − G7U n 4 = I S 2 + G3U S 3
1 A 5
I 4 = (U n 4 − U n 2 + U S 4 )G4 =
1
4.含受控源的节点电压法 4.含受控源的节点电压法
R1 US1
§2-4 节点电压法( 节点电压法(节点分析法) 节点分析法)
µU12
§2-4 节点电压法( 节点电压法(节点分析法) 节点分析法)
4.含受控源的节点电压法 4.含受控源的节点电压法（ 含受控源的节点电压法（续）
解题步骤： 解题步骤： 特点： 特点：
§2-4 节点电压法(节点分析法)
1）选参考节点； 选参考节点；标出各支路电流参考方向和节点电压。 标出各支路电流参考方向和节点电压。 2）对独立节点列节点电流方程[ 对独立节点列节点电流方程[（n－1）个]。 3）通过KVL 通过KVL和元件特性用节点电压表示支路电流 KVL和元件特性用节点电压表示支路电流。 和元件特性用节点电压表示支路电流。 4）将以节点电压表示的支路电流代入步骤2 将以节点电压表示的支路电流代入步骤2）中的节点方程， 中的节点方程， 整理后可得以节点电压为变量的规范化的 整理后可得以节点电压为变量的规范化的电路方程 规范化的电路方程。 电路方程。 1）电路方程数少——只需独立节点数（ 只需独立节点数（n—1）个。 2）可根据电路图直接列写方程， 可根据电路图直接列写方程，且方程规范， 且方程规范，求解化 为数学上解代数方程组。 为数学上解代数方程组。 3）独立节点数少于独立回路数的电路。 独立节点数少于独立回路数的电路。 4）适用于平面或非平面电路。 适用于平面或非平面电路。 5）用于计算机求解电路， 用于计算机求解电路，如：PSPICE电路分析软件 PSPICE电路分析软件。 电路分析软件。
2.2 节点分析法
电路与模拟电子技术
节点分析法
节点分析法：以各节点电压为变量，列写 KCL方程(KCL方程数等于独立节点数)，联立 求解各个节点电压。 假设给定电路有n个节点，应用节点分析法， 首先必须选定任意一个为参考点，可以列写（ n －１）个KCL方程
Hengyang normal university
Department of P.&E.I.S.
u2 u1 10
Hengyang normal university
Department of P.&E.I.S.
电路与模拟电子技术
1
G4
G1 G2
电路含理想电流源与电阻串联
2 G3 处理： 与理想电流源串联 的电阻不计入自电 导、互电之内，当 作短路处理
IS1 3
IS3
IS2
(G1 G4 )u1 G4 u2 I S 1 G4u1 (G2 G4 )u2 I S 2 I S 3
电路与模拟电子技术
列写节点电压方程规律
节点电压方程：KCL方程 本节点自电导×本节点电压 — 相邻节点与本节点间互 电导×相邻节点电压 = 流入本节点所有电流源的代数和 1、自电导总是正的，互电导总是负的（互电导=公共 支路电导之和的负值） 2、如两节点间没有公共支路，则相应的互电导为 0 3、在列写节点电压方程时，事先必须指定参考节 点，参考节点电压为零 。不必事先指定各支路参 考方向，只当需要时才有必要。
电路与模拟电子技术
电路含理想电压源
处理： 电路含多个理想电压源， 则给每个电压源的支路设 定一个电流，当作理想电 流源电流代入方程，再补 充相应方程：电压源电压 与节点电压的关系
设节点4为Leabharlann 考点(1 0.1)u1 0.1u3 is1 (1 0.1)u2 u3 is1
节点分析法
节点分析法：以各节点电压为变量，列写 KCL方程(KCL方程数等于独立节点数)，联立 求解各个节点电压。 假设给定电路有n个节点，应用节点分析法， 首先必须选定任意一个为参考点，可以列写（ n －１）个KCL方程
Hengyang normal university
Department of P.&E.I.S.
u2 u1 10
Hengyang normal university
Department of P.&E.I.S.
电路与模拟电子技术
1
G4
G1 G2
电路含理想电流源与电阻串联
2 G3 处理： 与理想电流源串联 的电阻不计入自电 导、互电之内，当 作短路处理
IS1 3
IS3
IS2
(G1 G4 )u1 G4 u2 I S 1 G4u1 (G2 G4 )u2 I S 2 I S 3
电路与模拟电子技术
列写节点电压方程规律
节点电压方程：KCL方程 本节点自电导×本节点电压 — 相邻节点与本节点间互 电导×相邻节点电压 = 流入本节点所有电流源的代数和 1、自电导总是正的，互电导总是负的（互电导=公共 支路电导之和的负值） 2、如两节点间没有公共支路，则相应的互电导为 0 3、在列写节点电压方程时，事先必须指定参考节 点，参考节点电压为零 。不必事先指定各支路参 考方向，只当需要时才有必要。
电路与模拟电子技术
电路含理想电压源
处理： 电路含多个理想电压源， 则给每个电压源的支路设 定一个电流，当作理想电 流源电流代入方程，再补 充相应方程：电压源电压 与节点电压的关系
设节点4为Leabharlann 考点(1 0.1)u1 0.1u3 is1 (1 0.1)u2 u3 is1
2-2-3-3-电路分析-回路与节点法
16
节点分析法
在图示电路中，共有四个节点，选节点④为基准节点。
R3
i3 R6 i6
①
R5 i5 ② uS6 i1 i4 R4
④
R1 uS1
③ i2 R2
uS2
17
节点分析法
在右图电路中，已标出各支 路电流的参考方向。电路共 有四个节点，选节点④为基 准节点。
R3 i3 R6 i 6
①
R5 i5 ② uS6 i1 i4 R4
I1 R1 R3 I2 R4 R2 I3 R5
U S3
US4
虚网孔电流法：取一个网孔电流，且仅仅一个网孔电流流经电流源。 由于该网孔电流就等于电流源电流，该网孔电流如同虚设，故称虚 网孔电流法。
I1=IS
-R1I1+(R1+R3+R4)I2-R4I3=-US3-US4 -R2I1-R4I2+(R2+R4+R5)I3=US4
1
回路分析法
基本要求： 熟练掌握用视察法列回路方程和网孔方程 掌握含受控源电路回路方程的列写
用虚回路法列写无伴电流源电路回路方程
2
回路分析法
回路分析法是以各回路电流作为未知变量来列写 方程，所得方程称回路方程。
由于电路的独立回路数总小于支路数，所以，回 路分析法可以减少求解电路所需的联立方程数。
上式的解式为
1 m imi uSjj ji， i 1, 2, j 1
R11 R12 R22 Rm 2 R1m R2 m Rmm
,m
式中
R21 Rm1
8
回路分析法
如果取网孔作回路的回路分析法，称网孔分析法。 网孔分析法是以各网孔电流作为未知变量来列写方 程，所得方程称网孔方程。从网孔方程求得网孔电 流以后，再求出各支路电压和电流。 取网孔作回路所列方程一定是独立的，且比较方便。
第二章 网孔分析和节点分析
un3 20 50 105 175V U un3 1 20 195V
I ( un 2 90) / 1 120 A
返 回 上 页 下 页
＋
un1 100V
1 － U 20A ＋ 3 2 2
－
100V
1
5.节点分析和网孔分析的比较:
1.网孔分析只适于平面电路；
+ : 流过互电阻的两个回路电流方向相同
Rkk:自电阻(为正)
Rjk ＝Rkj :互电阻
- : 流过互电阻的两个回路电流方向相反 0 : 无关
返 回 上 页 下 页
2. 网孔分析法的一般步骤（只适于平面电路）：
(1) 选定m=b-(n-1)个网孔，并确定其绕行方向；
(2) 对m 个网孔，列写网孔方程（实质是KVL方程）； 自电阻、互电阻、电压升。方程个数为b-(n-1)。 (3) 求解上述方程，得到m个网孔电流； (4) 求各支路电流(用网孔电流表示)； (5) 其它分析。
(2) 用节点电压表示控制量。
u3 un 3 i un 2 R2
返 回 上 页 下 页
I
例
求U和I 。 应用节点法。
1
－ 90V ＋ 2
un 2 100 110 210V
注：与电流源串接的 电阻不参与列方程
0.5un1 0.5un 2 un3 20
＋ － 110V
b ( n 1)
a i1 R1 uS1 + – i2 R2 + – iM2 i3
与支路电流法相比， 方程数减少n-1个。
(R1+ R2) iM1-R2iM2=uS1-uS2
i M1
R3
uS2
节点分析法
（2-7）
电路分析基础——第一部分：2-2
7/23
进一步整理后得： G11un1+G12un2+G13un3= is11 G21un1+G22un2+G23un3= is22 G31un1+G32un2+G33un3= is33
（2-8）
自电导：G11、G22、G33。它们分别是各个节点上所 有电导之和，如： G22= G1+G2+G3 ；
= 0.175
– 0.1 = 0.0306 – 0.01 = 0.0206
– 0.1 0.175
6 – 0.1 1 = – 6 0.175 = 1.050 – 0.6 = 0.45
电路分析基础——第一部分：2-2
0.175 6 2 = – 0.1 – 6 = – 1.050 + 0.6 = – 0.45
电路分析基础——第二部分：第二章 目录
第二章 运用独立电流电压变量 的分析方法
1 网孔分析法 2 节点分析法 3 含运算放大器
的电阻电路 4 树的概念
5 割集分析法
6 回路分析法
7 线性电阻电路解答的 存在性和唯一性定理
电路分析基础——第一部分：2-2
1/23
2-2 节点分析法
内容回顾：如何选用完备独立的变量作为第一步求解
方程，因此与该节点有关的所有
电流都必须计算在内。
+
G1
Is33可一理般解在为此流种入情节况点下的，所I有s11已、知Is2的2、–
2 Us
电流源电流和未知的电压源电流的
G4
代数和。节点分析法都是如此处理
非接地电压源的！
1
G2
G3
2-3 割集电压分析法
-
解 （1）电感L1、L2 之间无耦合 画出网络的有向图，对节点和支路进行编号，选支路1 画出网络的有向图，对节点和支路进行编号，选支路1、2、 为树支，如图所示。 4为树支，如图所示。
& I6
& I s6
a
R6
C1 6 b C2 c 2 4 3 5
& I1
& I3
M L1 & I4 C4 & I 2 L2 & I5 R5
∆ = jω ( L1 L2 − M 2 )
割集电压方程的矩阵形式为： 割集电压方程的矩阵形式为：
1 1 L2 + + R 3 R6 ∆ 1 −M R6 ∆ 1 R3 1 M − R6 ∆ 1 1 L1 + + R5 R6 ∆ 1 − R5
1 & I s6 R3 & U q1 & 1 & = I − U s5 & U s6 − R5 q2 R5 & U q 3 U & 1 1 s5 + + j ωC 4 R R3 R5 5
割集电压方程的矩阵形式为： 割集电压方程的矩阵形式为：
1 1 1 + + R3 R6 jωL1 1 − R6 1 − R3 1 − R6 1 1 1 + + R5 R6 jωL2 1 − R5
1 − & R3 & I s6 U q1 & 1 U = I − U s 5 & & − q 2 s6 R R5 & U q 3 & 5 1 1 U s5 + + j ωC 4 R3 R5 R 5
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
i4
G1 G5 G11
G11为节点①的自电导，是所有 与节点①相连支路的电导之和 G22为节点②的自电导，是所有 与节点②相连支路的电导之和 G33为节点③的自电导，是所有 与节点③相连支路的电导之和
G1 G2 G3 G22
G3 G4 G5 G33
G5 ① G1
i5
un1 16 V un 2 12 V
G11un1 G12un 2 iS11
G21un1 G22un 2 iS 22
1 un1 8 2 1 un 2 6 2
[例题]求图示电路中的U1。 解：改画电路如 图所示，电路有 4 个 节点，以节点 4 为参 考节点，列节点方程 +12V
un1 U S
因此，只需对节点2和节点4列 出节点方程 节点2的自电导：
G12 G21 G1 G24 G42 G3 G41 G14 G2
电源输入节点2和4的电流：
G22 G1 G3 G4
节点4的自电导：
G44 G2 G3 G5
iS11 I , iS 22 0 iS 44 0
再令
iS11 iS iS 22 0 iS 33 0
G5 ① G1
i5
G3
iS
i1 ② i2
G2
i3
G4意到: iS11、iS22、iS33分别是电源输入给节点①、节点②、节点 ③的电流的代数和（流入节点取 “ + ”，从节点流出取 “－”） 节点电压方 程可改写成
G11 un1 G12 un 2 G13 un3 iS11 G21 un1 G22 un 2 G23 un3 iS 22 G31 un1 G32 un 2 G33 un3 iS 33
un2 = － 48 / 7 V Ia = － 24 / 7 A U1 = un1 = － 17.14 V
思考：本题若以节点2为参考点，所列节点方程有何不同？
① ② ③
2.节点方程的一般表示式
电路含有 k 个节点的节点电压方程（ k-1个）的表示式
G11 un1 G12 un 2 G1k 1 un k 1 iS11 G21 un1 G22 un 2 G2k 1 un k 1 iS 22
Gk 11 un1 Gk 12 un 2 Gk 1k 1 un k 1 iS k 1k 1 un (k-1)是下标 (k-1) 所示节点的节点电压；
式 中
G(k-1)(k-1)是下标 (k-1) 所示节点的自电导；
G12、G21、G23、G32 …是下标所示两节点间的互电导
iS(k-1)(k-1)是电源输入给节点（k-1）的电流的代数和
解方程组，可求出电路中各个节点的电压，再由各 个节点电压，可求出电路中各支路电压和支路电流。
3.应用举例
3I
un1 12
列节点方程
1 1 1 u 3I un1 n2 4 4 2
③
节点方程中含有 I ，因为 I 是受控电流源的控制量，它也是
一个未知量，所以必须补充一个方程，需将 I 用节点电压表示。
需要增 补方程
un1 12
联立 方程
1 I un1 un 2 4
§2-3 节点分析法
节点分析法------以节点电压为直接求解对象，依据KCL建 立电路方程（节点电流方程），来分析求解电路的方法。
1.节点电压方程的建立
图示电路共有4个节点，依 据KCL建立（n-1=3）个独立节 点的电流方程为
① G1
G5
i5
G3
i1 i5 iS 0 i1 i2 i3 0 i3 i4 i5 0
节点方程为
un1 U S G1un1 G1 G3 G4 un 2 G3un 4 0 G2un1 G3un 2 G2 G3 G5 un 4 0
注意：若以节点 4为参考点，电压源 US 跨接在节点1与节 点3之间，必须考虑电压源 US的电流 I 是流出节点1，流入节 点3。 [例题]求图示电路中 U 和 I 本题要点：含有电流控制电流源 I 4Ω ② ① 的节点方程的建立 + + 解：电路共有三个节点，以节点 12V 2Ω U 3为参考点。 － －
①
② ③
G1 G5 un1 G1un2 G5un3 iS G1un1 G1 G2 G3 un 2 G3un3 0 G5un1 G3un 2 G3 G4 G5 un3 0
G5
i5
G3
①
G1
iS
i1 ② i2
G2
i3
G4
③
④ （0） 令：
[例题]列出图示电路的节点方程 解：（1）设参考节点如图所示 （2）列节点方程
自电导 互电导
①
6A
②
1 1 1 1 G11 ; G22 6 3 2 2 G12 0 ; G21 0
2Ω 2A (0)
6Ω
3Ω
电源输入给节点的电流的代数和
列节点方程
iS11 2 6 8 iS 22 6
①+
3Ia
－
②
（1）选择节点3为参考节点
（2）列节点方程 节点① 节点②
+ 6Ω U1
－
I
4Ω
Ia
2Ω 17A
需补充
1 un1 9 I 6 1 1 u I 17 n2 4 2 un1 un 2 3I a 1 un 2 I a 2
③ 解得： un1 = －120 / 7 ≈17.14 V
iS
i1 ② i2
G2
i3
G4
③
④ （0）
i4
建立节点电压方程，就是设法将节点电流方程中的各支路 电流用节点电压来表示。下面分析节点方程的导出。 ★（1）先选择一个参考节点，如图选择节点4为参考节
点，节点①、②、③的节点电压分别为un1、un2、un3。
★（2）列KCL方程
①
②
③
i1 i5 is 0 i1 i2 i3 0 i3 i4 i5 0
以节点电压表示
G5 ① G1
i5
G3
iS
i1 ② i2
G2
i3
G4
③
④ （0）
i4
①
② ③
G1 un1 un 2 G5 un1 un3 iS 0 G1 un1 un 2 G2un 2 G3 un 2 un3 0 G3 un 2 un3 G4un3 G5 un1 un3 0
un1 2V
即
U1 un1 2V
[例题]列出图示电路的节点方程 1 I 要点：用节点分析法分析求解 G1 G2 电路时，参考点可任意设定。若尽 + G3 量使电压源跨接于节点与参考点之 2 US 4 间，可简化分析（例如，我们选择 － 节点 3 为参考点。注意到若选择节 G4 G5 3 点 4 为参考点，有何不同？）。 (0) 解：以节点3为参考点，则节 点1的节点电压为已知 节点间的互电导：
①
I 4Ω +
12V
－
② + 2Ω U
－
3I
1 1 1 un1 un 2 3I 4 4 2 1 I un1 un 2 4 un 2 = 8 V
解得
③
I= 1A
即 U = un 2 = 8 V
[例题]求图示电路中的 U1 。
[解]分析要点:不要忽略 电流控制电压源的电流，设 9A 此电流为 I 。
②
电路可 改画为
5kΩ
U1 3kΩ
－4V
5kΩ ①
12V ③
U1
3kΩ 4V ④
un2=12V 已知 un3=－4V
因此，只需对节点1立节点方程
G11un1 G12un 2 G13un3 is11
即 解得
1 1 1 1 ( )un1 un 2 un3 0 5000 3000 5000 3000
G3
iS
i1 ② i2
G2
i3
G4
③
④ （0）
另令：
i4
G1 G12 G21
G3 G23 G32
G5 G31 G13
G12、G21为节点1和节点 2间的互电导，等 于节点1和节点2公共支路的电导的负值 G23、G32 为节点2和节点3间的互电导，是 节点2和节点3间公共支路的电导的负值 G31、G13 为节点3和节点1间的互电导，等 于节点3和节点1公共支路的电导的负值