1_2抽取与内插滤波器
PCM/CVSD系统中内插和抽取高效滤波算法

( h 4hRs r ntr E C, hi ha gt bi .0 1 C i ) Te5 t e ac st efC T S i zun t e 00 8 , h a e hl ia o j a e 5 n
Ab ta t Atf s ,h p lc to a k r u d o ntro ain a d d c main f tr te r atme c n e so y tm ewe n PCM nd src rt te a pi ain b c go n f i ep lt n e i t les,h e li o v rin sse b t e i o o i a
C D, nrd c d. h n, i l d e iin e in me d o tr oain a d d cma o l r a e n a ̄ f d f tri p ee t , VS i it u e T e a s s o mpe a f ce td sg  ̄o fi ep lt e i t n ft sb s d o n n o n i ie l mn e s rs n e l i d
音 采用 A律 6 b s P M编 码体 制 。为 了解决 这 4k p 的 C 2 不 同语 音 编 码 方 式 的通 信 网之 间 的互 通 , 要 种 需 对 内插 和抽 取 滤波器 的设 计 以半 带滤 波器 为基
础 , 特征 介绍 如下 : 其
① 半 带 FR滤 波 器 的 冲激 响应 除 了零 点 不 为 I
h l n e to al d mtrmeh d ba
0 引言
某 专 用 网话 音 部 分 采用 1 b s的连 续 可变 斜 6k p
1 内插 和 抽 取 滤 波器 的设 计
抽取与内插滤波器

2020年4月22日星期三
抽取滤波器和内插滤波器
抽取滤波器 • 2倍抽取滤波的矩阵表示
内插滤波器 2倍内插滤波的矩阵表示
抽取滤波器
X(ejW)
-p
可用理想低通滤波器滤除X(ejW)中的高频分量
W
p
但理想低通滤波器无法实现。
抽取滤波器
X(ejW)
W
-p
p
若Wm/M 为X(ejW)中需保留的最高频率分量,则有
第0列 h0[k] =h[2k] 第2列 h0[k-1] = h[2k-2]
第4列 h0[k-2] = h[2k-4] 第2n列 h0[k-n] = h[2k-2n]
第1列 第3列
h-1[k]=h[2k -1] h-1[k-1] = h[2k-3]
第5列 h-1[k-2] = h[2k-5] 第2n+1列 h-1[k-n] = h[2k-(2n+1)]
2倍内插滤波器的时域表示
内插滤波器的时域表示
例:2倍抽取滤波器hR[k]=h[-k]的矩阵表示
例:2倍内插滤波器hR[k]=h[-k]的矩阵表示
利用MATLAB 计算抽样率变换
(1) 抽取 y = decimate(x,M)
用8阶Chebyshev I 型 IIR 低通滤波器进行滤波。 为保证零相位,对序列进行正向和反向滤波。
第4行 h0[2-n]= h[4-2n]
第2k行 h0[k-n]= h[2k-2n]
第-1行 第1行 第3行 第2k-1行
h-1[-n] = h[-1-2n] h-1[1-n]= h[1-2n ] h-1[2-n]= h[3-2n ] h-1[k-n] = h[2k-1-2n]
可视电话系统中用于图像抽取与内插的FIR滤波器设计

可视电话系统中用于图像抽取与内插的FIR 滤波器设计罗虹(宁夏工业设计院有限责任公司)【摘要】实现了可视电话系统中应用于视频格式CCIR601与QCIF 相互转换的抽取与内插的FIR 数字滤波器的设计,并在已实现的H.263编解码系统中使用了这些滤波器,实验结果获得了很好的图像质量。
【关键词】抽取;内插;FIR 滤波器【Ab str act 】An implementatio n of decimatio n and interpo latio n FIR digital filters is propo sed in this paper .T hese filters can be applied into the conv ersion between CCIR601PAL and QCIF.A test has been don e in a H.263codec sy stem and the result v erifies these filters are very suitable for this v ideo format co nversio n.【Key wo r ds 】Decim ation;Interpo lation;FIR filter1.前言在可视电话H.263编解码系统[5]中,需要完成视频格式CCIR601PAL(704*576)与QCIF(176*144)的相互转换,这一过程主要是要完成图像数据采样率的转换。
在数字采样率变换方法中,提高采样率称为内插;降低采样率称为抽取。
从CCIR601变换到QC IF,需要降低采样率,因而采用抽取,相反地,从QCIF 变换到CCIR601,采用内插。
对于抽取和内插,我们分别设计了FIR 数字滤波器,实践表明,这组滤波器非常适合CCIR601与QCIF 的相互转换,可获得很好的图像质量。
图1X(!)Y(!)抽取频谱图Fig.1Figu re s o f decima tion s pe ctrumX(!)Y(!)2.抽取与内插的工作原理2.1抽取的工作原理以4:1下取样为例,设输入信号(数字序列)为x (n),输出信号为y(n),则y (n)=x (4n)n=0,1,2,…根据Fourier 变换的性质,x(n)、y (n )的频谱Y(!)、X(!)满足如下关系[1]Y(!)=14[X(!4)+X(!4-"2)+X(!4-")+X(!4-32")]图1(a)、(b)分别为X(!)、Y(!)频谱图。
抽取与内插滤波器

利用MATLAB计算抽样率变换
1
0.8 0.6 抽取后信号的谱 0.4 0.2 0 0 p /4 p /2 抽取滤波后 信号的谱 3p /4 p
原信号的谱
利用Matlab 计算抽样率变换
(2) 内插 [y,h] = interp(x,L)
使内插后的信号的均方误差最小来确定FIR滤波器。
h: 所用FIR的系数。 M=255; L=4; x = firls(M,[0 0.5 0.5 1],[1 1 x1=zeros(1,L*length(x)); x1(1:L:end)=x; x2=interp(x,4); w=linspace(0,pi,512); X=freqz(x,[1],w); X1=freqz(x1,[1],w); X2=freqz(x2,[1],w);
h0 h1 h2 h0 h3 h1 h2 h3
x 0 x1 x2 x 3 h0 h1
2倍内插滤波器的矩阵表示
内插矩阵[Ih]的列
h0 h1 h 2 h3 Ih h0 h1 h2 h0 h3 h1 h2 h3 h0 h1
1 π / M H (e ) 0 π / M π 但理想低通滤波器无法实现。
j
抽取滤波器
x[k ]
H (z )
M
y[k ]
X(ej)
-p
-
π M
-
m
M
m
M
π M
p
若m/M 为X(ej)中需保留的最高频率分量,则有
H (e
j
1 m / M ) 0 π / M π
数字信号处理讲义-2抽取与内插滤波器

L:内插的倍数 M:抽样的倍数。
例:离散信号x[k]是由抽样频率为10Hz,试求出抽样频
率为15Hz的序列y[k]。
f=0.35;N=40;
fs=10;fs1=15;
k=0:N-1;t=k/fs;
k1=0:N*1.5-1;t1=k1/fs1;
x=cos(2*pi*f*t);
xr=cos(2*pi*f*t1);
l=3时,要求的阻带为[(6p0.4p)/4,(6p+0.4p)/4]=[1.4p,1.6p]
综上所述,抽取滤波器阻带为 [0.4p,0.6p],[0.9p, p] 7
2021/3/18
x = firls(511,[0 0.1 0.1 0.5 0.5 1],[1 1 1 0 0 0]); f=[0.1 0.4 0.6 0.9];a=[1 0 0];dev=[0.01 0.001 0.001]; %设计滤波器 [N,fo,ao,w] = remezord(f,a,dev); h = remez(N,fo,ao,w); xd=filter(h,[1],x); y=xd(1:4:end); w=linspace(0,pi,512); mag=freqz(h,[1],w); subplot(3,1,1);plot(w/pi,20*log10(abs(mag))); xlabel('Normalized frequency'); ylabel('Gain, dB'); X=freqz(x,[1],w);Y=freqz(y,[1],w); subplot(3,1,2);plot(w/pi,(abs(X))); xlabel('Normalized frequency'); ylabel('magnitude');title('Spectrum of x'); Subplot(3,1,3);plot(w/pi,abs(Y)); xlabel('Normalized frequency'); ylabel('magnitude');title('Spectrum of y');
抽取及内插的频谱分析
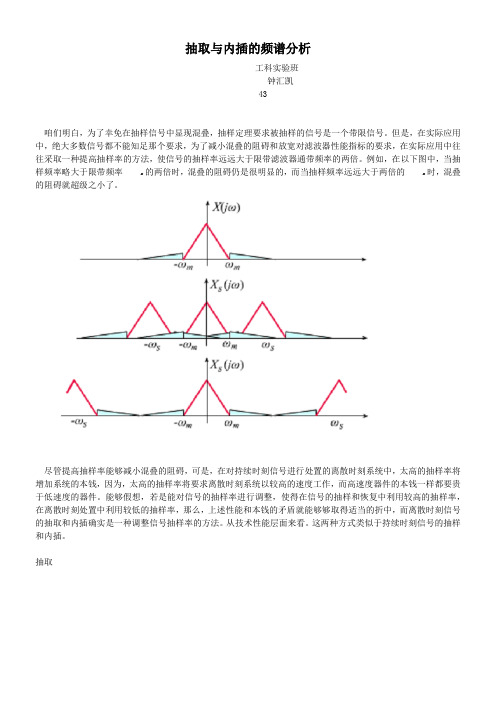
抽取与内插的频谱分析工科实验班钟汇凯43咱们明白,为了幸免在抽样信号中显现混叠,抽样定理要求被抽样的信号是一个带限信号。
但是,在实际应用中,绝大多数信号都不能知足那个要求,为了减小混叠的阻碍和放宽对滤波器性能指标的要求,在实际应用中往往采取一种提高抽样率的方法,使信号的抽样率远远大于限带滤波器通带频率的两倍。
例如,在以下图中,当抽样频率略大于限带频率m 的两倍时,混叠的阻碍仍是很明显的,而当抽样频率远远大于两倍的m 时,混叠的阻碍就超级之小了。
尽管提高抽样率能够减小混叠的阻碍,可是,在对持续时刻信号进行处置的离散时刻系统中,太高的抽样率将增加系统的本钱,因为,太高的抽样率将要求离散时刻系统以较高的速度工作,而高速度器件的本钱一样都要贵于低速度的器件。
能够假想,若是能对信号的抽样率进行调整,使得在信号的抽样和恢复中利用较高的抽样率,在离散时刻处置中利用较低的抽样率,那么,上述性能和本钱的矛盾就能够够取得适当的折中,而离散时刻信号的抽取和内插确实是一种调整信号抽样率的方法。
从技术性能层面来看。
这两种方式类似于持续时刻信号的抽样和内插。
抽取离散时刻信号的抽取包括信号抽样和尺度变换两个步骤:第一,以抽样距离N 对离散时刻信号进行抽样,然后再对抽样信号进行1/ N 的尺度紧缩变换。
以下图是离散时刻信号的抽取进程,图中,x [ n ] 是离散时刻信号,xs [ n ] 是抽样信号,抽样距离N=3,xd [ n ] 是抽取信号,它是xs [ n ] 进行1/N 尺度紧缩变换后所取得的结果。
由图可见,在抽样信号xs [ n ] 和抽取信号xd [ n ] 之间存在以下关系:(1)由于抽样信号xs [ n ] 在N 的整数倍上和离散时刻信号x [ n ] 相等,因此,式也可等效为:(2)尽管式(1)和式(2)在形式上完全相同,但二者的含义不同:式(1)的含义是,抽取信号xd [ n ] 是由抽样信号xs [ n ] 进行1/N 尺度紧缩变换的结果;而式(2)的含义是,抽取信号xd [ n ] 是从离散时刻信号x [ n ] 中每隔(N-1)个点取一个样本值所组成的一个新序列,那个进程就称为离散时刻信号的抽取。
数字信号处理7-2抽取滤波器和内插滤波器

M=2
抽取滤波器的基本概念
X(ej) 1
3 2/3 2/3
3
XD(ej)
1/2
3
序列抽取M倍不混叠的条件:
3
X(ej)=0,||>/M
x[k ]
H(z)
M
y[k ]
H(z) 2
D/A
fsam=32kHz
frec=16kHz
x(t)
x[k]
t
k
连续信号
抽样频率为32kHz的离散信号
问题解决:16 kHz 系统播放抽样频率 32 kHz信号
x[k]
w[k]
y(t)
x(t) A/D
H(z) 2
D/A
fsam=32kHz
frec=16kHz
w[k] k
频率转换后的离散信号
问题解决: 16 kHz 系统播放抽样频率 24 kHz信号
x(t)
x[k ]
A/D
2
fsam 24kHz
w[k ]
y(t)
H(z) 3
D/A
frec 16kHz
x(t)
连续信号号
问题解决: 16 kHz 系统播放抽样频率 24 kHz信号
...
/L /L
可用理想低通滤波器滤除内插后信号频谱XI(ej)中的镜像分量
H
(e
j
)
1, 0,
Ω π/L
π / L | | π
内插滤波器的基本概念
X(ej)
+m m
...
XI(ej)
m m
...
内插滤波器原理

内插滤波器原理内插滤波器原理是一种常见的信号处理方法,用于在信号处理中恢复或改变信号的特性。
内插滤波器可以在离散时间上对信号进行插值,以获得更高的频率分辨率或更准确的信号重建。
它的原理基于信号的局部特性和插值算法。
内插滤波器的基本原理是根据已知的离散信号点,通过插值算法来估计未知点的值。
插值算法可以是线性插值、多项式插值或样条插值等。
线性插值是最简单的插值算法,它通过已知点之间的线性关系来估计未知点的值。
多项式插值使用多项式函数来拟合已知点,并通过多项式函数来计算未知点的值。
而样条插值则使用分段函数来拟合已知点,并通过分段函数来计算未知点的值。
内插滤波器的具体实现可以使用数字滤波器的方法。
数字滤波器是一种通过离散时间上的运算来处理信号的滤波器。
内插滤波器可以将输入信号通过数字滤波器进行插值处理,从而获得更准确的输出信号。
数字滤波器可以是有限冲激响应(FIR)滤波器或无限冲激响应(IIR)滤波器。
FIR滤波器是一种只有有限个滤波系数的滤波器,它通过对输入信号的加权和来计算输出信号。
IIR滤波器是一种具有无限个滤波系数的滤波器,它通过对输入信号和输出信号的加权和来计算输出信号。
内插滤波器可以根据具体的需求选择合适的滤波器类型和滤波器参数。
内插滤波器在实际应用中具有广泛的应用。
例如,在音频处理中,内插滤波器可以用于音频信号的重采样和降噪。
在图像处理中,内插滤波器可以用于图像的放大和缩小。
在通信系统中,内插滤波器可以用于信号的调制和解调。
内插滤波器的应用范围广泛,不仅可以提高信号处理的效果,还可以减少信号处理的复杂度。
内插滤波器是一种常见的信号处理方法,它通过插值算法和数字滤波器来恢复或改变信号的特性。
内插滤波器在各个领域都有广泛的应用,它可以提高信号处理的效果,减少信号处理的复杂度,从而为人们提供更好的信号处理体验。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第0行 第1行 第k 行
抽取矩阵[Dh]的第k行第n 列
[ Dh ] k ,n h[2k - n]
2倍抽取滤波的矩阵表示
抽取矩阵[Dh]的列
h0 h2 h1 h0 [ Dh ] h h h h 3 2 1 0 h3 h2 h1 h0
y [Dh ]x
y0 h0 y h 1 2 y2 y3 h1 h3 h0 h2 h1 h3 h0 h2
h1 h0
2倍抽取滤波的矩阵表示
抽取矩阵[Dh]的行
h0 h2 h1 h0 [ Dh ] h3 h2 h1 h0 h3 h2 h1 h0
h0 h1 h2 h3
h0 h1 h2 h0 h3 h1
例:2倍内插滤波器hR[k]=h[-k]的矩阵表示
x
2
h[-k]
y
h0 h2 h1 h3 h h 0 2 h1 h3 [ I hR ] h0 h2 h1 h0
第-1行 第1行 第3行 第2k-1行
矩阵[Ih]的第k行第n 列
[ I h ] k ,n h[k - 2n]
2倍内插滤波器的时域表示
x
2
H
y
y [ I h ]x
[ I h ] k ,n h[k - 2n]
y[k ] [ I h ] k , n x[n] h[k - 2n]x[n]
第0列 h0[k] =h[2k]
第2列 h0[k-1] = h[2k-2] 第4列 h0[k-2] = h[2k-4] 第2n列 h0[k-n] = h[2k-2n] 第1列 h-1[k]=h[2k -1]
第3列
h-1[k-1] = h[2k-3]
第5列 h-1[k-2] = h[2k-5] 第2n+1列 h-1[k-n] = h[2k-(2n+1)]
为保证零相位,对序列进行正向和反向滤波。
M=255; x = firls(M,[0 0.25 0.25 0.5 0.5 1],[1 1 1 0 0 0]); x1=x(1:4:end); x2=decimate(x,4); w=linspace(0,pi,512); X=freqz(x,[1],w);X1=freqz(x1,[1],w); X2=freqz(x2,[1],w);
2倍抽取滤波的时域表示
x H(z)
2
y
y [Dh ]x
[ Dh ] k ,n h[2k - n]
y[k ] [ Dh ] k , n x[n] h[2k - n]x[n]
n n
M倍抽取滤波的时域表示
x[k ]
H(z)
v[ k ]
M
y[k ]
v[k] x[n]h[k - n]
h0[-n]= h[-2n] 第2行 h0[1-n] =h[2-2n] 第4行 h0[2-n]= h[4-2n] 第2k行 h0[k-n]= h[2k-2n] 第1行 h1[-n] = h[1-2n] 第3行 h1[1-n]= h[3-2n ] 第5行 h1[2-n]= h[5-2n ] 第2k+1行 h1[k-n] = h[2k+1-2n] 矩阵[Ih]的第k行第n 列
Wavelet and FilterBank
信号与系统系列课程组 国家电工电子教学基地
抽取滤波器和内插滤波器
抽取滤波器 2倍抽取滤波的矩阵表示 内插滤波器
2倍内插滤波的矩阵表示
抽取滤波器
x[k ]
H (z )
M
y[k ]
X(ej)
-p
-
π M
π M
p
可用理想低通滤波器滤除X(ej)中的高频分量
1 0]);
2 1 0
2 1 0
0
p/4
p/2 原信号的谱
3p/4
p
0
p/4
p/2 4倍内插后信号的谱
3p/4
p
5
0 0
p/4
p/2 4倍内插滤波后信号的谱
3p/4
p
利用MATLAB 计算抽样率变换
(3) 分数倍抽样滤改变 [y,h] = resample(x,L,M);
L:内插的倍数 M:抽样的倍数。 例:离散信号x[k]是由抽样频率为10Hz,试求出抽样频 率为15Hz的序列y[k]。 f=0.35;N=40; fs=10;fs1=15; k=0:N-1;t=k/fs; k1=0:N*1.5-1;t1=k1/fs1; x=cos(2*pi*f*t); xr=cos(2*pi*f*t1); y=resample(x,3,2); subplot(3,1,3);stem(k1,abs(y-xr)); title('error');
第0列 第1列 第2列 第n列 h[k] h[k -2] h[k -4] h [k-2n]矩阵[Ih]Fra bibliotek第k行第n 列
[ I h ] k ,n h[k - 2n]
2倍内插滤波器的矩阵表示
内插矩阵[Ih]的行 第0行
h0 h1 h 2 h3 Ih h0 h1 h2 h0 h3 h1 h2 h3 h0 h1
抽取滤波器
x[k ]
H (z )
M
y[k ]
更一般地,抽取滤波器的幅度响应可为
1, j H (e ) 0,
2 πl - m M
m / M
2 πl m M
, l 1, 2,, M - 1
X(ej
-p
m
M
π
0
p
M
X (e M )
[ I h ] k ,n h[k - 2n]
2倍内插滤波器的矩阵表示
内插矩阵[Ih]的行
h0 h1 h 2 h3 Ih h0 h1 h2 h0 h3 h1 h2 h3 h0 h1
n
y[k ] v[k M ]
y[ k ]
n
x [ n ]h[ M k - n ]
内插滤波器(interpolation filter)
x[k ]
L
xI [k ]
H ( z)
y[k ]
XI(ej
-
π
π
L
L
可用理想低通滤波器滤除XI(ej)中的镜像分量
1 π / L H (e ) 0 π / L π
1 π / M H (e ) 0 π / M π 但理想低通滤波器无法实现。
j
抽取滤波器
x[k ]
H (z )
M
y[k ]
X(ej)
-p
-
π M
-
m
M
m
M
π M
p
若m/M 为X(ej)中需保留的最高频率分量,则有
H (e
j
1 m / M ) 0 π / M π
利用MATLAB计算抽样率变换
1
0.8 0.6 抽取后信号的谱 0.4 0.2 0 0 p /4 p /2 抽取滤波后 信号的谱 3p /4 p
原信号的谱
利用Matlab 计算抽样率变换
(2) 内插 [y,h] = interp(x,L)
使内插后的信号的均方误差最小来确定FIR滤波器。
h: 所用FIR的系数。 M=255; L=4; x = firls(M,[0 0.5 0.5 1],[1 1 x1=zeros(1,L*length(x)); x1(1:L:end)=x; x2=interp(x,4); w=linspace(0,pi,512); X=freqz(x,[1],w); X1=freqz(x1,[1],w); X2=freqz(x2,[1],w);
h0 h1 h2 h3 h0 h1 h2 h3 [ DhR ] h h h h 0 1 2 3 h0 h1 h2 h3
[ DhR ] [ I h ]
T
h0 h1 h 2 h3 Ih
j
-p
- m
X (e
-p
j
2p m
M
π
M0
Mp
)
π
- m
M0 - 2π m
Mp
- m M0 - 2π m
2π - m M 2π m M
0
2倍抽取滤波的矩阵表示
x H(z)
2
y
x0 x 1 x2 x 3 x4 x 5 x6
2 πl m L
, l 1, 2,, L - 1
2倍内插滤波器的矩阵表示
x
2
H
y
y [ I h ]x
y0 h0 y1 h1 y h 2 2 y3 h3 y4 y 5 y6 y7
h0 h2 h1 h0 [ Dh ] h3 h2 h1 h0 h3 h2 h1 h0
T
[ I hR ] [ Dh ]
利用MATLAB 计算抽样率变换
(1) 抽取
y = decimate(x,M)
用8阶Chebyshev I 型 IIR 低通滤波器进行滤波。
