电路分析-第12章
《电路分析基础》习题参考答案

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) SOW; (2) 300 V、25V,200V、75V; (3) R=12.50, R3=1000, R4=37.5021-2 V =8.S V, V =8.S V, V =0.S V, V =-12V, V =-19V, V =21.S V U =8V, U =12.5,A mB D 'AB B CU =-27.S VDA1-3 Li=204 V, E=205 V1-4 (1) V A=lOO V ,V=99V ,V c=97V ,V0=7V ,V E=S V ,V F=l V ,U A F=99V ,U c E=92V ,U8E=94V,8U BF=98V, u cA=-3 V; (2) V c=90V, V B=92V, V A=93V, V E=-2V, V F=-6V, V G=-7V, U A F=99V, u c E=92V, U B E=94V, U BF=98V, U C A =-3 V1-5 R=806.70, 1=0.27A1-6 1=4A ,11 =llA ,l2=19A1-7 (a) U=6V, (b) U=24 V, (c) R=SO, (d) 1=23.SA1-8 (1) i6=-1A; (2) u4=10V ,u6=3 V; (3) Pl =-2W发出,P2=6W吸收,P3=16W吸收,P4=-lOW发出,PS=-7W发出,PG=-3W发出1-9 l=lA, U5=134V, R=7.801-10 S断开:UAB=-4.SV, UA0=-12V, UB0=-7.2V; S闭合:12 V, 12 V, 0 V1-12 UAB=llV / 12=0.SA / 13=4.SA / R3=2.401-13 R1 =19.88k0, R2=20 kO1-14 RPl=11.110, RP2=1000第2章习题参考答案2-1 2.40, SA2-2 (1) 4V ,2V ,1 V; (2) 40mA ,20mA ,lOmA 2-3 1.50 ,2A ,1/3A2-4 60 I 3602-5 2A, lA2-6 lA2-7 2A2-8 lOA2-9 l1=1.4A, l2=1.6A, l3=0.2A2-10 11=OA I l2=-3A I p l =OW I P2=-l8W2-11 11 =-lA, l2=-2A I E3=10V2-12 11=6A, l2=-3A I l3=3A2-13 11 =2A, l2=1A ,l3=1A ,14 =2A, l5=1A2-14 URL =30V I 11=2.SA I l2=-35A I I L =7.SA2-15 U ab=6V, 11=1.SA, 12=-lA, 13=0.SA2-16 11 =6A, l2=-3A I l3=3A2-17 1=4/SA, l2=-3/4A ,l3=2A ,14=31/20A ,l5=-11/4A12-18 1=0.SA I l2=-0.25A12-19 l=1A32-20 1=-lA52-21 (1) l=0A, U ab=O V; (2) l5=1A, U ab=llV。
第十二章非正弦周期电流电路

第十二章 非正弦周期电流电路一、是非题是非题(注:请在每小题后[ ]内用"√"表示对,用"×"表示错)1. 周期非正弦电流的有效值,不仅与其各次谐波的有效值有关, 而且还与各次谐波的初相位有关。
[×]2. 电压u(t)=3sinωt+2sin(3ωt + 60°)的相量表达式为mU &=(3∠00+2∠600) [×]3. 电压波形的时间起点改变时,波形对纵轴和原点的对称性将发生变化, 但不影响它是否为奇次谐波函数。
[√]4. 奇谐波函数一定不包含直流分量。
[√]二、选择题选择题(注:在每小题的备选答案中选择适合的答案编号填入该题空白处,多选或不选按选错论)1. 在图中,12,20i t i t ==, 则电流3i 的有效值为______。
(A) 1A; (B) 5A; (C) 7A。
解:I3=5A。
2. 欲测一周期非正弦量的有效值应用_____。
(A) 电磁式仪表; (B) 整流式仪表; C磁电式仪表。
解:电磁式仪表。
3. 下列四个表达式中,是非正弦周期性电流的为_____。
(A) t t t i π3cos 32cos 26)(++=, A (B) ()34cos 5cos36sin 5,i t t t t =+++ A (C) ()2sin(34sin(7),i t t t =+ A(D) t t t t i ωπωcos cos cos )(++= A解:()34cos 5cos36sin 5,i t t t t =+++1. 已知t t t t u ωπωπωω5cos 230)323sin(280)323sin(280sin 230+++−+=伏, 则u 的有效值为_____。
(A) U=30+80+80+30=220V(B) 120.83U ==V(C) 90.55U == V解:80∠(-2π/3)+80∠(2π/3)=160∠(2π/3)=-80, 323sin(280)323sin(280πωπω++−t t =)3sin(280πω−t V90.55U == V。
高中物理新教材同步必修第三册 第12章 闭合电路 专题强化9 闭合电路的功率 故障分析

例1 如图2所示,电路中E=3 V,r=0.5 Ω,R0=1.5 Ω,滑动变阻器的 最大阻值为10 Ω.
当输出功率为120 W时,由题图中P-I关系图线看出对应干路电流为4 A,
再从U-I图线读取对应的输出电压为30 V,D正确.
1234567
返回
图1
功率最大
D.当P移到滑动变阻器的右端时,电源的效率最高
1234567
解析 滑动变阻器的滑片P向右移动,电路总电阻减 小,根据I=RE总可知,电流表的示数变大,根据E=U +Ir可知电压表的示数减小,故A正确,B错误; 当P移到滑动变阻器的右端时,外电阻R最小,根据 I=RE总可知,电路中的电流最大,根据P内=I2r可知此时电源内部消耗的 电功率最大,故C正确; 根据效率η=R+R r×100%可知,此时电源的效率最低,故D错误.
(2)滑动变阻器接入电路的阻值R为多大时,滑动变 阻器上消耗的功率最大?最大为多大?
答案
2Ω
9 8
W
解析 将电阻R0和电源等效成新的电源,滑动变阻器上消耗的功率就是 等效电源的输出功率.
当R=r+R0=2 Ω时,滑动变阻器上消耗的功率最大,为: Pm=4ER2=4×322 W=98 W.
总结提升
图7
1234567
解析 电源的路端电压和电流的关系为:U
=E-Ir,显然直线①的斜率的绝对值等于r,
纵轴的截距为电源的电动势,从题图中看出
E=50 V,r=560--020 Ω=5 Ω,A正确,B
第12章 网络函数和频率特性 电路分析基础

0
理想带阻滤波器
12. 2 RC电路的频率特性
一、一阶RC低通滤波电路
如图所示RC 串联电路,其负载
端开路时电容电压对输入电压的转
移电压比为
1
H(j)U U12
jC
R 1
1
1jRC
jC
令
11
ωC
RC
将上式改写为
H(j)
1
H(j)
1j
C
i1
i2
+R
+
u1
C
u2
-
-
H(j)
1
1C2
幅频特性
arctan
2.调参数L、C ( 常改变C )。
2. 谐振时的电压和电流
Z(j0)R
IUS US ZR
I + U R - + U L -
+
R
j0L +
U S
-
1
U C
j 0C -
谐振时电阻、电感和电容上的电压分别为
U RRIU S
U Lj0L IjR 0LU SjQ U S
U Cj 1 0CIj01 RU C SjQ U S
三. 常见一阶滤波电路
一阶低通滤波电路
I R
+
+
U i
C
U O
–
–
一阶高通滤波电路
I
+
+
U i
C R
U O
–
–
I
+ U i
L R
+
U O
–
–
I
+ U i
R L
+
第十二章 非正弦周期电流电路

is1
is3
华东理工大学 上 页 下
页
§12-3 有效值、平均值和平均功率
一. 有效值
根据周期量有效值的定义, 为其方均根值:
I
1 T
0
T
[it ] dt U
2
1 T
0
T
[u t ]2 dt
it I 0 I km cos(k1t k )
k 1
P U 0 I 0 U k I k cos k
k 1
(三角函数的正交性)
U 0 I 0 U 1 I1 cos1 U 2 I 2 cos 2 U k I k cos k
Um Im 式中 : U k , Ik , k uk ik , k 1,2, 华东理工大学 2 2
0
ui
t
+ uo
③非正弦激励下的线性电路
0
-
+
0
t
ui
t
uo
0
t
页
- 华东理工大学 上 页 下
§12-2 周期函数分解为傅里叶级数 (谐波分析) 一. 数学分析
设非正弦周期电流i(t)=i(t+T) ,当满足狄里赫利条件 ( ① i(t)在一周期内连续or有有限多个第一类间断点; ② i(t)在一周期内有有限多个极大值与极小值 )时, 可展成收敛的傅里叶级数:
I av
1 T i dt 0 T
例:正弦电流的平均值 为 1 T 2 I av 0 I m cost dt I M 0.898 I M 0.637 I T 恒定分量(直流分量) 磁电系仪表:
电磁系仪表: 全波整流仪表:
邱关源《电路》第五版第12章-三相电路分析
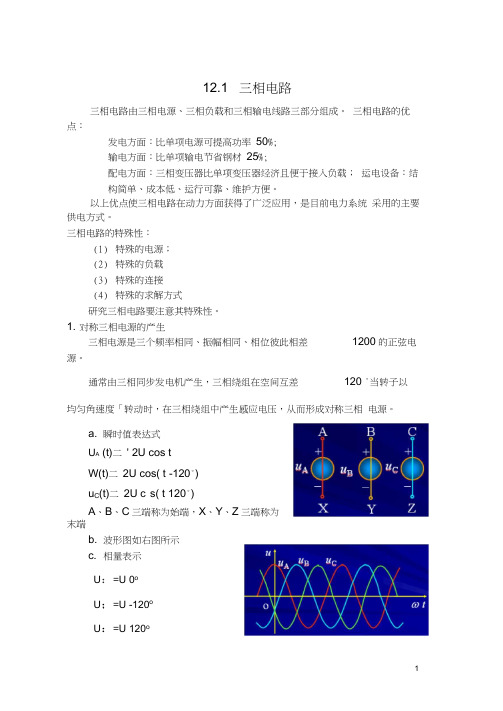
12.1 三相电路三相电路由三相电源、三相负载和三相输电线路三部分组成。
三相电路的优点:发电方面:比单项电源可提高功率50%;输电方面:比单项输电节省钢材25%;配电方面:三相变压器比单项变压器经济且便于接入负载;运电设备:结构简单、成本低、运行可靠、维护方便。
以上优点使三相电路在动力方面获得了广泛应用,是目前电力系统采用的主要供电方式。
三相电路的特殊性:(1)特殊的电源;(2)特殊的负载(3)特殊的连接(4)特殊的求解方式研究三相电路要注意其特殊性。
1. 对称三相电源的产生三相电源是三个频率相同、振幅相同、相位彼此相差1200的正弦电源。
通常由三相同步发电机产生,三相绕组在空间互差120 °当转子以均匀角速度「转动时,在三相绕组中产生感应电压,从而形成对称三相电源。
a. 瞬时值表达式U A (t)二' 2U cos tW(t)二2U cos( t -120°)u C(t)二2U c°s( t 120°)A、B、C三端称为始端,X、Y、Z三端称为末端b. 波形图如右图所示c. 相量表示U:=U 0oU;=U -120oU:=U 120od. 对称三相电源的特点U A U B U c = 0u A u;U C-oe. 对称三相电源的相序定义:三相电源各相经过同一值(如最大值)的先后顺序。
正序(顺序):A —B—C—A负序(逆序):A —C—B—A (如三相电机给其施加正序电压时正转,反转则要施加反序电压)以后如果不加说明,一般都认为是正相序。
2. 三相电源的联接(1)星形联接(Y联接)X, Y, Z接在一起的点称为丫联接对称三相电源的中性点,用N表示。
4〜C ------------------------------- °N (2)三角形联接e联接)注意:三角形联接的对称三相电源没有中点3. 三相负载及其联接三相电路的负载由三部分组成,其中每一部分称为一相负载,三相负载也有二种联接方式。
九年级物理第12章欧姆定律专题特训六动态电路分析习题新版北师大版
【答案】B
返回
返回
2.[2023·丹东]如图所示,电源电压保持不变,闭合开 关S,在滑动变阻器R的滑片P向右移动的过程中, 下列说法正确的是( D ) A.电压表示数变小 B.电压表示数变大 C.电流表A1示数变小 D.电流表A2示数变小
返回
3.小明用如图所示电路探究电流与电压的关系。R为定值 电阻,电源电压保持不变,闭合开关,当滑动变阻器 滑片P向左移动的过程中,
返回
6.[2023·益阳]如图所示电路中,电源电 压保持不变,R1和R2为定值电阻。 先闭合开关S1,再闭合S2后,电流表 和电压表的示数变化的情况是( A )
A.电流表示数增大,电压表示数不变
B.电流表示数增大,电压表示数减小
C.电流表示数减小,电压表示数增大
D.电流表示数不变,电压表示数增大
返回
7.如图所示电路中,电源电压恒定不变,开关都闭合 后,电路正常工作。当断开开关S1时,下列判断中 正确的是( A )
A.电流表示数变小 B.电压表示数变大 C.电压表和电流表示数之比变小 D.没有电流通过R0
返回
8.[2023·齐齐哈尔]如图所示,电源电压恒定,先只闭合 开关S1,两电表均有示数;再断开S1,同时闭合S2和 S3,此过程中( C ) A.电压表示数变大,电流表示数变小 B.电压表示数变小,电流表示数不变 C.电压表示数与电流表示数乘积变大 D.电压表示数与电流表示数比值不变
【点拨】由电路图可知,体重秤显示器串联在电路中,相当
于电流表,C 正确;开关闭合时,R1 与 R2 串联,体重秤显
示器(电流表)测电路中的电流,人体质量越大,压敏电阻 R1 的阻值越小,电路的总电阻越小,由 I=UR可知,电路中的
电流越大,由 U=IR 可知,定值电阻 R2 两端的电压越大,
高中物理人教必修三第12章第1节2闭合电路的四率问题
闭合电路的“四率”问题【知识梳理】1.电源的总功率(1)任意电路:P总=EI=U外I+U内I=P出+P内(2)纯电阻电路:P总=I2(R+r)=E2 R+r2.电源内部消耗的功率:P内=I2r=U内I=P总-P出3.电源的输出功率(1)任意电路:P出=UI=EI-I2r=P总-P内。
(2)纯电阻电路:P出=I2R=E2R(R+r)2=E2(R-r)2R+4r 讨论:如图所示①当R=r时,电源的输出功率最大为P m=E2 4r。
②当R>r时,随着R的增大输出功率越来越小。
③当R<r时,随着R的增大输出功率越来越大。
④当P 出<P m 时,每个输出功率对应两个可能的外电阻R 1和R 2,且R 1R 2=r 2。
4.电源的效率 (1)任意电路:η=P 出P 总×100%=UE ×100% (2)纯电阻电路:η=R R +r×100%=11+r R×100% 讨论:R 越大,η越大;当R =r 时,电源有最大输出功率,效率仅为50%。
【巩固训练】【例1】如图所示,已知电源电动势E =6 V ,内阻r =1 Ω,保护电阻R 0=0.5 Ω,求:当电阻箱R 读数为多少时,保护电阻R 0消耗的电功率最大,并求这个最大值。
[解析] 保护电阻消耗的电功率为P 0=E 2R 0(r +R +R 0)2,因R 0和r 是常量,而R 是变量,所以R 最小时,P 0最大,即R =0时,P 0max =E 2R 0(r +R 0)2=62×0.51.52 W =8 W 。
[答案] R =0 P 0max =8 W【变式训练1】在【例1】中,条件不变,求当电阻箱R 读数为多少时,电阻箱R 消耗的功率P R 最大,并求这个最大值。
[解析] 这时要把保护电阻R 0与电源内阻r 算在一起,据以上结论,当R =R 0+r ,即R =1 Ω+0.5 Ω=1.5 Ω时,电阻箱R 消耗的功率最大,P R max =E 24(r +R 0)=624×1.5 W =6W 。
视在功率、平均功率或有功功率、无功功率、功率因数
电感、电容无功功率:设任何时刻,单口网络上的关联参考方
向电流、电压表示为u(t) = Umcos(t+u),i(t) = Imcos(t+i),则 电容、电感的无功功率可表示为:
QL = XLI2 = LI2 =
1 L L
QC
=
XCI2
=
–
CU2
=
–
1 C
I2 =
无功功率的单位:为表示区别,无功功率的单位不是瓦(W),而 是反作用伏安(var,volt ampere reactive)。
电路分析基础——第三部分:12-4~6 10/13
jy QL
Q O
例12-10 工厂中的感应电机是感
性负载,功率因数较低,为提高功
率因数,可并联合适的电容器。设
有一220V,50Hz,50kW的感应电
Q = Q1 + Q2 + Q3 + Q4 = 25 – 35 – 10 + 20 = 0 (为什么?)
电路分析基础——第三部分:12-4~6 13/13
例12-13 电路如图12-21所示,试求每个负载吸收的总复功率, 及输入电流有效值。
解:由无功功率的定义,可得
I
• S1 = S1[cosZ1+ jsinZ1]
= 86600 var = 86.6 kvar
电路分析基础——第三部分:12-4~6 11/13
(2)根据电容与电感之间无功功率相互抵消的原理,并联后
电源提供的无功功率为:
Q = QL + QC = 0, QC = – QL = – 86.6 kvar = – CU2
C=
– QC U2
=
86600 100×2202
第十二章 非正弦周期电流电路和信号的频谱
k
)
其中:
A
0
: 恒定分量 (直流分量)
: 一次谐波。
A 1 m cos( t 1 )
也称为基波分量。
A km cos( k 1 t k )
k 2 ,3 , 4 ,
称为高次谐波(如2次谐波、3次谐波等等)。
二、 频谱(图):
(1) 幅度频谱: (2) 相位频谱:
A km k 1
(sin t
1 3
sin 3 t )
f(t) A
O
t
O
t
f1 ( t )
f 1 (t) 4 A /
4A
sin t
f 3 ( t) A
f3 (t )
4A
(sin t
1 3
sin 3 t
1 5
sin 5 t )
O
t
O
t
f (t ) f3 (t )
电容对低频电流有抑制作用, 电感对低频电流起分流作用。
12-6
付里叶级数的指数形式
一、 付里叶级数的指数形式:
付里叶级数的指数形式:
f (t )
其中:
ck 1 T
k
cke
jk 1 t
T
f (t )e
jk 1 t
dt
0
二、 说明:
因为: 且:
A km cos( k 1 t k ) 1 2 A km e
P
k 1
U k I k cos k Leabharlann pk ok
p
k o
k
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
us _
电路图
解:1、求大信号时工作点 u 0
10 u 2i u 4i 2i 2
2
u _
I Q 1A U Q 8V I Q 2(舍 去 )
+ us _
R
i
+
2、求动态电阻,作小信号等效电路图
du rd di
Rd
du di
可见,无论是静态电阻还是动态电阻都与电路工作状态有关。
例12-1
解:
设某非线性电阻的伏安特性为 u = 20 i+ 0.5 i 2。求 (1)i1 = 1A,i2 = 2A时所对应的电压u1、u2。 (2)i3 = i1+ i2时所对应的电压u3。 (3)i = 2cosωt时所对应的电压u。
例12-2 图示电路(a)中, 非线性电阻的伏安特 性及其分段线性化折 线逼近情况如图(b)所 示。求回路电流i。 解:由图(b)可得
RAi U 01 2i 1, u Rd i U 0 RB i U 02 0.4i 2.5,
15 U 0 得 i 5 Rd
1、串联适用都是单调型或流控型 电阻
则两电阻串联后满足 u = f1(i1) + f2(i2) = f1(i) + f2(i) = f (i) 串联后,等效于一个单调型或流控型非线性电阻。 若非线性电阻中有一个为压控型,则串联后的等效电阻无 法写出如上式的解析式,此时可利用图解法求出串联等效电阻 的伏安特性如图 (c)所示。
某一非线性电阻伏安特性曲线近似于直线区域的一段, 当电路工作在此区域时,此非线性电阻伏安特性可用一条 直线来近似代替这一段曲线。即在此区域工作的非线性电 阻的特性可由下式直线方程表示: u = U0 + Rdi 从而把非线性电阻支路转化为线性含源支路。近似线 性化后,就可按照线性电路的计算方法进行分析计算了。 这种方法称为近似线性化法,也称直线近似法。
由电路两类约束条件, 可列电路方程
U 0 Δus Ri u i g ( u)
小信号分析法过程(续1)
A
用大信号求解静态工作点
当us=0,即电路中仅有直流电源作用时,由上式可得
i u U0 R R
i = g (u)
两式联立求解,即可求得电路的 工作点Q,如图 (c)所示。
(1)i1 = 1A时, u1 = 20i1+0.5i12 = 201+0.512 = 20.5 V i2 = 2A时, u2 = 20i2+0.5i22 = 202+0.522 = 42 V
(2)i3 = i1+ i2时,u3 = 20(i1+ i2)+0.5(i1+ i2)2 = 203+0.532 = 64.5 V 显然,u3 u1 + u2, 即叠加定理不适用于非线性电阻。
12.2.3、分段线性化--简介举例
在0 < i < IB区间,曲线AB段可近似用斜率为1/RAB的直线 AB代替,该直线方程为 u = RAB i 0 < i < IB
直线AB过坐标原点,其可等效为一线性电阻
在IB < i < IC区间,曲线BC段可近似用u轴截距为UBC、 斜率为负1/RBC的直线BC代替,该直线方程为 u = RBC i + UBC IB < i < IC 等效为一线性电压源串联一个负电阻支路 在i > IC区间,曲线CD段可近似用u轴截距为UCD、 斜率为1/RCD的直线CD代替,该直线方程为 u = RCD i + UCD i > IC 其可等效为一线性含源支路
第12章
非线性电路基础
非线性电路指在电路中含有非线性元件的电路。从严格的 意义上讲一切实际电路器件都是非线性的,只是对于那些非线 性程度相对较弱的器件或是仅应用器件的线性部分工作的电路 而言,可采用线性电路模型进行分析;而当器件的非线性特性 不容忽略或是需要利用器件的非线性特性时,则应采用非线性 电路模型进行分析。本章简要介绍非线性电路的基本概念和分 析方法。
q dq C , Cd u du
dq dq du du i Cd dt du dt dt
12.1.3、非线性电感
1、特点
电流控制型电感 Ψ = f (i)
磁链控制型电感 i = g (Ψ )
2、参数
非线性电感元件同样具有静态电感 L , L和动态电感Ld之分,如图 (b)所示 i
教学要点
非线性电阻元件,简单的非线性电阻电路分析,非线 性电阻电路的静态工作点和负载线、分段线性化方法;非 线性电容元件的库——库伏特性;非线性电感元件的磁通 链——电流特性;非线性电路方程的编写;小信号分析法; 含有二极管的电路 。
教学提示
充分掌握非线性电阻元件,简单的非线性电阻电路 分析;充分掌握小信号分析法分析含有非线性电阻元件 的电阻电路的方法;本章的其他知识一般了解。
u
_
rd
(b)等效电路
非线性电路问题转化为线性问题进行求解
小信号分析法过程(续3)
C 最后合成总的电路响应- -既有小信号又有大信号
把A、B求得的大信号(UQ、IQ )和小信号 Δi或Δu 合成
u U Q Δu i I Q Δi
为最后所求。
例
Hale Waihona Puke 用小信号分析法求图中电压u。直流电压源U0=10V,其 中干扰的小信号uS 10mv ,已知非线性电阻的伏安特 性为 4i 2 2i 2 i0 i 2 u + i0 0 + +
12.2.1、含一个非线性元件的电路
可以把电路中除了非线性元件之外的线性电路部分视 为一个线性含源一端口网络,利用戴维南定理将其等效化 简为电压源串联电阻支路。
含一个非线性元件的电路及图解 然后 联立两个方程 i = g (u) 求解静态工作点 或图解曲线相交
u = uoc R0 i
12.2.2、非线性电阻的串联/并联
2、非线性电阻参数-静态、动态电阻
由于非线性电阻元件伏安特性的非线性,所以非线 性电阻不能像线性电阻那样用常数表示电阻值。对于非 线性电阻元件通常引用静态电阻和动态电阻的概念。
非线性电阻元件在某一工作状 态下的静态电阻定义为该点的电压 与电流之比
u UQ R i IQ
非线性电阻元件在某一工作点 Q的动态电阻为该点的电压对电流 的导数 点Q称为此时该非线性 电阻的工作点。UQ称为工作 点电压,IQ称为工作点电流。
2、非线性电阻的并联
并联适用都是单 调型或压控型电阻
两电阻并联后满足 i = g1(u1)+ g2(u2) = g1(u) + g2(u) = g (u) 若非线性电阻中有一个为流控型,则并联后的等效电阻 无法写出如上式的解析式,与非线性电阻的串联类似,可采 用图解法求出等效电阻的伏安特性。
12.2.3、分段线性化 --非线性伏安特性的直线近似
(3)i = 2cosωt时,u1 = 202cosωt +0.522cos2ωt = 1+ 40cosωt +cos2ωt V
12.1.2、非线性电容
1、特点 电压控制型电容 q = f (u) 电荷控制型电容 u = g (q ) 2、参数 静态电容C定义为非线性电容在某一工作点Q上的电 荷与电压之比,动态电容Cd定义为非线性电容在某一工 作点Q上的电荷对电压的导数,动态电容Cd又称为增量 电容。 关联参考方向 时
di Δi du
1 Δu gd Δu Δu u U Q rd
小信号分析法过程
如图 (a)所示含一个非线性元件电路,电路线性部分可 用戴维南定理等效为一电压源us串联电阻R支路,其中电源 电压us在一恒定电压U0上有一个微小变化量us,us满足 us << U0 。 对于给定的这一电路,us会使电路中的各电压、电流 产生相应的变化。 us=U0+us 如图 (a) 所示,电源电压 us:
i 1
u
_
8i 2 i 1 10
3、磁滞回线
d Ld di
图(c)所示为电子技术中常使用的铁芯、磁芯电感的Ψi特 性,通常称为磁滞回线,其既非流控又非磁控,曲线对I、对 Ψ都是多值函数。
12.2 非线性电阻电路
仅由非线性电阻元件、线性电阻元件、独立电源以及受 控源组成的电路称为非线性电阻电路。 分析非线性电路的基本依据仍是KCL、KVL和元件的伏 安关系。KCL、KVL仅与电路连接的结构有关,而与所连接 元件的特性无关,所以,由KCL、KVL所列出的仍是线性方 程。 表征元件约束的元件伏安特性中,对于线性元件是线性 方程,对于非线性电阻元件则是非线性方程。求解一般非线 性方程的解析解很困难,通常可借助于计算机求解非线性方 程的数值解。 如电路中仅有一个非线性元件、多个非线性元件可等效 化简、非线性元件具有分段折线性以及在小信号工作条件下 等,可采用较简单的方法求解非线性电路。
U0/R IQ
i i = g ( u)
Q
U0+us = R(IQ+i)+UQ+u IQ+i = g(UQ+u)
0 UQ U0 u
在u = UQ处将g(u)展开为泰勒级数:
(c) 小信号分析图解
di I Q Δi g(U Q ) du
u U Q
Δu 高 阶 项
由于u足够小,略去高阶项,且IQ = g(UQ),
AP段 PB段
i 1, 1 u 3 1 i 5, 3 u 4.5
15 U 02 15 2.5 i 2.315 A 5 RB 5 0.4
15 U 02 15 2.5 i 2.315 A 5 RB 5 0.4
