速率分布函数
麦克斯韦速率分布函数

=21/2N0xexp(x2)xdx2 =21/2N0xxd[exp(x2)] =21/2N[xexp(x2)|0x
+0xexp(x2)dx]
=N[21/2xexp(x2) +21/20xexp(x2)dx]. 定义误差函数erf(x)为
erf(x)=21/20xexp(x2)dx,
器壁的碰撞次数,把nvxf(vx)dvx 在从0到的区间内积分,就能
得到分子通量J.
而从(6)式可以看出:式 中的两个积分内的被积函 数nvxf(vx)dvx和(n/4)vf(v)dv 的地位相当,它们的物理 意义相似,因而在这两者 之间可以进行类比推理。
现在既然(n/4)vf(v)dv在从0 到的区间内积分,也能得到 分子通量 J. 可见 (n/4)vf(v)dv 就表示速率取值在 v到 v+dv间 隔内的气体分子在单位时间内 对单位面积器壁的碰撞次数。 据此处理某些相关问题,有时 往往会比较简捷。
f(v).
三、速率分布函 数类比质点运动 中的时间分布函 数
类比法是一种在物理学 研究中常用的逻辑推理方 法。使用类比法时,根据 两类对象之间在某些方面 的相似或相同,来推出它 们在其他方面也可能相似 或相同.
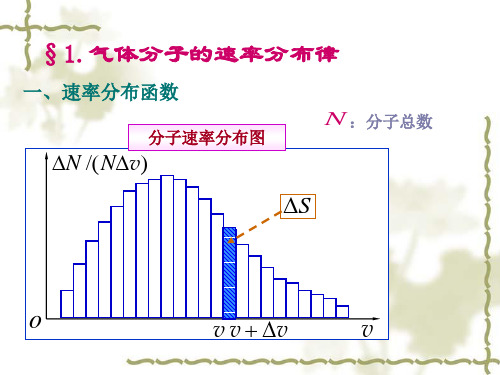
为了描述处于平衡态下的气体 的分子数在不同的速率间隔内的 分布情况,可以取分子速率 v 为 横坐标值,画出速率取值在v至v +v间隔内的分子数 N 占总分 子数 N 的比率的直方图(条形统 计图)。
因此,如果在热学 中学习速率分布函数 时,类比力学中的速 率-时间函数,就能 够比较容易地认识到 其物理意义。
不仅如此,用 f(v) 类比 f(t),还利于正确理解为什 么说 “不应该问速率刚 好等于特定值 v 的分子有 多少个?如果非要这样问, 那这种分子其实一个都没 有。”
分子热运动的速度和速率统计分布规律

f (v )
C
o
vo
v
解:
0
f (v)dv Cdv Cvo 1
0
vo
1 C vo
v vf (v)dv
0
vo
0
vo 1 v vo 2 2
2 o
2 vo Cvdv C 2
v v f (v)dv
2 2 0
voΒιβλιοθήκη 01 2 Cv dv vo 3
S1
Ag
例:利用麦克斯韦速率分布求:V
m 3 2 ) e 解: f (V ) 4π( 2πkT m 2 V 2 kT
p
V2 V
V2
kT 1.41 m
1.60 kT m
df (V ) 0 dV
2kT 2 RT Vp m M
8kT 8RT V πm πM
V V 2 f (V )dV
5
P 1.013 10 25 -3 N n 2.7 10 m -23 kT 1.38 10 273.15
M 28 10 kg mol
-3
-3
-1
M 28 10 -26 m 4.65 10 kg 23 N A 6.022 10
2 m N N e 2πkT
2 y
) g (v
2 z
)
2
+ v
2 y
g (v ) e
2 -av x
F (V ,V ,V ) Ae -aV
x y z
2
常数的确定:
---
F(v ,v ,v )dvdv dv 1
x y z x y z
麦克斯韦速率分布函数的归一化条件

麦克斯韦速率分布函数的归一化条件
麦克斯韦速率分布函数是描述理想气体中分子速度分布的概率密度函数。
它的归一化条件是指该函数在整个速度空间上的积分等于1,也就是概率的总和为1。
麦克斯韦速率分布函数的表达式是:
f(v) = (m/2πkT)^(3/2) * 4πv^2 * exp(-mv^2/2kT)
其中,f(v)是速率分布函数,m是分子的质量,k是玻尔兹曼常数,T 是气体的温度,v是分子的速度。
要满足归一化条件,我们需要对速率分布函数在整个速度空间上进行积分。
∫f(v) dv = 1
在球坐标系下,速度分布函数可以写成:
f(v) = (m/2πkT)^(3/2) * 4πv^2 * exp(-mv^2/2kT)
进行变量替换,令x = mv^2/2kT,则速率分布函数可以重写为:
f(x) = (m/2πkT)^(3/2) * exp(-x)
通过变量替换,速度范围从0到无穷变为了0到无穷。
进一步进行计算,我们可以得到速率分布函数在整个速度空间上的积分:
∫[0,∞] f(x) dx = (m/2πkT)^(3/2) * ∫[0,∞] exp(-x) dx
对指数函数进行积分,我们可以得到:
∫[0,∞] exp(-x) dx = 1
因此,归一化条件可以表示为:
(m/2πkT)^(3/2) * 1 = 1
通过简化,我们得到:
(m/2πkT)^(3/2) = 1
进一步整理,可以得到麦克斯韦速率分布函数的归一化条件:
(m/2πkT)^(3/2) = 1
这个条件保证了麦克斯韦速率分布函数在整个速度空间上的积分等于1,即概率的总和为1。
经典:第四讲-速度分布函数-麦克斯韦速率

f (v) dN Ndv
速率分布函数
理解分布函数的几个要点:
1.条件:一定温度(平衡态)和确定的气体系统,T和m是一定的; 2.范围:(速率v附近的)单位速率间隔,所以要除以dv;
3.数学形式:(分子数的)比例,局域分子数与总分子数之比。
8
物理意义:
速率在 v 附近,单位速率区间的分子数占总分子数
• dN/N 是 v 的函数; •当速率区间足够小时(宏观小,微观大), dN/N还应与
区间大小成正比。
为此,规定以单位速率间隔为比较标准,即 dN ,这样,比
Ndv
值 dN
Ndv
就反映出了分布随速率v的改变而改变。为此我们规定;
7
定义:处于一定温度下的气体,分布在速率v附近的
单位速率间隔内的分子数占总分子数的百分比只是
(2) 氢气在该温度时的最概然速率和方均根速率
解 (2)
vp
2RT
M
RT 2 103
1000
m/s
RT
f(v)
(v p )H2 103
1.41 103 m/s
( v 2 )H2
3RT M
1.73103 m/s
He H2
1000
v
29
例2 有N 个粒子,其速率分布函数为
f (v )
(2) 因为速率分布曲线下的面积代表一定速率区间内 的分子与总分子数的比率,所以
v v0 的分子数与总分子数的比率为
N
N
v0a
v0
2 3v 0
2 3
N 2 N
3
因此, v>v0 的分子数为 ( 2N/3 ) f (v )
第三章气体分子速率及能量分布ppt课件
麦克斯韦主要从事电磁理论、分子物理学、统计物理学、光学、力学、 弹性理论方面的研究。尤其是他建立的电磁场理论,将电学、磁学、光学统 一起来,是19世纪物理学发展的最光辉的成果,是科学史上最伟大的综合 之一。
麦克斯韦大约于1855年开始研究电磁学,在潜心研究了法拉第关于电 磁学方面的新理论和思想之后,坚信法拉第的新理论包含着真理。于是他抱 着给法拉第的理论“提供数学方法基础”的愿望,决心把法拉第的天才思想 以清晰准确的数学形式表示出来。他在前人成就的基础上,对整个电磁现象 作了系统、全面的研究,凭借他高深的数学造诣和丰富的想象力接连发表了 电磁场理论的三篇论文:《论法拉第的力线》(1855年12 月至1856年2 月);《论物理的力线》(1861至1862年);《电磁场的动力学理论》 (1864年12月8日)。对前人和他自己的工作进行了综合概括,将电磁场 理论用简洁、对称、完美数学形式表示出来,经后人整理和改写,成为经典 电动力学主要基础的麦克斯韦方程组。据此,1865年他预言了电磁波的存 在,电磁波只可能是横波,并计算了电磁波的传播速度等于光速,同时得出 结论:光是电磁波的一种形式,揭示了光现象和电磁现象之间的联系。 1888年德国物理学家赫兹用实验验证了电磁波的存在。。
(
m
2 kT
)3/
2
em
(
v
2 x
v 2y
vz2
)
/
2kT
dvx dv y dvz
引用速度空间的概念,可以对这个定律得到更直 观的理解。
速度空间:以vx, vy, vz为轴的直角坐标系(或 以v、θ、φ为坐标的球坐标系)所确定的空间。
速率分布公式:
dN 4 ( m )3/ 2 emv2 / 2kTv2dv
07气体动理论2

EH 2 EO 2
i1 / 2 RT = = 1 :1 i2 / 2 RT
对1g氢气和1g氧气来说,都是双原子分子( i = 5), 但它们的摩尔数不同。
EH 2 EO 2
m1 M = 1 m2 M2
i1 RT M 32 2 = 2 = = 16 : 1 i2 RT M 1 2 2
3.理想气体的内能是 温度 的单值函数,平衡态时 能量按 自由度 均分, 理想气体分子的平均动能 , 1mol理想气体分子的内能
p = nkT
可知,V不变,P 要增大。
三、计算题
1.容积为10升的容器中储有 10克的氧气。若气体分子的方均 根速率 v 2 =600m ·s-1,则此气体的温度和压强各为多少? =600m· 由方均根速率公式 解: 解:由方均根速率公式
v2 =
3RT M
3 × 8.31 T ⇒ T = 462K 600 = −3 32 ×10 m pV = RT 由 M m 10 × 10 −3 p= RT = × 8.31× 462 可得 -3 −3 VM 10 × 10 × 32 ×10
B
dN/N表示dv间隔内的分子数占总分子数的百分比。所以 f (v)表示速率分布在v附近的单位速率间隔中的分子数占 总分子数的百分比。
2.若某种气体在温度 T2 时的最概然速率与它在温度 T1 时的 方均根速率相等,那么这两个温度之比 T1 : T2为: ( A )2 : 3 ; ( C )7 : 8 ; 解: 最概然速率 方均根速率 两者相等 可得 (B) 3 : 2 ; (D) 8 : 7
= 1.2 ×105 Pa
2.有N个气体分子,其速率分布如图所示,当 v>2v0时, 粒子的数目为零。求 : (1)常数a;
麦克斯韦速率分布函数的物理意义
速率分布函数[1]是一个描述分子运动速率分布状态的函数。
一个符合玻尔兹曼分布的粒子体系,如理想气体,其体系中粒子运动速率的分布可以用如下的速率分布函数来描述:通常速率分布函数也采用依动量和依动能分布的形式,虽然形式上有所不同但因为动量动能和速率的相关关系,这些表达方式本质上和依速率表示的速率分布函数还是一样的在处理某些特殊体系的情况下可能会用到二维和一维的速率分布函数,如固体表面吸附的理想气体就可以看做是在二维平面上运动的一个二维独立粒子体系,当处理这个体系有关分子运动速率的问题的时候就要用到二维速率分布函数在平衡状态下,当分子的相互作用可以忽略时,分布在任一速率区间v~v+△v间的分子数dN占总分子数N的比率(或百分比)为dN / N .dN / N是v 的函数,在不同速率附近取相等的区间,此比率一般不相等.当速率区间足够小时(宏观小,微观大),dN / N 还应与区间大小成正比:其中f(v)是气体分子的速率分布函数.分布函数f(v)的物理意义是:速率在v 附近,单位速率区间的分子数占总分子数的比率.分布函数f(v)满足归一化条件:大量分子的系统处于平衡态时,可以得到速率分布函数的具体形式:式中T是热力学温度,m为分子质量,k为玻尔兹曼常数.上式就是麦克斯韦速率分布律.麦克斯韦速率分布是大量分子处于平衡态时的统计分布,也是它的最概然分布.大量分子的集合从任意非平衡态趋于平衡态,其分子速率分布则趋于麦克斯韦速率分布,其根源在于分子间的频繁碰撞.上图是麦克斯韦速率分布函数f(v)示意图,曲线下面宽度为dv 的小窄条面积等于分布在此速率区间内的分子数占总分子数的比率dN/N .我们可以看到:同一种理想气体在平衡状态下,温度升高时速率分布曲线变宽、变平坦,但曲线下的总面积不变.随着温度的升高,速率较大的分子在分子总数中的比率增大.同一温度下,分子质量m越小,曲线越宽越平坦,在分子总数中速率较大的分子所占比率越高.。
大学物理第二十二讲 麦克斯韦、玻尔兹曼分布
v vf v dv
0
v v 2 f v dv
2 0
9
v vf v dv
0
0
m 4 e 2 kT
2
3
mv 2 2 kT
v 3dv
8kT 8RT RT v 1.60 m M M
3.方均根速率 v 2 ●分子速率平方的平均值的平方根
T2 T1
v
6
6.曲线随分子量的变化关系
m 2 f v 4 e 2 kT
3
mv 2 2 kT
v
2
☆分子质量越大,曲线峰值越向左,峰值也越高; 反之,质量越小,曲线峰值越向右,峰值也越低。 ☆分子质量越小,曲线越平坦。
f (v )
O2
He
mO2 mHe
f (v )
2 a 5v0
a 0
(v0 v 3v0 ) (v 3v0 )
a
o
2. v vf (v )dv
0
v0
3 v0
v
v0
o
3v0 2 2v 26 v ( 2 )dv vdv v0 v0 5v 5v0 15 0
3. N
2.5v0
1.5v0
Nf (v )dv
o
vP
v
5
5.曲线随温度的变化关系
m f v 4 e 2 kT
2
3
mv 2 2 kT
v
2
☆温度升高,曲线右移。即 T 增大时速率大的分子 增多,速率小的分子减少。 ☆因曲线下的总面积恒等于1,故此时曲线变得较为 平坦。
高二物理竞赛利用麦克斯韦速率分布函数计算微观量的平均值课件
vo
[例题] 求速率在区间vp—1.
f (v)dv Cdv C v 1 因此, v>v0 的分子数为 ( 2N/3 )
0
0
o
( vo> v > 0) ( v > vo )
C 1 vo
o
vo v
9
v vo vf (v)dv vo Cvdv C vo2
0
0
2
v 1 vo2 vo vo 2 2
v2
v2 f (v)dv
0
vo 0
Cv2dv
1 3
vo2
v2
3 3
vo
10
例3. 由麦氏分布律导出理想气体分子按平动动能的分布律,并找
出最可几动能是什么?一个分子的平均平动动能是什么?
解:一个分子的平动动能: 1 mv 2 d mvdv
由麦氏分布律:
2
dN f (v)dv 4(
3.nf (v)dv N dN dN VN V
—— 单位体积内分子速率分布在速率 v 附近 v ~ v + dv 速率区间内的分子数。
14
)
kT
)
分子的平均平动动能为:
0
f
(
)d
0
2(
1 kT
3
)
2
3
2
e
kT
d
3 kT 2
从理论上 已经得到过:
t
3 2
kT
理论与实验符合得很好。
12
思考题
说明下列各量的物理意义:
1. f (v)dv
2.Nf (v)dv
3.nf (v)dv
5. v2 Nf (v)dv v1
7. v 2 f (v)dv 0
麦克斯韦速率分布函数
麦克斯韦速率分布函数
麦克斯韦速率分布函数(Maxwell speed distribution)是物理场论中用来描述微粒物质的一种速度分布。
它表示了物质在由统计力学所确定的不同速度级别上所占有的百分比。
它表明,物质以恒定的密度分布在越来越大的速度上,但其最高速度是有限的。
该分布首先由美国物理学家约翰·麦克斯韦提出,他认为这种物质的速度可以满足类似高斯分布的概率分布函数。
根据统计力学,该函数包含物质的速率,总能量和温度,可以描述它们在温度和速度方向上的随机运动。
麦克斯韦速率分布函数可以通过以下方程表示:
f(v) = (m/2πkT)^(3/2) * 4πv^2 * e^(-mv^2/2kT)。
其中,m为微粒的质量,v为微粒的速度,k是玻尔兹曼常数,T为微粒的温度。
因此根据该函数可以确定物质在温度和速度方向上的随机运动,以及物质以恒定的密度分布在不同速度上的分布情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
粒子数按空间 位置 X 分布曲线
N: x x+x的 粒子数
...................................... ......................................................... ........................................
N 1 v附近单位速率区间的分 : N v 子数占总分子数的百分比
定义:函数:
(v x , v y , v z )
v
d Nv
(1)是速率 v 的函数
(2)是温度 T 的函数
vx
vy
速度空间
v附近单位速率区间的 分子数占总分子数的百 分比
对一定量理想气体,处于平衡状 态麦克斯韦证明: f v N
(5)T、m 变化对曲线的影响。
vp
m 一定
f (v)
T低
2kT m
T 一定
f (v)
m大 m小
T高 0
v 0
v
(6) 气体分子按平动动能的分布规律
麦克斯韦速率分布定律
N m 3 / 2 2 m v 2 / 2 kT 4 π( ) v e v N 2π kT
1 mv 2 2
2kT m
0
vp
2 RT M mol
(3)算术平均速率
v
N
v
0
vdN N
0
vNf v dv
vf v dv
0
得:
8kT v m
8 RT M mol
高斯积分:
0 e d x 2 1 2 x 1 x 0 x e d 2 2 x x 0 x e d 4 3 2
v
物理意义是所有速率区间内分子数 百分比之和应等于1。
讨论: (2)最概然速率
f (v)
o vp 其意义为:速率在 vp 附近 单位速率间隔的分子数占总分子 数比率最大。
v
df ( v ) 0 dv
4 ( / ) 2 ve
3/ 2 2
m 2kT
v 2
v 2
v 2 ve
两边微分
mvv
/ kT
代入上式得
N 4 2π 1 2 f ( ) e 32 N (2π kT )
意义: 上式表明理想气体在平衡态下,分子动能在
~ + 区间内的分子数与总分子数的比率。
思考 最概然平动动能是否等于最概然速率所对应的平
动动能?
统计规律的特点:
x
Δx
1. 分布函数 概率(几率):
一定条件下,某偶然事件出现的可能性的大小
设 N---实验总次数,Ni---事件A出现次数,
则
Ni f i lim N N Ni 即 fi N
fi 随Ni变化的函数式--分布函数
对所有事件:
Ni fi N
N 1 N
i
--分布函数是归一化的
Nv
v 0
m 3 / 2 mv 2 / 2 kT 2 4 ( ) e v 2kT f (v)
dN f ( v )dv N
o dv
v
讨论:
f (v)
(1)归一化条件:
dN f (v)= N dv
dN f ( v )dv N
v dv
f ( v )dv 1
0
x 2
2
2
1 0 x e d x 2 2 3 4 x 2 x x e d 52 0 8
3 x 2
(4)方均根速率
v
2
2
v
2
0
v dN N
2
v f ( v ) dv
0
3kT m
v
2
3kT m
3 RT M mol
v
2
3kT v m
800~900 > 900
速率区间 百分数 (m/s) 1859年麦克 1.4 % <100 斯韦从理论上 100~200 8.1 % 得到速率分布 分 200~300 16.5 % 定律。 子 实 300~400 21.4 %
2.0 % 0.9 %
三、麦克斯韦分子速率分布定律
设 N 为气体分子总数,N为 v v+v 区间内气体分子数。 N v v+ v 速率区间 的分子 : 数占总分子数的百分比 N
:
真实值 (统计平均值)
二、分子速率分布的测定—斯特恩实验
φ
v
金属 蒸汽 方向选择
ω
t2
L
ω
屏
L t1 v
速率选择器
t1 t 2
v L
葛正权测定分子速率实验:
B G
热原子炉
速 验 400~500 20.6 % 1920年斯特 率 数 500~600 15.1 % 恩从实验上证 分 据 600~700 9.2 % 实了速率分布 布 700~800 4.8 % 定律。 的
§6 麦克斯韦
分子速率分布定律
§5 麦克斯韦分子速率分布定律
一、统计规律
[伽尔顿板实验]
粒子落入其中一 格是一个偶然事 件,大量粒子在 空间的分布服从 统计规律。
...................................... ......................................................... ........................................
fi 的取值范围:
0 fi 1
2.统计平均值
测得物理量M: M1、M2、Mn出现的次数分别为 N1、N2、Nn M的算术平均值:
M1 N 1 M 2 N 2 M n N n M N1 N 2 N n
M i N i M i f i N
平均值
N
统计规律是对大量偶然事件整体起作 用的规律。 统计规律从本质上不同于每一事件的 动力学规律。 统计规律总是伴随着涨落(起伏)现 象
说明下列各式的物 理意义: v v+ d v 速率区间 的分子 f ( v )dv
8kT m
2
vp
2kT m
f (v)
v v vp
o
vp v
v
2
v
说明
f(v)
T
p
( 一般三种速率用途各 不相同 讨论速率分布一般用 v · 讨论分子的碰撞次数用 v · 讨论分子的平均平动动 · 能用
O
vp v
v
v
2
v2
(2) 同一种气体分子的三种速率的大小关系: v 2 v v p
