一次函数第一课时演示文稿1
《一次函数》PPT课件(第1课时)

④y=x-6.
③
(1)其中过原点的直线是________;
④
( 2)函数y随x的增大而增大的是_______;
②
(3)函数y随x的增大而减小的________;
①
(4)图象在第一、二、三象限的________
.
(1.5,0)
3.直线y =2x-3 与x 轴交点的坐标为________;与y
2 了解分段函数的表示及其图象.
1
3
能初步应用一次函数模型解决现实生活中的
问题,体会一次函数的应用价值.(难点)
新课导入
1.复习
3
y
2
x
画出函数
和 y x 3 的图象.
2
2.反思
你在作这两个函数图象时,分别描了几个点?
你为何选取这几个点?有不同的取法吗?
3.思考
反过来,已知一个一次函数的图象经过
数学课件:www.1ppt.c om/keji an/shuxue/
美术课件:www.1ppt.c om/keji an/mei shu/
物理课件:www.1ppt.c om/keji an/wuli /
生物课件:www.1ppt.cc om/keji an/lishi /
科学课件:/keji an/kexue/
化学课件:/keji an/huaxue/
地理课件:/keji an/dili/
PPT素材:/s ucai/
PPT图表:/tubiao/
PPT教程: /powerpoint/
手抄报:/shouc haobao/
语文课件:/keji an/yuwen/
英语课件:/keji an/ying yu/
13.2一次函数 第一课时

13.2一次函数第一课时13.2一次函数一、教学目标1、理解一次函数的概念,并能根据实际上问题列出简单的一次函数的表达式2、理解一次函数的图象是一条直线,熟练地作出一次函数的图象二、教学重点、难点1、重点:一次函数的概念,及一次函数的图象2、难点:实际问题中一次函数解析式的确定。
三、课时:第1课时四、课型:新授五、教学方法:讲授法六、教学过程(一)新课导入在上节的学习中,我们遇到过这样一些函数:h=30t+1800; Q=-25t+300; y=2x; y=-2x; s=80t. 问:这些函数有什么共同特点?答:不难看出,这些函数都是用自变的量的一次式表示的. 可以写成:y=kx+b的形式.(二)新课讲解定义:一般地,如果有:y=kx+b(k,b为常数,且k≠0),那么,y叫做x的一次函数.其中,当b=0时,一次函数y=kx+b 就成为y=kx(k≠0).如上面的y=2x、y=-2x、s=80t,这些函数中两个变量间的关系,就是小学学过的正比例关系.因此,y=kx(k≠0)中y叫做x的正比例函数. 可见,正比例函数是一次函数的特殊情形. 下面,来研究一次函数的图象与性质.前面画过函数y=2x、y=-2x及另外一些正比例函数的图象,可见正比例函数y=kx(k≠0)的图象是一条直线,通常我们把正比例函数y=kx(k≠0)的图象叫做直线y=kx.因为两点确定一条直线,所以画正比例函数的图象,只要先描出两点,再过这两点画直线,就可以了. 例1 在同一坐标系里,画下列函数的图象: y=1/2x, y=x, y=3x.解列表:(为便于比较,三个函数值计算表排在一起) x y=1/2x y=xy=3x … … … … 0 0 0 0 1 1/2 1 3 … … … … 如图13-11,过两点(0,0),(1,1/2)画直线,得y=1/2x的图象;过两点(0,0),(1,1)画直线,得y=x的图象;过两点(0,0),(1,3)画直线,得y=3x的图象;(三)课堂练习课本P35 ,第1、2 (四)课堂小结这节课我们学习了一次函数的定义,能够在直角坐标系中画出一次函数的图像。
一次函数1-PPT资料16页

正比例函数是 一次函数的特例
函数 正比例函数
一次函数
概念说明
特别注意:
一个关自键变点量:的次数是1次 两个控制器:一次项系数k,常数项b
概念辨析
判断下列函数是不是一次函数,如果是一次函数,
是不是正比例函数?
(1)y=
3 2
x-1
是一次函数,不是正比例函数
(6)某种汽油8元/L,加油应付油费y元随加油量xL面所列出的函数式进行分类吗?
自觉感悟
y=40-5x
y=10-x
L=4x
y=8x
• 你能把上面所列出的函数式进行分类吗?
是一次函数
不是一次函数
概念产生
一般地,如果2个变量x与y之间的函数关系, 可以表示为y=kx+b(k、b为常数,且k≠0)的 形式,那么称y是x的一次函数.
小试牛刀
1.若y=(m-1)x+5是一次函数,
则m ≠1 。
2.若y=2x m2-3 - 4是一次函数,
则m =±2 。
小试牛刀
课堂小结 通过本节课的学习,你有哪些收获?
谢谢你的阅读
知识就是财富 丰富你的人生
(2)y=3x2+2 不是一次函数
(3)m=-5n 是一次函数, 是正比例函数
(4)y=6 - 3x 是一次函数,不是正比例函数
(5)y=2(t-5) 是一次函数,不是正比例函数 (6)2y=x-1 是一次函数,不是正比例函数
概念辨析
是 是 否 是 是
是
-1 0
是
0
否
3 -3
否
12
典型例题
例:已知函数 y(m1)xm21 (1)m取何值时,该函数是一次函数? (2) m取何值时,该函数是正比例函数?
一次函数(1)PPT教学课件
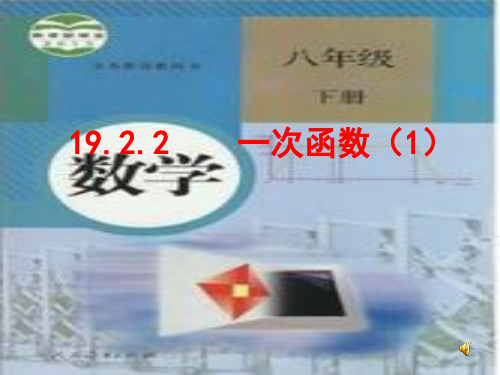
y=k1x+ k2(x-2)
当x=1时,y=0,得:0=k1+k2(1-2)
①
当x=-3时,y=4,得:4=-3k1+k2(-3-2) ②
2020/12/10
16
①②组合得:
0k1k2(1-2) 4-31k k2(--32)
解之得:
k
1
-1 2
k2
-1
2
∴ y与x之间的函数关系式为: y=- x+1
y=0.3x+5
思考:这个函数是正比例函数吗?
2020/12/10
3
学习目标:
1、掌握一次函数解析式的特点及意义; 2、理解一次函数与正比例函数的关系。
2020/12/10
4
二、自主预习
1、正比例函数一般式: y=kx(k是常数,k≠0)
2、正比例函数的图象:
一条经过原点和(1,k)的直线
y y= kx (k>0)
( 3) y=-0.5x-1
( 4) y=5x26
2、下列说法正确的是 ① ③ (填序号)
①正比例函数一定是一次函数;
②一次函数一定是正比例函数;
③若y-1与x成正比例,则y是x的一次函数;
④若y=kx+b,则y是x的一次函数。
2020/12/10
13
3、 已知方程3x-2y=1,把它写成y是x的一次函数的形 式是_y__=_1.5x-_0_._5_ ,当 x = 1时, y =__1__;当 y = 4 时, x =__3__。
9
(3)某城市的市内电话的月收费额y(单位: 元)包括月租费22元和拨打电话x min的计时费
(按0.1元/min收取).
y = 0.1x + 22
《一次函数的性质》第一课时说课稿

《一次函数的图象和性质》第一课时说课稿
高安二中谢红莲
各位同行,你们好!
我今天说课的内容是《一次函数的图象和性质》,现在我来说说我是怎样跟学生一起学习这节内容的,希望各位多加指导!我将就以下几个方面向大家汇报。
一、教材分析
1
2
3
四、学法分析
贯彻以“学生发展”为本,把学习的主动权还给学生,倡导积极主动、勇于探索的学习方式。
因此重要采用学生动手,自主探索,与合作交流的方式,自觉实现知
识的建构,促进学生的全面发展。
五、教具准备
直尺、坐标纸
七、板书设计
《一次函数的图象和性质》教学设计
高安二中谢红莲
教学任务分析
教学过程设计
板书设计
欢迎共阅 时间安排
1、创设情境,复习引入1
2、合作交流:性质探究18。
19.2.2 一次函数的概念 课件(共23张PPT)
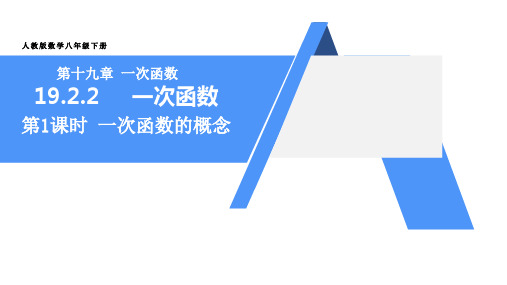
(1)求小球速度v(单位:m/s) 关于时间t(单位:s)的函数解析式. 它是一次函数吗?
(2)求第2.5 s 时小球的速度; (3)时间每增加1 s,速度增加多少,速度增加量是否随着 时间的变化而变化?
解:(1)小球速度v关于时间t的函数解析式为v=2t,是一次函数. (2)当t=2.5时,v=2×2.5=5(m/s). (3)时间每增加1 s,速度增加2 m/s,速度增加量不随着 时间的变化而变化.
答:此人本月工资是4140元.
例4 如图,△ABC是边长为x的等边三角形.
(1)求BC边上的高h与x之间的函数解析式.h是x的
一次函数吗?如果是,请指出相应的k与b的值.
解: (1)因为BC边上的高AD也是BC边上的中线,
A
所以,BD=x/2.在Rt△ABD中,由勾股定理,得
h AD AB2 BD2 x2 1 x2 3 x,
度 t(单位:℃)有关,且 c 的值约是 t 的7 倍与35的差;
c=7t -35(20≤t≤25)
(2)一种计算成年人标准体重G(单位:kg)的方法是,
以厘米为单位量出身高值 h ,再减常数105,所得差是G 的
值;
G=h-105
(3)某城市的市内电话的月收费额 y(单位:元)包括月租 费22元和拨打电话 x min 的计时费(按0.1元/min收取);
y = k(常数) x + b(常数)
知识要点
一般地,形如y=kx+b (k, b 是常数,k≠0) 的函数,叫做一次函数. 思考:一次函数与正比例函数有什么关系? (1)当b=0时,y=kx+b 即y=kx(k≠0),此时该一次函数是 正比例函数.
一次函数(第一课时)课件.ppt
形成概念
定义:一般地,形如y=kx+b(k,b是 常数,k≠0)的函数,叫做一 次函数. 当b=0时, y=kx+b即变成y=kx,
所以说正比例函数是一种特殊的一 次函数.
课堂练习
练习1 下列函数中哪些是一次函数,哪些又是正
比例函数?
(1)y=-8x
(2)y=
-8 x
(3)y=5x2 +6
(4)y=-0.5x-1 (5)y= x -1
y = 5 - 6x 也可以写为 y = -6x + 5
(2)登山队员向上登高多少千米时,他们所 在位置的气温是0 ℃ 呢?
当y=0时,0=-6x+5 所以x=5 /6(km)
问题1
某登山队大本营所在地的气温为5 ℃,海拔每升高1 km 气温下降6 ℃.登山队员由大本营向上登高x km时, 他们所处位置的气温是 y ℃. 试用函数解析式表示 y 与 x 的关系.
(4)把一个长10 cm,宽5 cm的矩形的长减少 x cm, 宽不变,矩形面积 y(单位:cm2)随x的值而变化.
问题3
观察以上出现的四个函数解析式,分别说出哪些是 自变量、自变量的函数和常数.
函数解析式 自变量的函数 自变量 常数
(1)c=7t-35
c
t
7,35
(2)G=h-105
G
h
-105
(3)y=0.1x+22
y
x
0.1,22
(4)y= -5x+50
y
x
-5,50
思考:上面这些函数解析式有什么共同特征呢? 它们都是常数与自变量的乘积与另一常数的和的形式.
形成概念
定义:一般地,形如y=kx+b(k,b是 常数,k≠0)的函数,叫做一 次函数.
一次函数第一课时PPT
课后作业
作业:教科书第99页第3,6题; 其中,第6 题增加以下两个小题:
(1)当x 取-3,-2,-1,0,1,2,3,4 时,求对 应的函数值,并列表表示对应关系;
(2)从表中观察,当自变量的值每增加1 时,对应 的函数值怎样变化?当自变量的值每增加2呢?
收取);
y=0.1x+22
(4)把一个长10 cm,宽5 cm的矩形的长减少 x cm, 宽不变,矩形面积 y(单位:cm2)随x的值而变化.
y=-5x+50(0≤x≤10)
观察以上出现的四个函数解析式, 很显然它们不是正比例函数,这些 函数关系式有什么特点?
(1) c = 7t-35 (2) G=h-105
(1) y 8x (2) y 5x2 6
(3) y 8 (4) y 0.5x 1
(5) y
x
x
1
2
(7)y=2(x-4)
(6) y 2 13 x
(8) y x 3 2
你能举出一些一次函数的例子吗?
课堂练习
练习2 请写出若干个变量 y 与 x 之间的函数解析 式,让同桌判断是否是一次函数;如果是,请说出其一 次项系数与常数项.
当b=0时,y=kx+b就变成了y=kx,所以 说正比例函数是一种特殊的一次函数。
一次函数 正比例函数
例1.下列函数关系式中,那些是一次函数? 哪些是正比例函数?
(1)y=2πx
(3)y 1 x
(2)y=-x-4 (4)y=x2 -3x
(5) y=8x2+x(1-8x)
试一试下列函数中哪些是一次函数,哪些又 是正比例函数?
海拔每升高1㎞气温下降6 ℃,登山队员由大本 营向上登高x㎞时,他们所在位置的气温是y ℃ ,试用解析式表示y与x的关系。
《一次函数1》课件1
思考 当b=0 时,y=kx+b是什么函数?
课堂练习
练习1 下列函数中哪些是一次函数,哪些又是正
比例函数?
(1)y=-8x ;
(2)y=
-8 x
;
(3)y=5x2+6 ;
(4)y=-0.5x-1 ; (5)y= x -1 ;
收取);
y=0.1x+22
(4)把一个长10 cm,宽5 cm的矩形的长减少 x cm, 宽不变,矩形面积 y(单位:cm2)随x的值而变化.
y=-5x+50(0≤x≤10)
问题3 观察以上出现的四个函数解析式,很显然它 们不是正比例函数,那么它们有什么共同特征呢?
c=7t-35(20≤t≤25) G=h-105 y=0.1x+22 y=-5x+50(0≤x≤10)
(6)y=
2
-13
2 ;(7)y=2(x-4);(8)y=
x 请写出若干个变量 y 与 x 之间的函数解析 式,让同桌判断是否是一次函数;如果是,请说出其一 次项系数与常数项.
课堂练习
练习3 已知一次函数 y=kx+b,当 x=1时,y=5;当 x=-1时,y=1.求 k 和 b 的值.
八年级 下册
19.2.2 一次函数(1)
课件说明
• 本课是在学习正比例函数的基础上,进一步学习一 次函数的概念.一次函数的概念是在观察一类具体 函数的解析式的特点的基础上,通过抽象得到的函 数模型.
课件说明
• 学习目标: 1.结合具体情境理解一次函数的意义,能结合实际 问题中的数量关系写出一次函数的解析式; 2.能辨别正比例函数与一次函数的区别与联系; 3.初步体会用待定系数法求一次函数解析式的方法.
《一次函数》第一课时PPT课件
12.甲乙两地相距500千米,汽车从甲地以 每小时80千米的速度开往乙地.
(1)写出汽车离乙地的距离s(千米)与开 出时间t(小时)之间的函数关系围; (3)汽车从甲地开出多久,离乙地为 100千米?
达标小测
2.若函数y=(m-1)x|m|+m是关于x 的一次函数,试求m的值.
m=1
小结与收获
同学们 要记得做作业呀
作业:
习题17.3 1, 2
成功的人找方法 失败的人找借口
师 生 共
勉
知识大门常打开,开放怀抱等你; 书山有路方法为径,学海无涯快乐作舟。 困难之虎常拦路,一片浓云迷雾; 合作探究,团结互助, 定能把困难克服!
⑴面积为10cm2的三角形的底a(cm)与这边上的高 h(cm);
⑵长为8(cm)的平行四边形的周长L(cm)与宽b (cm);
⑶食堂原有煤120吨,每天要用去5吨,x天后还剩 下煤y 吨;
⑷汽车每小时行40千米,行驶的路程s(千米)和 时间t(小时)。
1.已知函数y=(2-m)x+2m-3.求当m为何值时, (1)此函数为正比例函数? (2)此函数为一次函数?
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
2.一次函数的一般形式是什么?
3.什么是正比例函数?它的一般 形式是什么?
一次函数的有关概念
1.用自变量的一次整式表示的函数。 称为一次函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正比例函 数
下列函数关系式中,哪些是一次 函数,哪些是正比例函数? (1)y=-x-4 它是一次函数,不是正比例函数。
(2)y=5x2+6 它不是一次函数,也不是正比例函数。 (3)y=2πx 它是一次函数,也是正比例函数。
(4) y
8 x
它不是一次函数,也不是正比例函数
(5)y=-8x
5. 已知函数y=(k+1)x+k2-1,当k为什么 值时,它是一次函数;当k什么值时,它 是正比例函数?
6.汽车油箱中原有油50升,如果行驶中每 小时用油5升,求油箱的油量y(单位:升)随 行使时间x(单位:时)变化的函数关系式, 并写出自变量x的取值范围.y是x的一次 函数吗? 解:由题意得,函数关系式为y=50-5x.
Y=-6x+5Biblioteka 思考 Y=-6x+5
• 1、这个函数是正比例函数吗? • 2、它与正比例函数有什么不同? • 3、这种形式的函数还会有吗?
• 1、有人发现,在20—25oc时蟋蟀每分钟鸣 叫次数c与温度t(oc)有关,即c的值是t的 7倍与35的差; C=7t-35 2、一种计算成年人标准体重G(单位:千 克)的方法是,以厘米为单位量出身高值h, 再减常数105,所得差是G的值;
一次函数
(第一课时) 辉南县永康中学 王新红
复习:
1、什么叫做正比例函数? 2、正比例函数的结构形式? 3、正比例函数的解析式的特点?
• 1、某登山队大本营所在地的气温为5oc, 海拔每升高1km气温下降6oc,登山队员由大 本营向上等高xkm时,他们所在位置的气温 yoc,试用解析式表示y与x的关系。
其中有一格不慎被墨汁遮住了,想想看,该 空格里原来填的数是多少?解释你的理由。
气温随着高度的增加而下降,下降的一般规律是 从地面到高空11km处,每升高1 km,气温下降 6℃.高于11km时,气温几乎不再变化,设地面的 气温为38℃,高空中x km的气温为y℃. (1)求y与x之间的关系式; (2)求当x=5、11时,y的值; (3)求离地面13 km的高空处气温是多少度? (4)当气温是-16℃时,问在离地面多高的地方? 当气温是- 28oC时,离地面多高?
y=-6x+5 C=7t-35 G=h-105
y=0.1x+22 Y=-5x+50
类似于正比例函数的结构的形式 为: 函数=常数 ⅹ自变量+另一个常数
y=kx+b(k、b是常数,k≠ 0)
学习目标
• 1、 掌握一次函数的定义; • 2、灵活应用一次函数的定义进行解题。
一次函数:
一般地,形如y=kx+b(k,b是常数,k≠0)的函 数,叫做一次函数。 当b=o时,y=kx+b即y=kx,所以 说正比例函数是一种特殊的一次 函数
(C)正比例函数是特殊的一次函数
(D)不是正比例函数就不是一次函数
1.已知函数y=(m-3)x +m是 一次函数,求m的值?
2.已知函数y=(2-m)x+2m-3.求当m为何值时, (1)此函数为正比例函数 (2)此函数为一次函数
m2-8
3.若函数y=(m-1)x|m|+m是关于x的一次函数, 试求m的值. 4.要使y=(m-2)xn-1+n是关于x的一次 函数,n,m应满足什么条件?
它是一次函数,也是正比例函数。
x 1 y x ;s=60t;y=100-25x,其中表示 2
1 1.已知下列函数:y=2x+1; y x
一次函数的有( D ) (A )1个 ( B)2个 ( C)3个 ( D)4个
2.下列说法不正确的是( D )
(A)一次函数不一定是正比例函数
(B)不是一次函数就一定不是正比例函数
G=h-105
3、某城市的市内电话的月收费额y(元)包 括:月租费22元,拨打电话x分钟的计时费 (按0.1元/分收取) Y=0.1x+22 4、把一个长10cm、宽5cm的长方形的长 减少xcm,宽不变,长方形的面积y(cm2) 随x的值而变化。 Y=(10-x)×5 = -5x+50
≠
观察下列解析式有什么共同点:
解: (1)
y=38-6x
(0≤x≤11)
y=-28
(
x≥11
)
(2)当x=5、11时y的值分别是80、-280. (3)在离地面13 km的高空处气温是-280.
(4)当y=-16时,-16=38-6x,解得x=9(km)
当y=-28时,x≥11
自变量x的取值范围是0≤x≤10
y是x的一次函数.
• 1、已知在y=kx+b中,当x=2时,y=5;当 x=0时,y=1;求k和b的值。 • 2、在y=kx+b中,当x=1时y=2;当x=-1时 y=0;求当x=2时 y的值.
3 小明根据某个一次函数关系式填写了下 表:
x y -2 3 -1 0 1 1 0
